Artikel Transformasi Affine

TRANSFORMASI AFFINE Sinta Sintia

(1600522)

Program Studi Pendidikan Teknik Bangunan Fakultas Pendidikan Teknologi dan Kejuruan

Universitas Pendidikan Indonesia Email: sintassintia@gmail.com

ABSTRAK

Suatu geometri adalah suatu studi tentang sifat-sifat dari suatu himpunan S yang tetap tidak berubah bilamana element-element S ditransformasikan olehn sekelompok transformasi. Definisi ini menetapkan geometri transformasi sebagai suatu cara memahami hubungan-hubungan diantara semua geometri, euclid, dan non euclid. Salah satu bentuk geometri yang dapat dikenal yaitu transformasi affine, yaitu hubungan geometri yang mempertahankan bentuk dasar dan integritas bangun geometri. Dengan mempelajari transformasi affine kita dapat menentukan rotasi, translasi, dan dilatasi dari suatu objek.

PENDAHULUAN

Geometri Affine menarik banyak perhatian para ilmuan dalam sepuluh tahun belakangan ini. Latar belakang yang mendasari lahirnya Geometri Affine adalah geometri terurut. Bidang Affine dipandang sebagai keadaan khusus dari bidang terurut.

Awalnya Euler mengidentifikasi bahwa banyak sifat-sifat Affine yang sudah dikenal dari geometri Euclid, tetapi juga berlaku di ruang Minkowski . Sifat-sifat geometri Euclid ini dikembangkan dengan proyeksi paralel dari satu bidang ke bidang lainnya yang disebut dengan Affine. Akibatnya, geometri Affine merupakan perluasan dari geometri Euclidean yang bercirikan kemiringan dan skala distorsi. Dalam bahasa program Erlangen Klein, yang mendasari simetri dalam geometri Affine adalah grup afinitas, yaitu grup transformasi yang dihasilkan oleh transformasi linear dari ruang vektor dan translasi vektor.

PEMBAHASAN

SEJARAH TRANSFORMASI AFFINE

Transformasi affine pertama kali diperkenalkan oleh Leonhard Euler dari Jerman (1707 – 1793). Dalam geometri ini, garis paralel tunggal, sesuai Postulat Playfair, “ Melalui satu titik yang diketahui, tidak pada suatu garis yang diketahui, hanya dapat dibuat satu garis yang paralel dengan garis itu”, memegang peranan yang penting sekali. Karena dalam geometri ini lingkaran tidak disebut-sebut dan sudut-sudut tidak pernah diukur, maka dapat dikatakan, bahwa geometri ini mempunyai dasar aksioma I dan II, dari aksioma Euclides. Aksioma III dan IV tidak berarti sama sekali.

Geometri Absolut pertama kali dikenalkan oleh J. Bolyai dari Hongaria (1802 – 1860). Geometri ini didasarkan pada 4 aksioma pertama dari Euclides dan melepaskan aksioma V. Dengan demikian, geometri Affine dan geometri Absolut mempunyai dasar persekutuan yaitu pada Aksioma I dan Aksioma II. Ada pula suatu inti dari dalil-dalil yang berlaku untuk keduanya, yaitu pengertian Keantaraan ( Intermediacy ). Pengertian itu terkandung dalam definisi keempat dari Eulides.

Geometri yang menjadi dasar dari geometri Affine dan geometri Absolut ini disebut Geometi Ordered ( Geometri Terurut ), karena dalam hal ini urutan memegang peranan penting. Geometri Terurut ini berdasarkan dua aksioma pertama dari Euclides, tetapi penyajiannya lebih teliti. Jadi Geometi Affine dan geometri absolut termuat dalam Geometri terurut, sedangkan Geometri Euclides termuat dalam Geometri Affine dan Geometri absolut.

PENGERTIAN TRANSFORMASI AFFINE

Transformasi Affine adalah hubungan geometri yang mempertahankan bentuk dasar dan integritas bangun geometri. Transformasi Affine dapat berupa rotasi, translasi, dan dilatasi. Transformasi Affine bersifat linier (perubahan yang kecil pada transformasi akan mengakibatkan perubahan yang kecil pada objek yang ditransformasikan), tetapi akan membentuk fraktal nonlinier jika beberapa transformasi digabungkan dan diiterasi.

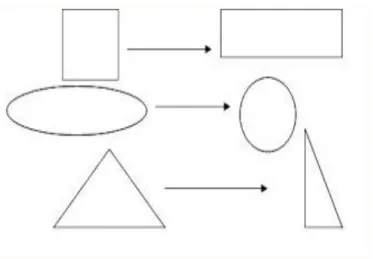
Transformasi affine tidak mengawetkan kesebangunan. Hal ini dikarenakan factor pengali pada x tidak sama dengan pengali pada y. Perhatikan gambar dari beberapa bangun oleh transformasi affine berikut. Pada transformasi Affine tidak memperhatikan kesebangunan. Hal ini dikarenakan faktor pengali padax tidak sama dengan pengali pada y.

MACAM-MACAM TRANSFORMASI AFFINE Transformasi affine dibagi menjadi 2 yaitu :

1. Transformasi affine 2D

Transformasi Affline 2D adalah transformasi yang sering digunakan untuk mentransformasikan nilai-nilai koordinat dari suatu sistem koordinat dua dimensi ke sistem koordinat dua dimensi lainya. Penentuan nilai parameter suatu transformasi ditentukan berdasarkan ketersediaan data koordinat titik-titik sekutu dari masing-masing sistem dua dimensi dan teknik hitungan penentuan parameter transformasi. Parameter- parameter transformasi yang dihasilkan dari kedua metode tersebut relatif sama, akan tetapi ketelitian ( standar kesalahan ) pada 1 sigma untuk metode implisit relatif lebih baik.

Rumus transformasi Affine 2D antar bidang datar adalah : x’ = a1x + b1y + c1

y’ = a2x + b2y + c2

Dimana a1, b1 c1, a2, b2, dan c2 (6 buah) merupakaan parameter trasformasi,

a1 ≠ b2, a2 ≠ b1. Dengan rumus transformasi tersebut, tidak menghasilkan bentuk

conform. Jadi, akan terjadi perubahan sudut dan jarak. Untuk dapat memecahkan parameter transformasi yang banyaknya 6 buah, diperlukan minimal 3 buah titik sekutu dari setiap titik sekutu memberikan 2 buah persamaan. Pemecahan 6 parameter dari 6 persamaan mudah dilakukan yaitu dengan cara eliminasi crammer.

Apabila dikehendaki nilai-nilai parameter yang lebih teliti, gunakan titik sekutu lebih dari tiga buah, dan pemecahannya dengan perataan kuadrat terkecil. Sebaliknya apabila dikehendaki hasil yang tidak perlu teliti maka cara grafis dapat ditempuh. Misalnya cara grafis dari VAN GLEUNS atau VAN DER TASS. Selain itu, cara lain yang dapat ditempuh yaitu denga mencari dahuliu koreksi sudut dan jaraknya.

Untuk keperluan transformasi koordinat titik P dan Q dalam 2D dinyatakan sebagai :            1 y x P P P dan            1 y x Q Q Q

Hal ini berarti titik P berada pada lokasi P = Px i + Py j + 

Dimana  adalah titik pusat koordinat (tidak harus selalu (0,0)).

Transformasi dari titik P menuju titik Q menggunakan fungsi T() berikut ini.

                     z y x z y x P P P T Q Q Q atau ringkasnya Q = T(P)

Transformasi Affine mempunyai bentuk seperti berikut ini.

                         1 1 23 22 21 13 12 11 m P m P m m P m P m Q Q y x y x y x

dalam bentuk persamaan matriks persamaan di atas dapat diubah menjadi

                               1 1 0 0 1 23 22 21 13 12 11 y x y x P P m m m m m m Q Q

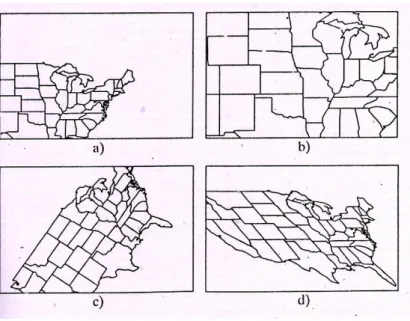
Transformasi Affine berpengaruh pada 4 transformasi dasar, yaitu : translasi, skala, rotasi dan shear.

Gambar 2. Transformasi Dasar. a pengaruh translasi, b. pengaruh skala, c. pengaruh rotasi, dan d. pengaruh shear.

Transformasi Affine untuk translasi diberikan oleh persamaan berikut ini.

                               1 1 0 0 m 1 0 m 0 1 1 23 13 y x y x P P Q Q

atau lebih ringkasnya

                       1 m P m 1 23 y 13 x y x P Q Q

Vektor (m13 , m23) adalah vektor offset yang menyatakan besarnya pergeseran.

Transformasi Affine untuk skala melakukan penskalaan dengan menggunakan dua faktor skala yaitu Sx dan Sy masing-masing untuk koordinat x dan y.

Persamaan transformasinya diberikan pada persamaan berikut ini. ( Qx, Qy ) = ( Sx Px , Sy Py )

sehingga matriks untuk transformasi skala adalah :

          1 0 0 0 0 0 0 y x S S

Qx = Px cos() – Py sin(),

Qy = Px sin() – Py cos(),

Matriks transformasinya adalah sebagai berikut .

           1 0 0 0 ) cos( ) sin( 0 ) sin( ) cos(    

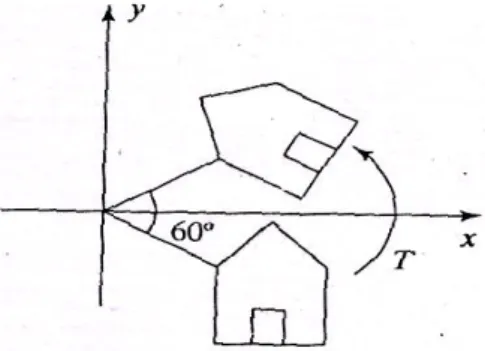
Rotasi mempunyai pengertian diputar dengan pusat titik asal (0,0) ke arah berlawanan jarum jam sebesar sudut . Lebih jelasnya dapat dilihat pada gambar berikut ini.

Gambar 3. Transformasi Rotasi

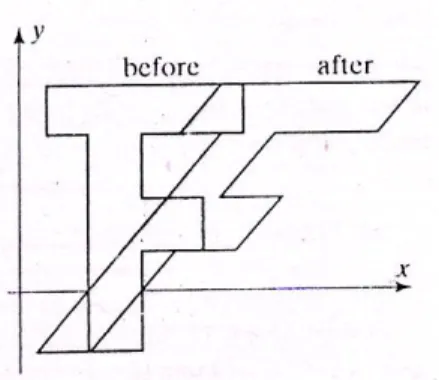
Transformasi Affine untuk shearing diberikan oleh persamaan berikut ini. Qx = Px + hPy

Qy = Py

Dimana h menyatakan besarnya perubahan P pada sumbu y. Matrik transformasinya adalah sebagai berikut.

          1 0 0 0 1 0 0 1 h

Gambar 4. Transformasi Shear 2. Transformasi Affine 3D

Seperti pada transformasi Affine 2D, transformasi Affine 3D juga menggunakan koordinat frame. Titik P dinyatakan dengan :

P = Px i + Py j + Pz k +  atau              1 z y x P P P P

Dan transformasinya secara umum dinyatakan dengan persamaan transformasi berikut ini.                          1 1 z y x z y x P P P M Q Q Q

dengan M nya adalah

             1 0 0 0 34 33 32 31 24 23 22 21 14 13 12 11 m m m m m m m m m m m m M

Untuk translasi matrik M tersebut adalah sebagai berikut

            1 0 0 0 1 0 0 0 1 0 0 0 1 34 24 14 m m m

, (m14, m24, m34) adalah besarnya translasi yang diinginkan.

            1 0 0 0 0 0 0 0 0 0 0 0 0 z y x S S S

, dimana (Sx, Sy, Sz) adalah besarnya skala yang diinginkan.

Untuk shearing matriks transformasinya adalah sebagai berikut.

            1 0 0 0 0 1 0 0 0 0 1 0 0 0 1 f

Jika matrik transformasi dikalikan dengan titik P akan menghasilkan Q = (Px,

fPx + Py , Pz). Jadi komponen Px, dan Pz tetap, sedangkan komponen Py berubah

secara proporsional, dimana f adalah konstanta yang kita inginkan. Untuk rotasi ada 3 macam transformasi, yaitu rotasi terhadap sumbu x, sumbu y, dan sumbu z.

a. Rotasi dengan sumbu x, matrik rotasinya adalah

             1 0 0 0 0 0 0 0 0 0 0 1 c s c c

b. Rotasi dengan sumbu y, matrik rotasinya adalah

             1 0 0 0 0 0 0 0 1 0 0 0 c s s c

c. Rotasi dengan sumbu z, matrik rotasinya adalah

             1 0 0 0 0 1 0 0 0 0 0 0 c s s c

Dimana c dalam matriks adalah cos() dan s adalah sin(), untuk  yang diinginkan.

TEOREMA-TEOREMA AFFINE

Teorema-teorema geometri Euclidean adalah teorema-teorema Affine. Itu berarti pernyataan dan bukti juga melibatkan konsep yang dipertahan kan oleh transformasi affine. Secara kasar, teorema-teorema affine dapat dibuktikan dengan metode vektor tanpa menggunakan norm atau dot atau hasil kali vektor.

1. Tengah-tengah dari suatu segitiga bertemu pada sebuah titik (coincident).

Gambar 5. Tengah-Tengah Segitiga Bertemu pada Sebuah Titik

Jika sebuah segitia mempunyai garis-garis a, b and c maka mudah diperiksa bahwa garis tengahnya akan bertemu pada suatu titik (a + b + c) /3.

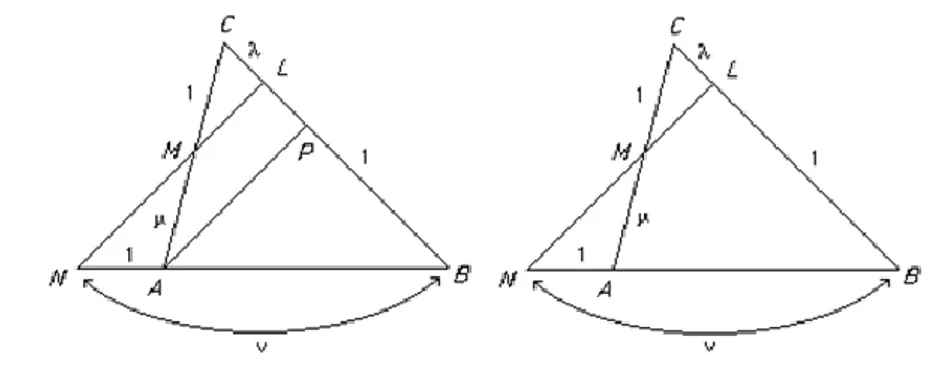
2. Teorema Ceva

Jika sisi-sisi BC, CA, AB pada suatu segitiga dibagi oleh titik-titik L, M, N dengan perbandingan 1 : , 1 : , 1 : maka ketiga garis AL, BM, CN setitik (konkurent) jika dan hanya jika hasil kali = 1.

Gambar 6. Teorema Ceva

Dalam kenyataan, kita akan membuktikan ini tidak dengan menggunakan metode affine.

= CL/LB = CLA/ LBA = CLP/ LBP = CAP/ ABP. Dengan cara yang sama = AM/MC = ABP/ BCP and = BN/NA

= BCP/ CAP dan diperoleh hasil tersebut 3. Teorema Menelaus

Jika sisi-sisi segitiga dibagi oleh titik-titik L, M, N dalam perbandingan 1 : , 1 : , 1 : maka ketiga titik L, M, N adalah segaris jika dan hanya jika hasil kali

= -1.

Gambar 7. Teorema Menelaus

Perlu dicatat bahwa perbandingan dimana titik L membagi sebuah interval AB adalah negatif jika L berada diluar sisi AB (perpanjangan AB).

Garis AP sejajar ML. Maka 1/ = CM/MA = CL/LP dan 1/ = AN/NB = PL/LB. Maka 1/( ) = CL/LP . PL/LB = -CL/LB = - dan diperoleh hasil tersebut.

KESIMPULAN

Transformasi Affine adalah hubungan geometri yang mempertahankan bentuk dasar dan integritas bangun geometri. Transformasi Affine dapat berupa rotasi, translasi, dan dilatasi. Transformasi Affine bersifat linier (perubahan yang kecil pada transformasi akan mengakibatkan perubahan yang kecil pada objek yang ditransformasikan), tetapi akan membentuk fraktal nonlinier jika beberapa transformasi digabungkan dan diiterasi. Transformasi affine tidak mempertahankan jarak dan sudut, Luas dan volum. Namun transformasi affine mempertahankan kesegarisan, kesejajaran, dan perbandingan.

DAFTAR PUSTAKA

http://en.wikipedia.org/wiki/Introductio_in_analysin_infinitorum Diakses pada tanggal 19 November 2017, pukul 06.09 WIB.

http://en.wikipedia.org/wiki/Affine_space Diakses pada tanggal 19 November 2017, pukul 06.09 WIB.

Nomizu, Katsumi dan Takeshi Sasaki. 1994. Affine Differential Geometry. New York : Cambridge University Press.