PENYELESAIAN NUMERIS BEDA HINGGA PERSAMAAN
DIFERENSIAL PARSIAL
TUGAS AKHIR
Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Matematika
Program Studi Matematika
Oleh: Ria Ayu Agustin
153114006
PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI
UNIVERSITAS SANATA DHARMA YOGYAKARTA
i
PENYELESAIAN NUMERIS BEDA HINGGA PERSAMAAN
DIFERENSIAL PARSIAL
TUGAS AKHIR
Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Matematika
Program Studi Matematika
Oleh: Ria Ayu Agustin
153114006
PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI
UNIVERSITAS SANATA DHARMA YOGYAKARTA
ii
FINITE DIFFERENCE NUMERICAL SOLUTION TO
PARTIAL DIFFERENTIAL EQUATIONS
FINAL PROJECT
Presented as Partial Fulfillment of the
Requirements to Obtain the Degree of Sarjana Matematika Mathematics Study Program
Written by: Ria Ayu Agustin
153114006
MATHEMATICS STUDY PROGRAM DEPARTMENT OF MATHEMATICS FACULTY OF SCIENCE AND TECHNOLOGY
SANATA DHARMA UNIVERSITY YOGYAKARTA
vi
HALAMAN PERSEMBAHAN
Tugas Akhir ini kupersembahkan untuk orang tua saya yaitu Bapak Agustinus Purjianto dan Ibu Agustina Rustinah yang selalu mendukung dengan berbagai aspek. Dosen pembimbing yaitu Bapak Sudi Mungkasi yang dengan sabar membimbing agar dapat menyelesaikan tugas akhir tepat waktu. Adik saya yaitu Lusia Chrisanti yang setia mendengar keluh kesah serta semua orang yang mengasihi saya.
vii
ABSTRAK
Tugas akhir ini menyelesaikan persamaan diferensial parsial menggunakan metode beda hingga. Hasil perhitungan numeris mengkonfirmasi keunggulan metode beda hingga dalam menyelesaikan persamaan diferensial parsial. Metode beda hingga menghasilkan error yang cukup kecil, sehingga dapat dipercaya sebagai metode penyelesaian yang handal.
viii
ABSTRACT
This final project solves partial differential equations using the finite difference method. The results of numerical calculations confirm the superiority of the finite difference method in solving partial differential equations. The finite difference method results in a fairly small error, so it can be trusted as a reliable method of resolution.
Keywords: numerical method, finite difference method, partial differential equation
xii
DAFTAR ISI
HALAMAN JUDUL ... i
TITLE PAGE ... ii
HALAMAN PERSETUJUAN PEMBIBING ... iii
HALAMAN PENGESAHAN ... iv
PERNYATAAN KEASLIAN KARYA ... v
HALAMAN PERSEMBAHAN ... vi
ABSTRAK ... vii
ABSTRACT ... viii
LEMBAR PERNYATAAN PERSETUJUAN ... ix
KATA PENGANTAR ... x
DAFTAR ISI ... xii
BAB I PENDAHULUAN... 1 A. Latar Belakang ... 1 B. Rumusan Masalah ... 2 C. Batasan Masalah... 2 D. Tujuan Penulisan ... 2 E. Metode Penulisan ... 3 F. Manfaat Penulisan ... 3 G. Sistematika Penulisan ... 3
BAB II PERSAMAAN DIFERENSIAL... 5
A. Turunan ... 5
B. Klasifikasi Persamaan Diferensial ... 6
xiii
D. Analisis Galat ... 9
BAB III PERSAMAAN DIFERENSIAL PARSIAL ... 11
BAB IV PENYELESAIAN NUMERIS PERSAMAAN DIFERENSIAL ... 17
BAB V KESIMPULAN DAN SARAN ... 31
A. Kesimpulan ... 31
B. Saran ... 31
1
BAB I
PENDAHULUAN
A. Latar Belakang
Peran matematika tidak dapat dilepaskan dalam membantu manusia di berbagai aspek kehidupan. Contohnya saja terhadap fenomena-fenomena yang terjadi di lingkungan sekitar. Para peneliti dapat mendiskripsikan atau menganalisis sesuatu dengan bantuan ilmu matematika. Hal ini dilakukan agar mendapatkan solusi yang sesuai dalam pemecahan masalah. Biasanya masalah yang akan diselesaikan dimodelkan secara matematis ke dalam bentuk sistem persamaan matematika.
Persamaan diferensial adalah persamaan yang menghubungkan suatu fungsi dengan turunan-turunannya (Boyce dan DiPrima, 2013). Beberapa contoh fenomena fisik yang melibatkan tingkat perubahan antara lain: dinamika populasi, gerak sistem mekanis, dan gerakan fluida. Persamaan diferensial dapat diklasifikasikan menjadi dua macam berdasarkan banyaknya varibel bebas yang bersangkutan. Persamaan diferensial biasa adalah persamaan diferensial yang melibatkan satu variabel bebas. Persamaan diferensial parsial adalah persamaan diferensial yang melibatkan lebih dari satu variabel bebas.
Tidak semua persamaan dapat diselesaikan secara analitis. Hal itu dapat diatasi dengan menyelesaikan secara numeris. Salah satu penyelesaian secara numeris yang digunakan adalah metode beda hingga. Metode beda hingga adalah suatu metode alternatif untuk mengonstruksi diskretisasi terhadap persamaan diferensial yang bertujuan menemukan solusi numeris. Metode beda hingga dapat diaplikasikan dalam berbagai macam bidang, seperti biologi, kesehatan, ekologi, teknik, kimia, dan lain-lain.
B. Rumusan Masalah
Rumusan masalah yang bersangkutan di dalam tugas akhir berdasarkan latar belakang adalah:
1. Bagaimana merumuskan skema beda hingga?
2. Bagaimana penggunaan skema beda hingga dalam menyelesaikan persamaan diferensial?
C. Batasan Masalah
Permasalahan tugas akhir yang akan dibahas dibatasi dengan penggunaan skema beda hingga pada masalah persamaan diferensial agar menemukan solusi numeris.
D. Tujuan Penulisan
Tujuan penulisan tugas akhir ini adalah: 1. Menjelaskan tentang skema beda hingga.
2. Memaparkan penggunaan skema beda hingga dalam penyelesaian persamaan diferensial.
E. Manfaat Penulisan
Manfaat penulisan dari tugas akhir ini adalah penulis dan pembaca mendapat pengetahuan baru tentang skema beda hingga.
F. Metode Penelitian
Metode penelitian yang digunakan dalam penulisan tugas akhir ini adalah studi pustaka, dengan membaca jurnal-jurnal, makalah ilmiah, dan buku-buku yang berhubungan dengan skema beda hingga. Selain itu akan digunakan bantuan aplikasi komputer untuk simulasi numeris.
G. Sistematika Penulisan BAB I PENDAHULUAN A. Latar Belakang B. Rumusan Masalah C. Batasan Masalah D. Tujuan Penelitian E. Manfaat Penulisan F. Metode Penelitian G. Sistematika Pemulisan
BAB II PERSAMAAN DIFERENSIAL A. Turunan
B. Klasifikasi Persamaan Diferensial C. Deret Taylor
D. Analisis Galat
BAB III PERSAMAAN DIFERENSIAL PARSIAL
BAB IV PENYELESAIAN NUMERIS PERSAMAAN DIFERENSIAL BAB V PENUTUP
A. Kesimpulan B. Saran
5
BAB II
PERSAMAAN DIFERENSIAL
A. Turunan
Definisi 2.1
Turunan fungsi f adalah fungsi f yan didefinisikan sebagai
, ) ( ) ( lim ) ( 0 h x f h x f x f h
di setiap titik x sehingga limit fungsi tersebut ada dan berhingga (bukan atau
).
Contoh: Jika f(x)5x32x1, carilah f(x). Penyelesaian: h x f h x f x f h ) ( ) ( lim ) ( ' 0
h x x h x h x h 1 2 5 1 ) ( 2 ) ( 5 lim 3 3 0
h x x h x h xh h x x h 1 2 5 1 2 2 15 15 5 lim 3 3 2 2 3 0 h h h xh h x h 2 15 15 lim 3 2 2 0 2 15 15 lim 2 2 0 x xh h h 2 15 2 x .B. Klasifikasi Persamaan Diferensial
Dalam sub bab ini akan membahas tentang klasifikasi pada persamaan diferensial.
Definisi 2.2
Persamaan diferensial adalah persamaan yang menghubungkan suatu fungsi satu variabel atau lebih dengan turunan-turunannya.
Contoh:
(2.1.1)
( )
(2.1.2)(2.1.3)
(2.1.4) Definisi 2.3
Persamaan diferensial biasa adalah persamaan diferensial yang melibatkan tepat satu variabel bebas.
Contoh:
Persamaan diferensial biasa dapat dilihat pada persamaan (2.1.1) dan (2.1.2). Variabel bebas untuk persamaan (2.1.1) adalah t , sedangkan variabel terikatnya
adalah v. Pada persamaan (2.1.2) melibatkan t sebagai varibel bebas dan y
sebagai varibel terikat. Definisi 2.4
Persamaan diferensial parsial adalah persamaan diferensial yang melibatkan lebih dari satu variabel bebas.
Contoh:
Persamaan diferensial parsial dapat dilihat pada persamaan (2.1.3) dan (2.1.4). Variabel bebas untuk persamaan (2.1.1) adalah t dan u sedangkan variabel terikatnya adalah v. Pada persamaan (2.1.2) melibatkan t dan z sebagai
variabel bebas dan v sebagai variabel terikat.
C. Deret Taylor
Definisi 2.5
Andaikan dan turunanya , kontinu di selang , -. Misalkan , -, maka nilai-nilai untuk disekitar dan , -, ( ) dapat diperluas ke dalam deret Taylor.
( ) ( ) ( ) ( ) ( ) ( ) ( )
( ) .
Contoh:
Tentukan perluasan fungsi ( ) ( ) ke dalam deret Taylor di sekitar .
Penyelesaian:
Menentukan turunan ( ) terlebih dahulu, ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )( ) ( ) dan seterusnya.
Berdasarkan Definisi 2.5, ( )dihampiri dengan deret Taylor,
( ) ( ) ( ) ( ( )) ( ) ( ( )) ( ) ( ( )) ( ) ( ( )) .
Bila dimisalkan , maka
( ) ( ) ( ( )) ( ( )) ( ( ))
( ( ))
Kasus khusus adalah bila fungsi diperluas di sekitar , maka deretnya dinamakan deret Maclaurin, yang merupakan deret Taylor baku. Deret Taylor yang dipotong sampai suku orde ke- dinamakan deret Taylor terpotong dan dinyatakan oleh:
( ) ( ) ( ) ( ) ( ) ( ) ( )
( ) ( ).
Yang dalam hal ini,
( ) ( )
( )( ) ,
disebut galat atau sisa (residu).
D. Analis Galat
Galat berasosiasi dengan seberapa dekat solusi hampiran terhadap solusi sebenarnya. Semakin kecil galat maka semakin teliti solusi numerik yang didapatkan.
Pada penurunan rumus turunan numeris dengan deret Taylor, rumus galat dalam penurunan rumus turunan numeris dapat langsung diperoleh. Akan tetapi dengan polinom interpolasi harus dicari rumus galat tersebut dengan bantuan deret Taylor.
Contoh:
Tentukan rumus galat dan orde dari rumus turunan numeris hampiran beda-pusat:
( )
Nyatakan E sebagai ruas kiri persamaan, lalu ekspansi ruas kanan dengan deret Taylor disekitar ,
( ) *( ) ( )+ ( ) , ( )
Jadi hampiran beda pusat memiliki galat , , dengan orde ( ).
11
BAB III
PERSAMAAN DIFERENSIAL PARSIAL
Dalam bab ini akan dibahas tentang persamaan diferensial dan klasifikasinya.
Klasifikasi Persamaan Diferensial Parsial
Benda berkeadaan isotropik jika konduktivitas termal pada setiap titik dalam benda tidak tergantung pada arah panas yang rendah melalui titik tersebut. Andaikan , , dan adalah fungsi dari ( ) dan masing-masing mewakili, konduktivitas termal, panas spesifik, dan kepadatan isotropik benda pada ( ). Maka suhu, ( ), dalam suatu benda dapat ditemukan dengan menyelesaikan persamaan diferensial parsial
. / . / . / ,
Ketika , , dan adalah konstanta, persamaan ini dikenal sebagai persamaan panas tiga dimensi yang sederhana dan dinyatakan sebagai
.
Jika batas benda relatif sederhana, solusi untuk persamaan ini dapat ditemukan menggunakan deret Fourier.
Dalam sebagian besar situasi di mana , , dan tidak konstan atau ketika batas tidak ditentukan, solusi untuk persamaan diferensial parsial harus diperoleh dengan teknik penaksiran.
Persamaan Eliptik
Persamaan diferensial parsial umumnya dikategorikan dengan cara yang mirip dengan bagian kerucut. Persamaan diferensial parsial yang akan dibahas melibatkan ( ) ( ) dan merupakan persamaan eliptik. Persamaan
eliptik tertentu yang akan ditinjau dikenal sebagai persamaan Poisson:
( ) ( ) ( ).
Dalam persamaan ini, diasumsikan bahwa menggambarkan input ke masalah pada bidang daerah dengan batas . Persamaan dari tipe ini muncul dalam studi berbagai masalah fisik yang tidak tergantung waktu seperti distribusi stabil dari panas dalam suatu daerah bidang, energi potensial dari suatu titik dalam bidang yang digerakkan oleh gaya gravitasi di bidang tersebut dan masalah yang melibatkan cairan yang tidak bisa dimampatkan.
Kendala tambahan harus dikenakan untuk mendapatkan solusi unik untuk persamaan Poisson. Sebagai contoh, studi tentang distribusi panas tunak di daerah bidang membutuhkan ( ) , menghasilkan penyederhanaan persamaan Laplace
( ) ( ) .
Jika suhu dalam suatu daerah ditentukan oleh distribusi temperatur pada batas daerah, kendalanya disebut kondisi batas Dirichlet, yang diberikan oleh
( ) ( ),
untuk semua ( ) pada , batas wilayah . (Lihat Gambar 3.1).
Gambar 3.1. Ilustrasi domain dan kondisi batasnya.
Persamaan Parabolik
Ditinjau masalah yang melibatkan persamaan diferensial parsial parabolik bentuk
( )
( ) .
Masalah fisik yang dipertimbangkan di sini menyangkut aliran panas sepanjang batang (lihat Gambar 3.2) yang memiliki suhu yang seragam dalam setiap elemen penampang. Ini membutuhkan batang untuk diisolasi dengan sempurna
pada permukaan lateral. Konstanta diasumsikan tidak tergantung pada posisi pada batang. Ini ditentukan oleh sifat konduktif panas dari bahan yang batangnya disusun.
Gambar 3.2. Ilustrasi domain satu dimensi.
Salah satu kondisi untuk masalah aliran panas jenis ini adalah untuk menentukan distribusi panas awal dalam batang,
( ) ( ),
dan untuk menggambarkan perilaku di ujung tongkat. Misalnya, jika ujungnya ditahan pada suhu konstan dan , syarat batasnya berbentuk
( ) dan ( ) ,
dan distribusi panas mendekati distribusi temperatur yang membatasi adalah ( ) .
Sebaliknya, jika batang diisolasi sehingga tidak ada panas yang mengalir melalui ujung, kondisi batasnya
( ) dan
Maka tidak ada panas yang keluar dari batang dan dalam kasus pembatas suhu pada batang konstan. Persamaan diferensial parsial parabolik juga penting dalam studi difusi gas; pada kenyataannya, ini dikenal di beberapa kalangan sebagai persamaan difusi.
Persamaan Hiperbolik
Persamaan gelombang satu dimensi dan merupakan contoh dari persamaan diferensial parsial hiperbolik. Misalkan sebuah tali elastis dengan panjang direntangkan di antara dua penyangga pada tingkat horizontal yang sama (lihat Gambar 3.3).
Gambar 3.3. Ilustrasi gelombang yang merambat satu dimensi.
Jika tali diatur untuk bergetar dalam bidang vertikal, perpindahan vertikal ( ) dari titik pada waktu memenuhi persamaan diferensial parsial
asalkan efek redaman diabaikan dan amplitudo tidak terlalu besar. Untuk memberikan batasan pada masalah ini, asumsikan bahwa posisi awal dan kecepatan tali diberikan oleh
( ) ( ) dan
( ) ( ), untuk .
Jika titik akhir ditetapkan, maka diperoleh ( ) dan ( ) .
Masalah fisik lainnya yang melibatkan persamaan diferensial parsial hiperbolik terjadi dalam studi balok bergetar dengan satu atau kedua ujung dijepit dan dalam transmisi listrik pada garis panjang di mana ada beberapa kebocoran arus ke tanah.
17
BAB IV
PENYELESAIAN NUMERIS PERSAMAAN DIFERENSIAL
Persamaan diferensial parsial eliptik yang dipertimbangkan adalah persamaan Poisson,
( )
( ) ( ) ( ) (4.1)
pada *( )| +, dengan ( ) ( ) untuk ( ) , dimana menunjukkan batas . Jika dan kontinu di domain mereka, maka ada solusi unik untuk persamaan ini.
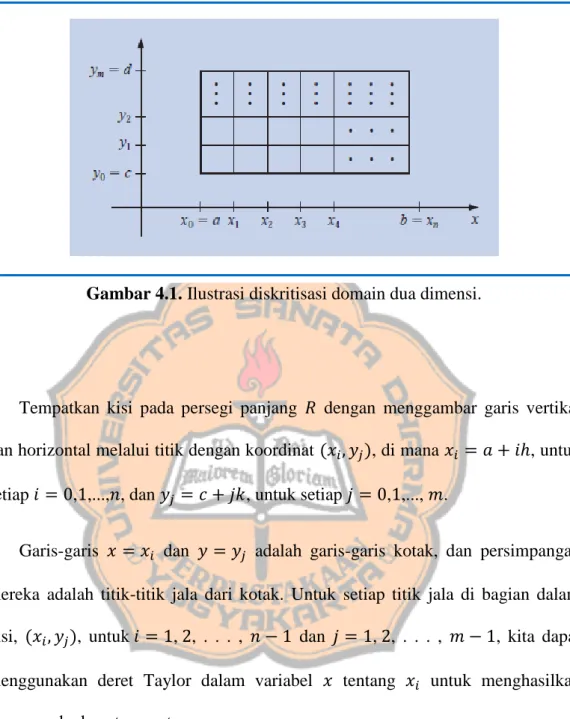
Metode yang digunakan adalah adaptasi dua dimensi dari metode beda-hingga untuk masalah nilai batas-linear. Langkah pertama adalah memilih bilangan bulat dan untuk menentukan ukuran langkah ( ) ⁄ dan ( ) ⁄ . Partisi interval , - menjadi bagian yang sama lebar dan interval , - menjadi bagian yang sama dengan lebar (lihat Gambar 4.1).
Gambar 4.1. Ilustrasi diskritisasi domain dua dimensi.
Tempatkan kisi pada persegi panjang dengan menggambar garis vertikal dan horizontal melalui titik dengan koordinat ( ), di mana , untuk setiap , ,..., , dan , untuk setiap , ,..., .
Garis-garis dan adalah garis-garis kotak, dan persimpangan mereka adalah titik-titik jala dari kotak. Untuk setiap titik jala di bagian dalam kisi, ( ), untuk , , . . . , dan , , . . . , , kita dapat menggunakan deret Taylor dalam variabel tentang untuk menghasilkan rumus perbedaan terpusat.
( )
( ) ( ) ( )
( ), (4.2)
di mana ( ). Dapat juga menggunakan deret Taylor dalam variabel tentang untuk menghasilkan rumus perbedaan terpusat
( )
( ) ( ) ( )
( ), (4.3)
dimana ( ).
Menggunakan rumus ini dalam persamaan (4.1) memungkinkan untuk mengekspresikan persamaan Poisson pada titik ( ) sebagai
( ) – ( ) ( )
( ) – ( ) ( )
( )
( ) ( ),
untuk setiap , , . . . , dan , , . . . , . Kondisi batasnya adalah
( ) ( ) dan ( ) ( ), untuk setiap , , . . . , ; ( ) ( )dan ( ) ( ), untuk setiap , ,..., .
Metode Beda-Hingga
Dalam bentuk persamaan-beda, ini menghasilkan metode beda-hingga:
*( ) + ( ) ( ) ( )
( ), (4.4)
( ) dan ( ), untuk setiap , , . . . , ; (4.5) ( ) dan ( ), untuk setiap , , . . . , ;
di mana mendekati ( ). Metode ini memiliki kesalahan pemotongan
lokal pada orde ( ).
Persamaan (4.4) melibatkan perkiraan untuk ( ) pada titik-titik ( ), ( ), ( ), ( ), dan ( ).
Mebentuk bagian grid di mana titik-titik ini berada (lihat Gambar 4.2) menunjukkan bahwa setiap persamaan melibatkan perkiraan dalam wilayah berbentuk bintang tentang X biru di ( ).
Digunakan informasi dari kondisi batas persamaan (4.5) kapan pun sesuai dalam sistem yang diberikan oleh persamaan (4.4); yaitu pada semua titik ( ) yang berdekatan dengan titik batas jala.
Ini menghasilkan ( )( ) ( )( ) sistem linier dengan yang tidak diketahui adalah perkiraan ke ( ) pada titik jala interior.
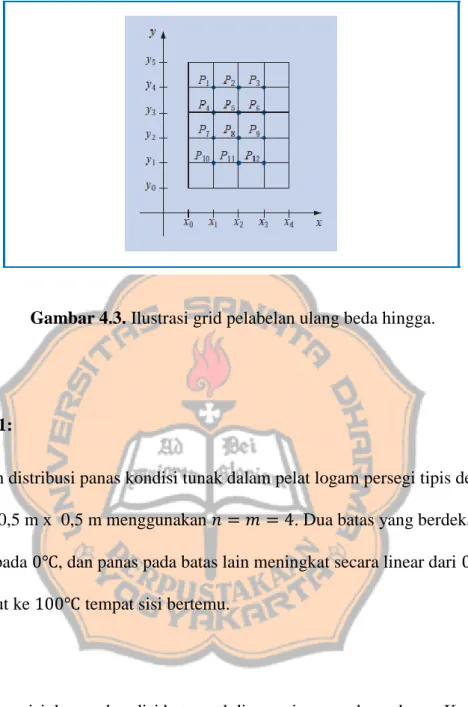
Sistem linier yang melibatkan hal-hal yang tidak diketahui ini diekspresikan untuk perhitungan matriks secara lebih efisien jika pelabelan ulang titik-titik jala interior diperkenalkan. Pelabelan yang direkomendasikan untuk titik-titik ini adalah
( ) dan ,
dimana ( )( ), untuk setiap , , . . . , dan , , . . . , . Ini memberi label titik-titik jala secara berurutan dari kiri ke kanan dan atas ke bawah. Memberi label titik dengan cara ini memastikan bahwa sistem yang diperlukan untuk menentukan adalah matriks berpita dengan lebar pita paling banyak .
Misalnya, dengan dan , hasil pelabelan ulang dalam kotak yang poinnya ditunjukkan pada Gambar 4.3.
Gambar 4.3. Ilustrasi grid pelabelan ulang beda hingga.
Contoh 1:
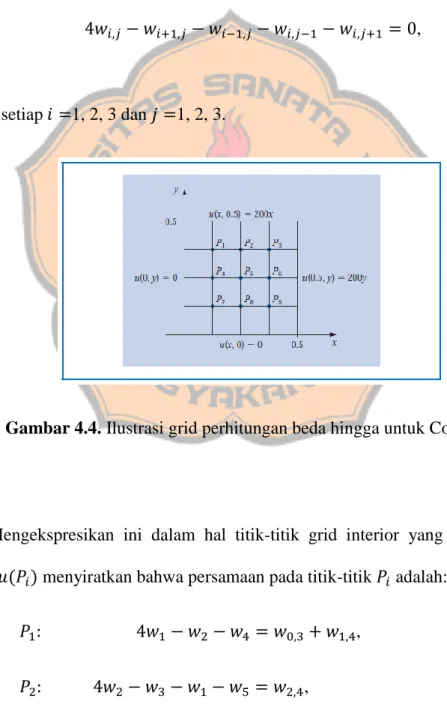
Tentukan distribusi panas kondisi tunak dalam pelat logam persegi tipis dengan dimensi 0,5 m x 0,5 m menggunakan . Dua batas yang berdekatan ditahan pada , dan panas pada batas lain meningkat secara linear dari di satu sudut ke tempat sisi bertemu.
Solusi:
Tempatkan sisi dengan kondisi batas nol di sepanjang sumbu dan . Kemudian masalahnya dinyatakan sebagai
untuk ( ) di domain *( )| +. Kondisi batasnya adalah
( ) , ( ) , ( ) , dan ( ) .
Jika , masalah memiliki grid yang diberikan pada Gambar 4.4, dan persamaan beda (4.4) adalah
,
untuk setiap 1, 2, 3 dan 1, 2, 3.
Gambar 4.4. Ilustrasi grid perhitungan beda hingga untuk Contoh 1.
Mengekspresikan ini dalam hal titik-titik grid interior yang dilabel ulang ( ) menyiratkan bahwa persamaan pada titik-titik adalah:
, ,
, , , , , , , di mana sisi kanan persamaan diperoleh dari kondisi batas.
Faktanya, syarat batas menyiratkan hal itu
,
, , and .
Jadi, sistem linear yang terkait dengan masalah ini memiliki bentuk
[ ][ ] [ ]
Nilai , ,. . . , , ditemukan dengan menerapkan metode Gauss-Seidel ke matriks tersebut, diberikan pada Tabel 4.1.
Tabel 4.1. Tabel hasil perhitungan untuk Contoh 1. 1 18.75 2 37.50 3 56.25 4 12.50 5 25.00 6 37.50 7 6.25 8 12.50 9 18.75
Jawaban-jawaban ini tepat (solusi-solusi tersebut adalah eksak), karena solusi yang benar, ( ) , miliki bentuk
,
dengan error nol pada setiap langkah.
Masalah yang dibahas dalam Contoh 1 memiliki ukuran jala yang sama, 0.125, pada setiap sumbu dan hanya membutuhkan penyelesaian sistem linier 9 × 9. Ini menyederhanakan situasi dan tidak memperkenalkan masalah komputasi yang hadir ketika sistem lebih besar.
Persamaan Poisson Beda-Hingga
Untuk memperkirakan solusi untuk persamaan Poisson
( ) ( ) ( ), , ,
tunduk pada ketentuan batas
( ) ( ) jika atau dan dan
( ) ( ) jika atau dan .
Meskipun prosedur iteratif Gauss-Seidel dimasukkan ke dalam algoritma untuk kesederhanaan, disarankan untuk menggunakan teknik langsung seperti eliminasi Gaussian ketika sistemnya kecil, pada urutan 100 atau kurang, karena kepastian positif memastikan stabilitas sehubungan dengan kesalahan pembulatan.
Berikut ini adalah Algoritma Metode Beda Hingga menurut Burden dan Faires (2011):
Contoh 2
Gunakan metode beda hingga Poisson dengan , , dan toleransi
untuk mendekati solusi
( ) ( ) , , ,
dengan syarat batas
( ) , ( ) , , ( ) , ( ) , , dan bandingkan hasilnya dengan solusi perhitungan ( ) . Solusi:
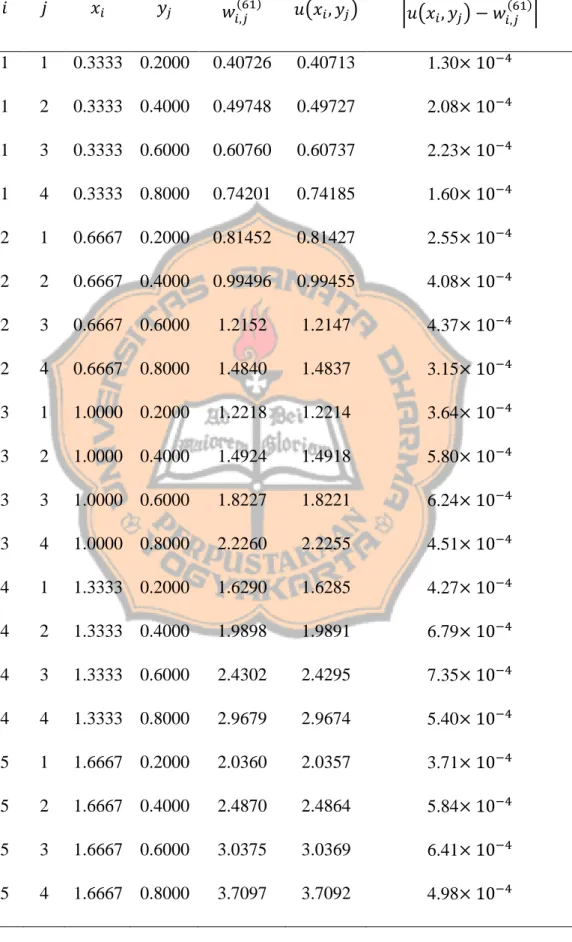
Gunakan algoritma sebelumnya dengan jumlah iterasi maksimum yang ditetapkan pada memberikan hasil pada Tabel 4.2. Kriteria berhenti untuk metode Gauss-Seidel pada Langkah 17 mengharuskan itu
| ( ) ( )| ,
untuk setiap 1, . . . ., 5 dan 1, . . . ., 4. Solusi untuk persamaan perbedaan diperoleh secara akurat, dan prosedur dihentikan pada . Hasilnya, bersama dengan nilai-nilai yang benar, disajikan pada Tabel 4.2.
Tabel 4.2. Hasil perhitungan beda hingga untuk Contoh 2. ( ) ( ) | ( ) ( )| 1 1 0.3333 0.2000 0.40726 0.40713 1.30 1 2 0.3333 0.4000 0.49748 0.49727 2.08 1 3 0.3333 0.6000 0.60760 0.60737 2.23 1 4 0.3333 0.8000 0.74201 0.74185 1.60 2 1 0.6667 0.2000 0.81452 0.81427 2.55 2 2 0.6667 0.4000 0.99496 0.99455 4.08 2 3 0.6667 0.6000 1.2152 1.2147 4.37 2 4 0.6667 0.8000 1.4840 1.4837 3.15 3 1 1.0000 0.2000 1.2218 1.2214 3.64 3 2 1.0000 0.4000 1.4924 1.4918 5.80 3 3 1.0000 0.6000 1.8227 1.8221 6.24 3 4 1.0000 0.8000 2.2260 2.2255 4.51 4 1 1.3333 0.2000 1.6290 1.6285 4.27 4 2 1.3333 0.4000 1.9898 1.9891 6.79 4 3 1.3333 0.6000 2.4302 2.4295 7.35 4 4 1.3333 0.8000 2.9679 2.9674 5.40 5 1 1.6667 0.2000 2.0360 2.0357 3.71 5 2 1.6667 0.4000 2.4870 2.4864 5.84 5 3 1.6667 0.6000 3.0375 3.0369 6.41 5 4 1.6667 0.8000 3.7097 3.7092 4.98
31
BAB V
KESIMPULAN DAN SARAN
A. KESIMPULAN
Metode beda hingga berhasil diterapkan untuk menyelesaikan masalah persamaan diferensial parsial. Metode beda hingga mempunyai keuntungan bahwa metode ini mudah untuk diprogram secara numeris. Namun demikian, pembahasan dalam Tugas Akhir ini masih perlu dikaji lebih lanjut terkait teori kestabilan metode beda hingga untuk menyelesaikan masalah persamaan diferensial parsial tersebut.
B. SARAN
Penulis menyarankan agar metode beda hingga dalam Tugas Akhir ini dianalisis lebih lanjut terkait kestabilan dan konvergensinya sehingga pembaca lebih yakin dengan keunggulan metode beda hingga.
32
DAFTAR PUSTAKA
Boyce W. E., DiPrima, R.C. (2012). Elementary Differential Equations and Boundary Value Problems, edisi ke-10, New York: John Wiley & Sons, Inc.
Burden R. L., Faires J. D. (2011). Numerical Analysis, edisi ke-9, Boston:
Brooks/Cole, Cengage Learning.
Hong Q., Li J., Wang Q. Supplementary variable method for structure-preserving
approximations to partial differential equations with deduced equations, 2020, Applied Mathematics Letters, 110, 106576, 10.1016/j.aml.2020.106576
Patel K.S., Mehra M. Fourth order compact scheme for space fractional
advection-diffusion reaction equations with variable coefficients, 2020, Journal of Computational and Applied Mathematics, 380, 112963, 10.1016/j.cam.2020.112963
Salama F.M., Hj. Mohd. Ali N., Abd Hamid N.N. Efficient hybrid group iterative methods in the solution of two-dimensional time fractional cable equation, 2020, Advances in Difference Equations, 2020, 1, 257, 10.1186/s13662-020-02717-7
Varberg, Purcell, Ringdon. (2010). Kalkulus (Terjemahan), edisi ke-9, Jakarta:
Penerbit Erlangga.
Wongsaijai B., Oonariya C., Poochinapan K. Compact structure-preserving
2020, Mathematics and Computers in Simulation, 178, 125-150, 10.1016/j.matcom.2020.05.002
Zhang H., Yang X., Liu Y., Liu Y. An extrapolated CN-WSGD OSC method
for a nonlinear time fractional reaction-diffusion equation, 2020, Applied Numerical Mathematics, 157, 619-633, 10.1016/j.apnum.2020.07.017