PENYELESAIAN PROGRAM NONLINEAR DENGAN METODE KUADRATIK PADA PORTOFOLIO SAHAM
Oleh Efria Lemadona
11305144029
ABSTRAK
Pembentukan portofolio merupakan salah satu penerapan permasalahan program nonlinear. Salah satu metode yang dapat digunakan untuk menyelesaikan permasalahan program nonlinear yaitu metode kuadratik. Tujuan dari penulisan skripsi ini adalah menjelaskan pembentukan model nonlinear pada pembentukan portofolio saham dan penyelesaiannya menggunakan metode kuadratik sehingga diperoleh penyelesaian yang optimal.
Metode kuadratik merupakan bentuk khusus dari program nonlinear yang memiliki fungsi tujuan berbentuk kuadratik dan fungsi kendala berbentuk linear. Metode kuadratik dapat diselesaikan dengan menggunakan persyaratan Karush Kuhn Tucker. Persyaratan Karush Kuhn Tucker dibentuk dengan menurunkan fungsi tujuan dan dipisahkan berdasarkan masing-masing variabel keputusan lalu ditambahkan variabel lambda sebagai pengali. Langkah-langkah untuk menyelesaikan permasalahan program nonlinear dengan metode kuadratik yaitu dengan mentransformasi fungsi tujuan yang berbentuk nonlinear menjadi linear dan menyelesaikan dengan metode simpleks.
Dalam pembentukan portofolio optimal menggunakan data harga penutupan saham harian perbankan dari perusahaan BNI, BRI, Bank Mandiri, BCA dan Bank Danamon periode 2 Januari 2014 sampai 30 Desember 2014. Model nonlinear pada portofolio saham perbankan
. Penyelesaian metode Kuadratik untuk portofolio optimal adalah berdasarkan pada perhitungan dengan dibantu program QSB diperoleh nilai , dan Proporsi dana yang diinvestasikan di Bank Mandiri yaitu 30%, BCA yaitu 50% dan Bank Danamon 20%.
BAB 1 PENDAHULUAN
A. Latar Belakang
Setiap perusahaan atau organisasi memiliki keterbatasan atas sumber daya, baik keterbatasan dalam jumlah bahan baku, mesin dan peralatan, ruang, tenaga kerja, jam-kerja, maupun modal. Dengan keterbatasan ini, perusahaan perlu merencanakan strategi yang dapat mengoptimalkan hasil yang ingin dicapai, baik itu berupa memaksimumkan keuntungan atau meminimumkan biaya. Program linear adalah salah satu model matematika yang dapat digunakan untuk memodelkan upaya perusahaan tersebut dalam memperoleh solusi yang optimal (Eddy Herjanto, 2007: 43).
Adanya fungsi tujuan (objective function) dari variabel keputusan dan dapat digambarkan dalam fungsi linear. (3) Keterbatasan sumber daya maupun sumber dana dapat digambarkan dalam fungsi linear.
Ketika permasalahan tidak dapat dimodelkan dalam bentuk model matematika linear, maka permasalahan ini dapat diselesaikan dengan program nonlinear (Jerome Bracken, 1968:vii). Permasalahan program nonlinear
banyak ditemui dalam berbagai disiplin ilmu tergantung pada karateristik fungsi tujuan dan fungsi kendala, seperti pada ilmu ekonomi, teknik, industri, fisika, dll. Menurut Hillier (2001:664) terdapat beberapa metode yang dapat digunakan untuk menyelesaikan permasalahan program nonlinear antara lain metode separable, metode kuadratik, metode newton raphson, dll. Model kuadratik digunakan untuk menyelesaikan permasalahan program nonlinear dengan fungsi tujuan berbentuk kuadratik dan fungsi kendala berbentuk linear (Hillier, 2001:683). Metode kuadratik dapat diselesaikan dengan menggunakan persyaratan Karush Kuhn Tucker. Persyaratan Karush Kuhn Tucker dibentuk dengan menurunkan fungsi tujuan dan dipisahkan
berdasarkan masing-masing variabel keputusan lalu ditambahkan variabel lambda sebagai pengali.
keuntungan di masa mendatang. Ketika melaksanakan investasi dalam bentuk portofolio saham, investor dihadapkan dengan masalah risiko turunnya harga saham. Seorang investor membeli portofolio saham bertujuan memperoleh keuntungan dari kenaikan harga saham ataupun sejumlah pengembalian laba (dividen) di masa yang akan datang, sebagai imbalan atas waktu dan risiko yang terkait dengan investasi tersebut.
Menurut Abdul Halim (2005:12) saham merupakan surat berharga yang menunjukkan kepemilikan perusahaan sehingga pemegang saham memiliki hak klaim atas dividen atau distribusi lain yang dilakukan perusahaan kepada pemegang saham lainnya. Fluktuasi harga saham ditentukan oleh kemampuan perusahaan dalam memperoleh laba. Apabila laba yang diperoleh perusahaan relatif tinggi, maka kemungkinan besar bahwa dividen yang dibayarkan juga relatif tinggi. Hal ini akan berpengaruh positif terhadap harga saham di bursa, dan investor akan tertarik untuk membelinya. Akibatnya permintaan akan saham tersebut meningkat, sehingga harga saham juga akan meningkat.
perlu dibentuk portofolio (Frank J.Fabozzi, 1999:61). Dalam melakukan penyusunan portofolio, yang menjadi bahan pertimbangan adalah expected return (harapan keuntungan atau tingkat pengembalian) dan risiko. Salah
satu pengukuran risiko adalah standar deviasi.
B. Batasan Masalah
Pada penulisan tugas akhir ini, permasalahan dibatasi pada penyelesaian model nonlinear portofolio saham menggunakan metode Kuadratik dengan persyaratan Karush Kuhn Tucker. Portofolio saham dibentuk dari penutupan harga saham harian Bank Negara Indonesia (BNI), Bank Rakyat Indonesia (BRI), Bank Mandiri, Bank Central Asia (BCA) dan Bank Danamon periode 2 Januari 2014 sampai 30 Desember 2014.
C. Rumusan Masalah
Dalam tulisan ini, masalah yang dibahas adalah:
1. Bagaimana membentuk model nonlinear pada pembentukan portofolio saham perbankan?
2. Bagaimana penyelesaian model nonlinear pada portofolio saham perbankan dengan metode Kuadratik?
D. Tujuan Penelitian
Tujuan yang ingin dicapai dari penyusunan tugas akhir ini adalah
1. Menjelaskan pembentukan model nonlinear portofolio pada investasi saham di bidang perbankan.
E. Manfaat Penelitian
Manfaat yang didapat dari penyusunan skripsi ini adalah: 1. Bagi Penulis
a. Menambah pengetahuan penulis mengenai penyusunan portofolio optimal.
b. Menambah pengetahuan penulis mengenai langkah penyelesaian portofolio optimal menggunakan Metode Kuadratik.
c. Menambah pengetahuan penulis mengenai penerapan portofolio optimal menggunakan Metode Kuadratik pada investasi harga saham perbankan.
2. Bagi Jurusan Pendidikan Matematika
Menambah pengetahuan dan referensi untuk Portofolio Optimal menggunakan Metode Kuadratik yang diterapkan pada investasi saham perbankan.
3. Bagi Pembaca
a. Menambah pengetahuan calon investor dalam mengoptimalkan keuntungan yang diharapkan dengan tingkat risiko tertentu.
BAB II
KAJIAN PUSTAKA
Berikut diberikan landasan teori mengenai Teori Portofolio, Turunan Parsial, Supremum dan Infimum, Himpunan Konveks, Program Nonlinear, Matriks Definit Positif dan Definit Negatif, Persyaratan Karush Kuhn Tucker, Metode Kuadratik, Permasalahan Komplementaritas Linear, Langkah-langkah Metode Kuadratik dan Program Linear.
A. Teori Portofolio
1. Pengertian Portofolio
2. Return
Return merupakan hasil yang diperoleh dari investasi. Adanya
hubungan positif antara return dan risiko dalam berinvestasi yang dikenal dengan high risk- high return, yang artinya semakin besar risiko yang ditanggung, semakin besar pula return yang diperoleh. Hal ini dimaksudkan sebagai harus ada pertambahan return sebagai kompensasi dari pertambahan risiko yang akan ditanggung oleh investor. (Jogiyanto, 2014:19).
Return realisasi (realized return) merupakan return yang telah
terjadi. Return realisasi banyak digunakan sebagai data untuk investasi, termasuk digunakan sebagai data analisis portofolio. Return realisasi (realized return) dihitung dengan menggunakan data historis. Menurut Jogiyanto (2003:109) return historis juga berguna sebagai dasar penentuan return ekspektasi (expected return) dan risiko di masa mendatang. Return ekspektasi (expected return) adalah return yang diharapkan akan diperoleh oleh investor di masa mendatang. Berbeda dengan return realisasi yang sifatnya sudah terjadi, return ekspektasi sifatnya belum terjadi.
a) Return realisasi portofolio adalah rata-rata tertimbang dari return realisasi setiap aset tunggal di dalam portofolio (Jogiyanto, 2014:94). Secara matematis untuk n aset, return realisasi portofolio dapat ditulis:
Keterangan:
: return realisasian portofolio
: proporsi dana yang diinvestasikan pada saham i : return realisasian dari aset ke-
: jumlah dari aset tunggal
b) Jika seseorang menginvestasikan dananya pada saham ke-i periode dengan harga dan harga pada periode selanjutnya
adalah , maka return total pada periode sampai adalah
. Return total dapat digambarkan sebagai
pendapatan relatif atau tingkat keuntungan (profit rate).
Dengan demikian, return total dapat dinyatakan sebagai berikut (Jogiyanto, 2003:206)
= (2.2)
Keterangan:
: return total realisasi portofolio
: Harga penutupan saham ke-i pada periode ke- : Harga penutupan saham i pada periode
ke-3. Expected Return
Menurut Jogiyanto (2014:24) return ekspekatasi (expected return) merupakan return yang diharapkan dari investasi yang akan dilakukan. Return ekpektasi merupakan return yang penting karena dapat digunakan
menggunakan data historis dapat dihitung berdasarkan beberapa cara sebagai berikut:
1) Metode rata-rata (mean method) 2) Metode tren (trend method)
3) Metode jalan acak (random walk method)
Diantara ketiga metode yang paling banyak digunakan adalah metode rata-rata (mean method) dibandingkan dengan metode rata-rata aritmatika (arithmetic mean) dan rata-rata geometrik (geometric mean).
a. Expected return saham individual
= (2.3)
Keterangan:
: nilai ekspektasi
: return aset ke- pada periode ke-
: banyaknya return yang terjadi pada periode observasi b. Expected return Portofolio
Menurut Jogiyanto (2014:19) return ekspektasian portofolio dapat dihitung dari rata-rata return ekspektasian masing-masing aset tunggal di dalam portofolio. Untuk aset, return ekspektasian portofolio dapat dinyatakan secara matematis sebagai berikut:
= (2.4)
Keterangan:
: proporsi dari aset ke-i terhadap seluruh aset di portofolio
: nilai harapan return aktiva ke-i
: banyaknya return yang terjadi pada periode observasi 4. Risiko
Menurut Abdul Halim (2003:42) risiko didefinisikan sebagai besarnya penyimpangan antara tingkat pengembalian yang diharapkan (expected return) dengan tingkat pengembalian yang dicapai secara nyata (realized return). Semakin besar penyimpangannya maka semakin besar pula tingkat risikonya. Apabila risiko dinyatakan sebagai seberapa jauh hasil yang diperoleh dapat menyimpang dari hasil yang diharapkan, maka digunakan ukuran penyebaran adalah varians atau deviasi standar.
Risiko dalam investasi dibedakan menjadi dua, yaitu: a. Risiko saham individual
Risiko saham invidual dihitung dengan menggunakan rumus sebagai berikut:
(2.5)
Keterangan:
σi2 : varians dari investasi pada saham i
: nilai harapan return aktiva ke-i : return aset ke-i pada periode ke-t
b. Risiko Portofolio
Menurut Jogiyanto (2014:59) salah satu pengukur risiko adalah standar deviasi atau varian (variance) yang merupakan kuadrat dari standar deviasi. Risiko portofolio dapat diukur dengan ukuran besarnya standar deviasi atau varian dari nilai-nilai return aktiva tunggal. Dengan demikian, varian return portofolio yang merupakan risiko portofolio dapat ditulis sebagai berikut:
(2.6)
Dimana , sehingga persamaan (2.6)
menjadi:
Jika persamaan (2.7) ditulis dalam simbol-simbol diperoleh persamaan sebagai berikut:
(2.8)
(2.9)
Keterangan:
σi2 : varians dari investasi pada saham i
: Risiko portofolio
: nilai harapan return aktiva ke-i
: return aktiva ke-i pada periode ke-t
: banyaknya return yang terjadi pada periode observasi 5. Model Mean Variance Markowitz
Model mean variance markowitz pertama kali diperkenalkan tahun 1952 oleh Harry Markowitz dala paper berjudul portofolio selection tentang pemilihan portofolio optimal secara kuantitatif.
Dalam paper tersebut, Harry Markowitz mengidentifikasi expected return dan risiko menggunakan varians return, dimana varians tersebut
diminimalkan untuk tingkat ekspektasi tertentu.
Teori portofolio optimal menggunakan model Markowitz didasarkan pada empat asumsi sebagai berikut (Jogiyanto, 2003:204):
3) Prefensi investor hanya didasarkan pada expected return dan risiko dari portofolio
4) Tidak adanya pinjaman dan simpanan bebas risiko
Menurut Moehring (2013) portofolio optimal menggunakan model mean-variance Markowitz berdasarkan prefensi investor adalah
sebagai berikut:
a. Meminimumkan risiko untuk tingkat return tertentu Fungsi tujuan:
Meminimumkan (2.10)
dengan kendala:
(2.11)
artinya jumlah proporsi dana sama dengan satu (2.12)
(2.13)
b. Memaksimumkan return dengan tingkat risiko tertentu Fungsi tujuan:
Memaksimumkan (2.14)
dengan kendala:
(2.15)
artinya jumlah proporsi dana sama dengan satu
B. Turunan Parsial
Definisi 2.1 (Purcell dan Varberg, 2001:141)
Jika terdefinisi dalam domain D dibidang , sedangkan turunan pertama terhadap dan disetiap titik ada maka:
Turunan pertama di (selain dianggap konstan) adalah
Turunan pertama di (selain dianggap konstan) adalah
Dapat dinotasikan sebagai
1. Turunan parsial fungsi n variabel
Diberikan fungsi n variabel dari dengan persamaan , maka turunan-turunan parsialnya yaitu:
, , ....,
Khusus untuk fungsi tiga variabel dari dengan persamaan , maka turunan-turunan parsialnya yaitu:
, ,
2. Turunan Parsial Derajat Dua
C. Supremum dan Infimum
Berikut ini diperkenalkan konsep tentang batas atas dan batas bawah dari suatu himpunan bilangan real.
Definisi 2.2 (Robert G. Bartle, 1927:35) Diberikan S subset tak kosong
(a) Himpunan S dikatakan terbatas ke atas (bounded above) jika terdapat suatu bilangan sedemikian hingga untuk semua . Setiap bilangan u seperti ini disebut dengan batas atas (upper bound) dari S. (b) Himpunan S dikatakan terbatas ke bawah (bounded below) jika terdapat
suatu bilangan sedemikian hingga untuk semua . Setiap bilangan w seperti ini disebut dengan batas bawah (lower bound) dari S. (c) Suatu himpunan dikatakan terbatas (bounded) jika terbatas ke atas dan
Definisi 2.3 (Robert G. Bartle, 1927:35) Diberikan S subset tak kosong ℝ .
(a) Jika S terbatas ke atas, maka suatu bilangan u disebut supremum (batas atas terkecil) dari S jika memenuhi kondisi berikut:
(1) u merupakan batas atas S, dan
(2) jika v adalah sebarang batas atas S, maka . Ditulis u = sup S .
(b) Jika S terbatas ke bawah, maka suatu bilangan w disebut infimum (batas bawah terbesar) dari S jika memenuhi kondisi berikut:
(1) w merupakan batas bawah S, dan
(2) jika t adalah sebarang batas bawah S, maka . Ditulis w = inf S
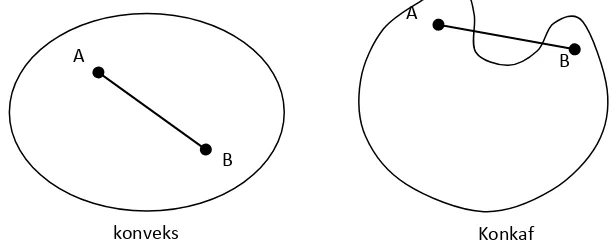
D. Himpunan Konveks
Menurut Mokhtar S Bazaraa (1979:34) konsep konveks sangat penting dalam permasalahan optimasi. Konsep fungsi konveks berhubungan langsung dengan himpunan konveks. Jika adalah fungsi konveks maka
kumpulan titik-titik yang terletak pada membentuk himpunan konveks.
Definisi 2.4 (Mokhtar S Bazaraa, 1979:34)
Perbedaan fungsi konveks dan konkaf tampak pada gambar di bawah ini:
1. Fungsi Konveks
Definisi 2.5 (Mokhtar S Bazaraa, 1979:80)
Diketahui dimana S adalah himpunan konveks yang tidak kosong di . Fungsi dikatakan fungsi konveks di S ketika
untuk setiap dan untuk (0,1).
Fungsi dikatakan fungsi konveks ketat ketika tanda ≥ dapat diganti dengan dan merupakan fungsi konkaf (fungsi konkaf ketat) jika dapat diganti dengan . Untuk fungsi dengan satu variabel ketika fungsi memiliki turunan kedua, maka bersifat konveks jika dan
hanya jika , untuk setiap nilai .
Dapat disimpulkan bahwa:
a. Fungsi konveks jika dan hanya jika , untuk setiap nilai
... (2.16) A
B
Konkaf A
B
[image:19.595.175.483.117.240.2]konveks
b. Fungsi konveks ketat jika dan hanya jika , untuk setiap
nilai .
c. Fungsi konkaf jika dan hanya jika , untuk setiap nilai .
d. Fungsi konkaf ketat jika dan hanya jika , untuk setiap
nilai .
2. Fungsi konveks dan fungsi konkaf dengan banyak variabel
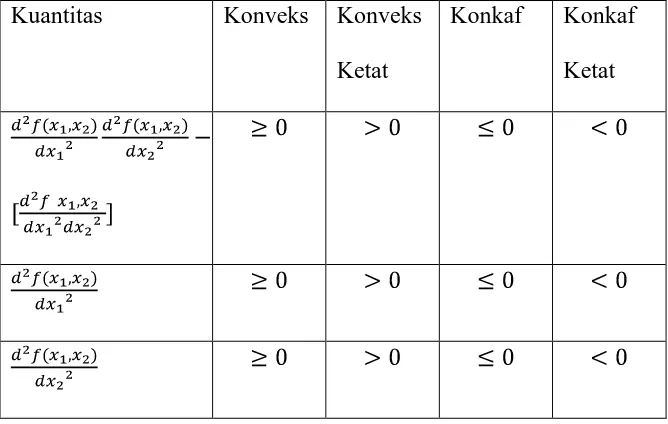
[image:20.595.163.497.413.625.2]Turunan parsial kedua dapat digunakan untuk menguji konveks atau konkafnya suatu fungsi dengan banyak variabel. Sebagai contoh terdapat dua variabel maka untuk mengetahui fungsi konveks atau konkaf seperti pada tabel dibawah ini:
Tabel 1 Fungsi Konveks dan Konkaf Dengan Variabel Banyak Kuantitas Konveks Konveks
Ketat
Konkaf Konkaf Ketat
3. Pseudoconvex
Definisi 2.6 (Mokhtar S Bazaraa, 1979:106)
S bukan himpunan kosong di dan terdiferensial di S. Fungsi dikatakan pseudoconvex ketika untuk setiap dengan
, maka . Ekuivalen dengan ketika
, maka . Fungsi dikatakan
pseduconcave jika adalah pseudoconvex.
Perbedaan pseudoconvex dan bukan pseudoconvex tampak pada Gambar 2 di bawah ini:
(i) Pseudoconvex (ii) bukan pseudoconvex Gambar 2. Perbedaan Pseudoconvex
4. Quasiconvex
Definisi 2.7 (Mokhtar S Bazaraa, 1979:100)
Terdapat dimana S himpunan konveks yang tidak kosong di
. Fungsi dikatakan quasiconvex ketika untuk setiap
, .
Fungsi dikatakan quasiconcave jika – adalah quasiconvex. Dari definisi di atas, fungsi quasiconvex jika
dimana lebih besar atau sama dengan fungsi dari semua kombinasi konveks dan . Fungsi dikatakan quasiconcave jika
dimana fungsi dari semua kombinasi konveks dan lebih besar atau sama dengan .
Perbedaan quasiconvex, quasiconcave dan bukan keduanya tampak pada Gambar 3 di bawah ini:
(i) Quasiconvex (ii) Quasiconcave (iii)Bukan keduanya
Gambar 3. Perbedaan Quasiconvex
5. Closure And Interior Of A Convex Set
Definisi 2.8 (Mokhtar S Bazaraa, 1979:38)
Diketahui S himpunan di , titik dikatakan closure dari dinotasikan
Adapun teorema-teorema yang berkaitan dengan fungsi Konveks dan akan berkaitan dengan syarat Karush Kuhn Tucker antara lain yaitu:
(i) Teorema 2.1 (Mokhtar S Bazaraa, 1979:45)
Jika S himpunan konveks tertutup tak kosong di dan , maka ada vektor taknol p dan skalar α sedemikian sehingga dan
untuk . Bukti:
Karena S himpunan konveks tertutup tak kosong di dan , maka ada titik minimum khusus sedemikian sehingga
untuk . Perhatikan bahwa
(a)
Karena untuk , maka persamaan (a)
menjadi untuk yang lain, dimana
. Terlihat bahwa untuk .
Diperoleh α=sup{ }.
(ii) Teorema 2.2 (Mokhtar S Bazaraa, 1979:48)
Diketahui S himpunan konveks tak kosong di . Jika , maka ada
sebuah hyperplane yang mendukung S pada yaitu ada sebuah vektor taknol p sedemikian sehingga untuk yang lain. Bukti:
Karena , ada sebuah barisan yang bukan pada sedemikian sehingga . Berdasarkan pada Teorema 2.1, berkorespondensi
yang lain. Karena adalah terbatas, sehingga memiliki sebuah subbarisan yang konvergen dengan limit p dengan panjang adalah
sama dengan satu. Mempertimbangkan subbarisan ini memiliki
untuk yang lain. Menentukan dan memilih limit seperti mendekati . Sehingga . Jadi ada hyperplane
yang mendukung S untuk .
(iii)Teorema 2.3 (Mokhtar S Bazaraa, 1979:49)
Jika dan adalah himpunan konveks tak kosong sehingga
, maka ada hyperplane pemisah dan , dan juga ada vektor bukan
nol p di sedemikian sehingga inf{ sup{ . Bukti:
Ada dan .
S= . Perhatikan bahwa S adalah konveks dan karena akan mengakibatkan menjadi tidak kosong. Karena S
adalah himpunan konveks maka ada vektor p bukan nol dimana p sedemikian sehingga untuk setiap . Ini berarti
untuk setiap dan (iv) Epigraph (Epi)
Definisi 2.9 (Mokhtar S Bazaraa, 1979:84)
(v) Teorema 2.4 (Mokhtar S Bazaraa, 1979:85)
Diketahui S himpunan konveks tak kosong di , dan jika
maka fungsi konveks jika dan hanya jika epi adalah himpunan konveks.
Bukti:
Dengan mengasumsikan bahwa adalah konveks, dan jika ( dan
( epi , maka , dan . Untuk
berlaku
Dimana pertidaksamaan di atas mengikuti konvektivitas dan
. Demikian juga karena epi adalah konveks maka epi . Bertentangan dengan asumsi bahwa epi adalah konveks, dan jika maka
dan termasuk dalam epi . Dengan mengikuti konvektivitas
epi maka epi untuk
Dengan kata lain, karena
untuk sehingga adalah konveks.
(vi) Teorema 2.5 (Mokhtar S Bazaraa, 1979:87)
Diketahui S himpunan konveks tak kosong di , dan jika
bagian khusus untuk yang lainnya,sehingga adalah sebuah subgradient dari untuk .
Bukti:
Berdasarkan pada Teorema 2.4, epi adalah konveks. Dilain sisi [ )] menjadi batas dari epi . Dan berdasarkan Teorema 2.2 ada
vektor taknol sedemikian sehingga
untuk semua (a)
Perhatikan bahwa adalah tidak positif karena pertidaksamaan di atas akan terjadi kontradiksi dengan memilih y yang cukup besar. Akan diperlihatkan bahwa , dengan cara kontradiksi, dan didukung oleh
, maka untuk semua Karena , ada
sedemikian sehingga , dan karena
berimplikasi bahwa dan ( . Terjadi kontradiksi dengan ( adalah sebuah vektor taknol. Walaupun begitu,
Menunjukkan oleh dan dengan membagi pertidaksamaan (a)
dengan , diperoleh untuk semua
epi (b)
Secara khusus, hyperplane
didukung epi pada [ )]. Dengan pada persamaan (b),
(vii) Lemma 2.1 (Mokhtar S Bazaraa, 1979:90)
Diketahui S himpunan konveks tak kosong di , dan fungsi
konveks. Jika terdiferensial di maka ada subgradient untuk adalah himpunan tunggal { }.
Bukti:
Karena terdiferensial di dan S himpunan konveks yang tak
kosong, maka subgradient untuk juga tidak kosong. Dimisalkan Ɛ adalah subgradient untuk . Untuk beberapa vektor d dan diperoleh
(a)
(b) Dengan mengurangi persamaan (a) dan (b) dari pertidaksamaan,
diperoleh
Jika membagi persamaan (c) dengan diperoleh
jika atau berdasarkan pada Definisi 2.2 nilai
maka . Untuk d= , sehingga
. Misal sehingga jelas
bahwa . Jadi sehingga .
E. Matriks Hessian
(2.17)
F. Vektor Gradien
Definisi 2.10 (Mokhtar S Bazaraa, 1979:89)
Terdapat S bukan himpunan kosong di dan . dikatakan
terdiferensial di jika ada vektor gradien f(x) yaitu:
x d df x f x f x f x f n . . ) ( 2 1 (2.18)
Suatu fungsi sedemikian sehingga
dengan .
Contoh 2.1 6 8 6 4 2 3 )
( 1 2 1 2
2 2 2
1 x xx x x
x x f
8 4 4 6 4 6 ) ( 2 1 2 1 2 1 x x x x x f x f x f
Dengan memenuhi syarat perlu keoptimalan, yaitu
0
x
f 6x1 4x2 6 0.
0 8 4
4x1 x2
2x1 2 0
x1 1 x2 3
Jadi
3 1 *
x adalah titik optimal dari f x .
G. Titik Kritis
Teorema 2.6 (Edwin J Purcell, 2010:248)
(Teorema Titik Kritis) andaikan fungsi didefinisikan pada selang I yang
memuat titik c. Jika adalah nilai ekstrem, maka haruslah berupa suatu titik kritis, yakni berupa salah satu dari:
(i) Titik ujung dari I
Bukti:
Dengan berupa nilai maksimum pada I , maka untuk
semua dalam I, yaitu . Jadi, jika sehingga , maka
(1)
Sedangkan jika , maka
(2)
Akan tetapi, ada karena c bukan titik singular. Akibatnya, apabila
dalam persamaan (1) dan dalam persamaan (2), maka diperoleh dan . Sehingga dapat disimpulkan bahwa
.
Titik kritis untuk penyelesaian program nonlinear dapat digolongkan sebagai maksimum atau minimum lokal. Maksimum atau minimum global akan diperoleh dengan membandingkan minimum lokal dan maksimum lokal dan kemudian menguji nilai dari fungsi tersebut.
Teorema 2.7 (Hillier, 2001:664)
Jika fungsi diketahui konveks maupun konkaf, maka titik kritis pasti merupakan minimum global maupun maksimum global.
Bukti:
Perhatikan masalah optimisasi berikut Min
Jika S adalah himpunan konveks, adalah fungsi konveks dan adalah titik minimum lokal untuk masalah optimasi maka adalah titik
minimum global dari pada himpunan S.
Misalkan bukan titik minimum global atau titik minimum lokal, maka terdapat yєS yang memenuhi . Sebut saja
yang merupakan kombinasi konveks dari dan y, untuk . Hal ini mengakibatkan , untuk .
Karena adalah fungsi konveks maka berlaku
untuk setiap . Hal ini kontradiksi dengan asumsi bahwa adalah minimum lokal. Dengan demikian haruslah merupakan titik minimum global.
H. Program Nonlinear
menentukan nilai yang merupakan variabel-variabel keputusan dengan fungsi tujuan:
Maksimum / minimum (2.19)
Fungsi kendala: (2.20)
untuk i = 1, 2, ..., m dengan merupakan konstanta tak negatif. Menurut Hillier (2001:664) terdapat 3 bentuk permasalahan program nonlinear, yaitu: 1. Program Nonlinear Tanpa Kendala
Program nonlinear tanpa kendala merupakan optimasi yang tidak memiliki kendala dengan fungsi tujuan berbentuk nonlinear. Bentuk model program nonlinear tanpa kendala untuk menentukan nilai
dengan
Fungsi tujuan: maksimum / minimum (2.21) Untuk menyelesaikan permasalahan program nonlinear tanpa kendala terdapat dua syarat keoptimalan, yaitu:
a. Syarat Perlu Keoptimalan
Syarat perlu keoptimalan digunakan untuk mencari titik-titik
optimal x pada pendekatan analitis. Syarat perlu keoptimalan * mengatakan bahwa :
Bila x* adalah titik optimal dari f(x) maka :
f x* 0 (2.22)
Dengan f(x)merupakan vektor gradien. *
x yang memenuhi
b. Syarat Cukup Keoptimalan
Syarat cukup keoptimalan digunakan untuk menentukan apakah titik optimal yang didapatkan dari syarat perlu keoptimalan merupakan titik minimum atau titik maksimum.
Syarat cukup keoptimalan yaitu :
Bila f x* 0 dan H x* definit positif maka x titik minimum *
...(2.23)
Bila f x* 0 dan H x* definit negatif maka x titik maksimum *
...(2.24)
Contoh 2.2
Suatu fungsi :
( ) 3 2 4 1 2 6 1 8 2 6
2 2 2
1 x xx x x
x x
f :
Pada contoh 2.1 telah didapatkan titik optimal
3 1 *
x dan
didapatkan matrik Hessiannya adalah :
4 4 4 6 ) (x*
Jadi,
3 1 *
x adalah titik minimum dengan
3 6 24 6 12 18 3 * x f
2. Program Nonlinear Dengan Kendala Linear
Program nonlinear dengan kendala linear merupakan optimasi dengan kendala berbentuk fungsi linear dan fungsi tujuan berupa fungsi nonlinear. Untuk menentukan nilai dengan bentuk umum adalah:
Maksimum / minimum : (2.25)
dengan kendala : (2.26)
untuk m=1,2,..., n.
3. Program Nonlinear Berkendala
Menurut Taha (2007:699) program nonlinear berkendala merupakan masalah optimasi dengan fungsi tujuan nonlinear dan fungsi kendala nonlinear. Program nonlinear berkendala dibedakan menjadi dua yaitu:
a. Untuk bentuk umum program nonlinear dengan kendala kesamaan (equality) adalah
Fungsi tujuan : Maksimum / minimum : (2.27)
Fungsi kendala : (2.28)
dimana menunjukkan jumlah kendala dan menunjukkan jumlah variabel dengan .
Maksimum / minimum : (2.29) dengan kendala : 0 untuk i = 1, 2, ..., n (2.30)
I. Matriks Definit Positif dan Definit Negatif
Ada dua pendekatan/cara untuk menentukan apakah suatu matriks persegi merupakan matriks definit positif atau matriks definit negatif atau tidak definit. Pendekatan pertama lebih bersifat teoritis, seperti dijelaskan berikut ini.
Definisi 2.11 (Howard Anton, 1995:320)
A matriks persegii (nxn), maka secara teoritis berlaku :
a. A disebut Definit Positif x Rn
b. A disebut Definit Negatif x Rn
c. A disebut Semi Definit Positif x Rn
Didefinisikan suatu matriks persegi A
Didefinisikan minor – minor utama dari matriks A adalah sebagai berikut :
11 1 a A 22 21 12 11 2 a a a a A 33 32 31 23 22 21 13 12 11 3 a a a a a a a a a A
Sehingga cara/pendekatan kedua untuk menentukan kedefinitan suatu matriks adalah sebagai berikut :
a. A disebut Definit Positif det , i= 1, 2, ..., n (2.31)
b. A disebut Definit Negatif det , i= 1, 2, ..., n (2.32)
c. A disebut Semi Definit Positif det 0, i= 1, 2, ..., n (2.33)
Contoh 2.3
Diketahui matriks
4 4
4 6
H dan dan adalah minor-minor matriks
H. Determinan minor – minor matriks H adalah
det H1 6 6 > 0
det 24 16 8
4 4
4 6 2
H > 0. Jadi, matriks H adalah Definit Positif
J. Pengali Lagrange (Lagrange Multiplier)
Menurut Purcell dan Varberg (1987:303) fungsi lagrange digunakan untuk menyelesaikan permasalahan optimasi (penentuan harga ekstrim), dimana terdapat batasan-batasan (constrains) tertentu.
1. Satu Pengali Lagrange
Prinsip dari metode ini adalah mencari harga ekstrim (optimasi) suatu fungsi objektif dengan batasan-batasan tertentu yang harus dipenuhi, yaitu .
Cara: dibentuk Fungsi Lagrange
Dengan syarat ekstrim:
, dan
2. Lebih dari satu pengali Lagrange
Jika pengali Lagrange melibatkan lebih dari satu kendala, maka penggunaan parameter yang dipilih dapat ditambahkan menjadi , atau
parameter yang lain.
Misalnya untuk memperoleh nilai ekstrim dengan kendala dan maka fungsi Lagrangenya adalah:
Cara penyelesaiannya adalah
, , dan
Metode ini dapat diperluas untuk n variabel dengan k kendala
, ,...,
Sebagai Fungsi Lagrangenya adalah:
Dengan cara penyelesaiannya adalah:
,
Dengan adalah pengali Lagrange.
K. Persyaratan Karush Kuhn Tucker (KKT)
berkendala baik itu permasalahan linear ataupun nonlinear. Menurut Mokhtar S Bazaraa (1979:123) untuk fungsi konveks, syarat perlu dan syarat cukup untuk mencari titik optimum dapat menggunakan syarat Karush Kuhn Tucker. Tetapi untuk fungsi nonkonveks, syarat Karush Kuhn Tucker merupakan syarat perlu saja, akan tetapi belum cukup untuk mencapai nilai optimal. Jadi untuk fungsi konveks, syarat Karush Kuhn Tucker menjadi syarat perlu dan syarat cukup untuk mencapai nilai minimum \ maksimum global.
Adapun teorema-teorema dan definisi yang berkaitan dengan syarat Karush Kuhn Tucker antara lain yaitu:
1) Definisi 2.12 (Mokhtar S Bazaraa, 1979:124)
d adalah descent direction untuk apabila ada d yang memenuhi dan ada dan є(0, sedemikian sehingga
.
2) Definisi 2.13 (Mokhtar S Bazaraa, 1979:127)
Jika S bukan himpunan kosong di En, dan єcl S. Cone of feasible
direction dari S untuk , dinotasikan dengan D, diberikan oleh
untuk setiap dan Vektor bukan nol yang lainnya disebut feasible direction. 3) Teorema 2.8 (Mokhtar S Bazaraa, 1979:128)
meminimumkan dengan kendala .
Diketahui dan S himpunan tak kosong di dan
, dimana dan D adalah cone feasible direction S untuk
Bukti:
Dengan cara kontradiksi, andai , ada d , berarti d dan d .
Berdasarkan pada Definisi 2.12, maka ada , sehingga
untuk є(0, (a)
Dan juga berdasarkan pada Definisi 2.13, maka ada sehingga
untuk є(0, . (b)
Dari persamaan (a) dan (b) jelas ada dan
. Hal ini bertentangan dengan asumsi awal bahwa adalah solusi optimum lokal. Jadi
4) Teorema 2.9 (Mokhtar S Bazaraa, 1979:129) Diketahui:
untuk , dan himpunan terbuka yang tidak kosong di . Mempertimbangkan permasalahan meminimumkan
dengan kendala untuk , dan . adalah titik yang mungkin, dan diketahui . Dengan dan untuk
terdiferensial di dan untuk adalah kontinu di . Jika adalah solusi optimum lokal, maka , dimana
Bukti:
Dengan dan dimana adalah himpunan terbuka,
berdasarakan pada Definisi 2.13 maka ada sehingga
untuk є(0, (a)
Karena dan adalah kontinu di untuk ada sehingga
karena dan untuk
є(0, dan (b)
Karena , <0 untuk dan dengan Definisi 2.2, ada sehingga
untuk є(0, dan (c)
Dari persamaan (a), (b), dan (c) diperoleh bahwa adalah solusi yang mungkin dari permasalahan P untuk є(0, , dimana =
minimum ( ). Jelas bahwa untuk sembarang
berimplikasi dengan , sehingga Berdasarkan pada Teorema
2.8, karena adalah solusi lokal untuk permasalahan P, dan . Karena diketahui sehingga . Karena jelas bahwa
.
5) Teorema 2.10 (Mokhtar S Bazaraa, 1979:140)
Diketahui X himpunan tak kosong di , , untuk
, dan untuk . Masalah P
dinyatakan dalam bentuk
Dengan kendala : , dengan , dengan
solusi optimum lokal dari masalah P, . Diketahui untuk kontinu di , dan , untuk terdiferensial di , dan
untuk terdiferensial kontinu di . Jika untuk adalah bebas linear, maka
, dimana
untuk
untuk Bukti:
Dengan cara kontradiksi, andai , ada
sedemikian sehingga , untuk dan
dimana adalah sebuah matriks yang berukuran yang mana kolom th tersebut adalah . Untuk , didefinisikan dengan mengikuti persamaan diferensial dan syarat batas:
(a)
(b)
Dimana adalah matriks yang dibangun untuk beberapa vektor di
mempunyai rank yang sempurna dan adalah terdiferensial secara kontinu di , sehingga adalah kontinu di . Karena kontinu maka integralnya juga kontinu seperti pada persamaan (b) sehingga
dan .
Untuk dan cukup kecil, adalah kemungkinan dan dan dari persamaan (a), diperoleh:
(b)
Untuk yang lain. Pada khususnya, adalah ruang null di , sehingga untuk diperoleh . Oleh sebab itu dari persamaan (b) dan diketahui bahwa , diperoleh:
(c)
Untuk yang lain. Hal ini berimplikasi dengan untuk dan cukup kecil. Untuk , , dan adalah kontinu di , dan untuk yang cukup kecil. adalah terbuka, untuk yang cukup kecil. Karena sudah terpenuhi, maka hanya perlu membuktikan bahwa . Dengan teorema nilai rata-rata, diperoleh:
(d)
Dengan petunjuk, adal di ruang null dari dan dari persamaan di atas, diperoleh . Subtitusikan ke persamaan
(d), dan mengikuti . Karena benar untuk yang lain, hal ini mengikuti adalah solusi yang mungkin dari permasalahan P untuk yang cukup kecil. Sehingga persamaan (c) diperoleh:
Dan karena untuk dan cukup kecil. Hal ini bertentangan dengan adalah solusi optimum lokal. Jadi
6) Teorema 2.11 (Mokhtar S Bazaraa, 1979:142)
(The Fritz John Conditions) Diketahui himpunan tak kosong di ,
, untuk , dan untuk
. Masalah P dinyatakan dalam bentuk
Minimum :
Dengan kendala : , dengan
, dengan
solusi yang mungkin dari masalah P, . Diketahui
pula untuk kontinu di , dan , untuk terdiferensial di , dan untuk terdiferensial kontinu di .
untuk
Dengan adalah vektor yang komponennya ada untuk dan
. Selanjutnya, jika untuk yang terdiferensial di , maka Fritz John Condition dengan bentuk dan
dapat ditulis menjadi:
untuk untuk
Bukti:
Ketika untuk adalah bergantung linear, maka ada
yang tidak nol, sedemikian sehingga .
Dimana untuk sama dengan nol, kondisi pada bagian pertama trivial.
Ketika untuk adalah bebas linear. Jika adalah
sebuah matriks dimana baris matriksnya berupa dan
untuk . Dan adalah sebuah matriks dimana baris matriksnya berupa untuk .Sehingga dari Teorema 2.10, solusi lokal dari berimplikasi dengan
sehingga menjadi tidak konsisten karena tidak didefinisikan secara jelas seperti pada Teorema 2.10.
Diberikan dua himpunan sebagai berikut:
Dimana dan adalah himpunan konveks tak kosong sehingga
, berdasarkan pada Teorema 2.3 maka ada vektor tak nol dan sehingga
untuk dєEn dan ( .
Diketahui untuk . dimana dan maka dapat dipilih angka negatif besar. Dan juga ( . Sehingga
diperoleh . Jika , hal ini
mengikuti , dan .
Ada vektor tak nol dengan sehingga
. Hal ini menunjukkan oleh dan , dan = . Bukti selesai.
7) Teorema 2.12 (Mokhtar S Bazaraa, 1979:146)
(Teorema Syarat Perlu Kuhn Tucker) Menurut Mokhtar S Bazaraa (1979:146) jika x bukan himpunan kosong di dan ,
untuk i=1, ..., m dan dengan bentuk umum
dengan kendala : , dengan i=1,2,..., m (2.36) , dengan i=1,2,..., l (2.37)
Dimana adalah variabel keputusan, adalah fungsi tujuan dan , adalah fungsi kendala. Misalkan fungsi , ,
adalah fungsi kontinu dan terdiferensial. Diasumsikan
merupakan solusi yang mungkin, dimana dan
saling bebas linear. Maka terdapat skalar ,
sedemikian sehingga
(2.38)
untuk i= 1, ..., m (2.39) Dengan kendala
untuk i=1,..., m (2.40)
untuk j=1, ..., p (2.41)
Dengan kata lain syarat perlu Kuhn Tucker yaitu nilai turunan pertama dari fungsi objektif maupun fungsi kendala akan sama dengan nol. Dari persamaan di atas dapat didefinisikan persamaan Lagrange sebagai berikut:
(2.42)
Bukti:
Perhatikan bahwa , karena jika maka akan terjadi
kontradiksi dengan asumsi bebas linear dan . Hasil pertama
lalu diikuti dengan nilai dan . Bentuknya sama dengan
kondisi perlu dengan nilai . Sehingga kondisi Kuhn Tucker dapat dinyatakan dalam bentuk sebagai berikut
8) Teorema 2.13 (Mokhtar S Bazaraa,1979:147)
(Teorema Syarat Cukup Kuhn Tucker) Menurut Mokhtar S Bazaraa (1979:146) jika x bukan himpunan kosong di dan , untuk i=1, ..., m dengan permasalahan bentuk umum P adalah
minimum : (2.43)
dengan kendala : , dengan i=1,2,..., m (2.44) , dengan i=1,2,..., l (2.45) Dimana adalah variabel keputusan, adalah fungsi
tujuan dan , adalah fungsi kendala.
Misalkan fungsi pseudoconvex, adalah quasiconvex terdiferensial. Diasumsikan merupakan solusi yang mungkin dan merupakan solusi optimum global, dimana ada yang merupakan skalar nonnegative sedemikian sehingga
Dengan kata lain, jika , adalah konveks dan karena keduanya pseudoconvex dan quasiconvex, maka kondisi Kuhn Tucker menjadi
cukup. Bukti:
Misal x adalah solusi yang mungkin dari permasalahan P. Untuk ,
karena dan . Dengan quasiconvexity dari untuk dan mengikuti
Untuk setiap . Hal ini berimplikasi bahwa bukan penambahan dengan mengganti dari sepanjang arah , sehingga
, untuk (a)
Dengan cara yang sama, karena adalah quasiconvex untuk dimana
dan adalah quasiconcave untuk dimana , sehingga
, untuk (b)
, untuk (c)
Dengan mengalikan persamaan (a), (b) dan (c), dan nilai , , dan penambahan, diperoleh
Dengan mengalikan persamaan (2.40) dengan dan tanpa ,
Dengan pseudoconvexity dari untuk , sehingga , dan terbukti.
Definisi 2.14 Hillier (2001:680)
Diasumsikan merupakan fungsi tujuan dan
merupakan fungsi kendala yang dapat diturunkan maka
merupakan nilai optimal untuk permasalahan program nonlinear hanya jika terdapat sejumlah m bilangan sehingga semua syarat kondisi KKT (Karush Kuhn Tucker) terpenuhi:
(i) pada untuk j=1, 2, ..., n (2.47)
(ii) pada untuk j=1, 2, ..., n (2.48)
(iii) untuk i= 1, 2, .., m (2.49)
(iv) untuk i=1, 2, ..., m (2.50)
(v) untuk j=1, 2, ..., m (2.51)
(vi) untuk j=1, 2, ..., m (2.52)
Dari kondisi (ii) dan (iv) memerlukan hasil kali dua kuantitas sama dengan nol. Oleh karena itu, setiap kondisi ini menyatakan bahwa setidaknya salah satu dari kuantitas harus sama dengan nol. Hal ini berakibat kondisi (iv) dapat dikombinasi dengan kondisi (iii), sehingga dapat dinyatakan dalam bentuk lain sebagai berikut:
atau (2.53)
atau (2.55)
jika untuk j= 1, 2, ..., m (2.56)
Contoh 2.4: Maksimum
dengan kendala , ,
Kondisi KKT untuk contoh di atas yaitu:
1. Untuk j=1,
Untuk j=2,
2. Untuk j=1,
Untuk j=2,
3. 4.
5. ,
6.
Langkah penyelesaian kondisi KKT untuk contoh di atas: 1. , dari kondisi 1 (j=2)
, dari kondisi 5.
2.
3. , dari kondisi 2 (j=1)
4. , berimpilkasi dari kondisi 4
6. , berimplikasi dari kondisi 2 (j=2) 7. Tidak ada kondisi yang dilanggar oleh
Sehingga diperoleh solusi atau x*=(0,3).
L. Metode Kuadratik
Menurut Mokhtar S Bazaraa (1979:447) metode kuadratik merupakan bentuk khusus dari program nonlinear yang memiliki fungsi tujuan berbentuk kuadratik dan kendala linear.
Bentuk umum dari model kuadratik yaitu:
Minimum (2.57)
dengan kendala (2.58)
Dimana:
: vektor kolom dari fungsi tujuan
: matriks kendala
: matriks kolom dari variabel keputusan
: vektor kolom dari kendala bagian kanan
: matriks Hessian
Notasi dari perkalian vektor Lagrange dengan kendala dan
oleh dan . Notasi dari variabel slack yaitu , sehingga kondisi KKT dapat dinyatakan sebagai:
(2.59)
(2.60)
(2.61)
diperoleh:
(2.62)
M. Permasalahan Komplementaritas Linear (The Linear Complementary Problem)
Kondisi KKT dan model kuadratik dapat dinyatakan dalam permasalahan komplementaritas, dengan algoritma ini dapat digunakan untuk menyelesaikan permasalahan nonlinear dengan metode kuadratik.
Definisi 2.15 (Mokhtar S Bazaraa,1979:438)
Jika M adalah sebuah matrik berukuran pxp, dan q merupakan vektor p. Permasalahan komplementaritas linear untuk menentukan vektor w dan z yaitu:
, untuk j= 1, 2, ..., p (2.64)
untuk j= 1, 2, ..., p (2.65)
Dimana:
( ) : variabel komplemen
q : vektor kolom
M : matriks pxp yang diketahui.
Algoritma yang efisien telah dikembangkan untuk memecahkan permasalahan komplemen linear dengan asumsi pada matriks M. Algoritma yang digunakan yaitu pemutaran (pivoting) dari satu solusi BF (Basic Feasible) ke solusi selanjutnya, seperti pada metode simpleks dalam program
linear. Jika q bilangan nonnegative dengan dan , maka penyelesaian dari (1), (2), (3) yaitu:
(2.66)
, , untuk j= 1, 2, ..., p (2.67)
untuk j= 1, 2, ..., p (2.68)
N. Langkah-langkah Penyelesaian Metode Kuadratik
a. Menentukan turunan dari fungsi tujuan.
b. Menentukan matriks Hessian seperti pada persamaan (2.17).
c. Menentukan Persyaratan Karush Kuhn Tucker (KKT)
Berdasarkan pada Definisi 2.14 diperoleh persyaratan Karush Kuhn Tucker sebagai berikut:
(i) pada untuk j=1, 2, ..., n
(ii) pada untuk j=1, 2, ..., n
(iii) untuk i= 1, 2, .., m
(iv) untuk i=1, 2, ..., m
(v) untuk j=1, 2, ..., n
(vi) untuk j=1, 2, ..., m
d. Menyatakan permasalahan dalam bentuk umum model kuadratik seperti pada persamaan (2.57), dimana komponen-komponen pembentukan model kuadratik seperti pada persamaan (2.60).
sehingga
Model umum Kuadratik yaitu meminimumkan
Dengan kendala
e. Mengubah kondisi Karush Kuhn Tucker yang berbentuk pertidaksamaan menjadi persamaan dengan menambah slack variabel.
Untuk mengubah pertidaksamaan pada persyaratan Karush Kuhn Tucker kondisi (i) dan (iii) menjadi persamaan yaitu dengan
memindahkan konstanta ke sisi sebelah kanan dan menambahkan slack variabel nonnegative yang dilambangkan dengan .
(i)
f. Menentukan kendala komplementaritas.
Kendala komplementaritas diperoleh dengan mensubstitusikan hasil perhitungan point e pada kondisi Karush Kuhn Tucker yang berbentuk persamaan yaitu kondisi (ii) dan kondisi (iii).
(ii)
(iii) .
Setiap pasang , ..., dan merupakan variabel
komplementer karena hanya satu dari dua variabel tersebut yang dapat bernilai nol. Kendala komplementer tersebut digabung menjadi satu kendala yaitu:
g. Membentuk permasalahan komplementaritas dengan menambah variabel artificial.
Model kuadratik pada persamaan (2.57) telah ditransformasi menjadi model linear, sehingga fungsi tujuan yang akan diselesaikan dengan metode simpleks yaitu:
meminimumkan dimana
dengan semua kendalanya yaitu:
, , , ,
h. Menyatakan persamaan komplementer dalam bentuk matriks.
Meminimumkan
Dengan kendala:
i. Menyelesaikan model linear dengan metode simpleks.
Secara komputasi perhitungan dapat diselesaikan dengan bantuan QSB.
O. Program Linear
1. Pengertian Program Linear
persoalan secara matematis. Menurut Zulian Yamit (1991:1), syarat-syarat yang harus dipenuhi agar suatu persoalan dapat dipecahkan dengan program linear secara lengkap sebagai berikut:
a. Fungsi tujuan harus didefinisikan secara jelas dan dinyatakan sebagai fungsi obyektif yang linear.
b. Fungsi tujuan dan fungsi kendala dinyatakan dalam hubungan linear. c. Variabel keputusan harus positif.
d. Sumber-sumber dan aktifitas mempunyai sifat dapat dibagi, artinya solusi tidak harus merupakan bilangan integer (bilangan bulat).
e. Sumber-sumber dan aktifitas mempunyai jumlah yang terbatas.
f. Aktifitas harus proporsional terhadap sumber-sumber, artinya adanya proposionalitas dalam fungsi tujuan dan fungsi kendala.
g. Model programming deterministik , artinya sumber dan aktifitas diketahui secara pasti.
2. Model Program Linear
Menurut Zulian Yamit (1991:2), untuk menyelesaikan permasalahan optimasi dengan program linear, hal pertama yang dilakukan adalah mengidentifikasi masalah kemudian membuat model matematis dari masalah tersebut. Langkah-langkah yang dilakukan untuk merumuskan model program linear adalah
b. Tentukan batasan dari variabel keputusan, dan nyatakan dalam bentuk persamaan linear atau ketidaksamaan linear.
c. Tentukan tujuan yang akan dicapai dari variabel keputusan.
Menurut B. Susanta (1994: 6), model program linear secara umum adalah
Mencari dengan tujuan:
Memaksimumkan/meminimumkan:
(2.69)
dengan kendala :
. . . . . . . . .
, ,
Keterangan:
: fungsi tujuan : variabel keputusan
: koefisien teknis (koefisien dalam kendala utama)
: suku tetap
: koefisien biaya (koefisien dalam fungsi tujuan)
Perumusan di atas dapat ditulis sebagai berikut: mencari , j=1,2,...,n
mak/min (2.70)
dengan kendala , i=1,2,...,m
Fungsi tujuan pada rumusan program linear di atas yaitu merupakan tujuan yang akan dicapai atau dioptimalkan. Selanjutnya, persamaan atau pertidaksamaan yang merepresentasikan keterbatasan atau kendala yang membatasi pencapaian fungsi tujuan dinamakan fungsi kendala. Untuk m kendala pertama disebut kendala utama. Syarat bahwa nilai variabel keputusan harus lebih dari atau sama dengan nol ( ) dinamakan kendala-kendala tidak negatif.
Rumusan program linear di atas menunjukkan bahwa setiap kendala dapat berbentuk kendala pertidaksamaan atau persamaan.
Menurut B. Susanta (1994: 81-82), terdapat tiga jenis bentuk masalah program linear sebagai berikut:
a) Masalah program linear berbentuk kanonik yaitu masalah program linear yang semua kendala utamanya berbentuk persamaan.
Mencari , j = 1, 2, ..., n dengan tujuan:
memaksimumkan (atau meminimumkan) (2.71)
dan memenuhi susunan kendala berikut: = , i=1,2,...,m
b) Masalah program linear berpola maksimum yaitu masalah program linear yang memaksimumkan fungsi tujuan dengan model sebagai berikut:
Mencari , j = 1, 2, ..., n
yang memaksimumkan (2.72)
dengan kendala ( ≥, ≤, =) , i=1,2,...,m
x=1,2,...,n.
Jika relasi setiap kendala utama pada masalah program linear berpola maksimum adalah kurang dari atau sama dengan (≤), maka disebut
model berpola maksimum baku.
c) Masalah program linear berpola minimum yaitu masalah program linear yang meminimumkan fungsi tujuan dengan model sebagai berikut:
Mencari , j = 1, 2, ..., n
yang meminimumkan (2.73)
dengan kendala: ( ≥, ≤, =) , i=1,2,...,m
, x=1,2,...,n.
Contoh 2.5
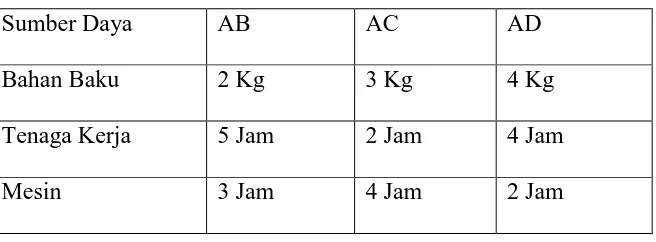
[image:64.595.151.479.355.476.2]Sebuah perusahaan sedang mencari alternatif kombinasi produksi dari produk yang dihasilkan, agar memperoleh keuntungan yang maksimum. Pada saat ini perusahaan memproduksi 3 jenis produk yang diberi merek AB, AC dan AD. Ketiga produk tersebut dibuat dengan menggunakan sumber daya berupa: bahan baku, mesin, tenaga kerja. Bagian penelitian dan pengembangan hasil produksi memberikan informasi bahwa untuk membuat ketiga jenis produk setiap unitnya memerlukan sumber daya seperti terlihat dalam tabel berikut ini:
Tabel 2. Sumber daya produksi
Sumber Daya AB AC AD
Bahan Baku 2 Kg 3 Kg 4 Kg
Tenaga Kerja 5 Jam 2 Jam 4 Jam
Mesin 3 Jam 4 Jam 2 Jam
a. Menentukan variabel keputusan
Aktivitas yang diketahui adalah produksi bulanan dari ketiga jenis produk.
Misalkan: x adalah banyak produksi bulanan dari jenis AB y adalah banyak produksi bulanan dari jenis AC
z adalah banyak produksi bulanan dari jenis AD
b. Menentukan batasan/kendala
Untuk setiap unit produk jenis AB memerlukan 2 Kg bahan baku, sehingga untuk x unit produk AB memerlukan bahan baku. Model AC memerlukan dan model AD memerlukan . Dengan demikian kebutuhan bahan baku secara total ketiga jenis produk tersebut adalah yang tidak boleh melebihi 200 Kg. Demikian pula halnya untuk sumber daya jam tenaga kerja dan jam kerja mesin. Apabila ketiga batasan tersebut dibuat dalam satu set fungsi linear, akan berbentuk sebaagai berikut:
bahan baku tenaga kerja
jam mesin
c. Menentukan tujuan yang akan dicapai
Dari ketiga langkah tersebut, diperoleh model linearnya adalah Maksimum
Dengan batasan / kendala 1)
2) 3)
untuk harga .
3. Operasi Elementer
Operasi elementer dibutuhkan untuk mengetahui langkah-langkah penyelesaian pada metode simpleks.
Definisi 2.16 (Howard Anton, 1995: 5)
Operasi elementer adalah operasi yang dilakukan pada suatu matriks. Langkah-langkah operasi elementer yaitu:
1) Mengalikan sebuah baris atau kolom dengan sebuah konstanta yang tidak sama dengan nol.
2) Mempertukarkan dua baris atau kolom.
3) Mengalikan suatu baris atau kolom dengan sebuah konstanta yang tidak nol, kemudian ditambahkan pada baris atau kolom yang lain. Contoh 2.6
Diberikan contoh penerapan operasi elementer pada sebuah matriks. Misal terdapat matriks A sebagai berikut:
4. Metode Simpleks
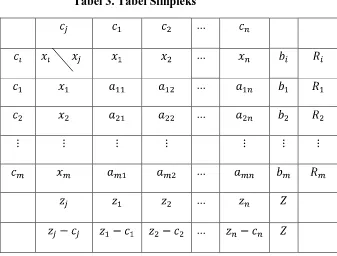
Tabel 3. Tabel Simpleks ...
...
...
...
...
...
...
Keterangan:
: perubah-perubah lengkap
: koefisien teknis (koefisien dalam kendala utama)
: suku tetap (tak negatif)
: koefisien biaya (koefisien dalam fungsi tujuan)
: perubah yang menjadi basis dalam tablo yang ditinjau : koefisien ongkos milik perubah basis
: (hasil kali dari dengan kolom )
: (hasil kali dari dengan )
: selisih zj dengan cj
Berikut diberikan langkah-langkah penyelesaian model program linear menggunakan metode simpleks menurut B. Susanta(1994: 87-108):
1) Langkah Awal: Membuat Tabel Awal Simpleks
Langkah awal metode simpleks adalah mengubah bentuk model masalah program linear yang ada ke bentuk kanonik, kemudian memasukkan masalah tersebut pada tabel awal simpleks yang disusun seperti Tabel Simpleks pada Tabel 3. Variabel slack dan artificial menjadi variabel basis karena variabel-variabel ini berada dalam matriks identitas dengan koefisien . Apabila ada penambahan variabel slack, surplus, dan artificial pada suatu model maka dibuat fungsi tujuan baru, yaitu fungsi tujuan yang memuat variabel-variabel tersebut. Koefisien biaya variabel slack dan surplus adalah nol, variabel artificial adalah –M untuk kasus memaksimumkan dan +M untuk kasus meminimumkan fungsi tujuan. M mewakili suatu bilangan yang sangat besar.
2) Langkah Kedua: Menguji Keoptimuman Penyelesaian
Langkah kedua ini bertujuan untuk memeriksa penyelesaian yang diperoleh tabel simpleks pada suatu iterasi. Suatu penyelesaian layak basis masalah program linear kasus memaksimumkan fungsi tujuan dikatakan telah optimum apabila , sedangkan
penyelesaian yang diperoleh tabel pada suatu iterasi telah optimum, maka langkah metode simpleks berhenti. Namun, apabila penyelesaian yang diperoleh belum optimum, tabel simpleks perlu diperbaiki untuk memperoleh penyelesaian yang lebih baik yaitu penyelesaian yang lebih mengoptimumkan fungsi tujuan. Memperbaiki tabel simpleks ini merupakan langkah ketiga dari metode simpleks.
3) Langkah Ketiga: Memperbaiki tabel
Tahap ini bertujuan untuk membuat tabel simpleks baru yang menghasilkan penyelesaian yang lebih baik dari tabel sebelumnya. Hal tersebut dilakukan dengan cara memilih satu variabel non-basis untuk dijadikan variabel basis baru pada tabel simpleks baru yang akan dibuat dan pemilihan satu variabel basis yang keluar dari basiskarena akan digantikan oleh variabel basis baru yang terpilih. Setelah diperoleh tabel baru dilanjutkan menguji keoptimuman penyelesaian. Apabila penyelesaiannya telah optimal maka iterasi dihentikan, tetapi apabila penyelesaiannya belum optimal maka dilanjutkan langkah ketiga yaitu tahap memperbaiki tabel. Variabel non-basis yang menjadi variabel basis untuk kasus memaksimumkan fungsi tujuan adalah variabel non-basis pada kolom ke-k yang memiliki nilai paling kecil (j = 1, 2, ..., n). Pada kasus
meminimukan, variabel non-basis dari kolom ke-k yang memiliki
kolom yang memiliki nilai yang sama, maka dapat dipilih
salah satu diantaranya secara acak. Selanjutnya kolom yang terpilih tersebut dinamakan kolom kunci.
Variabel basis yang harus keluar baik pada kasus memaksimumkan atau meminimumkan fungsi tujuan adalah sama yaitu variabel yang diperoleh dari baris yang terkecil. Nilai
diperoleh dari perhitungan berikut: dengan . Baris
yang terpilih dinamakan sebagai baris kunci. Unsur yang menjadi perpotongan kolom dan baris kunci dinamakan unsur kunci, yang digunakan untuk memperbaiki tabel. Nilai unsur kunci ini harus dibuat sama dengan 1 dan nilai-nilai lainnya pada kolom yang sama harus nol dengan melakukan beberapa kali operasi baris elementer. 5. Langkah-langkah pada QSB
QSB digunakan untuk membantu perhitungan permasalahan portofolio optimal. Dimana fungsi dari QSB sama dengan metode simpleks. Hanya saja perhitungan dengan QSB menggunakan program, sedangkan untuk metode Simpleks secara manual. Langkah-langkah pada QSB secara lengkap dapat dilihat pada Lampiran III.
a. Buka Program QSB .
b. Pilih Linear Programming .
e. Menginput hal-hal yang akan ditinjau seperti: fungsi tujuan, banyaknya kendala, banyaknya variabel, dll.
f. Menginput variabel.
g. Menginput data permasalahan seperti fungsi tujuan dan fungsi kendala.
h. Menentukan Solusi Permasalahan. Ada beberapa pilihan seperti solusi per langkah, ataupun solusi akhirnya.
i. Solusi akhir dari permasalahan.
Berikut diberikan contoh penyelesaian persamaan nonlinear dengan metode kuadratik.
Contoh 2.8 :
Diketahui fungsi tujuan:
Meminimumkan
Dengan kendala
Penyelesaian:
a. Menentukan turunan parsial dari fungsi tujuan.
b. Menentukan matriks Hessian seperti pada persamaan (2.17).
Det H
Jadi matriks H adalah definit positif
Nilai dari dan
Jadi fungsi merupakan fungsi konkaf.
c. Menentukan persyaratan Karush Kuhn Tucker 1. Untuk j=1,
Untuk j=2,
2. Untuk j=1, Untuk j=2, 4.
5.
6. ,
7.
Dari soal diatas diperoleh
Sehingga model umumnya yaitu meminimumkan
Dengan kendala
e. Mengubah kondisi Karush Kuhn Tucker yang berbentuk pertidaksamaan menjadi persamaan dengan menambah slack variabel.
Untuk mengubah pertidaksamaan pada kondisi KKT 1. untuk , dan kondisi 3 menjadi persamaan yaitu dengan memindahkan konstanta ke sisi sebelah kanan dan menambahkan slack variabel nonnegative yang dilambangkan dengan .
Untuk j=2,
3.
f. Menentukan kendala komplementaritas.
Perhatikan kondisi 2 untuk j=1 dan dari point (e) untuk j=1, sehingga
Nilai yang memenuhi yaitu atau
Dengan cara yang sama, kondisi 1untuk j=2 dan dari point (e) untuk j=2, sehingga
Nilai yang memenuhi yaitu atau
Dengan cara yang sama untuk kondisi 4 dapat dinyatakan sebagai berikut:
Nilai yang memenuhi yaitu atau
Setiap pasang , , dua variabel tersebut merupakan variabel komplementer karena hanya satu dari dua variabel tersebut yang dapat bernilai nol. Bentuk baru kondisi 2 untuk (j=1), kondisi 2 untuk (j=2) dan 4 dapat digabung menjadi satu kendala yaitu:
Dengan mengalikan -1 pada kondisi 1 untuk (j=1) dan untuk (j=2) untuk mendapatkan ruas kanan nonnegative, sehingga kondisi secara keseluruhan yaitu:
, , , , ,
g. Membentuk permasalahan komplementaritas dengan menambah variabel artificial.
Permasalahan komplementaritas adalah meminimumkan nilai variabel artificial pada Karush Kuhn Tucker. Masalah program linear yang diselesaikan dengan metode simpleks adalah
Meminimumkan
, , , , , , ,
h. Menyatakan permasalahan komplementaritas dalam bentuk matriks.
i. Menyelesaikan dengan metode simpleks
Tabel berikut menunjukkan hasil dari penerapan metode simpleks untuk menyelesaikan masalah di atas.
Langkah awal:
0 0 0 0 0 0 1 1
B R
1 4 -4 1 -1 0 0 1 0 15 -
1 -4 8 2 0 -1 0 0 1 30
0 1 2 0 0 0 1 0 0 30 15
0 4 3 -1 -1 0 1 1 45
0 3 -1 -1 0 0 0
Iterasi pertama
OBE: ,
0 0 0 0 0 0 1 1
B R
1 2 0 1 -1 -1 0 1 1 30 15
0 1 0 0 0 -
[image:77.595.104.526.206.550.2]0 2 0 0 1 0
2 0 2 -1 -1 0 1 1 30
0 2 -1 -1 0 0 0
Iterasi kedua
OBE: , ,
0 0 0 0 0 0 1 1
B R
1 0 0 -1 -1 1
0 0 1 0 0 75
0 1 0 0 0 -
0 0 -1 -1 1
0 0 -1 -1 0
Iterasi ketiga
OBE: , ,
0 0 0 0 0 0 1 1
b R
2
0 0 0 1
0 0 1
0 1 0 0
0 0 0 0 0
0 0 0 0 0 -1 -1
DAFTAR PUSTAKA
Abdul,Halim. (2005). Analisis Investasi. Jakarta: Salemba Empat.
Amalia. (2009). Peranan Persyaratan Karush Kuhn Tucker Dalam Menyelesaikan Pemrograman Kuadratik. Sumatra Utara: USU.
Anton,Howard. (1987). Aljabar Linear Elementer. Jakarta: Erlangga.
Bazaraa,Mokhtar S. & C.M.Shetty. (1979). Nonlinear Programming. Singapore: John Wiley and Sons.
Bartle, Robert G. (2000). Introduction To Real Analysis. USA: John Willey and Sons.
Birbil,S.I. (2006). An Elementary Proof Of The Fritz John And Karush-Kuhn-Tucker Condition In Nonlinear Programming. European Journal Of Operation Research. vol. 4. No. 012.
Bracken,Jerome&Garth.P.Mc.Cormick. (1968). Selected Aplication of Nonlinear Programming. Virginia: Mc.Lean.
B.Susanta. (1994). Program Linear. Yogyakarta: Departemen Pendidikan dan Kebudayaan Direktorat Jenderal Pendidikan Tinggi.
Eddy,Herjanto. (2007). Manajemen Operasi Edisi Ketiga. Jakarta: Grasindo. Fabozzi,Frank J. (1999). Manajemen Investasi. (Alih B