PEMBAHASAN SOAL UN MATEMATIKA SMP TA 20112012 (Paket A64)

(1)

PEMBAHASAN SOAL UN MATEMATI KA SMP TA 2011/ 2012

Soal ini menguji kemampuan menyelesaikan masalah yang ber kaitan dengan oper asi

tambah, kur ang, kali atau bagi pada bilangan bul at

Alternatif car a penyelesaian:

Operasi perkalian dan pembagian mempunyai hir ar ki yang lebi h ti nggi dibandi ngkan

oper asi penjumlahan dan pengur angan. Bilangan yang ada dalam tanda kurung,

dipri or itaskan untuk dikerjakan ter lebih dahulu, sebelum dioper asikan dengan

bilangan lai n yang ada di luar tanda kurung. Soal ini dapat di selesaikan dengan mudah

sebagai ber ikut:

17−(3 × (−8)) = 17−(−24) = 17 + 24 = 41

Jadi diper ol eh hasil sama dengan 41.

(B)

tambah, kur ang, kali atau bagi pada bilangan pecahan

Operasi perkalian dan pembagian mempunyai hir ar ki yang lebi h ti nggi dibandi ngkan

oper asi penjuml ahan dan pengurangan. Soal i ni dapat disel esaikan dengan mudah

(2)

21

jumlah uang mereka adalah …

A. Rp160.000,00

Per bandingan dua besar an mer upakan suatu pecahan dalam bentuk seder hana yaitu

bentuk atau : , dengan , merupakan bilangan asli, ≠0.

Dar i soal diketahui per bandingan uang Wati dan uang Dini adalah1: 3 dan selisi h uang

Wati dan Dini adal ah Rp120.000,00.

Selisih per bandingan uang Wati dan uang Dini adal ah 3−1 = 2

Jumlah perbandingan uang Wati dan uang Dini adalah 3 + 1 = 2

Jumlah uang Wati dan uang Dini adalah 4

2× 120.000 = 240.000

Jadi jumlah uang mer eka adal ah Rp240.000,00.

(C)

Soal ini menguji kemampuan menyelesaikan masalah yang ber kaitan dengan bil angan

(3)

Soal ini menguji kemampuan menyelesaikan masalah yang ber kaitan dengan bil angan

dal am bentuk akar .

Dengan menggunakan si fat pada bi langan bentuk akar yaitu

a) _√ ×√ =√

setahun. Tabungan kakak saat di ambi l sebesar Rp920.000,00. Lama menabung adalah

….

(4)

Ada dua jeni s bunga yai tu

a. Bunga tunggal, jika yang mendapat bunga hanya modalnya saja sedangkan

bunganya tidak ber bunga lagi

b. Bunga majemuk, ji ka yang mendapat bunga tidak hanya modalnya saja tetapi

bunganya juga akan ber bunga lagi

Dar i soal diketahui bahw a besarnya modal adalah Rp800.000,00 dan bunga dalam

setahun adalah 9% = 9% × 800000 = 72000

Bunga dal am setahun sebesar Rp72.000,00

Sehingga bunga dal am satu bulan sebesar 72000

12 = 6000

Bunga dal am satu bulan sebesar Rp6.000,00

Ji ka kakak mengambi l tabungan sebesar Rp920.000,00 maka selisih tabungan kakak

dengan modal sebesar 920000−800000 = 120000

Jadi pada saat kakak mengambi l tabungan sebesar Rp920.000,00 lama menabung

kakak adalah 120000

6.000 × 1 bulan = 20 bulan.

Soal ini menguji kemampuan menyelesaikan masal ah yang ber kaitan dengan bar isan

bilangan dan deret.

Dar i soal diketahui bar i san bil angan yai tu 3, 4, 6, 9 ,…, … kemudian dicar i dua suku

ber ikutnya. Untuk i tu per lu dicar i ter lebih dahulu seli si h dua suku seper ti beri kut.

(5)

8. Suatu bar isan ar itmetika diketahui 6 = 18dan 10= 30. Jumlah 16 suku per tama dar i

bar isan tersebut adalah …

A. 896

B. 512

C. 448

D. 408

bilangan dan deret.

Di ketahui 6= 18dan 10= 30

Kar ena sudah diketahui mer upakan bar isan ar itmetika maka = −1 +

Misal 1=

2= +

3= 2+ = + + = + 2

6= + 5 = 18 ……(1)

10= + 9 = 30 ……(2)

Dar i per samaan (1) dan (2) dengan menggunakan eliminasi diperoleh nil ai = 3.

Kar ena b_{= 3 maka}

+ 9 = 30

+ 27 = 30

= 3

16= + 15 = 3 + 15 × 3 = 3 + 45 = 48

=1

2 ( 1+ )

Dengan demikian

16=

1

2× 16 × ( 1+ 16) =1

2× 16 × (3 + 48)

= 408

Jadi, jumlah 16 suku pertama dar i bar isan tersebut adalah 408

(6)

9. Dalam setiap 20 menit amuba membelah dir i menjadi dua. Ji ka mula-mula ada 50

amuba, selama 2 jam banyaknya amuba adalah …

A. 1.600

B. 2.000

C. 3.200

D. 6.400

bilangan dan deret.

Dar i soal diket ahui bahw a 1= 50dan dalam seti ap 20 menit amuba membelah dir i

menjadi 2.

Sehingga dal am 120 menit atau 2 jam, banyaknya amuba adalah 3200.

Atau dengan menggunakan bar isan geometr i

1= 50

mendapatkan banyaknya amuba. Jadi sel ama 20 menit di per oleh

7= 1∙ −1

Soal i ni menguji kemampuan menyelesai kan masalahmenentukan pemfaktoran

(7)

Kar ena kedua suku mer upakan bentuk kuadrat, maka dengan menggunakan

pemfaktor an selisi h dua kuadrat diper oleh

81 2 – 16 2= 92 2−42 2

persamaan linear atau per tidaksamaan linear satu var iabel.

−7 + 8 < 3 −22

12.Jumlah ti ga bilangan ganjil ber urutan adal ah 63. Jumlah bi langan ter besar dan ter kecil

dar i bi langan ter sebut adal ah …

A. 38

B. 42

C. 46

D. 54

tambah, kur ang, kali atau bagi pada bilangan.

Tiga bil angan ganjil ber urutan yai tu 2 + 1,2 + 3, 2 + 5

Jumlah ti ga bilangan ganjil ber urutan adalah 63

( 2 + 1) + ( 2 + 3) + ( 2 + 5) = 63

6 + 9 = 63

6 = 54

(8)

Bilangan ter besar adalah 2 + 5, bilangan ter kecil adalah 2 + 1

2 + 1 + 2 + 5 = 4 + 6

= 4 × 9 + 6

= 42

Jadi jumlah bilangan terbesar dan ter kecil dar i ketiga bilangan ter sebut adalah 42.

(B)

13.Ada 40 peserta yang ikut lomba. Lomba baca puisi dii kuti oleh 23 or ang, lomba baca

puisi dan menuli s cer pen diikuti 12 or ang. Banyak peser ta yang mengikuti

l ombamenuli s cer pen adalah …

A. 12 orang

B. 28 orang

C. 29 orang

D. 35 orang

Soal i ni menguji kemampuan menyelesai kan masalah yang ber kaitan dengan

himpunan

Kita dapat menyelesaikan soal ini dengan membuat gambar berupa diagram Venn

kemudian menyusun per samaan dari infor masi yang di ketahui .

Untuk menyelesai kan per masalahan ter kait himpunan diaw al i dengan menghitung

banyaknya elemen yang mendukung himpunan tersebut. Pada soal diketahui jumlah

selur uh peser ta lomba 40 or ang, 23 or ang mengikuti lomba baca puisi dan 12 or ang

mengikuti lomba baca pui si dan menulis cer pen. Ber dasar kan infromasi ter sebut,

dapat diketahui bahw a peserta yang mengikuti lomba baca puisi saja sebanyak

23−12 = 11 peser ta.Kar ena juml ah selur uh peser ta 40 or ang, sedangkan 23 peser ta

sudah terdaft ar mengikuti lomba, sehingga sisanya 17 or ang mer upakan peserta untuk

l omba menul is cer pen saja. Dar i i nfor masi yang diketahui di atas, maka dapat di buat

(9)

Dan dar i diagr am Venn di atas dapat diketahui bahw a banyaknya peser ta yang

mengikuti lomba menuli s cer pen adalah 29 orang.

(C)

14.Fungsi f didefinisikan dengan r umus ( ) = + . Ji ka ( 3) = −10 dan (−2) = 0,

maka (−7)adalah …

A. 18

B. 10

C. 10

D. 18

Soal ini menguji kemampuan menyelesai kan masal ah yang ber kaitan dengan fungsi .

Di ketahui:

( ) = +

Kar ena ( 3) = −10 maka −10 = 3 + ...(i )

Kar ena (−2) = 0 maka 0 = −2 + ... (ii)

Dar i (i) dan (ii ) dengan metoda eliminasi di per oleh = −2 dan = −4.

Dengan demiki an nilai dar i (−7) dapat diper oleh sebagai ber ikut:

(−7) = −7 +

= −7(−2) + (−4)

= 10

(C)

12

11 17

Lomba baca puisi

Lomba menuli s cer pen

(10)

15.Di ketahui rumus fungsi ( ) = −2 + 5. Nil ai (−4) adalah …

A. −13

B. −3

C. 3

D. 13

Soal ini menguji kemampuan menyelesai kan masal ah yang ber kaitan dengan fungsi

Ni lai (−4) dapat langsung dihitung dengan car a mensubstitusikan = −4 ke dalam

r umus fungsi ( ) = −2 + 5 sebagai ber i kut:

(−4) = −2(−4) + 5

= 13

Jadi nilai (−4) adalah 13

(D)

16.Gradien gar is dengan per samaan 4 −6 = 24 adalah …

A.

B.

C. −

D. −

Soal ini menguji kemampuan menentukan gr adien, per samaan gar i s atau gr afiknya.

Per samaan gar i s 4 −6 = 24 ter lebih dahulu dinyatakan dalam bentuk eksplisit

= + sebagai ber ikut:

4 −6 = 24

−6 = −4 + 24

= 2

3 −4

Dengan demiki an gr adien gar is dengan per samaan 4 −6 = 24 adal ah .

(11)

17.Keli ling suatu per segipanjang 28 cm. Jika panjangnya 2 cm lebih dar i lebar nya, luas

per segi panjang ter sebut adalah …

A. 28 cm2

B. 30 cm2

C. 48 cm2

D. 56 cm2

Soal ini menguji kemampuan menyelesai kan masalah yang ber kaitan dengan luas

bangun datar

Di ketahui keliling per segipanjang 28 cm.

Misalkan lebar persegipanjang , maka panjang per segipanjang = + 2.

Kelili ng = 2( + )

Luas per segi panjang dapat dihi tung sebagai ber i kut:

Luas = ×

= 8 × 6

= 48

Dengan demiki an luas per segipanjang ter sebut adalah 48 cm2.

(C)

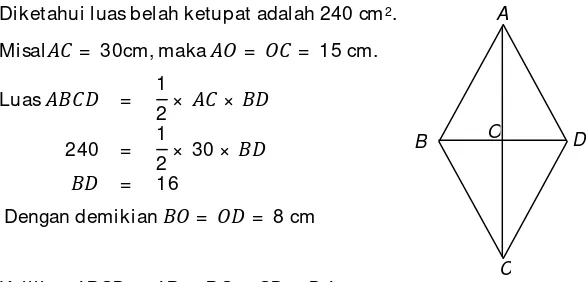
18.Di ketahui luas bel ahketupat 240 cm2 _{dan panjang salah satu diagonal nya 30 cm.}

Keli ling belahketupat ter sebut adalah…

A. 60 cm

B. 68 cm

C. 80 cm

D. 120 cm

Soal ini menguji kemampuan menyelesaikan masal ah yang ber kaitan dengan kel iling

(12)

P Q

Di ketahui luas belah ketupat adalah 240 cm2_.

Misal = 30cm, maka = = 15 cm.

digunakan, sehingga = 17.

Keli ling = 4 × 17 = 68.

Jadi kel iling belahketupat adalah 68 cm.

(B)

Soal ini menguji kemampuan menyelesaikan

masalah yang ber kaitan dengan luas bangun datar

Dar i gambar jelas bahw a daer ah yang diar sir t er letak pada per segi dan

sekali gus ter l etak pada persegipanjang . Sehi ngga l uas daer ah yang diar sir akan

ter hitung dua kali. Dengan demikian untuk menghitung luas daerah yang tidak di ar sir ,

digunakan car a sebagai ber ikut:

A

B

C

(13)

Luas = + −2 × Luas

156 = × + × −2 × Luas

156 = 12 × 12 + 10 × 5−2 × Luas

Luas = 19

Sehingga luas daer ah yang diar sir adalah 19 cm2

(A)

20.Di atas sebidang tanah berbentuk per segipanjang dengan ukur an 15 m × 6 makan

dibuat pagar di sekelili ngnya. Untuk kekuatan pagar , setiap jarak 3 m ditanam ti ang

pancang. Banyak tiang pancang yang ditanam adalah …

A. 12

B. 13

C. 14

D. 15

Soal ini menguji kemampuan menyel esaikan masalah ber kait an dengan luas dan

keliling bangun datar .

Di ketahui bidang tanah berbentuk persegi panjang dengan ukur an 15 m × 6 m.

Kel iling bi dang tanah = 2( + )

= 2( 15 + 6)

= 42

Kar ena jar ak antar ti ang pancang adalah 3 m, maka banyak tiang pancang yang

ditanam adalah = 14.