PARALELISASI DE-NOISING CITRA BERDASARKAN TRANSFORMASI WAVELET DISKRIT PADA GPU DENGAN ARSITEKTUR CUDA
Rudy Cahyadi Hario Pribadi, S.ST 1*, Dr. Nanik Suciati, S.Kom, M.Kom 1, Wahyu Suadi, S.Kom, MM, M.Kom 1
Jurusan Teknik Informatika, Fakultas Teknologi Informasi, Institut Teknologi Sepuluh Nopember, Surabaya, Indonesia 1
Abstrak
Sebuah citra seringkali terkontaminasi oleh noise pada saat akuisisi atau transmisi. Proses de-noising citra yang bagus adalah sebuah proses untuk menghilangkan noise pada suatu citra, dengan tetap mempertahankan dan tidak mendistorsi kualitas citra yang diproses. Proses rekonstruksi dari transformasi wavelet diskrit bersifat lossless, sehingga dapat digunakan untuk de-noising citra. Waktu komputasi dari transformasi wavelet diskrit baik pada proses dekomposisi maupun proses rekonstruksi adalah cukup besar, sehingga kurang bisa memenuhi kebutuhan secara real-time.
Dengan bertumbuhnya perangkat keras yang mendukung komputasi
secara paralel seperti GPU (Graphic Processing Unit) , permasalahan waktu komputasi suatu program dapat teratasi. GPU keluaran NVidia, sekarang dilengkapi dengan suatu arsitektur komputasi paralel yang bernama CUDA (Compute Unified Device Architecture). CUDA menyediakan mekanisme pemrosesan data dalam jumlah besar secara paralel. Penelitian ini memparalelkan proses de-noising citra berdasarkan transformasi wavelet diskrit pada arsitektur
GPU CUDA. Hasil eksperimen menunjukkan bahwa paralesisasi proses
de-noising pada penelitian ini lebih cepat sekitar 2 kali lipat dibanding dengan hasil penelitian sebelumnya.
Katakunci: De-noising, Transformasi Wavelet Diskrit, GPU, CUDA
1. Pendahuluan
Sebuah citra seringkali terkontaminasi oleh noise pada saat akuisisi atau transmisi. Proses de-noising yang bagus adalah sebuah proses untuk menghilangkan noise pada suatu citra, sementara tetap mempertahankan dan tidak mendistorsi kualitas citra yang diproses. Teknik pemfilteran noise secara konvensional seperti median fitering, dan homomorphic Wiener filtering sering mengaburkan tepi-tepi citra [1]. Karena itu, representasi signal dengan skala tunggal baik dalam waktu dan frekuensi sering tidak cukup memadai ketika digunakan untuk memisahkan signal dari data noise.
de-noising citra [2]. Akan tetapi, waktu komputasi dari transformasi wavelet diskrit dalam kaitan dengan sifat operasi dekomposisi dan rekonstruksi data yang multilevel, mengurangi performansi dan implementasi untuk aplikasi real-time, terutama ketika berhadapan dengan ukuran citra yang besar [3]. Kompleksitas waktu dari transformasi wavelet adalah O(N2), N adalah ukuran citra, dan waktu proses komputasi bertambah secara signifikan sesuai dengan ukuran citra [4].
Penelitian sebelumnya [3] mengimplementasikan proses de-noising citra
berdasarkan wavelet menggunakan GPU (Graphics Processing Unit) dengan pustaka OpenGL. Transformasi wavelet diskrit 2D diimplementasikan dengan menerapkan Transformasi wavelet diskrit 1D masing-masing sepanjang arah horisontal dan vertikal. Hasil penelitian tersebut menyimpulkan bahwa transformasi wavelet diskrit menggunakan GPU Geforce GTX 9700 dapat mempercepat proses komputasi dengan faktor percepatan 5,9 sampai 9,6 kali terhadap implementasi proses de-noising pada CPU Pentium IV 2,6GHz .
Pada [5] didapatkan hasil bahwa kinerja menggunakan arsitektur CUDA lebih baik dari implementasi menggunakan OpenGL. Pada implementasi OpenGL dibutuhkan pengetahuan khusus tentang grafika komputer, sehingga diperlukan lebih banyak waktu implementasi. Selain itu, versi GPU NVIDIA Tesla, yang merupakan perangkat keras khusus komputer berkinerja tinggi tidak mendukung OpenGL. Pada [6] didapatkan hasil bahwa implementasi CUDA lebih cepat dari OpenGL. Penggunaan CUDA memudahkan pemrograman dan tidak membutuhkan pengetahuan khusus tentang grafika komputer. Selain itu, CUDA mengekspos secara detil manajemen thread dan memori pada GPU, sehingga programmer dapat mengontrol memori, thread, intensitas aritmetik secara lebih baik.
Pada penelitian ini kami mengusulkan suatu paralelisasi proses de-noising citra berdasarkan transformasi wavelet diskrit pada GPU dengan arsitektur CUDA. Transformasi wavelet diskrit digunakan untuk proses de-noising suatu citra, dan arsitektur CUDA digunakan untuk mempercepat proses de-noising suatu citra pada GPU secara real-time.
2. Metoda
2.1 Lingkungan Percobaan & data uji coba
Dalam penelitian ini kami menggunakan Hardware CPU Quad Core @2,666Ghz 4GB RAM DDR2 dengan GPU Geforce GTS 450 1GB GDDR3 AMP! Edition. Software Microsoft Visual Studio 2008 Professional, Matlab R2010a, CUDA toolkit 3.2, Windows 7 64bit.
Data uji coba yang digunakan dalam penelitian ini adalah citra berwarna RGB dengan berbagai ukuran piksel.
2.2 Algoritma De-noising Citra Berdasarkan Transformasi Wavelet Diskrit Algoritma de-noising citra berdasarkan transformasi wavelet diskrit meliputi: 1. Dekomposisi transformasi wavelet diskrit 2D.
2. Soft Global thresholding.
3. Rekonstruksi transformasi wavelet diskrit 2D.
Daubechies4 mempunyai 4 koefisien fungsi wavelet / high-pass filter dan 4 koefisien fungsi skala / low-pass filter.
Koefisien fungsi skalanya adalah :
Koefisien fungsi waveletnya adalah :
; ; ;
Dekomposisi transformasi wavelet diskrit 2D dibagi kedalam dua transformasi wavelet diskrit 1D, pemfilteran secara horisontal/baris dan pemfilteran secara vertikal/kolom. Misal D(0,0), D(0,1), ..., D(n-1,n-1), n=2k, k N adalah signal array 2D (citra) yang akan dedekomposisi. Untuk pemfilteran secara horisontal, low-pass values didapatkan dengan melakukan perhitungan konvolusi yang melibatkan 4 data asli citra dan 4 koefisien fungsi skala, seperti pada persamaan (1). High-pass values didapatkan dengan melakukan perhitungan konvolusi yang melibatkan 4 data asli citra dan 4 koefisien fungsi wavelet, seperti pada persamaan (2). Demikian juga untuk pemfilteran secara vertikal, cara kerja sama dengan pemfilteran horisontal. Data output dari hasil pemfilteran horisontal dijadikan sebagai data input untuk pemfilteran vertikal.
(1)
(2)
Dimana lpv adalah low-pass values ; hpv adalah high-pass values ; D adalah data input. Setiap iterasi index i ditambah 2.
Soft Global thresholding, digunakan untuk menghasilkan sebuah threshold dan menerapkannya melalui soft tresholding pada koefisien-koefisien detil secara global.
Rekonstruksi transformasi wavelet diskrit 2D juga menggunakan basis wavelet Daubhecies4. Rekonstruksi transformasi wavelet diskrit 2D juga dibagi kedalam dua transformasi wavelet diskrit 1D, pemfilteran secara horisontal/baris dan pemfilteran secara vertikal/kolom. Cara kerja secara umum adalah merekonstruksi citra yang noise-nya sudah di-threshold, dengan melakukan perhitungan konvolusi seperti pada persamaan (3) dan (4), yang melibatkan 4 data hasil dekomposisi yang sudah di-threshold, 2 low-pass values dan 2 high-pass values.
(3)
(4)
Dimana D adalah data piksel citra yang direkonstruksi, d adalah data hasil dekomposisi yang sudah dithreshold, dimana d0 sampai dhalf-1 adalah low-pass value, dan dhalf sampai
dn-1 adalah high-pass value.
2.3 Eksploitasi paralelisme
Berdasarkan persamaan (1) dan (2) perhitungan setiap low-pass values dan high-pass values adalah tidak saling tergantung (independent) antara low-pass values dan high-pass values yang lainnya. Sehingga algoritma dekomposisi transformasi wavelet diskrit bisa diimplementasikan secara paralel (data paralelism ).
Berdasarkan persamaan (3) dan (4) perhitungan tiap D1 ,D2 sampai Dn tidak
tergantung satu sama lain (independent), Sehingga algoritma rekonstruksi transformasi wavelet diskrit bisa diimplementasikan secara paralel juga (data paralelism ).
2.4 Paralelisasi Dekomposisi Transformasi Wavelet Diskrit 2D menggunakan CUDA
Algoritma ini terdiri dari proses: Mentransfer citra dari host memory ke device memory, menerapkan pemfilteran horisontal dekomposisi 1D pada device, menerapkan pemfilteran vertikal dekomposisi 1D pada device, dan mentransfer citra hasil dekomposisi dari device memory ke host memory
Berdasarkan ekspolitasi paralelisme pada bab 3.2, perhitungan setiap low-pass value dan high-pass value dengan CUDA dilakukan oleh satu thread. Sehingga satu thread menghitung dua nilai.
Didalam proses dekomposisi dengan basis Daubechies4 menggunakan arsitektur CUDA, terdapat permasalahan batas block. Solusinya adalah melakukan periodic padding yaitu menambahkan beberapa jumlah elemen input data pada suatu block secara periodik. Jumlah padding adalah sama dengan jumlah basis Daubechies4 yaitu 4. Sehingga dalam satu block terdapat 2*(512 - npadding) perhitungan nilai.
Untuk pemfilteran horisontal dekomposisi, misal citra NxN membutuhkan grid
berdimensi 2 ( n BlockIdx.x, N BlockIdx.y ) dan tiap block mempunyai jumlah thread 512 ( 512 ThreadIdx.x, 1 ThreadIdx.y ).
n = 1, Jika N < (2*(512 - npadding)).
n = N/(2*(512 - npadding)), jika N%(2*(512-npadding)) = 0. n = N/(2*(512 - npadding)) + 1, jika N%(2*(512 - npadding)) <> 0.
Proses pemfilteran vertikal sama dengan pemfilteran horisontal, namun untuk pemfilteran vertikal yang diproses adalah dimensi kolom citra, sedangkan pemfilteran horisontal adalah dimensi baris citra. Sehingga, misal untuk citra berukuran NxN, maka dibutuhkan grid berdimensi 2 ( N BlockIdx.x, n BlockIdx.y ) dan tiap block mempunyai jumlah thread 512 ( 1 ThreadIdx.x, 512 ThreadIdx.y ).
Sebelum melakukan perhitungan, data dari global memory dimuat ke shared memory, karena shared memory lebih cepat dari global memory. Setiap thread pada block memuat 2 elemen input data dari global memory ke shared memory.
2.5 Paralelisasi Rekonstruksi Transformasi Wavelet Diskrit 2D menggunakan CUDA
Algoritma ini terdiri dari proses: Mentransfer citra dari host memory ke device memory, menerapkan pemfilteran horisontal rekonstruksi 1D pada device, menerapkan pemfilteran vertikal rekonstruksi 1D pada device, dan mentransfer citra hasil dekomposisi dari device memory ke host memory.
Berdasarkan eksploitasi paralelisme pada bab 3.2, perhitungan setiap data rekonstruksi dengan CUDA dilakukan oleh satu thread. Jadi satu thread menghitung satu data rekonstruksi.
Didalam proses rekonstruksi dengan basis Daubechies4 menggunakan arsitektur CUDA, terdapat proses zero padding diantara dua input data. Zero padding yaitu menambahkan beberapa elemen input data yang bernilai 0 diantara dua input data. Didalam satu block terdapat (512-2*npadding) perhitungan nilai data rekonstruksi.
Untuk pemfilteran horisontal rekonstruksi, misal untuk citra berukuran NxN, membutuhkan grid berdimensi 2 ( n BlockIdx.x, N BlockIdx.y ) dan tiap block mempunyai jumlah thread 512 ( 512 ThreadIdx.x, 1 ThreadIdx.y ).
n = 1, jika Nl<(512-2*npadding).
Nl adalah lebar citra pada suatu level dekomposisi.
Sama seperti pada proses dekomposisi, sebelum melakukan perhitungan, data dari global memory dimuat ke shared memory. Setiap thread pada block memuat 2 elemen input data dekomposisi yaitu low-pass value dan high-pass value dari global memory ke shared memory sendiri-sendiri.
2.6Evaluasi kinerja sistem
Evaluasi dilakukan dengan membandingkan waktu komputasi dan hasil akurasi[9] dari versi GPU-CUDA dengan versi CPU dengan berbagai ukuran citra berwarna RGB.
Evaluasi kinerja sistem diukur menggunakan:
Kecepatan = Tcpu / Tgpu (5)
Dimana Tcpu adalah waktu komputasi sekuensial CPU, sedangkan Tgpu adalah waktu komputasi paralel GPU.
(6)
Dimana mse adalah mean square error antara citra asli x dan citra ter-noise y dengan ukuran MxN:
(7)
3. Hasil dan Diskusi
Berdasarkan tabel 2. Waktu komputasi dekomposisi GPU-CUDA + transfer memori host-device dan sebaliknya mempunyai kecepatan 6 sampai 14 kali dari dekomposisi CPU. Tetapi jika tanpa mengikutsertakan waktu komputasi transfer memori, kecepatannya antara 39 sampai 80 kali. Demikian juga dengan waktu komputasi rekonstruksi GPU-CUDA + transfer memori host-device, mempunyai kecepatan 3 sampai 9 kali dari rekonstruksi CPU. Sedangkan jika tanpa transfer memori host-devie, kecepatannya antara 21 sampai 47 kali.
Berdasarkan hasil diatas waktu komputasi transfer memori host-device dan sebaliknya memberikan sumbangan waktu yang signifikan atau bisa dikatakan sebagai bottleneck dari komputasi paralel pada GPU-CUDA.
Pada tabel 1. Waktu komputasi proses de-noising citra menggunakan GPU-CUDA mempunyai kecepatan sampai 4 kali lipat dari versi CPU.
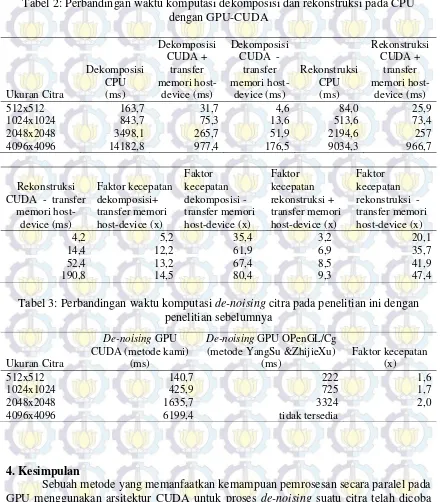
Gambar 6. Citra Asli
Gambar 7. Citra ter-noise dengan model noise gaussian (gambar kiri σ=0,01,tengah
σ=0.05, kanan σ=0.1)
Gambar 8. Citra hasil de-noising (gambar kiri psnr=32,84,tengah psnr=28,04, kanan psnr=24,9)
Pada gambar 8 adalah citra hasil de-noising dari citra noise model white noise gaussian dengan σ antara 0,01 sampai 0,1. Hasil PSNR menunjukkan kualitas citra, semakin besar nilai σ maka PSNR semakin kecil. Dengan kata lain semakin besar nilai σ maka semakin menurun kualitas citra.
Tabel 1: Perbandingan waktu komputasi de-noising citra pada CPU dan GPU-CUDA
Ukuran Citra
De-noising versi CPU (ms)
De-noising versi GPU CUDA (ms)
Faktor kecepatan (x)
512x512 313,6 140,7 2,2
1024x1024 1612,6 425,9 3,8
2048x2048 6686,3 1635,7 4,1
Tabel 2: Perbandingan waktu komputasi dekomposisi dan rekonstruksi pada CPU dengan GPU-CUDA Ukuran Citra Dekomposisi CPU (ms) Dekomposisi CUDA + transfer memori host-device (ms) Dekomposisi CUDA -
transfer memori host-device (ms) Rekonstruksi CPU (ms) Rekonstruksi CUDA + transfer memori host-device (ms) 512x512 163,7 31,7 4,6 84,0 25,9 1024x1024 843,7 75,3 13,6 513,6 73,4 2048x2048 3498,1 265,7 51,9 2194,6 257 4096x4096 14182,8 977,4 176,5 9034,3 966,7
Rekonstruksi CUDA - transfer
memori host-device (ms) Faktor kecepatan dekomposisi+ transfer memori host-device (x) Faktor kecepatan dekomposisi - transfer memori host-device (x) Faktor kecepatan rekonstruksi + transfer memori host-device (x) Faktor kecepatan rekonstruksi - transfer memori host-device (x)
4,2 5,2 35,4 3,2 20,1
14,4 12,2 61,9 6,9 35,7 52,4 13,2 67,4 8,5 41,9 190,8 14,5 80,4 9,3 47,4
Tabel 3: Perbandingan waktu komputasi de-noising citra pada penelitian ini dengan penelitian sebelumnya
4. Kesimpulan
Sebuah metode yang memanfaatkan kemampuan pemrosesan secara paralel pada GPU menggunakan arsitektur CUDA untuk proses de-noising suatu citra telah dicoba dan dievaluasi. Metode yang diterapkan sangat efektif bila menghadapi ukuran data citra yang sangat besar.Performansi secara kesuluruhan untuk kualitas visual citra dan efisiensi komputasional cukup baik.
Pada penelitian ini, metode yang diterapkan berlaku untuk pemrosesan citra dua dimensi 2D. Namun beberapa aplikasi video atau CCTV, sekumpulan citra video diperlakukan sebagai volume 3D. Sehingga menjadi tantangan yang besar untuk efisiensi komputasi proses de-noising pada video.
Komputasi paralel pada GPU menggunakan arsitektur CUDA terbukti dapat mengatasi masalah efisiensi komputasi suatu aplikasi. Namun bottleneck komputasi terbesar terletak pada transfer data antar memori host/CPU-device/GPU dan sebaliknya. Sehingga diperlukan perbaikan metode untuk mengatasi hal ini kedepan.
Ukuran Citra
De-noising GPU CUDA (metode kami)
(ms)
De-noising GPU OPenGL/Cg (metode YangSu &ZhijieXu)
(ms)
Faktor kecepatan (x)
512x512 140,7 222 1,6
1024x1024 425,9 725 1,7
2048x2048 1635,7 3324 2,0
5. Pustaka
[1] Caballero., Mateo, L. (2008), “Methodological Approach to Reducing Spekle Noise in Ultrasound Image”, International Conference on Biomed. Engie. And Informatics, IEEE Computer Society, 978-0-7695-3118-2/08
[2] Unser, M., Aldroubi, A., Laine, A. (2003), “Wavelet in Medical Imaging” , IEEE Trans. Med. Imaging, hal 285-288.
[3] Yang Su, Zhijie Xu. (2010), “Parallel implementation of wavelet-based image denoising on programmable PC-grade graphics hardware”, Signal Processing volume 90, issue 8, Elsevier, hal. 2396-2411.
[4] Ajdari, J. (2010), “Parallel Implementation of 2D Haar and Daubechies D4 Transform in Mesh Architecture”, IJIIP 1(2), hal 55-64.
[5] Weinlich, A., Keck, B., Scherl, H., Kowarschik, M., Hornegger, J. (2008),
“Comparison of High-Speed Ray Casting on GPU using CUDA and OpenGL”, High
Performance and Hardware-Aware Comuting (HipHac), ed R Buchty and J-P Weiss, hal 25-30.
[6] Amorim, R. (2009), “Comparing CUDA and OpenGL implementation for a Jacobi
iteration”, High Performance Computing & Simulation, IEEE, 978-1-4244-4906-4. [7] Mallat, S, (1987), "A compact multiresolution representation: the wavelet model,"
Proceeding Workshop Computer Vision, IEEE.
[8] NVIDIA CUDA Toolkit 3.2.
http://developer.nvidia.com/object/cuda_download.html