4.1. Pendahuluan
Seorang peneliti dari suatu perusahaan manufaktur melakukan riset pasar di suatu pusat perbelanjaan. Penelitian itu bertujuan untuk mengetahui respon konsumen terhadap produk yang baru dipasarkan. Meskipun pengunjung di pusat perbelanjaan tersebut lebih dari 2.000 ribu orang tersebut pengunjung, namun hanya 100 orang pengunjung
Pembaca setelah mempelajari bab ini diharapkan dapat : Menjelaskan pengertian teknik sampling
Menjelaskan konsep tentang metode pengambilan sampel pada penelitian
Menentukan sample dengan teknik penentuan yang benar Menjelaskan konsep distribusi sample rata-rata dan
teorima batas tengah
Menjelaskan cara penentuan besarnya anggota sample Menghitung besarnya anggota sample dalam penelitian Pembaca setelah mempelajari bab ini diharapkan dapat : Menjelaskan pengertian teknik sampling
Menjelaskan konsep tentang metode pengambilan sampel pada penelitian
Menentukan sample dengan teknik penentuan yang benar Menjelaskan konsep distribusi sample rata-rata dan
teorima batas tengah
yang digunakan. Mengapa peneliti pasar memutuskan menggunakan 100 orang pengunjung dari semua pengunjung pusat perbelanjaan tersebut yang jumlahnya lebih dari 2.000 orang? Alasan pertama adalah keterbatasan waktu dan menghindari pembiayaan tinggi dari penelitian pasar tersebut, jika melibatkan semua pengunjung. Selama akurasi dari sampel dapat dipertanggungjawabkan, maka respon dari semua pengunjung tidak diperlukan. Pada bagian ini akan menjawab pertanyaan seperti berapa jumlah sampel yang sebaiknya digunakan? Bagaimana memilih sampel? Bagaimana mengetahui sampel yang digunakan dapat menggambarkan populasi yang sebenarnya?
Cold storage yang akan membeli udang pada suatu tambak udang tidak mungkin menggunakan semua udang yang terdapat di dalam tambak untuk menentukan ukurannya. Petugas dari Cold Storage mengambil sebagian udang, kemudian udang tersebut ditimbang untuk menentukan ukuran udang yang ada pada tambak tersebut.
Manajer tersebut tidak mungkin melibatkan semua masyarakat yang di pasar tersebut di dalam penelitiannya, cukup melibatkan sebagian saja dari mereka untuk memperoleh gambaran tentang opini masyarakat terhadap produk yang akan dipasarkan.
Manajer keuangan suatu perusahaan besar yang sering melakukan pembelian tidak akan menggunakan semua faktur pembelian untuk mengetahu persentase kekeliruan pencatatan dalam suatu periode akuntansi. Untuk keperluan itu, manajer keuangan cukup menggunakan sebagian faktur pembelian untuk memperoleh gambaran mengenai persentase kekeliruan pencatatan pada faktur penjualan.
1. Obyek yang akan diteliti memiliki anggota yang banyak sekali (infinite), sehingga tidak mungkin mengumpulkan semua anggota dari obyek tersebut.
2. Biaya yang harus dikeluarkan dalam suatu penelitian yang menggunakan data populasi terlalu besar.
3. Penelitian yang menggunakan data populasi memerlukan banyak tenaga peneliti yang handal. Padahal biasanya pada setiap penelitian hanya terdapat sedikit peneliti yang handal.
4. Obyek yang akan diteliti mempunyai kemungkinan terdapat pada kelompok-kelompok kecil dan menyebar di tempat yang berjauhan antara kelompok satu dengan yang lainnya.
5. Perlu adanya waktu dalam penelitian yang menggunakan data populasi.
Dari beberapa kesulitan tersebut, maka biasanya penelitian hanya melibatkan sebagian anggota populasi (data sampel) saja. Penentuan sampel yang baik akan dapat memberi gambaran karekteristik populasinya.
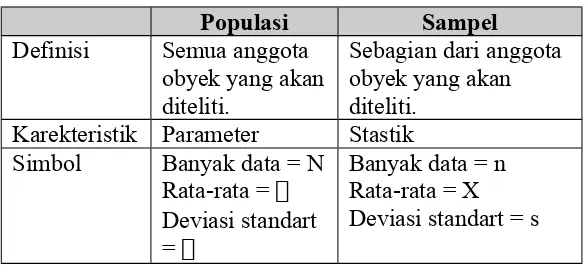
median, modus, dan standart deviasi. Apabila ukuran-ukuran tersebut mencerminkan suatu nilai dari sampel disebut statistik (statistic) dan apabila ukuran-ukuran tersebut menggambarkan suatu nilai dari populasi disebut parameter (parameters). Jadi nilai statistik adalah karekteristik dari sampel dan nilai parameter adalah karakteristik dari populasi. Tabel 4.1 menunjukkan perbedaan antara populasi dengan sampel.
Tabel 4.1. Perbedaan antara Populsi dengan Sampel.
Populasi Sampel
Definisi Semua anggota obyek yang akan diteliti.
Sebagian dari anggota obyek yang akan diteliti.
Karekteristik Parameter Stastik Simbol Banyak data = N
Rata-rata = Deviasi standart =
Banyak data = n Rata-rata = X Deviasi standart = s
4.2. Sampling
baik diperlukan metode yang baik dalam pemilihan anggota sampel. Metode pengambilan anggota sampel yang baik sangat tergantung dari kondisi populasinya. Metode pengambilan sampel dari populasinya dikelompokkan menjadi dua, yaitu Random Sampling dan Nonrandom Sampling.
4.2.1. Sampel Random (Random Sampling).
Ciri yang mendasar dari pemilihan sampel dengan menggunakan metode random sampling adalah bahwa semua anggota populasi mempunyai kesempatan yang sama untuk menjadi anggota sampel. Random sampling disebut juga Probability sampling, karena dalam metode ini memberikan kesempatan yang sama pada setiap anggota populasi untu menjadi anggota sampel. Pemilihan sampel dengan menggunakan cara ini cukup obyektif untuk menaksirkan karekteristik populasi dari sampel yang dipilih, dan obyektivitas taksiran yang dihasilkan dapat dijelaskan.
lengkap sebelum anggota sampel diambil dari anggota populasi tertentu.
Proses pemilihan anggota sampel dengan menggunakan random sampling terdapat empat metode, yaitu sampel random sederhana (simple random sampling), sampling sistimatis (syistematic sampling), sampel bertingkat (statified sampling) dan sampel berkelompok (cluster sampling).
a. Sampel random sederhana (simple random sampling)
BC, BD, CD. Karena terdapat enam pasangan yang mungkin terjadi, maka masing-masing pasangan mempunyai kesempatan (probabilitas) yang sama, yaitu 1/6. Untuk mengetahui kesempatan setiap pelamar yang dipilih untuk mengikuti tes wawancara adalah sebagai berikut :
P(A) = P(AB) + P(AC) + P(AD) = 3/6 = ½ . P(B) = P(AB) + P(BC) + P(BD) = 3/6 = ½ . P(C) = P(AC) + P(CB) + P(CD) = 3/6 = ½. P(D) = P(AD) + P(BD) + P(CD) = 3/6 = ½.
b. Sampel sistematis (systematic sampling)
Pengambilan anggota sampel berikutnya pedagang kaki lima pada urutan kelima berikutnya pada daftar tersebut. Selama penentuan urutan diambil, dilakukan secara random, maka Sampling Sitematis ini merupakan random sampling. Karena pada akhirnya setiap nomor urut mempunyai kesempatan yang sama bagi setiap anggota populasi untuk dipilih menjadi anggota sampel.
c. Sampel bertingkat (stratified sampling)
dalam penelitian merupakan penjumlahan dari anggota masyarakat yang bekerja sebagai pedagang, pegawai negeri, dan pegawai swasta dipilih secara acak.
d. Sampel berkelompok (Cluster Sampling)
Kecamatan Banjar Utara, dan Kotamadya). Pada masing-masing lokasi (kecamatan) dipilih beberapa keluarga secara acak untuk membentuk sampel yang diperlukan dalam penelitian.
4.2.2. Sampel Nonrandom (Nonrandom Sampling)
Pemilihan sampel dari sesuatu populasi tidak harus memberikan kesempatan yang sama kepada semua anggota populasi untuk menjadi anggota sampel. Pemilihan sampel dengan cara ini menggunakan pengetahuan dan opini dari peneliti terhadap obyek yang akan diteliti. Karena pemilihan sampel dengan cara non random sampling hanya berdasar pada pengetahuan dan opini peneliti, maka cara pengambilan sampel seperti ini disebut juga Judgement Sampling. Baik tidaknya sampel yang diperoleh dari pemilihan sampel dengan metode Nonrandom Sampling (sampel kebijaksanaan) ini sangat tergantung dari kemampuan peneliti.
Ukuran statistik deskriptif yang diperoleh dari sampel, yaitu rata-rata, median, modus, strandart deviasi, dan lain-lain, tidak hanya dapat digunakan untuk memberi gambaran statistik saja. Ukuran-ukuran itu dapat juga digunakan untuk membuat inferens (penafsiran) mengenai parameter populasi, estimasi, dan uji hipotesis.
Konsep distribusi sampling sangat erat hubungannya dengan pemikiran mengenai variasi kesempatan (fluktuasi kesempatan) yang ditekankan dalam pembahasan mengenai ukuran variabelitas. Pada bagian ini, pembahasan ditekankan hanya pada rata-rata sampel dan distribusi samplingnya.
Ada dua pendekatan mengenai distribusi sampel, yaitu distribusi sampel teoritis (Teoritical Sampling Distribution) dan distribusi sampel experimen (Experimental Sampling Distribution). Distribusi sampling teoritis didasarkan atas teori matematis yang relevan. Sebagai contoh digunakan penghitungan terhadap ditribusi sampling teoritis rata-rata pada kasus berikut ini :
Populasi yang beranggotakan 3, 5, 7, 9, 11 dipilih dua anggota sebagai sampel secara acak. Rata-rata () dan
5
Varians populasinya adalah
8
2
Distribusi sampling rata-rata dan deviasi standartnya dapat dicari dengan cara sebagai berikut :
Rata-rata distribusi sampling rata-rata adalah : Variasi distribusi rata-rata sampling adalah
3
Sedangkan standart deviasi distribusi rata-ratanya adalah
populasinya dan standar deviasi dari distribusi sampling elemen tidak terbatas (infinite), maka antara standart deviasi sampel (x) dengan standart deviasi populasi () dapat
ditulis sebagai berikut :
n X
Apabila elemen populasi terbatas (finite), maka hubungan antara variasi sampel (x) dengan standart deviasi
populasi () dapat ditulis sebagai berikut :
sampelnya kurang atau sama dengan 30 (sampel kecil), harus menggunakan faktor koreksi. Dengan menggunakan faktor koreksi, maka variasi sampel rata-rata sampel akan sama dengan variasi populasinya. Masalah ini dapat dibuktikan secara matematis sebagai berikut :
penentuan nilai statistik menggunakan distribusi sampling teoritis.
4.4. Teorima Batas Tengah (Central Limit Theorem) Teorima batas tengah penting untuk mengetahui kenormalan suatu distribusi data. Misalnya X1, X2, …, Xn
adalah sampel acak yang berasal dari populasi yang tidak terbatas dengan rata-rata populasi () dan standart deviasi
(), serta X1 adalah variabel acak independen. Apabila
sampel (n)-nya besar, maka bentuk teorima batas tengah adalah :
n X Z
/
Ini merupakan perkiraan distribusi normal standart dengan nilai X terdistribusi mendekati nilai rata-rata
populasi () dan standart deviasi x / n
teorima batas tengah adalah teorima ini memberikan indikasi bahwa kita dapat menggunakan teori distribusi normal untuk membuat penaksiran tentang rata-rata populasi tanpa harus mengetahui terlebih dahulu sifat populasinya, asalkan sampel yang digunakan cukup banyak.
4.5. Penentuan Besarnya Anggota Sampel (sample size) Besar anggota sampel harus dihitung berdasarkan teknik-teknik tertentu agar kesimpulan yang berlaku untuk populasi dapat dipertanggungjawabkan. Di samping itu harus pula memenuhi teknik sampling.
Besarnya anggota sampel yang dipilih berdasarkan pertimbangan-pertimbangan :
1. Pertimbangan Praktis
Pertimbangan praktis menyangkut :
a) Unsur-unsur biaya, waktu, tenaga dan kemampuan; b) Unsur eksploratori (exploratory) atau penemuan atau
c) Jika kita memilih anggota sampel yang banyak, maka tingkat prediksi relatif tepat, kesalahan mentabulasi dan menghitung besar, reliabilitas besar, dan power meningkat, demikian pula sebaliknya.
2. Ketepatan
Semakin kecil kita memilih taraf signifikansi atau alpha ( ), semakin banyak anggota sampelnya. Dengan demikian semakin tepat atau teliti ramalan kita.
3. Pertimbangan Nonrespons
4.6. Teknik Menghitung Besarnya Anggota Sampel Secara umum teknik untuk menghitung besarnya anggota sample dapat dilakukan dengan dua cara yaitu;
1. Proporsi,
2. Ketelitian estimasi
4.6.1. Proporsi
Perhitungan besarnya anggota sample dengan menggunakan cara proporsi dapat menggunakan sejumlah rumus. Salah satu rumus tersebut adalah;
2 1/2
Z pq
n
di mana :
n = jumlah anggota sampel minimal p = proporsi kelompok pertama q = proporsi kelompok kedua = (1-p)
Contoh 4.1 :
Suatu daerah diketahui anggota populasi penduduknya yang berstatus sebagai PNS sebanyak 400.000 orang. Di antaranya 100.000 orang belum menjalankan KB secara efektif. Berapa besar anggota sampel yang perlu diteliti dalam rangka mengungkapkan partisipasi terhadap program KB ?
Penyelesaian :
Misalkan digunakan = 0.05, maka didapatkan :
dibulatkan menjadi 294 orang.
4.6.2. Ketelitian Estimasi a). Ketelitian estimasi
s = standard deviasi (diketahui) SEx = standard error
b). Rumus dasar confidensi interval :
n z 2 1/2
w
di mana :
w = interval estimasi
= simpangan baku populasi (diketahui)
n = besarnya anggota sampel
= taraf signifikansi Z1/2 = nilai z tabel
Contoh 4.2 :
Diketahui 2 = 100, w = 5, = 0.05. Berapa banyaknya
61
Sebenarnya tidak ada aturan yang tegas mengenai berapa besarnya anggota sampel yang disyaratkan suatu penelitian. Demikian pula apa batasannya bahwa sampel itu besar atau kecil. Yang jelas ialah jika sampelnya besar, maka biaya, tenaga, waktu yang disediakan harus besar pula. Demikian sebaliknya. Meskipun demikian, mutu suatu penelitian tidaklah ditentukan oleh besarnya anggota sampel yang digunakan, melainkan oleh kuatnya dasar-dasar teori yang mendukung teknik pengambilan anggota sampel tersebut. Sesungguhnya tidak ada anggota sampel yang 100 persen representatif, kecuali anggota sampelnya sama dengan anggota populasinya (total sampling).
Kesalahan-kesalahan umum yang sering dijumpai dalam menentukan besarnya anggota sampel antara lain :
1. Peneliti gagal dalam menetapkan jumlah anggota populasi yang dapat dipercaya;
2. Peneliti menggunakan anggota sampel yang terlalu kecil untuk setiap subgrupnya, sehingga analisis statistika parameter tidak berlaku, pada populasi sebenarnya cukup besar;
3. Peneliti tidak menggunakan teknik sampling startified yang disyaratkan untuk menentukan anggota sampel subgrupnya;
4. Peneliti mengubah prosedur teknik sampling;
5. Peneliti mengubah rumus untuk menghitung besarnya anggota sampel;
6. Peneliti memilih anggota sampel yang tidak sesuai dengan tujuan penelitiannya;
8. Peneliti tidak memberikan alasan-alasan mengapa rumus dan teknik sampling tertentu yang ia gunakan di dalam penelitiannya itu;
9. Kekeliruan sampling biasanya terjadi karena pemeriksaan yang kurang teliti dan lengkap terhadap populasi yang hanya dilakukan terhadap sampel serta penelitian dilakukan dengan menggunakan prosedur yang sama;
10. Kekeliruan nonsampling ini bisa terjadi dalam setiap penelitian, apakah itu berdasarkan sampling atau berdasarkan sensus, penyebabnya adalah :
a) Populasi tidak didefinisikan sebagaimana mestinya. b) Penyimpangan populasi tidak dipelajari.
c) Kuesioner tidak dirancang sesuai dengan keperluan. d) Rumusan dan istilah tidak dipergunakan
sebagaimana mestinya.
e) Peneliti kurang memahami isi dari kuesioner sehingga jawaban responden kurang sesuai dengan keinginan.
Latihan :
1. Sebutkan tujuan teknik pengambilan sampel! 2. Apa arti teknik sampling? Jelaskan dengan contoh! 3. Sebut dan jelaskan cara teknik sampling!
4. Bagaimana cara menghitung besar sampel ? Sebutkan pertimbangan menentukan besar anggota sampel !
5. Dari suatu kebun percobaan dijumpai empat kelompok tanah. Tiap kelompok tanah berisi bawang putih dengan varietas yang berbeda. Kelompok 1 adalah varietas lumbu hijau, kelompok 2 adalah varietas lumbu putih, kelompok 3 adalah varietas tawangmangu baru, dan kelompok 4 adalah varietas local. Populasi tanaman pada tiap-tiap kelompok adalah sebagai berikut :
Kelompok 1 = 450 Kelompok 2 = 245 Kelompok 3 = 300 Kelompok 4 = 290
6. Andaikan bahwa tinggi badan dari 3000 mahasiswa laki-laki suatu universitas mempunyai distribusi normal dengan nilai rata-rata sebesar 68.0 inci dan simpangan baku sebesar 3.0 inci. Apabila diambil 80 sampel yang masing-masing terdiri atas 35 mahasiswa, tentukanlah nilai rata-rata dan simpangan baku yang diharapkan apabila :
a). sampel diambil dengan pengembalian b). sampel diambil tanpa pengembalian
7. Suatu populasi sebanyak 12000 unit mempunyai nilai rata-rata 100 dan simpangan baku 60. Hitunglah nilai rata dan simpangan baku dari distribusi sample rata-rata :
a). jika diambil sampel sebanyak n = 100; b). jika diambil sampel sebanyak n = 900!
8. Perusahaan PT MUTIARA memiliki karyawan sebanyak 800 orang, akan dipilih beberpa orang untuk disekolahkan. Pemilihan dilakukan secara acak.
b). Jika dipilih 20 orang, tentukan nomor-nomor yang akan diambil (gunakan tabel bilangan acak seribu angka keempat, kolom 10, 11, dan 12 baris 5)! 9. Dari 400 orang peserta penataran “Teknik Pemasaran”
suatu perusahaan yang berasal dari 4 divisi, hendak diambil sample berlapis sebesar 20%. Bagaimana penentuan jumlah atau besar sampel untuk setiap stratum apabila terjadi hal berikut ini ?
a). Seperempat dari besar sampel dialokasikan pada masing-masing stratum.
b). Divisi I terdiri dari 100 orang, divisi II terdiri atas 75 orang, divisi III sebanyak 150 orang, dan divisi IV sebanyak 175 orang, alokasi pada masing-masing stratum dilakukan secara proposional.