Çeviren: Yrd. Doç. Dr. Cemalettin YILDIZ
Geometri Öğrenimi
ÖKLİD’İN ETKİSİ
Geometri, İngiltere’de 21. yüzyılın başına kadar çoğunlukla erkeklerden oluşan ve ilkokulu bitirerek eğitimlerine devam etme şansı olan küçük bir grubun okul müfredatlarında görme imkânına sahip olduğu bir derstir. Geometri müfredatı, kitaplardaki hâliyle teorem ve bunların ispatlarını içeren ders kitabı formundaki Öklid’in Öğeleri’nden meydana gelmekteydi. Bu durum, geometri öğrenimine geniş bir bakış açısıyla bakan, Öklid’in çalışmasının anlamını ve amacını anlayan birkaç öğrenci dışında kaçınılmaz bir başarısızlık getirmiştir. Başarılı ve yetenekli olan öğrenciler bile geometriye yönelik son derece sınırlı bir bakış açısı kazanabilmiştir. Öğrencilerin problem çözerek, cebirsel metodlar kullanarak veya düşüncelerini matematik dünyasının dışında kalan diğer uygulamalarla ilişkilendirerek uygulama yapma anlamında çok az fırsatları vardı.
Geometri öğretiminde Öklid’e olan katı bağlılığın öğretmenlerde sebep olduğu endişe, 1871 yılında Geometri Öğretimini Geliştirme Derneği’nin kurulmasıyla son bulmuştur. Derneğin ilgi alanı, geometrinin sınırlarını aşmış ve bu kurum 1897 yılında Matematik Derneği adını almıştır. Bu dönemde, Oxford ve Cambridge üniversitelerinin kabul koşullarına kadar az bir ilerleme kaydedilebilmiştir. Memurluk ve orduya giriş sınavlarında ise Öklid ile ilgili birebir bilgiler istenmemiştir.On dokuzuncu yüzyılın ilerleyen dönemlerinde, okullarda teorik ispat yerine geometri uygulamaları ile ilgili daha fazla girişimde bulunulmuş ve Öklid’in ispat anlayışına olan bağlılık son bulmuştur. Price (1994) ve Howson (1973, 1982)’un çalışmalarında bu gelişmelere ayrıntılı olarak değinilmiştir. Bu reform hareketlerinde aktif olarak rol oynayan iki isim Profesör
John Perry (1850-1920) ve okul müdürü Charles Godfrey (1873-1924)’dir. Bu
kişiler, birbirinden oldukça farklı iki perspektiften yola çıkarak okul geometrisinin 50 yıl boyunca göstereceği ilerlemede son derece önemli etkiler oluşturmuştur. Ayrıca bu insanlar, 1903 yılında üniversitelerin Öklid’e olan katı bağlılığını azaltmıştır. Perry, tümdengelimli Öklidispatlarını fazla vurgulamadan uygulamaya dayalı okul geometrisini savunmuştur. Godfrey ise uygulama sürecini Öklid içerisindeki teoremlerin geliştirilmesine yönelik bir araç olarak görmüştür. Aynı zamanda çeşitli ispat yöntemleri ve teoremler ile bağlantılı problemlerin de üzerinde durmuştur.
Yeni yüzyılın ilk yıllarında, birçok yeni geometri ders kitabı basılmıştır. Bunlardan en dikkat çekici olanı Godfrey ve Siddons (1903) tarafından yazılan
Temel Geometri kitabıdır. Öklid’in sunduğundan daha zengin bir geometri bakış
açısına sahip olan bu kitap, yıllarca basılmıştır. Ölçme, kesme ve katlama üzerine deneysel faaliyetler, formal ispatlar ve sonuçların informal gösterimleri tümdengelimli bir bakış açısıyla kitaba dâhil edilmiştir.
ortaya koyan Matematik Derneğinin (1923) geometri öğretimi üzerine hazırladığı ilk raporda açıklanmıştır. Bu üç aşama fikri, derneğin ikinci raporunda daha da geliştirilmiştir. Radikal değişimlerin ortaya atıldığı ve kabul görmeye başlandığı 1960’lara kadar, üç aşama fikrinin Matematik Derneğinin (1938) geometri öğretimi ve ders kitapları üzerinde önemli etkisi olmuştur.
A aşaması, deneysel bir aşamadır. Öğrenciler, bu aşamada geometrik özellikleri incelemek için ölçme, kesme ve katlama gibi faaliyetlere katılırlar. Ayrıca öğrenciler, geometrik nesneler ve ilişkilere yönelik sezgisel bir anlayış geliştirmeye başlarlar. Örneğin, bir üçgenin iç açılarının ölçülerinin toplamının 180° olduğu gerçeği, bir açıölçer yardımıyla açıların ölçüleri bulunarak veya üçgenin iç açılarının düz bir çizgi üzerinde doğru açı oluşturduğunun görülmesiyle kazandırılabilir. Bu durum, Öklid’edayalı ölçmenin kullanılmadığı, öğrencilerin geometri derslerinde açıölçer ve pergel kullanmayı öğrenmediği çalışma biçiminden farklılık göstermektedir. A aşamasının önemini vurgulayan temel düşünce, günümüzde bile hâlâ geçerliğini koruyan Matematik Derneği’nin (1938) ikinci geometri raporunda aşağıdaki gibi ifade edilmiştir:
“Matematik öğretiminde yapılan en büyük hatalardan biri, zihinlerimizi bunlara hazırlamadan soyutlamalar yapmaktır.”
B aşaması, tümdengelimli bir aşamadır. Bu aşamada, fikirler büyük bir hassasiyetle tanımlanır ve sonuçlar teoremler olarak sunulur. Ayrıca bu aşamada, teoremler ispatlanırken matematik ve cebir de kullanılabilir. Çember teoremleri gibi yeni bir teoremle karşılaşıldığında, B aşamasına geçmiş olmak A aşamasına geri dönmeyi engellemez.
Son aşama olan C aşamasında, konulara daha evrensel bir bakış açısıyla bakılırken, teoremler arasında bağlantılar kurulmaya, sonuçlara mantıksal bir sistematikle yaklaşmaya çalışılır. Bu aşamada, aksiyomlar referans gösterilerek en başta kabul edilen varsayımlar açıklığa kavuşturulmaya çalışılır. Son aşama oldukça gölgede kalan bir yapıya sahiptir ve öğrencilerin küçük bir kısmını ilgilendirmektedir.
Yirminci yüzyılın başlarında devlet tarafından açılan ilkokul sayısının artmasıyla,
ortaokullara daha fazla sayıda erkek ve kız öğrenci geçişi olmuştur. Bu durum,
okullarda öğretilen matematikle ilgili yeni değişiklikleri beraberinde getirmiştir. Matematik derslerine çizim ve trigonometrinin dâhil edilmesi, geometrik ispatlar ve problemler üzerinde iki önemli değişikliğin yapılması ihtiyacını ortaya çıkarmıştır. Öğrencilerin grafiklere olan aşinalığı, konik kesitlerle bağlantılı koordinat geometrisine değinmenin yolunu açmıştır. Bu durum, ortaokulun son
senesinde verilen matematik derslerinin ortak bir özelliği haline gelmiştir.
1960’LARDAN İTİBAREN MÜFREDAT DEĞİŞİMİ
matematik olarak ifade edilen bu değişikliklerin, müfredat içeriği ve öğretim yöntemleri üzerinde önemli etkileri olmuştur. Öğretim yöntemleri ile ilgili yapılan değişiklikler, A aşamasında deneysel ve keşfedici yaklaşımların daha fazla kullanılması yönündeydi. İçerik değişiklikleri arasında kümelerin, matrislerin, olasılığın ve istatistiğin müfredata eklenmesi; bilgisayarlardan bahsedilmesi ve geleneksel güçlü Öklid etkisindeki tümdengelimli geometriye alternatif olarak dönüşüm geometrisinin dâhil edilmesi yer almaktadır. Kümeler konusunun üzerinde durulması o dönem için oldukça çelişkiliydi. Amerika Birleşik Devletleri’nde bukonuya İngiltere’ye göre daha fazla odaklanılmış fakat bu durumun müfredat üzerinde uzun dönemli etkisi olmamıştır. Olasılık ve İstatistik konuları yaygınlaşmış ve matematik müfredatı şaşırtıcı bir görünüm almıştır. Okul matematiğinde bilgisayarların kullanımına yönelik ilk çabalar oldukça sınırlı kalmıştır. Ülkeler ve ülkelerdeki okullar arasında farklılıklar görülse de bilgisayarların okul matematiğinde yaygın olarak kullanımı 1990’lara kadar pek mümkün olmamıştır. Bilgisayarların matematik öğretimindeki etkisi, oldukça değişkenlik göstermiştir. Her ne kadar LOGO ve dinamik geometri gibi yazılımlar büyük oranda kabul görmüş olsalar da bilgisayarın matematik öğretiminde önemli bir rol oynaması gerektiği konusunda sınırlı bir fikir birliği sağlanmıştır.
İngiltere’de 1960’larda geometri müfredatında son derece önemli değişiklikler yapılmıştır. 1961 yılında yürütülen Okul Matematiği Projesi (OMP) bu değişiklikleri olumlu yönde etkilemiştir. OMP (1965) isimli kitabın ve bunu takip eden yeni kitapların yayımlanması, öğrencileri Godfrey ve Siddon’un Temel Geometri isimli kitabındaki standart teoremler ve bunların uygulamasına yönelik
formal tümdengelimli yaklaşıma yönlendiren A aşamasındaki etkinliklere kıyasla geometride önemli değişiklikler meydana getirmiştir. OMP adlı esere, A aşamasındaki geometrik şekillerin temel özellikleri ile yansıma, dönme, öteleme ve büyütme gibi dönüşümler dâhil edilmiştir. Bir üçgenin iç açılarının ölçüleri toplamı, çokgenlerin açılarla ilgili özellikleri ve Pisagor teoremi gibi konular ders kapsamına alınmıştır. Öklid tarafından derinleştirilen ispat yaklaşımının izlendiği formal teorem üzerinde ise çok az durulmuştur. Eş üçgenlerden çok az bahsedilmiş olsa da, ölçek katsayısı fikri ve büyütme dönüşümü kullanılarak benzerlik üzerinde önemle durulmuştur.
1980’lere gelindiğinde, yaygın olarak kullanılan ortak bir müfredat ortaya çıkmıştır. Bu müfredatta Öklid tarzındaki teoremlere ve ispatlara çok az yer verilmiştir. 1982’de okul matematiği hakkında yayımlanan Cockcroft raporu şunu belirtmektedir: “Modern” ve “geleneksel” matematik arasındaki fark, daha az
hissedilir hâle gelmiştir (Cockcroft, 1982). Bu dönemin en önemli düşüncesi,
1960’lardaki reformlardan çok fazla etkilenmediği gözlenmiştir. Matematik Öğretmenleri Ulusal Konseyi (NCTM) yayımladığı standartlarda (1989, 2000b) informal yaklaşımlara vurgu yapan müfredatla ilgili düşüncelere daha fazla yer vermiştir. Ayrıca bu konsey, tümdengelimli unsurları kaybetmeden matematik konuları arasında ilişkiler kurmaya çalışmıştır.
Matematik Derneği’nin (1923,1938) geometri öğretimine yönelik önerdiği üç aşamalı model, öğrencilerin geometriyi nasıl öğrendiğiyle ilgili karmaşık bir modelin öncüsü olarak görülebilir. Inhelder ve Piaget (1958), öğrencilerin düşüncelerinin soyut işlem döneminde özel örnekler üzerinde düşünme sürecinden daha genel ve soyut ifadeleri düşünme yeteneğine doğru değiştiğini belirtmişlerdir. Bu durum, somuttan soyuta doğru geçişin belirli zamanlarda ve kolay bir biçimde olduğu, öğretmenin oluşturduğu sınıf ortamındaki görevlerin doğasından etkilenmediği anlamına gelmemelidir. Adey ve Shayer (1994) bilişsel hızlanma ile ilgili araştırmalarında, öğrencilerin daha yüksek düzeylerde düşünebilme kabiliyetlerinin, genel düşünce kabiliyetlerini geliştirmek için yapılandırılan sınıf görevlerinden etkilenebildiğini göstermişlerdir.
Van Hiele (1986), geometri ile ilgili beş düzey tanımlamıştır. Van Hiele’nin bu
çalışması, öğrencilerin geometri öğrenmeye başladıklarında karşılaşacakları hiyerarşik düzeyleri tanımlamaya yönelik önemli bir girişimdir ve geometri dersinin nasıl yapılandırılması gerektiği konusuna rehberlik etmektedir. Van Hiele (1986)’nin önerdiği beş düzey aşağıdaki gibidir:
Düzey 1: Şekiller, parçalar veya özellikler algılanmaya veya tanınmaya başlanmadan önce bir “bütün” olarak algılanır. Bu düzeydeki bir çocuk, çemberi veya kareyi bu şekillerin sahip olduğu özelliklerin güçlü etkisi altında kalmadan ya da elips veya dikdörtgenden ayırt etme yeteneğine gerek duymadan tanıyabilir.
Düzey 2: Bu düzeyde, öğrenciler şekillerin kendilerine has özelliklerini tanımaya başlar ve bu özelliklerle onları tanımlayabilir. Böylece kare, dört eşit
uzunlukta kenara ve her köşesinde dik açılara sahip bir şekil olarak görülür.
Ayrıca öğrencilerde karede eş köşegenlerin dik açıyla kesiştiği bilinci bu düzeyde ortaya çıkar. Ancak karenin eşkenar dörtgenle veya dikdörtgenle ilişkisi öğrenciler tarafından fark edilemez.
Düzey 3: Bu düzeyde, şekillere ve bu şekillerin diğer şekillerle ilişkilerine yönelik tanımlar daha iyi anlaşılmaya başlanır. Tanım ve özellikleri listeleme arasındaki ayrım, daha açık ve net hâle gelir. Ayrıca öğrencilerin şekiller arasındaki ilişkiyi algılayabilmesi daha da netleşir. Örneğin kare, eşkenar dörtgen veya dikdörtgenin özel bir hâlidir. Bununla birlikte kare, aynı zamanda Şekil 2.1’de gösterildiği gibi paralelkenarın özel bir hâlidir.
eşit olduğu sonucu çıkarılabilir.
Düzey 5: Son düzeyde, başlangıçtaki varsayımlardan türetilen ve teorem sistemi ile karakterize edilen geometrinin, sistematik gelişiminde aksiyomların rolü daha iyi anlaşılır.
Öğrenmeyi karakterize etmeye çalışan her çaba gibi van Hiele düzeyleri de gerçekliği, farklı fikirlerin değişken kavramsal zorluklarını hesaba katmadan, düzeyler arasında küçük ilerlemelerle geçiş yaparak açıklamaya çalışır. Öğrenciler, üzerinde çalıştıkları konulardaki bilgi düzeylerine göre düzeyler arasında ileri ve geri gidebilirler. Böylece, Düzey 4’te bilindik bir materyal üzerinde işlem yapmaktan oldukça mutlu olan bir öğrenci, yeni fikirlerle karşılaştığında daha önceki düzeylere geri dönebilir. Düzey 2’deki bir öğrencinin fikirleri, deneysel olarak keşfedilebileceği gibi zor problemlerin çözümü sırasında da açığa çıkarılabilir.
Şekil 2.1 Bazı dörtgenler arasındaki ilişkiler
UZAMSAL FARKINDALIK VE
GEOMETRİK SEZGİ
Bölüm 1’de ifade edildiği gibi, okul geometrisinin amaçlarından biri, öğrencilerin uzamsal farkındalıklarını geliştirmektir. Bu durum, inşaatçılar, mimarlar, arazi ölçüm mühendisleri, denizciler gibi kişiler arasında geometrik sezgi gerektiren gerçek dünya ile ilgili bir husus olarak algılanmaktadır. Rafların yapımı,
perdelerin dikimi, bir gezi planlarken harita çözümleme veya şehirde bir yerin
bulunması gibi günlük hayatımızdaki bazı işlerde de benzer bir ilişki söz konusudur. Bu pratik uygulamalar ile sınıfta yapılan faaliyetler arasındaki bağlantı açık değildir. Uzamsal beceri gerektiren faaliyetlerin bu tür görevlerdeki performansı artırabileceği tahmin edilirken, okul dışında gerçekleştirilen öğrenmenin sınıfta yapılan faaliyetler üzerindeki etkisini ayırt etmek oldukça güçtür. Örneğin, oyuncaklarla kazanılan çocukluk tecrübeleri, okullardaki geometri derslerinden daha etkili olabilir. Ayrıca çocukluk tecrübeleri, okul geometrisindeki başarıya olumlu katkı sağlayabilir.
Geometriye A ve B aşamaları yaklaşımının ve van Hiele’nin düzeylerinin ortak özelliği, tümdengelimin geometri ile ilişkili olarak kullanılmasıyla elde edilen başarının farklı pratik deneyimlere bağlı olmasıdır. Fischbein (1982), ispat konusunda sezgiyi tartışırken “sezginin temel özelliklerinden biri olan belirginlik özelliğinden” bahseder. Fischbein, Pisagor teoremi gibi aşikâr olmayan matematiksel gerçeklerle dikey karşıt açıların açıkça görülen eşitliğini karşılaştırır. Geometri öğrenimi, hem sezgisel hem de analitik unsurları içinde barındırır. Sezgiler, geometrik şekillerin açık, kritik ve gizli özelliklerini tespit etme, varsayımlar üretme, geometrik problemleri çözerken kullanışlı yapıları belirleme gibi önemli görevleri içerir.
Analitik beceriler-muhakeme etme yeteneği-belli ölçüde sistematik olarak
öğrenilebilirken, geometrik şekillerle ilgili tecrübelerimizin bir ürünü olan sezgisel becerilerin nasıl geliştirilebileceği çok belirgin bir durum değildir. Ancak okul geometrisinin şekiller üzerinde gözlemleme, uğraşma, yönlendirme, ilişkilendirme, tartışma ve açıklama yoluyla geometrik sezgiyi ve analitik becerileri geliştirmesi gerektiği oldukça açıktır.
GEOMETRİDE KAVRAM YANILGILARI
A açısı, B açısından daha büyüktür. (%33) B açısı, A açısından daha büyüktür. (%4) A ve B açısı aynı büyüklüktedir. (%52) Bir şey söylenemez. (%4)
Şekil 2.2Açılardan hangisi daha büyüktür?
İki açı, kareli kâğıt üzerine bir eğim yapacak biçimde çizilmiştir. Eşit ölçülere sahip bu açılar, şekillerden birinde açı kolu diğerinin yaklaşık iki katı olacak biçimde gösterilmiştir. Cevap veren öğrencilerin büyük bir bölümü, bu soruyu yanlış cevaplamışlardır. Yanıt verenlerin büyük bir kısmının, açıların ölçülerinin eşit olduğunu neden anlamadıkları ve doğru cevapların da nasıl oluşturulduğu konusunda elimizde bir kanıt yoktur. Yanıt verenlerin büyük bölümü, akıl yürütmeden açıların yaklaşık olarak aynı olduğu biçiminde düşünerek yorum yapmışlardır. Öğrencilerin açıları dönme veya çevirmenin bir ölçütü olarak kavrayamamalarının ve açıların genellikle statik diyagramlarda gösterilmesinin
bu durumu engellediğinden hiç şüphe yoktur. Geometri öğreniminin erken
aşamalarında yapılan pratik uygulamalar son yıllarda bilgisayar görüntülerinin sağladığı çeşitli imkânlarla desteklenmiş olmasına rağmen, açı fikrinin dönme fikriyle ilişkilendirilmesi ile ilgili zorluklar hâlen devam etmektedir.
Şekil 2.2’deki örneğe geri dönecek olursak; bu tür hatalarda izlenecek tek yol, öğrencilerin açıölçeri nasıl kullanacaklarını bildiklerini varsayarak öğrencilerden ilgili açı çiftini ölçmelerini istemektir. Açıların ölçülerinin eşit olduğunu düşünen öğrenciler, bir çelişkiye maruz kalırlar. Çünkü onlar bir açının diğerinden daha büyük olduğuna yönelik doğru olmayan sezgisel algı ile açıların ölçüm
A
sonuçlarını karşılaştırmak zorundadırlar. Sezgisel algı ve ölçümün sunduğu kanıt arasında bir çelişki oluşturmak, öğrencilerin mevcut düşüncelerinin yetersizliğine dikkat çekerek onlara fikirlerini değiştirmede yardımcı olmaktadır. Adey ve Shayer (1994), öğrencilerin bilişsel becerilerinin geliştirilmesinde yardımcı bir araç olarak bilişsel çelişkinin önemini vurgulamışlardır. Araştırmacılar, bilişsel çelişkiyi kafa karıştırıcı, önceki tecrübe veya bilgilerle uyumsuz olan “olay veya gözlem” biçiminde tanımlarlar. Hatalar ve kavram yanılgıları, öğrencilerin bir
duruma ve kabul edilen bir açıklamaya yönelik algıları arasındaki çelişkiyi içeren
durumlar için değerli kaynaklar olabilirler.
Sıkça karşılaşılan bir diğer zorluk kaynağı, çevre ve alan arasındaki kafa karışıklığıdır. Daha ileriki aşamalarda, yüzey alanı ve hacim arasındaki karışıklık karşımıza çıkmaktadır. Karışıklık bir nebze de olsa dilden yani kelimelerin anlamından kaynaklanmış olabilir. Ancak öğrencilere şekillerin çevresi ve alanlarının birbiriyle orantılı olduğunu yani birindeki artışın diğerinde de artışa
neden olacağını düşündürecek daha ciddi bir kavram yanılgısı bulunabilir.
Öğrencilerin Şekil 2.3’teki gibi çevre uzunluğundaki bir değişimin alan üzerinde ve alandaki değişimin de çevre uzunluğunda değişim yapacağı anlamına gelmediğini gösteren örneklerle çalışmaları faydalı olacaktır. Ancak diğer kavram yanılgıları gibi, alan ve çevreyle ilgili bu çelişkinin oldukça kalıcı ve tek bir karşı örneğin referans gösterilmesiyle veya sabit bir alana sahip dikdörtgenlerin çevrelerinin incelenmesiyle giderilmesi mümkün olmayacaktır. Bu durumu ortadan kaldırmak için hatalı sezgi ve geometrik gerçekler arasındaki çelişkinin farklı örneklerle karşılaştırılması gerekmektedir.
Şekil 2.3 Çevre ve alan ile ilgili kavram yanılgıları
Basit düzeydeki çelişkiler, kelimelerin anlamlarının yanlış anlaşılmasından dolayı ortaya çıkabilmektedir. Fielker (1973), Şekil 2.4’teki gibi a,b,c olarak adlandırılan
üç paralel doğru ile ilgili bir örnek sunmuştur. On bir yaşındaki öğrenciler, “a, b’ye ve b de c’ye paraleldir.” demişlerdir. Fakat Fielker “a da c’ye paraleldir.”
dediğinde, öğrenciler “hayır, çünkü b iki doğru arasındadır!” biçiminde cevap
vermişlerdir. Öğrencilerin paralelin anlamı konusunda doğruların birbiriyle yan yana olmaları gerektiği biçiminde sınırlı bir bakış açısına sahip oldukları anlaşılmaktadır. Öğretmenlerin demiryolu rayları veya dikdörtgenlerin karşıt kenarları gibi sürekli aynı doğru çiftlerini örnek olarak vermeleri, bu durumun
muhtemel sebebi olabilir. Demiryolu rayları, yanıltıcı bir örnek olabilir. Çünkü perspektifin etkisi ile raylar uzak bir noktada birleşiyor gibi görünmektedir. Bir diğer kavram yanılgısı, küçük çocukların oldukça uzun iki doğru parçasının paralelliklerini gözleyemediklerini ifade eden Kerslake (1979) tarafından dile getirilmiştir. Bu örnekler, paralel doğrular gibi basit görünen durumlarda bile şaşırtıcı kavram yanılgılarının ortaya çıkabileceğini göstermektedir. Gal ve Vinner (1997), benzer zorluklara dik açılarda da karşılaşıldığını ifade etmişlerdir. Paralel doğrulardan farklı olarak eğer a, b’ye, b de c’ye dikse; iki boyutlu bir düzlemde a’nın c’ye dik olduğu doğru değildir. Dolayısıyla öğrencilerin zamanla farklı
örnekleri tecrübe etmeleri, öğretmenlerin de beklenmeyen ve şaşırtıcı yanlış
yorumlamalara karşı olmaları gerekmektedir.
Şekil 2.4 Paralel üç doğru
Birçok kelime, günlük anlamlarından farklı matematiksel anlamlara sahiptir. “Benzer” kelimesi buna net bir örnek teşkil etmektedir. Köşegen kelimesiyle ilgili çarpıcı bir örnek Pimm (1987) tarafından ortaya atılmıştır. Bir öğrenciden, farklı çokgenlerin köşegen sayılarını bulması istenmiştir. Öğrencinin verdiği cevaplardan ikisi Şekil 2.5’te gösterilmiştir. Öğrenci, dikdörtgenin herhangi bir köşegene sahip olmadığını ancak üçgenin üç tane köşegeninin olduğunu belirtmiştir. Bu açıklamadan öğrencinin kavram yanılgısına sahip olduğu söylenebilir. Sonuç olarak öğrencinin köşegenin günlük hayatta kullanılan anlamını düşünerek eğime sahip kenarları saydığı sonucuna varılabilir.
4 KENAR
3 KENAR
0 KÖŞEGEN
3 KÖŞEGEN
Şekil 2.5 Köşegenlerle ilgili kavram yanılgısı a
b
Pimm (1987)’in de ifade ettiği gibi, matematiksel kelimeleri ilgilendiren bu tür yanlış anlamalara yönelik benim en sevdiğim örnek, bir derste yaptığım gözleme dayanmaktadır. Öğretmen, 12 yaşındaki öğrencilerinden farklı üçgenler ve hayal edebildikleri diğer çokgenleri çizmelerini ve adlandırmalarını istemiştir. Şekil 2.6’dan, erkek öğrencilerden birinin dik kenar gösteriminden ziyade sağ tarafın solun tam karşısında olması gerektiğini düşündüğü anlaşılmaktadır.
SAĞ-AÇILI ÜÇGEN SOL-AÇILI ÜÇGEN
Şekil 2.6 Dik açılı ne anlama gelir?
Matematiksel kelimeler, genel durumları dışlayacak biçimde kelimelerin ‘olağan’ anlamlarını alırlar. Şekil 2.7’de farklı beşgen türleri gösterilmektedir. Beşgen kelimesi, genelde düzgün bir beşgenle ilişkilendirilmektedir. Bir kişiden beşgen çizmesi istendiğinde, bu kişi tabanda yatay bir kenara sahip düzgün bir beşgen çizecektir. Ancak beşgenlerin düzgün ve kenarlarının aynı uzunlukta olması gerekmez. Ayrıca beşgeninbir kenarının yatay hatta konveks olması da zorunlu değildir. Şekil 2.7’de gösterilen beşgenlerin hepsi eşit uzunlukta kenarlara sahiptir. Bu beşgenlerden sadece ilki düzgün çokgendir ve genel “alışıldık” pozisyondadır. Bu örnekler, öğrencilerin dikkatlerini “düzgün” kelimesinin anlamına çekmek için faydalıdır. Bu noktada, düzgün çokgenlerin sadece kenar uzunluklarının değil, açılarının ölçülerinin de eşit olması gerekmektedir. Birbirine uçlarından serbest biçimde eklenen beş eşit plastik çubukla veya dinamik geometri yazılımıyla bir beşgen oluşturmak, düzgün bir çokgenin eş açılara sahip olduğunu vurgulama anlamında iyi bir yöntemdir.
Şekil 2.7 Eşit kenar uzunluklarına sahip bazı beşgenler
Zorluklar, çoğunlukla ilişkiler hakkındaki varsayımların belirli bir şekil temel alınarak oluşturulmasından kaynaklanmaktadır. Şekil 2.8, birbiriyle ilişkili iki örneği göstermektedir. Bunlardan birincisinde, kenarortayın açıyı ikiye ayırdığını
şekildeki üçgen ikizkenar değil ise, hatalı bir biçimde açıortayın karşı kenarı ikiye böldüğü varsayılabilir. Yapılacak çizimlerle veya dinamik geometri yazılımları kullanılarak, benzer özelliklere sahip şekiller üzerinden değerlendirme yapmanın yanlışlığı ve muhtemel hatalar vurgulanabilir.
Şekil 2.8 Uygun olmayan şekillerden çıkarılan hatalı sonuçlar
Şekil 2.9’da düzgün bir beşgenin tepe açısını üç eşit parçaya bölen iki köşegen gösterilmektedir. Burada, sezginin doğru sonuca yönlendirmesi ile ilgili bir problemimiz bulunmaktadır. Ancak sezgi, sonucun doğru olduğundan emin olmak için tek başına yeterli değildir. Bir açının üçe bölünmesi durumu, Şekil 2.9’daki üç ikizkenar üçgenin açıları ölçülerek gösterilebilir. Bu durum, çember içerisine bir beşgen çizilerek ve bir köşedeki üç açının eşit uzunluklardaki yaylara karşılık geldiği gösterilerek de ispatlanabilir.
Şekil 2.9 Düzgün çokgendeki bir açı, köşegenlerle niçin üçe ayrılır?
Şekil 2.10 Bu bir küp müdür yoksa bir altıgen içerisindeki üç eşkenar dörtgen midir?
Benzer zorluklar, katı cisimlerin açık hallerinin çizimi sırasında veya öğrencilerden bu tür çizimler yapmaları istendiğinde de ortaya çıkmaktadır. Şekil 2.11, altı karenin iki farklı konumunu göstermektedir.Birinci şeklin bir küpün açık hâli olduğu anlaşılmaktadır. Ancak ikinci şekil, bir küpün açık hâli değildir. Çünkü karelerin ikisi katlandığında bu kareler üst üste gelecektir. Katı cisimlerin açık hallerinin zihinde nasıl canlandırılacağı, hangisinin bir küp meydana getireceğini ve hangisinin bir küp oluşturmayacağını belirlemek için şeklin nasıl katlanacağı çoğu insan açısından kolay bir durum değildir. Uygun biçimde tasarlanmış faaliyetler kullanılarak, görselleştirme gücü geliştirilebilir.
Şekil 2.11 Bir küpün muhtemel açık hali hangisi olabilir?
İSPAT YAPMAYI ÖĞRENMEK
Matematikte ispat, genel olarak varsayımların doğrulanmasıyla gösterilir. Bu süreci, kanıtın veya varsayımın makul olduğunun, makul değilse de en azından hatalı olmasının pek de mümkün olmadığının gösterilmesi takip eder. Matematiksel ispat, kesinlik içerir. Ayrıca matematiksel ispat, iddianın mevcut kanıtlara bağlı olduğu ve yeni kanıt ortaya çıktıkça değişime maruz kaldığı bilimsel veya hukuki bağlamdaki ispatlardan farklıdır.
1800 olduğunu, üçgenin açılarını ölçmek suretiyle deneysel kanıta dayanarak
bilmektedirler. Bu açıklamalar, öğrencilerin ispat yapmayı öğrenmeyle ilgili motivasyonlarındaki iki önemli zorluğu işaret etmektedir.
Birinci zorluk, neyin açık olduğu ile ilgilidir. Tümdengelim, kabul edilen varsayımlar temel alınarak oluşturulmalıdır. Ancak doğru olarak kabul edilen başlangıç noktaları, yeni başlayanlar için daha kabul edilebilirdir. Okul geometrisi, öğrencilere muhakeme zincirini izleme ve kendi tümdengelimli iddialarını geliştirebilme yeteneği ile birlikte varsayımlarını temellendirecekleri başlangıç noktalarını ifade etme dili ve geometrik fikirleri anlama yetisi kazandırmalıdır.
Öklid geometrisindeki zorluklardan biri, ikizkenar üçgenin taban açılarının ölçülerinin eşitliğinden çok sonuç çıkarma ile ilgilidir. Şekil 2.12’de kenar -kenar-kenar benzerlik kuralı kullanılmıştır. İspat, Öklid geometrisinde verilmiş olmasına rağmen açık olarak görülebilecek bir sonuç da ortaya çıkmaktadır. Bu tür gerçekleri formal yoldan ispatlamak çoğu öğrencinin motivasyonunu bozmaktadır. Çünkü doğru olduğu açık bir biçimde görülen bir durumun ispatlanmaya çalışılması, öğrenciler tarafından anlamsız bir çaba olarak görülmektedir. Her iki örnek, sezgi ve deneyin birlikte kullanılması nedeniyle doğru sonuçları göstermektedir. Bu durum, eşit kenar özelliğinin ikizkenar üçgeni tanımladığını anlama konusunda öğrencilere yardımcı olur. Ancak ikizkenar üçgeni doğru bir biçimde çizmek için gerekli bilgilerin göz önünde bulundurulması gerekmektedir. Bir sonraki aşamada, Şekil 2.12’deki teoremi ispatlarken benzerliği kullanmak öğrenciler için yönlendirici olabilir. Üçgenlerin benzer olması, kenarortayın A köşesindeki açıyı ikiye bölmesi ve BC kenarına dik olması anlamına gelir. Fakat bu tür özellikler, öğrencilerin çoğu tarafından ikizkenar üçgenlerin simetrisinden kaynaklanan durumlar olarak kabul edilmektedir.
ABC üçgeninde, AB ve AC kenarları eşit uzunluktadır.
D noktası, BC’nin orta noktası olsun.
Buna göre ABD ve ACD üçgenleri benzerdir. Çünkü AB = AC, BD = CD ve AD ortaktır.
Böylece ABD ve ACD açılarının ölçüleri eşittir.
Şekil 2.12 İkizkenar üçgenin taban açılarının eşit olduğunu ispatlama
İkinci zorluk, tümdengelimli ispat ile Balacheff’in (1988) naif deneycilik (naive empiricism) olarak nitelediği ölçüm sonucunu kabul etme arasında bir ayrım yapabilmektir. Üçgenin iç açılarının ölçülerinin toplamının 1800olduğunun aşikâr
gerçeğinden hareketle, bu tür durumlar için tümdengelimli iddianın önemli bir yeri vardır. Ancak öğrenciler sonucun doğru olduğunu kabul ettikten sonra böyle bir tartışmayla karşılaştıklarında, ispat yapmanın amacını anlayamayabilirler. Hoyles (1997), öğrencilerin “gördüklerinin” doğru olduğunu düşündükleri konularda deneysel bir çalışmayla karşılaştıklarında, varsayımın neden doğru olduğuna dair içsel bir zorunluluk geliştirdiklerinden bahsetmektedir. De Villiers (1998)’a göre ispat, önerinin doğruluğunugöstermede iddiadan daha fazlasıdır. Çünkü ispat, fikirlere derinlemesine bir bakış ve açıklama sunar. Bunun yanında, iddianın marifeti veya netliği kendi doğrusunu açık bir biçimde ortaya koyabilir. İspatlar öğrencilerle tartışılırsa kavramsal anlamalarını genişletmede, matematiksel iddiaların ve sonuçların sunduğu sezgi ve uyarılara cevap vermede matematikçiler gibi düşünmeleri konusunda onları teşvik etmiş oluruz.
Problem çözümünde olduğu gibi, ispatları anlamak ve geliştirmek, geometrik
fikirleri anlamaktan ve muhakeme etme yeteneğinden fazlasını gerektirmektedir.
Bir öneriyi ispatlamada veya bir geometrik problemi çözmede başarısız olma sık karşılaşılan bir durumdur. Başka birinin iddiasını takip ederken zorlanmama, küçük bir özelliği gözden kaçırdığını anlayarak şaşırma veya çözüm yapan kişinin kendi çözüm stratejisini nasıl kullandığına şahit olma da sık karşılaşılan durumlardandır. Öğrencilerin, yeni yollar keşfetmelerini, geometrik şekilleri farklı açılardan görmelerini ve diğer fikirlerle bağlantı kurmalarını sağlamak için çeşitli stratejilerle donatılmış olmaları gerekmektedir.
BİLGİSAYARLARIN ROLÜ
Bilgisayar yazılım ve donanımının hızlı gelişimi, geometrinin sunumu ve keşfi ile ilgili yeni yolların ortaya çıkmasını sağlamıştır. Her birinin iki öğretim türüyle ilişkilendirildiği iki kapsamlı tür bulunmaktadır. Bu türler, Şekil 2.13’teki tabloda gösterilmiştir.
TÜM SINIF BİREYSEL VEYA
KÜÇÜK GRUP
AÇIK
KAPALI
Şekil 2.13 Sınıfta bilgisayar kullanımı ile ilgili iki boyut
tahtayla entegre olan bir bilgisayarla donatılmıştır. Bu sınıflar, belirli bir konuyu hızlı bir biçimde göstermek veya yeni fikirleri denemek için kullanılabilir. Şekil 2.13’ün diğer boyutu, öğrencilerin üzerinde çalıştığı görevlerin niteliğine göre açık veya kapalı kullanım türüyle ilişkilidir. Kapalı görevler hassas yönlendirmeleri ve rutin egzersizleri temel alırken, açık görevler girişimcilik ve yaratıcılık becerisi gerektiren daha açıklayıcı problem-odaklı faaliyetleri içermektedir. Aynı sınıflandırma, kapalı soruları veya öğrencilerin düşüncelerini yönlendirebilecek daha açık uçlu tartışmaları ve uygulamaları içermektedir. Bu sınıflandırma, sınıfın tümüne uygulanan faaliyetler için de kullanılabilir. Her iki kategori de bu aralığın uç noktalarını teşkil etmektedir. Çünkü birçok ders, her iki boyutun bileşenlerini içerebilir. Yazılımlar ve buna eşlik eden kaynaklar akılda
genel olarak belirli kullanım türlerine göre tasarlanmaktadır.
Yazılım, farklı kategorilerde sınıflandırılabilir:
Küçük yazılım, belli becerileri geliştirmek, bir süreç veya konu hakkındaki fikirleri güçlendirmek için kullanılmaktadır. Bu yazılımlar, çeşitli zorluk seviyelerindeki bulmacalar ve oyunlar aracılığıyla, öğrencilere becerilerini kontrol etme imkânı veren ilgi çekici araçlardır.
Üretken yazılım, çok farklı amaçlar için kullanılabilir. LOGO, Cabri Geometry ve Geometer’s Sketchpad gibi dinamik yazılım paketleri sıkça kullanılan örnekler arasında yer almaktadır. Ayrıca grafik çizimleri yapabilen ve dönüşüm geometrisini keşfetmeye olanak sağlayan Omnigraph ve Autograph da bu yazılıma örnek olarak verilebilir. Bu özellikler, grafik özellikli hesap makinelerinde de bulunmaktadır. Bu makinelerin küçük ve düşük çözünürlüklü olmaları, bilgisayar monitörlerine olan ilgiyi arttırmıştır.
Öğretim ve kaynak paketleri: Bu paketler, genel olarak DVD veya CD -ROM formatında bulunurlar. Ayrıca bunlar interaktif olmaları, zihinde daha fazla canlandırma sağlamaları ve esnek yapıları itibarıyla kitap gibi kaynaklardan farklılık gösterirler.
Bunun yanında internet, çeşitlilik açısından zengin ve sürekli olarak büyüyen bilgi ve düşünce kaynağını teşkil eder. Ayrıca diğer türlerin tüm örneklerini bünyesinde barındırır.
Şekil 2.14 Simetri ve dönüşüm: SMILE programı
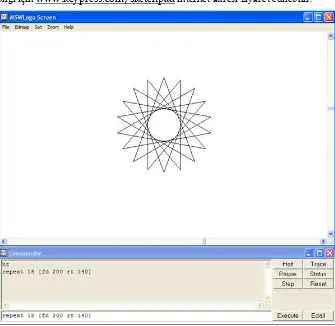
MSW LOGO, www.softronix.com tarafından LOGO programlama dilinin bir
versiyonu olarak ücretsiz olarak sunulmaktadır. Yazılım, öğrencilere basit ve çok yönlü bir ortam sağlamaktadır. Bunun yanında kolay öğrenilebilen, küçük ama güçlü bir komut kümesi kullanılarak geometrik şekilleri çizebilme yeteneği de kazandırmaktadır. Şekil 2.15’te gösterilen örnek, 18 tane sivri uca sahip bir yıldızdır. Bu şekil, 200 birim uzunluğun 1400’lik açıyla döndürülmesi ve bu iki
komutun 18 defa tekrar edilmesiyle çizilmiştir. Bu yazılım, Bölüm 4’te detaylı olarak incelenen bir konu olan, düzgün çokgenlerin özelliklerinin keşfedilmesinde kullanılan LOGO’nun en basit uygulamalarından birinin eklentisidir.
Dinamik geometri yazılımları, geometrik şekillerin ekranda çizilmesini ve sonrasında noktaların sürüklenerek değiştirilmesini sağlamaktadır. Şekil 2.16’da Cabri Geometry ekranı ve bir üçgenin üç kenarortayı gösterilmektedir. Eğer üçgen köşelerinden herhangi biri kullanılarak sürüklenirse, üçgenin şekli değişmekte ancak kenarortaylar hâlâ ortak bir noktada kesişmektedir. Yazılım aynı zamanda parçaların uzunluklarını da göstermektedir. Bölüm 7’de tartışılacağı üzere, her kenarortaya ait parçaların uzunluklarının 2:1 oranında olduğu yazılım aracılığıyla kolaylıkla görülebilir. Cabri Geometry, Texas Instruments tarafından üretilmiştir. Bu programla ilgili daha fazla bilgi edinmek için education.ti.com internet adresine girilebilir. Yazılım, Fransa’da Grenoble Üniversitesi’nde üretilmiştir ve yazılımla ilgili interaktif örneklerden bazıları
www-cabri.imag.fr adresinde bulunmaktadır. The Geometer’s Sketchpad
bilgi için www.keypress.com/sketchpad internet adresi ziyaret edilebilir.
Şekil 2.15 LOGO programında 18 tane sivri uca sahip yıldızın çizimi
Grafik çizim programlarının çoğunda, kendi ana fonksiyonlarının yanında, şekillerin kolayca çizilmesi ve bunların dönüştürülmesi için standart uygulamalar bulunmaktadır. Şekil 2.17’de, Autograph programı kullanılarak oluşturulan bir ekran görüntüsü görülmektedir. Birinci bölgedeki üçgen, y eksenine, sonraki görüntü ise y = x doğrusuna göre yansıtılmıştır. Bu iki yansımanın, saat yönünde
orjin etrafında 900’lik bir döndürmeyle eş oldukları görülebilir. İki dönüşüm ters
sırayla yapılırsa aynı sonuç elde edilemez. Üçgenin eşini meydana getiren tek dönüşüm, daha önceki gibi 900’lik bir dönüştür ancak bu dönüş saat yönünün
tersi yönde yapılmalıdır. Aynı sonuç, üçgenin birinci bölgede önce y = x
doğrusuna göre, sonra görüntünün y yerine x eksenine göre yansıtılmasıyla da elde edilebilir.
Grafik çizim yazılımı olan Autograph ile ilgili daha fazla detay
Software tarafından çıkarılan ve yaygın olarak kullanılan bir diğer grafik çizim programıdır. Bu program ile ilgili ayrıntılı bilgiler www.spasoft.co.uk adresinden edinilebilir.
Şekil 2.18’de www.mathsnet.net web sitesinden alınmış interaktif bir geometri sayfası görülmektedir. Bir doğru üzerinde, simetrisi B olan bir A noktası ve
hareket edebilen bir Xnoktası bulunmaktadır. Bu şekilde, hareket edebilen A ve
B noktaları ile AX ve XB mesafeleri gösterilmektedir. Bir öğrenciden üç ifade
arasından bu şekille ilgili bir seçim yapması istenmiştir. Doğru olan ifade, X’in AB’nin orta dikmesi boyunca hareket ettiği biçimindeki ifadedir. Bu web sitesi, farklı geometrik durumları matematiksel kaynaklarıyla birlikte göstermektedir. Ayrıca bu site, öğrenciler ve öğretmenler için matematik öğrenimi ile ilgili önemli
sitelerden biridir. ces.hull.ac.uk/people/DougFrench internet adresi, sınıf
kaynaklarını ve diğer sitelere erişim linklerini içermektedir.
Şekil 2.17 Autograph ekranında dönüşümler
Şekil 2.18 Mathsnet: İnternette interaktif geometri
SONUÇ
On dokuzuncu yüzyıldaki okullarda Öklid’e temelden bağlı olan geometrinin karakteristik özelliği, geometrik öğelere yönelik sezgisel hissin altında yatan noktaları fazla göz önüne almadan tümdengelime daha çok önem vermesidir. İngiltere’de 20. yüzyılın ilk yarısında, pratik tecrübe üzerine giderek artan bir vurgu yapılmıştır. Fakat 1960’lara kadar öğrencilerin çoğu geometriyi anlaşılmaz
teorem-ispat ve çözümü imkânsız problemlerin sıkıcı bir rutini olarak görmeye
devam etmişlerdir. Yirminci yüzyılın ikinci yarısında, geometrinin tümdengelimli yönüne yönelik güçlü bir akım ortaya çıkmıştır. Böylece pratik ve deneysel bakış açıları ile cebirsel yaklaşımlar daha baskın bir duruma gelmiştir. Pratik üzerine daha fazla ağırlık verilmesi ile ilgili durum, birçok ülke için de geçerlidir.
Geometrinin geleceği konusunda geniş çapta bir tartışma bulunmakla birlikte,
İngiltere’de ispat ve muhakeme yapmaya doğru bir yönelim söz konusudur. Geometri öğretiminde bilgisayarların kullanımı gittikçe artmaktadır. Bilgisayarların oynayabilecekleri hassas rol veya geometri öğreniminde deneysel aşamanın ötesinde sergileyebilecekleri etkinliklerle ilgili çok az ortak görüş bulunmaktadır. Ancak akıllıca kullanıldıklarında öğrencilerin motivasyonunu önemli derecede arttırıcı ve anlamalarını geliştirmeye yönelik potansiyel anlamında değerli kaynaklar oldukları yönünde güçlü bir algı bulunmaktadır.
kullanımını gerektirmektedir. Sezgi geometrik şekiller ve pratik etkinlikler ile ilgili tartışmalarla farklı tecrübeler kazanılması temeline dayanmaktadır. Tümdengelim sanatı, öğretmen ve ders kitapları tarafından sunulan örneklerle öğrenilir. Bunun yanında, öğrenciler öğretmenlerinin vereceği bireysel veya grup görevlerine ihtiyaç duymakta ve bu hususlar iddialarını geliştirmede kendileri için fırsat sunmaktadır.