BAB 2
LANDASAN TEORI
2.1 Sistem Pakar
Sistem pakar (Expert System) adalah sistem yang berusaha mengadopsi pengetahuan manusia kedalam komputer, agar komputer dapat menyelesaikan masalah seperti yang dilakukan oleh para ahli. Dan perancangan sistem yang dibangun harus benar-benar dari narasumber yang ahli dibidangnya, sehingga ketika sistem selesai dibuat, sistem tersebut memang dapat membantu pengguna dalam menyelesaikan masalah dan tidak menimbulkan masalah berikutnya.
Sistem pakar merupakan cabang dari AI (Artificial Intelligent) yang membuat penggunaan pengetahuan yang dikhususkan secara ekstensif untuk memecahkan masalah pada level human “ahli”. Seorang yang ahli yaitu mempunyai pengetahuan atau keterampilan
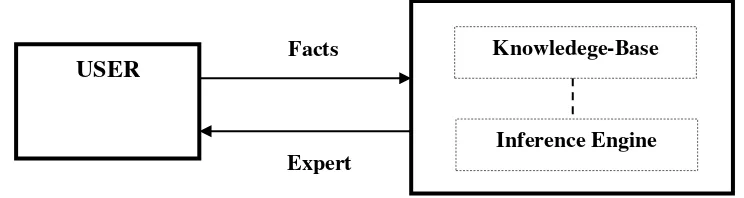
tertentu yang tidak diketahui atau ada untuk kebanyakan orang. Seorang ahli dapat memecahkan masalah yang tidak dapat dipecahkan sama sekali oleh orang lain atau memecahkanya dengan lebih efisien (tetapi tidak mudah). Berikut adalah konsep dasar dari fungsi sistem pakar :
Gambar 2.1 : Konsep dari Fungsi Sistem Pakar
USER Knowledege-Base
Inference Engine Facts
2.1.1 Manfaat dan Kelemahan Sistem Pakar
Adapun manfaat yang dari sistem pakar adalah sebagai berikut (Kusrini, 2006) : 1. Memungkinkan orang awam bisa mengerjakan pekerjaan para ahli.
2. Bisa melakukan proses secara berulang secara otomatis. 3. Menyimpan pengetahuan dan keahlian para pakar. 4. Meningkatkan output dan produktivitas
5. Meningkatkan kualitas
6. Mampu mengambil dan melastarikan keahlian para pakar (terutama yang termasuk keahlian angka).
7. Mampu beroperasi dalam lingkungan yang berbahaya. 8. Memiliki kemampuan untuk mengakses pengetahuan. 9. Memiliki reabilitas.
10.Meningkatkan kapabilitas sistem komputer.
11.Memiliki kemampuan untuk bekerja dengan informasi yang tidak lengkap dan mengandung ketidakpastian.
12. Sebagai media pelengkap dalam pelatihan.
13. Meningkatkan kapabilitas dalam penyelesaian masalah. 14. Menghemat waktu dalam mengambil keputusan.
Selain memilki manfaat yang begitu banyak sistem pakar juga memiliki kelemahan yaitu sebagai berikut :
1. Biaya yang diperlukan untuk membuat dan memeliharanya sangat mahal.
2. Sedikitnya ketersediaan pakar dibidangnya sehingga sistem pakar sulit dibuat atau dikembangkan.
2.2 Metode Demspter Shafer
Teori Dempster Shafer pertama kali diperkenalkan oleh Arthur P. Dempster dan Glenn Shafer. Yang melakukan percobaan ketidakpastian dengan range probabilities dari pada sebagai probabilities tunggal. Kemudian pada tahun 1976 Shafer mempublikasikan teori Dempster pada buku yang berjudul Mathematical Theory of Evident. Secara umum teori Dempster Shafer ditulis dalam suatu interval :
[Belief, Plausibility]
Belief (Bel) adalah ukuran kekuatan evidence dalam medukung suatu himpunan proposisi. Jika bernilai 0 maka mengindikasikan bahwa tidak ada evidence, dan jika bernilai 1 menunjukkan adanya kepastian. Plausibility (Pl) dinotasikan sebagai berikut:
Pl (A) = 1 – Bel(Ᾱ) ... (1)
Plausibility juga bernilai 0 sampai 1. Jika kita yakin akan Ᾱ, maka dapat dikatakan bahwa Bel(Ᾱ) = 1, dan Pl(A) = 0. Plausibility akan mengurangi tingkat kepercayaan dari evidence. Fungsi kombinasi m1 dan m2 sebagai m3 dibentuk dengan persamaan (Sentz & Ferson, 2002) :
... (2)
Dengan :
1) m1 (X) adalah mass function dari evidence X 2) m2 (Y) adalah mass function dari evidence Y 3) m3 (Z) adalah mass function dari evidence Z
Pada contoh kasus berikut akan dijelaskan bagaimana metode Demspter-Shafer melakukan perhitungan dan menentukan hasil analisis berdasarkan gejala atau ciri yang dihasilkan dari penarikan kesimpulan. Contoh kasusnya adalah :
Tomy adalah seorang calon mahasiswa universitas X berasal dari Kota Kabupaten di Sumatera. Terdapat 3 jurusan yang diminati oleh Tomy yaitu Teknik Informatika (I), Ekonomi (E) dan Pariwisata (P). Untuk itu dia mencoba mengikuti beberapa tes uji coba. Uji coba pertama adalah tes logika dengan hasil tes menunjukkan bahwa probabilities densitas m1{I,E} = 0,75 Lalu pada tes kedua adalah tes matematika, hasil tes menunjukkan bahwa
probabilitas densitas m2{I} = 0,8. Tes ketiga adalah wawancara, hasil tes menunjukkan bahwa
densitas probabilitas m3{P} = 0,3 maka tentukan probabilitas densitas dari kombinasi gejala
(hasil tes) yang didapat oleh Tomy.
Hal pertama yang harus diperhatikan adalah ciri-ciri atau hasil tes yang didapat oleh calon mahasiswa baru, setelah itu maka akan dijabarkan satu per satu dan menghitung densitas probabilitas masing-masing dari ciri tersebut, caranya adalah sebagai berikut :
Anggota θ = {I,E,P}, dengan : I = Teknik Informatika E = Ekonomi
P = Pariwisata
Berikutnya, perhitungan densitas setiap gejala/ciri menggunakan persamaan (1) :
1. Gejala/Ciri 1 : Nilai Tes Logika
Dari hasil tes logika yang didapat oleh Tomy, diberikan densitas sebesar 0,75. Maka nilai probabilitasnya adalah :
m1{I,E} = 0,75
m1{θ} = 1 – 0,75 = 0,25
Dari hasil tes matematika yang didapat oleh Tomy, diberikan densitas sebesar 0,8 maka nilai probabilitasnya adalah :
m2{I} = 0,8
m2{θ} = 1 – 0,8 = 0,2
Munculnya ciri baru maka harus dilakukan perhitungan densitas baru untuk beberapa kombinasi (m3). Untuk memudahkan perhitungan maka himpunan-himpunan bagian dibuat
kebentuk tabel.
Tabel 2.1 : Aturan Kombinasi untuk m3
{I} (0,8) θ (0,2)
{I,E} (0,75) {I} (0,6) {I,E} (0,15)
θ (0,25) {I} (0,2) θ (0,05)
Penjelasan tabel :
1. Kolom pertama berisikan semua himpunan bagian pada gejala pertama dengan m1 sebagai fungsi densitas.
2. Barisan kedua berisikan semua himpunan bagian pada gejala kedua dengan m2 sebagai fungsi densitas.
3. Baris kedua dan ketiga pada kolom kedua merupaka irisan dari kedua himpunan.
Selanjutnya dihitung densitas baru untuk beberapa kombinasi (m3) dengan persamaan Dempster Shafer, rumus yang digunakan adalah persamaan (2) dengan perhitungan densitas barunya adalah sebagai berikut :
m3{I}
m3{I,E}
Keterangan :
1. Terlihat bahwa pada mulanya dengan hanya gejala/ciri nilai tes logika, m{I,E}= 0.75, namun setelah ada gejala baru (tes matematika), maka nilai m{I,E} = 0,15.
2. Namun pada gejala/ciri tes matematika, m{I} = 0.8 tidak terjadi perubahan nilai densitas atau tetap.
3. Dengan adanya dua gejala/ciri tesebut maka nilai densitas paling tertinggi adalah m{I} = 0.8.
4. Namun jurusan belum dapat ditentukan karena masih terdapat satu gejala/ciri lagi yaitu nilai tes pariwisata dengan densitas m{P} = 0.3, sehingga harus dicari lagi nilai kombinasi dari m5.
3. Gejala/Ciri 3 : Nilai Tes Wawancara
Dari hasil tes wawancara yang didapat oleh Tomy, diberikan densitas sebesar 0,3 maka nilai probabilitasnya adalah :
m4{P} = 0,3
m4{θ} = 1 – 0,3 = 0,7
Tabel 2.2 : Aturan Kombinasi untuk m5
{P } (0,3) θ (0,7) {I} (0,8) ∅ (0,24) {I} (0,56)
{I,E} (0,15) ∅ (0,045) {I,E} (0,105)
θ (0,05) {P} (0,015) θ (0,035)
Dari hasil tabel kombinasi untuk m5 diatas maka nilai densitas dari m5 dapat ditentukan dengan rumus persamaan (2) sebagai berikut :
m5{I}
m5{P}
m5{θ}
Maka dapat disimpulkan bahwa calon mahasiswa baru yang bernama Tomy lulus pada jurusan Teknik Informatika, dengan nilai densitas yang paling tidak jauh berbeda dengan nilai densitas awalnya yaitu dengan nilai m{I} = 0.783.
2.3 Metode Certainty Factor (Faktor Kepastian)
Certainty factor menampilkan derajat kepastian sama seperti teori Dempster-Shafer yang
menggunakan notasi Bel. Certainty factor menggambarkan derajat kepercayaan atau ketidak percayaan, dimana hasil dari penjumlahan keduanya tidak selalu berjumlah 1. Certainty factor menggunakan MB(H|E) untuk menggambarkan nilai kepercayaan dari hipotesis H, Gejala E,
dan MD(H|E) untuk nilai ketidakpercayaan dari hipotesis H, gejala E. Karena keterangan atau
fakta bagian dari gejala salah satunya menyangkal hipotesis, MB(H|E) atau MD(H|E) maka
nilainya harus nol untuk setiap H dan E. Jadi rumus untuk Certainty factor adalah sebagai berikut (Coppin, 2004) :
CF(H|E) = MB(H|E) – MD(H|E) ... (3)
Keterangan :
CF(H|E) : Certainty factor dari hipotesis H yang dipengaruhi oleh gejala (evidence) E. Besarnya CF berkisar antara -1 sampai dengan 1. Nilai -1 menunjukkan ketidakpercayaan mutlak sedangkan 1 menunjukkan kepercayaan mutlak.
MB(H|E) : ukuran kenaikan kepercayaan (measure of increased belief) terhadap hipotesis H
yang dipengaruhi oleh gejala E.
MD(H|E) : ukuran kenaikan ketidakpercayaan (measure creased disbelief) terhadap hipotesis
E : Evidence (Peristiwa atau fakta)
Certainty Factor untuk kaidah dengan kesimpulan yang serupa (Similiarly Concluded Rules) :
CFCombine CF[H|E]1,2 = CF[H|E]1 + CF[H|E]2 * [1 – CF[H|E]1] ... (4)
CFCombine CF[H|E]old,3 = CF[H|E]old + CF[H|E]3 * [1 – CF[H|E]old] ... (5)
2.3.1 Contoh Kasus dan Perhitungan Certainty Factor (CF) pada Penelitian Sistem Pakar Penyakit Kulit Pada Manusia Menggunakan Metode Certainty Factor Berbasis Web (Yastita et al.,)
Pada contoh kasus berikut akan dijelaskan bagaimana metode Certainty Factor (CF) melakukan perhitungan dan menentukan hasil diagnosa berdasarkan gejala atau ciri yang dihasilkan dari penarikan kesimpulan. Contoh Kasus :
Seorang pasien mengalami suatu jenis penyakit kulit yang belum diketahui. Gejala yang dialami adalah sebagai berikut :
1. Gatal-gatal
2. Gatal diduga setelah mengkonsumsi makanan dan obat-obatan 3. Gatal yang dirasakan kurang dari 14 hari
4. Mempunyai riwayat alergi
Dari gejala yang telah diuraikan, sistem akan melakukan proses dengan metode CF. Setelah proses perhitungan selesai, maka sistem akan menyimpulkan jenis penyakit yang diderita oleh pasien. Perhitungan manual dari contoh kasus :
Tabel 2.3 Nilai Kepercayaan Gejala
Gejala Panu Dermatitis Alergi
MB MD MB MD
Gatal yang dirasakan kurang dari 14 hari 0,75 0,02 0,8 0,02 Gatal diduga setelah mengkonsumsi makanan
atau obat-obatan
0,02 0,8 0,8 0,02
Mempunyai riwayat alergi 0,02 0,8 0,8 0,02
Penyelesaian :
1. Perhitungan pada penyakit panu menggunakan rumus persamaan (4) dan persamaan (5). Perhitungan MB Panu (Measure Belief) :
Gatal – gatal ^ Gatal kurang dari 14 hari = 0,75 + 0,75 * (1 -0,75)
= 0,9375
Gatal – gatal ^ Gatal kurang dari 14 hari ^ = 0,9375 + 0,02 * (1 – 0,9375) Gatal yang disebabkan mengkonsumsi = 0,93875
Makanan atau obat-obatan
Gatal – gatal ^ Gatal kurang dari 14 hari ^ = 0,9387 + 0,02 * (1 – 0,9387) Gatal yang disebabkan mengkonsumsi = 0,93998
Makanan atau obat-obatan ^ Alergi
Perhitungan MD Panu (Measure Disbelief) :
Gatal – gatal ^ Gatal kurang dari 14 hari = 0,01 + 0,02 * (1 -0,01)
= 0,0298
Gatal – gatal ^ Gatal kurang dari 14 hari ^ = 0,0298 + 0,8 * (1 – 0,0298) Gatal yang disebabkan mengkonsumsi = 0,80596
Makanan atau obat-obatan
Gatal – gatal ^ Gatal kurang dari 14 hari ^ = 0,80596+ 0,8 * (1 – 0,80596) Gatal yang disebabkan mengkonsumsi = 0,96119
Makanan atau obat-obatan ^ Alergi
Certainty Factor (CF) = MB – MD = 0,93998 – 0,96119
= - 0,21217
2. Perhitungan pada penyakit Dermatitis Alergi menggunakan rumus persamaan (4) dan persamaan (5). Perhitungan MB Dermatitis Alergi (Measure Belief) :
Gatal – gatal ^ Gatal kurang dari 14 hari = 0,75 + 0,8* (1 - 0,75) = 0,95
Gatal – gatal ^ Gatal kurang dari 14 hari ^ = 0,95 + 0,8 * (1 – 0,95) Gatal yang disebabkan mengkonsumsi = 0,99
Makanan atau obat-obatan
Gatal – gatal ^ Gatal kurang dari 14 hari ^ = 0,99 + 0,8 * (1 – 0,99) Gatal yang disebabkan mengkonsumsi = 0,998
Makanan atau obat-obatan ^ Alergi
Perhitungan MD Dermatitis Alergi (Measure Disbelief) :
Gatal – gatal ^ Gatal kurang dari 14 hari = 0,01 + 0,02 * (1 -0,01) = 0,0298
Gatal – gatal ^ Gatal kurang dari 14 hari ^ = 0,0298 + 0,02 * (1 – 0,0298) Gatal yang disebabkan mengkonsumsi = 0,049204
Makanan atau obat-obatan
Gatal – gatal ^ Gatal kurang dari 14 hari ^ = 0,0492+ 0,8 * (1 – 0,0492) Gatal yang disebabkan mengkonsumsi = 0,06821
Makanan atau obat-obatan ^ Alergi
Certainty Factor (CF) = MB – MD = 0,998 – 0,068
= 0,929
Maka dari hasil diagnosa dan perhitungan menggunakan metode Certainty Factor (CF) nilai tertinggi yaitu penyakit Dermatitis Alergi dengan nilai dengan nilai 0,929.
2.4 Psikopat
Psikopat adalah perilaku psikologis dimana pelaku terus menerus mencari gratifikasi (pembeneran diri) atas tindakan-tindakan keliru yang dilakukannnya. Seseorang psikopat tidak memiliki kemampuan mengenali dan belajar dari kesalahan. Namun dia memiliki daya analisa yang tinggi dan seringkali tergolong orang yang sangat cerdas namun ada juga psikopat yang kecerdasannya dibawah rata-rata. Ada beberapa psikopat yang akan dibahas pada skripsi ini yaitu sebagai berikut :
2.4.1 Pedophilia (Pedofilia)
Pedofilia kata ini berasal dari bahasa Yunani : paidophilia, pais, (“anak atau anak –anak”) dan philia (cinta yang bersahabat atau persahabatan). Pedofilia digunakan sebagai ungkapan untuk
“cinta anak” atau “kasih anak” dan sebagian besar dalam konteks ketertarikan romantis atau seksual dengan berbagai cara, yang paling banyak dengan sodomi. Pedofilia juga merupakan gangguan psikoseksual, yang mana fantasi atau tindakan seksual dengan anak-anak pra-pubertas merupakan cara untuk mencapai gairah dan kepuasan seksual.
2.4.2. Sexual Sadism (Sadisme Seksual)
Sadisme Seksual adalah gangguan dan penyimpangan seksual dimana rangsangan seksualnya berhubungan dengan menyakiti atau menghina. Adapun ciri-ciri dari sadisme seksual menurut Diagnostic and Statistical Manual IV (2000) adalah sebagai berikut :
1) Selama paling tidak 6 bulan, fantasi, dorongan dan perilaku yang merangsang secara seksual yang melibatkan tindakan dimana penderitaan orang lain menimbulkan rangsangan seksual yang muncul berulang kali secara intens.
2) Orang mewujudkan dorongan, fantasi dan perilaku seksualnya itu terhadap orang yang tidak menyetujui tindakannya, sehingga mengakibatkan distress atau hambatan yang signifikan.
2.4.3. Transvestic Fetishism
Transvestic Fetishism (Tranvetisme Fetehistik) adalah gejala keadaan seseorang yang mencari