DIGRAF DWIWARNA
Pada bab ini akan dibahas beberapa konsep dasar seperti definisi dan teore-ma yang dijadikan landasan teori dalam penelitian ini. Konsep dasar tersebut berkaitan dengan digraf dwiwarna, primitifitas, scrambling index, dan batas -batas scrambling index.
2.1 Digraf Dwiwarna
Sub-bab ini akan membahas definisi digraf dwiwarna dan beberapa istilah yang digunakan pada digraf dwiwarna, serta representasi digraf dwiwarna menggu-nakan grafis dan matriks.
2.1.1 Definisi Digraf Dwiwarna
Sebuah digraf D adalah sebuah objek terdiri atas sebuah himpunan berhingga dan tak kosong V ={v1, v2, v3,· · · , vr} yang unsur - unsurnya disebut titik dari digraf D, bersama dengan sebuah himpunan B = {b1, b2, b3,· · · , bs} merupakan himpunan bagian dari himpunanV ×V yang unsur - unsurnya disebut busur dari digraf D. Sebuah digraf D dengan himpunan titik - titik V dan busur - busur B dinotasikan dengan D{V, B}. Bila b1 = (v1, v2) subset V ×V adalah sebuah
busur dari digraf D, maka titik v1 disebut sebagai titik asal dan titikv2 disebut
sebagai titik terminal dari busur b1.
Fornasini dan Valcher (1997) memperkenalkan digraf dengan dua jenis busur yaitu setiap busur pada suatu digraf D diberi dua warna, namun tidak sekaligus kedua warna tersebut berada pada busur yang sama. Digraf tersebut disebut sebagai digraf dwiwarna (D(2)). Warna yang dipergunakan adalah warna merah
dan warna biru. Secara aplikasi digraf dwiwarna dapat direpresentasi ke dalam grafis dengan cara sebagai berikut :
• Setiap busur b = (vi, vj) direpresentasikan dengan menggunakan garis be-rarah dari titik vi ke titik vj. Busur berwarna merah dan berwarna biru masing - masing ditandai dengan garis berarah tak putus dan garis berarah putus - putus.
Terdapat beberapa istilah dalam digraf dwiwarna, diantaranya yaitu jalan, lintasan dan cycle. Untuk bilangan bulat tak negatif h dan ℓ, suatu (h, ℓ)-jalan pada digraf D(2) adalah suatu jalan dengan h busur merah dan ℓ busur biru. Sebuah jalan dengan panjang k = h+ℓ yang menghubungkan titik vi dan vj, dinotasikan denganvi
k
→vj, merupakan sebuah barisan berhinggak busur dalam bentuk
{vi =v0, v1},{v1, v2},{v2, v3},· · · ,{vk−1, vk =vj},
juga dapat dinotasikan dalam bentuk
vi =v0 →v1 →v2 →v3 → · · · →vk−1 →vk =vj.
Untuk sebuah jalanWvivj diD(2), dinotasikan bahwar(Wvivj) danb(Wvivj) masing - masing merupakan banyaknya busur merah dan busur biru dari titik vi ke vj di W. Vektor (r(Wvivj), b(Wvivj))
T adalah komposisi pada jalan W
vivj. Jalan tersebut disebut tertutup jika titik vi = vj dan jalan disebut terbuka jika titik vi 6=vj.
Suatu jalan dari titikvike titikvj memuat titik yang berbeda - beda disebut sebagai lintasan, dinotasikan dengan Pvivj. Vektor (r(Pvivj), b(Pvivj))T adalah komposisi pada lintasanPvivj, denganr(Pvivj) danb(Pvivj) adalah masing - masing banyaknya busur merah dan busur biru diPvivj. Jika titikvi =vj diPvivj disebut sebagai lintasan tertutup atau cycle. Jarak antara dua titik berbeda dari vi ke vj padaPvivj, dinotasikan dengan d(vi, vj), didefinisikan sebagai panjang lintasan (r(Pvivj) +b(Pvivj)) yang dilewati dari titik vi ke titik vj.
Suatu digrafD(2)dikatakan sebagai digraf Hamilton dwiwarna jika terdapat cycleHamilton yaitu sebuahcycleyang memuat setiap titik pada digrafD(2)tepat
sekali kecuali kedua titik ujung pada barisan cycle tersebut.
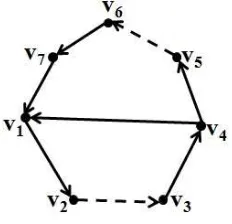
Contoh 2.1.1. Himpunan V = {v1, v2, v3, v4, v5, v6, v7} bersama dengan him-punan busur merah R = {(v1, v2),(v3, v4),(v4, v1),(v4, v5),(v6, v7),(v7, v1)} dan
himpunan busur biru B = {(v2, v3),(v5, v6)} adalah suatu digraf dwiwarna
Gambar 2.1 : Digraf Hamilton Dwiwarna dengan 7 titik dan 8 busur.
Dari gambar 2.1 dapat ditemukan contoh jalan, lintasan dan cycle antara lain sebagai berikut:
• Barisan v1 →r v2 →b v3 →r v4 →r v1 →r v2 adalah jalan terbuka dari v1 ke v2 dengan komposisi (4,1)T.
• Barisan v7 →r v1 →r v2 →b v3 →r v4 →r v1 →r v2 →b v3 →r v4 →r v5 →b v6 →r v7 adalah jalan tertutup dariv7 kev7 dengan komposisi (8,3)T.
• Barisan v6 →r v7 →r v1 →r v2 →b v3 →r v4 →r v5 adalah lintasan terbuka dari v6 ke v5 dengan komposisi (5,1)T.
• Barisan v1 →r v2 →b v3 →r v4 →r v1 adalah lintasan tertutup atau cycle dari v1 ke v1 dengan komposisi (3,1)T.
• Barisan v1 →r v2 →b v3 →r v4 →r v5 →b v6 →r v7 →r v1 adalah cycle Hamilton dengan komposisi (5,2)T, sehingga gambar 2.1 merupakan digraf Hamilton dwiwarna dengan panjang cycle Hamilton adalah 7.
2.1.2 Matriks Ketetanggaan Digraf Dwiwarna
titik vi, dinotasikan dengan od(vi), adalah banyaknya busur yang insiden dari titik vi yakni banyaknya busur dengan titik asal vi. Derajat dari sebuah titik vi adalah jumlahan dari derajat masuk dan derajat keluar dari titik tersebut.
Representasi digraf dwiwarna dengan matriks menggunakan konsep kete-tanggaan. AndaikanD(2)adalah sebuah digraf dwiwarna atasntitikv
1, v2,· · ·, vn.
Matriks ketetanggaan dari sebuah digraf D(2) didefiniskan sebagai berikut:
1. Matriks ketetanggaan merah dariD(2) adalah sebuah matriks bujursangkar R= (rij) dengan ordo n yang setiap entri didefinisikan sebagai
rij =
2. Matriks ketetanggaan biru dari D(2) adalah sebuah matriks bujursangkar B = (bij) dengan ordo n yang setiap entri didefinisikan sebagai
bij =
Contoh 2.1.2. Berikut adalah representasi menggunakan matriks yang diperoleh dari gambar 2.1.
AndaikanRdanB adalah matriks tak negatif berordon×ndan andaikanh dan ℓ adalah bilangan bulat tak negatif. Suatu (h, ℓ)-Hurwitz product dari R dan B didefinisikan secara rekursif, yang dinotasikan dengan (R, B)(h,ℓ), adalah
jumlah keseluruhan matriks dari hasil perkalianRsebanyakhkali danBsebanyak ℓ kali yaitu,
(R, B)(h,0) =Rh, (R, B)(0,ℓ)=Bℓ dan
Contoh 2.1.3.
(R, B)(1,0) =R, (R, B)(2,0) =R2, (R, B)(0,1) =B,
(R, B)(1,1) =R(R, B)(0,1)+B(R, B)(1,0) =RB+BR, maka
(R, B)(2,1) =R(R, B)(1,1)+B(R, B)(2,0) =R(RB+BR) +B(R2)
=R2B+RBR+BR2.
Lemma 2.1.4. Andaikan D(2) adalah digraf dwiwarna atasn titik dan andaikan R dan B adalah matriks ketetanggaan merah dan matriks ketetanggaan biru dari D(2). Maka (R, B)(h,ℓ) adalah banyaknya (h, ℓ)-jalan dari titik v
i ke vj.
Bukti. Pembuktian ini akan dilakukan dengan cara induksi. Pertama, dibuk-tikan bahwa untuk (h, ℓ) = (1,0) atau (h, ℓ) = (0,1), pernyataan (R, B)(h,ℓ)
benar merupakan banyaknya (h, ℓ)-jalan dari setiap titik vi ke vj. Perhatikan bahwa ketika (h, ℓ) = (1,0) diperoleh (R, B)(h,ℓ) = (R, B)(1,0) = R merupakan
jalan dengan dari titik vi ke vj dengan komposisi (1,0)T di D(2). Dan bahwa ketika (h, ℓ) = (0,1) diperoleh (R, B)(h,ℓ)= (R, B)(0,1) =B merupakan jalan dari
titik vi kevj dengan komposisi (0,1)T di D(2).
Kedua, asumsikan bahwa (R, B)(h,ℓ)adalah banyaknya (h, ℓ)-jalan dari titik
vi ke vj. Akan diperlihatkan bahwa untuk semua bilangan bulat tak negatif h+ℓ+ 1, pernyataan (R, B)(h+1,ℓ) benar merupakan banyaknya (h+ 1, ℓ)-jalan
dari setiap titik vi kevj dengan pembuktian mengikuti persamaan (2.1) yaitu
(R, B)(h,ℓ)=R(R, B)(h−1,ℓ)+B(R, B)(h,ℓ−1),
maka diperoleh
(R, B)(h+1,ℓ)=R(R, B)(h,ℓ)+B(R, B)(h+1,ℓ−1).
Berdasarkan asumsi maka R(R, B)(h,ℓ) merupakan jalan dari titik v
i ke vj yang dimulai dengan busur merah dan dilanjutkan oleh (h, ℓ)-jalan, danB(R, B)(h+1,ℓ−1)
merupakan jalan dari titik vi ke vj yang dimulai dengan busur biru dan dilan-jutkan oleh (h+ 1, ℓ−1)-jalan, sehingga (R, B)(h+1,ℓ)adalah banyaknya (h+ 1,
ℓ)-jalan dari titik vi ke vj. Karena langkah pertama dan kedua telah diperlihatkan maka terbukti bahwa (R, B)(h,ℓ)adalah banyaknya (h, ℓ)-jalan dari titikv
Contoh 2.1.5. Perhatikan matriks tak negatif dan matriks positif berikut.
S =
3 0 5 0 10 0 7 1 4
, T =
13 10 25 2 10 9 23 4 17
.
matriks tak negatif matriks positif
2.2 Primitifitas
Pada sub-bab ini akan dijelaskan tentang digraf dwiwarna terhubung kuat dan digraf dwiwarna terhubung kuat yang primitif.
2.2.1 Digraf Dwiwarna Terhubung Kuat
Berikut akan didiskusikan konsep keterhubungan kuat pada sebuah digraf dwi-warna. Suatu digraf dwiwarna dikatakan terhubung kuat bila untuk dua titik vi dan vj di D(2) terdapat sebuah jalan berarah dari vi ke vj dan terdapat se-buah jalan berarah dari vj ke vi, tanpa memperhatikan setiap warna busur yang dilalui. Sebaliknya, suatu digraf dwiwarna dikatakan tidak terhubung kuat bila untuk dua titik vi dan vj di D(2) terdapat sebuah jalan berarah dari vi ke vj, tetapi tidak terdapat jalan berarah dari vj kevi.
Contoh 2.2.1. Berikut diberikan contoh digraf dwiwarna terhubung kuat dan tidak terhubung kuat.
Gambar 2.2 : Digraf Dwiwarna Terhubung Kuat dan Tidak Terhubung Kuat.
Berikut diberikan sebuah sifat khusus dari digraf dwiwarna terhubung kuat yang berkaitan dengan keberadaan cycle.
Proposisi 2.2.2. AndaikanD(2) adalah sebuah digraf dwiwarna terhubung kuat. Setiap titik di D(2) terletak pada sebuah cycle.
Bukti. Andaikan vi adalah sebarang titik di D(2). Karena D(2) merupakan se-buah digraf dwiwarna terhubung kuat maka terdapat titik vj di D(2) sehingga (vi, vj) adalah sebuah busur di D(2). Karena D(2) merupakan sebuah digraf dwi-warna terhubung kuat, terdapat lintasan sederhanaPvjvi darivj kevi. Kemudian, busur (vi, vj) dilanjutkan dengan lintasan sederhanaPvjvi adalah sebuah lintasan tertutup atau cycle yang memuat titik vi. Dengan perkataan lain bahwa setiap titik vi di D(2) terletak pada sebuah cycle.
2.2.2 Primitifitas Digraf Dwiwarna Terhubung Kuat
Andaikan D(2) adalah sebuah digraf dwiwarna terhubung kuat. Digraf D(2) dikatakan primitif jika terdapat bilangan bulat tak negatif h dan ℓ sehingga un-tuk setiap pasangan titik vi dan vj di D(2) terdapat jalan vi
(h,ℓ)
−→ vj dan jalan vj
(h,ℓ) −→vi.
Andaikan C = {C1, C2,· · · , Cq} adalah himpunan semua cycle di D(2). Definisi matriks cycle M dari D(2) adalah matriks yang banyak kolom diper-oleh dari himpunan C dan banyak baris diperoleh dari banyak warna pada D(2), sehingga
M =
r(C1) r(C2) · · · r(Cq)
b(C1) b(C2) · · · b(Cq)
.
Content dari matriksM2×qdidefinisikan menjadi 0 jika rank dari M kurang dari 2 dan pembagi persekutuan terbesar dari determinan submatriks 2×2.
Teorema 2.2.3. (Fornasini dan Valcher, 1998) Andaikan D(2) memiliki
Contoh 2.2.4. Berdasarkan gambar 2.1 terdapat dua cycle yaitu cycle satu adalah v1
r
→ v2
b
→ v3
r
→ v4
r
→ v1 dengan komposisi C1 = (3,1)T dan cycle dua
yaitu v1
r
→v2
b
→ v3
r
→v4
r
→v5
b
→ v6
r
→v7
r
→v1 dengan komposisi C2 = (5,2)T.
Maka diperoleh matrikscycle dari digraf Hamilton dwiwarna tersebut, yaitu:
M =
3 5 1 2
karena det(M) = 1, maka D(2) tersebut terhubung kuat dan primitif.
2.3 Scrambling Index
Pada sub-bab ini akan didiskusikan mengenai definisi scrambling index lokal an-tara dua titik, scrambling index dari digraf dwiwarna primitif dan definisi scram-bling index dengan menggunakan matriks ketetanggaan dari digraf dwiwarna primitif.
Untuk dua titik berbedavidanvj diD(2), scrambling index lokal darividan vj adalah bilangan bulat positifkvi,vj(D(2)) yang didefinisikan sebagai berikut:
kvi,vj(D
(2)) = min
vw∈V(D(2)){kvi,vj(vw)} = min
vw∈V(D(2)){min(h+ℓ) :vi
(h,ℓ)
−→vw dan vj
(h,ℓ) −→vw}
Scrambling index dari digraf dwiwarna primitif, yang dinotasikan dengan k(D(2)), adalah bilangan bulat positif terkecil (h+ℓ) untuk semua bilangan bulat
tak negatif h busur merah dan ℓ busur biru sedemikian sehingga untuk setiap pasangan titik vi dan vj di D(2) terdapat sebuah titik vw di D(2) dengan sifat bahwa terdapat sebuah jalan vi
(h,ℓ)
−→vw dan sebuah jalanvj
(h,ℓ)
−→vw. Dari definisi k(D(2)) dan k
vi,vj(D(2)), diperoleh hubungan k(D(2))≥max
vi6=vj{kvi,vj(D
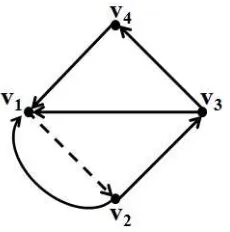
Contoh 2.3.1. Berikut scrambling index lokal dari digraf Hamilton dwiwarna primitif pada gambar 2.3.
Gambar 2.3 : Digraf Dwiwarna Primitif.
kv1,v2(D(2))=minv1,v2,v3,v4{(2,1),(3,2),(4,2),(5,2)}=min{(3),(5),(6),(7)}= 3, kv1,v3(D(2))=minv1,v2,v3,v4{(2,1),(3,2),(3,2),(5,2)}=min{(3),(5),(5),(7)}= 3, kv1,v4(D(2))=minv1,v2,v3,v4{(2,1),(3,2),(4,2),(7,3)}=min{(3),(5),(6),(10)}= 3, kv2,v3(D
(2))=minv
1,v2,v3,v4{(2,1),(1,1),(4,2),(6,2)}=min{(3),(2),(6),(8)}= 2, kv2,v4(D
(2))=minv
1,v2,v3,v4{(2,1),(1,1),(4,2),(6,2)}=min{(3),(2),(6),(8)}= 2, kv3,v4(D
(2))=minv
1,v2,v3,v4{(1,0),(1,1),(2,1),(6,2)}=min{(1),(2),(3),(8)}= 1. Dari definisi diperoleh bahwa k(D(2)) ≥ max
vi6=vj{kvi,vj(D
(2))}, sehingga k(D(2)) ≥
max{3,3,3,2,2,1}= 3. Selanjutnya, perhatikan bahwa untuk dua titik berbeda vi dan vj yaitu {(v1, v2),(v1, v3),(v1, v4),(v2, v3),(v2, v4),(v3, v4)} terdapat titik
v1, sehingga terdapat jalan dari vi ke v1 dan vj ke v1 dengan komposisi (2,1).
Hal ini menunjukkan k(D(2)) ≤ 3. Oleh karena itu, dapat disimpulkan bahwa
k(D(2)) = 3.
Berdasarkan Lemma 2.1.4, scrambling index dari suatu digraf dwiwarna D(2) dapat dicari dengan menggunakan matriks ketetanggaan R dan B di D(2).
Scrambling index dari matriks ketetanggaan R dan B adalah bilangan bulat positif terkecil (h, ℓ) sehingga (R, B)(h,ℓ) adalah sebuah scrambling matriks, yaitu
untuk setiap dua baris (R, B)(h,ℓ) terdapat sedikitnya satu entri yang nilainya
positif pada kolom yang sama, maka (h, ℓ) merupakan scrambling index dari digraf dwiwarna D(2).
Contoh 2.3.2. Dari gambar 2.3 diperoleh matriks ketetanggaan merah dan ma-triks ketetanggaan biru sebagai berikut:
R=
0 0 0 0 1 0 1 0 1 0 0 1 1 0 0 0
dan B =
0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
Berikut scrambling index menggunakan matriks ketetanggaan di atas.
Scrambling index dariD(2) bukanlah (1,0), karena setidaknya ada dua baris pada matriks (R, B)(1,0), yaitu baris pertama dan baris ketiga
tidak memiliki entri positif pada kolom yang sama.
b. (R, B)(0,1) =B =
Scrambling index dariD(2) bukanlah (0,1), karena setidaknya ada dua baris pada matriks (R, B)(0,1), yaitu baris kedua dan baris keempat
tidak memiliki entri positif pada kolom yang sama.
2. Untukh+ℓ= 2, diperoleh
Scrambling index dariD(2) bukanlah (2,0), karena setidaknya ada dua baris pada matriks (R, B)(2,0), yaitu baris pertama dan baris keempat
tidak memiliki entri positif pada kolom yang sama.
b. (R, B)(1,1) =RB+BR=
Scrambling index dariD(2) bukanlah (1,1), karena setidaknya ada dua baris pada matriks (R, B)(1,1), yaitu baris pertama dan baris kedua
tidak memiliki entri positif pada kolom yang sama.
c. (R, B)(0,2) =B2 =
Scrambling index dariD(2) bukanlah (0,2), karena setidaknya ada dua baris pada matriks (R, B)(0,2), yaitu baris kedua dan baris ketiga tidak
3. Untukh+ℓ= 3, diperoleh
Scrambling index dariD(2) bukanlah (3,0), karena setidaknya ada dua baris pada matriks (R, B)(3,0), yaitu baris pertama dan baris keempat
tidak memiliki entri positif pada kolom yang sama.
b. (R, B)(1,2) =RB2+BRB+B2R=
Scrambling index dariD(2) bukanlah (1,2), karena setidaknya ada dua
baris pada matriks (R, B)(1,2), yaitu baris pertama dan baris kedua
tidak memiliki entri positif pada kolom yang sama.
c. (R, B)(0,3) =B3 =
Scrambling index dariD(2) bukanlah (0,3), karena setidaknya ada dua baris pada matriks (R, B)(0,3), yaitu baris kedua dan baris ketiga tidak
memiliki entri positif pada kolom yang sama.
d. (R, B)(2,1) =R2B+RBR+BR2 =
Scrambling index dariD(2)adalah (2,1), karena untuk setiap dua baris
(R, B)(2,1) terdapat sedikitnya satu entri yang nilainya positif pada
kolom yang sama yaitu kolom satu.
2.4 Batas - Batas Scrambling Index
Pada sub-bab ini akan membahas mengenai batas - batas pada scrambling index yaitu batas atas dan batas bawah pada scrambling index digraf dwiwarna primitif.
mengiku-ti hubungan berikut:
untuk beberapa lintasanPvivj darivi kevj dan beberapa vektor bulat tak negatif z.
Batas atas scrambling index dari digraf dwiwarna primitif dinyatakan dalam proposisi berikut.
Proposisi 2.4.1. (Mulyono dan Suwilo, 2014) Andaikan D(2) adalah digraf dwiwarna primitif terdiri dari dua cycle C1 dan C2. Andaikan vj adalah sebuah
titik yang terletak pada kedua cycle. Jikahdanℓadalah bilangan bulat tak negatif, terdapat sebuah lintasan Pvivj dari vi ke vj sehingga sistem
Mz+
mempunyai sebuah solusi bilangan bulat tak negatif, maka ada jalan vi
(h,ℓ) −→vj di D(2).
Bukti. Asumsikan solusi dari sistem (2.2) adalah z = (z1, z2)T. Solusi tersebut
dibagi menjadi empat kasus berikut:
1. Jika z1 > 0 dan z2 > 0, maka jalan dimulai dari titik vi bergerak ke ke titik vj sepanjang (r(Pvivj), b(Pvivj))-lintasan Pvivj, kemudian mengelilingi C1 sebanyak z1 kali dan C2 sebanyak z2 kali, dan kembali ke titikvj adalah
sebuah (h, ℓ)-jalan dari vi ke vj.
2. Jika z1 = 0 dan z2 > 0, maka jalan dimulai dari titik vi bergerak ke ke titik vj sepanjang (r(Pvivj), b(Pvivj))-lintasan Pvivj, kemudian mengelilingi C2 sebanyak z2 kali, dan kembali ke titik vj adalah sebuah (h, ℓ)-jalan dari vi ke vj.
3. Jika z1 > 0 dan z2 = 0, maka jalan dimulai dari titik vi bergerak ke ke titik vj sepanjang (r(Pvivj), b(Pvivj))-lintasan Pvivj, kemudian mengelilingi C1 sebanyak z1 kali, dan kembali ke titik vj adalah sebuah (h, ℓ)-jalan dari vi ke vj.
4. Jika z1 = z2 = 0, maka (r(Pvivj), b(Pvivj))-lintasan Pvivj adalah sebuah
Andaikan D(2) adalah digraf dwiwarna primitif terdiri dari dua cycle dan andaikan vi dan vj adalah dua titik yang berbeda di D(2). Untuk beberapa titik vw, andaikan bahwa kvi,vj(vw) diperoleh dari (h, ℓ)-jalan. Berikut Lemma untuk menentukan batas bawah untuk kvi,vj(D(2)) dan karenanya akan diperoleh batas bawah scrambling index.
Lemma 2.4.2. (Mulyono, Sumardi dan Suwilo, 2015)AndaikanD(2)adalah
digraf dwiwarna primitif terdiri dari dua cycle dengan matriks cycle M dan andaikan det(M) = 1. Andaikan vi dan vj adalah dua titik berbeda di D(2). Jika kvi,vj(vw) diperoleh dari (h, ℓ)-jalan, maka
Bukti. Karena det(M) = 1, terdapat bilangan bulat e1 dan e2 sehingga
Karena setiap jalan dapat dikomposisi ke dalam lintasan dan beberapa cycle, maka
untuk beberapa lintasan Pvivw dari titik vi ke vw dan beberapa vektor bilangan bulat tak negatif z. Bandingkan persamaan (2.3) dan (2.4), diperoleh
untuk beberapa lintasan Pvjvw dari titik vj ke vw dan beberapa vektor bilangan bulat tak negatif z. Bandingkan persamaan (2.3) dan (2.5), diperoleh
z=
e1
e2
−M−1
r(Pvjvw) b(Pvjvw)
≥0
karenanya
e1
e2
≥M−1
r(Pvjvw) b(Pvjvw)
=
b(C2)r(Pvjvw)−r(C2)b(Pvjvw) r(C1)b(Pvjvw)−b(C1)r(Pvjvw)
.
Sehingga diperoleh e2 ≥ r(C1)b(Pvjvw)−b(C1)r(Pvjvw) untuk beberapa lintasan Pvjvw dari titik vj kevw. Jikakvi,vj(vw) diperoleh dari (h, ℓ)-jalan, maka
h ℓ
= M
e1 e2
≥M
b(C2)r(Pvivw)−r(C2)b(Pvivw) r(C1)b(Pvjvw)−b(C1)r(Pvjvw)
(2.6)
dan karenanya
kvi,vj(vw)≥ℓ(C1)[b(C2)r(Pvivw)−r(C2)b(Pvivw)]+ℓ(C2)[r(C1)b(Pvjvw)−b(C1)r(Pvjvw)]