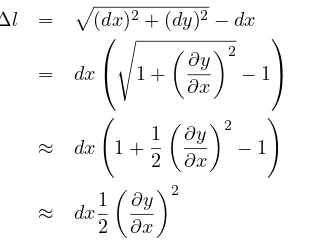SOLUSI DAWAI RELATIVISTIK BEROTASI PADA RUANG ADS5 ×

SOLUSI DAWAI RELATIVISTIK BEROTASI PADA RUANG

ADS

5

×

S

5

M. AFIF ISMAIL NRP 1113100090 Dosen Pembimbing Agus Purwanto, D.Sc

DEPARTEMEN FISIKA

Fakultas Matematika dan Ilmu Pengetahuan Alam Institut Teknologi Sepuluh Nopember

SOLUSI DAWAI RELATIVISTIK BEROTASI PADA RUANG

ADS

5

×

S

5

M. AFIF ISMAIL NRP 1113100090

Dosen Pembimbing Agus Purwanto, D.Sc

DEPARTEMEN FISIKA

Fakultas Matematika dan Ilmu Pengetahuan Alam Institut Teknologi Sepuluh Nopember

ROTATING RELATIVISTIC STRING SOLUTIONS IN

ADS

5

×

S

5

M. AFIF ISMAIL NRP 1113100090

Supervisor

Agus Purwanto, D.Sc

Department of PHYSICS

SOLUSI DAWAI RELATIVISTIK BEROTASI PADA RUANG ADS5×S5

Nama : M. AFIF ISMAIL NRP : 1113100090 Jurusan : Fisika FMIPA Pembimbing : Agus Purwanto, D.Sc

ABSTRAK

Dawai merupakan objek yang mempunyai dua parameter gerak yaitu waktu dan panjang dawai, yang merupakan generalisasi dari partikel yang mem-punyai satu parameter gerak berupa waktu. Pada penelitian ini, digu-nakan kondisi batas dawai berupa dawai tertutup. Dawai relativistik berg-erak pada ruang-waktu dengan lintasan berupa sebuah luasan yang diben-tuk oleh dua parameter, lintasan ini biasa disebut lembaran dunia (world-sheet). Dawai relativistik ini juga mempunyai dua aksi yang disebut aksi Nambu-Goto dan aksi Polyakov. Aksi Nambu-Goto dibangun dengan menggunakan(world-sheet). Sedangkan aksi Polyakov merupakan ben-tuk lain dari aksi Nambu-Goto dengan penambahan alat matematis berupa metrik(auxilliary field)yang dapat menyederhakan pengerjaan aksi. Pada penelitian ini digunakan aksi Polyakov dengan metrik (auxilliary field) berupa metrik minkowski. Dengan menggunakan aksi Polyakov, digu-nakan model dawai bergerak pada bidang datar dan ditentukan energi be-serta momentum sudut dari dawai. Selanjutnya, digunakan model dawai bergerak pada ruangAdS5×S5dan ditentukan energi serta momentum

sudut dari dawai. Dari perhitungan yang telah dilakukan, energi dawai yang berputar padaAdS5×S5mempunyai bentuk yang ekivalen dengan

energi dawai yang berputar pada bidang datar.

ROTATING RELATIVISTIC STRING SOLUTIONS INADS5×S5

Name : M. AFIF ISMAIL NRP : 1113100090 Department : Physics

Supervisor : Agus Purwanto, D.Sc

ABSTRACT

String is an object that possess two movement parameters, time and string length, generalization from particle that possess one movement pa-rameter that is time. In this thesis a restriction is used which is closed string. Relativistic string move in space-time with trajectory in form of area made of two parameters, this trajectory is called world-sheet. Rela-tivistic string have two action called Goto and Polyakov. Nambu-Goto action built using world-sheet. While Polyakov is the other form of Nambu-Goto with addition of mathmetical tool that is auxilliary field ma-trix that can simplify execution of actions. In this thesis Polyakov action is used with minkowski matrix as the auxilliary field matrix. By using Polyakov action, moving string model is used on flat plane also the en-ergy and angular momentum of the string is determine. Next, moving string model is used on Ad5 x S5 also the energy and the angular momen-tum of the string is determine. From the calculation that had been made, energy of spinning string on Ad5 x S5 have a form equivalent with energy on spinning string on a flat plane.

Alhamdulillaahirabbil’alamiin

Puji syukur penulis panjatkan kehadirat ALLAH SWT karena atas karunia-Nya penulis dapat menyelesaikan Tugas Akhir dengan judul ”SO-LUSI DAWAI RELATIVISTIK BEROTASI PADA RUANGAdS5×

S5”. Tugas akhir ini diharapkan dapat membantu rekan-rekan mahasiswa

S1 yang ingin belajar lebih mendalam tentang Fisika terutama di sekitar topik Teori Dawai.

Terselesaikannya tugas akhir ini tidak luput dari bantuan berbagai pi-hak. Penulis mengucapkan terima kasih dengan setulus hati kepada:

1. Umi dan Ayah atas segala yang telah diberikan kepada penulis den-gan penuh kasih sayang. Penulis tidak akan mampu membalasnya.

2. Bapak Agus Purwanto D.Sc, atas segala bimbingan selama berada di ITS hingga penyelesaian tugas akhir. Penulis memohon maaf yang sebesar-besarnya atas segala kesalahan yang telah dilakukan.

3. Bapak Dr. Yono Hadi Pramono selaku Ketua Departemen Fisika FMIPA-ITS.

4. Dr. Sheng-Lan Ko atas segala bimbingan selama penulis mempela-jari teori dawai diInstitute for Fundamental Study. dan Mas Chandra atas bantuannya selama penulis menyelesaikan Tugas Akhir di Thailand.

5. Bapak Dr. rer. nat Bintoro Anang Subagyo, Bapak I Nengah Artawan M.Si, Bapak Heru Sukamto M.Si, Bapak Lila Yuwana M.Si serta Bapak dan Ibu dosen yang telah mengajarkan ilmu kepada penulis.

6. Sahabat-sahabat di LaFTiFA, Dwi, Ira, Afidah, Anom, Adam, Bayu, Kasyfil, Nusur sebagai teman diskusi. Terutama Fasya yang telah banyak membantu penulis selama pengerjaan tugas akhir.

7. Arek-arek Kontrakan, Dwi, Fahru, Tito, Senpai, Taufik, Erik yang telah banyak membantu penulis selama di Kontrakan.

8. Teman-teman seperjuangan Fisika 2013 (Supernova) atas bantuan-nya selama di Jurusan Fisika.

9. Kakak-kakak angkatan dan Alumni di Jurusan Fisika

10. Adik Fisika 2014,2015,2016. Semoga tetap terjaga keharmonisan di Jurusan Fisika.

11. Serta semua pihak yang telah membantu dan tidak dapat penulis sebutkan satu persatu.

Semoga Tugas Akhir ini dapat bermanfaat bagi pihak-pihak yang berke-pentingan serta dapat menjadi sumbangan bagi almamater tercinta dalam pengembangan sains kedepannya.

ABSTRAK ix

ABSTRACT xi

Kata Pengantar xiii

DAFTAR ISI xv

DAFTAR TABEL xvii

DAFTAR GAMBAR xix

1 PENDAHULUAN 1

1.1 Latar Belakang . . . 1

1.2 Perumusan Masalah . . . 2

1.3 Tujuan . . . 2

1.4 Batasan Masalah . . . 2

1.5 Metode Penelitian . . . 2

1.6 Sistematika Penulisan . . . 2

2 DAWAI RELATIVISTIK 5 2.1 Aksi Nambu-Goto . . . 5

2.2 Persamaan Gerak dari Aksi Nambu-Goto . . . 10

2.3 Invariansi Parameterisasi Ulang dari Aksi Nambu-Goto . . 12

2.4 Aksi Polyakov . . . 14

2.5 Persamaan Gerak dari Aksi Polyakov . . . 17

2.6 Invariansi Parameterisasi Ulang dari Aksi Polyakov . . . . 22

2.7 Momentum dan Momentum Sudut Konservatif . . . 24

3 SOLUSI DAWAI RELATIVISTIK PADA RUANG DATAR 27 3.1 Aksi Polyakov pada Ruang Datar . . . 27

3.2 Dawai Melingkar Berputar pada dua Bidang yang Saling Tegak Lurus . . . 31

4 SOLUSI DAWAI RELATIVISTIK PADA RUANGAdS5×S5 35 4.1 Aksi Polyakov pada RuangAdS5×S5 . . . 35

4.2 Dawai Melingkar Berputar padaRt×S5bagian dariAdS5×

S5 _{. . . 44}

4.3 Dawai Melingkar Berputar padaS3_⊃S5 _{. . . 47}

4.4 Dawai Melingkar Berputar hanya padaAdS5 . . . 50

4.5 Dawai Melingkar Berputar padaAdS5danS5 . . . 53

5 PENUTUP 59 5.1 Kesimpulan . . . 59

5.2 Saran . . . 59

DAFTAR PUSTAKA 61 A Lampiran 63 A.1 Dawai Non-Relativistik . . . 63

A.2 Partikel Relativistik . . . 67

A.3 Bentuk Umum dari Model Dawai . . . 76

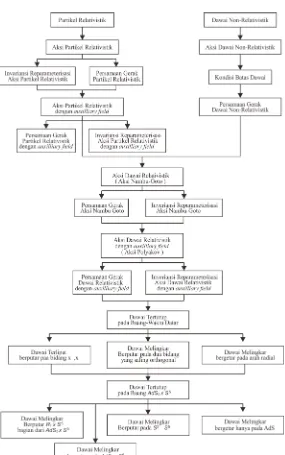
1.1 Skema pengerjaan tugas akhir . . . 4

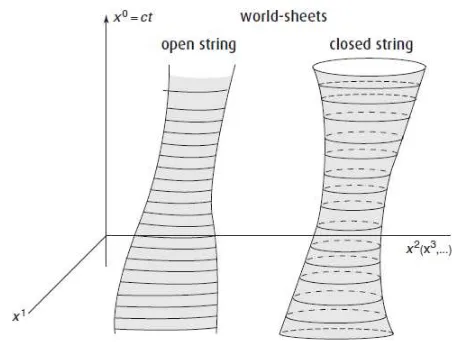
2.1 Gambaran dariworld-sheet. Disebelah kiri berupa dawai terbuka, dan yang disebelah kanan berupa dawai tertutupΣ 6 2.2 Area dari permukaan jajargenjangΣ . . . 7

3.1 dawai berputar pada bidang(x1_{, x}2₎ . . . 32

3.2 dawai berputar pada bidang(x3_{, x}4₎ . . . 33

A.1 dawai yang direnggangkan kearah transversal . . . 64

A.2 (a): dawai dengan kondisi batas Dirichlet. (b): dawai den-gan kondisi batas Neumann . . . 65

A.3 diagram ruang-waktu dengan beberapa world-line yang menghubungkan titik awal dengan(c tf, → xf) . . . 68

PENDAHULUAN

1.1 Latar Belakang

Benda yang berada disekitar kita dibentuk oleh sekumpulan atom yang saling berikatan. Atom merupakan objek yang terdiri dari partikel elek-tron, proton dan neutron. Elektron termasuk kedalam partikel tal, sedangkan proton dan neutron masih tersusun oleh partikel fundamen-tal yang disebut. Partikel fundamenfundamen-tal diyakini merupakan objek dengan ukuran paling kecil, sehingga tidak dapat dibagi lagi. Partikel fundamen-tal ini terbagi menjadi dua, yaitu fermion dan boson. Fermion merupakan partikel yang dapat berinteraksi. Sedangkan boson merupakan partikel pembawa interaksi antara fermion.

Pada tahun 1970, Yoichiro Nambu, Holger Bech Nelson, dan Leonard Susskind berargumen bahwasannya terdapat kandidat objek dasar penyusun materi berupa dawai. Argumen ini muncul dari penelitian Gabriele Veneziano tentang interaksi kuat pada partikel hadron. Yoichiro Nambu dan Tet-suo Goto merumuskan dawai tersebut dalam kerangka relativistik dengan melakukan generalisasi dari konsep partikel titik yang mempunyai nol di-mensi menjadi dawai dengan didi-mensi satu. Pada tahun 1974, Alexander Markovich Polyakov menguantisasi dawai relativistik dengan menerap-kan relasi komutasi posisi momentum dari memenerap-kanika kuantum sehingga didapatkan dawai bosonic. Teori dawai bosonic hanya dapat mendiskrip-sikan partikel elementer dengan spin bulat(partikel bosonic). Sehingga dibutuhkan teori dawai baru untuk menyempurnakan teori dawai dalam mendenkripsikan partikel fundamental lain berupa fermion. Teori dawai tersebut dinamakan teori dawai super. Teori ini ditemukan dengan meng-gabungkansupersymmetrydengan dawai bosonic. Hal ini menyebabkan munculnya dawai fermion.

Sekitar dua puluh tahun yang lalu, fisikawan menemukan sifat baru dari teori dawai. Ketika teori dawai super diterapkan dalam ruang-waktu anti de Sitter, dawai tersebut dapat menjelaskan fenomena fisika yang serupa dengan teori medan kuantum. Teori ini dikemukakan oleh Malda-cena dengan nama korespondensianti de Sitter/Conformal Field Theory (Ads/CFT). Maldacena berargumen bahwa dunia dengan dimensi (3+1) tanpa gravitasi dan ruang waktu anti de Sitter (4+1) saling berhubungan.

Pada tugas akhir ini, digunakan dawai relativistik untuk diterapkan

ke dalam ruang anti de sitter. Dengan menggunakan bentuk pergerakan dawai tertutup beroutar, dihitung energi dari dawai tersebut dan pengaruh dari penerapan dawai relativistik ke dalam ruang ruang-waktu anti de Sit-ter Sit-terhadap sifat fisis dari dawai Sit-tersebut. Pada perhitungan energi dawai, dilakukan pendekatan dawai berputar sangat cepat dan sangat lambat.

1.2 Perumusan Masalah

Rumusan masalah dari tugas akhir ini adalah bagaimana solusi dari dawai relativistik serta pengaruh dari penerapan dawai relativistik ke dalam ruang ruang-waktu anti de Sitter.

1.3 Tujuan

Tujuan yang ingin dicapai pada tugas akhir ini adalah menerapkan dawai Relativistik berputar menggunakan aksi Polyakov pada ruangAdS5×

S5, serta mengetahui energi dari beberapa model dawai dan mengetahui

Energi dawai pada ruangAdS5×S5Dengan ruang datar

1.4 Batasan Masalah

Pada tugas akhir ini permasalahan hanya dibatasi pada sampai pener-apan aksi polyakov pada ruangAdS5×S5

1.5 Metode Penelitian

Metode yang digunakan dalam penyusunan Tugas Akhir ini adalah metode analitis dari studi literatur. Skema pengerjaan tugas akhir ini diberikan pada gambar (1.1)

1.6 Sistematika Penulisan

datar dengan menggunakan 3 model dawai. Pada bab IV akan diturunkan solusi dawai relativistik pada ruang AdS5 ×S5 dengan menggunakan

4 model dawai. Bab V adalah kesimpulan dan saran. Lampiran berisi materi tambahan yang terkait dengan tugas akhir ini. Untuk menyeder-hanakan pengerjaan tugas akhir ini, digunakanc = 1. Digunakan notasi

DAWAI RELATIVISTIK

Dawai merupakan objek yang mempunyai dua parameter gerak yaitu panjang dawai dan waktu, seperti halnya partikel yang hanya mempunyai satu parameter gerak berupa waktu. Dawai relativistik merupakan dawai yang bergerak dengan kecepatan yang mendekati kecepatan cahayav_≈c pada pusat massanya terhadap suatu kerangka acuan.

2.1 Aksi Nambu-Goto

Untuk mendeskripsikan suatu sistem yang bergerak, dapat digunakan persamaan gerak yang dibangun dari persamaan aksi dari sistem tersebut. Dawai mempunyai 2 parameter dalam pergerakannya di ruang-waktuxµ yaitu panjang dawaiσdan waktu pergerakan dawaiτ. Aksi dapat diban-gun dari lintasan yang dilalui dawai pada ruang-waktu. Lintasan ini berupa area dua dimensi yang terdiri dari 2 parameter dawai seperti pada gambar (2.1). Area ini disebut lembaran-dunia (world-sheet)

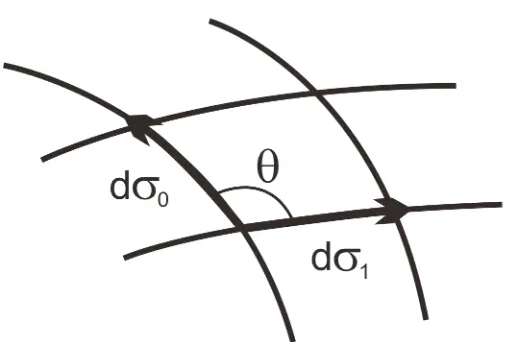
Di ambil bentuk umum dari lembaran-dunia berupa jajargenjang. Area dari permukaan pada jajargenjang kecil dibentuk oleh tangen vektor den-gan garisσ0danσ1seperti pada gambar (2.2). Dimanaσ0_≡τ, σ1_≡σ

dσ0dandσ1mempresentasikan perpindahan pada koordinat, bukan jarak sebenarnya. Metrikgabpada permukaanworld-sheetΣ,

mempresen-tasikan bagaimana mengubah perpindahan pada koordinat menjadi jarak yang sebenarnyads2.

(ds)2=gabdσadσb (2.1)

untuka, b= 0,1. Maka jarak sebenarnya dari perpindahan koordinatdσ0 ialah

||dσ0_||=√g00dσ0 (2.2)

dan untukσ1

||dσ1_||=√g11dσ1 (2.3)

Area dari jajargenjang merupakan hasil cross product dari dσ0 dan dσ1, maka didapatkan area dari jajargenjang

Gambar 2.1: Gambaran dariworld-sheet. Disebelah kiri berupa dawai terbuka, dan yang disebelah kanan berupa dawai tertutupΣ

||dσ0×dσ1|| = ||dσ0|| ||dσ1||sin(θ) = ||dσ0_{|| ||}dσ1_||√1−cos2_θ

= √||dσ0_||2_||dσ1_||2_{− ||dσ}0_||2_||dσ1_||2cos2_θ

= √||dσ0_||2_||dσ1_||2_{− ||dσ}0_.dσ1_||2

= √g00(dσ0)2g11(dσ1)2−(g01)2(dσ0)2(dσ1)2

= dσ0dσ1√g00g11−(g01)2 (2.4)

Tanda dibawah akar pada persamaan (2.4) bernilai negatif. Untuk mengetahuinya, dimisalkan menggunakan metrik Minkowski 2 dimensi

gµν =

(

−1 0

0 1

)

Gambar 2.2: Area dari permukaan jajargenjangΣ

maka didapatkang00g11−(g01)2 < 0. Agar dapat menghilangkan

ni-lai negatif. Maka suku pertama dan kedua didalam akar dibalik, sehingga tanda dibawah akar tidak bernilai negatif. Dengan melakukan hal ini, di-dapatkan bahwa

dA(areaΣ) = ||dσ0_×dσ1_||

= dσ0dσ1√(g01)2−g00g11

= dσ0dσ1√₋detgab

= dσ0dσ1√−g (2.6)

dengan penulisandet gabdituliskan dalam bentukg.

Metrik pada permukaanΣdapat dipetakan ke dalam koordinat

ruang-waktu. Dalam pemetaan permukaanΣkedalam ruang-waktu, maka

per-mukaan membutuhkan metrik yang disebut induced metric (metrik in-duksi). Untuk menentukan bentuk eksplisit dariinduced metricdidalam ruang-waktu. Dianggap jarak pada ruang-waktu diberikan dalam bentuk

(ds)2_=G

dimanaGµν merupakan metrik ruang-waktu. Jika perpindahan tetap

be-rada pada permukaanΣ, maka

dxµ=∂x

Dengan menggunakan persamaan (2.8) pada persamaands2_(2.7),

di-dapatkan

Jika perpindahan tetap berada pada permukaan Σ, maka persamaan

(2.9) dapat ditulis dalam bentuk metrik induksiinduced metrichabsebagai

berikut

(ds)2=habdσadσb (2.10)

dengan metrik induksinya diberikan dalam bentuk

hab=Gµν

∂xµ

∂σa

∂xν

∂σb (2.11)

dari permukaanΣialah dengan mendefiniskan bahwa∂x

∂τ ≡x,˙ ∂x ∂σ ≡x´

Diperkenalkan aksi dawai relativistik. Aksi ini sebanding dengan area world-sheetsebagai manaworld-linepada partikel relativistik. Area ini mempunyai satuan panjang kuadrat. Jika dilihat dari pers (2.12),xµ

mem-punyai satuan panjang, dan setiap suku dibawah akar memmem-punyai empat x. Satuan dariτdanσhilang, karena setiap suku dibawah akar mempun-yai dua turunanτ dan dua turunanσ. Didefiniskanσdanτ mempunyai satuan panjang dan waktu. Maka didapatkan satuan dari masing-masing besaran

[τ] =T, [σ] =L, [xµ] =L, [A] =L2 (2.14) dikarenakan aksiSharus mempunyai satuanM L2_{/T danAmempunyai}

satuanL2_{, maka dibutuhkan kuantitas dengan satuanM/T. Digunakan}

didapatkan kuantitas dengan satuanM/T. Selanjutnya, area pada pers (2.12) dikalikan denganT/cuntuk mendapatkan kuantitas dengan satuan aksi. Maka didapatkan aksi dari dawai relativistik

S=−T

Aksi dari dawai relativistik sering disebut sebagai aksi Nambu-Goto. Diru-muskan oleh fisikawan jepang yang mendapatkan penghargaan nobel tahun 2008 Yoichiro Nambu dan Tetsuo Goto.

2.2 Persamaan Gerak dari Aksi Nambu-Goto

Untuk mendapatkan persamaan gerak dari dawai terhadap ruang-waktu xµ, dilakukan variasi dari aksi terhadap ruang-waktu_xµ. Dimana aksi

akan stasioner sehingga bernilai nol pada saat divariasikan. Dari per-samaan (2.15)

denganLmerupakan rapat Lagrangian dari sistem, yang diberikan dalam

bentuk

L( ˙x,x´) =−T

c

√

( ˙x.x´)2−x˙2_x´2 (2.17)

DivariasikanS, denganLmerupakan fungsi darix˙danx´

δS =

dengan menggunakan momentum konjugat, yang mempunyai bentuk

dan menggunakan menggunakan syarat batas kondisi awalτidan kondisi akhirτfpada suku

pertama

δxµ(τi) =δxµ(τf) = 0 (2.22)

persamaan ini menggambarkan bahwa pada saat kondisi waktu awal dan kondisi waktu akhir, xµ berada pada posisi yang tetap. dan untuk suku

kedua digunakan syarat batas Dirichlet atau Neumann atau dawai tertutup

δxµ(σi) =δxµ(σf) = 0 (Dirichlet) (2.23)

persamaan (2.23) menggambarkan kondisi dawai yang kedua ujungnya terikat, sehingga variasi atau pergeseran pada kedua ujungnya bernilai nol.

Pσ

persamaan (2.24) menunjukan kondisi pada dawai dengan kedua ujung be-bas. Pada kondisi ini, tidak ada momentum yang dapat mengalir melebihi kedua ujung dawai. Hal ini mengindikasikan bahwa kedua ujung dawai dapat bergerak bebas pada ruang-waktu

δxµ(σi) = δxµ(σf)

Pσ

µ(σi) = Pµσ(σf) (dawai tertutup) (2.25)

persamaan (2.25) memberikan gambaran bahwa pada dawai tertutup, kon-disi pada ujung awal dan ujung akhir bernilai sama.

Dengan menggunakan persamaan (2.22) pada suku pertama dan per-samaan (2.23) atau (2.24) atau (2.25) pada suku kedua, maka didapatkan

δS = − Menggunakan prinsip aksi, dimana variasi dari aksi bernilai nol

δS Persamaan 2.27 merupakan persamaan gerak dari dawai relativistik ter-hadap ruang-waktu xµ _{dari aksi Nambu-Goto. Untuk menentukan}

per-samaan gerak ini diperlukanPτ

µdanPµσyang didapatkan dari lagrangian

sistem.

2.3 Invariansi Parameterisasi Ulang dari Aksi Nambu-Goto

Integral dari aksi pada lembaran dunia (world-sheet) diparamaterkan olehτdanσ. Lembaran dunia (world-sheet) hanya lintasan dawai melalui ruang-waktu sehingga tidak bergantung terhadap pemilihan parameter yang digunakan. Hal ini menyatakan bahwa aksi invariant terhadap parameter-isasi ulang.

Diperke-nalkan parameter baru yang berhubungan denganτdanσ. Denga paramtere baru mempunyai bentukeτ =τe(τ σ)danσe =σe(σσ). Untuk mengetahui

apakah aksi Nambu-Goto invarian terhadap parameterisasi, dilakukan pen-gubahan parameterτ σ_→eσ_eτ Dari perhitungan diatas dapat dilihat bahwa hasil parameterisasi aksi

2.4 Aksi Polyakov

Terdapat permasalahan pada aksi Nambu-Goto dikarenakan ruang-waktu xµ _{berada didalam akar, yang menyebabkan persamaan ini sulit untuk}

diselesaikan. Jika dilihat pada persamaan gerak dari aksi Nambu-Goto, persamaan ini terlihat rumit dikarenakanP merupakan turunan dari

la-grangian yang mempunyai ruang-waktuxµdidalam akar.

Terdapat aksi lain yang lebih sederhana yang disebut aksi Polyakov. Aksi ini terlihat cukup sederhana karena ruang-waktuxµtidak berada

di-dalam akar. Pada aksi ini diperkenalkan parameter gerak baru yang dina-makanauxilliary field. Auxilliary fieldtidak memberikan sifat fisis baru dari dawai, karenaauxilliary fieldhanya merupakan alat matematis agar mempermudah pengerjaan aksi Polyakov. Penambahan auxilliary field pada aksi menyebabkan aksi Polyakov mempunyai dua persamaan gerak. Aksi Polyakov dapat dibangun dari aksi Nambu-Goto

SN G = −

T c

∫

dσdτ√₋h

= −₂T_c

∫

dσdτ√₋hhαβhαβ

= −₂T

c

∫

dσdτ√₋hhαβ∂αxµ∂βxµ (2.29)

dengan mengganti metrik induksihαβmenjadi metrikworld-sheet_gαβ

yang tidak terikat denganxµ. Metrikworld-sheetini merupakanauxiliary

field. Karena, metrikgαβtidak memiliki variabel dinamik. Maka

didap-atkan aksi Polyakov sebagai berikut

SP =−2Tc

∫

dσdτ√₋g gαβ_∂

αxµ∂βxµ (2.30)

δSp = − Untuk memvariasikang. Diambilgαβberupa matrik2×2

gαβ=

Variasi dari determinangαβdapat dituliskan dalam bentuk

δ(−g) =δ(−detgαβ) =g01δg10+δg01g10−g00δg11−δg00g11(2.34)

jika dibandingkan persamaan (2.34) dengan komponen dari(−g)(gαβ₎

pada persamaan (2.33). Maka dapat persamaan (2.34) dapat dituliskan dalam bentuk

variasiδgαβharus dituliskan dalam bentukδgαβ.

selanjutnya, subtitusi persamaan (2.37) ke persamaan (2.31)

δSp = −

dengan menggunakan prinsip aksi,

1 faktor(gγρ_hγρ)tidak mempunyai indek bebas, persamaan ini memberikan

metrikgαβsebanding dengan metrik induksihαβ. Selanjutnya, diambil

bentuk determinan terhadap indekαdanβ,

dengann= 2merupakan ukuran dari metrik. jika disubtitusi hasil dari persamaan (2.39) kedalam aksi Polyakov

SP = − Hasil ini menunjukan bahwa aksi Polyakov dan aksi Nambu-Goto ekuiv-alen.

Dapat dilakukangauge fixing(menentukan parameter matematis dari medan)Auxilliary fieldpada aksi Polyakov kedalam bentuk paling seder-hana, dengan memberikan bentukAuxilliary fieldberupa metrik Minkowski 2-dimensi

2.5 Persamaan Gerak dari Aksi Polyakov

Polyakov pada persamaan (2.30

δSp = −

T

2c

∫

dσ dτ δ(√−ggαβ∂αxµ∂βxνGµν

)

(2.42) dilakukangauge fixing(2.41) padaauxilliary field, dimanaauxilliary field mempunyai bentuk sebagai ruang-waktu datar.

gαβ=µαβ=

(

−1 0

0 1

)

maka,

δSp = −

T

2c

∫

dσdτ δ(µαβ∂αxµ∂βxνGµν)

= −T

2c

∫

dσdτ δ(µτ τ∂τxµ∂τxνGµν+µσσ∂σxµ∂σxνGµν)

= −₂T_c

∫

dσdτ δ((−1)∂τxµ∂τxνGµν+ (1)∂σxµ∂σxνGµν)

= −₂T

c

∫

dσdτ(−δ(∂τxµ)∂τxνGµν−∂τxµδ(∂τxν)Gµν

−∂τxµ∂τxν δ(Gµν) +δ(∂σxµ)∂σxνGµν+∂σxµδ(∂σxνGµν) +∂σxµ∂σxνδ(Gµν))

= −₂T_c

∫

dσdτ

 

−δ(∂τxµ)∂τxνGµν−∂τxµδ(∂τxν)Gµν

| {z }

µ←→ν

−∂τxµ∂τxν δ(Gµν) +δ(∂σxµ)∂σxνGµν

+∂σxµδ(∂σxνGµν)

| {z }

µ←→ν

+∂σxµ∂σxνδ(Gµν)

  

= −₂T

c

∫

dσdτ(−δ(∂τxµ)∂τxνGµν−∂τxνδ(∂τxµ)Gνµ

= −₂T untuk suku pertama menggunakan kondisi batas pada persamaan 2.22, dan untuk suku kedua menggunakan kondisi batas

δxµ(σf) =δxµ(σi) = 0 (kondisi batas Dirichlet) (2.45)

persamaan (2.45) menggambarkan kondisi dawai yang kedua ujungnya terikat, sehingga variasi atau pergeseran pada kedua ujungnya bernilai nol.

∂xµ

∂σ (σi) = ∂xµ

dawai. ∂xµ

∂σ (σi) = ∂xµ

∂σ (σf) (kondisi batas dawai tertutup) (2.47) persamaan (2.47) memberikan gambaran bahwa pada dawai tertutup, kon-disi pada ujung awal dan ujung akhir bernilai sama. sehingga, didap-atkan

δS

δxµ = −

T

2c

∫

dσdτ (2∂τ(∂τxν)Gµν+ 2 ∂τxν∂τ(Gµν)

−∂τxγ∂τxν

∂(Gγν)

∂xµ −2∂σ(∂σx ν_)G

µν−2∂σxν∂σ(Gµν)

+∂σxγ∂σxν

∂(Gγν)

∂xµ

)

(2.48) dengan menggunakan prinsip aksi, dimana variasi dari aksi bernilai nol

0 = 2∂τ(∂τxν)Gµν+ 2 ∂τxν∂τ(Gµν)−∂τxγ∂τxν

∂(Gγν)

∂xµ

−2∂σ(∂σxν)Gµν−2∂σxν∂σ(Gµν) +∂σxγ∂σxν

∂(Gγν)

∂xµ

(2.49) persamaan (2.49) merupakan persamaan gerak dari aksi polyakov pada ruang-waktuxµ

2.6 Invariansi Parameterisasi Ulang dari Aksi Polyakov

Pada persamaan aksi (2.30) digunakan parameterτ danσ. Diperke-nalkan parameter baru yang berhubungan denganτdanσ. Denga paramterer baru mempunyai bentukeτ ≡ eτ(τ, σ)danσ_e ≡ eσ(τ, σ). Untuk

menge-tahui apakah aksi Polyakov invarian terhadap parameterisasi, dilakukan pengubahan parameterτ σ→eσeτ

SP = −

T

2c

∫

digunakan Dari perhitungan diatas dapat dilihat bahwa hasil parameterisasi aksi

2.7 Momentum dan Momentum Sudut Konservatif

Salah satu sifat utama dari lagrangian ialah dapat direduksi menjadi kuantitas yang konservatif. Kuantitas konservatif sangat berguna dalam mempelajari sistem dinamik. Kuantitas yang konservatif ini berupa mo-mentum konjuget, yang mempunyai bentuk

Pτ

µ =

∂L

∂(∂τxµ) P σ

µ =

∂L

∂(∂σxµ)

(2.52)

dari persamaan (2.52) dapat ditentukan momentum empat menggunakan momentum konjuget pada parameterτ

Pµ =

∫

dσPτ

µ (2.53)

integral terhadapσdigunakan karena momentum konjuget_Pτ

µ

menggu-nakan rapat lagrangianL.

Pada sistem dinamik perlu diketahui besar energi dari sistem terse-but. Energi dapat ditentukan dari momentum-empattime-likedenganµ= 0. Dikarenakanµ = 0mengindikasikan besaran yang berkaitan dengan

waktu, dan pada relativitas besaran tersebut ialah energi. Maka energi dari dapat ditentukan dengan persamaan

E ≡P0=−P0=−

∫

dσPτ

0 (2.54)

Momentum sudut dibutuhkan untuk kasus sistem berotasi. Momen-tum sudut dapat dibangun menggunakan momenMomen-tum konjuget yang dita-mbahkan sukuxµ. Dengan perubahan kecil dari momentum sudut dapat

didefinisikan dalam bentuk

ϵµνj_µνα = ∂L

∂(∂αxµ)

δxµ (2.55)

denganϵµνmerupakan metrik perubahan kecil terhadap momentum sudut

jα

la-grangian, sehingga

variasi darixµdiruas kanan, dapat dituliskan dalam bentuk metrik peruba-han kecilϵµν

Selanjutnya, dianalisa sifat dari metrikϵµν _{menggunakan perubahan}

kecil pada transformasi lorentz. Transformasi lorentz merupakan trans-formasi linear dari koordinatesxµ yang menyebabkan bentuk kuadratik

dariηµνxµxν invarian

memberikan bahwaϵµνmerupakan metrik antisimetrik

ϵµν =−ϵνµ (2.59)

Menggunakan sifat antisimetrik dariϵµν, maka persamaan (2.58) dapat

dituliskan dalam bentuk

didefinisikan arus jµνα dengan menghilangkan −1 pada ruas kanan dan

α=τ, didapatkan arus lorentztime-likeyang ekivalen dengan memontum sudut dari dawai

j_µντ = 1 2

∫

dσ

(

∂L

∂(∂τxν)

xµ−

∂L

∂(∂τxµ)

xν

)

SOLUSI DAWAI RELATIVISTIK PADA RUANG DATAR

3.1 Aksi Polyakov pada Ruang Datar

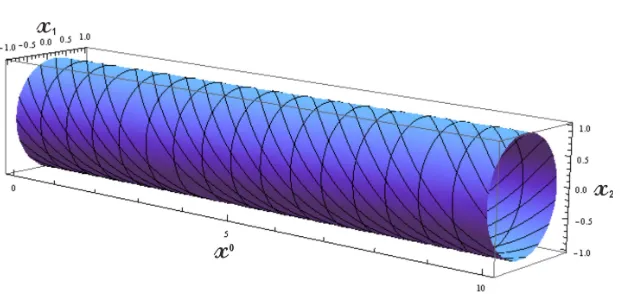
Akan dipelajari dawai tertutup dengan menggunakan Aksi Polyakov (2.30). Dawai tertutup mempunyaiworld-sheetberbentuk silinder dengan kondisi dimana kedua ujung dawai menyambung.

xµ(τ, σ) =xµ(τ, σ+ 2π) (3.1)

dilakukangauge fixing(2.41) padaauxilliary field, sehingga metrik aux-illiary fielddiberikan dalam bentuk metrik minkowski 2-d.

gαβ=ηαβ (3.2)

Pada kasus ini, dipelajari dawai relativistik didalam ruang-waktu datar. Sehingga metrik ruang-waktu diberikan dalam bentuk metrik minkowski 5-d

Gαβ=ηαβ (3.3)

dengan

ηαβ=

     

−1 1

1 1

1

    

 (3.4)

Sehingga aksi Polyakov pada persamaan (2.30) dapat dituliskan dalam bentuk

SP =

∫

dτ dσ_L (3.5)

denganLmerupakan rapat lagrangian

L=−₂T_c ηαβ∂αxµ∂βxνηµν (3.6)

Untuk menentukan energi dari dawai, digunakan momentum-empat time-likepada persamaan (2.55)

Pµ =

denganµ= 0untuk suku energi, maka

E_≡P0=−P0=

T c

∫

dσx˙0 (3.8)

Persamaan ini digunakan untuk menentukan besar energi dari sistem, be-sar energi tersebut hanya bergantung pada koordinat waktu dari ruang-waktuxµ Untuk menentukan momentum sudut dari dawai digunakan

persamaan (2.60) menggunakan rapat lagrangian pada persamaan (3.6). Ditentukan terlebih dahulu turunan lagrangian pada suku pertama dan kedua diruas kanan

maka, momentum sudut dari dawai dapat dituliskan dalam bentuk

Sµν ≡jτµν =

∫

dσ T

2c( ˙xνxµ−x˙µxν)

(3.11)

Untuk menentukan persamaan gerak dawai pada ruang datar digu-nakan persamaan 2.49

0 = 2∂τ(∂τxν)Gµν+ 2 ∂τxν∂τ(Gµν)−∂τxγ∂τxν

∂(Gγν)

∂xµ

−2∂σ(∂σxν)Gµν−2∂σxν∂σ(Gµν) +∂σxγ∂σxν

∂(Gγν)

∂xµ

digunakan metrik ruang-waktu datarGµν=ηµν

0 = 2∂τ(∂τxν)ηµν+ 2 ∂τxν∂τ(ηµν)−∂τxγ∂τxν

∂(ηγν)

∂xµ

−2∂σ(∂σxν)ηµν−2∂σxν∂σ(ηµν) +∂σxγ∂σxν

∂(ηγν)

∂xµ 0 = ∂τ(∂τxν)ηµν−∂σ(∂σxν)ηµν

0 = ∂τ(∂τxµ)−∂σ(∂σxµ)

(3.12)

Untuk persamaan gerak dari variasi aksi terhadap auxilliary fieldgαβ

atau biasa disebut konstrain pada aksi dikarenakan penmabahan auxilliary fieldauxilliary field

S = T

2c

∫

dτ dσ(₋√₋g gαβ∂αxµ∂βxνηµν

)

δS = T

2c

∫

dτ dσ δ(₋√₋g gαβ∂αxµ∂βxνηµν

)

= T

2c

∫

dilakukangauge fixingpada metrikauxilliary fieldberupa metrik minkowski gαβ=ηαβgγρ=ηγρdenganγ, ρ=τ, σ,αβ=τ, maka

0 = −1

2(g τ τ_∂

τxµ∂τxνηµν)

−1

2(g σσ_∂

σxµ∂σxνηµν)

−(∂τxµ∂τxνηµν)

= ∂τxµ∂τxνηµν+∂σxµ∂σxνηµν

(3.14) dari persamaan (3.13), jika digunakan metrik non-diagonal denganα, γ=

τ,danρ, β=σ. Maka didapatkan

0 =

(

1

2(−gτ σ)g τ σ₍

−∂τxµ∂σxνηµν)

)

+ (−∂τxµ∂σxνηµν)

= ∂τxµ∂σxνηµν (3.15)

3.2 Dawai Melingkar Berputar pada dua Bidang yang Saling

Tegak Lurus

Pada model dawai ini, dawai tertutup berputar terhadap waktu pada bidang(x1_{, x}2₎dan_(x3_{, x}4₎yang saling tegak lurus. Ansatz dari model

dawai ini ialah

x0 = κτ

x1 = acos(ωτ+σ)

x2 = asin(ωτ +σ)

x3 = acos(ωτ₋σ)

x4 = asin(ωτ −σ)

(3.16) denganamerupakan jari-jari dawai danωfrekuensi rotasi dari dawai.

Gambar 3.1:dawai berputar pada bidang(x1_{, x}2₎

= ∂τxµ∂τxνηµν+∂σxµ∂σxνηµν

= −κ2+a2ω2(cos2(ωτ+σ) +sin2(ωτ +σ)) +a2ω2(cos2(ωτ ₋σ) +sin2(ωτ₋σ))

+a2(cos2(ωτ+σ) +sin2(ωτ +σ))+a2(cos2(ωτ−σ) +sin2(ωτ −σ))

κ2 = 2a2(ω2+ 1)

jika digunakanω= 1, maka

κ= 2a (3.17)

Untuk energi dari dawai, digunakan persamaan (3.8)

E = T

∫ 2π

0

dσ ∂τ(κτ)

= T2πκ

Gambar 3.2: dawai berputar pada bidang(x3_{, x}4₎

Momentum sudut dari dawai pada bidang (x1_{, x}2) dapat ditentukan

menggunakan persamaan 3.11

S12 =

T

2

∫

dσ (acos(ωτ+σ)ω acos(ωτ +σ)

−asin(ωτ +σ)ω(−asin(ωτ+σ)))

= T

2 ω a

2∫ 2π 0

dσ

= T

2 ω a

2_{2π (3.19)}

Momentum sudut dari dawai pada bidang (x3_{, x}4) dapat ditentukan

menggunakan persamaan 3.11

S34 =

T

2

∫

dσ (acos(ωτ₋σ)ω acos(ωτ ₋σ)

−asin(ωτ ₋σ)ω(−asin(ωτ₋σ)))

= T

2 ω a

2∫ 2π

0

dσ

= T

2 ω a

Persamaan gerak dari dawai pada ruang-waktu xµ dapat ditentukan menggunakan persamaan (3.12)

0 = ∂τ(∂τxµ)−∂σ(∂σxµ)

= ∂τ(∂τx0) +∂τ(∂τx1) +∂τ(∂τx2) +∂τ(∂τx3) +∂τ(∂τx4) −∂σ(∂σx0)−∂σ(∂σx1)−∂σ(∂σx2)−∂σ(∂σx3)−∂σ(∂σx4)

= ∂τ(∂τκτ) +∂τ(∂τacos(ωτ+σ)) +∂τ(∂τasin(ωτ +σ)) +∂τ(∂τacos(ωτ−σ)) +∂τ(∂τasin(ωτ −σ))

−∂σ(∂σκτ)−∂σ(∂σacos(ωτ+σ))−∂σ(∂σasin(ωτ +σ))

−∂σ(∂σacos(ωτ−σ))−∂σ(∂σasin(ωτ−σ)) = 0−a ω2cos(ωτ+σ)−a ω2sin(ωτ+σ)

−a ω2cos(ωτ−σ)−a ω2sin(ωτ−σ) +0 +acos(ωτ+σ) +asin(ωτ +σ) +acos(ωτ−σ) +asin(ωτ −σ)

(3.21) Besar energi dapat diberikan dalam bentuk momentum sudut dengan menggunakanω= 1

SOLUSI DAWAI RELATIVISTIK PADA RUANG

ADS

5

×

S

5

4.1 Aksi Polyakov pada Ruang

AdS

5

×

S

5

RuangAdS5×S5merupakan penggabungan antara anti-de Sitter 5

dimensi dengan sperical 5 dimensi, sehingga ruang ini mempunyai total 10 dimensi. RuangAdS5×S5ini memberikan interprestasi fisis menarik

ketika dawai supersuperstringdipelajari dalam ruang tersebut. Pada tugas akhir ini akan dipelajari dawai klasik yang berotasi dalam ruangAdS5×S5 serta ditinjau energi dan momentum sudut dari dawai tersebut.

Ruang anti-de sitter merupakan ruang dengan kurvatur kuadratik kon-stan negatif ( jari-jari negatif). Ruang ini dapat direpresentasikan seba-gai hiperboloid yang berada pada permukaanR2,5−1_{, sehingga dapat}

di-tuliskan dalam bentuk

ηP QYPYQ =−Y02+Y12+Y22+Y32+Y42−Y52=−1 (4.1)

dengan diberikan jari-jari dari hiperboloid ialah 1. perpindahan dalam ru-angAdS5×S5berikan dalam persamaan

ds2=ηP QdYPdYQ ηP Q= (−1,1, ....,1,−1) (4.2)

Untuk ruang spherical 5-dimensi S5. dapat direpresentasikan pada permukaan dengan kurvatur kuadratik positif yang berada pada permukaan R5+1

XMXM =X12+X22+X32+X42+X52+X62= 1 (4.3)

dengan jari-jari bernilai 1.

BagianAdS5danS5dari aksi dawai terikat dengan interaksinya

ter-hadap metrikworld-sheet2-dimensigαβ. Aksi polyakov pada ruangAdS5×

S5merupakan penjumlahan dari aksi Polyakov padaAdS5danS5,sehingga

dapat diberikan dalam bentuk

S=

∫

dτ dσ(LAdS5+LS5) (4.4)

denganLAdS5danLS5merupakan rapat lagrangian pada ruangAdS5dan

Dengan Λe merupakan pengali lagrange untuk ruangAdS5dengan

kon-strainYP_YQ_η

P Q=−1danΛmerupakan pengali lagrange untuk ruang

S5dengan konstrain_X

MXM = 1

Pada persamaan ini terdapat 5 persamaan gerak dari variasi aksi ter-hadap auxilliary fieldgαβ,variasi aksi terhadap_X

M, variasi aksi terhadap

YP, variasi aksi terhadap pengali langrange_Λe dan_Λ

Energi dari dawai dapat ditentukan menggunakan persamaan momen-tum sudut-empattime-like. Dengan indekµ = 0, ν = 5. Hal ini

dikare-nakan dawai juga berputar pada bidang yang dibentuk koordinat waktu AdS5.

dilakukangauge fixing(2.41) padaauxilliary field, sehingga metrik aux-illiary fielddiberikan dalam bentuk metrik minkowski 2-d.

maka, energi dari dawai diberikan dalam bentuk Momentum sudut dari dawai yang berotasi pada bidangAdS5

SP Q≡jP Qτ =

dilakukangauge fixing(2.41) padaauxilliary field, sehingga metrik aux-illiary fielddiberikan dalam bentuk metrik minkowski 2-d.

= − ∂

maka, momentum sudut dawai pada ruangAdS5diberikan dalam bentuk

SP Q≡jP Qτ =

Momentum sudut dari dawai yang berotasi pada bidangS5

dengan,

dilakukangauge fixing(2.41) padaauxilliary field, sehingga metrik aux-illiary fielddiberikan dalam bentuk metrik minkowski 2-d.

= − ∂

maka, momentum sudut dawai pada ruangS5_{diberikan dalam bentuk}

JM N ≡jτM N =

Untuk persamaan gerak dari variasi aksi terhadap auxilliary fieldgαβ

δS dilakukangauge fixingpada metrikauxilliary fieldberupa metrik minkowski

gαβ=ηαβgγρ=ηγρdenganγ, ρ=τ, σ,αβ=τ, maka

dari persamaan (4.16), jika digunakan metrik non-diagonal denganα, γ=

τ,danρ, β=σ. Maka didapatkan

Untuk persamaan gerak dari variasi aksi terhadapYP

denganGP Q=ηP Q= (−1,1,1,1,1,−1)

Untuk persamaan gerak dari variasi aksi terhadapXM

dari persamaan (4.20) dan (4.3), bisa didapatkan bentuk dari pengali la-grange pada ruangS5

0 = ∂α∂αXM + ΛXM 0 = XM(∂α∂αXM+ ΛXM) 0 = XM∂α∂αXM +XMΛXM)

0 = ∂α(XM∂αXM)−∂αXM∂αXM+XMΛXM)

−Λ = ∂α(XM∂αXM

| {z }

0

)−∂αXM∂αXM

Λ = ∂αXM∂αXM

(4.21) Dari persamaan (4.19) dan (4.1), bisa didapatkan bentuk dari pengali la-grange pada ruangS5

0 = ∂α∂αYP−ΛeYP 0 = YP(∂α∂αYP −ΛeYP)

0 = YP∂α∂αYP+XPΛeXP) 0 = ∂α(YP_∂α_Y

P)−∂αYP∂αYP+YPΛeYP)

−Λe = ∂α(YP∂αYP

| {z }

0

)−∂αYP∂αYP

e

Λ = ∂αYP∂αYP

4.2 Dawai Melingkar Berputar pada

R

t

×

S

5

bagian dari

AdS

5

×

S

5

Pada model ini, dawai melingkar berputar padaS3dengan radius_a≤

1di dalamS5dengan radius₁Ansatz

Y0=cos(kτ) Y5=sin(kτ)

X1=

a

√

2cos(m(τ+σ)) X2=

a

√

2sin(m(τ+σ))

X3=

a

√

2cos(m(τ−σ)) X4=

a

√

2sin(m(τ−σ))

X5+iX6= √

1−a (4.23)

kmerupakan frekuensi rotasi dawai pada bidangY0Y1,mmerupakan frekuensi

rotasi pada bidangS5dan juga memberikan banyak lilitan dawai. Energi dari dawai dapat dihitung menggunakan persamaan (4.9)

E≡ S05 = T 2

∫ 2π

0

dσ(Y0Y˙5−Y5Y˙0

)

= T

2

∫ 2π

0

dσ(cos(kτ)kcos(kτ)−sin(kτ)(−sin(kτ)))

= T

2

∫ 2π

0

dσ k(cos2(kτ) +sin2(kτ))

Momentum sudut dari dawai pada bidangX1danX2dapat dihitung

menggunakan persamaan (4.15)

J12 = T

Momentum sudut dari dawai pada bidangX3danX4dapat dihitung

menggunakan persamaan (4.15)

J34 = T

Pengali lagrange pada ruangAdS5diberikan dalam bentuk

e

Λ = ∂αYP∂αYP

= ∂τY0∂τY0+∂σY0∂σY0+∂τY5∂τY5+∂σY5∂σY5

= k2sin2(kτ) + 0 +k2cos2(kτ) + 0

Pengali lagrange pada ruang S5 dari persamaan (4.21)diberikan dalam

Persamaan gerak dari dawai terhadapauxilliary field

hubun-gan (4.29)

E =T π k=√4m T π J (4.30)

solusi energi ini identik dengan solusi energi dawai berputar di ruang datar pada persamaan (3.22)

4.3 Dawai Melingkar Berputar pada

S

3

⊃

S

5

Pada model dawai ini, dawai melingkar dan berputar dengan dua mo-mentum sudut yang sama padaS3⊃S5. Model dawai ini identik dengan dawai pada persamaan (4.23), dimana a = 1danω = m. Ansatz dari

dawai ini diberikan dalam bentuk

Y0=cos(kτ) Y5=sin(kτ)

X1=

1

√

2cos(ωτ+mσ) X2= 1

√

2sin(ωτ +mσ)

X3=

1

√

2cos(ωτ−mσ) X4= 1

√

2sin(ωτ −mσ)

X5=X6= 0 (4.31)

Energi dari dawai dapat dihitung menggunakan persamaan (4.9)

E_{≡ S}05 =

T

2

∫ 2π

0

dσ(Y0Y˙5−Y5Y˙0

)

= T

2

∫ 2π

0

dσ(cos(kτ)kcos(kτ)−sin(kτ)(−sin(kτ)))

= T

2

∫ 2π

0

dσ k(cos2(kτ) +sin2(kτ))

= T π k (4.32)

menggunakan persamaan (4.15)

Momentum sudut dari dawai pada bidangX3danX4dapat dihitung

meng-gunakan persamaan (4.15)

J34 =

terhadapgαβ jika digunakan persamaan gerak ini pada solusiE_≡S05, maka

E = √m2_+ω2_{T π} untuk dawai berputar dengan sangat cepatJ >>1

4.4 Dawai Melingkar Berputar hanya pada

AdS

5

Pada model dawai ini, dawai berputar pada ruangAdS5yang

mem-punyai jari-jarir. Dawai berputar pada dua bidang yang dibentuk koordi-nat ruangAdS5dan bidang tersebut saling tegak lurus. Ansatz dari model

dawai ini

Energi dari dawai dapat dihitung menggunakan persamaan (4.9)

E≡S05 =

Momentum sudut dari dawai pada bidangY1danY2dapat dihitung

meng-gunakan persamaan (4.12)

Momentum sudut dari dawai pada bidangY3danY4dapat dihitung

meng-gunakan persamaan (4.12)

S34 = T

Persamaan gerak dari persamaan (4.17) (variasi aksi terhadapgαβ

Pengali lagrange pada ruangAdS5(4.22)diberikan dalam bentuk

e

Λ = ∂αYP∂αYP

= ∂τY0∂τY0+∂σY0∂σY0+∂τY5∂τY5+∂σY5∂σY5 −∂τY1∂τY1+∂σY1∂σY1−∂τY2∂τY2+∂σY2∂σY2 −∂τY3∂τY3+∂σY3∂σY3−∂τY4∂τY4+∂σY4∂σY4

= (1 + 2r2)k2(cos2(kτ) +sin2(kτ))

−r2ω2(cos2(ωτ +σ) +sin2(ωτ+σ))−r2ω2(cos2(ωτ+σ) +sin2(ωτ+σ)) +r2(cos2_{(ωτ−σ) +sin}2₍

ωτ−σ)) +r2(cos2_{(ωτ −σ) +sin}2₍

ωτ−σ))

= (1 + 2r2)k2₋2r2ω2+ 2r2 (4.43)

Untuk mendapatkan hubungan antarakdenganr, digunakan persamaan gerak dawai terhadapY0pada ruang_AdS

5,

0 = ∂α∂αY0−ΛeY0

0 = −ω2₋Λe

0 = −ω2−(1 + 2r2)k2+ 2r2ω2−2r2

menggunakan persamaan (4.42), maka didapatkan

0 = 2k2r2₋k2₋2k2r2+ 4r2

r2 = 1 4k

2 _(4.44)

Momentum sudut dari dawai dapat dituliskan dalam fungsikdengan menggunakanr2=k2

2 danω= √

k2_{+ 1}

S12=S34≡ S= = 1

4k

2√_k2_{+ 1}

0 = k6+k2₋16S2

(4.45) dengan melakukan ekspansi terhadapkdengan limitS <<1

selanjutnya disubtitusi nilaikpada persamaan4.46kedalam bentuk energi

persamaan energi ini menunjukan energi dari dawai pada dawai yang berputar sangat lambat. Jika diambil suku pertama dari solusi energi diatas, didap-atkan hasil yang identik dengan solusi energi dawai berputar di ruang datar pada persamaan (3.22)

4.5 Dawai Melingkar Berputar pada

AdS

5

dan

S

5

Pada model dawai ini, dawai melingkar berputar pada bidang yang dibentuk oleh ruangAdS5dan ruangS5. Dawai ini mempunyai ansatz

Y0=

Energi dari dawai dapat dihitung menggunakan persamaan (4.9)

E_≡S05 =

meng-gunakan persamaan (4.12)

S12 = T 2

∫ 2π

0

dσ(Y1Y˙2−Y2Y˙1

)

= T

2

∫ 2π

0

dσ r2(cos(ωτ +σ)ωcos(ωτ +σ)

−sin(ωτ +σ)ω(−sin(ωτ +σ)))

= T

2r

2∫ 2π 0

dσ ω (cos2(ωτ+σ) +sin2(ωτ+σ))

= r2T πω (4.49)

Momentum sudut dari dawai pada bidangX1danX2dapat dihitung

meng-gunakan persamaan (4.15)

J12 = T 2

∫ 2π

0

dσ(X1X˙2−X2X˙1

)

= T

2

∫ 2π

0

dσ a2(cos(ωτ −σ)ωcos(ωτ −σ)

−sin(ωτ −σ)ω(−sin(ωτ −σ)))

= T

2a

2∫ 2π 0

dσ ω (cos2(ωτ−σ) +sin2(ωτ−σ))

= a2T π (4.50)

persamaan gerak dari persamaan (4.18) variasi aksi terhadapgαβ

0 = ∂τYP∂σYQGP Q+∂τXM∂σXM

0 = ∂τY0∂σY0(−1) +∂τY5∂σY5(−1) +∂τY1∂σY1(1) +∂τY2∂σY1(2) +∂τX1∂σX1+∂τX2∂σX2

= −0−0 +r2ωsin2(ωτ +σ) +r2ωcos2(ωτ+σ)

−a2sin2(τ₋σ)−a2cos2(τ₋σ) = 2r2ω−2a2

persamaan gerak dari persamaan (4.17) variasi aksi terhadapgαβ

0 = ∂τYP∂τYQGP Q+∂σYP∂σYQGP Q +∂τXM∂τXM +∂σXM∂σXM 0 = ∂τY0∂τY0(−1) +∂τY5∂τY5(−1)

+∂τY1∂τY1+∂τY2∂τY2+∂τX1∂τX1+∂τX2∂τX2

+∂σY1∂σY1+∂σY2∂σY2+∂σX1∂σX1+∂σX2∂σX2

0 = −(1 +r2)k2(sin2(kτ))−(1 +r2)k2(cos2(kτ)) +r2ω2sin2(ωτ+σ) +r2ω2cos2(ωτ+σ) +a2ω2sin2(ωτ ₋σ) +a2ω2cos2(ωτ ₋σ) +a2sin2(ωτ+σ) +a2cos2(ωτ +σ) +a2sin2(ωτ₋σ) +a2cos2(ωτ ₋σ) 0 = −(1 +r2)k2+r2ω2+r2+a2+a2 k2(1 +r2) = r2(ω2+ 1) + 2a2

dengan menggunakan persamaana2_=r2ω, maka

k2(1 +r2) = r2ω2+r2+ 2r2ω k2+k2r2 = r2(ω2+ 1 + 2ω)

k2 = r2(ω2+ 1 + 2ω−2k2)

dengan menggunakan persamaanω2_=k2_{+ 1}

k2 = r2(k2+ 1 + 1 + 2√k2_{+ 1−k}2₎

k2 = r2(2 + 2√k2_{+ 1)}

r2 = k

2

2(1 +√k2_{+ 1)} (4.52)

jika persamaanr2= k2

r2ω

solusi untukk

k=±

Tanda±pertama diambil positif, karena nilai energi harus bernilai positif.

Tanda ±kedua diambil positif, karena nilai dibawah akar harus dalam

bentuk real.

Untuk dapat menentukan nilai E dalam pendekatan dawai berputar cepat dan lambat, persamaanEdiekspresikan dalam fungsiS, maka

E = T π(1 +r2)k dengan menggunakan softwaremathematicadidapatkan solusiE untuk dawai berputar sangat cepatS >>1

E=T π

untuk dawai yang berputar dengan sangat lambatS <<1

E=√4T πS

PENUTUP

5.1 Kesimpulan

Dalam tugas tugas akhir ini, didapatkan kesimpulan

1. Telah diterapkan dawai relativistik menggunakan aksi Polyakov dalam ruang waktu datar pada model dawai melingkar yang berputar pada dua bidang yang saling tegak lurus. Selanjutnya, didapatkan energi, momen-tum sudut, dan persamaan gerak dari dawai tersebut.

2. Telah diterapkan dawai relativistik menggunakan aksi Polyakov dalam ruang waktu AdS5 ×S5 pada model dawai Melingkar pada Rt ×S5

bagian dariAdS5×S5, dawai Melingkar padaS3⊃S5, dawai Melingkar

Berputar hanya padaAdS5, dan dawai Melingkar Berputar padaAdS5dan

S5_{. Lagrangian dari aksi Polyakov dalam ruang waktuAdS}

5×S5

men-dapatkan suku tambahan berupa konstrain dari ruangAdS5×S5. Karena

penambahan konstrain, suku tersebut dikalikan dengan pengali lagrange. Didapatkan 2 persamaan gerak dari variasi aksi Polyakov terhadap ru-angAdS5, ruang S5, dan dua konstrain dari variasi aksi terhadap

aux-illiary field. Selanjutnya, didapatkan energi, momentum sudut, dan per-samaan gerak dari 4 model tersebut. Pada dawai di dalam ruang waktu AdS5×S5, besar energi dapat diberikan dalam bentuk momentum sudut

menggunakan empat persamaan gerak dan dua konstrain. Pada model dawai melingkar berputar padaAdS5danS5, dawai yang berputar pada

ruang AdS5 juga terikat dengan perputarannya di ruang S5. Sehingga

besar momentum sudutnya bernilai sama. Energi pada dawai melingkar berputar padaAdS5danS5mempunyai bentuk polinomial, dan dapat

di-lakukan pendekatan untuk mencari besar energi pada saat berputar sangat cepat dan berputar sangat lambat. Pada dawai yang berputar sangat lam-bat, didapatkan energi yang identik terhadap solusi energi dawai berputar di ruang datar dengan penambahan faktor bernilai 2.

5.2 Saran

Untuk penelitian selanjutnya, bisa dilakukan pengerjaan pada dawai relativistik yang sudah terkuantisasi. Kuantisasi yang dapat dilakukan bisa

[1] B. Zwiebach,A First Course In String Theory, Cambridge University Press, 2009

[2] B. Hatfield,Quantum Field Theory Of Point Particles And Strings, Avalon Publishing, 1998

[3] D. McMahon, String Theory Demystified, McGraw Hill Profes-sional, 2008

[4] K. Fujikawa, 1988, Phys. Lett. B 213

[5] L. McAllister, 2010, Notes on String Theory from Liam McAllister Physics 7683,Cornel University, New York, United Stated of Amer-ica

[6] B. Hattfield,Quantum Field Theory of Point Particles and Strings, Perseus Books, 1991

[7] A.A Tseytlin, 2010,Review of AdS/CFT Integrability, Chapter II.1, Imperial College London, arXiv:1012.3982

[8] S. Frolov, A.A Tseytlin, 2003, Nucl.Phys. B668, arXiv:hep-th/0304255

LAMPIRAN

A.1 Dawai Non-Relativistik

Dawai ialah objek 1 dimensi yang dapat berisolasi terhadap titik setimbangnya. Arah sepanjang dawai disebut arah longitudinal dan arah tegak lurus dengan dawai disebut arah transversal. Dawai non-relativistik merupakan dawai yang dapat bergerak dengan kecepatan yang jauh lebih kecil jika dibandingkan dengan kecepatan cahayav << cterhadap suatu kerangka acuan.

Dimisalkan dawai dengan dengan rapat massaµ0, konstanta

tegan-gan dawaiT0, dan ujung dawai terletak padax = 0danx = a.

Energi kinetik suatu dawai merupakan penjumlahan energi kinetik dari potongan kecil dari dawai. Maka energi kinetik dawai dapat dituliskan dalam bentuk

T =

∫ a

0

1

2(µ0dx)

(

∂y ∂t

)2

(A.1)

energi potensial dari dawai berasal usaha yang dikerjakan untuk meregangkan dawai. Pada keadaan setimbang, elemen kecil dawai terbentang dari(x,0)hingga(x+dx,0). Jika elemen kecil dawai

diregangkan ke arah transversal dari(x, y)menjadi(x+dx, y+dy)

seperti pada gambar (A.1). Dengan mengambil osilasi dari dawai sangat kecil∂y/∂x << 1, maka perubahan panjang∆l dari ele-men kecil dawai ialah

∆l = √(dx)2_{+ (dy)}2_−dx

= dx

 

√

1 +

(

∂y ∂x

)2 −1

 

≈ dx

(

1 + 1 2

(

∂y ∂x

)2 −1

)

≈ dx1

2

(

∂y ∂x

)2

(A.2)

kerja elemen kecil dawai yang diregangkan ialahT0∆l. Maka total

energi potensial pada dawai dengan panjanga

V =

∫ a

0

dx1

2T0

(

∂y ∂x

)2

(A.3)

Gambar A.1:dawai yang direnggangkan kearah transversal

pers (A.1) dan (A.3) didapatkan lagrangian dari string

dengan L merupakan rapat lagrangian dari sistem dawai

non-relativistik

Untuk mempermudah menganalisa dawai diperkenalkan kondisi batas pada dawai. Terdapat 2 kondisi batas pada dawai yaitu kondisi batas Dirichlet dan kondisi batas Neumann. Diasumsikan dawai ter-bentang pada sumbu-xdan dawai akan berosilasi pada arah sumbu-y. Untuk kondisi batas Dirichlet memberikan kondisi spesifik dari

Gambar A.2:(a): dawai dengan kondisi batas Dirichlet. (b): dawai den-gan kondisi batas Neumann

ujung dawai yang diikatkan pada suatu dinding seperti pada gambar (A.2). Maka kondisi batas Dirichlet dapat dituliskan dalam bentuk

∂y(t, x= 0) =∂y(t, x=a) = 0 (A.7)

∂y

∂t(t, x= 0) = ∂y

∂t(t, x=a) = 0 (A.8)

Pada kondisi batas Neumann, kedua ujung dawai dikaitkan pada batang licin. Sehingga ujung dawai dapat bergerak bebas dalam arah vertikal pada sumbu-y seperti pada gambar A.2. Dimana kedua ujung dawai tidak bermassa dan dikaitkan pada batang licin, maka kemiringan dari dawai pada ujungx= 0, ayang merupakan turunan

∂y

∂x bernilai nol.

∂y

∂x(t, x= 0) = ∂y

∂x(t, x=a) = 0 (A.9)

Pada sistem yang bergerak, digunakan aksi untuk mendeskripsikan gerak dari sistem tersebut. Aksi merupakan integral dari lintasan terhadap lagrangian pada dua titik yang dilalui sistem. Sehingga aksi dapat dituliskan dalam bentuk

S =

∫ tf

ti

L(t)dt (A.10)

ter-hadap koordinaty,

menggunakan syarat batas pada suku pertama dan kedua. Serta menggunakan prinsip aksi, didapatkan

0 =

Persamaan ini merupakan persamaan gerak dari dawai non-relativistik

A.2 Partikel Relativistik

Dibayangkan partikel yang berada pada lintasan di ruang-waktu

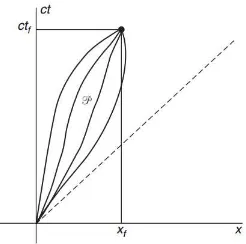
Gambar A.3: diagram ruang-waktu dengan beberapa world-line yang menghubungkan titik awal dengan(c tf,

→ xf)

yang dimulai dari titik asal hingga pada titik (c tf,

→

xf). Terdapat

beberapa kemungkinanworld-linesantara titik awal dan titik akhir, seperti pada gambar (A.3). DimisalkanPmengambarkanworld-line.

Perpindahan partikel relativistik pada ruang waktu diberikan dalam bentuk

(ds)2 = Gµνdxµdxν

(ds)2 = Gµν

dxµ dτ

dxν dτ (dτ)

2

ds =

√

Gµν

dxµ

dτ dxν

dτ dτ (A.12)

semua pengamat lorentz. Sehingga didapatkan aksi

Aksi partikel relativistik ini invariant terhadap reparameterisasi ulang. Jika diubah paramater kedalam bentuk lain, maka akan di-dapatkan bentuk aksi yang serupa

= −mc

∫

dτ

(

−∂x

µ

∂τ ∂xν

∂τ δx

αdGµν

dxα

−

[

−δxµ∂x

ν

∂τ d

dτ(Gµν)−δx

µ∂2xν

∂τ2 Gµν

]

−

[

−δxν∂x

µ

∂τ d

dτ(Gµν)−δx

ν∂2xµ

∂τ2 Gµν

])

+

(

δxν∂x

µ

∂τ Gµν

)τf

τi

+

(

δxµ∂x

ν

∂τ Gµν

)τf

menggunakan variasi pada kondisi awalτidan kondisi akhirτfyang

bernilai nol, maka suku kedua terakhir bernilai nol

persamaan ini, biasa disebut persamaan geodesik.

Persamaan aksi partikel relativistik (A.13) tidak dapat mendeskrip-sikan pergerakan dari partikel tidak bermassa, persamaan tersebut memberikan aksi bernilai nol dan tidak dari aksi tersebut tidak bisa didapatkan persamaan gerak dari partikel tidak bermassa.

Terdapat aksi lain yang lebih sederhana dengan penampahan param-eter baru yang disebutauxilliary fielde(τ). Aksi ini diberikan dalam

bentuk

Aksi ini merupakan integral terhadap lintasannya pada ruang-waktu xµ_{, sehingga tidak bergantung pada parameter yang digunakan. Hal}

ini mengindikasikan aksi (A.15) reparameterisasi invarian. Untuk menguji bahwa aksi (A.15) reparameter invarian, diperkenalkan pa-rameter baruτ _→eτ(τ) Hasil perhitungan ini memberikan bentuk aksi yang identik dengan aksi pada persamaan (A.15). Sehingga dapat dikatakan aksi pada per-samaan (A.15) reparameter invarian.

Persamaan aksi ini memberikan dua persamaan gerak, persamaan gerak terhadap ruang-waktuxµdan persamaan gerak terhadap

aux-illiary fielde

Jika persamaan gerak ini disubtitusikan kembali ke aksi partikel (A.15)

menggunakan variasi pada kondisi awalτidan kondisi akhirτfyang

bernilai nol, maka suku kedua terakhir bernilai nol

= −c solusi persamaan gerak ini memiliki bentuk yang identik dengan per-samaan gerak pada perper-samaan (A.14). Menunjukan bahwa penamba-hanauxilliary fieldterhadap aksi (A.15) tidak mengubah persamaan gerak dari dawainya

A.3 Bentuk Umum dari Model Dawai

lin-tasan dari objek tersebut

S =−κ

∫

dp+1σ√−dethαβ (A.20)

α, β = 0,1...., p,κmerupakan konstanta untuk menyetarakan di-mensi dari lintasan objek dengan didi-mensi dari aksi, dengan

hβ=

∂xµ

∂σα

∂xν

∂σβGµν (A.21)

xµ(σ0= 0, σ1, σ2, ...., σp),µ= 0,1, ..., D−1

Jika digeneralisasi metrikhαβmenjadi tidak terikat olehxµ. Maka

metrikhαβ menjadi metrikauxilliary fieldgαβ. dan metrik ini juga

disebut metrik yangnon-dynamic

Saux=−κ₂

∫

dp+1σ√₋detgαβ

(

gαβ∂x

µ

∂σα

∂xν

∂σβGµν−(p−1)

)

(A.22)

Salah satu objek yang dapat dideskripsikan dari bentuk umum dari model dawai ialah2−brane.2−branemerupakan objek dengan

(3 + 1)parameter(xµ_=xµ_(σ0_{=τ, σ}1_{, σ}2₎). Untuk merumuskan

aksi dari2−brane. digunakan persamaan (A.20) denganp= 2

S = −κ

∫

d2+1σ√−dethαβ

= −κ

∫

dτ dσ1dσ2√−dethαβ

(A.23)

denganα, β = 0,1,2. Untuk aksi denganauxilliary field

Saux = −κ₂ ∫

d2+1σ√−detgαβ

(

gαβ∂x

µ

∂σα

∂xν

∂σβGµν−(2−1)

)

= −κ₂

∫

dτ dσ1dσ2√₋detgαβ

(

gαβ∂xµ

∂σα

∂xν

∂σβGµν−1

)

(A.24)

A.4 Ruang

AdS

5

×

S

5

Anti de sitter AdSd merupakan ruang dengan kurvatur kuadratik

negatif sehingga dapat direpresentasikan sebagai hiperboloid yang berada pada permukaanR2,d−1

ηP QYPYQ =−Y02+Y12+...+Yd2−1−Yd2=−1 (A.25)

yang berada pada permukaanR2,d−1_{dengan radius dari hiperboloid}

ialah 1, dengan metrik

ds2=ηP QdYPdYQ ηP Q= (−1,1, ....,1,−1) (A.26)

Pada ruangAdS5_{digunakand= 5, dan diparameterisasi dengan 5}

koordinat global yang saling tidak terikat. Maka persamaan (A.25) dapat disederhakan

−1 = −Y₀2+Y₁2+Y₂2+Y₃2+Y₄2₋Y₅2

−1 = −(Y02+iY52

) (

Y02−iY52

)

+(Y12+iY22

) (

Y12−iY22

) (

Y32+iY42

) (

Y32−iY42

)

(A.27) diperkenalkan 3 parameter bebast, ϕ1, ϕ2

−1 = −(a1eit) (a1e−it)+(a2eiφ1) (a2e−φ1)+(a3eiφ2)+(a3e−iφ2)

diperkenalkan 2 parameter bebasρ, θ

−1 = −a2₁+ (a2₂+a2₃)

−1 = −cosh2ρ+sinh2ρ(sin2θ+cos2_θ)

(A.29) dengan

a1=coshρ (A.30)

a2=sinhρsinθ (A.31)

a3=sinhρcosθ (A.32)

Maka, didapatkan

Y0+iY5=a1eit=coshρ(cost+isint) (A.33)

Y1+iY2=a2eiφ1 =sinhρsinθ(cosϕ1+isinϕ1) (A.34)

Y3+iY4=a3eiφ2 =sinhρcosθ(cosϕ2+isinϕ2) (A.35)

untuk mendapatkan bentuk eksak darids2, maka ditentukan bentuk dari perpindahan pada setiap koordinat. UntukY02

Y0 = coshρsint (A.36) maka,

dY0 = sinhρsint dρ+coshρcost dt (A.37)

UntukY₁2

maka,

dY1 = coshρsinθcosϕ1dρ+sinhρcosθcosϕ1dθ

+sinhρsinθ(−sinϕ1)dϕ1 (A.39)

UntukY22

Y2 = sinhρsinθsinϕ1 (A.40)

maka,

dY2 = coshρsinθsinϕ1dρ+sinhρcosθsinϕ1dθ

+sinhρsinθcosϕ1dϕ1 (A.41)

UntukY32

Y3 = sinhρcosθcosϕ2 (A.42)

maka,

dY3 = coshρcosθcosϕ2dρ+sinhρ(−sinθ)cosϕ2dθ

+sinhρcosθ(−sinϕ2)dϕ2 (A.43)

UntukY42

Y4 = sinhρcosθsinϕ2 (A.44)

maka,

dY4 = coshρcosθsinϕ2dρ+sinhρ(−sinθ)sinϕ2dθ

+sinhρcosθcosϕ2dϕ2 (A.45)

UntukY2 5

Y5 = coshρcost (A.46) maka,

dari persamaan (A.37),(A.39),(A.41),(A.43),(A.45),(A.47), bisa di-dapatkan perpindahaan pada ruangAdS5

ds2 = ηP QdYPdYQ

= η00dY0dY0+η11dY1dY1+η22dY2dY2+η33dY3dY3

+η44dY4dY4+η55dY5dY5

= (−1)dY0dY0+ (1)dY1dY1+ (1)dY2dY2+ (1)dY3dY3

+(1)dY4dY4+ (−1)dY5dY5

(A.48) dengan,

dY0dY0 = (sinhρsint dρ)2+ (coshρcost dt)2 +2 (sinhρsint dρ) (coshρcost dt) (A.49)

dY1dY1 = (coshρsinθcosϕ1dρ)2+ (sinhρcosθcosϕ1dθ)2

+ (sinhρsinθ(−sinϕ1)dϕ1)2

+2 (coshρsinθcosϕ1dρ) (sinhρcosθcosϕ1dθ)

+2 (coshρsinθcosϕ1dρ) (sinhρsinθ(−sinϕ1)dϕ1)

+2 (sinhρcosθcosϕ1dθ) (sinhρsinθ(−sinϕ1)dϕ1)

(A.50)

dY2dY2 = (coshρsinθsinϕ1dρ)2+ (sinhρcosθsinϕ1dθ)2

+ (sinhρsinθcosϕ1dϕ1)2

+2 (coshρsinθsinϕ1dρ) (sinhρcosθsinϕ1dθ)

+2 (coshρsinθsinϕ1dρ) (sinhρsinθcosϕ1dϕ1)

+2 (sinhρcosθsinϕ1dθ) (sinhρsinθcosϕ1dϕ1)

dY3dY3 = (coshρcosθcosϕ2dρ)2+ (sinhρ(−sinθ)cosϕ2dθ)2

+ (sinhρcosθ(−sinϕ2)dϕ2)2

+2 (coshρcosθcosϕ2dρ) (sinhρ(−sinθ)cosϕ2dθ)

+2 (coshρcosθcosϕ2dρ) (sinhρcosθ(−sinϕ2)dϕ2)

+2 (sinhρ(−sinθ)cosϕ2dθ) (sinhρcosθ(−sinϕ2)dϕ2)

(A.52)

dY4dY4 = (coshρcosθsinϕ2dρ)2+ (sinhρ(−sinθ)sinϕ2dθ)2

+ (sinhρcosθcosϕ2dϕ2)2

+2 (coshρcosθsinϕ2dρ) (sinhρ(−sinθ)sinϕ2dθ)

+2 (coshρcosθsinϕ2dρ) (sinhρcosθcosϕ2dϕ2)

+2 (sinhρ(−sinθ)sinϕ2dθ) (sinhρcosθcosϕ2dϕ2)

(A.53)

dY5dY5 = (sinhρcost dρ)2+ (coshρ(−sint)dt)2 +2 (sinhρcost dρ) (coshρ(−sint)dt) (A.54)

maka, persamaan dapat disederhanakan menjadi

(ds2)AdS5 = dρ 2

−cosh2ρ dt2+sinh2ρ(dθ2+sin2θdϕ2₁+cos2θdϕ2₂) (A.55)

Selanjutnya, untuk ruang spherical 5-dimensiS5. dapat

direpresen-tasikan pada permukaan dengan kurvatur kuadratik positif yang be-rada pada permukaanR5+1

XmXm=X1X1+X2X2+X3X3+X4X4+X5X5= 1(A.56)

koor-dinat global yang saling tidak terikat. Maka persamaan (A.56) dapat disederhakan, dengan memperkenalkan 3 parameterψ1, ψ2, ψ3

1 = (X1+iX2)(X1−iX2) + (X3+iX4)(X3−iX4)

+(X5+iX6)(X5−iX6)

1 = b1eiψ 1

b1e−iψ 1

+b2eiψ 2

b2e−iψ 2

+b3eiψ 3

b3e−iψ 3

1 = (b2₁+b2₂) +b2₃ (A.57) diperkenalkan parameter 2 parameterγ, φ

(b2₁+b2₂) +b2₃ = 1

sin2

γ(cos2φ+sin2φ) +cos2 = 1 (A.58)

dengan

b1=sinγcosφ (A.59)

b2=sinγsinφ (A.60)

b3=cosγ (A.61)

maka, didapatkan

(X1+iX2) =b1eiψ 1

=sinγcosφ(cosψ1+isinψ1) (A.62)

(X3+iX4) =b2eiψ 2

=sinγsinφ(cosψ2+isinψ2) (A.63)

(X5+iX6) =b3eiψ 3

=cosγ(cosψ3+isinψ3) (A.64)

di-tentukan bentuk dari perpindahan pada setiap koordinat. UntukX12

dX1 = cosγcosφcosψ1dγ+sinγ(−sinφ)cosψ1dφ

+sinγcosφ(−sinψ1)dψ1

(A.65)

UntukX2 2

dX2 = cosγcosφsinψ1dγ+sinγ(−sinφ)sinψ1dφ

+sinγcosφcosψ1dψ1

(A.66)

UntukX32

dX3 = cosγsinφcosψ2dγ+sinγcosφ)cosψ2dφ

+sinγsinφ(−sinψ2)dψ2

(A.67)

UntukX2 4

dX4 = cosγsinφsinψ2dγ+sinγcosφ)sinψ2dφ

+sinγsinφcosψ2dψ2

(A.68)

UntukX52

dX5 = (−sinγ)cosψ3dγ

+cosγ(−sinψ3)dψ3

(A.69)

UntukX2 6

dX6 = (−sinγ)sinψ3dγ

+cosγcosψ3dψ3

dari persamaan (A.65),(A.66),(A.67),(A.68),(A.69),(A.70), bisa di-dapatkan perpindahaan pada ruangAdS5

ds2 = dXMdXM

= dX0dX0+dX1dX1+dX2dX2+dX3dX3

+dX4dX4+dX5dX5

(A.71) dengan,

dX1dX1 = (cosγcosφcosψ1dγ)2+ (sinγ(−sinφ)cosψ1dφ)2

+ (sinγcosφ(−sinψ1)dψ1)2

+2 (cosγcosφcosψ1dγ) (sinγ(−sinφ)cosψ1dφ)

+2 (cosγcosφcosψ1dγ) (sinγcosφ(−sinψ1)dψ1)

+2 (sinγ(−sinφ)cosψ1dφ) (sinγcosφ(−sinψ1)dψ1)

(A.72)

dX2dX2 = (cosγcosφsinψ1dγ)2+ (sinγ(−sinφ)sinψ1dφ)2

+ (sinγcosφcosψ1dψ1)2

+2 (cosγcosφsinψ1dγ) (sinγ(−sinφ)sinψ1dφ)

+2 (cosγcosφsinψ1dγ) (sinγcosφcosψ1dψ1)

+2 (sinγ(−sinφ)sinψ1dφ) (sinγcosφcosψ1dψ1)