STUDI PENGARUH PERUBAHAN PENAMPANG SALURAN TERHADAP KECEPATAN PADA MODEL SALURAN TERBUKA

(1)

SKRIPSI

STUDI PENGARUH PERUBAHAN PENAMPANG SALURAN TERHADAP KECEPATAN PADA MODEL SALURAN TERBUKA

WISARDI / 105 81 947 09 A.ROBIANSYAH / 105 81 1142 09

JURUSAN TEKNIK SIPIL FAKULTAS TEKNIK

UNIVERSITAS MUHAMMADIYAH MAKASSAR 2014

(2)

ABSTRAK

Wisardi dan A.robiyansyah : Saluran terbuka adalah saluran dimana air mengalir dengan muka air bebas.Pada semua titik disepanjang saluran, tekanan dipermukaan air adalah sama, yang biasanya tekanan atmosfir.

Pengaliran melalui suatu pipa (saluran tertutup) yang tidak penuh (masih ada muka air bebas) masih termasuk aliran dalam saluran terbuka. Oleh karena itu melalui saluran terbuka harus mempunyai muka air bebas, maka aliran ini biasanya berhubungan dengan zat cair dan umumnya adalah air Penampang saluran alam umumnya sangat tidak beraturan, biasanya bervariasi dari bentuk seperti parabola sampai trapesium. Istilah penampang saluran (channel section) adalah tegak lurus terhadap arah aliran, sedangkan penampang vertikal melalui titik terbawah atau terendah dari penampang. Oleh sebab itu pada saluran mendatar penampangnya selaluh merupakan penampang vertikal.maka untuk memudahkan dalam menentukan jenis aliran dalam setiap aliran pada penampang yang berbeda maka perluh mencari berapa besar nilai Froude dan reynolnya dengan perbandingan kecepatan yang diperoleh pada saat penelitian

Kata kunci : Kecepatan, bilangan Froude, bilangan reynold, Luas Penampang

(3)

KATA PENGANTAR

Puji syukur penulis panjatkan khadirat Allah SWT., atas segala rahmat dan hidayah-Nyalah sehingga penulis dapat menyusun dan menyelesaikan tugas akhir ini, dan Alhamdulillah dapat kami selesaikan dengan baik.

Tugas akhir ini kami susun sebagai salah satu persyaratan akademik yang harus ditempuh dalam rangka menyelsaikan Program Studi pada Jurusan dan Perencanaan Fakultas Teknik Universitas Muhammadiyah Makassar. Adapun judul tugas akhir kami adalah: “STUDI PENGARUH PERUBAHAN PENAMPANG SALURAN TERHADAP KECEPATAN PADA MODEL SALURAN TERBUKA”.

Penulis menyadari sepenuhnya bahwa di dalam penulisan skripsi ini masih terdapat banyak kekurangan, hal ini disebabkan sebagai manusia biasa yang tidak luput dari kesalahan dan kekurangan, baik dari segi segi teknis penuliusan maupun dari perhitungan-perhitungan. Oleh karena itu, penulis menerima dengan senang hati atas segala koreksi dan perbaikan guna penyempurnaan tulisan ini agar kelak suatu saat dapat bermanfaat.

Skripsi ini dapat terwujud berkat adanya bantuan, arahan dan bimbingan dari berbagai pihak. Oleh karena itu, dengan segala ketulusan dan kerendahan hati, kami mengucapkan terima kasih dan penghargaan yang setinggi-tingginya kepada :

(4)

1. Bapak Hamzah Al Imran, ST.MT Selaku Dekan Fakultas Teknik Universitas Muhammadiyah Makassar.

2. Bapak Muh. Syafaat S. Kuba, ST. Sebagai ketua Jurusan Fakultas Teknik Universitas Muhammadiyah Makassar.

3. Ibu Ir. Hj. Ratna Musa , M . S . selaku pembimbing I dan Ibu Nurnawati , ST.,MT. selaku pembimbing II, yang telah banyak meluangkan waktu dalam membimbing kami.

4. Bapak dan ibu dosen serta staf pegawai pada Fakultas Teknik atas segala waktunya telah mendidik dan melayani penulis selama mengikuti proses belajar mengajar di Universitas Muhammadiyah Makassar.

5. Ayahanda dan ibunda tercinta, penulis mengucapkan terima kasih yang sebesar-besarnya atas segala limpahan kasih sayang, doa dan pengorbanannya terutama dalam bentuk materi dalam menyelesaikan kuliah.

6. Saudara-saudaraku serta rekan-rekan mahasiswa Fakultas Teknik terkhusus Angkatan 2009 yang dengan keakraban dan persaudaraannya banyak membantu dalam menyelesaikan tugas akhir ini.

(5)

Semoga semua pihak tersebut di atas mendapat pahala yang berlipat ganda di sisi Allah SWT. Dan skripsi yang sederhana ini dapat bermanfaat bagi penulis, rekan-rekan, masyarakat serta Bangsa dan Negara. Amin.

Makassar, juli, 2014

Penulis

(6)

DAFTAR ISI

Halaman

ABSTRAK……….. i

HALAMAN PERSETUJUAN………... ii

KATA PENGANTAR ... iii

DAFTAR ISI ... v

DAFTAR GAMBAR ... vii

DAFTAR NOTASI DAN LAMBANG ... ix

DAFTAR TABEL……… xi

BAB 1 PENDAHULUAN ... 1

A. Latar Belakang... 1

B. Rumusan Masalah... 3

C. Tujuan Penelitian... 3

D. Manfaat Penelitian... 4

E. Batasan Masalah... 4

F. Sistematika Penelitian... 5

BAB II TINJAUN PUSTAKA ... 6

A. Aliran Pada Saluran Terbuka ... 6

B. Geometri Saluran ... 7

(7)

C. Klasifikasi Aliran... 8

D. Energi Spesifik ... ………... 12

E. Bilangan Froude... 14

F. Bilangan Reynold... 17

G. Profil Muka Air ... 21

H. Persamaan Aliran Saluran Terbuka ... 22

BAB III METODOLOGI PENELITIAN ... 24

A. Lokasi dan Waktu Penelitian ... 24

B. Jenis Penelitian dan Sumber Data ... 24

C. Alat dan Bahan ... 25

D. Variabel Yang Diteliti ... 26

E. Prosedur / Langkah Penelitian ... 26

F. Simulasi Penelitian... 27

G. Diagram Penelitian Laboratorium... 30

BAB IV ANALISA DAN PEMBAHASAN ... 31

4.1. Perhitungan Pada Running Kosong……… 31

4.2. Perhitungan Luas Penampang Saluran (A) dan jari- jari hidrolis (R)………..………. 32

4.3. Perhitungan Bilangan Froude (Fr) dan Bilangan Reynold (Re)……… 38

4.4. Perhitungan Energi Spesifik……….. 57

(8)

BAB V PENUTUP ... 65

A. Kesimpulan………... 65

B. Saran……….. 66

DAFTAR PUSTAKA ...

LAMPIRAN ………...

(9)

DAFTAR GAMBAR

Nomor halaman

1. Penampang saluran persegi panjang 7

2. Aliran seragam dan aliran tak seragam 11

3. Parameter energi spesifik 12

4. Profil aliran melalui penyempitan 13 5. Pola penjalaran gelombang di saluran terbuka 16 6. Pembentukan aliran seragam pada saluran 17

7. Aliran turbulen dan laminar 20

8. Hitungan profil muka air 22 9. Rancangan model saluran 29

10. Diagram penelitian laboratorium 30

11. Hubungan antara luas penampang dengan kecepatan pada Q1 36 12. Hubungan antara luas penampang dengan kecepatan pada Q2 37 13. Hubungan antara luas penampang dengan kecepatan pada Q3 37 14. Hubungan antara luas penampang dengan kecepatan

pada Q1, Q2, Q3 38

15. Hubungan antara kecepatan dengan bilangan reynol pada Q1 47 16. Hubungan antara kecepatan dengan bilangan reynol pada Q2 47 17. Hubungan antara kecepatan dengan bilangan reynol pada Q3 48 18. Hubungan antara kecepatan dengan bilangan reynol

pada Q1, Q2, Q3 48

(10)

19. Hubungan antara luas penampang dengan bilangan reynold

pada Q1 49

pada Q2 50

pada Q3 50

pada Q1, Q2, Q3 51

23. Hubungan antara kecepatan dengan bilangan Froude

pada Q1 52

24. Hubungan antara kecepatan dengan bilangan froude

pada Q2 52

pada Q3 53

pada Q1, Q2, Q3 54

27. Hubungan antara luas penampang dengan bilangan Froude

pada Q1 54

28. Hubungan antara luas penampang dengan bilangan froude

pada Q2 55

pada Q3 56

(11)

pada Q1, Q2, Q3 56

31. Hubungan antara kecepatan dengan energy spesific

pada Q1 60

32. Hubungan antara kecepatan dengan energy spesifik

pada Q2 60

pada Q3 61

pada Q1, Q2, Q3 61

35. Hubungan antara tinggi muka air dengan energy spesific

pada Q1 62

36. Hubungan antara tinggi muka air dengan energy spesifik

pada Q2 63

37. Hubungan antara tinggi muka air dengan energy spesifik

pada Q3 63

(12)

DAFTAR NOTASI DAN LAMBANG A : Luas penampang basah

B : Lebar dasar saluran

Fr : Bilangan froude

H : Tinggi muka air

X , L : Panjang saluran

Q : Debit aliran

g : Gaya grafitasi bumi

R : Jari-jari hidraulik

T : Waktu pengaliran

V : Kecepatan aliran

Re : Bilangan Reynolds

P : Keliling basah

E : Energi spesifik

I : Kemiringan dasar saluran

@ : Sudut kemiringan saluran

µ : Kekentalan kinematik

(13)

DAFTAR TABEL

Nomor halaman

1. Tabel kekentalan kinematik 18

2. Tabel rancangan simulasi penelitian 28 3. Tabel hasil perhitungan luas penampang dan jari-jarii

hidrolis 35

4. Tabel hasil perhitungan bilangan Froude dan bilangan

Reynold 46 5. Tabel hasil perhitungan energy spesifik 59

(14)

BAB I PENDAHULUAN A. Latar Belakang

Peranan sungai maupun saluran sebagai pelengkap dan penunjang kehidupan manusia untuk memenuhi kebutuhannya saat ini tidak bisa dipungkiri lagi. Oleh karena itu fungsi sungai dan saluranterbuka bukan hanya sebagi sarana untuk mengalirkan air, melainkan dapat memberi manfaat lain baik ditinjau dari segi ekonomis maupun pemenuhan kebutuhan lainnya seperti, penyediaan air baku, pembangkit listrik, pertanian dan lain sebagainya.

Aliran saluran terbuka adalah aliran air yang memiliki permukaan bebas.MenurutChow(1992:17),Saluran yang mengalirkan air dengan suatu permukaan bebas disebut saluran terbuka (open channel). Menurut asalnya saluran dapat digolongkan menjadi saluran alam (natural) dan saluran buatan (artificial). Saluran alam meliputi semua alur air yang terdapat secara alamiah di bumi,mulai dari anak selokan kecil di pegunungan,selokan kecil, sungai kecil dan sungai besar sampai kemuara sungai.Sungai merupakan suatu saluran drainase yang terbentuk secara alami yang mempunyai fungsi sebagai saluran.Air yang mengalir pada saluran terbuka akan mengakibatkan proses-proses penggerusan.Penggerusan yang terjadi secara terus menerus akan membentuk lubang-lubang gerusan dan berbagai dampak lain yang dapat

(15)

di timbulkan oleh oleh gejala-gejala tersebut.Proses gerusan dapat terjadi karena adanya pengaruh morfologi yang berupa tikungan atau adanya penyempitan saluran dan lain sebagainya.

Pada saluran terbuka semua titik di sepanjang saluran, tekanan di permukaan air adalah sama, parameter saluran sangat tidak teratur baik terhadap ruang dan waktu. Parameter tersebut adalah tampang lintang saluran, kekerasan, kemiringan dasar, belokan, pembendungan debit aliran dan sebagainya. Jadi secara umum dapat di katakan bahwa, aliran pada saluran terbuka merupakan aliran yang bergerak secara bebas, namun di pengaruhi oleh berbagai kontraksi-kontraksi yang terjadi karena adanya pengaruh seperti tampang saluran, kemiringan, penyempitan saluran, kecepatan aliran dan lain sebagainya. Oleh karena itu akibat pegaruh-pengaruh tersebut akan menimbulkan berbagai masalah. Hal ini merupakan suatu permasalahan pada saluran yang menarik untuk diteliti.

Maka dari itu penulis ingin melakukan penelitian dengan mengambil judul,

“STUDI PENGARUH PERUBAHAN PENAMPANG SALURAN TERHADAP KECEPATAN PADA MODEL SALURAN TERBUKA”.

(16)

B. Rumusan Masalah

Berdasarkan latar belakang yang disebutkan di atas maka penelitian studi pengaruh perubahan penampang saluran terhadap kecepatan pada model saluran terbuka dapat dibuat rumusan masalah sebagai berikut :

1. Berapa besar pengaruh antara luas penampang dengan kecepatan.

2. Berapa besar pengaruh energy spesifikterhadap kecepatan pada saluran terbuka.

3. Berapa besar pengaruh antara kemiringan dengan kecepatan

C.Tujuan Penelitian

Berdasarkan latar belakang dan rumusan masalah sebagaimana yang diuraikan diatas, maka penulis merumuskan tujuan penelitian sebagai berikut :

1. Mengkaji kontraksi perubahan luas penampang dengan kecepatan yang terjadi pada saluran terbuka.

2. Mengkaji hubungan antara energy spesifik dengan kecepatan saluran terbuka.

3. Mengkaji hubungan antara kecepatan aliran dengan jenis aliran sesuai dengan bilangan Froude dan bilangan reynold pada saluran terbuka

(17)

D.Manfaat Penelitian

Manfaat dari penelitian ini adalah agar pihak-pihak yang berkepentingan dapat memperoleh gambaran mengenai masalah-masalah atau kontraksi yang terjadi pada aliran saluran terbuka, sehingga dapat menjadi atau memberikan sumbangan pemikiran dalam merencanakan bangunan-bangunan air pada saluran terbuka, oleh karena itu manfaat yang dapat di peroleh adalah :

1. Hasil penelitian ini dapat berguna untuk mengkaji seberapa pengaruh antara kemiringan, luas penampang dan kecepatan penampang pada saluran terbuka.

2. Hasil penelitian sebagai bahan perbandingan dalam menentukan kecepatan pada saluran terbuka dengan metode yang berbeda.

3. Sebagai masukan untuk pengembangan kajian ilmiah atau referensi bagi penelitian pada saluran terbuka.

E.Batasan Masalah

Pada penelitian ini di batasi beberapa masalah-masalah, masalah tersebut adalah sebagai berikut :

1. Penelitian dilakukan pada saluran terbuka dengan saluran segi empat.

2. Pembuatan penampang dari kecil ke besar dan sebaliknya.

3. Kemiringan saluran di kondisikan dengan open chanel yang ada di laboratorium.

(18)

F.Sistematika Penulisan

Penulisan ini merupakan susunan yang serasi dan teratur, oleh karena itu dibuat dengan komposisi bab-bab mengenai pokok uraian sehingga mencakup pengertian tentang apa, dan bagaimana. Sistematika penulisan skripsi ini dapat diuraikan sebagai berikut :

Bab I. Merupakan bab pendahuluan, yang isinya meliputi latar belakang, rumusan masalah, tujuan penelitian, manfaat penelitian, batasan masalah, dan sistematika penulisan.

Bab II. Merupakan tinjauan pustaka, yang meliputi aliranpada saluran terbuka, geometri saluran, klasifikasi saluran, energy spesifik ( Spesicific Energy ), profil muka air, persamaan aliran saluran terbuka,

Bab III. Merupakan metodologi penelitian, meliputi lokasi dan waktu penelitian, jenis penelitian dan sumber data, alat dan bahan, variabel yang diteliti, prosedur/langkah penelitian,simulasi penelitian, diagram penelitian laboratorium.

Bab IV. Merupakan analisa dan pembahasan yang terdiri dari perhitungan pada running kosong, perhitungan luas penampang (A), perhitungan jari-jari hidrolis (R), perhitungan bilangan Froude (Fr) dan bilangan Reynolds (Re),Perhitungan energy spesifik

Bab V. Merupakan penutup, yang terdiri dari kesimpulan dan Saran.

(19)

BAB II

TINJAUAN PUSTAKA

A. Aliran Pada Saluran Terbuka

Saluran terbuka adalah saluran dimana air mengalir dengan muka air bebas.Pada semua titik disepanjang saluran, tekanan dipermukaan air adalah sama, yang biasanya tekanan atmosfir. Pengaliran melalui suatu pipa (saluran tertutup) yang tidak penuh (masih ada muka air bebas) masih termasuk aliran dalam saluran terbuka. Oleh karena itu melalui saluran terbuka harus mempunyai muka air bebas, maka aliran ini biasanya berhubungan dengan zat cair dan umumnya adalah air , (Bambang Triatmodjo: 2008)

Berbagai permasalahan teknik yang berhubungan dengan aliran terkadang tidak dapat diselesaikan dengan analitis,maka harus melakukan pengamatan dengan membuat suatu bentuk saluran atau alat peraga,bentuk saluran ini mempunyai bentuk yang sama dengan permasalahan yang diteliti, tetapi ukuran dimensi lebih kecil dari yang ada dilapangan.

Saluran digolongkan menjadi dua macam yaitu aliran alam (natural) dan saluran buatan (artificial).Saluran alam meliputi semua saluran air yang terdapat secara alamiah di bumi,melalui dari anak selokan kecil di pegunungan, sungai kecil dan sungai besar sampai ke muara sungai.Sifat- sifat hidrolik saluran alam biasanya tidak menentu. Dalam beberapa hal

(20)

dapat dibuat anggapan pendekatan yang cukup sesuai dengan pengamatan sesungguhnya. Sehingga persyaratan aliran pada saluran ini dapat diterima untuk penyelesaian analisa hidrolika teoritis. Saluran buatan merupakan saluran yang dibuat manusia untuk tujuan dan kepentingan tertentu seperti saluran irigasi,saluran drainase,saluran pembawa pada pembangkit listrik tenaga air dan saluran untuk industri. Saluran buatan memiliki penampang yang teratur dan lebih mudah dalam melakukan analisa dibanding saluran alami.

B. Geometri Saluran

Penampang saluran alam umumnya sangat tidak beraturan, biasanya bervariasi dari bentuk seperti parabola sampai trapesium. Istilah penampang saluran (channel section) adalah tegak lurus terhadap arah aliran, sedangkan penampang vertikal melalui titik terbawah atau terendah dari penampang. Oleh sebab itu pada saluran mendatar penampangnya selaluh merupakan penampang vertikal.

Gambar 1. Penampang saluran persegi panjangSumber: Bambang Triatmojo, 2008

(21)

Luas (A) = b x h ... (1)

Keliling basah (P) = b+2h ...……...(2)

Jari-jari hidrolik (R) = ...(3)

Dengan lebar b = lebar dasar saluran, dan h = tinggi kedalaman air C. Klasifikasi Aliran

Aliran saluran terbuka dapat digolongkan menjadi beberapa jenis dan diuraikan dengan berbagai cara sebagai berikut (Rangga raju, 1981) : 1. Aliran tunak (steady flow) dan aliran tak tunak (unsteady flow)

Aliran dalam saluran terbuka dikatakan tunak (steady) bila kedalaman aliran tidak berubah atau dianggap konstan selama selang waktu tertentu. Aliran dikatakan tak tunak (unsteady) bila kedalaman berubah sesuai dengan waktu. Sebagian besar persoalan tentang saluran terbuka umumnya hanya memerluhkan penelitian mengenai perilaku aliran dalam keadaan tunak. Debit (Q) pada suatu penampang saluran untuk sembarang aliran dinyatakan dengan persamaan :

Q = V. A………...………...(4) dengan V = kecepatan rata-rata dan A = luas penampang melintang tegak lurus terhadap aliran.

Sebagian besar persoalan aliran tunak, berdasarkan suatu pertimbangan, maka debit diasumsikan tetap disepanjang bagian saluran yang luas, dengan kata lain aliran bersifat tunak kontinu (continous steady flow)sehingga dari persamaan (1) :

(22)

Q = V1A1 =V2A2………...………...(5) Dengan subscript 1 dan 2 menunjukkan penampang saluran yang berlainan. Persamaan (2) tidak dapat dipakai bila debit aliran tunak tak seragam disepanjang saluran karena terjadi limpahan. Jenis aliran ini dikenal sebagai aliran berubah beraturan (spatially varied flow) atau aliran diskontinu yang terdapat pada pelimpah samping, air pembilas melalui saringan, cabang saluran sekitar tangki pengolah air buangan, saluran pembuang utama dan saluran pembawa dalam sistem irigasi.

2. Aliran seragam

Aliran pada saluran terbuka dikatakan seragam jika kedalaman aliran sama pada setiap penampang saluran. Suatu aliran seragam dapat bersifat tunak atau tidak tunak, tergantung apakah kedalamannya berubah sesuai dengan perubahan waktu. Aliran seragam yang tunak (steady uniform flow) merupakan jenis aliran pokokyang dibahas dalam hidrolika saluran terbuka dengan kedalaman aliran tidak berubah selama waktu tertentu yang telah diperhitungkan. Penetapan bahwa suatu aliran bersifat seragam tak tunak (unsteady uniform flow) harus dengan syarat bahwa permukaan air berfluktuasi sepanjang waktu dan tetap sejajar dasar saluran tetapi hal ini merupakan suatu keadaan yang praktis tidak mungkin terjadi.

Aliran disebut berubah (varied) bila kedalaman aliran berubah disepanjang saluran dan dapat bersifat tunak maupun tidak tunak. Karena aliran seragam yang tak tunak jarang terjadi, istilah tak tunak disinii

(23)

selanjutnya khusus dipakai untuk aliran tak tunak yang berubah. Untuk perhitungan hidrolika, kecepatan rata-rata aliran seragam turbulen dalam saluran terbuka biasanya dinyatakan dengan perkiraan yang dikenal dengan rumus aliran seragam dan sebagian besar persamaannya dapat dinyatakan dalam bentuk umum, yaitu :

V = C R x Sy ...(6) Dengan V: kecepatan rerata (m/det), R : jari-jari hidrolik (m), S : kemiringan energi, x dan y adalah eksponen, C : faktor tekanan aliran yang bervariasi menurut kecepatan rerata, jari-jari hidrolik, kekasaran saluran, dan berbagai faktor lainnya.

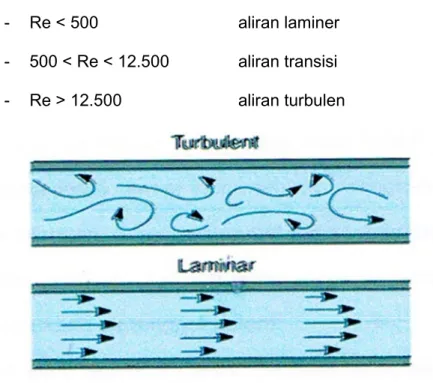
3. Aliran turbulen dan aliran laminer

Aliran fluida khususnya air diklasifikasikan berdasarkan perbandingan antara gaya-gaya inersia (inertial forces) dengan gaya-gaya akibat kekentalan (fiscous force) menjadi tiga bagian, yaitu aliran laminer, aliran transisi, dan aliran turbulen. Variabel yang dipakai untuk klasifikasi ini adalah bilangan Reynolds yang didefinisikan sebagai :

Re = Dimana:

Re = bilangan Reynold V = kecepatan (m/det) R = jari-jari hidraulik (m)

v = kekentalan kinematik (m²/det)

Selanjutnya klasifikasi aliran berdasarkan bilangan Reynolds dapat

(24)

dibedakan menjadi tiga kategori, yaitu Re < 500 = aliran laminer, 500 <Re >

12,500 = aliran peralihan, dan Re > 12,500 = aliran turbulen. Umumnya pada saluran terbuka mempunyai Re > 12,500 sehingga aliran termasuk dalam katergori aliran turbulen. (Robert, J.K.,2002)

Gambar 2. (a) Aliran seragam, (b) Aliran tak seragamSumber : Robert, J.K.,2002

4. Aliran kritis dan superkritis

Aliran dikatakan kritis apabila bilangan Froude (F) sama dengan satu (1), sedangkan aliran disebut subkritis atau kadang-kadang dinamakan aliran tenang (trianguil flow) apabila F > 1. Perbandingan kecepatan aliran dengan gaya gravitasi (per satuan volume) dikenal sebagai bilangan Froude dan dapat dirumuskan sebagai berikut (Rangga Raju, 1981) :

Fr = V/√ ...(7) Dengan F = bilangan Froude, V = kecepatan rata-rata aliran (m/det), g = percepatan gravitasi (m²/det), L = panjang karakteristik (m).

Pada aliran terbuka biasanya digunakan kedalaman hidraulis D

(25)

sebagai panjang karakteristik, sehinnga F dapat ditulis sebagai :

Fr = V/√ ...(8)

D. Energi Spesifik (Specific Energy)

Besarnya energi spesifik dapat dirumuskan sebagai berikut (Ven Te Chow,1959 dalam Robert,J.K.,2002) :

E = + ...(9) dengan E = energi spesifik.

Gambar 3.Parameter energi spesifikSumber : Robert J.K., 2002

Dasar saluran diasumsikan mempunyai kemiringan landai atau tanpa kemiringan. Z adalah ketinggian dasar diatas diatas garis referensi yang dipilih, h adalah kedalaman aliran, dan faktor koreksi energi (α) dimisalkan sama dengan satu. Energi spesifik aliran pada setiap penampang tertentu dihitung sebagai total energi pada penampang itu dengan menggunankan dasar saluran sebagai referensi (Rangga Raju, 1981). Persamaan energii secara umum adalah :

(26)

Sehingga persamaan energi untuk saluran datar (Ə = 0), adalah :

E = + ...……(10)

Berhubung Q = v x A, maka rumus energi spesifik menjadi

E = + ...(11) Denagn H = tinggi energi (cm), z = tinggi suatu titik terhadap bidang referensi (cm), α = koefisien energi, pada perhitungan selanjutnya α = 1, E

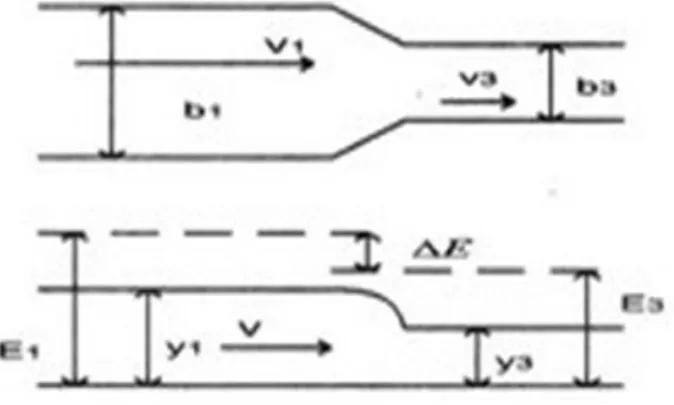
= energi spesifik (cm), h = kedalaman aliran (cm), v = kecepatan aliran rata-rata (cm/detik), A = luas penampang (cm²), g = percepatan gravitasi (cm/detik²), dan Q = debit (m³/det). Perbedaan energi sebelum penyempitan dan energi setelah penyempitan dikenal sebagai keehilangan energi, yaitu ∆E = E1– E2sebagaimana ditunjukkan pada gambar 4 berikut.

Gambar 4. Profil aliran melalui penyempitan Sumber Ven Te Chow, 1992 Dari gambar 4 diperoleh persamaan besarnya kehilangan energi sebagai berikut:

∆E = y1+ - y3- ...… (12)

(27)

Dengan ∆E = kehilangan energi (cm), y1 = tinggi air sebelum penyempitan (cm), y3 = tinggi air pada penyempitan (cm), v1 = kecepatan air sebelum penyempitan (cm/det), dan v3 = kecepatan air pada penyempitan (cm/det).

Kecepatan dapat diturunkan dari persamaan sebelumnya, sehingga persamaan (1) menjadi:

∆E = y1+ - y3- ...(13)

Dengan A1= luas penampang titik 1 dan A3 = luas penampang titik 3.

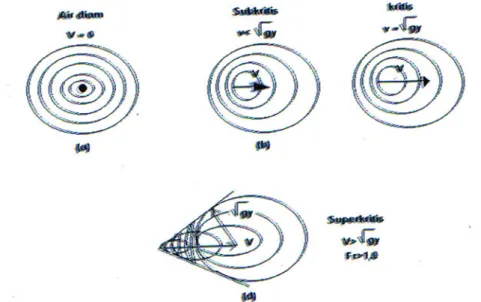
E. Bilangan Froude

Berdasarkan gaya berat terhadap inersia, aliran dapat merupakan aliran sub kritis, kritis dan super kritis. Ketiganya dipengaruhi oleh bilangan froude yang merupakan fungsi dari kecepatan (V) dan kedalaman aliran (h). Perbandingan gaya inersia dengan berat suatu aliran disebut bilangan froude.

Fr =

Dimana:ss

Fr = bilangan froude

V = kecepatan rata-rata (m/det) g = gaya gravitasi (m/det²) h = kedalaman aliran (m)

ada 3 macam aliran (Rinaldi,2002:20) sebagai berikut:

1. Aliran Sub Kritis

Aliran dkatakan Sub Kritis apabila gaya berat lebih besar dari pada

(28)

gaya inersia, sehingga air akan mengalir dengan kecepatan rendah.

Pada aliran Sub Kriits V < dan Fr < 1.

Dalam mekanisme gelombang dapat disamakan dengan kecepatan perambatan gelombang dangkal. Jika V < maka kecepatan perambatan gelombang akan lebih besar dari pada kecepatan rata-rata aliran, sehingga gelombang dapat bergerak kearah hulu.

2. Aliran super Kritis

Aliran dikatakan super kritis apabila gaya berat sangat lemah bila dibanding dengan gaya inersia, sehingga air akan mengalir dengan kecepatan tinggi.

Pada aliran super kritis V > dan Fr > 1.

Jika V > maka kecepatan perambatan gelombang akan lebih kecil dari pada kecepatan rata-rata aliran, sehingga gelombang hanya bergerak kearah hilir.

3. Aliran kritis

Antara keadaan Sub kritis dan super kritis terdapat keadaan kritis pada aliran kritis V = maka kecepatan perambatan gelombang sama dengan kecepatan rata-rata aliran, sehingga tidak ada pergerakan gelombang.

(29)

Kedalaman pada keadaan kritis disebut kedalaman kritis.

Gambar 5. Pola penjalaran gelombang disaluran terbuka Sumber:Bambang Triatmojo, 2008

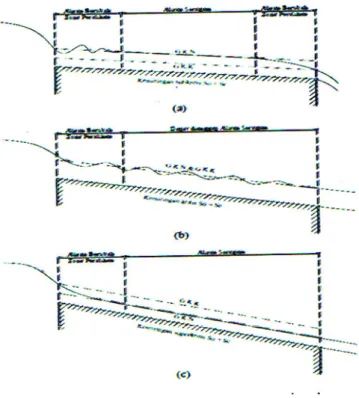
Pada gambar 5. Diperlihatkan suatu saluran panjang dengan tiga jenis kemiringan, subkritis, kritis dan superkritis. Pada kemiringan subkritis permukaan air di zona peralihan tampak bergelombang. Aliran dibagian tengah saluran bersifat seragam namun kedua ujungnya bersifat berubah.

Pada kemiringan kritis permukaan air dari aliran kritis ini tidak stabil.

Dibagian tengah dapat terjadi gelombang tetapi kedalaman rata-ratanya konstan dan alirannya dapat dianggap seragam. Pada kemiringan subkritis permukaan air beralih dari keadaan subkritis menjadi superkritis setelah melalui terjunan hidrolik lambat laun. Di hilir zona peralihan aliran mendekati seragam. Kedalam air seragam disebut kedalaman normal (normal depth). Pada gambar 6 tersebut, garis panjang terputus-putus

(30)

menyatakan garis kedalaman normal, disingkat dengan G.K.N. dan garis pendek terputus-putus atau garis titik-titik menyatakan garis kedalaman kritis atau G.K.K.

Panjang zona peralihan tergantung pada debit dan keadaan fisik saluran, seperti keadaan tempat permukaan air, bentuk kemiringan dan kekasarannya.

Gambar 6. Pembentukan aliran seragam pada saluran

Sumber: Ven Te Chow., E.V. nensi Rosalina, 1989 F. Bilangan Reynolds

Keadaan aliran di saluran terbuka dipengaruhi oleh kekentalan dan gaya berat berhubungan dengan gaya inersia dari aliran. Berdasarkan pengaruh kekentalan inersia, aliran dapat merupakan aliran laminer,

(31)

turbuler dan aliran peralihan. Ketiganya dipengaruhi oleh bilangan reynolds yang merupakan fungsi dari kecepatan (V), jari-jari hidraulik (R) dan kekentalan kinematik (v). Perbandingan dari gaya inersia terhadapa gaya kekentalan kinematik (viscositas kinematik) per satuan waktu dikenal sebagai bilangan reynolds.

Re = Dimana:

Re = bilangan reynold V = kecepatan (m/det) R = jari-jari hidraulik (m)

v = kekentalan kinematik (m²/det)

Tabel 1 : kekentalan kinematik terhadap bilangan reynold

Temperatur (°C) Viskositas ( 10 Ns/m² )

0 1,79 x 10

5 1,51 x 10

10 1,31 x 10

15 1,14 x 10

20 1,00 x 10

25 8,91 x 10

(32)

30 7,96 x 10

35 7,20 x 10

40 6,53x 10

50 5,47 x 10

60 4,66 x 10

70 4,04 x 10

80 3,54 x 10

90 3,15 x 10

100 2,82 x 10

Sumber : Piyantoro,1991

Aliran dikatakan laminer apabila tahanan antara lapisan-lapisan zat cair lebih besar jika dibandingkan dengan gaya inersia, sehingga kekentalan lebih menentukan sifat aliran. Pada keadaan ini garis arus tampak lurus karena butir-butir air bergerak secara teratur menurut garis arus.

Aliran disebut turbulen apabila tahanan antara lapisan-lapisan zat cair sangat lemah dibandingkan gaya inersia. Pada keadaan ini garis arus tampak bergelombang karena butir-butir air bergerak secara teratur.

(33)

Antatra aliran laminer dan turbulen terdapat keadaan campuran yang disebut keadaan peralihan.

Secara jelasnya klasifikasi aliran berdasarkan bilangan reynolds dapat dibedakan menjadi tiga kategori seperti berikut:

- Re < 500 aliran laminer - 500 < Re < 12.500 aliran transisi - Re > 12.500 aliran turbulen

Gambar 7. Aliran turbulen dan laminersumber: Amazon.com

Umumnya aliran pada saluran terbuka mempunyai Re > 12.500 sehingga alirannya termasuk dalam kategori aliran turbulen (Frenc, 1980;

Rajartman, 1987)

Suatu kombinasi dari efek viskositas dan gravitasi menghasilkan salah satu dari empat regimen aliran, yang disebut:

(a) Subkritis-laminer (subtricical-laminer), apabila Fr lebih kecil dari pada satu dan Re berada dalam rentang laminer;

(b) Superkritis_laminer (supercritcal-laminer), apabila Fr besar dari pada

(34)

satu dan Re berada dalam rentang laminer;

(c) Superkritis-turbulent (supercritical-turbulrnt), apabila Fr lebih besar dari pada satu dan Re berada dalam rentang laminer;

(d) Subkritis-turbulen (subcritical-turbulent), apabila Fr lebih kecil dari pada satu dan Re berada dalam rentang turbulen.

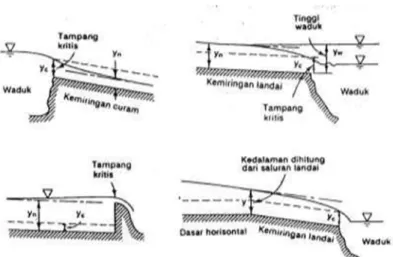
G. Profil Muka Air

Kedalaman aliran di sepanjang saluran dapat dihitung dengan menyelesaikan persamaan difrensial untuk aliran berubah beraturan.

Hitungan biasanya dimulai dari satu tampang dimana hubungan antara elevasi muka air (kedalaman) dan debit diketahui. Tampang tersebut dikenal dengan tampang (titik) kontrol seperti pada (Gambar 6).

Hitungan profil muka air biasanya dilakukan secara bertahap dari satu tampang berikutnya yang berjarak cukup kecil sehingga permukaan air diantara kedua tampang dapat di dekati dengan garis lurus. Apabila aliran adalah subkritis hitungan dimulai dari titik paling hilir dan menuju ke arah hulu. Sedang jika aliran adalah superkritis hitungan dilakukan dari hulu ke hilir.

(35)

Gambar 8. Hitungan profil muka air Sumber: Bambang Triatmojo, 2008

H. Persamaan Aliran Saluran Terbuka

Pada umumnya persamaan aliran di saluran terbuka hanya digunakan pada aliran tetap dengan debit dinyatakan :

Q = A. V...(14) Keterangan :

Q = debit (m³/s)

A = luas penampang melintang saluran (m) V = kecepatan rata-rata aliran (m/s)

Sementara itu, debit di sepanjang aliran dianggap seragam dengan kata lain aliran bersifat kontinu, sehingga :

Q1 = Q2 A1 . V1 = A2 . V2 ...(15) Namun demikian, tidak dapat dipungkiri bahwa akibat material yang berbeda pada setiap saluran, terutama saluran terbuka seperti sungai, aliran akan mengalami gesekan dengan material salurannya. Oleh sebab

(36)

itu perlu juga dilakukan perhitungan kecepatan aliran yang memperhatikan faktor gesekan tersebut. Persamaan Manning dapat digunakan untuk melakukan perhitungan yang dimaksud. Koefisien Manning (n) memperhitungkan koefisien kekasaran saluran pada perhitungannya.

Koefisien kekasaran merupakan pengerem dari aliran air baik di saluran (channel) maupun dataran banjir (flood plain). Nilai n pada saluran ditentukan dengan mengevaluasi pengaruh-pengaruh yang ditimbulkan oleh faktor-faktor kekasaran di dalam saluran.

(37)

BAB III

METODE PENELITIAN A. Lokasi dan Waktu Penelitian

Penelitian dilaksanakan di labotatorium Fakultas Teknik Sipill Universitas Muhammadiyah Makassar dengan rencana waktu penelitian selama 3 bulan yaitu dimulai bulan november sampai dengan bulan januari, dimana pada bulan pertama yakni di bulan november merupakan kajian literatur, pada bulan kedua yakni bulan desember merupakan pengambilan data dan pada bulan ketiga yakni bulan januari merupakan tahap pegelolaan data.

a. Jenis Penelitian dan Sumber Data 1. Jenis Penelitian

Jenis penelitian yang digunakan adalah simulasi eksperimental, dimana kondisi tersebut dibuat dan diatur sendiri oleh peneliti dengan mengacu pada literatur yang berkaitan dengan judul penelitian tersebut.

2. Sumber Data

Penelitian ini menggunakan dua sumber data, yang terdiri dari :

a. Data primer yakni data yang diperoleh langsung dari simulasimodel fisik di laboratorium.

(38)

b. Data sekunder yaitu data yang didapatkan dari literatur, hasil penelitian yang telah ada, baik yang telah dilakukan di laboratorium maupun di tempat lain yang berkaitan dengan penelitian karakteristik aliran saluran terbuka.

b. Alat dan Bahan 1. Alat :

a. Model saluran terbuka dengan penampang segi empat lebar 25 cm, tinggi 25 cm dan panjang 2,50 m.

b. Bak penampungan air dengan kapasitas tampungan 0,5 m³. c. Pompa air, untuk pengaliran

d. Current meter.

e. Meter lipat.^.

f. Pipa dan slang ukuran 3” untuk mengalirkan/menaikkan air dari bak air kesaluran.

g. Kamera digital digunakan untuk pengambilan dokumentasi dokumentasi.

2. Bahan : a. Air bersih.

b. Perekat silicone flubbers atau plastising untuk membentuk saluran.

(39)

c. Variabel Yang Diteliti

a. Sesuai tujuan penelitian ini, pengujian model hidrolik dilaksanankan pada model saluran terbuka (flume), dengan kajian perubahan penampang saluran terhadap kecepatan pada model saluran terbuka.

b. Model fisik ini dimaksudkan untuk mempelajari dan mengetahui pola aliran pada perubahan penampang saluran dengan mengamati lebar penampang saluran (B), Tinggi muka air (H) dengan pengamatan yang dilakukan secara manual di titik pengamatan.

d. Prosedur / Langkah Penelitian

Adapun langkah-langkah yang di lakukan dalam penelitianadalah sebagai berikut :

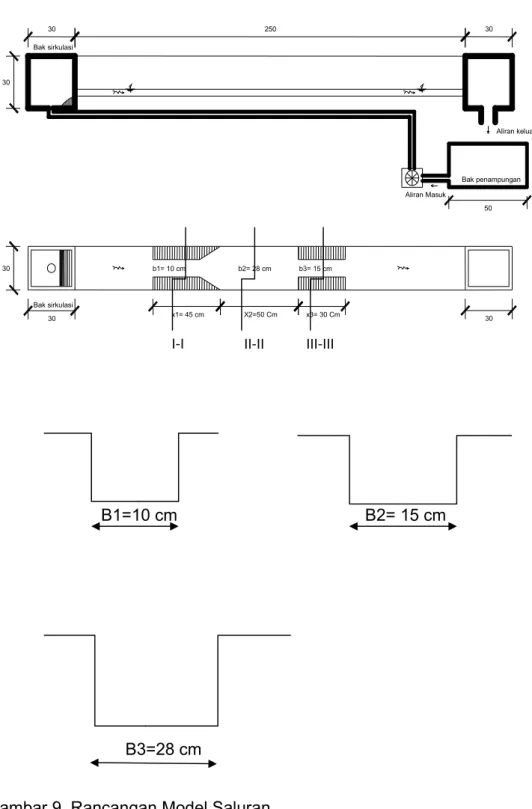
1. Mempersiapkan peralatan di laboratorium termasuk membuat modell fisik saluran terbuka dengan membuat tiga macam variasi lebar penampang pada satu aliran, yaitu B1, B2 dan B3.

2. Kalibrasi semua peralatan yang akan digunakan khususnya alat ukur kecepatan.

3. Melakukan pengaliran awal untuk mengetahui layak atau tidaknya saluran yang akan digunakan dalam pengaliran (Running kosong) 4. Melakukan pengukuran pada saat pengaliran yaitu mengukur lebar

bawah saluran (B) yaitu B1, B2 dan B3. Pengukuran tinggi muka air (H) yaitu H1, H2, dan H3 dan pengukuran kecepatan aliran (V) yaitu V1, V2

(40)

dan V3. Ketiga pengukuran tersebut dilakukan pada titik-titik pengamatan yang telah ditentukan dengan variasi debit pertama (Q1).

5. Kemiringan saluran dibuat dengan perbandingan 1:1 dan 1:2.

6. Mengamati pola aliran yang terjadi secara langsung pada variasi model penampang saluran.

7. Selanjutnya mengulangi langkah (4) untuk variasi debit Q2 dan Q3

e. Simulasi Penelitian

Rangkaian simulasi yang dilakukan dalam penelitian studi pengaruh perubahan penampang terhadap kecepatan pada model saluran terbuka diklasifikasikan dalam dua parameter, yaitu variasi perubahan lebar saluran (B),dengan mengubah masing-masing lebar penampang bawah saluran untuk mendapatkan perbedaan sampel yang diteliti (B1, B2 dan B3).

Sedangkan parameter pengamatan meliputi tinggi muka air (H1, H2, dan H3) dan kecepatan aliran (V1, V2 dan V3) pada aliran dan penentuan debit sebanyak 3 kali yaitu Q1 sebesar 1000 cm³/det, Q2 sebesar 2500 cm³/det , Q1 sebesar 5000 cm³/det.Penentuan debit ini dilakukan dengan cara 3 kalii perputaran.

Adapaun rancangan simulasi penelitian dapat dilihat pada tabel 2 sebagaii berikut :Tabel 2. Rancangan simulasi penelitian

(41)

NO Q

(cm3/det ) B

(cm)

H

(cm)

V

(cm/det) T

(det)

Fr Re

1 Q1 B1

H1 V1 T1 ……. …….

H2 V2 T2 ……. …….

H3 V3 T3 ……. …….

2

Q2 ( Salu

ran diper

besar )

B2

H1 V1 T1 ……. …….

H2 V2 T2 ……. …….

H3 V3 T3 ……. …….

3

Q2 ( Salu

ran diper

kecil )

B3

H1 V1 T1 ……. …….

H2 V2 T2 ……. …….

H3 V3 T3 ……. …….

Pada rancangan simulasi penelitian sebagaimana tabel 1 diatas, maka jumlah simulasi/running yang akan dilakukan dalam pelaksanaan penelitian ini adalah 3 simulasi/running dimana 3 variasi debit Q1, Q2 dan Q3, dengan masing-masing 3 variasi penampang (B).

(42)

B1=10 cm B2= 15 cm

B3=28 cm

Gambar 9. Rancangan Model Saluran

b1= 10 cm b2= 28 cm b3= 15 cm

30 x3= 30 Cm 30

III-III

X2=50 Cm

II-II

x1= 45 cm

I-I

Bak sirkulasi 30

Aliran keluar Bak sirkulasi

30

30 250 30

50 Bak penampungan Aliran Masuk

(43)

G. Diagram Penelitian Laboratorium

yes yes

Gambar 10 . Bagan alir penelitian

Mulai

Persiapan

Persiapan Alat Peraga

Laboratorium Persiapan Alat dan bahan

yang akan digunakan ya

Pengambilan Data

Variasi lebar saluran (b), diperlebar dan dipersempit

ya Data kecepatan

aliran (v)

Data tinggi muka air (h)

Verifikasi Data

Analisa Data

Selesai

(44)

BAB IV

ANALISA DAN PEMBAHASAN 4.1. Perhitungan pada running kosong

Diketahui :

B = 28 cm

H = 1,7 cm

t = 11,3 det

X = 250 cm

V = 22 cm/det

a. Mencari luas penampang basah (A)

A = B . H

A = 28 . 1,7

A = 47,6 cm²

b.Mencari Debit (Q)

Q = A . V Q = 47,6 . 22 Q = 1047,2 cm³/det

(45)

3.2. Perhitungan luas penampang saluran (A) dan Jari-jari Hidrolis (R)

Diketahui data hasil penelitian sebagai berikut :

B1 = 10 cm X1 = 45 cm

B2 = 28 cm X2 = 50 cm

B3 = 15 cm X3 = 30 cm

H1 = 1,79 cm t1 = 0,81 det

H2 = 0,73 cm t2 = 1,02 det

H3 = 1,48cm t3 = 0,67 det

V1 = 56 cm/det

V2 = 49 cm/det

V3 = 45 cm/det

a. Mencari luas penampang basah (A)

Untuk mencari luas penampang saluran dapat digunakan rumus sebagai berikut:

Luas (A) = B x H

Dimana : A = Luas penampang (cm²)

B = Lebar dasar saluran (cm)

(46)

H = Tinggi muka air (cm)

A1 = B1 . H1 A2 = B2 . H2 A3 = B3 . H3

= 10 .1,79 = 28 . 0,73 = 15 . 1,48

= 17,9 cm² = 20,44 cm² = 22,2 cm²

b. Mencari jari-jari hidrolis (R)

Diketahui : A1 = 17,9 cm²

A2 = 20,44 cm²

A3 = 22,2 cm²

B1 = 10 cm

B2 = 28 cm

B3 = 15 cm

H1 = 1,79 cm

H2 = 0,73 cm

H3 = 1,48 cm

Untuk mencari jari-jari hidrolis maka dapat dihitung dengan menggunakan rumus sebagai berikut:

=A P

(47)

Dimana : R = Jari-jari hidrolis (cm)

A =Luas penampang (cm²)

P = Keliling basah (cm)

P1 = B1 + 2 H1 P2 = B2 + 2 H2

P1 = 10 + 2 . 1,79 P2 = 28 + 2 . 0,73

P1 = 10 + 3,58 P2 = 28 + 1,46

P1 = 13,58cm P2 = 29,46 cm

P3 = B3 + 2 H3

P3 = 15 + 2 . 1,48

P3 = 15 + 2,96

P3 = 17,96cm

Jadi R dapat dihitung :

1 = 2 =

1 =

_,^,

2 =

^,_,

1 = 1,32 cm 2 = 0,69 cm

(48)

3 = 3 =

_,^,

3 = 1,24 cm

Perhitungan selanjutnya dapat dilihat pada tabel 4

Tabel 4 : Tabel perhitungan luas penampang, jari-jari hidrolis

Q (cm³/det) P (cm) A (cm²) R (cm) TIPE

(1) (2) (3) (4) (5)

Q1=1000

13,58 17,9 1,32 A

29,46 20,44 0,69 B

17,96 22,2 1,24 C

Rata-rata 20,33 20,18 1,08 -

Q2 = 2500

12,58 29 1,31 A

31,87 61,6 0,89 B

16,31 30 1,01 C

Rata-rata 20,25 40,2 1,07 -

(49)

Q3= 5000

14,87 17,8 1,21 A

29,43 32,76 0,99 B

18,35 21,6 0,72 C

Rata-rata 20,88 24,05 0,97 -

Sumber :Hasil perhitungan

Gambar 11.Grafik hubungan antara luas penampang dengan kecepatan Pada Q1

Pada percobaan Q1,luas penampang yang sebesar 17.9 cm² menghasilkan kecepatan sebesar 56 cm/det,luas penampang yang sebesar 20.44 cm² menghasilkan kecepatan sebesar 49 cm/det,luas penampang yang sebesar 22.2 cm² menghasilkan kecepatan sebesar 45 cm/det.

56

49 45

0 10 20 30 40 50 60

17.9 20.44 22.2

Kecepatan (cm/det)

Luas Penampang (cm²)

Hubungan antara luas penampang

dengan kecepatan pada Q1

(50)

Gambar 12.Grafik hubungan antara luas penampang dengan kecepatan Pada Q2

Pada percobaan Q2,luas penampang yang sebesar 29 cm² menghasilkan kecepatan sebesar 85 cm/det,luas penampang yang sebesar 30 cm² menghasilkan kecepatan sebesar 83 cm/det,luas penampang yang sebesar 61.6 cm² menghasilkan kecepatan sebesar 40cm/det.

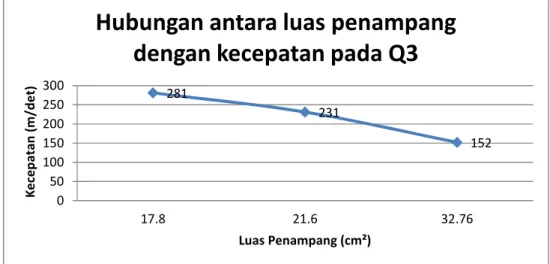
Gambar 13.Grafik hubungan antara luas penampang dengan kecepatan pada Q3

85 83

40

0 20 40 60 80 100

29 30 61.6

Kecepatan (cm/det)

Hubungan antara luas penampang dengan kecepatan pada Q2

281

231

152

0 50 100 150 200 250 300

17.8 21.6 32.76

Kecepatan (m/det)

Hubungan antara luas penampang

dengan kecepatan pada Q3

(51)

Pada percobaan Q3,luas penampang yang sebesar 17.8 cm² menghasilkan kecepatan sebesar 281 cm/det,luas penampang yang sebesar 21.6 cm² menghasilkan kecepatan sebesar 231 cm/det,luas penampang yang sebesar 32.76 cm² menghasilkan kecepatan sebesar 152cm/det.

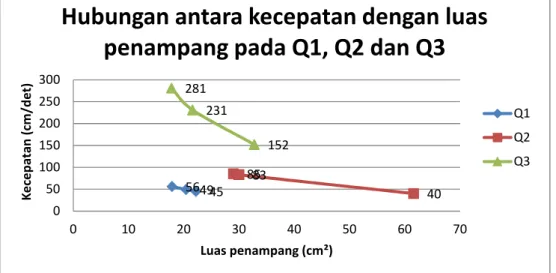
Gambar 14.Grafik hubungan antara luas penampang dengan kecepatan pada Q1,Q2,Q3.

Bahwa grafik diatas menunjukkan bahwa hubungan antara kecepatan dengan luas penampang adalah berbanding terbalik artinya jika luas penampang saluran besar maka kecepatan aliran pada saluran kecil begitupula dengan sebaliknya.

4. 3.Perhitungan bilangan Froude (Fr) dan bilangan reynold (Re) a. Mencari bilangan froude (Fr)

Berdasarkan gaya berat terhadap inersia, aliran dapat merupakan aliran sub kritis, kritis dan super kritis. Ketiganya dipengaruhi oleh bilangan

564945 8583

40 281

231

152

0 50 100 150 200 250 300

0 10 20 30 40 50 60 70

Kecepatan (cm/det)

Luas penampang (cm²)

Hubungan antara kecepatan dengan luas penampang pada Q1, Q2 dan Q3

Q1 Q2 Q3

(52)

froude yang merupakan fungsi dari kecepatan (V) dan kedalaman aliran (h). Perbandingan gaya inersia dengan berat suatu aliran disebut bilangan froude.

Fr =

Dimana:

Fr = bilangan froude

V = kecepatan rata-rata (m/det) g = gaya gravitasi (m/det²) R = Jari-jari hidrolis (m)

Fr1 =

_.

Fr1 =

√ . ,

Fr1 = 0,67

Fr1< 1,0 berarti alirannya subkritis

Fr2 =

_.

Fr2 =

√ . ,

Fr2 = 0,57

Fr2 < 1,0 berarti alirannya subkritis

(53)

Fr3 =

_.

Fr3 =

√ . ,

Fr3 = 0,82

Fr3< 1,0 berarti alirannya subkritis

b. Mencari bilangan reynold (Re)

Perbandingan dari gaya inersia terhadapa gaya kekentalan kinematik (viscositas kinematik) per satuan waktu dikenal sebagai bilangan reynolds.

Re = Dimana:

Re = bilangan reynold V = kecepatan (m/det) R = jari-jari hidraulik (m)

v = kekentalan kinematik (m²/det) R

e1 =

^.

Re1 =

_,^{. ,}

Re1 = 664,1

500 < Re1 < 12.500 berarti aliran transisi

(54)

Re2 =

^.

Re2 =

_,^{. ,}

Re2 = 474,67

Re2 < 500 berarti aliran laminar

Re3 =

^.

Re3 =

_,^{. ,}

Re3 = 397,59

Re3< 500 berarti aliran laminar

c. Menghitung aliran transisi

pada Aliran transisi terjadi pada saat tinggi muka air sebesar 1,79 cm pada percobaan Q1 , tinggi muka air sebesar 2,2 cm pada percobaan Q2 dan tinggi muka air sebesar 1,17cm pada percobaan Q3

untuk menghitung kecepatan pada saat terjadi aliran terjadi maka dapat digunakan rumus kontinuitas sebagai berikut:

= .

Dimana :Q = debit (cm³/det)

A = luas penampang (cm²)

(55)

V = kecepatan transisi (cm/det)

Untuk tinggi muka air sebesar 1,79 cm dengan debit 1000 cm³/det maka kecepatan aliran transisinya adalah:

Mencari H rata-rata :

H rata − rata = 1 + 2 2

H rata − rata = 1,79 + 0,73 2

H rata − rata = 1,26 cm

Mencari B rata-rata :

B rata − rata = 1 + 2 2

B rata − rata =10 + 28 2 B rata − rata = 19 cm

Mencari luas penampang (A)

A = B + (m + H ) . H

A = 19 + (1 + 1,26 ) . 1,26

A = 19 + 2,848

A = 21,848 cm²

(56)

Jadi kecepatan transisinya adalah:

= .

V =

V = 1000 21,848

V = 45,771 cm/det

Untuk tinggi muka air sebesar 2,2 cm dengan debit sebesar 2500 cm³/det maka kecepatan aliran transisii adalah ;

H rata − rata = 1 + 2 2

H rata − rata = 2,2 + 2,9 2

B rata − rata = 1 + 2 2

B rata − rata =10 + 28 2

B rata − rata = 19 cm

(57)

A = B + (m + H ) . H

A = 19 + (1 + 2,55 ) . 2,55

A = 19 + 9,053

A =38,053 cm²

= .

V =

V = 2500 38,053

V = 65,698 cm/det

Untuk tinggi muka air sebesar 1,17 cm dengan debit sebesar 5000 cm³/det maka kecepatan aliran transisii adalah ;

H rata − rata = 1 + 2 2

H rata − rata = 1,17 + 1,78 2

(58)

B rata − rata = 1 + 2 2

B rata − rata =10 + 28 2 B rata − rata = 19 cm

A = B + (m + H ) . H

A = 19 + (1 + 1,475 ) . 1,475

A = 19 + 3,65

A = 22,65 cm²

= .

V =

V = 5000 22,65

V = 220,751 cm/det

(59)

Perhitungan selanjutnya dapat dilihat pada tabel 5

Tabel 5. Hasil perhitungan bilangan Froude dan bilangan reynold

V (cm/det)

A

(cm²) Re Fr Vtransisi

(cm/det) Jenis Aliran TIPE

56 17,9 664,10 0,67 45,771 Transsisi / subkritis A

49 20,44 474,67 0,57 _ Laminer / subkritis B

45 22,2 397,59 0,46 _ Laminer / subkritis C

85 29 466,04 1.01 _ Laminer / subkritis A

40 61,6 263,09 0.28 65,698 transisi / superkritis B

83 30 318,06 0.59 _ Laminer / subkritis C

281 17,8 681,08 1 _ Laminer / subkritis A

152 32,76 104,42 0.47 220,751 Transisi / kritis B

231 21,6 377,03 0.72 _ Laminer / superkritis C Sumber : Hasil Perhitungan

(60)

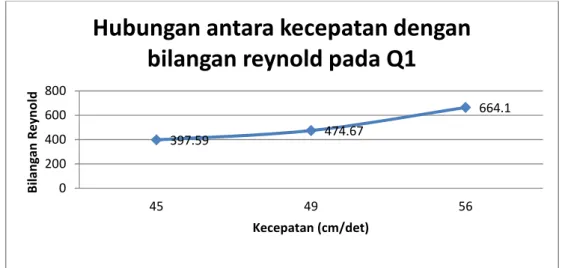
Gambar 15: Hubungan antara kecepatan dengan bilangan reynold pada Q1

Pada percobaan Q1,kecepatan yang sebesar 45 cm/det menghasilkan bilangan reynold sebesar 397.59,kecepatan yang sebesar 49 cm/det menghasilkan bilangan reynold sebesar 474.67,kecepatan yang sebesar56 cm/det menghasilkan bilangan reynold sebesar 664.1.

Pada percobaan Q2,kecepatan yang sebesar 40cm/det menghasilkan bilangan reynold sebesar 263.09,kecepatan yang sebesar83 cm/det

397.59 474.67

664.1

0 200 400 600 800

45 49 56

Bilangan Reynold

Kecepatan (cm/det)

Hubungan antara kecepatan dengan bilangan reynold pada Q1

263.09 318.06

466.04

0 100 200 300 400 500

40 83 85

Bilangan Reynold

Kecepatan (m/det)

Hubungan antara kecepatan dengan

bilangan reynold pada Q2

(61)

menghasilkan bilangan reynold sebesar 318.06,kecepatan yang sebesar 85 cm/det menghasilkan bilangan reynold sebesar 466.04.

Pada percobaan Q3,kecepatan yang sebesar 152 cm/det menghasilkan bilangan reynold sebesar 104.42,kecepatan yang sebesar 231 cm/det menghasilkan bilangan reynold sebesar 377.03,kecepatan yang sebesar 281 cm/det menghasilkan bilangan reynold sebesar 681.08.

Gambar 18: Hubungan antara kecepatan dengan bilangan reynold pada Percobaan Q1, Q2, Q3.

104.42

377.03

681.08

0 200 400 600 800

152 231 281

Bilangan Reynod

Hubungan antara kecepatan dengan bilangan reynold pada Q3

397.59474.67 664.1

263.09 318.06 466.04

104.42

377.03

681.08

0 200 400 600 800

0 50 100 150 200 250 300

Bilangan Reynold (Re)

Kecepatan (V)

Hubungan antara kecepatan dengan bilangan reynold pada Q1, Q2 dan Q3

Q1 Q2 Q3

(62)

Bahwa grafik diatas menunjukkan bahwa hubungan antara kecepatan dengan bilangan reynold adalah berbanding lurus artinya jika kecepatan aliranya yang terjadi pada saluran besar maka bilangan reynoldnya akan semakin besar pula..

Gambar 19: Hubungan antara bilangan reynold dengan luas penampang Pada Q1.

Pada percobaan Q1,luas penampang yang sebesar 17.9 cm² menghasilkan bilangan reynold sebesar 664.1,luas penampang yang sebesar 20.44 cm² menghasilkan bilangan reynold sebesar 474.67,luas penampang yang sebesar 22.2 cm² menghasilkan bilangan reynold sebesar 397.59.

664.1

474.67

397.59

0 100 200 300 400 500 600 700

17.9 20.44 22.2

Luas Penampang (A)

Hubungan antara bilangan reynold (Re)

dengan luas penampang (A) pada Q1

(63)

Gambar 20: Hubungan antara bilangan reynold dengan luas penampang (A) pada Q2

Pada percobaan Q2,luas penampang yang sebesar 29 cm² menghasilkan bilangan reynold sebesar 466.04,luas penampang yang sebesar 30 cm² menghasilkan bilangan reynold sebesar 318.06,luas penampang yang sebesar 61.6 cm² menghasilkan bilangan reynold sebesar 263.09.

Gambar 21: Hubungan antara bilangan reynold dengan luas penampang Pada Q3

466.04

318.06

263.09

0 100 200 300 400 500

29 30 61.6

Hubungan antara bilangan reynold (Re) dengan luas penampang (A) pada Q2

681.08

377.03

104.42 0

200 400 600 800

17.8 21.6 32.76

Hubungan antara bilangan reynold (Re)

dengan luas penampang (A) pada Q3

(64)

Pada percobaan Q3,luas penampang yang sebesar 17.8 cm² menghasilkan bilangan reynold sebesar 681.08,luas penampang yang sebesar 21.6 cm² menghasilkan bilangan reynold sebesar 377.03,luas penampang yang sebesar 32.76 cm² menghasilkan bilangan reynold sebesar 104.42.

Gambar 22: Hubungan antara bilangan reynold dengan luas penampang Pada Q1, Q2, Q3.

Bahwa grafik diatas menunjukkan bahwa hubungan antara bilangan reynold dengan luas penampang adalah berbanding terbalik artinya jika luas penampang saluran besar maka bilangan reynoldnya pada saluran kecil begitupula dengan sebaliknya.

466.04 318.06

263.09 681

377.03

104.42 0

100 200 300 400 500 600 700 800

0 10 20 30 40 50 60 70

Bilangan Reynold

Hubungan antara luas penampang dengan bilangan reynold pada Q1, Q2 dan Q3

Q1 Q2 Q3

(65)

Gambar 23: Hubungan antara kecepatan dengan bilangan Froude pada Q1

Pada percobaan Q1,kecepatan yang sebesar 45 cm/det menghasilkan bilangan froude sebesar 0.46,kecepatan yang sebesar 49 cm/det menghasilkan bilangan froude sebesar 0.57,kecepatan yang sebesar 56 cm/det menghasilkan bilangan froude sebesar 0.67.

0.46 0.57 0.67

0 0.2 0.4 0.6 0.8

45 49 56

Bilangan Froude

Hubungan antara kecepatan dengan bilangan froude pada Q1

0.28

0.59

1.01

0 0.2 0.4 0.6 0.8 1 1.2

40 83 85

Bilangan Froude

Hubungan antara kecepatan dengan

bilangan froude pada Q2

(66)

Pada percobaan Q2,kecepatan yang sebesar 40 m/det menghasilkan bilangan froude sebesar 0.28,kecepatan yang sebesar 83 m/det menghasilkan bilangan froude sebesar 0.59,kecepatan yang sebesar 85 m/det menghasilkan bilangan froude sebesar 1.01.

Pada percobaan Q3,kecepatan yang sebesar 1.52 m/det menghasilkan bilangan froude sebesar 0.47,kecepatan yang sebesar 2.31 m/det menghasilkan bilangan froude sebesar 0.72,kecepatan yang sebesar 2.81 m/det menghasilkan bilangan froude sebesar 1.0.

0.47

0.72

1

0 0.2 0.4 0.6 0.8 1 1.2

152 231 281

Bilangan Froude

Hubungan antara kecepatan dengan

bilangan froude pada Q3

(67)

Gambar 26: Hubungan antara kecepatan dengan bilangan Froude pada Q1, Q2, Q3

Bahwa grafik diatas menunjukkan bahwa hubungan antara kecepatan dengan bilangan reynold adalah berbanding lurus artinya jika kecepatan aliran yang terjadi pada saluran besar maka bilangan reynoldnya akan semakin besar pula..

Gambar 27: Hubungan antara bilangan Froude (Fr) dengan luas Penampang (A) pada Q1.

0.460.570.67 0.28

0.59 1.01

0.47

0.72 1

0 0.2 0.4 0.6 0.8 1 1.2

0 50 100 150 200 250 300

Bilangan Froude

Kecepatan (cm/det)

Hubungan antara kecepatan dengan bilangan Froude pada Q1, Q2 dan Q3

Q1 Q2 Q3

0.67 0.57

0.46

0 0.2 0.4 0.6 0.8 1

17.9 20.44 22.2

Bilangan froude (Fr)

Hubungan antara bilangan froude (Fr)

dengan luas penampang (A) pada Q1

(68)

Pada percobaan Q1,luas penampang yang sebesar 17.9 cm² menghasilkan bilangan froude sebesar 0.67,luas penampang yang sebesar 20.44 cm² menghasilkan bilangan froude sebesar 0.57,luas penampang yang sebesar 22.2 cm² menghasilkan bilangan froude sebesar 0.46.

Pada percobaan Q1,luas penampang yang sebesar 29 cm² menghasilkan bilangan froude sebesar 1.01,luas penampang yang sebesar 30 cm² menghasilkan bilangan froude sebesar 0.59,luas penampang yang sebesar 61.6 cm² menghasilkan bilangan froude sebesar 0.28.

1.01

0.59

0.28

0 0.2 0.4 0.6 0.8 1 1.2

29 30 61.6

Bilangan Froude (Fr)

Hubungan antara bilangan froude (Fr)

dengan luas penampang (A) pada Q2

(69)

Pada percobaan Q1,luas penampang yang sebesar 17.8 cm² menghasilkan bilangan froude sebesar 1.0,luas penampang yang sebesar 21.6 cm² menghasilkan bilangan froude sebesar 0.72,luas penampang yang sebesar 32.76 cm² menghasilkan bilangan froude sebesar 0.47.

Gambar 30: Hubungan antara bilangan Froude (Fr) dengan luas Penampang (A) pada Q1, Q2, Q3.

1

0.72

0.47

0 0.2 0.4 0.6 0.8 1 1.2

17.8 21.6 32.76

Bilangan froude (Fr)

Hubungan antara bilangan froude (Fr) dengan luas penampang (A) pada Q3

0.670.570.46 1.01

0.59 0.47 0.28 1 0.72

0 0.5 1 1.5

0 10 20 30 40 50 60 70

Bilangan Froude

Hubungan antara luas penampang dengan bilangan froude pada Q1, Q2 dan

Q3

Q1 Q2 Q3

(70)

Bahwa grafik diatas menunjukkan bahwa hubungan antara bilangan froude dengan luas penampang adalah berbanding terbalik artinya jika luas penampang saluran besar maka kecepatan aliran pada saluran kecil begitupula dengan sebaliknya.

4. 4.Perhitungan energy spesipic Diketahui :

H1 = 1,79 cm

H2 = 0,73 cm

H3 = 1,48 cm

V1 = 56cm/det

V2 = 49cm/det

V3 = 45cm/det

Untuk mencari energy spesifik digunakan rumus sebagai berikut:

= 2. +

Dimana : E = Energi spesifik (cm)

V = Kecepatan aliran (cm/det)

g = Gaya gravitasi bumi (cm/det²)