ABSTRAK
Kesetimbangan Hardy-Weinberg menegaskan adanya seleksi alam, mutasi, migrasi, perkawinan yang tidak acak, penyimpangan genetik yang acak, aliran gen, frekuensi genotip, dan frekuensi alel dari sebuah populasi tetap konstan dari generasi ke generasi.
Penyimpangan dari proporsi Hardy-Weinberg merupakan hasil dari kekuatan evolusi seperti perkawinan sedarah, perkawinan yang asortatif dan ukuran sampel yang kecil. Penyimpangan dari proporsi Hardy-Weinberg diuji dengan membandingkan perbedaan antara frekuensi genotip yang diobservasi dengan yang diduga.
Pengujian terhadap kesetimbangan Hardy-Weinberg menggunakan Uji Chi-Square Pearson dan uji Eksak F. Uji Chi-Square Pearson digunakan untuk melihat ada tidaknya perbedaan antara frekuensi genotip pengamatan dan frekuensi genotip harapan dari data. Data yang akan diuji dikategorikan ke dalam tabel kontingensi. Apabila frekuensi genotip harapan dari data (sel pada tabel kontingensi) cukup kecil maka digunakan Uji Eksak F. Frekuensi alel dan frekuensi genotip merupakan dua parameter yang digunakan pada kedua uji tersebut.
ABSTRACT
Hardy-Weinberg’s equilibrium states that natural selection, mutation, migration, non-random mating, random genetic deviation, genetic drift, genotype frequencies and allele frequencies remain constant from a generation to another generation.
Deviation from Hardy-Weinberg proportion is the result of evolution power such as inbreeding, assortative mating and small sample space. The deviation of Hardy-Weinberg proportion is tested by comparing the difference between observed genotype frequencies and expected genotype frequencies.
The test of Hardy-Weinberg equilibrium employs Chi-Square Pearson test and F Exact Test. Chi-Square Pearson test is used to see whether there is any difference between observed genotype frequencies and expected genotype frequencies from data. The data which is going to be used is categorized into a contingency table. If the expected genotype frequencies from data (cell in contingency table) is rather small, F Exact Test is used. Allele frequency and genotype frequency are the required parameters for both of the tests.
PENGUJIAN KESETIMBANGAN GENETIKA
HARDY-WEINBERG DENGAN UJI CHI-SQUARE PEARSON
DAN UJI EKSAK F
Skripsi
Diajukan untuk Memenuhi Salah Satu Syarat
Memperoleh Gelar Sarjana Program Studi Matematika
Oleh:
Amanda Alexandra Tanne
NIM: 123114024
PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA
FAKULTAS SAINS DAN TEKNOLOGI
UNIVERSITAS SANATA DHARMA
YOGYAKARTA
THE TESTING OF HARDY-
WEINBERG’S GENETIC
EQUILIBRIUM USING CHI-SQUARE PEARSON TEST
AND F EXACT TEST
Thesis
Presented as a Partial Fulfillment of the Requirements
to Obtain Sarjana Sains Degree in Mathematics
By:
Amanda Alexandra Tanne
Student Number: 123114024
MATHEMATICS STUDY PROGRAM/DEPARTMENT OF MATHEMATICS
FACULTY OF SCIENCE AND TECHNOLOGY
SANATA DHARMA UNIVERSITY
YOGYAKARTA
HALAMAN PERSEMBAHAN
Skripsi ini saya persembahkan untuk:
Tuhan Yesus atas kasih-Nya, berkat, tuntunan dan penyertaannya.
Papa dan Mama tercinta, Robby Tanne dan Leonora
Lawalata.
Bapak Ir. Ig. Aris Dwiatmoko, M. Sc., selaku
pembimbing skripsi terbaik.
Siapapun yang berpikir matematika tidak dapat
ABSTRAK
Kesetimbangan Hardy-Weinberg menegaskan adanya seleksi alam, mutasi, migrasi, perkawinan yang tidak acak, penyimpangan genetik yang acak, aliran gen, frekuensi genotip, dan frekuensi alel dari sebuah populasi tetap konstan dari generasi ke generasi.
Penyimpangan dari proporsi Hardy-Weinberg merupakan hasil dari kekuatan evolusi seperti perkawinan sedarah, perkawinan yang asortatif dan ukuran sampel yang kecil. Penyimpangan dari proporsi Hardy-Weinberg diuji dengan membandingkan perbedaan antara frekuensi genotip yang diobservasi dengan yang diduga.
Pengujian terhadap kesetimbangan Hardy-Weinberg menggunakan Uji Chi-Square Pearson dan uji Eksak F. Uji Chi-Square Pearson digunakan untuk melihat ada tidaknya perbedaan antara frekuensi genotip pengamatan dan frekuensi genotip harapan dari data. Data yang akan diuji dikategorikan ke dalam tabel kontingensi. Apabila frekuensi genotip harapan dari data (sel pada tabel kontingensi) cukup kecil maka digunakan Uji Eksak F. Frekuensi alel dan frekuensi genotip merupakan dua parameter yang digunakan pada kedua uji tersebut.
ABSTRACT
Hardy-Weinberg’s equilibrium states that natural selection, mutation, migration, non-random mating, random genetic deviation, genetic drift, genotype frequencies and allele frequencies remain constant from a generation to another generation.
Deviation from Hardy-Weinberg proportion is the result of evolution power such as inbreeding, assortative mating and small sample space. The deviation of Hardy-Weinberg proportion is tested by comparing the difference between observed genotype frequencies and expected genotype frequencies.
The test of Hardy-Weinberg equilibrium employs Chi-Square Pearson test and F Exact Test. Chi-Square Pearson test is used to see whether there is any difference between observed genotype frequencies and expected genotype frequencies from data. The data which is going to be used is categorized into a contingency table. If the expected genotype frequencies from data (cell in contingency table) is rather small, F Exact Test is used. Allele frequency and genotype frequency are the required parameters for both of the tests.
KATA PENGANTAR
Puji dan syukur patut penulis panjatkan ke hadirat Tuhan Yang Maha Esa atas segala berkat, rahmat dan penyertaanNya sehingga penulis dapat menyelesaikan skripsi ini dengan baik. Skripsi yang berjudul “Pengujian
Kesetimbangan Genetika Hardy-Weinberg dengan Uji Chi-Square Pearson dan Uji Eksak F” ini merupakan salah satu syarat untuk memperoleh gelar sarjana
Matematika pada Fakultas Sains dan Teknologi Universitas Sanata Dharma Yogyakarta.
Tidak dapat dipungkiri bahwa penyusunan skripsi ini dapat diselesaikan dengan baik karena dukungan dan bantuan dari berbagai pihak, walaupun menemui beberapa kendala baik dari dalam maupun luar diri penulis. Oleh sebab itu, dengan tulus hati penulis ingin menyampaikan ucapan trima kasih kepada:
1. Bapak Ir. Ig. Aris Dwiatmoko, M. Sc., selaku dosen pembimbing skripsi yang telah dengan penuh kesabaran telah meluangkan waktu, pikiran, tenaga serta memberikan berbagai masukan, arahan dan nasihat kepada penulis.
2. Bapak YG. Hartono, S.Si., M.Sc., Ph.D., selaku Ketua Program Studi dan Dosen Pembimbing Akademik yang juga selalu bersedia meluangkan waktunya untuk memberikan masukan berkenaan dengan perkuliaan. 3. Bapak Sudi Mungkasi, S.Si., M.Math.Sc., Ph.D. selaku dekan Fakultas
Sains dan Teknologi.
Herawati, S.Si., M.Si., dan Ibu Lusia Krismiyati Budiasih, S.Si., M.Si. selaku dosen-dosen prodi matematika yang telah banyak membagikan ilmunya selama masa perkuliahan.
5. Perpustakaan Universitas Sanata Dharma dan staf sekretariat Fakultas Sains dan Teknologi yang juga telah banyak membantu dalam proses administrasi.
6. Kedua orang tua yang sangat ku kasihi untuk setiap dukungan, doa, dorongan, nasihat, semangat dan kesabarannya hingga terselesaikannya skripsi ini. Kakak yang ku sayangi untuk semangat dan doanya.
7. Bonifasius Endo Gauh Perdana, partner yang luar biasa yang selalu memberikan dorongan semangat, mengingatkan dan menguatkan penulis dalam penulisan skripsi ini. Dewita dan Anggun, sahabat perkuliahan yang selalu saling mengingatkan dan menyemangati.
8. Sahabat-sahabat Genesis, Odi, Ria, Nirmala dan Dina atas semangatnya dan kepeduliannya.
9. Teman-teman Program Studi Matematika 2012: Dewita, Anggun, Risma, Oxi, Putri, Sila, Budi, Rian, Bobi, Happy, Ega, Amalya, Arum, Ajeng, Ilga, Juli, Tika, Ferny dan Noni yang telah memberikan dukungan dan kenangan selama perkuliahan.
10.Semua pihak yang telah membantu dengan memberikan bantuan, semangat dan motivasi hingga terselesaikannya skripsi ini.
DAFTAR ISI
HALAMAN JUDUL ... i
HALAMAN JUDUL DALAM BAHASA INGGRIS ...ii
HALAMAN PERSETUJUAN PEMBIMBING ... iii
HALAMAN PENGESAHAN ... iv
HALAMAN PERSEMBAHAN ... v
HALAMAN PERNYATAAN KEASLIAN KARYA ... vi
HALAMAN ABSTRAK ...vii
HALAMAN ABSTRACT ... viii
LEMBAR PERNYATAAN PERSETUJUAN PUBLIKASI ... ix
KATA PENGANTAR ... x
DAFTAR ISI ... xiii
BAB I PENDAHULUAN ... 1
Latar Belakang Masalah... 1
A. Rumusan Masalah ... 4
B. Batasan Masalah ... 4
C. Tujuan Penulisan ... 5
D. Manfaat Penulisan ... 5
E. Metode Penulisan ... 5
F. Sistematika Penulisan ... 5
A. Pengertian Istilah-istilah dalam Genetika ... 8
B. Probabilitas ... 25
C. Variabel Acak Diskrit ... 26
D. Variabel Acak Kontinu ... 32
E. Fungsi Probabilitas Bersama ... 36
F. Kovariansi Variabel Acak ... 42
G. Distribusi Probabilitas Binomial ... 47
H. Distribusi Probabilitas Multinomial ... 52
I. Distribusi Hipergeometrik ... 56
J. Distribusi Chi-Square ... 62
K. Fungsi Pembangkit Momen... 68
L. Uji Hipotesis ... 72
M. P-value ... 74
BAB III PENDUGAAN PARAMETER DISTRIBUSI MULTINOMIAL, UJI CHI-SQUARE PEARSON DAN UJI EKSAK F ... 77
A. Penduga Parameter dengan Metode Penduga Kemungkinan Maksimum .... 77
B. Penduga Parameter Distribusi Multinomial ... 79
C. Penduga Kemungkinan Maksimum Lokus yang Tidak Memenuhi HWE .. 81
D. Lokus dengan Lebih dari Dua Alel ... 84
E. Uji Chi-Square Pearson ... 85
BAB IV UJI CHI-SQUARE PEARSON DAN UJI EKSAK F TERHADAP
KESETIMBANGAN HARDY-WEINBERG... 102
A. Tabel Kontingensi ... 103
B. Uji Kesesuaian Chi-Square ... 108
C. Uji Eksak F ... 112
D. Kasus yang Memenuhi Kesetimbangan Hardy-Weinberg ... 118
E. Kasus yang Tidak Memenuhi Kesetimbangan Hardy-Weinberg ... 122
F. Pengujian Kasus Terhadap Kesetimbangan Hardy-Weinberg ... 126
BAB V PENUTUP ... 132
A. Kesimpulan ... 132
B. Saran ... 133
DAFTAR PUSTAKA ... 134
BAB I
PENDAHULUAN
A. Latar Belakang
Kesetimbangan Hardy-Weinberg merupakan salah satu prinsip yang sangat penting dalam genetika populasi. Castle, Hardy dan Weinberg (1908) secara independen menemukan prinsip ini. Kesetimbangan Hardy-Weinberg menegaskan adanya seleksi alam, mutasi, migrasi, perkawinan yang tidak acak, penyimpangan genetik yang acak, aliran gen, frekuensi genotip, dan frekuensi alel dari sebuah populasi tetap konstan dari generasi ke generasi. Frekuensi genotip dapat dinyatakan sebagai fungsi yang sederhana dari frekuensi alel. Prinsip Hardy-Weinberg secara luas mempelajari penyakit-penyakit manusia untuk mendeteksi perkawinan sedarah, stratifikasi populasi dan kesalahan pada genetika. Dugaan frekuensi genotip disebut proporsi Hardy-Weinberg. Penyimpangan dari proporsi Hardy-Weinberg diuji dengan membandingkan perbedaan antara frekuensi genotip yang diobservasi dengan yang diduga.
negatif). Perkawinan asortatif juga dapat meningkatkan homosigositas dari gen yang terkait dengan fenotip. Ukuran sampel yang kecil juga dapat meningkatkan homosigositas di dalam populasi. Pada populasi yang kecil, frekuensi alel dapat bergeser dari generasi ke generasi, proses ini dikenal dengan pergeseran genetik. Pergeseran genetik dapat mengakibatkan perubahan acak pada frekuensi genotip, hal ini bisa melanggar prinsip Hardy-Weinberg. Penyimpangan dari proporsi Hardy-Weinberg yang berpengaruh pada individu juga dapat memberikan bukti adanya hubungan antara variasi genetika dan penyakit.
Untuk menguji penyimpangan dari proporsi Hardy-Weinberg di dalam populasi, digunakan hipotesis nol (H0) yang menunjukkan bahwa tidak ada perbedaan yang signifikan antara frekuensi genotip yang diobservasi dengan frekuensi genotip yang diduga terhadap proporsi Hardy-Weinberg. Hipotesis alternatif (Ha) menunjukkan bahwa terdapat perbedaan yang signifikan di antara frekuensi genotip yang diobservasi dengan yang diduga. Pendekatan yang umum digunakan dalam pengujian Hardy-Weinberg adalah uji kesesuaian Chi-Square Pearson dan uji Eksak F. Uji kesesuaian Chi-Square Pearson merupakan pendekatan yang paling umum digunakan untuk menguji penyimpangan proporsi Hardy-Weinberg.
1. Uji Chi-Square Pearson
2. Uji Eksak F
lima. Pengujian ini dilakukan dengan menghitung kemungkinan terhadap hipotesis nol (H0) dari semua kemungkinan kombinasi genotip yang memiliki frekuensi alel serta ukuran total sampel yang sama dengan sampel yang diobservasi.
B. Rumusan Masalah
Rumusan masalah yang akan dibicarakan pada tugas akhir ini, adalah: 1. Bagaimana prinsip Hardy-Weinberg dalam bidang genetika populasi? 2. Bagaimana penyimpangan-penyimpangan terhadap prinsip
Hardy-Weinberg dirumuskan, diselesaikan dan dianalisa?
3. Bagaimana dasar-dasar matematika uji Chi-Square Pearson dan uji Eksak F?
4. Bagaimana uji kesesuaian chi-square Pearson dan uji eksak F diterapkan untuk menguji penyimpangan terhadap kesetimbangan Hardy-Weinberg?
C. Batasan Masalah
Tugas akhir ini akan dibatasi pada masalah-masalah sebagai berikut : 1. Kesetimbangan Hardy-Weinberg yang akan dibahas adalah penerapan uji
Chi-Square Pearson dan uji Eksak F dalam pengujian penyimpangan terhadap prinsip Hardy-Weinberg.
2. Penyimpangan yang dibahas adalah penyimpangan secara umum dan analisis kasus secara umum, tidak menitikberatkan pada suatu kasus penyimpangan tertentu.
3. Penyimpangan yang dibahas ialah penyimpangan yang terjadi pada manusia.
D. Tujuan Penulisan
Tujuan dari penulisan tugas akhir ini adalah untuk menganalisa penyimpangan terhadap kesetimbangan Hardy-Weinberg dengan menggunakan uji kesesuaian Chi-Square Pearson dan uji Eksak F.
E. Manfaat Penulisan
Manfaat yang dapat diperoleh dari penulisan tugas akhir ini adalah kita dapat mengetahui tentang proporsi Hardy-Weinberg, penyimpangan-penyimpangan yang terjadi terhadap proporsi Hardy-Weinberg dan manfaat uji kesesuaian Chi-Square Pearson dan uji Eksak F dalam pengujian penyimpangan terhadap prinsip Hardy-Weinberg.
F. Metode Penulisan
Metode yang digunakan penulis dalam penulisan tugas akhir ini adalah metode studi pustaka, yaitu dengan membaca dan mempelajari buku-buku atau jurnal-jurnal yang berkaitan dengan kesetimbangan Hardy-Weinberg, penyimpangan-penyimpangannya.
G. Sistematika Penulisan
D. Tujuan Penulisan E. Manfaat Penulisan F. Metode Penulisan G. Sistematika Penulisan
BAB II LANDASAN TEORI
A. Pengertian Istilah-istilah Dalam Genetika B. Probabilitas
C. Variabel Acak Diskrit D. Variabel Acak Kontinu E. Fungsi Probabilitas Bersama F. Kovariansi Variabel Acak G. Distribusi Probabilitas Binomial H. Distribusi Probabilitas Multinomial I. Distribusi Hipergeometrik
J. Distribusi Chi-Square K. Fungsi Pembangkit Momen L. Uji Hipotesis
M. P-value
A. Penduga Parameter dengan Metode Penduga Kemungkinan Maksimum
B. Penduga Parameter Distribusi Multinomial
C. Penduga Kemungkinan Maksimum Lokus yang Tidak Memenuhi HWE
D. Lokus dengan Lebih dari Dua Alel E. Uji Chi-Square Pearson
F. Uji Eksak Fisher
BAB IV UJI CHI-SQUARE PEARSON DAN UJI EKSAK F TERHADAP KESETIMBANGAN HARDY-WEINBERG
A. Tabel Kontingensi
B. Uji Kesesuaian Chi-Square C. Uji Eksak F
D. Kasus yang Memenuhi Kesetimbangan Hardy-Weinberg E. Kasus yang Memenuhi Kesetimbangan Hardy-Weinberg F. Pengujian Kasus Terhadap Kesetimbangan
Hardy-Weinberg
BAB V PENUTUP
A. Kesimpulan
BAB II
LANDASAN TEORI
A. Pengertian Istilah-istilah dalam Genetika
1. Alel
Tiap organisme berasal dari satu sel. Dalam sel tersebut terdapat bahan sifat keturunan. Bahan sifat keturunan ini terdapat di dalam inti sel (nucleus). Di dalam inti sel terdapat kromatin yang banyak sekali menghisap zat warna. Kromatin merupakan benang-benang halus yang akan berubah menjadi kromosom pada saat sel sedang giat membelah diri. Kromosom inilah yang merupakan bahan sifat keturunan. Kromosom terdiri atas dua bagian, yaitu :
1. Kinetokor yang merupakan pusat atau kepala kromosom. 2. Lengan yang merupakan badan kromosom sendiri.
Jika diamati lebih dekat lagi dengan mikroskop, sebuah kromosom akan terlihat terdiri dari bagian-bagian sebagai berikut :
1. Selaput (membrane), lapisan tipis menyelaputi badan kromosom. 2. Kandung (matrik), mengisi seluruh lengan, terdiri dari satu cairan
yang bening.
3. Kromonema, yakni benang halus yang berada di dalam kandung (matrik). Kromonema berasal dari benang kromatin sendiri.
inilah yang menumbuhkan dan mengatur pertumbuhan suatu karakter. Ada gen yang bertugas menumbuhkan karakter hidung, ada gen yang mengatur pertumbuhan bentuk dan warna rambut, ada gen yang mengatur pigmentasi kulit, gen yang mengatur susunan darah, dll.
Suatu tubuh organisme memiliki kromosom berpasangan yaitu terdapat sepasang yang homolog (kromosom yang berpasangan pada proses pembelahan), maka gen juga berpasangan karena gen terletak pada masing-masing kromosom yang berpasangan itu sendiri. Kedudukan gen pada kromosom selalu tetap. Untuk setiap individu dari suatu spesies bahkan untuk setiap kromosom dalam satu tubuh, kedudukan gen selalu tetap. Tempat kedudukan gen itu diukur berdasarkan berapa jarak gen tersebut dari ujung kromosom. Tempat kedudukan gen pada kromosom disebut lokus (jamaknya : loci). Umpamanya ada gen A, lokusnya adalah 28. Artinya, jarak gen tersebut dari ujung kromosom adalah 28 unit. Setiap sel tubuh kromosom adalah sepasang, maka gen-gen pada kromosom juga berpasangan. Pasangan-pasangan gen tersebut terletak pada lokus yang sama.
dikalahkan oleh gen A. Gen A disebut dominan terhadap a. Kedua gen ini masih terletak pada lokus yang sama. Gen-gen yang terletak pada lokus yang sama tetapi memiliki karakteristik yang berbeda tetapi untuk satu tugas yang sama disebut alel, dengan kata sifatnya yaitu sealel. A sealel dengan a. A disebut alel dominan, a disebut alel resesif.
Pasangan kedua alel yang sama pada suatu individu (memiliki simbol yang persis sama) disebut homozigot.
Contoh : AA (homozigot dominan), aa (homozigot resesif)
Pasangan kedua alel yang berbeda pada suatu individu (memiliki simbol yang berbeda) disebut heterozigot.
Contoh : Aa, Rr’.
2. Frekuensi Alel
Pada level yang lebih luas, pergeseran frekuensi alel di dalam populasi dapat mengakibatkan perubahan kecil pada susunan genetika, hal ini disebut dengan evolusi mikro, yang secara kolektif hal ini dapat mengakibatkan evolusi.
Frekuensi genotip dapat mengalami perubahan jika kondisi-kondisi berikut terpenuhi, di antaranya :
1. Individu dari satu genotip memiliki kemungkinan untuk menghasilkan keturunan dengan genotip yang sama, dibandingkan dengan yang berbeda genotip.
2. Migrasi individu yang terjadi di antara populasi.
3. Terisolasi untuk bereproduksi dalam grup-grup kecil atau terpisah dari populasi yang lebih besar (hanyutan genetik).
4. Mutasi yang mengakibatkan terbentuknya alel baru dalam suatu populasi.
5. Individu dengan genotip tertentu lebih berpotensi untuk menghasilkan keturunan yang layak dan subur pada kondisi lingkungan yang spesifik daripada individu-individu dengan genotip yang lain (seleksi alam).
populasi dari kesuksesan memproduksi keturunan yang subur secara bersamaan, evolusi makro, atau bentuk dari spesies yang baru telah terjadi.
3. Menghitung Frekuensi Alel
Perhatikan lokus autosomal (tubuh, tidak bergantung pada jenis kelamin), frekuensi alel dapat dihitung dengan menggunakan dua cara, yaitu :
1. Cara pertama yaitu menghitung gen :
Frekuensi alel a, diperoleh dengan :
Frekuensi dari alel a, dapat ditulis dengan f(a). Homozigot memiliki dua dari alel yang diberikan dan heterozigot hanya memiliki satu, serta banyaknya alel-alel adalah dua kali banyaknya individu (masing-masing individu membawa dua alel), frekuensi alel dapat dihitung dengan memperhatikan contoh berikut ini : Sebagai contoh, distribusi fenotip dari tipe darah MN (alel M dan N) dari dua ratus orang yang dipilih secara acak di Ohio sebagai berikut :
Tipe M (genotip MM) = 114 Tipe MN (genotip MN) = 76 Tipe N (genotip NN) = 10 Total = 200 Andaikan p adalah frekuensi relatif alel M
q adalah frekuensi relatif dari N Maka, p = f(M) =
q = f(N) =
secara alternatif, frekuensi relatif dari dua alel M dan N akan berjumlah satu (p Jika diketahui p = 0.76, maka q = 1 – 0.76 = 0.24.
2. Cara kedua untuk menghitung frekuensi alel yaitu dengan menggunakan frekuensi genotip. Pada contoh di atas, diperoleh frekuensi sebagai berikut :
f(MM) = 114/200 = 0.57 f(MN) = 76/200 = 0.38 f(NN) = 10/200 = 0.05
perhitungan nilai p dan q berdasarkan pada frekuensi genotip adalah sebagai berikut :
Kedua cara di atas secara aljabar memberikan hasil yang sama (identik).
4. Kesetimbangan Hardy-Weinberg
Ilmu biologi mendefinisikan evolusi sebagai jumlahan total perubahan genetika di dalam individu yang merupakan anggota dari kolam gen. Kolam gen merupakan jumlah keseluruhan alel dalam sebuah populasi tunggal. Hal ini menunjukkan bahwa efek dari evolusi akan dirasakan oleh individu, tetapi yang berevolusi di sini adalah populasi secara keseluruhan. Evolusi secara sederhana merupakan perubahan di dalam frekuensi alel di dalam kolam gen dari sebuah populasi.
Definisi evolusi ini secara independen dikembangkan oleh Godfrey Hardy, seorang matematikawan Inggris dan Wilhelm Weinberg, seorang fisikawan Prancis pada tahun 1908. Mereka menggunakan aljabar untuk menjelaskan bagaimana frekuensi alel dapat digunakan untuk memprediksi frekuensi genotip dan fenotip di dalam suatu populasi.
Menurut Hardy dan Weinberg, evolusi tidak akan terjadi jika dalam suatu populasi memenuhi 7 kondisi, di antaranya :
3. Ukuran populasi yang besar 4. Tidak adanya perkawinan sedarah 5. Perkawinan acak
6. Frekuensi alel yang sama antara laki-laki dan perempuan (setiap orang memproduksi jumlah keturunan yang sama)
7. Tidak adanya migrasi di dalam atau di luar populasi.
Suatu kondisi di mana ketujuh kondisi di atas dipenuhi disebut kesetimbangan Hardy-Weinberg.
Kesetimbangan Hardy-Weinberg jarang terjadi pada gen yang mengafeksi fenotip karena penampilan dan kesehatan organisme yang mempengaruhi kemampuan reproduksi organisme tersebut. Gen yang memberi pengaruh pada fenotip dikeluarkan dari populasi pada seleksi alam. Kesetimbangan Hardy-Weinberg terjadi pada kondisi yang tidak memberi pengaruh pada fenotip, maka kesetimbangan Hardy-Weinberg hanya memperhatikan frekuensi genotip di dalam suatu populasi. Dengan kata lain, jika ketujuh kondisi di atas tidak dipenuhi maka dapat menyebabkan terjadinya evolusi.
Tabel 2.1. Punnet Square
Alel
A a
p q
Alel A p AA = p
2
Aa = pq
Tabel 2.1 menunjukkan bagaimana ekspansi Binomial dapat diperoleh dari frekuensi alel.
Ekspresi dari genetika populasi di dalam aljabar dimulai dengan persamaan sederhana ,
dengan p = proporsi alel dominan pada gen q = proporsi alel resesif pada gen
ekspresi ini secara sederhana mempunyai arti bahwa semua alel dominan dan semua alel resesif mencakup semua alel-alel untuk gen dalam suatu populasi. Frekuensi genotip AA atau ditulis dengan f(AA) = p2, frekuensi genotip Aa atau ditulis dengan dan frekuensi genotip aa atau ditulis dengan f(aa) = q2.
Hardy dan Weinberg mendeskripsikan frekuensi genotip-genotip yang mungkin untuk gen dengan dua alel menggunakan bentuk ekspansi Binomial
dengan p2 = persentase dari individu dengan genotip homozigot dominan 2pq = persentase heterozigot
generasi ke generasi selanjutnya maka gen tidak mengalami evolusi, dengan kata lain dalam kondisi ini kesetimbangan Hardy-Weinberg terpenuhi.
5. Penyimpangan Hardy Weinberg
Telah dijelaskan sebelumnya bahwa kesetimbangan Hardy-Weinberg dipenuhi ketika kondisi-kondisi tertentu terpenuhi. Jika kondisi-kondisi tersebut tidak dipenuhi dengan kata lain terjadi penyimpangan pada kesetimbangan Hardy-Weinberg maka akan mengakibatkan perubahan pada frekuensi alel. Perubahan pada frekuensi alel dapat mengubah frekuensi genotip. Penyimpangan Hardy-Weinberg dapat disebabkan oleh hal-hal sebagai berikut :
1. Perkawinan Sedarah
perkawinan sedarah (F) yang bernilai 0 adalah ekuivalen, dan penyimpangan terhadap proporsi Hardy-Weinberg dapat mengindikasikan perkawinan sedarah di dalam populasi yang mana koefisien perkawinan sedarah yang bernilai tak 0 dapat mengindikasikan baik kelebihan heterozigot (F bernilai negatif) atau kelebihan homozigot (F bernilai positif) dibandingkan dengan proporsi Hardy-Weinberg yang diduga.
2. Perkawinan Asortatif
Perkawinan asortatif merupakan perkawinan dengan pasangan yang memiliki fenotip yang sama (perkawinan asortatif positif) atau fenotip yang berbeda (perkawinan asortatif negatif), yang dalam hal ini dapat mengakibatkan peningkatan homozigot dari gen yang yang berasosiasi dengan fenotip. Hubungan antara derajat perkawinan asortatif pada orang tua diukur dengan menggunakan kovarian tertimbang.
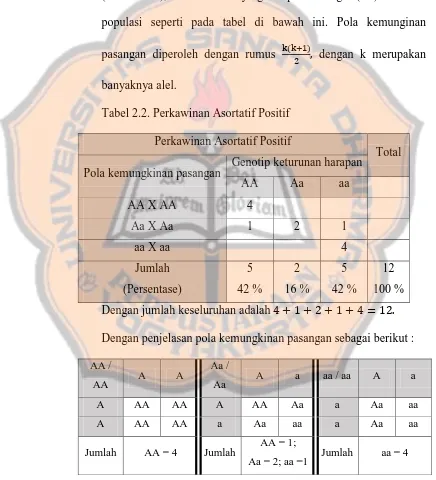
a. Perkawinan Asortatif Positif
autosomal, homozigot dominan dengan homozigot dominan (AA x AA), heterozigot dengan heterozigot (Aa x Aa) dan homozigot resesif dengan homozigot resesif (aa x aa). Efek dari perkawinan asortatif positif adalah meningkatnya jumlah genotip homozigot (AA dan aa), dan menurunnya genotip heterozigot (Aa) di dalam Pola kemungkinan pasangan Genotip keturunan harapan
Notasi / merupakan notasi untuk persilangan. Sebagai contoh notasi AA/AA adalah persilangan antara pasangan alel AA (homozigot) dengan pasangan alel AA (homozigot).
b. Perkawinan asortatif negatif
Pola perkawinan tak acak yang umum yang lainnya ada dimana seseorang memilih sifat fenotip pasangan yang berbeda dengan dirinya. Dalam aturan genetika, ada 6 kemungkinan pola perkawinan asoratatif negatif yang diperhatikan pada dua alel-alel autosomal, seperti ditunjukkan pada tabel 2.3.
Dengan penjelasan pola kemungkinan pasangan sebagai berikut : heterozigot (Aa) dan menurunnya frekuensi genotip homozigot (AA dan aa) dalam suatu populasi. Dengan kata lain, perkawinan asortatif negatif memiliki efek yang berlawanan dengan perkawinan asortatif positif.
3. Ukuran populasi yang kecil
pada frekuensi genotip sebagai hasil dari hanyutan genetik. Pada populasi yang terisolasi secara reproduktif, keadaan-keadaan khusus dapat mengakibatkan perubahan pada frekuensi gen yang independen sebagai akibat dari mutasi dan seleksi alam. Perubahan ini semata-mata terjadi sebagai faktor peluang. Semakin kecil populasi, semakin rentan populasi terhadap perubahan-perubahan tersebut. Feneomena inilah yang disebut dengan hanyutan genetik.
4. Mutasi
Mutasi merupakan perubahan pada materi genetika. Mutasi terjadi selama duplikasi DNA pada saat pembelahan sel. Mitosis dan meiosis merupakan proses mekanikal yang dalam prosesnya terjadi banyak operasi kompleks yang harus tepat selesai agar duplikasi DNA dapat terjadi, sehingga mutasi berpotensi terjadi pada saat mitosis dan meiosis sedang berlangsung.
Ada 4 kategori umum mutasi :
a. DNA yang berbasis substitusi, penyisipan dan penghapusan b. Persilangan yang tidak sama dan modifikasi struktural
kromosom yang terkait.
c. Inversi dan duplikasi parsial atau lengkap gen d. Jumlah kromosom yang tak beraturan
litium, merkuri organik dan beberapa bahan-bahan kimia, virus dan mikroorganisme juga dapat mengakibatkan terjadinya mutasi. Dalam hal mutasi sebagai subyek dari seleksi alam, mutasi harus ditunjukkan dalam fenotip dari individu. Walaupun mutasi memproduksi alel resesif yang mana jarang ditunjukkan pada fenotip, alel resesif menjadi bagian dari variabilitas yang tersembunyi yang dapat muncul pada generasi berikutnya. Alel resesif yang berbahaya tersebut ditambah ke dalam muatan genetik (genetic load). Muatan genetik (genetic load) merupakan ukuran dari semua alel resesif yang berbahaya di dalam populasi atau garis keturunan.
5. Seleksi alam
penyakit-penyakit yang menginfeksi. Jika infeksi membunuh sebelum saat reproduksi, penyebarannya akan disingkirkan dari kerentanan suatu individu terhadap infeksi.
6. Aliran gen
Evolusi dapat pula terjadi sebagai hasil dari gen yang ditransfer dari satu generasi ke generasi selanjutnya. Migrasi yang menyebabkan terjadinya aliran gen. pengurangan atau penjumlahan orang dapat dengan mudah mengubah frekuensi kolam gen walaupun tidak ada mekanisme operasi evolusi. Dampak dari aliran gen adalah adanya perubahan frekuensi alel dan genotip pada populasi asli.
B. Probabilitas
Definisi 2.1
Ruang sampel dari sebuah percobaan merupakan himpunan yang terdiri dari semua kemungkinan titik sampel. Ruang sampel dinotasikan dengan S.
Definisi 2.2
Sebuah ruang sampel diskrit memuat berhingga atau tak terhingga terbilang titik sampel.
Definisi 2.3
Sebuah kejadian di dalam ruang sampel diskrit S merupakan koleksi dari titik-titik sampel, yang merupakan himpunan bagian dari S.
Definisi 2.4
Misalkan S sebuah ruang sampel yang berasosiasi dengan sebuah percobaan. Untuk setiap kejadian A pada S (A merupakan himpunan bagian dari S), P(A) merupakan probabilitas dari A, sehingga memenuhi Aksioma sebagai berikut : Aksioma 1 :
Aksioma 2:
Aksioma 3: jika , , ,… membentuk barisan dari pasangan pada kejadian di S, maka
∑
Definisi 2.5
Probabilitas bersyarat dari kejadian A, dengan kejadian B yang telah terjadi yaitu
dengan . Simbol | dibaca probabilitas A yang diberikan oleh B. Definisi 2.6
Dua kejadian A dan B dikatakan saling bebas jika salah satu dari hal-hal di bawah ini dipenuhi :
|
|
Jika tidak dipenuhi, maka kejadian tersebut tidak saling bebas. Definisi 2.7
Variabel acak merupakan fungsi bernilai real dengan domainnya berupa ruang sampel.
Definisi 2.8
Misalkan N dan n secara berturut-turut merepresentasikan banyaknya elemen-elemen dalam populasi dan sampel. Jika sebarang sampel diambil dan mengakibatkan masing-masing dari ( ) sampel memiliki probabilitas yang sama, sampel tersebut dikatakan acak, dan hasilnya disebut sebagai sampel acak.
C. Variabel Acak Diskrit
Definisi 2.9
Definisi 2.10
Probabilitas variabel acak Y bernilai y, , didefinisikan sebagai jumlahan dari probabilitas dari semua titik sampel di S yang menentukan nilai y. juga dinotasikan dengan notasi lain .
Definisi 2.11
Distribusi probabilitas untuk variabel diskrit Y dapat direpresentasikan dengan sebuah rumus, tabel atau grafik yang menetapkan untuk semua y.
Definisi 2.12
Untuk sebarang distribusi probabilitas diskrit memenuhi hal-hal sebagai berikut: 1. , untuk semua y
2. ∑ , penjumlahan untuk semua nilai y yang memiliki probabilitas tak nol.
Contoh 2.1 :
Seorang supervisor pada sebuah perusahaan memiliki 3 pria dan 3 wanita yang bekerja pada perusahaan tersebut. Dia ingin memilih 2 pekerja untuk sebuah pekerjaan yang khusus. Dia akan melakukan pemilihan secara acak agar tidak menimbulkan bias pada pemilihan. Misalkan Y menotasikan banyaknya wanita yang dipilih. Tentukan distribusi probabilitas dari Y.
3 pria, misalkan A, B, C. 3 wanita, misalkan 1, 2, 3.
- Ruang sampel terpilihnya 2 pekerja adalah S = {AB, AC, AC, 1A, 1B, 1C, 2A, 2B, 2C, 3A, 3B, 3C, 12, 13, 23)
Supervisor tersebut dapat memilih 2 pekerja dari 6 pekerja dalam 15 cara. S memuat 15 titik sampel , yang diasumsikan sama karena sampelnya merupakan sampel acak.
untuk . Nilai untuk Y yang memiliki probabilitas tak nol adalah 0, 1, dan 2. Banyaknya cara memilih Y = 0 wanita adalah ( )( ) karena supervisor harus memilih 0 pekerja dari 3 wanita dan 2 pekerja dari 3 pria. Maka ada ( )( ) titik sampel pada kejadian Y = 0, dan
( )( )
secara sama,
( )( )
( )( )
atau dengan ( ) .
Akan ditunjukkan bahwa contoh di atas memenuhi definisi 2.12 1. Secara jelas terlihat bahwa , untuk semua y.
Definisi 2.13
Misalkan Y merupakan variabel acak diskrit dengan fungsi probabilitas p(y). Maka, nilai harapan dari Y, yang disimbolkan dengan E(Y) didefinisikan dengan
∑
Teorema 2.1
Misalkan Y merupakan variabel acak diskrit dengan fungsi probabilitas dan
merupakan fungsi bernilai real dari Y. Maka nilai harapan dari yaitu
∑
Bukti :
Misalkan variabel acak Y merupakan jumlahan berhingga dari nilai-nilai
∑ ∑
( )
∑ ( ) ( )
Definisi 2.14
Jika Y merupakan variabel acak dengan rata-rata , variansi dari variabel acak Y didefinisikan sebagai nilai harapan dari , yaitu
Standar deviasi dari Y merupakan akar pangkat dua positif dari Teorema 2.2
Misalkan Y merupakan variabel acak diskrit dengan fungsi probabilitas dan c merupakan suatu konstanta. Maka
Bukti :
Perhatikan fungsi . Dengan menggunakan Teorema 2.1,
∑ ∑
Tetapi ∑ (definisi 2.12), maka Teorema 2.3
Misalkan Y merupakan variabel acak diskrit dengan fungsi probabilitas ,
merupakan fungsi dari Y, dan c merupakan konstanta. Maka
Bukti :
∑ ∑
Teorema 2.4
Misalkan Y merupakan variabel acak diskrit dengan fungsi probabilitas dan
merupakan sejumlah k fungsi dari Y. Maka,
Bukti :
Dengan menggunakan induksi matematika : f(y)
,dengan k merupakan fungsi dari Y
Akan dibuktikan dengan menggunakan induksi matematika.
(i) Langkah awal
Pernyataan benar untuk k = 1, yaitu
∑
(ii) Hipotesa
Diandaikan benar untuk k = n, yaitu
(iii) Langkah induksi
Akan dibuktikan benar untuk k = n + 1.
∑ ∑
D. Variabel Acak Kontinu
Definisi 2.15
Misalkan Y menotasikan sebarang variabel acak. Fungsi distribusi dari Y, dinotasikan dengan , didefinisikan sebagai untuk
Definisi 2.16
Jika merupakan fungsi distribusi, maka 1.
2.
3. merupakan fungsi tak turun dari y. [Jika dan merupakan sebarang nilai sehingga , maka
Definisi 2.17
Variabel acak Y dengan fungsi distribusi dikatakan kontinu jika kontinu untuk
Definisi 2.18
Misalkan merupakan fungsi distribusi untuk variabel acak kontinu Y. Maka
yaitu
bila turunannya ada, merupakan fungsi probabilitas (fungsi densitas) untuk variabel acak Y.
Menurut definisi 2.16 dan definisi 2.17, dapat ditulis sebagai
∫
Definisi 2.19
Jika merupakan fungsi densitas untuk variabel acak kontinu, maka 1. untuk semua y,
1. Secara jelas terlihat untuk semua y.
2. ∫ ∫ ∫ Definisi 2.20
Nilai harapan dari variabel acak kontinu Y, yaitu
∫
Teorema 2.5
Misalkan merupakan fungsi dari Y. Maka nilai harapan dari yaitu
∫
Bukti : analog dengan bukti Teorema 2.1 Teorema 2.6
Misalkan Y merupakan variabel acak kontinu dengan fungsi probabilitas dan c merupakan suatu konstanta. Maka
Bukti :
Perhatikan fungsi . Dengan menggunakan Teorema 2.5,
∫
∫
Tetapi ∫ (definisi 2.18), maka Teorema 2.7
Misalkan Y merupakan variabel acak kontinu dengan fungsi probabilitas ,
merupakan fungsi dari Y, dan c merupakan konstanta. Maka
Dengan mengunakan Teorema 2.5,
∫
∫
Teorema 2.8
Misalkan Y merupakan variabel acak kontinu dengan fungsi probabilitas dan
merupakan sejumlah k fungsi dari Y. Maka,
Bukti :
Dengan menggunakan induksi matematika : f(y)
,dengan k merupakan fungsi dari Y
Akan dibuktikan dengan menggunakan induksi matematika.
(iv) Langkah awal
Pernyataan benar untuk k = 1, yaitu
∫
(v) Hipotesa
Diandaikan benar untuk k = n, yaitu
(vi) Langkah induksi
Akan dibuktikan benar untuk k = n + 1.
∫ ∫
E. Fungsi Probabilitas Bersama
Definisi 2.21
Misalkan dan merupakan variabel acak diskrit. Fungsi probabilitas bersama untuk dan ditunjukkan sebagai
Definisi 2.22
Misalkan dan merupakan variabel acak diskrit dengan fungsi probabilitas bersama, maka
1. 2. ∑
Contoh 2.2:
Misalkan 3 bola diambil dari sebuah kantong yang berisi 3 bola merah, 4 bola putih dan 5 bola biru. Jika X adalah banyaknya bola merah yang terambil dan Y adalah banyaknya bola putih yang terambil. Carilah fungsi peluang bersama dari X dan Y.
Penyelesaian :
Banyaknya cara mengambil 3 bola dari 12 bola adalah ( ) .
Banyaknya cara mengambil 0 bola dari 3 bola merah, 0 bola dari 4 bola putih, dan 3 bola dari 5 bola biru adalah ( )( )( ) . Diperoleh
Banyaknya cara mengambil 1 bola dari 3 bola merah, 0 bola dari 4 bola putih, dan 2 bola dari 5 bola biru adalah ( )( )( ) . Diperoleh
, dan seterusnya.
Banyaknya kemungkinan bola merah dan bola putih yang terambil ditunjukkan lewat tabel 2.4 di bawah ini.
Tabel 2.4. Peluang Terambilnya Bola Merah dan Putih
P(x,y) x
y 0 1 2 3 Total baris
0 10/220 30/220 15/220 1/220 56/220
1 40/220 60/220 12/220 112/220
2 30/220 18/220 48/220
3 4/220 4/220
Total kolom 84/220 108/220 27/220 1/220 1
Definisi 2.23
Untuk sebarang variabel dan , fungsi distribusi bersama didefinisikan sebagai
Misalkan dan merupakan variabel acak kontinu dengan fungsi distribusi bersama Jika terdapat fungsi tak negatif seperti
∫ ∫
untuk semua maka dan disebut sebagai variabel acak kontinu bersama. Fungsi disebut fungsi probabilitas bersama.
Definisi 2.25
Misalkan dan merupakan variabel acak kontinu bersama dengan fungsi densitas bersama yang dilambangkan dengan , maka
1. 2. ∫ ∫
Contoh 2.3:
Sebuah perusahaan cokelat mendistribusikan kotak-kotak cokelat yang berisi isian jenis: krim, kopi dan kacang. Terdapat 2 jenis cokelat yaitu cokelat hitam dan cokelat putih. Misalkan dipilih secara acak 1 kotak, dan variabel acak X dan Y menyatakan persentase dari cokelat putih dan cokelat hitam yang berisi krim dengan fungsi probabilitas bersama sebagai berikut:
Jawab :
1. 2. ∫ ∫
∫ ∫
∫ [ ]
∫ [ ]
]
Teorema 2.9
Misalkan dan merupakan variabel acak kontinu yang saling bebas dan dan hanya merupakan fungsi-fungsi dari dan . Maka,
Bukti :
Misalkan menotasikan fungsi densitas bersama dari dan .
berturut-turut merupakan fungsi dari dan . Oleh karena itu, menurut definisi dan asumsi bahwa dan bebas diperoleh,
∫ ∫
∫ ∫
∫ dikatakan bebas jika dan hanya jika
Untuk setiap pasangan bilangan real Definisi 2.27
{
Tentukan E( .
Penyelesaian :
Berdasarkan definisi 2.23, diperoleh :
∫ ∫
∫ ∫
∫ ∫
Teorema 2.10
Misalkan dan merupakan variabel acak diskrit yang saling bebas dan dan hanya merupakan fungsi-fungsi dari dan . Maka,
Bukti :
Misalkan menotasikan fungsi densitas bersama dari dan .
merupakan fungsi dari dan . Oleh karena itu, menurut definisi dan asumsi bahwa dan bebas diperoleh,
∑ ∑
∑ ∑
∑
∑
∑
Teorema 2.11
Misalkan merupakan fungsi dari variabel acak dan dan misalkan c merupakan suatu konstanta. Maka,
Bukti : analog dengan bukti Teorema 2.3 dan 2.6 Teorema 2.12
Misalkan dan merupakan variabel acak dan , ,
merupakan fungsi dari dan . Maka
Bukti : analog dengan bukti Teorema 2.4 dan 2.8
F. Kovariansi Variabel Acak
Definisi 2.28
Misalkan dan merupakan variabel acak dengan rata-rata dan secara berturut-turut, kovarian dari dan adalah
Teorema 2.13
Jika merupakan variabel acak dengan rata-rata dan berturut-turut, maka
Bukti :
Dengan berdasar pada Teorema 2.11 dan Teorema 2.12, diperoleh
Karena dan , diperoleh
Contoh menghitung kovariansi :
Tentukan kovariansi antara jumlah stok dan jumlah penjualan di berdasarkan fungsi densitas berikut :
{
Penyelesaian :
dan berdistribusi densitas bersama dengan fungsi .
Maka ∫ ∫ ∫ ]
∫
∫ ∫ ∫ ∫
( ]
Menggunakan Teorema 2.13, diperoleh
( )
Teorema 2.14
Misalkan dan merupakan variabel acak dengan
dan ( ) Definisikan
∑
∑
untuk konstanta-konstanta dan . Maka beberapa hal berikut terpenuhi, yaitu :
a. ∑ .
b. ∑ ∑ ∑ ( ),
dengan penjumlahan ganda meliputi seluruh pasang dengan . c. ∑ ∑ .
Bukti :
[∑
Dengan menggunakan definisi variansi dan kovariansi, diperoleh
∑
Langkah-langkah yang sama dapat digunakan untuk memperoleh bagian (c).
∑ ∑
∑ ∑ ( )
Contoh 2.5:
Misalkan , , merupakan variabel acak, dengan , ,
, , , , ,
, . Tentukan nilai harapan dan variansi dari
. Jika . Tentukan . Penyelesaian :
, dengan , , dan (Menurut Teorema 2.13)
Perhatikan bahwa , dengan dan . Maka diperoleh,
G. Distribusi Probabilitas Binomial
Beberapa percobaan terdiri dari pengamatan dengan urutan ulangan yang identik dan saling bebas. Masing-masing ulangan tersebut memberikan hasil yang terdiri dari dua hasil. Misalnya pada masing-masing tembakan yang mengenai target hanya ada dua kemungkinan yaitu mengenai target atau meleset. Percobaan ini dikenal dengan nama percobaan Binomial yang memenuhi beberapa karakteristik seperti ditunjukkan pada definisi berikut :
Definisi 2.29
Sebuah percobaan Binomial memenuhi beberapa sifat sebagai berikut : 1. Percobaan terdiri dari n ulangan yang identik.
2. Masing-masing ulangan memberikan dua kemungkinan hasil yaitu S (sukses) atau F (gagal).
3. Probabilitas diperolehnya sukses pada sebuah ulangan tunggal disimbolkan dengan p dan tetap sama dari satu ulangan ke ulangan lain. Probabilitas dari gagal disimbolkan dengan q, dengan q = 1 – p.
4. Ulangan-ulangan yang dilakukan saling bebas.
Distribusi probabilitas Binomial p(y) diperoleh dengan menerapkan pendekatan titik sampel untuk menemukan probabilitas banyaknya sukses yang disimbolkan dengan y.
Definisi 2.30
Variabel acak Y dikatakan berdistribusi Binomial dengan n ulangan dan peluang sukses p jika dan hanya jika
( )
Contoh 2.6: Pada genetika, distribusi Binomial dapat dilihat dalam menentukan probabilitas alel dominan dan resesif dari suatu individu.
dengan q = 1 - p
Bentuk percobaan Binomial diperoleh dari fakta bahwa hasil dari masing-masing percobaan merupakan salah satu dari dua kemungkinan hasil dan probabilitasnya disimbolkan dengan p(y), untuk y = 0, 1, 2, …, n, adalah suku-suku dari ekspansi Binomial.
( ) ( ) ( ) ( ) .
Dengan ( ) ( ) dan secara umum . p(y) memenuhi sifat penting untuk sebuah fungsi probabilitas karena p(y) bernilai positif untuk y = 0,1,…n dan karena q + p =1 maka diperoleh
p = probabilitas alel dominan
∑ ∑ ( )
Teorema 2.15
Andaikan Y merupakan variabel acak Binomial didasarkan pada n ulangan dan probabilitas suskses disimbolkan dengan p, maka
dan Bukti :
Definisi 2.31
Misalkan Y adalah variabel acak diskrit dengan fungsi probabilitas p(y). maka nilai harapan dari Y, yang disimbolkan dengan E(Y) didefinisikan sebagai :
∑
Berdasarkan definisi 2.29 dan definisi 2.30 diperoleh
∑ ∑ ( )
Perhatikan bahwa bentuk pertama dalam penjumlahan adalah 0, diperoleh
∑
∑
Jumlahan pada baris terakhir merujuk pada bentuk distribusi Binomial. Jika faktor np dikeluarkan dari bentuk jumlahan dan z = y -1, maka diperoleh
∑
∑ ( )
Perhatikan bahwa p(z) = ( ) merupakan fungsi probabilitas Binomial dengan (n-1) kali ulangan. Diketahui ∑ , maka diperoleh
Definisi 2.32
Jika Y merupakan variabel acak dengan rata-rata . Variansi dari variabel acak Y didefinisikan sebagai nilai harapan dari . Diperoleh,
Standar deviasi dari Y adalah akar kuadrat positif dari V(Y). Teorema 2.16
Misalkan Y adalah variabel acak diskrit dengan fungsi probabilitas p(y) dan rata=rata , maka
Bukti :
berdasarkan teorema 2.8. Perhatikan bahwa merupakan suatu konstanta, diperoleh
Tetapi , sehingga
Berdasarkan teorema 2.16, diketahui bahwa . dapat
dan
H. Distribusi Probabilitas Multinomial
Sebuah percobaan yang terdiri dari n ulangan untuk variabel acak Binomial akan memberikan dua hasil untuk masing-masing ulangan. Percobaan Multinomial merupakan perumuman dari percobaan Binomial dengan banyaknya kemungkinan hasil lebih dari dua untuk masing-masing ulangan.
Definsi 2.33
Sebuah percobaan Multinomial memenuhi beberapa sifat sebagai berikut : 1. Percobaan terdiri dari n ulangan yang identik.
2. Hasil dari masing-masing ulangan berada pada satu dari sejumlah k kelas atau sel.
3. Probabilitas untuk hasil pada ulangan tunggal untuk sel i disimbolkan dengan pi untuk i = 1, 2, …, k tetap sama antara satu ulangan dengan yang lainnya. Perhatikan bahwa p1 + p2 + p3+ … + pk = 1.
4. Ulangan-ulangan adalah saling independen.
Definisi 2.34
Asumsikan bahwa p1, p2, … , pk sedemikian sehingga ∑ dan untuk i = 1, 2, … , k. variabel acak Y1, Y2, … , Yk dikatakan berdistribusi Multinomialdengan parameter n dan p1, p2, … , pk jika fungsi probabilitas dari Y1, Y2, … , Yk diberikan sebagai berikut
dengan untuk setiap i dan ∑ .
Contoh : Menurut teori genetika, persilangan tertentu sejenis marmot akan menghasilkan keturunan berwarna merah, hitam, putih dalam perbandingan 8 : 4 : 4. Menentukan peluang bahwa 5 dari 8 turunan akan berwarna merah, 2 hitam dan 1 putih dapat menggunakan distribusi Multinomial sebagai berikut :
Jika Y1 adalah banyaknya marmot berwarna merah dengan p1 = 0.5, Y2 adalah marmot berwarna hitam dengan p2 = 0.25 dan Y3 adalah marmot berwarna putih dengan p3 = 0.25, maka
Akan ditunjukkan bahwa contoh di atas memenuhi sifat-sifat distribusi probabilitas Multinomial :
1. Percobaan terdiri dari n ulangan yang identik.
4. Ulangan-ulangan bersifat indepeden.
5. merupakan banyaknya ulangan dengan hasilnya berada pada sel ke – i. Dalam contoh ini, i = 1, 2, 3. Ditunjukkan Y1 + Y2 + Y3= n, yaitu :
Banyak percobaan yang melibatkan klasifikasi merupakan percobaan Binomial. Sebagai contoh : mempelajari bagaimana reaksi tikus ketika diberikan stimulus tertentu pada eksperimen dalam bidang psikologi. Jika tikus-tikus tersebut bereaksi terhadap satu dari tiga cara ketika diberikan stimulus, percobaan tersebut memberi hasil sebuah nomor yang menunjukkan tikus tersebut akan masuk ke kelas yang mana.
Dari penjelasan di atas ditunjukkan bahwa percobaan Binomial merupakan kasus khusus dari percobaan Multinomial ketika terdapat kelas yang disimbolkan dengan k bernilai 2.
Probabilitas dua sel, yaitu p dan q = 1 – p dari percobaan Binomial diganti dengan probabilitas sejumlah k sel, yaitu p1, p2,…, pk yang merupakan percobaan Multinomial.
Teorema 2.17
Jika Y1, Y2, … , Yk berdistribusi Multinomial dengan parameter n dan p1, p2,…, pk maka
1.
Bukti :
Misalkan diinterpretasikan sebagai banyaknya ulangan pada sel i. Bayangkan semua sel, tidak termasuk sel i, digabungkan menjadi sel yang lebih besar. Kemudian setiap ulangan akan memberi hasil pada sel i atau sel lain selain sel i, dengan probabilitas berturut-turut dan . Maka berdistribusi probabilitas Binomial. Sehingga diperoleh,
Pembuktian dari bagian yang kedua dengan menggunakan Teorema 2.14, misalkan sebuah percobaan Multinomial sebagai sebuah barisan dari sejumlah n ulangan yang bebas dan definisikan, untuk s ≠ t,
{
dan
{
Maka,
∑
∑
dan tidak dapat bernilai 1 bersama-sama. Maka, hasil dari selalu bernilai 0 dan Untuk mengevaluasi Cov ( , akan ditunjukkan sebagai berikut :
( )
Kovarian yang diperoleh bernilai negatif, yang diduga karena hasil yang bernilai cukup besar pada sel s akan mengakibatkan nilai pada sel i menjadi kecil.
I. Distribusi Hipergeometrik
Misalkan terdapat sebuah populasi yang terdiri dari sejumlah berhingga N elemen yang memiliki satu dari dua karakteristik. Elemen-elemen yang berwarna merah disimbolkan dengan r dan elemen-elemen yang berwarna hitam disimbolkan dengan b, dengan . Sampel yang terdiri dari sejumlah n elemen dipilih secara acak dari populasi. Variabel acak Y merupakan banyaknya elemen yang berwarna merah di dalam sampel. Variabel acak inilah yang diketahui sebagai distribusi probabilitas hipergeometrik.
n-tuple tersebut berkorespondensi pada terpilihnya sejumlah n elemen dari total N. Jika masing-masing elemen pada populasi diberi nomor dari 1 sampai N, titik sampel mengindikasikan item-item yang terpilih adalah 5, 7, 8, 64, … , 87. Item -item ini akan muncul sebagai n-tuple
(5,7,8,64,17,…,87).
n posisi
Jumlahan total dari titik sampel pada S akan berjumlah sama dengan banyaknya cara memilih himpunan bagian yang terdiri dari sejumlah n elemen dari keseluruhan N populasi atau ( ). Pengambilan secara acak mengimplikasikan bahwa semua titik sampel memiliki peluang yang sama. Hal ini menyebabkan probabilitas dari titik sampel adalah
( )
Banyaknya titik sampel pada kejadian numerik Y=y merupakan jumlahan banyaknya cara mengkombinasikan sebuah himpunan yang terdiri dari sejumlah y elemen yang berwarna merah dan sejumlah (n-y) elemen yang berwarna hitam. Dengan menggunakan aturan perkalian diperoleh . Penjumlahan dari probabilitas-probabilitas dari titik sampel pada kejadian numerik Y=y (mengalikan banyaknya titik-titik sampel dengan probabilitas untuk masing-masing titik sampel) menghasilkan fungsi probabilitas hipergeometri.
Definisi 2.35
Sebuah variable acak Y dikatakan berditsribusi probabilitas hipergeometri jika dan hanya jika
( )
dengan y merupakan bilangan bulat 0, 1, 2, … , n, dengan batas
Seperti diketahui ( )= 0 jika b > a, hal ini dengan jelas menunjukkan bahwa p(y) ≥ 0 pada probabilitas hipergeometrik. Fakta bahwa probabiltas
hipergeometri bila dijumlahkan akan bernilai 1 dapat dijelaskan sebagai berikut :
∑ ( ) ( )
Bukti :
Mengaplikasikan ekspansi Binomial pada masing-masing faktor pada persamaan
( ) ( ) ( )
( ) ( )
( ) ( ) ( )
( ) ( )
( ) ( )
( ) (
)
( )
Dengan membandingkan koefisien pada kedua sisi, diperoleh
( ) ( ) ( ) (
)
( ) ( ) ( ) ( )
( ) ( )
( ) ( ) ( ) ( ) ( ) ( ) ( )
Akan diberikan bukti bahwa ( )( ) ( )( ) ( )( ) ( ), sebagai berikut :
∑ ( ) demikian akan memunculkan suku . Jadi koefisien -nya adalah
( ) ( ) ( ) (
Rata-rata dan variansi dari variabel acak yang berditribusi hipergeometrik dapat diperoleh dari definisi 2.13 dan definisi 2.14.
p(y) dapat diinterpretasikan sebagai peluang keberhasilan y yang diambil dari sejumlah n elemen secara acak dengan r adalah sukses dan N – r adalah yang gagal.
Teorema 2.18
( ) ( )
Bukti :
Akan dibuktikan sifat dari koefisien Binomial. Diketahui bahwa
Variansi dari X (Var(X)) ditunjukkan sebagai berikut :
∑ ( )
( ) merupakan nilai harapan dari distribusi hipergeometrik,
∑ ( )( ) ( )
jumlahannya bernilai 1 karena merupakan jumlah keseluruhan dari semua kemungkinan pada distribusi. Sehingga diperoleh,
∑ (
merupakan jumlahan keseluruhan probabilitas dari distribusi hipergeometrik dan bernilai 1. Diperoleh,
masuk ke kotak 1, maka berdistribusi Binomial sehingga rata-rata (nilai harapan) diperoleh sebagai berikut :
Menurut distribusi Multinomial (Teorema 2.17), masing-masing dari ni berdistribusi Binomial dengan parameter n dan pi dan nilai-nilai harapan yang masuk ke dalam kotak i adalah
Nilai-nilai dari diduga dengan nilai-nilai tertentu dan dikalkulasikan nilai harapannya untuk masing-masing sel. Jika hipotesis ini benar, banyaknya masing-masing kotak yang disimbolkan dengan tidak akan memberikan hasil yang berbeda jauh dengan nilai harapan untuk i = 1,2,…, k.
Dengan kata lain, secara intuitif dapat digunakan statistik uji yang melibatkan sejumlah k selisih.
Karl Pearson mengajukan sebuah statistik uji, yang merupakan fungsi dari kuadrat selisih banyaknya pengamatan dengan nilai-nilai harapannya.
∑
∑
Misalkan , , … , merupakan variabel acak yang berdistribusi independen dan identik dengan dan . Definisikan dimiliki oleh variabel acak di dalam sebuah sampel sebagai berikut :
Tuliskan :
( )
Akhirnya,
Persamaan (2) merupakan fungsi pembangkit momen untuk sebuah variabel acak normal standar. Menggunakan Teorema 2.23, dapat disimpulkan bahwa memiliki fungsi distribusi yang konvergen ke fungsi distribusi normal standar. Z mendekati distribusi normal standarakan ditunjukkan sebagai berikut :
misalkan Y merupakan banyaknya sukses dari n percobaan, sebagai jumlahan dari sampel yang terdiri dari 0 dan 1, yaitu
∑
dengan
{
Variabel acak untuk adalah bebas (karena percobaan-percobaannya bebas) dan diperoleh dan untuk
. Ketika n besar,
∑ ̅
berdistribusi normal dengan rata-rata dan variansi
distribusi yang sama dengan U, dengan U berdistribusi normal dengan rata-rata
dan variansi Secara ekuivalen untuk n yang besar, Y memiliki distribusi yang sama dengan W, dengan W berdistribusi normal dengan rata-rata dan variansi
Untuk menunjukkan bahwa berdistribusi Chi-Square diperlukan Teorema 2.20 sebagai berikut :
Teorema 2.20
Misalkan , , … , merupakan sampel acak dengan ukuran n yang berdistribusi normal dengan rata-rata dan variansi . Maka merupakan variabel acak normal standar yang independen dengan i = 1, 2, … , n
dan
∑ ∑ ( )
berdistribusi Chi Square ( dengen derajat bebeas n. Bukti :
Andaikan berdistribusi normal dengan rata-rata i dan variansi i, berdistribusi normal standar dengan rata-rata 0 dan variansi 1. Dengan menggunakan metode Fungsi Pembangkit Momen diperoleh bahwa merupakan variabel acak yang berdistribusi Chi-Square dengan derajat bebas 1. Demikian,
diperoleh ∑ ,
Persamaan (3) merupakan FPM dari distribusi Chi-Square dengen derajat bebas 1. Sehingga menurut Teorema Ketunggalan (Teorema 2.23), V berdistribusi Chi-Square dengan derajat bebas n.
Diperoleh, kuadrat dari sebuah variabel acak normal standar berdistribusi Chi-Square, maka untuk k=2 dan untuk n yang besar, mendekati distribusi Chi-Square dengan derajat kebebasan 1.
K. FUNGSI PEMBANGKIT MOMEN (FPM)
Definisi 2.36
Momen ke-k dari sebuah variable acak Y didefinisikan sebagai dan dinotasikan sebagai .
Definisi 2.37
Nilai harapan dari momen ke-k dari sebuah variabel acak Y didefinisikan sebagai:
Dinotasikan sebagai . Definisi 2.38
Fungsi pembangkit momen m(t) dari sebuah variabel acak Y didefinisikan sebagai berikut:
Fungsi pembangkit momen dari Y ada jika terdapat sebuah konstanta b yang positif sehingga m(t) berhingga untuk| | . disebut fungsi pembangkit momen, melalui ekspansi baris dari , diperoleh
Asumsikan berhingga untuk k = 1, 2, 3, …, diperoleh
Argumen di atas melibatkan pertukaran penjumlahan yang hanya diperoleh jika m(t) ada. merupakan fungsi dari semua momen . merupakan koefisien dari pada ekspansi baris dari m(t).
Teorema 2.21
Jika m(t) ada, maka untuk sebarang bilangan bulat positif k,
Dengan kata lain, jika terdapat turunan ke-k dari m(t) terhadap t dan pada t = 0, hasilnya akan menjadi .
Bukti :
atau , merupakan turunan ke-k dari m(t) terhadap t. Karena
diperoleh
Secara umum dapat ditulis sebagai berikut :
Ketika t = 0 untuk masing-masing turunan di atas, diperoleh
Operasi-operasi di atas memuat turunan dan penjumlahan tak berhingga yang hanya dapat dioperasikan jika m(t) ada.
Teorema 2.22
Misalkan X merupakan variabel acak dengan momen . Misalkan dan merupakan variabel acak dengan fungsi pembangkit momen dan yang konvergen ketika | | Maka,
Secara umum, jika , , … , merupakan variabel acak yang independen dengan fungsi pembangkit momen yang konvergen ketika | | , maka
Jika semua variabel-variabel acak memiliki fungsi pembangkit momen yang sama misal , maka sisi kanan akan menjadi .
Bukti :
Bukti dari teorema di atas merujuk pada fakta bahwa nilai harapan dari variabel acak yang independen merupakan hasil kali nilai-nilai harapan. Jika dan
saling bebas, maka dan juga bebas (untuk suatu t). Diperoleh, [ ]
Teorema 2.23 (Teorema Ketunggalan)
Misalkan X dan Y merupakan variabel acak diskrit yang terdiri dari bilangan bulat positif tak nol dengan fungsi pembangkit momen MX(t) dan MY(t), masing-masing konvergen untuk |t| < δ. Maka X dan Y memiliki distribusi yang sama jika dan hanya jika MX(t) = MY(t) untuk |t| < δ.
Dengan kata lain, distribusi probabilitas diskrit secara “unik” ditentukan oleh
fungsi pembangkit momennya (bila konvergen).
Bukti :
Jika X dan Y memiliki distribusi yang sama maka secara trivial jelas bahwa MX(t) = MY(t). Untuk bukti arah sebaliknya, akan dibuktikan sebagai berikut :
Jika X dan Y merupakan bilangan berhingga yang tak nol. Misalkan X bernilai tak nol 0 ≤ < < … < dengan probabilitas positif , … , dan misalkan Y bernilai tak nol 0 ≤ < < … < dengan probabilitas positif , … , . Diketahui bahwa fungsi pembangkit momen keduanya sama, berdasarkan teorema 2.19 semua momen bernilai sama seperti ditunjukkan sebagai berikut :
L. UJI HIPOTESIS