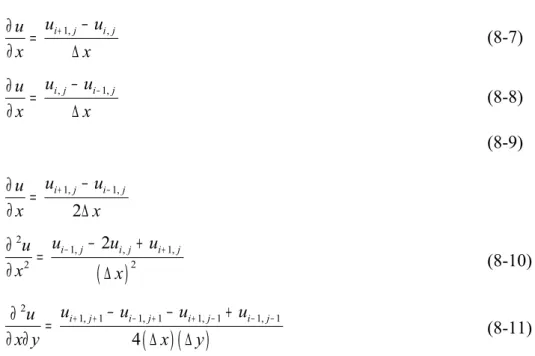BAB VI
PERSAMAAN DIFERENSIAL PARSIAL (PDP)
1 Pendahuluan
Persamaan diferensial parsial memegang peranan penting di dalam penggambaran keadaan fisis, dimana besaran-besaran yang terlibat didalamnya berubah terhadap ruang dan waktu. Sebagai contoh, jika kita meninjau topik-topik fisika lanjut (advanced physics), seperti halnya mekanika klasik lanjut yang membicarakan tentang gelombang elektromagnetik, hidrodinamik dan mekanika kuantum (gelombang Schroedinger), maka kita akan menemukan penggunaan persamaan diferensial parsial yang digunakan untuk menggambarkan fenomena fisis yang berkaitan dengan masalah-masalah tersebut. Masalah-masalah tersebut dalam kenyataannya sulit untuk dipecahkan dengan cara analitik biasa, sehingga metode numerik perlu diterapkan untuk menyelesaikannya. Penggunaan persamaan diferensial tidak terbatas pada masalah fisika saja, tetapi lebih luas lagi dalam bidang sains dan teknologi.
2 Pendekatan Beda Hingga
Untuk memahami dengan benar masalah persamaan diferensial ini, sebelumnya pada bab 5 kita sudah membahas bahwa suatu derivatif dapat didekati dengan beda hingga, sehingga persamaan diferensial dapat didekati dengan persamaan beda hingga pula. Dalam bab ini metode beda hingga yang telah dikenalkan sebelumnya akan diperluas lagi untuk kasus di dalam ruang multidimensi yang lebih tepat dikaji dengan menggunakan persamaan diferensial parsial.
Pada bab V yang lalu, kita sudah menggunakan pendekatan beda hingga untuk mendekati ungkapan turunan pertama dan kedua. Namun pada pembahasan yang lalu kita masih membatasi pada pendekatan untuk turunan pada ruang dimensi satu. Saat ini, kita masih akan menggunakan kaidah-kaidah pendekatan tersebut namun ditingkatkan untuk ruang dimensi dua.
Pada pembahasan tentang persamaan diferensial biasa di bab 7 yang lalu, kita telah melakukan pendekatan beda hingga pada penyelesaiannya. Nah di bab ini, kita juga
akan melakukan hal sama pada bentuk derivatif parsialnya. Mengapa? Karena untuk masalah-masalah yang melibatkan dua atau lebih variabel bebas, prinsip-prinsip tersebut masih tetap dapat diterapkan.
Di dalam pembahasan tentang persamaan diferensial biasa, variabel bebas yang terlibat dalam masalah hanya satu, sedangkan untuk persamaan diferensial parsial variabel bebas berjumlah lebih dari satu. Tentu saja, hal ini saja membuat permasalahan akan semakin kompleks. Untuk memberikan ilustrasi dan mempermudah pemahaman kita tentang masalah ini, sekarang marilah kita tinjau sebuah jaring kotak yang menggambarkan dua variabel bebas x dan y seperti terlihat pada gambar 8.1. Setiap kotak dalam jaring tersebut memiliki lebar ∆x dan y∆ . Oleh karena itu, panjang variabel bebas x setelah langkah ke i dinyatakan oleh
( )
0,1,...,i x
x = ∆i x i= N (8-5)
dan panjang variabel y setelah langkah ke j adalah
( )
0,1,...,j t
y = j ∆t j= N (8-6)
Dengan menggunakan titik-titik jaring pada gambar 8.1, diferensial orde pertama dan kedua dapat didekati oleh:
Persamaan Diferensial Parsial
Gambar 8.1. Jaring titik-titik hitungan pada pendekatan beda hingga dengan variabel bebas x dan y.
Δ y Δ y Δx Δx
1, , i j i j u u u x x + − ∂ = ∂ ∆ (8-7) , 1, i j i j u u u x x − − ∂ = ∂ ∆ (8-8) 1, 1, 2 i j i j u u u x x + − − ∂ = ∂ ∆ (8-9)
( )
2 1, , 1, 2 2 2 i j i j i j u u u u x x − − + + ∂ = ∂ ∆ (8-10)( ) ( )
2 1, 1 1, 1 1, 1 1, 1 4 i j i j i j i j u u u u u x y x y + + − − + − + − + − − ∂ = ∂ ∂ ∆ ∆ (8-11)Dalam beberapa masalah fisika dan teknik persamaan diferensial ada yang dinyatakan dalam turunan pertama terhadap waktu dan turunan kedua terhadap ruang, misalnya pada persamaan difusi. Untuk persamaan diferensial parsial yang mengandung variabel ruang dan waktu ini, pendekatan beda hingga dapat dinyatakan dalam jaring (jaring) bidang x dan t (lihat gambar 8.2).
Δx Δx Δ t
Gambar 8.2. Jaring titik-titik hitungan pada pendekatan beda hingga 1, i j
u
−u
i j,u
i j, +1 , 1 i ju
+Jaring kotak yang menyatakan variabel ruang dan waktu dibagi menjadi pias-pias dengan interval ruang dan waktu ∆x dan ∆t. Panjang variabel ruang x setelah interval ke i dinyatakan sebagai
( )
0,1,...,i x
x = ∆i x i= N (8-12)
Sedangkan untuk variabel waktu t setelah interval waktu ke j adalah
( )
0,1,...,j t
t = j ∆t j= N (8-13)
Bentuk turunan pertama terhadap waktunya dapat dituliskan sebagai
, 1 , i j i j u u u t t + − ∂ ≈ ∂ ∆ (8-14)
Ungkapan (8-14) dapat pula dituliskan sebagai
1 j j i i u u u t t + − ∂ ≈ ∂ ∆ (8-15)
dengan indeks bawah menyatakan harga u pada langkah waktu, dan indeks atas menunjukkan harga u pada langkah ruang. Sedangkan untuk derivatif kedua terhadap variabel ruang seperti dinyatakan pada persamaan (8-10) dapat dituliskan kembali
( )
2 1 1 2 2 2 j j j i i i u u u u x x − − + + ∂ = ∂ ∆ (8-16)8.1 Klasifikasi Persamaan Diferensial Parsial
Persamaan diferensial parsial dibagi menjadi tiga jenis, yaitu persamaan diferensial eliptik, parabolik dan hiperbolik. Untuk membedakan ketiga jenis persamaan diferensial parsial tersebut, marilah sekarang kita meninjau sebuah persamaan diferensial parsial orde dua dalam dua variabel ruang x dan waktu t,
2 2 2 2 2 , , , , 0 u u u u u A B C D x t u x x t t x t ∂ + ∂ + ∂ + ∂ ∂ = ∂ ∂ ∂ ∂ ∂ ∂ (6-1)
dimana A,B dan C merupakan fungsi dari x dan t, dan D adalah fungsi dari u dan
derivatif u x ∂ ∂ dan u t ∂
∂ , serta x dan t. Kita juga akan memperkenalkan variabel baru
sedemikian hingga suku-suku yang mengandung derivatif campuran akan sama dengan nol. Selanjutnya, pembedaan atas tiga klas persamaan diferensial parsial tersebut didasarkan pada harga diskriminan 2
4
B − AC dari persamaan (8-1) tersebut. Pertama, jika kita meninjau pada suatu titik
(
x t dan di titik tersebut 0, 0)
memenuhi syarat bahwa harga diskriminan
(
)
(
) (
)
2
0, 0 4 0, 0 0, 0 0
B x t − A x t C x t > (8-2)
maka persamaan diferensial parsial tersebut dikatakan hiperbolik pada titik
(
x t . 0, 0)
Selajutnya, jika persamaan tersebut hiperbolik pada seluruh titik di dalam ranah (domain) yang ditinjau, maka persamaan diferensial parsial tersebut dikatakan sebagai
persamaan hiperbolik. Sebagai contoh, jika kita meninjau persamaan gelombang
yang mengambil bentuk
Persamaan gelombang 2 2 2 2 2 0 u u c t x ∂ − ∂ = ∂ ∂
Dalam persamaan gelombang tersebut harga A= −c2, B= 0 dan C = 1, sehingga
harga diskriminannya berharga positip. Ini berarti persamaan gelombang benar-benar masuk dalam klasifikasi persamaan diferensial hiperbolik. Persamaan (8-1) tersebut memiliki dimensi ruang satu dengan c adalah kecepatan gelombang cahaya di ruang hampa. Persamaan tersebut menjelaskan dengan sederhana bahwa derivatif kedua dari penyelesaiannya berbanding lurus dengan derivatif kedua lainnya dengan konstanta kesebandingan c .2
Kedua, Jika pada suatu titik
(
x t memenuhi persyaratan0, 0)
(
)
(
) (
)
2
0, 0 4 0, 0 0, 0 0
B x t − A x t C x t = (8-3)
maka persamaan tersebut dikatakan parabolik pada titik
(
x t . Dan jika di seluruh 0, 0)
titik dipenuhi harga diskriminan (8-3), maka persamaan tersebut disebut persamaan
parabolik. Contoh dari persamaan diferensial parabolik adalah persamaan difusi yang
mengambil bentuk Persamaan difusi 2 2 0 u u t κ x ∂ − ∂ = ∂ ∂
dengan A= −κ , B= 0 dan C= 0. Oleh sebab itu, harga deskriminannya sama dengan nol. Persamaan ini dikenal dengan persamaan panas, yang menggambarkan aliran (difusi) panas melalui sebuah penghantar. Dalam kasus ini κ adalah konduktivitas termal yang merupakan kebalikan dari R yang merupakan hambatan termal. Di dalam ilmu fisika persamaan diferensial yang mirip dengan persamaan difusi adalah persamaan Schroedinger yaitu,
Persamaan Schroedinger
(
)
2 2 , , 0 2 u V x y z u i m t − ∇ + − ∂ = ∂ h hPersamaan Schroedinger ini memegang peran penting di dalam mekanika kuantum.
Ketiga, jika pada suatu titik
(
x t berlaku syarat0, 0)
(
)
(
) (
)
2
0, 0 4 0, 0 0, 0 0
B x t − A x t C x t < (8-4)
maka persamaan tersebut dikatakan eliptik pada titik
(
x t , dan jika di seluruh titik 0, 0)
dipenuhi syarat tersebut, maka persamaan tersebut masuk dalam klas persamaan
eliptik. Contoh dari persamaan eliptik adalah persamaan Poisson dan Laplace yang di
dalam ruang dimensi dua masing-masing mengambil bentuk
Persamaan Poisson
(
)
2 2 2 2 , u u S x y x y ∂ + ∂ = ∂ ∂ Persamaan Laplace 2 2 2 2 0 u u x y ∂ + ∂ = ∂ ∂Persamaan Poisson memperkenalkan sumber panas ke dalam sistem yang ditinjau. Sedangkan persamaan Laplace merupakan kasus khusus dari persamaan Poisson tanpa sumber. Disamping itu, persamaan Laplace juga bisa diturunkan dari persamaan difusi. Jika sebuah objek diisolasi dari lingkungan, maka akan dicapai distribusi suhu dalam keadaan mantap, suatu kondisi setimbang yang digambarkan oleh derivatif waktu sama dengan nol pada persamaan difusi. Keadaan mantap suatu aliran panas ditunjukkan oleh kuantitas yang sama antara panas yang keluar dan masuk suatu tampang lintang. Dari kenyataan bahwa derivatif waktu pada persamaan difusi sama dengan nol, maka diperoleh persamaan Laplace. Oleh karena tidak ada
variabel waktu yang gayut, maka penyelesaian untuk persamaan Laplace maupun Poisson tersebut adalah tak gayut waktu.
Persamaan menarik lain yang menggambarkan persamaan eliptik dan agak mirip dengan persamaan Poisson adalah persamaan Helmholtz yaitu,
Persamaan Helmotz 2 2 2 2 0 u u u x y λ ∂ + ∂ + = ∂ ∂
8.1 Persamaan Beda Hingga 8.1.1 Persamaan Hiperbolik Persamaan Gelombang
Contoh klasik dari persamaan hiperbolik adalah persamaan gelombang yang dinyatakan oleh 2 2 2 2 2 u u c t x ∂ = ∂ ∂ ∂ (8-17)
Persamaan ini muncul dalam berbagai masalah dari elastisitas dan akustik sampai hidraulika. Oleh sebab itu, dari tiga bentuk persamaan diferensial parsial yang kita ketahui, persamaan hiperbolik merupakan persamaan yang paling banyak dikaji oleh ilmuwan komputasi. Jika persamaan gelombang (8-17) didekati menggunakan pendekatan beda hingga, maka dapat dituliskan sebagai
( )
( )
1 1 2 1 1 2 2 2 2 0 j j j j j j i i i i i i u u u u u u c t x + − + − − + − − + = ∆ ∆ (8-18) dengan(
,)
j i i j u = u x t (8-19)Dengan memecahkannya untuk variabel uij 1
+
maka kita memperoleh
( )
( )
(
)
( )
( )
2 2 2 2 1 1 1 1 2 2 1 2 j j j j j i i i i i t c t c u u u u u x x + − + − ∆ ∆ = + + − − ∆ ∆ (8-20)Persamaan ini menjelaskan kepada kita bahwa apabila kita mengetahui u pada seluruh x pada saat-saat i t dan j tj−1, maka kita dapat menentukan harga u pada
seluruh x pada langkah waktu berikutnya. Hal ini disebut dengan metode eksplisit. i
Tetapi, ada sedikit masalah pada permulaan perhitungan, karena secara umum kita tidak mengetahui harga u pada dua waktu berturut-turut. Sedangkan, kita harus mengetahui harga u x
(
i,0)
dan derivatif ∂u x(
i,0)
∂tdi seluruh harga x . Oleh sebab iitu, dengan mengetahui ungkapan
( )
( )
1 1 0 , 2 t i i i t u x t u u t − = ∂ = − ∂ ∆ (8-21) atau( ) ( )
1 1 0 , 2 i i i t u x t u u t t − = ∂ = − ∆ ∂ (8-22)maka, kita dapat menyatakan 1
i u sebagai
( )
( )
(
)
( )
( )
( ) (
)
2 2 2 2 1 0 0 0 1 1 2 2 ,0 1 2 i i i i i t c t c u x u u u u t t x + − x ∆ ∆ ∂ = + + − + ∆ ∂ ∆ ∆ (8-23) Persamaan AdveksiPersamaan adveksi merupakan satu-satunya persamaan di dalam dinamika fluida yang munculnya lebih sering dibandingkan persamaan difusi. Persamaan ini memerikan cara suatu besaran kekal (conserved) seperti halnya suhu potensial ataupun momentum dibawa bersama aliran udara atau air.
Untuk menjelaskan secara fisika tentang masalah adveksi ini, sekarang misalnya ada seorang pengamat berdiri di suatu lapangan dengan membawa sebuah termometer. Di tempat tersebut bertiup angin dari arah barat membawa udara lebih hangat menuju ke arah timur yang bersuhu udara lebih dingin. Dalam hal ini sebut saja bahwa arah barat ke timur adalah x . Selajutnya, apa yang dilihat oleh pengamat tersebut dengan termometer yang dibawanya? Ternyata angka yang ditunjukkan oleh termometer semakin besar, yang berarti bahwa keadaan suhu di tempat tersebut semakin hangat. Hal ini disebabkan oleh pergantian udara yang terjadi di tempat tersebut, yaitu dari keadaan udara yang dingin diganti dengan udara yang lebih hangat.
Jika yang terjadi adalah bahwa angin yang berhembus ke arah pengamat tersebut tidak mengalami perubahan suhu, maka pengamat tersebut tidak dapat memberi informasi bahwa terjadi kenaikan suhu. Nah, karena kenyataannya terjadi perubahan suhu maka ada yang disebut gradien suhu. Laju perubahan suhu yang terjadi di tempat itu bergantung kepada besarnya gradien maupun laju perpindahan udara, yaitu
Laju perubahan suhu = -(Laju perpindahan udara) x (Gradien suhu)
Tanda minus menyatakan bahwa suhu hanya akan naik apabila gradien suhu turun, atau dengan kata lain udara akan menjadi lebih hangat jika kita bergerak ke arah x atau dari arah timur ke barat, yakni bergerak ke arah berlawanan dengan arah angin. Dalam bahasa matematika, pernyataan di atas dapat diungkapkan dalam bentuk
u u
c
t x
∂ = − ∂
∂ ∂ (8-24)
dengan u menyatakan suhu potensial yang merupakan besaran kekal yang dalam hal ini merupakan variabel yang diadveksi. Dalam kaitannya dengan masalah ini, maka kita hanya akan membahas untuk harga c konstan. Penyelesaian umum untuk persamaan (8-24) adalah
(
)
u F x ct= − (8-25)
Persamaan adveksi diatas merupakan contoh yang sangat bagus bahwa antara pendekatan numerik dengan analitis tidak selalu menemukan hasil yang sama. Di dalam pasal ini kita akan membahas beberapa pendekatan numerik yang dapat digunakan untuk mendekati persamaan (8-24) tersebut dan setiap metode akan kita kaji stabilitas dan akurasinya
Metode FTCS (Forward-Time Centered-Space)
Untuk menyelesaikan persamaan (8-24) kita akan mengimplementasikan sebuah metode dengan menggunakan pendekatan beda terpusat (metode Leap-Frog) untuk derivatif ruangnya dan metode Euler maju untuk derivatif waktunya.
( )
(
)
( )
1 2 1 1 0 2 n n n n j j j j u u u u O t c O x t x + + − − − + ∆ + + ∆ = ∆ ∆ (8-26) atau(
)
1 1 1 2 n n n n j j j j c t u u u u x + + − ∆ ≈ − − ∆ (8-27)dimana indeks bawah j menyatakan langkah ruang dan indeks atas n menyatakan
langkah waktu. Dengan menggunakan analogi terhadap pembahasan tentang metode Euler dan metode Leap-Frog pada bab yang lalu, maka kita dapat menyimpulkan bahwa ketelitian untuk metode ini adalah orde pertama untuk t -nya dan orde kedua untuk x ,
Pendekatan beda hingga untuk persamaan adveksi (8-26) inilah yang disebut dengan forward in time, centered in space atau lebih dikenal dengan metode FTCS. Pertanyaan selanjutnya apakah metode ini stabil saat mendekati persamaan adveksi tersebut?
Untuk mengetahui apakah metode yang kita gunakan untuk mendekati persamaan tersebut stabil atau tidak, maka kita perlu melakukan uji kestabilan dengan menggunakan analisa stabilitas Von Neuman. Ide dari bentuk analisis kestabilan ini, kita dapat membayangkan bahwa koefisien-koefisien dari persamaan beda berubah
sangat lambat ketika diperlakukan sebagai konstanta dalam ruang dan waktu. Dalam kasus demikian, penyelesaian bebasnya atau swamode dari persamaan beda mengambil bentuk
(
)
exp n n j u = ξ ikj x∆ (8-28)dengan k menyatakan bilangan gelombang ruang real yang dapat berharga sembarang, sedangkan ξ ξ=
( )
k adalah bilangan komplek yang bergantung pada k.Jika kita mensubstitusikan persamaan (8-28) ke persamaan hampiran (8-27), maka dengan mudah diperoleh
(
)
1 sin 2 c t i k x x ξ = − ∆ ∆ ∆ (8-29)Dari persamaan (8-29) dapat diketahui modulus dari ξ yaitu
(
)
2 2 1 sin 2 c t k x x ξ = + ∆ ∆ ∆ (8-30)Persamaan (8-30) memberi arti bahwa penguatan (amplification) penyelesaiannya berhrga 1≥ , ini berarti bahwa metode FTCS tidak stabil mutlak untuk mendekati persamaan adveksi. Skema untuk metode FTCS dapat diilustrasikan seperti gambar 8.4
Dalam gambar (8-4) tersebut bulatan kosong menggambarkan titik baru yang akan ditentukan nilainya, sedangkan bulatan hitam merupakan harga-harga fungsi yang sudah diketahui yang akan digunakan untuk memperoleh penyelesaian pada bulatan kosong. Garis sambung menghubungkan antara titik-titik yang akan
digunakan untuk menghitung derivatif ruang, sedangkan garis putus-putus menghubungkan titik-titik yang akan digunakan untuk menghitung derivatif waktu
Metode BTCS (Backward-Time Centered-Space)
Dengan menggunakan pendekatan beda mundur untuk langkah waktunya dan beda terpusat untuk langkah ruangnya, maka persamaan adveksi dapat didekati dengan
( )
(
1 1)
( )
1 2 1 1 0 2 n n n n j j j j u u u u O t c O x t x + + + + − − − + ∆ + + ∆ = ∆ ∆ (8-31)atau dapat disusun kembali menjadi
(
)
1 1 1 1 1 2 n n n n j j j j c t u u u u x + + + + − ∆ ≈ − − ∆ (8-32)Penggunaan analisa stabilitas Von Nouman pada pendekatan BTCS untuk persamaan adveksi ini menghasilkan
(
)
1 2 ik x ik x c t e e x ξ ∆ ξ ∆ ξ − ∆ = + − ∆ (8-33) atau(
)
1 1 sin 2 c t i k x x ξ = ∆ + ∆ ∆ (8-34)Persamaan (8-34) menunjukkan bahwa faktor penguatannya adalah
(
)
1 1 1 sin 2 c t k x x ξ = ≤ ∆ + ∆ ∆ (8-35)yang berarti, skema (8-31)) adalah stabil mutlak.
Metode Centered-Time Centered-Space (CTCS)
Untuk persamaan adveksi, penggunaan metode Euler maju untuk langkah waktu (forward-time) tidak stabil mutlak, apakah ini berarti dengan menggunakan pendekatan beda terpusat (centered-space) akan stabil? Untuk menjawab pertanyaan ini, marilah kita lakukan pendekatan persamaan adveksi tersebut dengan skema CTCS ini.
Dengan menggunakan skema CTCS, maka persamaan adveksi dapat didekati menjadi
( )
( )
1 1 2 1 1 2 0 2 2 n n n n j j j j u u u u O t O x t x + − + − − − + ∆ − + ∆ = ∆ ∆ (8-36)Persamaan (8-36) dapat disusun kembali menjadi bentuk
(
)
1 1 1 1 n n n n j j j j c t u u u u x + − + − ∆ ≈ − − ∆ (8-37) StabilitasKita dapat mengetes stabilitas dari skema ini dengan analisa stabilitas Von Nouman. Dengan mensubstitusi mode Fourier adveksi yang didefinisikan (8-28) pada persamaan (8-37) maka diperoleh
(
)
2 1 i c tsin k x
x
ξ = − ξ ∆ ∆
∆ (8-38)
Persamaan (8-38) merupakan persamaan kuadrat dalam ξ , sehingga harga-harga untuk ξ dapat dinyatakan oleh
(
)
(
)
2 12 sin sin 4 2 c t c t i k x k x x x ξ ∆ ∆ − ∆ ± − ∆ + ∆ ∆ = (8-39)Modulus dari masing-masing akar adalah 1, sedangkan syarat stabil adalah ξ ≤2 1, ini berarti bahwa metode CTCS stabil untuk menyelesaikan persamaan adveksi.
8.7 Metode Lax
Metode Lax merupakan sebuah metode yang dimaksudkan untuk memodifikasi metode FTCS dari sisi perbaikan terhadap stabilitasnya. Caranya adalah dengan mengganti u dalam derivatif waktu dengan rerata ruangnyanj
(
1 1)
1 2 n n n j j j u → u + + u − (8-40)sehingga persamaan adveksi menjadi
(
)
(
)
1 1 1 1 1 1 2 2 n n n n n j j j j j c t u u u u u x + + − ∆ + − = + − − ∆ (8-42)Dengan mensubstitusi bentuk mode Fourier ke persamaan (8-28) ke persamaan beda (8-42) diperoleh cosk x ic tsink x x ξ = ∆ − ∆ ∆ ∆ (8-43)
Modulus dari ξ adalah
(
)
2(
)
2 2 2 cos k x c t sin k x x ξ = ∆ + ∆ ∆ ∆ (8-44)Pernyataan (8-44) mengisyaratkan kepada kita bahwa metode Lax stabil untuk
1 c t x ∆ ≤ ∆ . Untuk harga 1 c t x ∆ <
∆ faktor penguatannya berkurang. Faktor penguatan ini
dinyatakan oleh
(
)
2(
)
2 2 cos k x c t sin k x x ξ = ∆ + ∆ ∆ ∆ (8-45) Untuk harga t 1 x υ ∆ =∆ , penyelesaiannya adalah eksak karena faktor penguatannya
berharga 1 atau tidak mengalami penguatan, sehingga
1 1 n n j j u + = u − (8-46) Kriteria stabilitas c t 1 x ∆ ≤
∆ dikenal dengan syarat Courant. Secara intuitif, syarat
stabilitas ini dapat dideskripsikan seperi pada gambar (8.6). Gambar tersebut menerangkan bahwa kuantitas unj+1 dalam persamaan (8-42) dapat diketahui setelah
diperoleh informasi titik-titik j−1 dan j+ 1 pada saat n . Dengan kata lain, xj−1 dan
Persamaan Diferensial Parsial
Gambar 8.5. Deskripsi untuk skema beda Lax
Gambar 8.6 Daerah dibawah garis putus-putus secara fisis adalah menurut
1
j
x+ merupakan batas yang memungkinkan untuk memberikan informasi pada besaran unj+1.
Hasil yang mengagumkan pada pendekatan Lax adalah bahwa penggantian u nj
dengan reratanya seperti terlihat pada ungkapan (8-41) dapat menstabilkan skema FTCS. Skema Lax pada (8-42) selajutnya dapat ditampilkan dalam bentuk
1 1 1 1 1 2 1 2 2 n n n n n n n j j j j j j j u u u u u u u c t x t + + − + − − − − + = − + ∆ ∆ ∆ (8-47)
yang merupakan representasi dari metode FTCS
( )
2 2 2 2 x u u u c t x t x ∆ ∂ = − ∂ + ∂ ∂ ∂ ∆ ∂ (8-48)Dalam persamaan (8-48) ini, kita memiliki suku difusi. Oleh sebab itu, skema Lax ini dikatakan memiliki disipasi numerik.
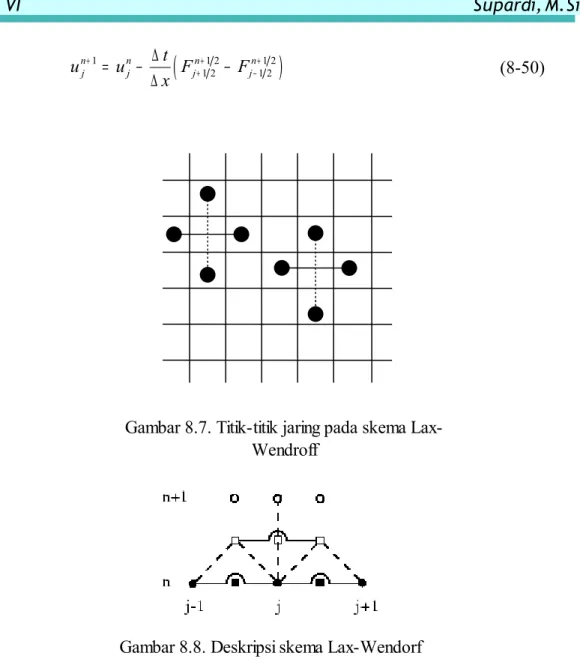
8.8 Skema Lax-Wendroff
Skema Wendroff merupakan metode dengan akurasi orde kedua terhadap waktu. Jika kita mendefinisikan suatu harga intermediet unj++1 21 2 pada langkah waktu
1 2
n
t + dan langkah ruang xj+1 2. Jika ini dihitung dengan menggunakan metode Lax, maka akan diperoleh
(
)
(
)
1 2 1 2 1 1 1 2 2 n n n n n j j j j j t u u u F F x + + = + + − ∆∆ + − (8-49)Sedangkan, harga terbaru untuk unj+1dapat dihitung dengan pernyataan terpusat
(
)
1 1 2 1 2 1 2 1 2 n n n n j j j j t u u F F x + + + + − ∆ = − − ∆ (8-50)Selanjutnya, kita akan mengkaji stabilitas dari metode ini untuk persamaan adveksi dengan mensubstitusi F cu= . Dengan mensubstitusi pernyataan (8-49) ke ungkapan (8-50), maka diperoleh
(
)
(
)
1 1 1 1 1 2 2 n n n n n n j j j j j j c t c t u u u u u u x x + + + ∆ ∆ = − + − − ∆ ∆(
1)
(
1)
1 1 2 2 n n n n j j j j c t u u u u x − ∆ − − + + − ∆ (8-51)Dengan menggunakan uji stabilitas Von Nouman, maka dengan mudah diperoleh
Persamaan Diferensial Parsial
Gambar 8.8. Deskripsi skema Lax-Wendorf Gambar 8.7. Titik-titik jaring pada skema
(
)
2 1 ic tsink x c t 1 cosk x x x ξ = − ∆ ∆ − ∆ − ∆ ∆ ∆ (8-52)Harga modulus dari ξ adalah
(
)
2 2 2 2 1 c t 1 cosk x c tsink x x x ξ = − ∆ − ∆ + ∆ ∆ ∆ ∆ (8-53) atau(
)
2 2 2 2 1 c t 1 c t 1 cosk x x x ξ = − ∆ − ∆ − ∆ ∆ ∆ (8-54)Kriteria stabilitas yang harus dipenuhi adalah ξ ≤2 1, hal ini mensyaratkan harga
2 1 c t x ∆ ≤ ∆
atau lebih dikenal sebagai kriteria Courant.
8.1.2 Persamaan Parabolik
Persamaan difusi, konduksi panas dan persamaan Schroedinger gayut waktu merupakan contoh dari persamaan diferensial parabolik. Persamaan parabolik memilki kemiripan dengan persamaan hiperbolik yakni batasnya yang terbuka. Di dalam Geofisika, persamaan difusi merupakan salah satu persamaan yang sangat penting yang muncul dalam berbagai konteks yang berbeda-beda. Di bawah ini diberikan bebarapa contoh persamaan diferensial parabolik yang dinyatakan dalam ungkapan matematis
a. Persamaan netron transien dalam ruang satu dimensi
( )
( )
2 2 , T x t T c k Q x t x ρ ∂ = ∂ + ∂ ∂b. Persamaan konduksi panas transien dalam ruang satu dimensi
( )
22 1 , a f x t D S t x ψ ψ ψ υ ψ υ ∂ = ∂ + + ∂ ∂∑
∑
dengan ψ menyatakan fluks netron.
( )
22u x D
tψ t ψ t ψ
∂ = − ∂ + ∂
∂ ∂ ∂
dengan ψ menyatakan rapat fluks spesies kimia, u x adalah kecepatan
( )
aliran dan D adalah konstanta difusi.8.1.2.1 Metode Eksplisit (Euler Maju)
Marilah kita ditinjau sebuah persamaan difusi yang mengambil bentuk
2 2 0 u u t κ x ∂ − ∂ = ∂ ∂ (8-55)
Dengan mengimpementasikan metode Euler maju untuk derivatif waktu seperti yang telah kita bahas pada bab persamaan diferensial biasa yang lalu, serta menggunakan pendekatan derivatif orde kedua terpusat pada turunan kedua terhadap variabel ruangnya, maka diskritisasi terhadap ungkapan (8-55) tersebut mengambil bentuk
(
)
( )
1 1 1 2 2 n n n n n j j j j j u u u u u t κ x + + − + − − = ∆ ∆ (8-56)atau dapat dituliskan kembali sebagai
( )
(
)
1 1 1 2 2 n n n n n j j j j j t u u u u u x κ + + − ∆ = + − + ∆ (8-57)Skema ini disebut sebagai metode eksplisit, karena jika u diketahui untuk seluruh in t n
pada titik-titik jaring, maka kita dapat menghitung uin+1 pada waktu tn+1 tanpa
menyelesaikan melalui persamaan simultan. Deskripsi skema ini dapat dilihat pada gambar 8.9.
Persamaan Diferensial Parsial
Gambar 8.9 Deskripsi metode eksplisit pada persamaan difusi
Apabila pendekatan penyelesaian persamaan difusi (8-57) dilakukan uji stabilitas menggunakan prosedur analisa stabilitas Von Nueman, maka dengan mudah dapat diperoleh bahwa
( )
2(
( )
)
1 2 k t cos kx 1 x ξ = + ∆ − ∆ (8-58) atau( )
2 2 1 1 4 sin 2 t k x x κ ξ = − ∆ ∆ ∆ (8-59)Dari hasil analisa stabilitas dapat ketahui bahwa metode yang kita gunakan untuk mendekati persamaan difusi tersebut stabil karena syarat stabil ξ ≤ 1 dipenuhi.
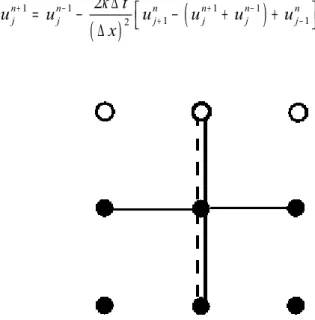
Metode Implisit (Euler Mundur)
Untuk memberikan gambaran tentang pendekatan metode implisit pada persamaan difusi yang kita miliki, sekarang marilah kita mengingat kembali tentang kemungkinan pendekatan persamaan tersebut dengan beda mundur. Jika persamaan difusi tersebut kita dekati dengan beda mundur, maka diperoleh
( )
1 1 1 2 2 n n n n n i i i i i u u u u u t κ x − + − − = − + ∆ ∆ (8-60)yang dapat disusun kembali menjadi ungkapan
( )
2(
1 2 1)
1 n n n n n i i i i i t u u u u u x κ − + − ∆ − − + = ∆ (8-61)Ungkapan (8-61) sebenarnya mengikuti suatu perjanjian, bahwa kuantitas yang belum diketahui harganya ditempatkan di ruas kiri, sedangkan besaran yang sudah diketahui ditempatkan diruas kanan. Dalam kasus ini, harga-harga u pada langkah waktu n dianggap tidak dketahui, harga-harga yang diketahui adalah pada langkah waktu ke n−1. Deskripsi skema implisit ini dapat dilihat pada gambar 8.10.
Dengan mengambil
( )
2 t x κ α ≡ ∆ ∆ (8-62)maka untuk setiap titik ruang x dengan j j= 1, 2,3,...,N−1, kita memperoleh
(
)
1 1 1 2 1 n n n n i i i i α ψ α ψ α ψ ψ − − + − + + − = (8-63)Jika syarat batas pada ujung-ujungnya diberikan yaitu u dan 0 u , maka kita N
persamaan (8-63) dapat ditampilkan dalam bentuk persamaan simultan linier sebagai berikut 1 n n− Ψ = Ψ Ag (8-64) dengan 1 0 0 . . 0 1 2 0 . 0 0 . . . 0 . . . . . . . . 1 2 . . . 0 0 1 α α α α α α − + − = − + − A (8-65)
Kita juga akan menggunakan analisa stabilitas Von Nouman untuk meyakinkan apakah skema implisit ini stabil atau tidak stabil. Jika kita mensubstitusikan mode Fourier ke persamaan (8-61), maka dengan mudah diperoleh
( )
2(
)
1 1 t cosk x 2 x κ∆ ξ − − ∆ − = ∆ (8-66)atau dapat disusun kembali menjadi
( )
2 1 1 1 sin 2 t k x x ξ = κ∆ + ∆ ∆ (8-67)Faktor penguatan yang memiliki bentuk semacam ini, tentunya harus berharga
≤ 1. Ini menunjukkan bahwa skema implisit yang kita gunakan untuk mendekati persamaan difusi adalah stabil mutlak.
8.1.2.2 Metode Dufort-Frankle
Metode ini merupakan salah satu dari beberapa metode yang digunakan untuk mengatasi masalah stabilitas yang ditemukan pada metode Euler maju atau FTCS. Metode Dufort-Frankle merupakan satu teknik yang memanfaatkan stabilitas tak bersyarat dari metode intrinsic untuk persamaan diferensial sederhana.
Selanjutnya kita dapat memodifikasi persamaan (8-61) menggunakan metode Dufort-Frankle sebagai berikut
( )
(
)
1 1 1 1 1 1 2 2 n n n n n n j j j j j j t u u u u u u x κ + − + − + − ∆ = − − + + ∆ (8-68) Jika diambil( )
2 2 t x κ β = ∆∆ , maka persamaan (8-68) dapat disusun kembali menjadi
bentuk
(
)
1 1 1 1 1 1 1 n n n n j j j j u α u α u u α α + − + − − = − + + + (8-69)Pengujian stabilitas terhadap pendekatan Dufort-Frankle menggunakan analisa Von Nouman memunculkan persamaan kuadrat dalamξ , hal ini dikarenakan
munculnya tiga pangkat konskutif pada ξ ketika prosedur Von Nueman disubstitusi ke dalam persamaan tersebut. Persamaan kuadrat tersebut adalah
2 2 cos 1 0 1 k x 1 α α ξ ξ α α − + ∆ − = + + (8-70)
Selanjutnya persamaan (8-70) memiliki dua penyelesaian yaitu
(
2 2)
1 cos 1 sin 1 k x k x ξ α α α = ∆ ± − ∆ + (8-71)Untuk mengetahui kestabilan skema ini, maka kita dapat mengecek bagaimana modulus dari ξ tersebut. Dengan menganggap α 2sin2k x∆ ≥ 1 dan α 2sin2k x∆ < 1,
maka kita akan memperoleh bahwa ξ ≤2 1. Ini menunjukkan bahwa skema Dufort-Frankle tersebut stabil mutlak.
Metode Cranck-Nicolson
Pendekatan metode Cranck-Nicolson untuk menyelesaikan persamaan diferensial parabolik didasarkan pada metode Euler termodifikasi seperti yang telah dibahas pada bab yang lalu. Dengan menggunakan metode ini, maka pendekatan pada persamaan difusi selanjutnya dapat ditulis kembali menjadi
( )
(
) (
)
1 1 1 1 1 1 1 1 2 2 2 2 n n n n n n n n i i i i i i i i t x ψ + ψ κ ψ ψ ψ ψ ψ ψ + + + − + − + − = − + + − + ∆ ∆ (8-72) atau( )
(
) (
)
1 1 1 1 1 1 1 1 2 2 2 2 n n n n n n n n i i i i i i i i t x κ ψ + ψ ψ + ψ + ψ + ψ ψ ψ − + − + ∆ = + − + + − + ∆ (8-73)Persamaan Diferensial Parsial
Dengan mendefinisikan
( )
2 2 t x κ γ = ∆∆ , maka ungkapan (8-73) juga dapat dinyatakan
dalam bentuk persamaan simultan sebagai berikut
(
)
(
)
1 1 1 1 1 2 1 1 1 2 1 n n n n n n j j j j j j γ ψ + γ ψ + γ ψ + γ ψ γ ψ γ ψ − + − + − + + − = + − + (8-74) atau 1 n+ = n Aψg B ψg (8-75)dengan matriks A dan B didefinisikan sebagai
1 0 0 . . 0 1 2 0 . 0 0 . . . 0 . . . . . . . . 1 2 . . . 0 0 1 γ γ γ γ γ γ − + − = − + − A (8-76) dan 1 0 0 . . 0 1 2 0 . 0 0 . . . 0 . . . . . . . . 1 2 . . . 0 0 1 γ γ γ γ γ γ − = − B (8-77)
Dengan menggunakan analisa stabilitas Von Nouman seperti yang telah kita terapkan pada metode-metode sebelumnya, maka diperoleh faktor penguatannya sebesar
(
)
(
)
2 2 1 2 sin 2 1 2 sin 2 k x k x γ ξ γ − ∆ = + ∆ (8-78)Faktor penguatan tersebut menunjukkan bahwa harganya selalu 1≤ . Ini menunjukkan bahwa skema ini stabil mutlak. Lebih lanjut lagi, karena pendekatan beda yang digunakan dalam metode ini adalah metode Euler termodifikasi, maka ketelitian metode ini lebih tinggi dibanding metode Euler maju ataupun mundur.
Contoh penggunaan skema Cranck-Nicolsan adalah pada penyelesaian persamaan Schroedinger.
8.13 Persamaan Schroedinger
Jika kita mengkaji secara serius ilmu fisika, maka kadang-kadang kita menemukan suatu masalah yang mengandung kendala (constraint), sebagai contoh persamaan Scrhoedinger gayut waktu di dalam Mekanika
Persamaan ini termasuk ke dalam persamaan diferensial parabolik untuk evolusi besaran kompleks ψ . Untuk persamaan diferensial parsial yang memerikan hamburan paket gelombang yang disebabkan oleh potensial V
( )
x dalam ruang 1D, maka persamaannya memiliki bentuk( )
2 2 2 2 i V x t m x ψ ψ ψ ∂ = − ∂ + ∂ ∂ h (8-79) Jika kita menggunakan satuan universal, sedemikian hingga konstanta Planck 1=
dan massa partikel m= 1/2, maka persamaan Schroedinger (8-79) akan mengmbil bentuk
( )
ψ ψ ψ V x x t i + ∂ ∂ − = ∂ ∂ 2 2 (8-80) Pengenaan syarat batas untuk masalah di atas adalah harga ψ pada saat awal atau(
x,t = 0)
ψ bersama dengan x→ ± ∞ yaitu ψ → 0. Selanjutnya langkah diskritisasi untuk persamaan gelombang (8-71) dapat dinyatakan dalam bentuk
( )
1 1 1 1 1 1 1 2 2 2 n n n n n j j j j j n j j i V t x ψ ψ ψ ψ ψ ψ + + + + + − + − − + = − + ∆ ∆ (8-81)Skema yang ditunjukkan pada persamaan beda (8-81) menggunakan skema implisit atau metode BTCS. Oleh sebab itu, factor penguatannya adalah
( )
2 2 1 4 1 sin 2 j t k x i V t x ξ = ∆ ∆ + + ∆ ∆ (8-82) atau( )
2 2 2 1 4 1 sin 2 j t k x V t x ξ = ∆ ∆ + + ∆ ∆ (8-83)Dengan harga ξ 2 di atas menunjukkan bahwa skema ini stabil mutlak. Sayangnya, skema ini tidak uniter. Mengapa harus uniter? Hal ini disebabkan oleh suatu syarat bahwa probabilitas total suatu partikel ditemukan dalam suatu range daerah yang terbentang dari − ∞ sampai ∞ adalah satu.
2 1 dx ψ ∞ − ∞ =
∫
(8-84)Persamaan (8-84) mensyaratkan fungsi gelombang awal ψ
( )
x,0 ternormalisir. Jika ungkapan persamaan Schroedinger (8-80) dinyatakan dalam bentuki H
t
ψ ψ
∂ =
∂ (8-85)
dengan H adalah operator hamiltonian yang mengambil bentuk
( )
2 2 H V x x ∂ = − + ∂ (8-86)maka penyelesaian persamaan (8-85) tersebut secara analitik adalah
( )
x t, e iHt( )
x,0ψ = − ψ
(8-87) Implementasi algoritma FTCS untuk mendekati persamaan (8-87) berbentuk
(
)
1 1 n n j iH t j ψ + = − ∆ ψ (8-88) dimana H dinyatakan oleh pendekatan beda hingga terpusat dalam x . Sedangkan, penggunaan skema implisit BTCS akan mengambil bentuk berbeda yaitu(
)
1 1 1 n n j iH t j ψ + = + ∆ − ψ (8-89)Dua metode yang digunakan di atas memiliki akurasi orde pertama dalam waktu, seperti telah dibahas di depan.
Dengan kenyataan bahwa metode eksplisit maupun implisit bukan metode yang baik untuk menyelesaikan persamaan Schroedinger gayut waktu ini, maka kita
akan menggunakan bentuk Cayleys untuk menyatakan wakilan beda hingga e−iHt
yang memiliki akurasi orde dua dan uniter yaitu 1 1 2 1 1 2 iHt iH t e iH t − − ∆ + ∆ ; (8-90)
dengan kata lain,
1 1 1 1 1 2 2 n n j j iH t ψ + iH t ψ + ∆ = − ∆ (8-91)
Selanjutnya dari persamaan (8-91), maka kita memiliki sistem tridiagonal. Skema tersebut adalah stabil, uniter dan memiliki akurasi orde kedua. Nah cara ini disebut sebagai metode Crank-Nicolson.
Contoh source code untuk menyelesaikan persamaan difusi Program Difusi
Integer*4 maxn, maxnplot
parameter( maxn = 300, maxnplot = 500 )
integer*4 n, i, j, iplot, nlangkah, plot_langkah, nplot, ilangkah real*8 tau, l, h, kappa, koef, tt(maxn), tt_baru(maxn)
real*8 xplot(maxn), tplot(maxnplot), ttplot(maxn,maxnplot) C initialisasi parameter (langkah waktu, pias, dll).
write(*,*) ‘masukkan langkah waktu: ' read(*,*) tau
write(*,*) ‘masukkan jumlah jaring: ' read(*,*) n
l = 1. h = l/(n-1) kappa = 1. koef = kappa*tau/h**2 if( koef .lt. 0.5 ) then
write(*,*) 'penyelesaian diharapkan stabil' else
write(*,*) 'warning: apakah penyelesaian diharapkan tidak stabil’ endif
C set syarat awal dan syarat batas. do i=1,n
tt(i) = 0.0
tt_baru(i) = 0.0 enddo tt(n/2) = 1/h iplot = 1 nlangkah = 300 plot_langkah = 6 nplot = nlangkah/plot_langkah + 1 do i=1,n xplot(i) = (i-1)*h - l/2 enddo do ilangkah=1,nlangkah do i=2,(n-1)
tt_baru(i) = tt(i) + koef*(tt(i+1) + tt(i-1) - 2*tt(i)) enddo
do i=2,(n-1)
tt(i) = tt_baru(i) enddo
if( mod(ilangkah,plot_langkah) .lt. 1 ) then do i=1,n ttplot(i,iplot) = tt(i) enddo tplot(iplot) = ilangkah*tau iplot = iplot+1 endif enddo nplot = iplot-1 open(11,file='tplot.txt',status='unknown') open(12,file='xplot.txt',status='unknown') open(13,file='ttplot.txt',status='unknown') do i=1,nplot write(11,*) tplot(i) enddo do i=1,n write(12,*) xplot(i) do j=1,(nplot-1) write(13,1001) ttplot(i,j) enddo write(13,*) ttplot(i,nplot) enddo 1001 format(e12.6,', ',$) stop end 8.2 Persamaan Eliptik
Contoh umum dari persamaan diferensial eliptik adalah persamaan Poisson yang berbentuk
(
)
2 2 2 2 , u u x y x y ρ ∂ + ∂ = − ∂ ∂ (8-92)Jika ρ
(
x y,)
= 0, maka disebut persamaan Laplace yang berbentuk2 2 2 2 0 u u x y ∂ + ∂ = ∂ ∂ (8-93)
Untuk menyelesaikan persamaan eliptik dibutuhkan syarat batas di ujung-ujungnya. Oleh sebab itu penyelesaian persamaan eliptik masuk dalam kategori masalah nilai batas.
Metode penyelesaian numerik untuk persamaan diferensial eliptik diklasifikasikan dalam dua kategori, yaitu metode beda hingga dan elemen hingga. Tetapi dalam pasal ini kita hanya akan menggunakan metode beda hingga untuk menangani persamaan ini. Metode beda hingga diturunkan dari jaring kotak. Penggunaan metode ini untuk menyelesaikan masalah diferensial eliptik memiliki banyak keuntungan. Adapun keuntungan metode elemen hingga diantaranya adalah bahwa persamaan diskritnya tidak terganggu oleh bentuk geometri yang rumit, sehingga metode ini fleksibel untuk diterapkan dalam bentuk geometri apapun. Namun akhir-akhir ini, metode beda hingga juga telah dikembangkan untuk mengatasi masalah geometri ini yaitu dengan cara transformasi koordinat.
Persamaan Beda dalam Geometri Rectangular
Dalam pasal ini kita tidak akan membahas metode beda hingga dalam geometri yang rumit, tetapi kita hanya akan membahas metode tersebut di dalam gometri kotak saja. Untuk memudahkan pemahaman kita tentang metode ini, sekarang marilah kita tinjau sebuah persamaan Laplace dalam koordinat kartesan seperti terlihat pada persamaan (8-93).
Untuk mempermudah pemahaman kita tentang masalah yang kita bahas ini, sekarang ditinjau untuk domain 0≤ ≤x Lx dan 0≤ ≤y Ly seperti terlihat pada
gambar 8.10. Syarat batas yang dikenakan pada sisi-sisinya adalah
Batas kiri u 0 x
∂ =
∂ (syarat batas Neumann)
Batas kanan u= 0 (syarat Dirichlet) Batas atas u= 0
Batas bawah u 0
y
∂ = ∂
Untuk menurunkan persamaan beda hingga pada persamaan Laplace, maka kita perlu membuat jaring pada kotak tersebut. Jika kita mengasumsikan bahwa lebar pias ∆ = ∆ = ∆x y, maka persamaan Poisson tersebut dapat didekati dengan pendekatan beda terpusat yang mengambil bentuk
(
2 2)
, , , 2 1 iui j j i ju i j δ + δ = ρ ∆ (8-94)atau secara eksplisit dapat ditunjukkan dalam bentuk deskrit
1, , 1, , 1 , , 1 , 2 2 1 1 2 2 i j i j i j i j i j i j i j u+ u u− u + u u − ρ − + + − + = ∆ ∆ (8-95) dengan ui j, ≡ u x y
(
i, j)
Masalah yang timbul dalam menangani persamaan beda (8-95) adalah bagaimana cara memberikan perlakuan pada titik-titik di syarat batas pada sisi kiri
0
u
x
∂ =
∂
∆
∆
i=1 2 3 4 … imax j= 1 2 3 4 … j maxx
L
y
L
0
x
0
=
y
=
0
u
y
∂ =
∂
0
u
=
0
u
=
dan bawah. Sedangkan persamaan beda di sisi atas dan kanan tidak penting, karena kita sudah mengetahui harga dari u.
Sekarang kita akan meninjau untuk persamaan beda di perbatasan sisi kiri.
Pada gambar tersebut terlihat bahwa syarat batas di sebelah kiri adalah u 0 x ∂ =
∂ .
Derivatif kedua dari u atau 2u2 x ∂
∂ pada titik-titik batas sebelah kiri selanjutnya dapat kita
dekati dengan 1 2 , , 2 2 1, 2 i j i j j u u x y u x + ∂ ∂ − ∂ ∂ ∂ ≈ ∂ ∆ (8-96)
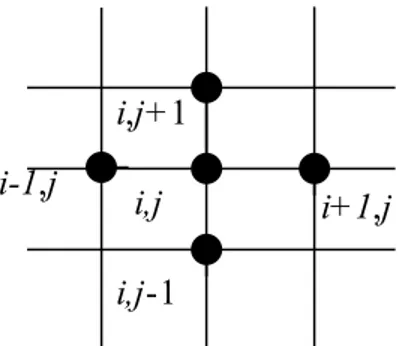
Sekarang, bagaimana cara kita mendekati derivatif pertama u terhadap x pada suku pertama pembilang pada persamaan beda (8-96) tersebut? Lihatlah gambar 8.15. Pada gambar tersebut tampak tiga titik terdekat yang mengelilingi titik (1,j). Dengan kenyataan itu, kita memang tidak bisa menerapkan persamaan beda untuk derivatif kedua seperti terlihat pada persamaan (8-95), karena kita harus memiliki empat titik yang mengitari titik pusat. Oleh sebab itu, kita berharap dengan pendekatan beda (8-96) tersebut permasalahan tersebut teratasi.
Persamaan Diferensial Parsial 1,j+1 1,j 1,j-1
2,j
Gambar 8.16. Titik-titik di perbatasan kiri i,j+1
i,j i,j-1
i+1,j
Gambar 8.15. Titik (i,j) dikelilingi empat titik terdekat. Pendekatan beda untuk derivatif kedua u terhadap x dinyatakan pada persamaan (88).
Selajutnya, suku pertama pembilang pada persamaan (8-96) dapat didekati dengan 2, 1, 1 1 , 2 j j j u u u x + − ∂ ≈ ∂ ∆ (8-97)
Oleh karena suku kedua pembilang pada persamaan beda (8-96) berharga sama
dengan nol, maka pendekatan beda 2u2 x ∂ ∂ adalah 2 2, 1, 2 1, 2 j 2 j j u u u x − ∂ ≈ ∂ ∆ (8-98)
Selanjutnya, persamaan beda derivatif kedua u terhadap x di perbatasan sisi kiri mengambil bentuk 2, 1, 1, 1 1, 1, 1 1, 2 2 1 1 2u j 2u j u j+ 2u j u j− ρ j − + − + = ∆ ∆ (8-99)
Dengan menggunakan cara yang sama, maka kita dapat mendekati derivatif pertama u terhadap x di perbatasan sisi bawah kotak adalah
2 ,2 ,1 2 ,1 2 i 2 i i u u u y − ∂ ≈ ∂ ∆ (8-100)
sehingga derivatif kedua u dapat didekati dengan persamaan beda
1,1 ,1 1,1 ,2 ,1 ,1 2 2 1 1 2 2 2 i i i i i i u+ u u− u u ρ − + + − = ∆ ∆ (8-101)
Persamaan Diferensial Parsial
i-1,j I,j i+1,j I,j+1
Dengan menggunakan persamaan beda () dan () untuk derivatif pertama u terhadap x, maka kita dapat menentukan pendekatan derivatif kedua dari u yang mengambil bentuk 2,1 1,1 1,2 1,1 1,1 2 2 1 1 u u u u ρ − + − = ∆ ∆ (8-102) Contoh
Ditinjau sebuah persamaan Laplace dalam ruang dimensi dua dengan domain
0≤ ≤x 8 dan 0≤ ≤y 6mengambil bentuk
2 2 2 2 0 x y ϕ ϕ ∂ + ∂ = ∂ ∂
dengan syarat batas yang diberikan adalah
Batas kiri u 0 x ∂ = ∂ Batas kanan u= 1 Batas atas u= 0 Batas bawah u 0 y ∂ = ∂ Penyelesaian
Untuk menyelesaikan persamaan di atas, maka kita membuat jaring dengan lebar pias sama yaitu 2. Harga titik-titik di perbatasan kotak atas dan kanan berharga
0
ϕ = , sedangkan titik-titik di perbatasan kiri dan bawah memenuhi ∂ϕ ∂ =x 0 dan 0
y
ϕ
∂ ∂ = . Dengan syarat batas yang diberikan tadi, kita akan menghitung titik-titik
Persamaan Diferensial Parsial 2
2 i=1 2 3 4 5 j = 1 2 3 4 0 u= x
L
yL
0
x
0
=
y
=
u 0 y ∂ = ∂0
u
=
8 0 u x ∂ = ∂ 6yang lain kecuali pada perbatasan atas dan kanan, karena di perbatasan ini harga ϕ sudah diketahui.
Dengan menggunakan persamaan beda hingga (8-95), (8-99) dan (8-101), maka kita dapat menuliskan persamaan simultan dalam ϕ yaitu
1. Titik (1,1) −4ϕ1,1+ 2ϕ2,1+ 2ϕ1,2 = 0 2. Titik (2,1) ϕ1,1− 4ϕ2,1+ ϕ3,1 + 2ϕ2,2 = 0 3. Titik (3,1) ϕ2,1− 4ϕ3,1+ ϕ4,1+ 2ϕ3,2 = 0 4. Titik (4,1) ϕ3,1 − 4ϕ4,1+ 2ϕ4,2 = −1 5. Titik (1,2) ϕ1,1− 4ϕ1,2 + 2ϕ2,2 + ϕ1,3 = 0 6. Titik (2,2) ϕ2,1+ ϕ1,2 + ϕ3,2 − 4ϕ2,2 + ϕ2,3 = 0 7. Titik (3,2) ϕ3,1 + ϕ2,2 − 4ϕ3,2 + ϕ4,2 + ϕ3,3 = 0 8. Titik (4,2) ϕ4,1+ ϕ3,2− 4ϕ4,2+ ϕ4,3 = −1 9. Titik (1,3) u1,2 − 4u1,3 + 2u2,3 = 0 10. Titik (2,3) u2,2 + u1,3 − 4u2,3+ u3,3 = 0 11. Titik (3,3) u3,2+ u2,3− 4u3,3 + u4,3 = 0 12. Titik (4,3)ϕ4,2 + ϕ3,3 − 4ϕ4,3 = −1
Jika persamaan simultan di atas dinyatakan dalam bentuk matriks, maka bentuknya
11 4 2 0 0 2 0 0 0 0 0 0 0 1 4 1 0 0 2 0 0 0 0 0 0 0 1 4 1 0 0 2 0 0 0 0 0 0 0 1 4 0 0 0 2 0 0 0 0 1 0 0 0 4 2 0 0 1 0 0 0 0 1 0 0 1 4 1 0 0 1 0 0 0 0 1 0 0 1 4 1 0 0 1 0 0 0 0 1 0 0 1 4 0 0 0 1 0 0 0 0 1 0 0 0 4 2 0 0 0 0 0 0 0 1 0 0 1 4 1 0 0 0 0 0 0 0 1 0 0 1 4 1 0 0 0 0 0 0 0 1 0 0 1 4 ϕ ϕ − − − − − − − − − − − − 21 31 41 12 22 32 42 13 23 33 43 0 0 0 1 0 0 0 1 0 0 0 1 ϕ ϕ ϕ ϕ ϕ ϕ ϕ ϕ ϕ ϕ − = − −
Jika persamaan simultan linier yang dinyatakan dalam bentuk matriks tersebut dinyakan oleh
=
A X bg
maka untuk menemukan harga setiap elemen matriks X dapat dilakukan dengan cara −
= 1
X A bg
Dengan menggunakan kaidah ini, maka elemen-elemen matriks X maka kita dapat menentukan harga ϕ pada setiap titik yaitu
11 21 31 41 12 22 32 42 13 23 33 43 0.3377, 0.3799, 0.5118 0.7379, 0.2955, 0.3351 0.4647, 0.7199, 0.1740 0.2003, 0.2920, 0.5030 ϕ ϕ ϕ ϕ ϕ ϕ ϕ ϕ ϕ ϕ ϕ ϕ = = = = = = = = = = = =
Metode Iteratif Jacobi
Sesuai dengan namanya, ide dari metode iteratif Jacobi adalah menemukan harga setiap titik-titik dalam kotak melalui jalan iterasi hingga ditemukan harga yang optimum. Iterasi awal dimulai dengan memberikan nilai tebakan pada variabel-variabelnya. Iterasi dilakukan terus menerus hingga selisih harga elemen kini dan sebelumnya melebihi toleransi yang diberikan.
Untuk lebih jelasnya, sekarang kita akan meninjau kembali persamaan Laplace seperti pada contoh 8.1 tetapi dengan syarat batas sebagai berikut
Batas kiri u = 0
Batas kanan u= 1 Batas atas u= 0 Batas bawah u = 1
Dengan syarat batas yang diberikan tersebut, maka kita dapat membentuk persamaan simultan baru sebagai berikut
1. Titik (2,2) 2,2 1,2 3,2 2,1 2,3 3,2 2,3 2,2 4 0 atau 4 ϕ ϕ ϕ ϕ ϕ ϕ ϕ ϕ − − − − = + = 2. Titik (3,2) 3,2 2,2 4,2 3,1 3,3 2,2 4,2 3,3 3,2 4 0 atau 4 ϕ ϕ ϕ ϕ ϕ ϕ ϕ ϕ ϕ − − − − = + + = 3. Titik (4,2) 4,2 3,2 5,2 4,1 4,3 3,2 4,3 4,2 4 0 1 atau 4 ϕ ϕ ϕ ϕ ϕ ϕ ϕ ϕ − − − − = + + = 4. Titik (2,3) 2,3 1,3 3,3 2,2 2,4 2,2 3,3 2,3 4 0 1 atau 4 ϕ ϕ ϕ ϕ ϕ ϕ ϕ ϕ − − − − = + + = 5. Titik (3,3) 3,3 2,3 4,3 3,2 3,4 2,3 4,3 3,2 3,3 4 0 1 atau 4 ϕ ϕ ϕ ϕ ϕ ϕ ϕ ϕ ϕ − − − − = + + + = 6. Titik (4,3) 4,3 3,3 5,3 4,2 4,4 3,3 4,2 4,3 4 0 2 atau 4 ϕ ϕ ϕ ϕ ϕ ϕ ϕ ϕ − − − − = + + = 0 0 0 1 1 1 1 1 1
Sebagai langkah awal, kita berikan tebakan awal seluruh titik sama dengan nol, kecuali pada batas-batas yang telah kita tentukan. Dari langkah ini, kita memiliki harga-harga pada setiap titik antara lain ϕ2,20 = 0,
0 3,2 0 ϕ = , ϕ4,20 = 0, 25, 0 2,3 0, 25 ϕ = , 0 3,3 0, 25
ϕ = , ϕ4,30 = 0,50. Dengan menggunakan bahasa pemrograman, maka arga
titik-titik pada iterasi berikutnya dapat kita temukan sampai toleransi yang diberikan. Program Iterasi_jacobi dimension pa(5,4),pb(5,4) real phip character*10 fname write(*,5) read 9,fname 9 format(15a)
5 format(23x,'nama file output:',\) open(8,file=fname)
c tebakan awal untuk seluruh titik diberikan sama dengan nol c kecuali pada batas-batas yang telah ditentukan
c syarat batas pada titik-titik jaring adalah pa(2,4)=1. pa(3,4)=1. pa(4,4)=1. pa(5,4)=1. pa(5,2)=1. pa(5,3)=1. c pb(2,4)=1. pb(3,4)=1. pb(4,4)=1. pb(5,2)=1. pb(5,3)=1. pb(5,4)=1. c do 25 iter=1,100 write(8,90)iter do 30 i=2,4 do 40 j=2,3 pb(i,j)=(pa(i-1,j)+pa(i+1,j)+pa(i,j-1)+pa(i,j+1))/4.
40 continue 30 continue do 35 i=2,4 do 45 j=2,3 pa(i,j)=pb(i,j) 45 continue 35 continue c write (8,22) pb(1,4),pb(2,4),pb(3,4),pb(4,4),pb(5,4) write (8,22) pb(1,3),pb(2,3),pb(3,3),pb(4,3),pb(5,3) write (8,22) pb(1,2),pb(2,2),pb(3,2),pb(4,2),pb(5,2) write (8,22) pb(1,1),pb(2,1),pb(3,1),pb(4,1),pb(5,1) write (*,22) pb(1,4),pb(2,4),pb(3,4),pb(4,4),pb(5,4) write (*,22) pb(1,3),pb(2,3),pb(3,3),pb(4,3),pb(5,3) write (*,22) pb(1,2),pb(2,2),pb(3,2),pb(4,2),pb(5,2) write (*,22) pb(1,1),pb(2,1),pb(3,1),pb(4,1),pb(5,1) 25 continue 90 format(i4) 22 format(5f10.6) close(8) stop end
Tabel 8.1 Contoh eksekusi program iterasi Jacobi
Iterasi ke-1 .000000 1.000000 1.000000 1.000000 1.000000 .000000 .250000 .250000 .500000 1.000000 .000000 .000000 .000000 .250000 1.000000 .000000 .000000 .000000 .000000 .000000 Iterasi ke-4 .000000 1.000000 1.000000 1.000000 1.000000 .000000 .406250 .574219 .738281 1.000000 .000000 .148438 .265625 .480469 1.000000 .000000 .000000 .000000 .000000 .000000 Iterasi ke-7 .000000 1.000000 1.000000 1.000000 1.000000 .000000 .451660 .634094 .784973 1.000000 .000000 .190125 .330688 .523438 1.000000 .000000 .000000 .000000 .000000 .000000 Iterasi ke-10 .000000 1.000000 1.000000 1.000000 1.000000 .000000 .460958 .648406 .794291 1.000000 .000000 .200234 .343851 .533567 1.000000 .000000 .000000 .000000 .000000 .000000 Iterasi ke-13 .000000 1.000000 1.000000 1.000000 1.000000
.000000 .463182 .651300 .796516 1.000000 .000000 .202281 .346998 .535614 1.000000 .000000 .000000 .000000 .000000 .000000 Iterasi ke-16 .000000 1.000000 1.000000 1.000000 1.000000 .000000 .463632 .651992 .796966 1.000000 .000000 .202770 .347634 .536103 1.000000 .000000 .000000 .000000 .000000 .000000 Iterasi ke-19 .000000 1.000000 1.000000 1.000000 1.000000 .000000 .463740 .652132 .797073 1.000000 .000000 .202869 .347786 .536202 1.000000 .000000 .000000 .000000 .000000 .000000 Iterasi ke-22 .000000 1.000000 1.000000 1.000000 1.000000 .000000 .463762 .652165 .797095 1.000000 .000000 .202892 .347817 .536226 1.000000 .000000 .000000 .000000 .000000 .000000 Iterasi ke-25 .000000 1.000000 1.000000 1.000000 1.000000 .000000 .463767 .652172 .797100 1.000000 .000000 .202897 .347824 .536230 1.000000 .000000 .000000 .000000 .000000 .000000 Iterasi ke-27 .000000 1.000000 1.000000 1.000000 1.000000 .000000 .463768 .652173 .797101 1.000000 .000000 .202898 .347825 .536231 1.000000 .000000 .000000 .000000 .000000 .000000 Iterasi ke-28 .000000 1.000000 1.000000 1.000000 1.000000 .000000 .463768 .652174 .797101 1.000000 .000000 .202898 .347826 .536232 1.000000 .000000 .000000 .000000 .000000 .000000 8.10 Metode Relaksasi
Konsep dari metode relaksasi didasarkan pada suatu ide bahwa konvergensi ke suatu penyelesaian dari pemberian terkaan awal tertentu dapat dicapai dengan cara mengulang-ulang iterasi setiap titiknya. Konsep dari iterasi berasal dari suatu ide bahwa perubahan perlahan-lahan (evolusi) terhadap waktu dapat dilihat ketika persamaan diferensial parsial eliptik dinyatakan dalam bentuk persamaan diferensial parabolik.
8.10.1 Metode RelaksasiGauss-Seidel
Metode relaksasi Gauss-Seidel telah terbukti memperoleh sukses besar dalam keberhasilannya menyelesaikan persamaan diferensial parsial eliptik. Untuk lebih jelasnya, sekarang kita akan menyatakan persamaan eliptik sebagai persamaan difusi
(
)
2 2 2 2 , u u x y x y ρ ∂ + ∂ = ∂ ∂ (8-72) menjadi(
)
2 2 2 2 , u u u x y t x y ρ ∂ = ∂ + ∂ − ∂ ∂ ∂ (8-73)Apabila pada t= 0 terdapat distribusi awal, maka kita dapat mengatakan bahwa bahwa ketika t→ ∞ penyelesaian sudah merelaks ke arah keadaan setimbang. Saat t→ ∞ tersebut, maka dipenuhi ∂u t/∂ → 0. Jika persamaan (8-73) kita lakukan diskritisasi menggunakan metode FTCS, maka ungkapan tersebut akan menjadi bentuk
(
)
1 , , 2 1, 1, , 1 , 1 4 , , n n n n n n n j j j j j j j j t u u u u u u u t x ρ + − + − + ∆ = + + + + − − ∆ ∆ ℓ ℓ ℓ ℓ ℓ ℓ ℓ ℓ (8-74)dengan indeks atas n mewakili variabel waktu, sedangkan indeks bawah menyatakan variabel ruang.
Dengan mengingat kembali bahwa di dalam ruang 1D metode FTCS stabil
hanya jika dipenuhi / 2 1 2 t
∆ ∆ ≤ , dan stabil dalam ruang 2D hanya jika / 2 1
4 t
∆ ∆ ≤ ,
maka ungkapan (8-74) dapat dinyatakan kembali dalam bentuk
(
)
2 1 , 1, 1, , 1 , 1 , 1 4 4 n n n n n j j j j j j u +ℓ = u − ℓ+ u + ℓ+ u ℓ− + u ℓ+ − ∆ ρ ℓ (8-75)Dari ungkapan (8-75), kita dapat menemukan harga terbaru dari u pada langkah