Staff Site Universitas Negeri Yogyakarta

(1)

量子力学

Quantum mechanics

School of Physics and Information Technology

(2)

CHAPTER 7

The variational principle

7.1 Theory

(3)

Suppose you want to calculate the ground-state energy

for a system described by the Hamiltonian , but you are

unable to solve the (time-independent) equation

g

E

..

schr o dinger

H

(4)

7.1 Theory

Theorem:

H

E

_g

≤

Ψ

≡

is any normalized function

That is, the expectation value of in the (presumably

in correct) state is certain to overestimate the ground-state

energy. Of course, if just happens to be one of the excited

states, then obviously exceeds .

H

Ψ

H

E

_g

(5)

Proof

Since the (unknown) eigenfunctions of form a complete

set ,we can express as a linear combination of them:

H

Ψ

, with

n n n n n

n

c H E

Ψ = Ψ Ψ = Ψ

And is normalized,

Ψ

2 *

1

m m n n

m n

m n m n n

m n n

c c

c c c

= Ψ Ψ = Ψ Ψ

(6)

2 *

m m n n

m n

m n n m n n n

m n n

H

c

H

c

c E c

E c

=

Ψ

=

Ψ Ψ

=

Meanwhile,

Since

E

_g

≤

E

_n ,we get

g n

n

g

c

E

H

≥

2

=

(7)

To find the ground-state energy

Aim

Processes

Examples

Processes

Step 1. Select a trial wave function

Step 2. Calculate in this state

Step 3. Minimize the

Step 4. Take as the appropriate ground-state energy

H

Ψ

min

(8)

Example 1. 2 2 2 2 2 1 d

H = − + m

ω

x

To find the ground-state energy for the one-dimensional

harmonic oscillator: ω 2 1 = g E

Of course, we already know the exact answer (see chapter 2):

2

2 2

H m x

m dx

ω

= − +

Pick a Gaussian function as our trial state

2

)

(

x

=

Ae

−bx

Ψ

where is a constant and is determined by normalization:b A

b A dx e A bx 2 1= 2 ∞ 2 2 = 2

π

(9)

The mean value of is

H

( )

2 2 2

2 2

2 ₂ 2 ₂ ₂

2 2 2 1 2 2 = 2 8

bx d bx bx

H A e e dx m A e x dx

m dx b m m b

ω

∞ ∞ − − − −∞ −∞ = − + +

We can get the tightest bound through minimizing withH

respect to :

b

0 8 2 2 2 2 = − = b m m H db d

ω

2

ω

m b =

Putting this back into ,we findH

ω

2 1

min =

(10)

Example 2.

To look for the ground state energy of the delta-function potential:

2 2

2

( )

2

d

H

x

m dx

αδ

= −

−

Again ,we already know the exact answer (see chapter 2):

2

g

b

E α

π

= −

2

m dx

The mean value of is

H

We also Pick a Gaussian function as our trial state:

2

)

(

x

=

Ae

−bx

(11)

2

0

d

a

H

=

−

=

2 2

2

m

α

b

=

Minimizing it,

(

)

2 2 2

2 2

2 2 ₂

2 2 ( ) 2 2 = 2

bx d bx bx

H A e e dx A e x dx

m dx b b m

α

δ

α

π

∞ ∞ − − − −∞ −∞ = − − −

0

2

d

a

H

db

=

m

−

π

b

=

4

2

π

α

m

b

=

2 2 min m H

α

π

= −

which is indeed somewhat higher than

E

_g ,since π > 2

(12)

Example 3.

To find an upper bound on the ground-state energy of

the one-dimension infinite square well, using the “triangular”

trial wave function (figure 7.1):

Figure 7.1: “triangular” trial wave function

for the infinite square well 2

a a x

( )x

(13)

3

2 ₂ ₂ ₂ 2

0

2

1 ( )

12

a _a

a

A x dx a x dx A

= + − =

A

2

3

a

=

Where is determined by normalization:A

In this case

The derivative of this step function is a delta function (see

problem 2.24b)

)

(

)

2

(

2

)

(

2

A

x

A

x

a

A

x

a

dx

d

−

+

−

=

Ψ

δ

(14)

2 2 2 2 2

12 (0) 2 ( ) ( )

2

A _a A

a

= − Ψ − Ψ + Ψ = =

and hence

2

( ) 2 ( ) ( ) ( )

2 2

A _a

H x x x a x dx

m

δ

= − − − + − Ψ

2

(0) 2 ( ) ( ) 2

2m a 2m 2ma

= − Ψ − Ψ + Ψ = =

The exact ground state is ( see chapter 2), so

the theorem works ( )

2 2 2

2

g

E

ma

π

=

2

(15)

write down a trial wave function

The variational principle is very powerful and easy to use

Advantages

Conclusions

Calculate

tweak the parameters to get the lowest possible value

H

Even if has no relation to the true wave function, one

often gets miraculously accurate values for

Ψ

g

(16)

Limitations

It applies only to the ground state

You never know for sure how close you are to the target You never know for sure how close you are to the target

and all you can certain of is that you have got an upper

(17)

7.2

The ground state of helium

Our task

:

To calculate the ground–state energy by using the

Variational Principle

(experimental)

ev 975 .

78

− =

g

E

(18)

[image:18.842.245.596.65.279.2]

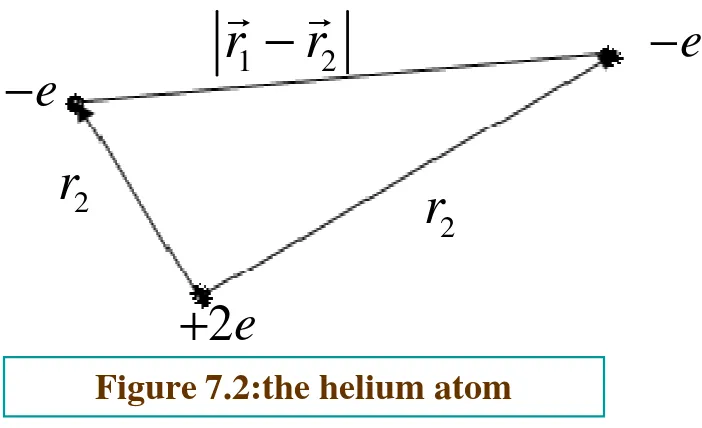
Figure 7.2:the helium atom

2

r

1 2

r

−

r

e

−

e

−

2

r

2

e

+

The Hamiltonian for the helium atom system (ignoring

fine structure and small correction) is

(

)

2 2

1 2

0 1 2 ₁ ₂

2 2 1

2 4

e H

m

πε

r r _r _r

= − ∇ + ∇ − + −

−

2

0 ₁ ₂

1 4

e e

e V

r r

π ε

=

−

(19)

( )

2( 1 2)

0 1 2 100 1 100 2 ₃ 8

, r r a

r r r r e

a

π

− +

Ψ ≡ Ψ Ψ =

Consequently ,the energy that goes with this simplified If we ignore the electron-electron repulsion is, the

ground-state wave function is just

ee

V

where is hydrogen-like wave function with . Ψ₁₀₀ Z = 2

picture is (see Chapter 5 ).8E₁ = −109 ev

(

)

0

8

1 ee 0

H

Ψ =

E

+

V

Ψ

In the following we will apply the variational principle ,

using the as the trial wave function. The eigenfunction of

(20)

Thus

1

8 _ee

H = E + V where

( 1 2)

2 ₄ 2

3 3 1 2 3

0 ₁ ₂

8

4

r r a

ee

e

V

d r d r

a

r

πε

π

− +

=

−

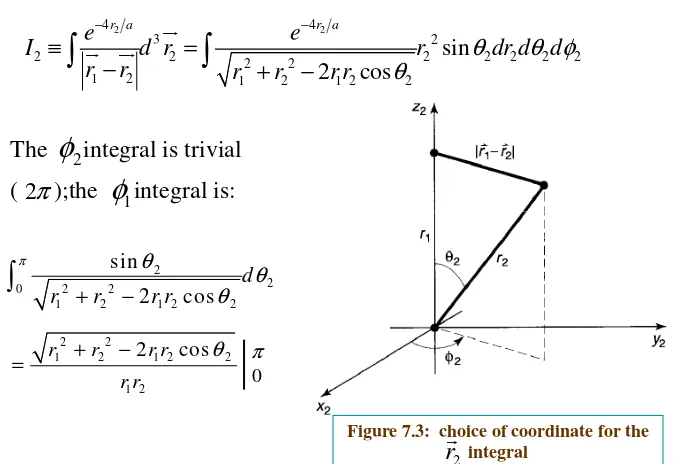
To get the above integral value conveniently, we do the

2

r

integral first and orient the coordinate system so that the

polar axis lies along (see Figure 7.3).

1

r

2

r

By the law of cosines,

2 2

1 2 1 2

2

1 2

cos

2

(21)

and hence

2 2

4 4

3 2

2 2 ₂ ₂ 2 2 2 2 2

1 2 1 2 1 2 2

sin 2 cos

r a r a

e e

I d r r dr d d

r r r r r r

θ θ φ

θ

− −

≡ =

− + −

The integral is trivial

( );the integral is:

[image:21.842.88.766.86.550.2]

2

φ

1

φ

π 2

Figure 7.3: choice of coordinate for the integral 2

r

2 2 2 2 0

1 2 1 2 2

sin

2 cos

d

r r r r

π θ

θ θ

+ −

2 2

1 2 1 2 2

1 2

2 cos

r r r r

(22)

(

)

(

)

2 2 2 2

1 2 1 2 1 2 1 2

1 2

1 2 1 2 1 2

1

2 2

1

r r rr r r rr

rr

r r r r rr

= + + − + −

= + − −

{

1 2 1

2 2 1

2 , if 2 , if

r r r

< >

=

Thus 1 2 2 1

4 2 4

2 2 2 2 2

0 1 3

1

4 r r a r a

r

I e r dr e r dr

r

π

∞ − − = + 1 3 4 1 1 2 1 1 8 r a r a e r a

π

− = − +

It follows that is equal to

V

_ee

1 1

2

4 4

1

1 1 1 1 1 3

0

2 8

1 1 sin

4

r a r a

r e

e e r dr d d

a a

θ

θ φ

πε

π

− −

(23)

2 2

4 8

0

2

5

128

r a

r

r a

a

re

r

e

dr

a

∞

− −

−

+

=

2

1 0

5

34

4

2

ee

e

V

E

ev

a

πε

=

= −

=

Finally , then,

The angular integals are easy( ),and the integal becomes

4

π

r

₁

0

4

a

4

πε

2

109

34

75

H

= −

ev

+

ev

= −

ev

And therefore

(24)

Can we think of a more realistic trial function

than

0

Ψ

(25)

We try the product function

1 2 3

( ) 1

( , )

1 2 ₃

Z r r a

Z

r r

e

a

π

− +

Ψ

≡

and treat Z as a variable rather than setting it equal to 2.

The idea is that as each electron shields the nuclear charge

seen by the other ,the effective Z is less than 2.

In the following, we will treat Z as a variational parameter,

(26)

Rewrite in the following form:

H

(

)

(

) (

)

2 2 2 2 2

1 2

0 1 2 0 1 2 ₁ ₂

2 2 ₁

2 4 4

Z Z

e Z Z e

H

m πε r r πε r r _r _r

− −

= − ∇ + ∇ − + + + +

−

The expectation value of is evidently

H

2

1

e

(

)

2 2

1

0

1

2 2 2

4 ee

e

H Z E Z V

r

πε

= + − +

r

1 1

r

Here is the expectation value of in the (one-particle)

(27)

And according to Chapter 6, we know

1 a

r = Z

The expection value of is the same as before ,except

that instead of ,we now want arbitrary Z—so we

multiply by :

2

=

Z

a

ee

V

multiply by :

a

Z ₂

2

1 0

5 5 8 4 4

ee

Z e Z

V E

a πε

= = −

Putting all this together, we find

(

)(

)

(

)

2 2

1 1

2 4 2 5 4 2 27 4

(28)

The lowest upper bound occurs when is minimized:

H

(

)

1

4 27 4 0

d

H Z E

dZ = − + =

from which it follows that

2 7

1 .6 9

Z = = 1 .6 9 1 6

Z = =

Putting in this value for Z, we find

6 1

1 3

77.5 2 2

H = E = − ev

(29)

7.3

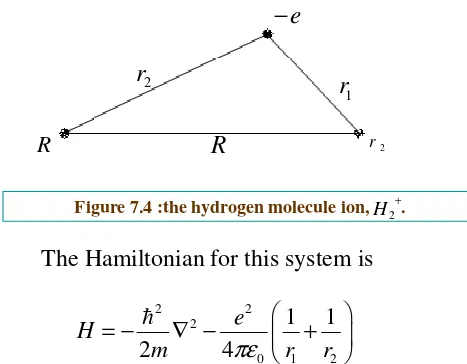
The hydrogen molecule ion

R R r 2

e

−

2

r

1

r

The Hamiltonian for this system is

2 2

2

0 1 2

1 1

2 4

e H

m πε r r

[image:29.842.166.633.130.494.2]

= − ∇ − +

Figure 7.4 :the hydrogen molecule ion, .+

2

(30)

To construct the trial wave function , imagine that the ion is

formed by taking a hydrogen atom in its ground state

a r

g

e

a

r

=

−

Ψ

3

1

)

(

π

and then bringing in proton from far away and nailing it down a

distance R away. If R is substantially greatly than the Bohr radius distance R away. If R is substantially greatly than the Bohr radius

a, the electron’s wave function probably isn’t changed very much.

But we would like to treat the two protons equally ,so that the electron

has the same probability of being associated with either one. So we

consider a trial function of the form

( )

1

( )

2

g g

A r r

(31)

Normalize this trial function:

( )

2

( )

2 ₃ ₂ 2 ₃ ₃ ₃

1 2 1 2

1= Ψ d r = A Ψ_g r d r + Ψ_g r d r + 2 Ψ_g r Ψ_g r d r

( )

2 ₃

1 2

2 A 1 _g r _g r d r

= + Ψ Ψ

( )

1 − r +r

Let

( )

( 1 2) 3

1 2 ₃

1 r r

a

g g

I r r e d r

a

π

− +

≡ Ψ Ψ =

Picking coordinates so that the pronton 1 is at the origin and

proton 2 is on the z-axis at the point R (Figure 7.5),we have

1

r = r 2 2

2 2 cos

(32)

and therefore

2 2

2 cos

2 3

1

sin

r R rR r

a a

I e e r drd d

a

θ

θ θ φ π

+ − − −

=

The integral is trivial ( ).

To do the integral ,let

φ

θ

π

[image:32.842.90.726.111.535.2]

2

Figure 7.5: coordinates for the calculation of I

2 2

2 cos

y ≡ r + R − rR

θ

( )

2

2 2 sin

d y = ydy = rR

θ θ

d

(33)

Then ( )

(

)

(

)

2 2 2 cos 0 1

sin r R

r R rR a y a

r R

r R a r R a

e d e ydy

rR a

e r R a e r R a

rR π θ θ θ + − + − − − − − − + = = − + + − − +

The integral is now straightforward:

r

2 ∞ R

(

)

(

)

(

)

2

2 ₀ ₀ 2

2

R R a r a R a

R a r a R

I e r R a e rdr e R r a rdr a R

e r R a e rdr

∞ − − − ∞ − = − + + + − + + − +

Evaluating the integrals, we find

2

1

1 ( ) (

3

)

R a R R

I e

a a

−

(34)

In the terms of , the normalization factor is

I

2 1 2(1 ) A I = +

Next we must calculate the expectation value of in the

trial state . Noting that

H

Ψ

( )

2 2 2

1 1 1 0 1

1

2 4 g g

e

r E r

m πε r

− ∇ − Ψ = Ψ

Where is the ground-state energy of atomic

hydrogen and the same with in place of ,we have ev

6 . 13

1 = −

E 1

r

2

r

( )

2 2 2 1 2

0 1 2

2

1 1 2

0 2 1

1 1 2 4 1 1 4 g g g g e

H A r r

m r r

e

E A r r

r r

πε

Ψ = − ∇ − + Ψ + Ψ

(35)

It follows that

( )

2 2

1 1 1 1 2

0 2 1

1 1

2

4 g g g g

e

H E A r r r r

r r

πε

= − Ψ Ψ + Ψ Ψ

Calculate the two remaining quantities ,the so-called direct integral,

( )

1

( )

1 2

1

g g

D a r r

r

≡ Ψ Ψ

2

1 R a

a a

D e

R R

−

= − +

1 a R a

X e

R

−

= +

and the exchange integral,

The results are

( )

1

( )

2

1

g g

X a r r

r

(36)

Putting all this together, and recalling that

we conclude that

( )

0 1 0 1 4 2 e E a πε = − 1 ( ) 1 2 (1 ) D X H E I + = + +

This is only the electron’s energy----there is also potential energy

associated with the proton-proton repulsion:

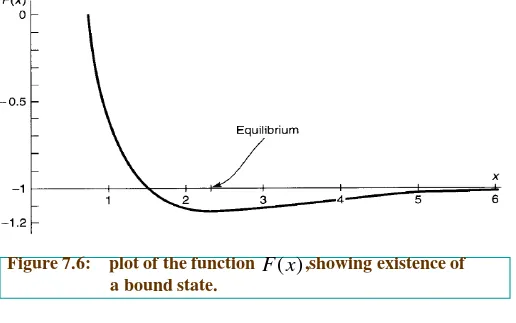
Thus the total energy of the system, in units of

and expressed as a function of ,is less than

1 E − R x a ≡ 2 2 2

2 (1 (2 / 3)

)

(1

)

( )

1

1 (1

(1/ 3)

)

x x

x

x e

F x

x

x e

(37)

[image:37.842.187.703.46.369.2]

Figure 7.6: plot of the function ,showing existence of a bound state.

) (x F

Evidently bonding does occur, for there exists a region in which the graph

goes below -1,indicating that the energy is less than that of a neutral atom plus

a free proton (to wit, ).The Equilibrium separation of the protons is

about 2.4 Bohr radii, or .

ev 6 . 13

−

A