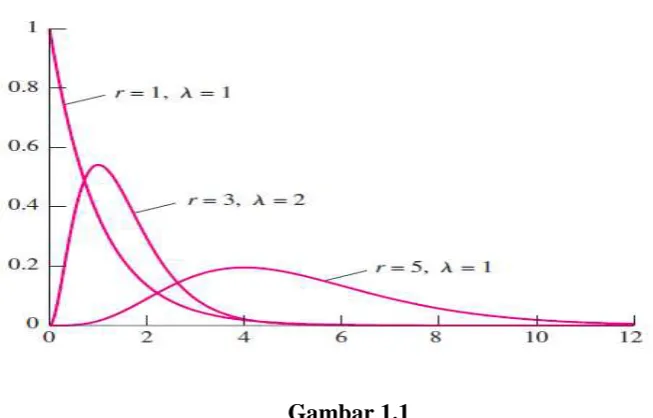
Gambar 1.1
BAB II
LANDASAN TEORI
2.1 Probabilitas Dasar
Andrei Kolgomorov (1903-1987) meletakkan landasan matematis teori peobabilitas dan teori acak. Dalam tulisannya, Kolgomorov menggunakan teori probabilitas dalam mempelajari pergerakan planet dan turbulensi aliran udara. Kontribusi penting lainnya adalah proses stokastik, informasi, mekanika statistik dan dinamika nonlinear.
ke-18, ketika Pierre de Laplace dan Karl F Gauss menggunakan aturan dasar probabilitas terhadap masalah fisis lainnya.
Beberapa definisi dan aksioma yang akan digunakan dalam hal ini berkaitan dengan peristiwa dan probabilitas acak.
Definisi 2.1
Eksperimen adalah suatu proses yang hasil dari keluarannya tidak diketahui secara pasti di mana eksperimen tersebut diasumsikan dapat di ulang dalam suatu waktu dan dibawah kondisi yang identik. Setiap pengulangan disebut sebagai repetisi. Eksperimen acak memenuhi tiga keadaan berikut:
a) Himpunan seluruh keluaran tidak diketahui pasti dalam tiap percobaan. b) Dalam kedaan khusus, tidak diketahui keluaran mana yang akan terjadi. c) Eksperimen dapat diulang dengan keadaan yang mirip.
2.2 Peubah Acak
Suatu eksperimen memuat sejumlah karakteristik yang terukur. Tetapi peneliti pada umumnya berkonsentrasi pada beberapa karakteristik tertentu pada suatu eksperimen. Apakah pada nilai karakteristik di sekitar pusat data atau pada penyebaran data. Pengelompokan keluaran suatu eksperimen diwakili oleh bilangan sederhana bertujuan untuk memudahkan deskripsi. Deskripsi tersebut diperlukan, tetapi di lain kasus hal itu berguna untuk menyatakan suatu bilangan sebagai perwakilan suatu keluaran di ruang sample.
Definisi 2.2
Peubah acak adalah seluruh nilai bernilai riil yang tiap-tiap nilainya diasosiasikan dengan keluaran dari suatu eksperimen acak.
2.2.1 Peubah Acak Diskrit
Jika himpunan seluruh nilai yang mungkin dari peubah acak � adalah suatu himpunan yang dapat dicacah sedemikian rupa, �1, �2, �3, … ,�� atau �1,
�2, �3, … sehingga X disebut sebagai variabel acak diskrit. Bagi suatu peubah acak diskrit �, didefinisikan fungsi massa peluang ��(�) sebagai:
��(�) =�(�=
�) 2.
Fungsi massa peluang �(�) bernilai positif , untuk sejumlah nilai � tercacah. Dengan kata lain, jika � mengambil salah satu dari nilai�1,�2, … maka peubah acak diskrit X dengan nilai yang mungkin �1, �2, �3, … ,�� fungsi massa peluang adalah fungsi yang memenuhi kriteria berikut:
1). �(��)≥0, �= 1,2, …
2). � �(��)
�
�=1
= 1
3). �(��) =�(�= ��)
2.2.2 Peubah Acak Kontinu
Definisi 2.5
Suatu peubah acak � berdistribusi kontinu jika terdapat fungsi � taknegatif, terdefinisi pada garis bilangan riil, sehingga setiap interval pada bilangan riil (berbatas atau tak berbatas), probabilitas bahwa X yang berada pada interval tersebut merupakan jumlahan daerah f pada interval tersebut. Sebagai contoh, keadaan yang menggambarkan definisi diatas, dengan batas dalam interval tertutup [�,�].
�(� ≤ � ≤ �) =∫ ��� (�)��
�(� ≥ �) =∫ ��∞ (�) dan �(� ≤ �) =
∫ �−∞� (�)�� 2.2
Berdasarkan karakteristik f distribusi variabel acak kontinu dengan cara yang sama menyatakan bahwa fungsi probabilitas berkarakteristik distribusi peubah acak kontinu. Fungsi kepadatan peluang � dapat digunakan untuk menggambarkan distribusi probabibilitas peubah acak kontinu. Jika suatu interval memuat kemiripan nilai X, probabilitasnya besar dan berkorespondensi dengan
�(�). Memenuhi ketiga kaidah berikut:
1). �(�)≥ 0
2). � �(�) �� = 1
∞
−∞
3). �(� ≤ � ≤ �) = � �(�) ��
�
�
Distribusi probabilitas adalah visualisasi peubah acak � dalam bentuk kurva. Ketika � merupakan peubah acak berbatas, himpunan probabilitas yang digambarkan terhadap nilai yang mungkin disebut distribusi probablitas �.
Jika � adalah peubah acak berbatas, dengan nilai-nilai �1,�2, …
maka daftar
distribusi probabilitas berkaitan dengan
�= �1, �= �2, …. Jumlah seluruh probabilitas selalu sama dengan 1.Ingat bahwa � merupakan variabel acak, sedangkan � merupakan nilai spesifik dari variabel acak �. Berakibat jika �= 2 maka probabilitas �(�=�) berarti
�(�= 2), probabilitas bahwa � adalah 2. Hal yang sama jika � merupakan peubah acak maka �(�=�) probabilitas � dengan nilai khusus �.
Dalam suatu pengukuran eksperimen, hasil pengukuran eksperimen seringkali menghasilkan variasi. Ukuran-ukuran yang menggambarkan karakteristik sampel berkorespondensi dengan karakteristik populasi. Secara sederhana karakteristik tersebut digambarkan sebagai nilai harapan atau lebih dikenal dengan mean. Secara matematis dinyatakan oleh formula berikut:
1). Peubah acak diskrit
�� =�[�]
=� ���(��)
�
�=1
2.3
2). Peubah acak kontinu
�� =�[�]
= � ��(�)��
∞
−∞
2.4
Sifat-sifat nilai ekspektasi 1. �[�] =�
2. �[��+�] =��[�] +�
3. �[�1+⋯+��] =�[�1] +⋯+�[��]
4. �[�(�,�) ± h(�,�)] = �[�(�,�)] ± E[h(�,�)]
5. �[�(�) ± h(�)] =�[�(�)] ± E[h(�)]
6. �(�.�) =�(�) E(�)
Bukti sifat 1.
Pada peubah acak kontinu berlaku;
�[�] = � ��(�)��
∞
−∞
�[�] =�
Sustitusi �= � maka �[�] =∫ ��−∞∞ (�)�� , karena b merupakan konstanta berlaku
�[�] =� � �(�)��
∞
� �(�)��
∞
−∞
= 1
�[�] =�
Bukti sifat 5.
�[�(�) ± h(�)] =�[�(�)] ± E[h(�)]
�[�] = � ��(�)��
∞
−∞
Substitusi Y = �(�) ± h(�) �[�] = � ��(�)��
∞
−∞
= �[ �(�) ± h(�)]�(�)��
∞
−∞ Berlaku
�[�] = � �[�]�(�)��± � ℎ[�]�(�)��
∞
−∞ ∞
−∞
�[�(�) ± h(�)] = � �[�]�(�)��± � ℎ[�]�(�)��
∞
−∞ ∞
−∞
�[�(�) ± h(�)] =�[�(�)] ±�[ℎ(�)]
2.3.2 Varians.
Pengukuran suatu variabel memungkinkan untuk mempermudah pemahaman mengenai suatu data. Untuk mengetahui seberapa besar tingkat variabilitas sampel yang berhubungan dengan populasi dinyatakan didefinisikan oleh
Var[X] =�[(� − �)2], secara jelas diperlihatkan oleh: 1). Variabel acak diskrit
�2
� = Var[X] = �(� �
�=10
− �)2�(��) 2.5
�2
� = Var[X] = �(�
∞
−∞
− �)2�(�)�� 2.6
Varians untuk kasus kontinu dapat dijabarkan sebagai berikut
Var[X] = �[(� − �)2]
Var[X] = �(� − �)2�(�)�� ∞
−∞
= �(�2−2��+�2)�(�)��
∞
−∞
= � �2�(�)�� −2� � ��(�)��+�2 � �(�)��
∞
−∞ ∞
−∞ ∞
−∞
Var[X] = �[�2]−2��[�] +�2
Karena �=�[X] maka diperoleh:
Var[X] =
�[�2]−(�[X])2 2.7 Sifat-sifat varians:
1. Var[c] = 0
2. Var[�X] =�2 Var[X]
3. Var[X + c] = Var[X]
4. Var[X1+⋯+ X�] = Var[X1] +⋯+ Var[X�]
Jika � adalah sebuah fungsi dan � merupakan satu titik interior pada domain �. Jika � memiliki nilai maksimum atau minimum lokal di �, maka
�′(�) = 0 atau �′(�) tidak ada
2.8
Teknik pengintegralan parsial
�
��[�(�)�(�)]
=�(�)�′(�)
+�(�)�′(�) 2.9
Misalkan
�= �(�) dan �= �(�)
��=�′(�) dan ��= �′(�)��
Persamaan 2.9 menjadi
� ��[��]
=�′�
+��′
Perhatikan persamaan (2.9) untuk memperoleh formula integral parsial, ruas kiri dan kanan dilakukan pengintegralan, sehingga diperoleh:
���� [�(�)�(�)] =� �(�)�′(�)��+� �(�)�′(�)��
� �′(�)�(�)��+� �(�)�′(�)��= �(�)�(�)
� �(�)�′(�)��= �(�)�(�)
� ���
= �� − � ��� 2.10
Definisi improper integral tipe-I
(a) Jika ∫ ��� (�)�� ada untuk setiap bilangan � ≥ �, maka;
� �(�)��
∞
�
= lim
�→∞� �(�)�� �
�
Menyatakan bahwa limit tersebut eksis.
(b) Jika ∫ ��� (�)�� eksis untuk setiap bilangan � ≤ �, maka
� �(�)��
�
−∞
= lim
�→−∞� �(�)�� �
�
Menyatakan limit tersebut eksis
Improper integral ∫ ��∞ (�)�� dan ∫ �−∞� (�)�� dikatakan konvergen jika limit yang dikaitkan ada dan divergen jika limitnya tidak ada.
(c) Jika ∫ ��∞ (�)�� dan ∫ �−∞� (�)�� konvergen, maka didefinisikan:
� �(�)��= � �(�)��
�
−∞ ∞
−∞
+� �(�)��
∞
�
2.4.1 Distribusi dan Fungsi Gamma
Andaikan suatu peristiwa Poisson terjadi dengan konstanta rate � per unit waktu. Misalkan variabel acak X menyatakann sebagai waktu tunggu kejadian ke− �. Maka X memiliki pdf ��(�), di mana
��(�) = �
�
(�−1)!�
�−1�−� ,
Pembuktian formula untuk ��(�) dilakukan dengan mendifferensialkan fungsi
Untuk memperoleh fungsi padat peluannya maka fungsi kumulatif pada kejadian yang berlangsung dalam interval [0, x] adalah variabel acak Poisson dengan
parameter λx, diturunkan terhadap x, diperoleh fungsi padat peluang sebagai
berikut
Berdasarkan aturan differensial dari perkalian dua buah fungsi pada persamaan
=��
Diberikan bilangan riil r > 0 dan λ > 0, peubah acak X dikatakan sebagai fungsi gamma pdf dengan parameter r dan λ jika:
Beberapa pembuktian fungsi gamma untuk membantu penurunan rumus dalam distribusi gamma. Mula-mula akan dicari nilai dari Γ�1
2�, substitusi nilai �=
= −∞3�−∞ + 03�−0+ 3 lim
Akan dicari formula ke-r untuk fungsi gamma sebagai berikut:
Pada persamaan terakhir diketahui bahwa nilai terakhir adalah perkalian berulang menurun maka untuk nilai �> 1 maka gamma � menjadi:
Γ(�) = (� −1)(� −2)(� −3){Γ(� −3)}
Γ(�) = (� −1)Γ(� −1)
Γ(�) = (� −1)(� −2)(� −3) … 3.2.1
Γ(�) = (� −1)!, di mana �> 1
Γ(�+ 1) = �Γ(�) =�! Γ(�) =Γ(�+ 1)
�
Γ(�) = Γ(�+�)
�(�+ 1) … (�+� −1) �+� > 0 �! = (�+�)!
(�+ 1)�
di mana (�+ 1)� =�(�+ 1) … (�+� −1) untuk � > 0
�! =�! (�+ 1)� (�+ 1)� =
�!�� (�+ 1)�
(�+ 1)� ��
lim
�→∞
�!��
(�+ 1)� = lim�→∞
�!��
�(�+ 1) … (�+� −1)
Diperoleh identitas
Γ(�) = lim
�→∞
�!��
�(�+ 1) … (�+� −1)
Identitas Weierstrass
�!��
�(�+ 1) … (�+� −1)
=�����(�)−1−
1 2−
1 3−⋯−
1 ��1
� ��1
1 +�/1 ��2
1 +�/2⋯ ���
lim
Kedua ruas dilogaritmakan diperoleh
��{Γ(�)} =−log(�)− γ�+� �� dinotasikan oleh ψ(�) untuk suatu bilangan bulat tak nol atau negatif dinyatakan dalam turunan logaritma Γ(�)
Estimator dalah kuantitas yang didasarkan dari observasi sampel yang nilainya diambil
sebagai indikator dari nilai parameter populasi yang tidak diketahui (sebagai contoh, rata-rata
parameter tak diketahui yang memiliki nilai dalam himpunan yang disebut ruang parameter.
Dalam estimasi, sampel acak diambil dari distribusi untuk memperoleh beberapa informasi dari parameter tak diketahui. Dilakukan perulangan sebanyak
� eksperimen independen, sampel observasi �1,�2, … ,�� dan lakukan pendugaan nilai parameter menggunakan observasi �1,�2, … ,��. Fungsi
�1,�2, … ,�� digunakan menduga nilai parameter, statistik �(�1,�2, … ,��) disebut sebagai penduga parameter yang dicari. Perhitungan �(�1,�2, … ,��) dilakukan mendekati nilai parameter sebenarnya. Karakteristik populasi oleh bilangan tunggal berdasarkan pada sampel data dan mewakili nilai yang menggambarkan karakteristik populasi disebut dugaan titik.
2.5.1 Moments Estimator (MMes)
Definisi 2.9
Secara sederhana estimasi � parameter berdasarkan metode momen adalah dengan menyamakan momen populasi dengan momen sampel yang bersesuaian, dituliskan oleh:
�
�1 = �1
�2 = �2
⋮ �� = ��
Persamaan di sisi sebelah kiri bergantung kepada distribusi parameternya. Persamaan di sisi sebelah kanan dapat dihiting berdasarkan data yang digunakan. Momen populasi ke− � didefinisikan sebagai
�� = E(��) Momen sampel ke− � disefinisikan oleh:
�� =
1 n� ��
� n
i=1
Misalkan �1, �2, … ,�� adalah peubah acak kontinu dan ��(�) merupakan fungsi padat peluang dengan � parameter tidak diketahui,
�1,�2, … ,��. Momen � pertama peubah �, jika ada diberikan oleh integral berikut:
�����= � �∞ � −∞ ��
(�,�1,�2, … ,��)��, �= 1,2, … ,�
Momen sampel ke− � merupakan aproksimasi terhadap moment teoretis ke− �.
Metode momen mengestimasi parameter tidak diketahui
��1,��2, … dan ��� terhadap model yang parameternya tidak diketahui adalah penyelesaian dari � persamaan simultan
� ���(�,�1,�2, … ,��)��=�
1 ��
∞
−∞
� �� �
�=1
� �2��(�,�1,�2, … ,��)��= �1 ��
∞
−∞
� ��2 �
�=1
⋮ ⋮
� ���
�(�,�1,�2, … ,��)��= �
1 ��
∞
−∞
� �� �
�=1
Peubah acak diskrit dengan pmf ��(�:�1,�2, … ,�� ) metode momen mengestimasi penyelesaian persamaan simultan
� �� �
��(�:�1,�2, … ,��) =�
1
�� � �� �
2.5.1.1 Prosedur Metode Moments
Tahapan pendugaan metode moments melibatkan tiga langkah dasar berikut ini: Misalkan terdapat � paramerter yang akan diestimasi, msalkan �= (�1, … ,��).
2. Tentukan hubungkan � momen sampel , ��, � = 1, 2, … ,�.
Banyaknya sampel moment harus sama banyak dengan parameter yang akan di estimasi.
3. Dari sistem persamaan, �� = ��, � = 1, 2, … ,�, selesaikan parameter
� = (�1, … ,��) yang merupakan penduga momen untuk ��.
2.5.2 Maximum Likelihood Estimation (MLE)
Definisi 2.6
Misalkan �1,�2, … ,�� merupakan sampel acak berukuran n dengan variabel acak diskrit pmf ��(�,�), di mana �(�1,�2, … ,��) adalah parameter tidak diketahui. Fungsi likelihood, L(θ), adalah perkalian pmf yang dikaitkan dengan n ke-k.
�(�) =�(�1 = �1, … ,�� =��)
�(�) =� �(�� = ��)
�
�=1
�(�) =� ��(��:�)
�
�=1
Andaikan �1,�2, … ,�� adalah sampel acak berukuran n dari pdf kontinu,
��(�,�) di mana �(�1,�2, … ,��) merupakan parameter tak diketahui, fungsi likelihood dituliskan:
�(�) =�(�1 =�1, … ,�� = ��)
�(�) =�(�1;�1,�2, … ,��).�(�2;�1,�2, … ,��) … .�(��;�1,�2, … ,��) Pandang sebagai fungsi �1,�2, … ,�� , disebut sebagai fungsi likelihood. Misalkan
[�1( �1,�2, … ,��), �2 ( �1,�2, … ,��), … ,��( �1,�2, … ,��)] Adalah tupel-k yang memaksimalkan � ( �1,�2, … ,�� ) sehingga:
��2 = �2(�1,�2, … ,��)
��3 = �3(�1,�2, … ,��)
⋮
��� = ��(�1,�2, … ,��)
Adalah penduga kemungkinan maksimum dari �1,�2, … ,��. Secara umum dapat dituliskan sebagai berikut
�(�) =� ��(��,�)
�
�=1
2.5.2.1 Prosedur untuk menentukan MLE
1. Definisikan Fungsi Likelihood, �(�). 2. Gunakan logaritma natural, ln[�(�)].
3. Ketika diterapkan, differensialkan ln[�(�)] terhadap �, dan samakan dengan nol.
4. Selesaikan parameter � dan akan diperoleh ��.
2.5.3 Sifat-sifat estimator
Sifat yang diharapkan dari sebuah penduga adalah bahwa penduga tersebut berada sedekat-dekatnya dengan nilai sebenarnya parameter yang tidak diketahui. Bila diperhatikan mean bukanlah satu-satunya lokasi yang mungkin parameter dimana parameter berada.. Untuk praktisi statisi, pertanyaan penting adalah mendapatkan sampel statistik seperti mean, median, observasi terkecil atau obeservasi terbesar, sebaiknya dipilih mempersentasikan seluruh sampel. Untuk memahami matematika pendugaan, maka pertama-tama ingat bahwa setiap penduga adalah fungsi dari sekelompok peubah acak
Estimator tidak bias adalah estimator yang nilai harapannya sama dengan nilai sesungguhnya dari parameter yang akan ditaksir.
Didefinisikan sebagai berikut
Andaikan �� merupakan estimasi titik untuk suatu parameter �. Maka �� disebut sebagai estimator tidak bias apabila �����= �. Jika ����� ≠ �, maka �� dikatakan bias. Bias suatu penaksir titik �� diberikan oleh �����= ����� − �.
2. Efisien
Jika distribusi Sampling dari dua buah statistik mempunyai mean atau ekspektasi yang sama, maka statistik varians yang lebih kecil disebut sebagai estimator efisien dari mean, sementara statistik yang kedua adalah estimator tak efisien. Nilai dari kedua statistik masing-masing disebut estimasi efisien dan estimasi tak efisien. Dan dinotasikan andaikan bahwa ��1 dan ��2 adalah dua penduga takbias untuk parameter �. suatu penduga adalah efisien terhadap � apabila penduga memiliki varians yang lebih kecil.
Ef(��2 ,��1) =
��� (��1) ��� (��2)
Ef���2 ,��1� =
E���1− �� 2
E���2− ��2
Ef���2 ,��1� =
E���1− ����1�� 2
E���2− ����2�� 2
Jika �� > 1 maka ��1 >��2 artinya secara relative ��2 lebih efisien daripada
��1, dan jika �� < 1 maka ��1 < ��2 secara relative ��1 lebih efisien daripada
��2.
3. Konsisten
meskipun ukuran sampel semakin lama semakin besar.
Suatu penduga dikatakan konsisten jika memenuhi syarat berikut:
1. Jika ukuran sampel bertambah maka penduga akan mendekati nilai parameter sebenarnya. Jika sampel menjadi tak terhingga maka penduga konsisten harus dapat memberi suatu titik yang sempurna terhadap parameternya. Sehingga, ��� � merupakan penduga konsisten, jika dan hanya jika:
� �θ� −E(θ)�2 →0 ������� → ∞