Informasi Dokumen
- Penulis:
- Putri Oktalinda Muttaqina
- I Nengah Adi Mahendra
- Ni Putu Amellia Artika
- I Putu Hendra Setiawan
- Ni Wayan Karmila Putri
- Made Arista Dewi
- I Dewa Made Agus Ariawan
- Ni Putu Ayu Novia Dewi
- Kadek Gede Doni Merta Marantika
- Ni Putu Eka Sucipta Dewi
- I Wayan Kumarayasa
- I Made Adi Wira Nata Putra
- Ni Ketut Indah Tiara
- Ni Luh Sinta Suryanti
- A.A. Gede Surya Pujawan
- Ni Wayan Dina Marziani
- Ni Kadek Rita Sri Utami
- Ni Putu Mirnawati
- Pengajar:
- Dr. Gede Suweken, M.Sc.
- Sekolah: Universitas Pendidikan Ganesha
- Mata Pelajaran: Pendidikan Matematika
- Topik: Gema Lomba Matematika (GLM) Untuk SMP Edisi 7
- Tipe: buku
- Tahun: 2013
- Kota: Singaraja
Ringkasan Dokumen
I. TEORI BILANGAN
Bab ini membahas konsep dasar teori bilangan yang penting untuk memahami keterbagian, bilangan kuadrat, dan teorema-teorema penting dalam matematika. Keterbagian menjelaskan hubungan antara dua bilangan, sedangkan bilangan kuadrat membahas sifat-sifat bilangan yang merupakan hasil kuadrat dari bilangan bulat. Teorema Eratosthenes dan kongruensi juga dibahas untuk memberikan pemahaman lebih dalam mengenai bilangan prima dan sifat-sifatnya. Materi ini sangat relevan untuk mencapai tujuan pendidikan matematika, yaitu mengembangkan kemampuan berpikir logis dan analitis siswa.
1.1 Keterbagian
Keterbagian merupakan konsep yang mendasar dalam teori bilangan. Suatu bilangan a disebut membagi b jika terdapat bilangan bulat c sehingga b = ac. Sifat-sifat keterbagian seperti sifat refleksif dan transitif sangat penting dalam membangun pemahaman lebih lanjut tentang bilangan. Pemahaman ini membantu siswa dalam menyelesaikan masalah yang berkaitan dengan pembagian, yang merupakan bagian penting dari kurikulum matematika di SMP.
1.2 Bilangan Kuadrat
Bilangan kuadrat adalah bilangan yang diperoleh dari hasil kuadrat suatu bilangan bulat. Dalam bagian ini, siswa diperkenalkan pada sifat-sifat bilangan kuadrat, termasuk angka satuan yang mungkin dan sifat pembagian. Pengenalan ini sangat penting dalam pengembangan kemampuan siswa untuk mengenali pola dan hubungan dalam bilangan, yang merupakan keterampilan dasar dalam matematika.
1.3 Teorema Eratosthenes
Teorema ini menjelaskan cara untuk menentukan bilangan prima. Dengan menggunakan metode penyaringan, siswa belajar untuk mengidentifikasi bilangan yang tidak dapat dibagi oleh bilangan prima lainnya. Ini adalah langkah awal yang penting untuk memahami konsep bilangan prima dan aplikasinya dalam teori bilangan.
1.4 Kongruensi
Kongruensi adalah konsep yang menunjukkan bahwa dua bilangan memiliki sisa yang sama ketika dibagi oleh bilangan tertentu. Pembelajaran tentang kongruensi membantu siswa memahami hubungan antar bilangan dan memperkenalkan mereka pada konsep yang lebih kompleks dalam matematika, seperti sistem bilangan modular.
1.5 FPB dan KPK
Faktor Persekutuan Terbesar (FPB) dan Kelipatan Persekutuan Kecil (KPK) adalah konsep penting dalam teori bilangan. Pembahasan ini mencakup metode untuk mencari FPB dan KPK, yang sangat berguna dalam menyelesaikan masalah yang melibatkan pembagian dan perkalian bilangan. Keterampilan ini sangat diperlukan dalam konteks pendidikan matematika di SMP.
1.6 Teorema Dasar Aritmatika
Teorema ini menyatakan bahwa setiap bilangan bulat positif dapat dinyatakan sebagai produk dari bilangan prima. Memahami teorema ini adalah kunci untuk penguasaan konsep faktorisasi, yang merupakan bagian penting dari aljabar dan teori bilangan.
1.7 Persamaan Diophantine
Persamaan Diophantine adalah persamaan yang mencari solusi dalam bilangan bulat. Pembelajaran tentang ini memperkenalkan siswa pada konsep solusi dari persamaan linear dan aplikasinya dalam konteks nyata. Ini juga meningkatkan kemampuan siswa dalam berpikir kritis dan analitis.
1.8 Induksi Matematika
Induksi matematika adalah teknik pembuktian yang digunakan untuk menunjukkan bahwa suatu pernyataan benar untuk semua bilangan bulat positif. Memahami induksi matematika membantu siswa dalam mengembangkan kemampuan berpikir logis dan sistematis, yang sangat penting dalam studi matematika.
II. ALJABAR
Bab ini membahas konsep-konsep dasar aljabar, termasuk persamaan polinom, ketaksamaan, dan nilai mutlak. Pemahaman yang kuat tentang aljabar sangat penting untuk mencapai hasil belajar yang diinginkan dalam pendidikan matematika, karena aljabar adalah fondasi bagi banyak konsep matematika yang lebih kompleks.
2.1 Persamaan Polinom
Persamaan polinom berderajat n adalah bentuk umum yang digunakan dalam aljabar. Pemahaman tentang akar-akar polinom dan sifat-sifatnya membantu siswa dalam menyelesaikan berbagai masalah aljabar. Teorema Vieta juga diperkenalkan untuk menghubungkan akar-akar polinom dengan koefisiennya, yang merupakan konsep penting dalam studi aljabar.
2.2 Ketaksamaan
Ketaksamaan adalah konsep yang membandingkan dua nilai dan menentukan hubungan antara mereka. Sifat-sifat dasar ketaksamaan sangat penting dalam menyelesaikan masalah yang melibatkan nilai-nilai yang tidak sama. Pembelajaran ini membantu siswa memahami konsep limit dan interval dalam aljabar.
2.3 Nilai Mutlak
Nilai mutlak adalah ukuran jarak dari nol pada garis bilangan. Memahami nilai mutlak dan sifat-sifatnya membantu siswa menyelesaikan masalah yang melibatkan jarak dan perbandingan, yang merupakan keterampilan penting dalam matematika.
2.4 Barisan dan Deret Bilangan
Barisan dan deret adalah konsep yang menggambarkan urutan bilangan. Siswa belajar tentang barisan aritmatika dan geometri, serta rumus untuk menghitung suku ke-n dan jumlah n suku pertama. Pemahaman ini sangat penting dalam analisis data dan pemecahan masalah.
2.5 Identitas Aljabar
Identitas aljabar adalah persamaan yang selalu benar untuk semua nilai variabel. Memahami identitas ini membantu siswa dalam menyederhanakan ekspresi aljabar dan menyelesaikan persamaan, yang merupakan keterampilan dasar dalam aljabar.
III. GEOMETRI
Bab ini membahas konsep dasar geometri, termasuk sudut, segitiga, dan lingkaran. Pemahaman yang kuat tentang geometri sangat penting untuk mencapai hasil belajar yang diinginkan dalam pendidikan matematika, karena geometri adalah bagian penting dari banyak aplikasi matematika di dunia nyata.
3.1 Sudut
Pembelajaran tentang sudut mencakup definisi, sifat-sifat, dan cara menghitung besar sudut dalam berbagai bangun datar. Memahami sudut adalah dasar untuk belajar tentang segitiga dan bentuk geometri lainnya.
3.2 Segitiga
Segitiga adalah bentuk dasar dalam geometri. Konsep dasar seperti sifat-sifat segitiga, luas, dan keliling dibahas untuk memberikan pemahaman yang mendalam. Ini juga mencakup teorema-teorema penting seperti Teorema Pythagoras.
3.3 Kongruensi
Kongruensi segitiga adalah konsep yang menunjukkan kesamaan bentuk dan ukuran. Siswa belajar tentang syarat-syarat kongruensi, yang penting dalam membuktikan sifat-sifat segitiga dan bentuk geometri lainnya.
3.4 Kesebangunan
Kesebangunan segitiga adalah konsep yang menunjukkan bahwa dua segitiga memiliki sudut-sudut yang sama dan sisi-sisi yang sebanding. Ini penting untuk memahami proporsi dan aplikasi dalam geometri.
3.5 Lingkaran
Lingkaran adalah bentuk dasar dalam geometri. Pembelajaran tentang sifat-sifat lingkaran, panjang dan luasnya sangat penting dalam memahami konsep geometri yang lebih kompleks.
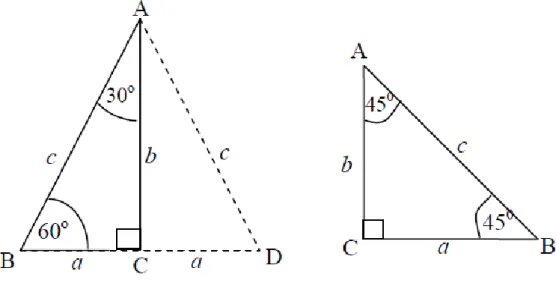
3.6 Trigonometri
Trigonometri membahas hubungan antara sudut dan sisi dalam segitiga. Pemahaman tentang fungsi trigonometri dan sudut-sudut khusus sangat penting dalam aplikasi matematika di bidang teknik dan sains.