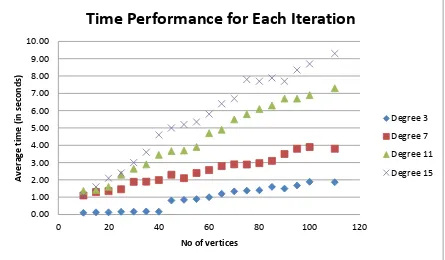
applicating cvd algorithm edge coloring special graphs
Teks penuh
Gambar
Dokumen terkait
Berdasarkan uraian di atas, perlu dilakukan penelitian ini untuk mengetahui Konsentrasi Hambat Minimun (KHM) minyak atsiri daun jeruk sambal ( Citrus microcarpa Bunge),
Seperti kebakaran lahan yang terjadi di Desa Pakning Asal Kabupaten Bengkalis, dalam 5 tahun terakhir dari hasil survey pada tanggal 28 Januari, lahan perkebunan
a) Membagi kuota dengan merujuk kepada persentasi zakat yang masuk dari kecamatan. b) Menurunkan surat kepada OPZ Kecamatan yang telah di setujui oleh pimpinan. c)
Penelitian ini bertujuan untuk melihat dan menjelaskan bagaimana pengaruh antara Disperinaker dan IKM dari faktor sosial, budaya, teknologi, waktu dan geografis terhadap
Aku dibesarkan dalam keluarga yang nomaden, Papa bekerja di perminyakan, kerjanya berpindah-pindah dari satu kota ke kota lainnya. Akibatnya, Papaku cenderung keras terhadap
As a result, the constellation can do the moving target identification work using the DRC mode on-board each satellite, and then estimate the true velocities of
Jumlah saham yang ditawarkan 600.000.000 Saham Biasa Atas Nama dengan nilai nominal Rp 100,- /saham Penjamin Pelaksana PT MANDIRI SEKURITAS, PT OSK NUSADANA SECURITIES
Dengan adanya pembangunan Hotel The Rayja yang dibangun diatas sumber mata air Umbul Gemulo memunculkan gerakan FMPMA, kemunculan gerakan FMPMA disebabkan oleh