UJI MODEL REGRESI.docx

UJI MODEL REGRESI

(Kajian lanjutan dari tugas kelompok 2 tentang Analisis Regresi)

A. Uji Regresi Linear Sederhana

1) Uji Signifikansi Regresi Linear Sederhana

Untuk menguji signifikansi dari suatu regresi maka perlu dihitung Jumlah Kuadrat (sum square) dan Rata-rata Jumlah Kuadrat (mean square) dari berbagai sumber variasi seperti Regresi a, regresi (b׀a), dan residu.

Dengan demikian pengujian terhadap signifikansi atau keberartian regresi

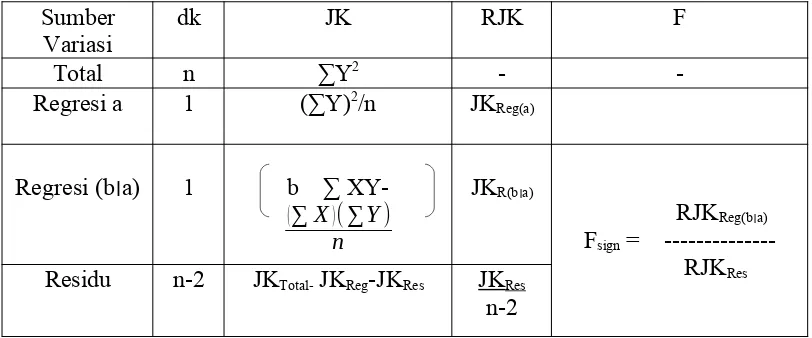
membutuhkan JK Regresi a, JK Regresi (b׀ a), JK Residu, dan JK Total. Tiap-tiap JK memiliki derajat kebebasan (dk) tersendiri, dan jika masing-masing JK dibagi oleh derajat kebebasannya maka diperoleh Rata-rata Jumlah Kuadrat (RJK). Untuk lebih jelasnya, nilai-nilai tersebut dapat dimasukkan ke dalam tabel analisis varians (ANAVA) berikut:

Tabel 9

Analisis Varians (ANAVA) Untuk Pengujian Signifikansi Regresi linear Sederhana Ŷ = 38,43 + 0,68X signifikan atau tidak. Sehubungan dengan itu kita membutuhkan nilai-nilai yang sudah tersedia dalam Tabel 3 di atas.

Nilai-nilai tersebut kemudian dimasukkan dalam rumus-rumus dalam Tabel 9 di atas sehingga diperoleh hasil sebagai berikut:

JKTotal = ∑Y2 _{= 117781}

JKReg a = (∑Y)2_{/n = (1525)}2_{/20 = 116281,25}

JKReg(b׀a) = b ∑ XY- (∑ X)_n(∑Y) = 0,68 86211 - (1114₂₀x1525) = 862,58

JKRes = JK(T) - JK(a) – JK(b׀a) = 117781 – 116281,25 – 862,58 = 637,13

RJKReg a = JKReg a = 116281,25 RJKReg(b׀a) = JKReg(b׀a) = 862,58

JKRes 637,13 637,13

RJKRes = --- = --- = --- = 35,396 = 35,4 n – 2 20 – 2 18

RJKReg(b׀a) 862,58

Fsign = --- = --- = 24,37 RJKRes 35,4

Nilai F hitung ini kemudian dibandingkan dengan nilai F tabel dengan dk pembilang = 1 dan dk penyebut = 18 pada taraf nyata α = 0,05 adalah 4,41 dan pada taraf nyata α = 0,01 adalah 8,28.

Kriterianya, jika nilai F hitung lebih besar daripada F tabel baik pada taraf nyata α = 0,05 maupun pada taraf nyata α = 0,01 maka regresi dikatakan signifikan. Karena nilai F hitung = 24,37 lebih besar dari F tabel maka regresi signifikan. Ternyata nilai F hitung lebih tinggi daripada nilai F tabel sehingga regresi sangat signifikan.

2) Uji Linearitas Regresi Linear Sederhana

JKтc = JKRes – JKE (1)

JKE = ∑ ∑Yi2 _{– (∑Yi)}2 ₍₂₎ x ni

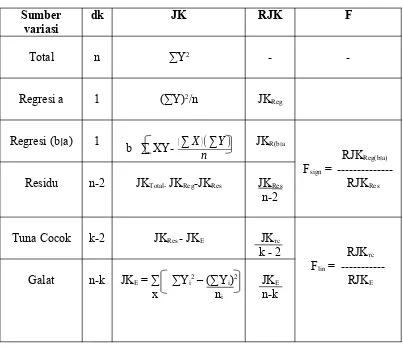
Untuk memudahkan perhitungan maka nilai-nilai ini dapat dimasukkan ke dalam tabel ANAVA dengan menggunakan Tabel 9 di atas.

Tabel 10

Analisis Varians untuk Pengujian Linearitas Regresi Linear Sederhana

Sumber

variasi dk JK RJK F

Total n ∑Y2 _-

-Regresi a 1 (∑Y)2_{/n JKReg}

Regresi (b׀a) 1 _{b ∑ XY-} (∑ X)(∑Y)

n JKR(b׀a RJKReg(b׀a) Fsign =

RJKRes Residu n-2 JKTotal- JKReg-JKRes JKRes

n-2

Tuna Cocok k-2 JKRes - JKE JKтc

k - 2 RJKтc Flin =

RJKE Galat n-k JKE = ∑ ∑Yi2 _{– (∑Yi)}2

x ni JKEn-k

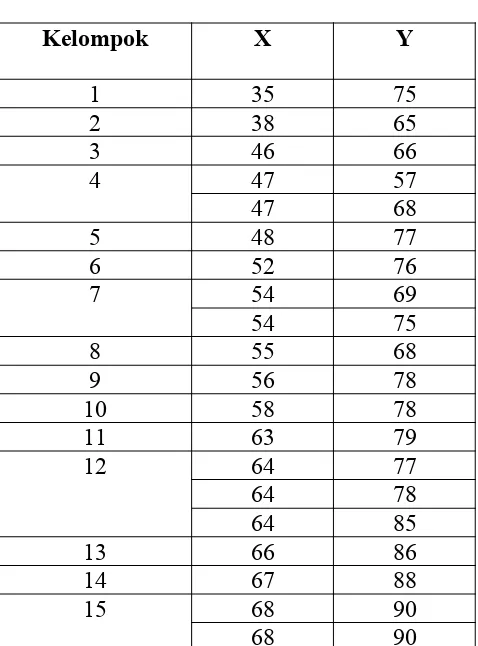
Untuk melakukan perhitungan terhadap JK Galat (JKG) maka data terlebih dahulu diurutkan dan dikelompokkan menurut variabel X. Dari hasil pengelompokkan itu diperoleh 15 kelompok sehinggga kemudian dapat dihitung jumlah kuadrat galat per kelompok seperti tercantum pada Tabel 11 berikut.

Tabel 11

Karena JKE sudah diketahui sebesar 116,5 maka JKтc sudah dapat dihitung sebagai berikut:

JKтc = JKRes - JKE = 637,17 – 116,5 = 520,67

RJKтc = JKтc k-2

= 520,67/(15-2) = 520/13 = 40,05 RJKE = JKE (n-k)

= 116,5/(20-15) = 116,5/5 = 23,3 Flin = RJKтc RJKE

= 40,05/23,3 = 1,72

Nilai Flin hitung ini harus dibandingkan dengan F tabel dengan menggunakan kriteria di atas. Nilai F tabel dengan dk pembilang = k-2 = 15-2 =13 dan dk penyebut = n-k = 20 – 15 = 5, sehingga dengan dk pembilang dan penyebut = (13,5) maka diperoleh nilai F tabel sebesar 4,68 (pada taraf nyata α = 0,05) dan 9,89 (pada taraf nyata α = 0,01).

Kriteria untuk menghitung linearitas regresi linear yaitu jika F hitung lebih kecil daripada F tabel maka regresinya bersifat linear. Karena Flin hitung lebih kecil dari F tabel maka regresi bersifat linear.

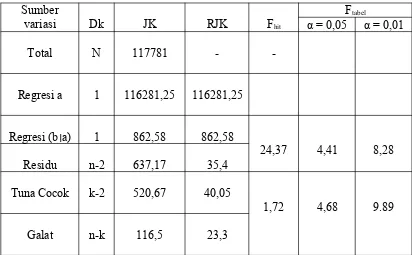
Tabel 12

Tabel ANAVA Ŷ = 38,43 + 0,68X

Sumber

variasi Dk JK RJK Fhit

Ftabel

α = 0,05 α = 0,01

Total N 117781 -

-Regresi a 1 116281,25 116281,25

Regresi (b׀a) 1 862,58 862,58

24,37 4,41 8,28

Residu n-2 637,17 35,4

Tuna Cocok k-2 520,67 40,05

1,72 4,68 9.89

Galat n-k 116,5 23,3

Dari hasil perhitungan menunjukkan bahwa:

1) Koefisien arah regresi bersifat signifikan karena nilai F hitung (24,37) lebih besar dari F tabel baik pada taraf nyata α = 0,05 maupun α = 0,01

2) Regresi bersifat linear karena nilai F hitung(1,72) lebih kecil dari F tabel baik pada taraf nyata α = 0,05 maupun α = 0,01.

Dengan demikian, model regresi ini dapat dipergunakan untuk membuat peramalan.

Selanjutnya, tafsiran terhadap regresi harus dilihat dalam konteks hubungan antara variabel X dan Y. Untuk itu, sebelum melakukan penafsiran terhadap regresi yang berujung pada peramalan, perlu diketahui derajat atau kuat lemahnya hubungan antara variabel X terhadap variabel Y dengan bantuan analisis korelasi. Karena itu, untuk dapat melakukan penafsiran terhadap hubungan antara X dan Y perlu dicari koefisien korelasi antara X dan Y dengan menggunakan rumus korelasi produk momen. Nilai-nilai yang sudah terdapat dalam tabel 5 di atas jika dimasukkan ke dalam rumus korelasi produk momen maka dapat diketahui koefisien korelasinya sebagai berikut:

r = [ n∑X2 _–(∑X)2_{] [n∑Y}2 _{– (∑Y)}2_] (20 x 86211) – (1114 x 1525)

= [(20 x 63918) – (1114)2_{] [(20 x 117781) – (1525)}2_]

1724220 – 1698850 =

---37364 x29995 = 25370/33477,3532 = 0,7578

Dari nilai r hitung ini kemudian dibandingkan dengan nilai r tabel dengan derajat kebebasan (n-2) = 20-2 = 18 diperoleh nilai r tabel = 0,378 (untuk taraf signifikansi 5%) dan 0,516 (pada taraf signifikansi 1%).

Kriteria untuk menentukan apakah korelasi antara variabel X dan Y adalah signifikan adalah jika nilai r hitung lebih besar dari nilai r tabel maka korelasinya signifikan.

Ternyata bahwa r hitung = 0,7578 jauh lebih besar daripada r tabel untuk kedua taraf signifikansi di atas, sehingga korelasinya sangat signifikan. Dengan demikian terdapat hubungan yang signifikan antara minat belajar matematika terhadap prestasi hasil belajar matematika siswa.

Analisis selanjutnya adalah menentukan indeks deteminasi berdasarkan koefisien korelasi tersebut dengan mengkuadratkan angka koefisien korelasi di atas. Dari nilai koefisien korelasi r = 0,7578 jika dikuadratkan diperoleh indeks determinasi sebesar 0,5743. Berdasarkan indeks determinasi ini dapat ditentukan kadar atau tingkat kontribusi dari variabel bebas X terhadap variabel terikat Y dengan mengalikan indeks deteminasi dengan 100% sehingga didapat 57,43%. Jadi dapat disimpulkan bahwa kontribusi relatif dari variabel minat belajar matematika terhadap nilai prestasi hasil belajar siswa adalah sebesar 57,43%. Artinya, sekitar 57,43% variasi dalam nilai prestasi hasil belajar matematika siswa ditentukan oleh minat belajar matematika mereka.

Dengan kata lain, dapat diramalkan bahwa kecendrungan nilai prestasi hasil belajar matematika siswa sebagiannya secara nyata bergantung kepada minat belajar matematika mereka. Dengan demikian, seandainya skor minat belajar matematika seorang siswa adalah 60 maka dapat diramalkan rata-rata nilai prestasi hasil belajar matematika siswa itu adalah 38,43 +0,68(60) = 79,23. Selanjutnya dapat diramalkan bahwa peningkatan skor minat belajar matematika siswa dapat diikuti dengan peningkatan nilai prestasi hasil belajar matematika mereka.

B. Uji Regresi Linear Berganda

1) Uji Keberartian Regresi Linear Berganda dengan 2 Prediktor

Untuk memastikan apakah regresi linear berganda dengan 2 prediktor yang telah ditentukan melalui persamaan regresi berarti atau tidak maka perlu dilakukan uji keberartian atau uji signifikansinya. Pengujian ini mutlak dilakukan jika kita ingin membuat kesimpulan berdasarkan analisis regresi ini. Jika asumsi-asumsi yang berlaku untuk regresi sudah terpenuhi maka uji keberartian dapat dilakukan, dan dengan demikian juga dapat dilakukan penarikan kesimpulan.

Pengujian keberartian atau signifikansi regresi linear berganda menggunakan statistik F berdasarkan analisis varians. Adapun rumus untuk menghitung keberartian regresi linear berganda dengan statistik F adalah:

F = JK Reg /k

JKRes/(n-k-1) ... (3) Dimana,

JKReg = b1∑x1y + b2∑x2y + ... + bk∑xky ... (4) JKRes = JKTotal + JKReg ... (5) JKTotal = ∑y2

k = banyaknya variabel prediktor n = banyaknya subjek

Sebelum dihitung keberartian maka perlu dihitung dahulu nilai-nilai berikut: ∑y2 _{= ∑Y}2 _{- (∑Y)}2_/n

∑x2y = ∑X2Y - [(∑Y)(∑X2)] ... (6) n

∑xky = ∑XkY - [(∑Y)(∑Xk)] n

Dari data tabel 6 dan rumus (6) di atas maka diperoleh:

∑y2 _{= ∑Y}2 _{- (∑Y)}2_{/n = 67258 – (1144)}2_{/20 = 1821,2} ∑x1y = ∑X1Y - [(∑Y)(∑X1)] = 20282– [(347)(1144)]/20 = 433,6

n

∑x2y = ∑X2Y - [(∑Y)(∑X2)] = 70635 – [(1211)(1144)]/20 = 1365,8 n

Jika dimasukkan ke dalam rumus (4) dan (5) di atas, dan lihat nilai b1 dan b2 hasil perhitungan pada tabel 6 maka diperoleh :

JKReg = (1,074 x 433,6) + (0,418 x 1365,8)= 1036,591 JKRes = (1821,2 – 1036,591) = 784,609

Dengan demikian nilai F dapat dihitung sesuai rumus (3) di atas sehingga diperoleh:

F = JK Reg /k

JKRes/(n-k-1)

= 1036,591/2 784,609/(20-2-1) = 518,296/46,153 = 11,23

Jika dibandingkan dengan nilai F tabel dengan derajat kebebasan(dk) pembilang = 2 dan dk penyebut = 17 maka diperoleh nilai F tabel sebesar 3,59 pada taraf signifikansi α = 0,05 dan 6,11 pada taraf signifikansi α = 0,01.

signikansi di atas, maka dapat dikatakan bahwa regresi signifikan atau berarti. Dengan demikian dapat dikatakan bahwa hubungan antara variabel X1 dan X2 dengan Y signifikan, dan variabel X1 dan X2 dapat digunakan untuk peramalan terhadap variabel Y.

Selanjutnya, tafsiran terhadap regresi harus dilihat dalam konteks hubungan antara variabel X1 dan X2 terhadap variabel Y. Untuk itu, sebelum melakukan penafsiran terhadap regresi yang berujung pada peramalan, perlu diketahui derajat atau kuat lemahnya hubungan antara variabel X1 dan X2 terhadap variabel Y dengan bantuan analisis korelasi. Karena itu, untuk dapat melakukan penafsiran terhadap hubungan antara X1 dan X2 terhadap variabel Y perlu dicari koefisien korelasi berganda. Nilai-nilai yang dibutuhkan untuk perhitungan koefisien korelasi berganda adalah:

JKReg = b1∑x1y + b2∑x2y = 1036,591

JKTotal = ∑y2 _{= 1821,2}

Sedangkan koefisien korelasi berganda dapat dicari dengan menggunakan rumus sebagai berikut:

R = (JKReg/ JKTotal) ... (7) Sehingga dengan menggunakan nilai-nilai yang ada maka dari rumus (7) didapat:

R = (JKReg/ JKTotal) = √1036,591/1821,2

= √0,57

= 0,755

Selanjutnya, untuk mengetahui hubungan dan kontribusi efektif (sumbangan murni) dari setiap variabel bebas terhadap variabel terikat dengan mengontrol variabel-variabel bebas lainnya dalam suatu hubungan linear berganda perlu dilakukan analisis korelasi parsial.

Dalam korelasi parsial dengan dua variabel prediktor terdapat dua pengontrolan terhadap variabel kriterium yakni 1) pengontrolan terhadap variabel X2 jika kita ingin mengetahui kontribusi relatif dari X1 terhadap Y, 2) pengontrolan terhadap variabel X1 jika kita ingin mengetahui kontribusi relatif dari X2 terhadap Y. Kedua jenis pengontrolan ini disebut: first order partial (parsial tingkat satu) karena hanya satu variabel prediktor yang dikontrol. Adapun rumus untuk menghitung korelasi parsialnya adalah sebagai berikut:

ry1.2 = ry1- ry2 r12 (1 - ry22_{)(1 - r12}2₎

ry2.1 = ry2- ry1 r12 ... (8) (1 - ry12_{)(1 - r12}2₎

Di mana: ry1.2 = korelasi parsial X1 dan Y dengan mengontrol X2 ry2.1 = korelasi parsial X2 dan Y dengan mengontrol X1 ry1 = korelasi sederhana X1 dan Y

ry2 = korelasi sederhana X2 dan Y r12 = korelasi sederhana X1 dan X2

dengan nilai-nilai ry1, ry2, dan r12 dapat dihitung dengan rumus-rumus berikut:

ry1 = n∑X1Y – (∑X1)(∑Y)

[n∑X12 _{– (∑X1)}2_{][ n∑Y}2 _{– (∑Y)}2_]

ry2 = n∑X2Y – (∑X2)(∑Y) ... (9) [n∑X22 _{– (∑X2)}2_{][ n∑Y}2 _{– (∑Y)}2_]

[n∑X12 _{– (∑X1)}2_{][ n∑X2}2 _{– (∑X2)}2_]

Dari data pada tabel di atas dan dengan menggunakan rumus (9) diperoleh hasil sebagai berikut:

ry1 = n∑X1Y – (∑X1)(∑Y)

[n∑X12 _{– (∑X1)}2_{][ n∑Y}2 _{– (∑Y)}2_] = 20(20282) – (347)(1144)

[20(6235) – (347)2_{][20(67258) – (1144)}2_] = 405640 - 396968

(124700– 120409)(1345160 – 1308736) = 8672

(4291)(36424) = 8672

156295384 = 8672/12501,815 = 0,694

ry2 = n∑X2Y – (∑X2)(∑Y)

[n∑X22 _{– (∑X2)}2_{][ n∑Y}2 _{– (∑Y)}2_] = 20(70635) – (1211)(1144)

[20(75345) – (1211)2_{][ 20(67258) – (1144)}2_] = 1412700 - 1385384

(40379)(36424) = 27316

1470764697 = 27316/38350,55 = 0,7123

r12 = n∑X1X2 – (∑X1)(∑X2)

[n∑X12 _{– (∑X1)}2_{][ n∑X2}2 _{– (∑X2)}2_] = 20(21497) – (347)(1211)

[20(6235) – (347)2_{][20(75345) – (1211)}2_] = 429940 – 420217

(124700–120409)(1506900–1466521) = 9723

(4291)(40379) = 9723

173266289 = 9723/13163,065 = 0,7387

Ry1.2 = r2_{y1 + r}2_{y2 - 2 ry1ry2 r12} 1 - r2

12

= 0,482+ 0,5074- 0,73 1 - 0,5457 = 0,2594

0,4543 = √0,57

= 0,755

R2

y1.2 = (0,755)2

= 0,57003

Jika dikalikan dengan 100% maka didapat persentase kontribusi relatif dari variabel X1 dan X2 terhadap Y yaitu sebesar 57%. Artinya sekitar 57% variasi dalam kemampuan mengelola pembelajaran guru ditentukan oleh pengalaman mengajar dan sikapnya terhadap siswa, dan sebesar 43% dipengaruhi oleh faktor lain.

Selanjutnya, untuk mengetahui hubungan dan kontribusi efektif (kontribusi murni) dari setiap variabel prediktor terhadap variabel prediktor lainnya dalam suatu hubungan linear berganda dapat dilakukan dengan analisis korelasi parsial.

Dalam korelasi parsial dengan dua variabel prediktor terdapat dua pengontrolan terhadap variabel kriterium yakni 1) pengontrolan terhadap variabel X2 jika kita ingin mengetahui kontribusi relatif dari X1 terhadap Y, 2) pengontrolan terhadap variabel X1 jika kita ingin mengetahui kontribusi relatif dari X2 terhadap Y. Kedua jenis pengontrolan ini disebut: first order partial (parsial tingkat satu) karena hanya satu variabel prediktor yang dikontrol.

Dari data-data nilai yang sudah ada dan dengan menggunakan rumus (8) di atas diperoleh hasil sebagai berikut:

ry1.2 = ry1- ry2 r12 (1 - ry22_{)(1 - r12}2₎

= 0,694 – 0,5262

(1 – 0,5074)(1 – 0,5457) = 0,1678

(0,4926)(0,4543) = 0,1678/0,2238 = 0,7498

ry2.1 = ry2- ry1 r12 (1 - ry12_{)(1 - r12}2₎

= 0,7123 – (0,694)(0,7387) [1 – ( 0,694)2_{][1 – (0,7387)}2_] = 0,7123 – 0,5127

(1 – 0,482)(1 – 0,5457) = 0,1996

(0,518)(0,4543) = 0,1996/0,4543 = 0,4394

Untuk menguji signifikansi dari koefisien korelasi parsial ini maka digunakan uji t dengan rumus sebagai berikut:

 Untuk ry1.2:

t = ry1.2 (n-k-1) ; k = banyaknya prediktor, n = banyaknya data (1- r2_y1.2)

= 0,7498 x

_√

(20−2−1)

√1−0,562

= 0,7498 x 4,123/√0,438

= 3,091/0,662 = 4,669  Untuk ry2.1:

t = ry2.1 (n-k-1) ; k = banyaknya prediktor, n = banyaknya data (1- r2_y2.1)

= 0,44x

_√

(20−2−1)

[ 1 – (0,44)2_] = 0,44 x √17

√1−0,1936

= 0,44 x 4,123/√0,8064

= 1,814/0,898 = 2,020

Dari hasil perhitungan itu kemudian diuji dengan membandingkan nilai t hitung dengan nilai t tabel pada taraf signifikansi α = 0,05 dengan derajat kebebasan dk = n-k-1 atau dk = 17. Nilai t tabel dengan dk = 17 pada taraf signifikansi α = 0,05 adalah 1,740.

Dengan demikian, kedua korelasi parsial di atas signifikan pada taraf signifikansi α = 0,05 karena t hitung lebih besar dari nilai t tabel.

a. Kontribusi efektif variabel pengalaman mengajar guru (X1) terhadap kemampuan guru dalam mengelola pembelajaran (Y) dengan mengontrol variabel sikap guru terhadap siswa (X2) adalah 56,22% (didapat dari 0,74982 _{x 100%). Hal ini berarti} sekitar 56,22% variasi kemampuan guru dalam mengelola pembelajaran ditentukan oleh variabel pengalaman mengajar guru.

2) Uji Keberartian Regresi Linear Berganda dengan 3 Prediktor

Seperti halnya juga pada regresi linear berganda dengan 2 prediktor, uji signifikansi atau keberartian terhadap regresi linear berganda dengan 3 prediktor juga dapat menggunakan uji F dengan rumus (3), (4), dan (5) di atas.

Dengan demikian untuk menguji apakah regresi linear berganda dengan persamaan regresi Ŷ = 10,64 + 0,17X1 + 0,081X2 + 0,1484X3 berarti ataukah tidak, kita membutuhkan nilai-nilai yakni Jumlah Kuadrat Regresi (JKReg), Jumlah Kuadrat

Total (JKTotal), dan Jumlah Kuadrat Residu (JKRes). Untuk mencari besaran dari JKReg

dibutuhkan nilai-nilai yang sudah tersedia di atas (lihat nilai-nilai hasil perhitungan pada tabel 8).

∑x1y = ∑X1Y – (∑X1) (∑Y) = 12952 – (545)(354) = 12952 – 12862 = 90 n 15

∑x2y = ∑X2Y – (∑X2) (∑Y) = 10422 – (439)(354) = 10422 – 10360,4 = 61,6 n 15

∑x3y = ∑X3Y – (∑X3) (∑Y) = 10580 – (446)(354) = 10580 – 10525,6 = 54,4 n 15

∑y2 _{= ∑Y}2 _{- (∑Y)}2_{/n = 8406 – (354)}2_{/15 = 8406 – 8354,4 = 51,6} Sehingga JKReg dan JKRes dapat dihitung sebagai berikut:

JKReg = b1∑x1y + b2∑x2y + b3∑x3y

= (0,17 x 90) + (0,081 x 61,6) + (0,148 x 54,4) = 15,3 + 4,99 + 8,05

= 28,34

JKRes = JKTotal - JKReg JKTotal = ∑y2 _{= 51,6} = 51,6 – 28,34

= 23,26

Dengan demikian, jika dimasukkan ke dalam rumus (3) di atas maka diperoleh hasil sebagai berikut:

JKRes/(n-k-1) = 28,34/3 23,26/ (15-3-1) = 28,34/3 23,26/11 = 9,447/2,115 = 4,47

Jika dibandingkan dengan nilai F tabel dengan derajat kebebasan pembilang = 3 dan derajat kebebasan penyebut = 11 diperoleh nilai F tabel = 3,59 pada taraf signikansi α = 0,05. Karena nilai F hitung lebih besar daripada nilai F tabel, maka regresi signifikan pada taraf signifikansi α = 0,05. Dengan demikian dapat dikatakan bahwa hubungan antara variabel X1, X2, dan X3 dengan Y signifikan, dan variabel X1, X2, dan X3 dapat digunakan untuk peramalan terhadap variabel Y.

Selanjutnya, tafsiran terhadap regresi harus dilihat dalam konteks hubungan antara variabel X1, X2, dan X3 terhadap variabel Y. Untuk itu, sebelum melakukan penafsiran terhadap regresi yang berujung pada peramalan, perlu diketahui derajat atau kuat lemahnya hubungan antara variabel X1, X2, dan X3 terhadap variabel Y dengan bantuan analisis korelasi. Karena itu, untuk dapat melakukan penafsiran terhadap hubungan antara X1, X2, dan X3 terhadap variabel Y perlu dicari koefisien korelasi berganda. Nilai-nilai yang dibutuhkan untuk perhitungan koefisien korelasi berganda adalah:

JKReg = b1∑x1y + b2∑x2y + b3∑x3y = 28,34 JKTotal = ∑y2 _{= 51,6}

Dengan rumus (7) di atas diperoleh harga R sebagai berikut:

R = (JKReg/ JKTotal) = √28,34/51,6 = √0,54922 = 0,741

sikap guru terhadap profesi guru, kemampuan komunikasi interpersonal guru, dan sikap guru terhadap siswa.

Selanjutnya, untuk mengetahui hubungan dan kontribusi efektif (sumbangan murni) dari setiap variabel bebas terhadap variabel terikat dengan mengontrol variabel-variabel bebas lainnya dalam suatu hubungan linear berganda perlu dilakukan analisis korelasi parsial.

Dalam korelasi parsial dengan tiga variabel prediktor, perhitungan korelasi parsial harus melewati dua tahap/dua tingkat yaitu:

 Pada tahap pertama dihitung dulu koefisien korelasi parsial antara satu variabel prediktor dengan variabel kriterium dengan mengontrol satu variabel prediktor lainnya, yang disebut: first order partial correlation yaitu ry1,2 ; ry1,3 ; ry2,1 ; ry2,3 ; ry3,1 ; ry3,2

 Pada tahap berikutnya, menghitung koefisien korelasi parsial antara satu variabel prediktor dengan variabel kriterium dengan mengontrol dua variabel prediktor lainnya, yang disebut: second order partial correlation yaitu ry1,23 ;; ry2,13 ;; ry3,12

Rumus untuk menghitung korelasi parsial dengan tiga variabel prediktor adalah sebagai berikut:

ry1.23 = ry1.2- ry3.2 r13.2 (1 - ry3.22_{)(1 - r13.2}2₎

ry2.31 = ry2.3- ry1.3 r12.3 ... (8) (1 - ry1.32_{)(1 - r12.3}2₎

ry3.12 = ry3.1- ry2.1 r23.1 (1 - ry2.12_{)(1 – r23.1}2₎

ry1.3 = korelasi parsial X1 dan Y dengan mengontrol X3 ry2.1 = korelasi parsial X2 dan Y dengan mengontrol X1 ry2.3 = korelasi parsial X2 dan Y dengan mengontrol X3 ry3.1 = korelasi parsial X3 dan Y dengan mengontrol X1 ry3.2 = korelasi parsial X3 dan Y dengan mengontrol X2 ry12.3 = korelasi parsial X1, X2 dan Y dengan mengontrol X3 ry13.2 = korelasi parsial X1, X3 dan Y dengan mengontrol X2 ry23.1 = korelasi parsial X2, X3 dan Y dengan mengontrol X1 ry1 = korelasi sederhana X1 dan Y

ry2 = korelasi sederhana X2 dan Y ry3 = korelasi sederhana X3 dan Y r12 = korelasi sederhana X1 dan X2 r13 = korelasi sederhana X1 dan X3 r23 = korelasi sederhana X2 dan X3

DAFTAR PUSTAKA

Irianto Agus, Dr., Statistik Pendidikan (1), Jakarta, Depdikbud, 1988.

Sudjana, Teknik Analisis Regresi dan Korelasi Bagi Para Peneliti, Bandung, Tarsito, 1996.

Sudjana, Metode Statistika, Bandung, Tarsito, 2005.

Sugiyono, Statistik untuk Penelitian, Bandung, CV Alfabeta, 2002.

Sutrisno Hadi, Prof.,M.A.,Drs., Analisis Regresi, Yogyakarta, ANDI OFFSET, 1994