commit to user
MODEL ENDEMIK SUSCEPTIBLE INFECTED RECOVERED
(SIR) DENGAN IMIGRASI, VAKSINASI DAN SANITASI
oleh
ANITA KESUMA ARUM M0108030
SKRIPSI
ditulis dan diajukan untuk memenuhi sebagian persyaratan memperoleh gelar Sarjana Sains Matematika
JURUSAN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SEBELAS MARET
commit to user
ABSTRAK
Anita Kesuma Arum. 2012. MODEL ENDEMIKSUSCEPTIBLE INFEC-TED RECOVERED (SIR) DENGAN IMIGRASI VAKSINASI DAN SANITASI. Fakultas Matematika dan Ilmu Pengetahuan Alam. Universitas Sebelas Maret.
Masalah penyebaran penyakit dapat dijelaskan dengan menggunakan mo-del matematika. Momo-del matematika yang dimaksud yaitu momo-del SIR. Ada dua jenis model SIR yaitu model epidemik SIR dan model endemik SIR. Model epi-demik SIR tidak memperhatikan faktor kelahiran dan kematian karena penyakit menyebar dalam waktu yang singkat, sedangkan model endemik SIR memper-hatikan faktor kelahiran dan kematian karena penyakit menyebar dalam kurun waktu yang lama. Imigrasi merupakan faktor yang dapat mempengaruhi penye-baran penyakit. Selain faktor imigrasi, upaya pencegahan yang dilakukan seperti program vaksinasi dan program sanitasi juga dapat mempengaruhi penyebaran suatu penyakit.
Tujuan penulisan ini adalah mengkonstruksikan model endemikSIRdengan imigrasi, vaksinasi dan sanitasi serta menentukan titik kesetimbangan dan tipe kestabilan titik kesetimbangan tersebut.
commit to user
Anita Kesuma Arum. 2012. ENDEMIC SUSCEPTIBLE INFECTED RE-COVERED (SIR) MODEL WITH IMMIGRATION VACCINATION AND SA-NITATION. Faculty of Mathematics and Natural Sciences, Sebelas Maret Uni-versity.
The disease outbreak problem can be explained using a mathematical model. The mathematical model mentioned is the model of SIR. There are two classic SIRmodels, namelySIRepidemic model and SIRendemic model. SIRepidemic models are used to describe the rapid outbreak, while theSIRendemic models are used for studying disease over longer periods. Immigration is a factor that able to influence the disease outbreak. In addition, prevention efforts such as vaccination programs and sanitation programs can also affect the disease outbreak.
The purposes of this research are to construct model of endemic SIR with immigration, vaccination and sanitation and to find the type of equilibrium points and the stability of the equilibrium points.
commit to user
KATA PENGANTAR
Segala puji dan syukur penulis panjatkan kepada Allah SWT yang telah melimpahkan rahmat dan hidayah-Nya, sehingga penulis dapat menyelesaikan skripsi ini. Penulis menyadari bahwa dalam penulisan skripsi ini tidak lepas dari bantuan, dorongan, serta bimbingan berbagai pihak. Oleh karena itu penulis mengucapkan terima kasih kepada
1. Bapak Dr. Sutanto, DEA. selaku Pembimbing I dan Ibu Dra. Purnami Widyaningsih, M.App.Sc selaku Pembimbing II yang telah membimbing dan mengarahkan dalam penyusunan skripsi ini.
2. Seluruh pihak yang telah membantu dalam penulisan skripsi ini.
Semoga skripsi ini dapat bermanfaat bagi pihak yang memerlukan.
Surakarta, September 2012
commit to user
PERSEMBAHAN
Sebuah karya sederhana ini kupersembahkan untuk
commit to user
DAFTAR ISI
HALAMAN JUDUL . . . i
HALAMAN PENGESAHAN . . . ii
ABSTRAK . . . iii
ABSTRACT . . . iv
KATA PENGANTAR . . . v
PERSEMBAHAN . . . vi
DAFTAR ISI . . . vii
DAFTAR TABEL . . . ix
DAFTAR GAMBAR . . . x
I PENDAHULUAN 1 1.1 Latar Belakang Masalah . . . 1
1.2 Perumusan Masalah . . . 3
1.3 Batasan Masalah . . . 4
1.4 Tujuan . . . 4
1.5 Manfaat . . . 4
II LANDASAN TEORI 5 2.1 Tinjauan Pustaka . . . 5
2.2 Teori Penunjang . . . 6
2.2.1 Sistem Autonomous. . . 6
2.2.2 Bidang Fase . . . 6
2.2.3 Model Endemik SIR dengan Imigrasi dan Vaksinasi . . . . 7
commit to user
2.3 Kerangka Berpikir . . . 12
III METODE PENELITIAN 14 IV PEMBAHASAN 16 4.1 Konstruksi Model . . . 16
4.2 Titik Kesetimbangan . . . 18
4.3 Kestabilan Titik Kesetimbangan . . . 20
4.4 Penerapan Kasus . . . 22
V PENUTUP 27 5.1 Kesimpulan . . . 27
5.2 Saran . . . 28
commit to user
DAFTAR TABEL
2.1 Kriteria kestabilan berdasarkan nilai eigen . . . 12
commit to user
DAFTAR GAMBAR
2.1 Dinamika populasi model endemikSIRdengan imigrasi dan
vak-sinasi . . . 9
2.2 Trajektori pada bidang fase . . . 13
4.1 Dinamika populasi modelSIRdengan imigrasi, vaksinasi dan sa-nitasi . . . 18
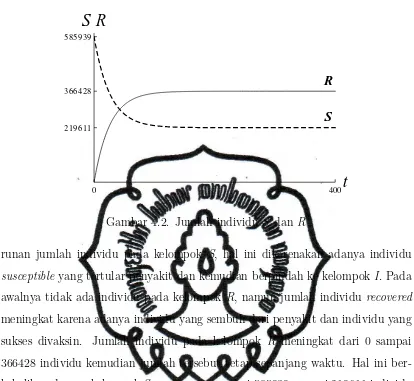
4.2 Jumlah individu S dan R . . . 23
4.3 Jumlah individu I . . . 23
commit to user
Bab I
PENDAHULUAN
1.1
Latar Belakang Masalah
Penyakit infeksi seperti rubella, measles, mumps, pertussis, cacar air dan hepatitis merupakan penyakit infeksi yang berbahaya. Kinbaby [13] menyebut-kan bahwa penyakit tersebut berbahaya karena dapat mengakibatmenyebut-kan komplikasi, kerusakan organ tubuh, cacat, kelumpuhan bahkan kematian. Penyakit tersebut disebabkan oleh virus yang dapat menyerang siapa saja. Penyebaran penyakit ini dapat melalui udara, batuk atau bersin, makanan, minuman dan kotoran manusia. Bagi anak-anak gejala yang ditimbulkan dari penyakit ini memang tidak begitu berbahaya, namun pada orang dewasa khususnya pada ibu hamil gejala tersebut bisa menjadi sangat berbahaya.
Piccolo dan Billings [15] menyebutkan penyakit infeksi seperti cacar air, rubella, measles, mumps dan pertussis merupakan masalah yang dihadapi setiap negara di dunia. Pada kota-kota besar imigrasi merupakan suatu hal yang wajar dan sering terjadi, sehingga faktor imigran menjadi salah satu faktor yang dapat mempengaruhi penyebaran suatu penyakit di wilayah tersebut. Individu baru yang masuk ke suatu wilayah mungkin membawa penyakit dari daerah sebelum-nya, sehingga individu tersebut dapat menularkan penyakit pada individu lain dalam daerah baru.
in-commit to user
dividu menjadi kebal terhadap suatu penyakit. Menurut WHO [16], pemberian vaksin MMR (Measles, Mumps, Rubella) telah terbukti dapat menekan jumlah kematian yang disebabkan penyakit measles, mumps dan rubella.
Pada umumnya, suatu penyakit akan cepat menyebar apabila didukung oleh keadaan lingkungan yang tidak sehat. Lingkungan yang tidak sehat ini dikare-nakan kurangnya akses masyarakat terhadap sanitasi serta kurangnya pelayanan kesehatan pada daerah tersebut. Menurut CDC [17], pada dasarnya sanitasi di-gambarkan sebagai suatu akses terhadap fasilitas pembuangan yang aman dari kotoran manusia (tinja dan urine), serta memiliki kemampuan untuk memper-tahankan kondisi higienis. Hetchote [9] menyebutkan bahwa, perbaikan sanitasi dapat mengurangi laju penyebaran penyakit. Upaya pencegahan penyebaran penyakit dapat dilakukan dengan meningkatkan sanitasi seperti mencegah ter-kontaminasinya makanan dan air oleh tinja, mencuci tangan setelah buang air besar dan sebelum makan, menjaga kebersihan saluran pembuangan, pengelolaan sampah rumah tangga serta gaya hidup sehat.
Menurut CDC [17], sanitasi total meliputi sumber air bersih, gaya hidup se-hat dan saluran pembuangan. Tingkat sanitasi dapat dilise-hat dari jumlah individu yang sakit tiap tahunnya. Hal ini berkorelasi dengan fasilitas sanitasi yang ada pada suatu daerah. Apabila di daerah tersebut banyak individu yang sakit tiap tahunnya, maka tingkat sanitasi di daerah tersebut kurang baik dan begitu pula sebaliknya. Guimaraens dan Code¸co [6] menyebutkan bahwa daerah yang memi-liki tingkat sanitasi rendah dapat menyebabkan endemik bagi penyakit hepatitis A. Selain hepatitis A, penyakit cacar air juga menjadi endemik pada daerah yang memikiki tingkat sanitasi yang rendah.
commit to user
pola penyebaran penyakit seperti ini dapat dijelaskan melalui model susceptible, infected, recovered (SIR).
Menurut Hethcote [8] ada dua model SIR klasik yaitu model epidemi SIR dan model endemik SIR. Karena penyakit ini bersifat endemik maka permasa-lahan penyebaran penyakit ini dapat dimodelkan dengan model endemik SIR. Kermack dan McKendrick [11] menyebutkan bahwa model endemik SIR berben-tuk sistem autonomous persamaan diferensial nonlinier orde satu. Penyelesaian sistem tersebut menyatakan jumlah individu susceptible (S), infected (I) dan recovered (R) setiap saat. Dengan demikian penyelesaian sistem tersebut dapat menjelaskan tentang bagaimana penyebaran penyakit pada suatu wilayah. Penye-lesaian sistem dengan sifat tertentu dimana jumlah individu susceptible, infected dan recovered tetap sepanjang waktu disebut titik kesetimbangan. Selanjutnya perlu diketahui sifat kestabilan dari titik kesetimbangan tersebut untuk menge-tahui bagaimana perilaku penyelesaian di sekitar titik kesetimbangan tersebut.
Piccolo dan Billings [15] telah meneliti tentang model endemiksusceptible, infected, recovered SIR yang mempertimbangkan faktor imigrasi dan vaksinasi dengan keefektifan vaksin 100%. Dalam hal ini, penulis ingin mengembangkan model endemik susceptible, infected, recovered (SIR) yang mempertimbangkan faktor imigrasi dan vaksinasi dengan keefektifan vaksin yang tidak 100% serta menambahkan faktor sanitasi dalam model. Selain itu penulis juga tertarik un-tuk mengetahui titik kesetimbangan serta kestabilan titik kesetimbangan model tersebut. Kemudian diberikan pula suatu contoh kasus untuk menginterpretasi-kan model endemik SIR dengan imigrasi, vaksinasi dan sanitasi.
1.2
Perumusan Masalah
Berdasarkan latar belakang yang telah diuraikan dapat diambil tiga perumusan masalah yaitu
commit to user
2. bagaimana menentukan titik kesetimbangan dan kestabilan di titik kese-timbangan?
3. bagaimana interpretasi model endemik SIR dengan imigrasi, vaksinasi dan sanitasi pada suatu kasus?
1.3
Batasan Masalah
Dalam penelitian ini, permasalahan dibatasi hanya pada fungsi sanitasi dengan nilai konstanta proporsionalitas pada fungsi tersebut lebih kecil atau sama dengan tingkat rata-rata kontaknya.
1.4
Tujuan
Penelitian ini bertujuan untuk
1. menurunkan model endemikSIR dengan imigrasi, vaksinasi dan sanitasi, 2. menentukan titik kesetimbangan dan kestabilan di titik kesetimbangan,
3. menginterpretasikan model endemik SIR dengan imigrasi, vaksinasi dan sanitasi pada suatu kasus.
1.5
Manfaat
commit to user
Bab II
LANDASAN TEORI
Pada bagian ini diberikan tinjauan pustaka yang berisi penelitian sebe-lumnya yang mendasari penelitian ini, teori penunjang yang berisi definisi dan teori yang diperlukan serta kerangka pemikiran yang menjelaskan alur pemikiran penulisan skripsi.
2.1
Tinjauan Pustaka
ModelSIRpertama kali diperkenalkan pada tahun 1927 oleh Kermack dan McKendrick [11]. Model ini berbentuk sistemautonomous persamaan diferensial. Menurut Hethcote [8], ada dua model SIR yaitu model epidemik SIRdan model endemikSIR. Model epidemikSIRdigunakan untuk menggambarkan penyebaran suatu penyakit yang bersifat epidemik, sedangkan model endemikSIRdigunakan untuk menggambarkan penyebaran suatu penyakit yang bersifat endemik. Model SIR sendiri telah dikembangkan oleh beberapa ilmuwan lain seperti Piccolo dan Billings [15], Guimaraens dan Code¸co [6] untuk mempelajari penyebaran penyakit pada kasus-kasus tertentu.
Dalam artikelnya, Piccolo dan Billings [15] telah mempelajari tentang pe-ngaruh vaksinasi pada modelSIRdengan imigrasi. Vaksinasi pada model tersebut memiliki keefektifan vaksin 100%. Kemudian pada tahun 2005, dalam artikelnya Guimaraens dan Code¸co [6] meneliti tentang pengaruh sanitasi pada penyebaran penyakit dengan model SIR dengan vaksinasi. Mereka mempelajari tentang pe-nyebaran penyakit hepatitis A pada masyarakat Brazil yang sangat kurang dalam pelayanan kesehatan dan kebersihan.
commit to user
dan Billings [15], namun dengan keefektifan vaksin yang tidak 100%. Kemudian model tersebut ditambahkan dengan faktor sanitasi seperti yang ditulis oleh Gui-maraens dan Code¸co [6]. Hal tersebut merupakan pengembangan dari yang telah dilakukan Arum dan Kuntari [1] yang membahas tentang simulasi level sanitasi pada model SIR dengan imigrasi dan vaksinasi.
2.2
Teori Penunjang
Pada bagian ini dijelaskan definisi dan teori yang mendukung dalam menca-pai tujuan penulisan. Selanjutnya diberikan definisi sistem autonomous, bidang fase, model endemik SIR dengan imigrasi dan vaksinasi, kesetimbangan serta kestabilan.
2.2.1
Sistem
Autonomous
Sistem persamaan diferensial nonlinear orde satu yang terdiri dari tiga persamaan mempunyai bentuk umum
dS
dt =f1(S, I, R) dI
dt =f2(S, I, R) dR
dt =f3(S, I, R),
(2.1)
dengan variabelS, I, danR bergantung padat. Fungsif1, f2, f3 merupakan per-samaan nonlinear yang kontinu. Dengan demikian ada jaminan bahwa sistem (2.1) memiliki penyelesaian. Menurut Boyce [3], suatu sistem persamaan diferen-sial dimana variabel bebas t tidak muncul secara eksplisit pada f1, f2, f3 disebut sistem autonomous.
2.2.2
Bidang Fase
commit to user
dapat membantu memberikan informasi tentang perilaku penyelesaian sistem no-nlinier tersebut. Dalam hal ini trajektori pada bidang fase dapat digunakan untuk mengetahui perilaku penyelesaian sistem.
Sistem (2.1) terdiri dari tiga persamaan diferensial orde satu yaitu
dS
Sistem (2.1) memiliki tiga kemungkinan persamaan bidang fase yaitu dS dI,
dS dR,dan dI
dR. Ambil contoh persamaan bidang fase dS
dI. Persamaan bidang fase dS
Penyelesaian persamaan bidang fase (2.2) tersebut dapat digambarkan sebagai kurva pada bidangS−I. Untuk selanjutnya bidangS−Itersebut disebut bidang fase. Sedangkan kurva yang dibentuk oleh penyelesaian persamaan bidang fase (2.2) yang disajikan pada bidang fase disebut trajektori.
2.2.3
Model Endemik
SIR
dengan Imigrasi dan
Vaksinasi
Penyakit yang bersifat endemik merupakan suatu penyakit yang menyebar pada suatu wilayah tertentu dalam kurun waktu yang lama. Menurut Hethcote [8], penyebaran penyakit endemik dapat dimodelkan kedalam model matematika yang disebut model endemik SIR.Karena terjadi dalam kurun waktu yang lama, faktor kelahiran dan kematian diperhatikan dalam model tersebut. Kemudian Piccolo dan Bilings [15] mengembangkan model endemik SIR dengan menam-bahkan faktor imigran dan vaksinasi. Dalam hal ini imigrasi dan program vak-sinasi juga memberikan pengaruh pada penyebaran suatu penyakit.
commit to user
bebas dari penyakit (R). Berikut adalah asumsi yang digunakan pada model endemik SIR dengan imigrasi dan vaksinasi.
1. Jumlah individu pada populasi konstan.
2. Setiap individu lahir dan imigran dalam keadaan sehat tetapi rentan pe-nyakit.
3. Populasi bercampur secara homogen, artinya setiap individu memiliki ke-mungkinan yang sama tertular suatu penyakit.
4. Hanya satu penyakit yang menyebar dalam populasi dengan masa inkubasi penyakit diabaikan.
5. Tidak terjadi emigrasi pada daerah tersebut.
6. Vaksinasi hanya diberikan pada individu susceptible, dengan keefektifan vaksin 100%.
Karena diasumsikan populasi konstan, sehingga jumlah individu pada po-pulasi tersebut tetap atauS(t)+I(t)+R(t) =N. Misal tingkat kelahiran sebesar
µ1, dan tingkat individu imigran sebesarµ2.Oleh karena itu jumlah individu lahir dan jumlah individu imigran pada daerah tersebut sebesar µ1N dan µ2N. Ting-kat kematian dalam tiap kelompok sama dengan tingTing-kat kelahiran dan tingTing-kat imigrasi yaitu (µ1+µ2). Misal tingkat vaksinasi pada individu lahir dan individu imigran sebesar σ1 dan σ2. Dengan demikian jumlah individu lahir dan imigran yang divaksin yaitu sebesar σ1µ1N dan σ2µ2N. Karena diasumsikan bahwa ke-efektifan vaksin 100%, maka individu yang telah berhasil divaksin langsung ma-suk pada kelompok R.
commit to user
vaksinasi disajikan dalam Gambar 2.1. Perubahan jumlah individu S, I dan R
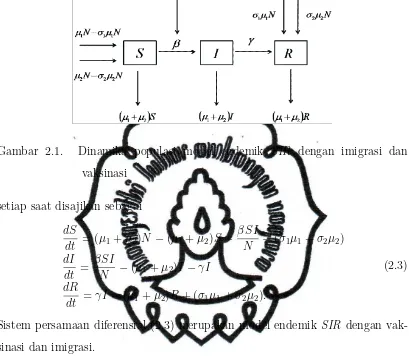
Gambar 2.1. Dinamika populasi model endemik SIR dengan imigrasi dan vaksinasi
setiap saat disajikan sebagai
dS
dt = (µ1+µ2)N −(µ1+µ2)S− βSI
N −(σ1µ1+σ2µ2) dI
dt = βSI
N −(µ1+µ2)I−γI dR
dt =γI−(µ1+µ2)R+ (σ1µ1+σ2µ2).
(2.3)
Sistem persamaan diferensial (2.3) merupakan model endemik SIR dengan vak-sinasi dan imigrasi.
2.2.4
Kesetimbangan dan Kestabilan
Panfilov [14] menyebutkan bahwa titik kesetimbangan dari suatu sistem merupakan suatu titik saat sistem tidak mengalami perubahan sepanjang wak-tu. Definisi titik kesetimbangan secara matematis disajikan pada Definisi 2.2.1 berikut.
Definisi 2.2.1. Titik(S∗, I∗, R∗)merupakan titik kesetimbangan sistem (2.1) jika memenuhi
f1(S∗, I∗, R∗) =f2(S∗, I∗, R∗) = f3(S∗, I∗, R∗) = 0.
commit to user
memberikan informasi tentang perilaku penyelesaian sistem tersebut. Menurut Finizio dan Ladas [5], titik kesetimbangan yang stabil berarti jika terjadi per-ubahan kecil pada titik kesetimbangan maka akan memberikan pengaruh kecil pada penyelesaian. Sedangkan stabil asimtotis berarti pengaruh dari perubahan kecil tersebut cenderung menghilang, dan suatu titik kesetimbangan yang tidak stabil berarti perubahan kecil yang terjadi pada titik kesetimbangan tersebut memiliki pengaruh besar dalam penyelesaiannya.
Jika (S, I, R) merupakan suatu titik disekitar titik kesetimbangan (S∗, I∗, R∗) pada sistem (2.1), maka (S, I, R) secara matematis dapat dituliskankan sebagai
(S, I, R) = (S∗+ ∆S, I∗+ ∆I, R∗+ ∆R).
Dengan demikian perubahan titik kesetimbangan pada sistem (2.1) dapat dituliskan sebagai
Menurut Khamsi [12], fungsi nonlinear f1, f2, f3 pada sistem (2.4) dapat didekati dengan menggunakan ekspansi deret Taylor
f1(S, I, R)≈f1(S∗, I∗, R∗) + (S−S∗)
Karena (S∗, I∗, R∗) merupakan titik kesetimbangan maka berdasarkan Definisi 2.2.1 berlaku
commit to user
Dengan demikian sistem (2.1) dapat didekati sebagai sistem linear dS
Sistem linear (2.5) dapat disajikan dalam bentuk matriks Bellomo dan Preziosi [2] nilai eigen dari matriks Jacobian pada sistem (2.6) dapat digunakan untuk menentukkan tipe kestabilan di titik kesetimbangan. Berikut ini teorema yang menyatakan hal tersebut.
Teorema 2.2.1. Jika λi merupakan nilai eigen matriks Jacobian J(S∗, I∗, R∗)
commit to user
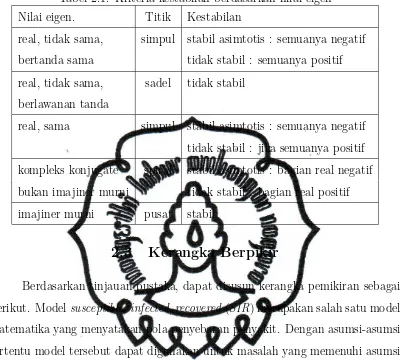
Tabel 2.1. Kriteria kestabilan berdasarkan nilai eigen Nilai eigen. Titik Kestabilan
real, tidak sama, simpul stabil asimtotis : semuanya negatif bertanda sama tidak stabil : semuanya positif real, tidak sama, sadel tidak stabil
berlawanan tanda
real, sama simpul stabil asimtotis : semuanya negatif tidak stabil : jika semuanya positif kompleks konjugate spiral stabil asimtotis : bagian real negatif bukan imajiner murni tidak stabil : bagian real positif imajiner murni pusat stabil
2.3
Kerangka Berpikir
Berdasarkan tinjauan pustaka, dapat disusun kerangka pemikiran sebagai berikut. Modelsusceptible, infected,recovered (SIR) merupakan salah satu model matematika yang menyatakan pola penyebaran penyakit. Dengan asumsi-asumsi tertentu model tersebut dapat digunakan untuk masalah yang memenuhi asumsi tersebut.
Penyakit infeksi seperti hepatitis,rubella, measles, mumps, hepatitis, cacar air dan pertussis merupakan penyakit infeksi yang dapat dimodelkan dengan model SIR. Penyakit tersebut bersifat endemik, oleh karena itu faktor kelahiran, kematian perlu diperhatikan dalam model. Selanjutnya individu imigran juga dapat mempengaruhi penyebaran suatu penyakit, untuk itu faktor imigrasi perlu diperhatikan dalam model.
commit to user
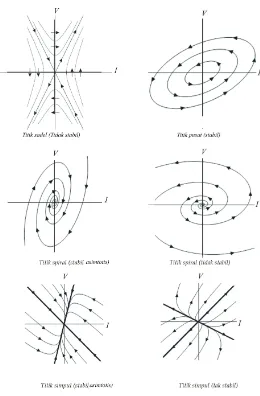
Gambar 2.2. Trajektori pada bidang fase
sangat berpengaruh dalam penyebaran penyakit. Oleh karena itu faktor sanitasi akan dimasukkan ke dalam model.
commit to user
Bab III
METODE PENELITIAN
Metode penelitian yang digunakan dalam penulisan skripsi ini adalah studi literatur. Langkah-langkah yang dilakukan untuk mencapai tujuan dalam pene-litian ini adalah sebagai berikut.
1. Mempelajari keadaan, perilaku, interaksi, serta kejadian dalam suatu popu-lasi konstan dimana terdapat individu imigran dengan individu didalamnya telah diberi vaksinasi, dan program sanitasi.
2. Menentukan asumsi, dan parameter yang diperlukan untuk mengkonstruksi model.
3. Mengkonstruksi model berdasarkan asumsi, dan parameter yang telah di-tentukan.
Langkah 1-3 dilakukan untuk mencapai tujuan pertama.
4. Menentukan titik kesetimbangan dari modelSIRdengan imigrasi, vaksinasi dan sanitasi menggunakan Definisi 2.2.1
5. Menganalisis tipe kestabilan di titik kesetimbangan menggunakan Teorema 7.1 dan Tabel 2.1.
Langkah 4-5 dilakukan untuk mencapai tujuan kedua.
6. Menentukan nilai parameter pada contoh yang diamati kemudian menen-tukan titik kesetimbangan serta kestabilan di titik kesetimbangan.
commit to user
9. Membandingkan hasil-hasil perubahan puncak endemik yang diperoleh dari langkah (8)
10. Menginterpretasikan hasil yang diperoleh.
commit to user
Bab IV
PEMBAHASAN
4.1
Konstruksi Model
Konstruksi model endemik SIR dengan imigrasi, vaksinasi dan sanitasi mengacu pada Piccolo dan Billings [15]. Penyebaran penyakit terjadi pada suatu daerah dengan asumsi dasar yang sama dengan asumsi pada model endemik SIR dengan imigrasi dan vaksinasi menurut Piccolo dan Billings [15].
Telah diasumsikan populasi konstan, sehingga jumlah individu pada popu-lasi tersebut tetap atau S(t) +I(t) +R(t) =N. Tingkat kelahiran pada populasi tersebut sebesar µ1, sedangkan tingkat individu yang masuk ke daerah tersebut (imigran) sebesar µ2. Tingkat kematian dalam tiap kelompok sama dengan de-ngan tingkat kelahiran dan tingkat imigrasi yaitu (µ1 +µ2). Tingkat vaksinasi pada individu lahir adalahσ1, sedangkan tingkat vaksinasi pada individu imigran adalah σ2 dengan 0 ≤σ1 ≤1 dan 0≤σ2 ≤1. Pada Piccolo dan Billings [15] di-asumsikan keefektifan vaksin 100%, namun pada penelitian ini didi-asumsikan bah-wa keefektifan vaksin tidak 100%. Oleh karena itu terdapat individu yang gagal vaksin dengan tingkat kegagalan vaksin sebesar θ.Tingkat kegagalan vaksin ter-sebut bernilai 0 ≤θ ≤1. Individu yang telah berhasil divaksin langsung masuk pada kelompokR, sedangkan individu yang mengalami kegagalan vaksin kembali ke kelompok S.
commit to user
kat kontak rata-rata tersebut. Guimaraens dan Code¸co [6] menyebutkan bahwa faktor sanitasi merupakan suatu fungsi linear kontinu yang mendeskripsikan efek sanitasi terhadap tingkat kontak rata-rata. Dengan demikian fungsi tersebut dapat didefinisikan sebagai c(H) = β−αH, dengan β merupakan tingkat kontak rata-rata,α merupakan sebuah konstanta proporsionalitas yang bernilai 0< α≤ β dan H merupakan tingkat sanitasi yang bernilai 0 ≤ H ≤ 1. Oleh karena itu kemungkinan jumlah individususceptible yang pindah ke kelompokI sebesar
(β−αH)SI
N .
Perubahan jumlah individu kelompokS setiap saat adalah jumlah individu lahir serta imigran sebesar (µ1 +µ2)N dikurangi dengan jumlah individu lahir dan imigran yang telah sukses divaksin sebesar (1−θ)(σ1µ1+σ2µ2)N. Jumlah individu kelompokS juga berkurang karena adanya individu yang terinfeksi atau pindah ke kelompok I sebesar (β−αH)SI
N serta adanya kematian pada kelompok S
sejumlah (µ1+µ2)S. Oleh karena itu perubahan jumlah individu pada kelompok
S setiap saat dapat diekspresikan sebagai
dS
dt = (µ1+µ2)N −(1−θ)(σ1µ1 +σ2µ2)N −(µ1+µ2)S−
(β−αH)SI
N . (4.1)
Individu pada kelompok I berasal dari individu pada kelompok S yang terinfeksi sebesar (β−αH)SI
N . Jumlah individu pada kelompok I berkurang karena
adanya kematian alami yang terjadi pada kelompok I sebesar (µ1 +µ2)I dan adanya individu yang sembuh. Misal tingkat kesembuhan γ, jumlah individu yang sembuh dan ke dalam kelompokR sejumlahγI. Perubahan jumlah individu pada kelompok I setiap saat dapat diekspresikan sebagai
dI dt =
(β−αH)SI
N −(µ1+µ2)I−γI. (4.2)
Individu pada kelompokR berasal dari jumlah individu yang telah berhasil divaksin (baik individu lahir maupun imigran) dan jumlah individu yang sembuh sebesar γI. Jumlah individu pada kelompok R berkurang dengan adanya kema-tian pada kelompok R sebesar (µ1 +µ2)R. Dengan demikian perubahan jumlah individu pada kelompok R setiap saat dapat diekspresikan sebagai
dR
commit to user
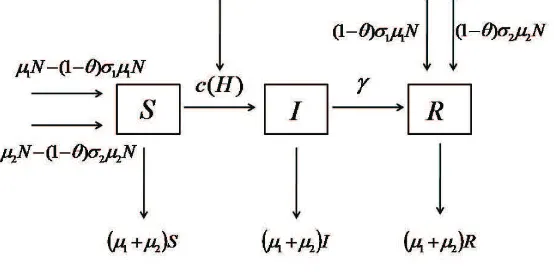
Dinamika populasi model SIR dengan imigrasi dan vaksinasi disajikan dalam Gambar 4.1. Dari persamaan (4.1), (4.2), dan (4.3) diperoleh model endemik
Gambar 4.1. Dinamika populasi model SIR dengan imigrasi, vaksinasi dan sanitasi
SIR dengan imigrasi, vaksinasi dan sanitasi yang dinyatakan sebagai
dS
dt = (µ1+µ2)N −(1−θ)(σ1µ1 +σ2µ2)N −(µ1+µ2)S−
(β−αH)SI N dI
dt =
(β−αH)SI
N −(µ1+µ2)I −γI dR
dt = (1−θ)(σ1µ1+σ2µ2)N +γI −(µ1+µ2)R.
(4.4)
Sistem persamaan diferensial (4.4) merupakan model endemik SIR dengan imi-grasi, vaksinasi dan sanitasi dengan parameter µ1, µ2, β, γ bernilai positif dan α merupakan suatu konstanta proporsionalitas. Penyelesaian dari sistem (4.4) be-rupa S(t), I(t) danR(t) yang menyatakan jumlah individu pada kelompokS,I,R setiap saat. Hal ini dapat digunakan untuk menjelaskan tentang penyebaran suatu penyakit.
4.2
Titik Kesetimbangan
commit to user
perubahan individu pada kelompokS dan I. Karena diasumsikan bahwa populasi konstan S(t) +I(t) +R(t) = N, maka nilai R(t) dapat diketahui apabila nilai
S(t) dan I(t) diketahui. Oleh karena itu sistem (4.4) dapat ditulis sebagai
dS
Dengan demikian berdasarkan Definisi 2.2.1 sistem akan setimbang jika
dS
H ≤ 1, maka sulit untuk menentukan titik kesetimbangannya. Sehingga harus dimasukkan suatu nilai H ke dalam sistem (4.4) agar dapat ditentukan titik kesetimbangannya. Untuk selanjutnya titik kesetimbangan hanya akan diselidiki pada H = 1. Hal ini dilakukan untuk mengetahui titik kesetimbangan dengan sanitasi maksimal (H = 1). Sedangkan untuk 0≤H <1 akan diselidiki melalui simulasi.
Untuk sanitasi maksimal atau H = 1, sistem (4.4) memenuhi keadaan se-timbang jika diperoleh. Dari persamaan (4.2) diperoleh dua jenis titik kesetimbangan dilihat dari ada tidaknya individu pada kelompok I.
1. Titik kesetimbangan bebas penyakit
E0 = (S0, I0, R0) =
commit to user
Nilai Ie yang tidak nol menunjukkan bahwa terdapat sejumlah individu
pada kelompok I yang menyebarkan penyakit dan menyebabkan endemik.
4.3
Kestabilan Titik Kesetimbangan
Menurut Bellomo dan Presziosi [2], kestabilan dari suatu sistem persamaan diferensial dapat ditentukan berdasarkan nilai eigen matriks Jacobian sistem yang dievaluasi pada titik kesetimbangannya. Karena diasumsikan populasi konstan
S+I +R = N, nilai R dapat diketahui apabila nilai S dan I telah diketahui. Dengan demikian sistem (4.4) dapat ditulis sebagai
dS
Matriks Jacobian dari sistem (4.5) adalah
J =
Seperti pada titik kesetimbangan, harus dimasukkan suatu nilai H pada sistem (4.5) agar dapat ditentukan nilai eigen dari matriksJ. Berikut kestabilan di titik kesetimbangan dengan H = 1.
1. Bebas penyakit
Matriks Jacobian sistem (4.5) untuk H = 1 yaitu
commit to user
Matriks Jacobian sistem (4.5) untuk H = 1 yaitu
J(Ee) =
ristik matriks Jacobian (4.7) yaitu
λ2+Aλ+B = 0 Nilai eigen dari matriks Jacobian (4.7) adalah λ1 = −A−
√
A2−4B
2 dan λ2 = −A+√A2−4B
2 . Berdasarkan Tabel 2.1 titik kesetimbangan tersebut akan sta-bil asimtotis apasta-bila nilai eigennya bernilai real negatif. Dengan demikian titik kesetimbangan akan stabil asimtotis apabila√A2−4B < Adan tidak stabil apabila√A2−4B > A dengan nilai A >0 dan A2
−4B >0. Selain itu titik kesetimbangan juga akan stabil asimtotis apabila bagian real nilai eigennya yang berbentuk kompleks konjugat bernilai negatif. Dengan demi-kian apabila nilai A >0 maka titik kesetimbangan stabil asimtotis, dengan
A2
commit to user
4.4
Penerapan Kasus
Penerapan kasus ini merupakan pengembangan dari Arum dan Kuntari [1]. Diberikan informasi tentang penyebaran penyakit cacar air. Penyakit cacar air merupakan penyakit infeksi yang menyebar melalui bersin, batuk, makanan dan bersentuhan langsung dengan luka yang diakibatkan oleh penyakit ini. Menurut Johnson [10] tingkat rata-rata kontak penyakit cacar air yaitu 0.65≤ β ≤0.85,
sedangkan tingkat kesembuhan penyakit sebesar γ = 0.3. Pada pembahasan ini ingin diketahui perilaku penyebaran penyakit cacar air dengan tingkat rata-rata kontak minimal, untuk itu digunakan tingkat rata-rata kontak minimal atauβ = 0.65. Sebagai contoh, suatu daerah yang memenuhi asumsi pada model memiliki jumlah penduduk yaitu N = 586039, dengan tingkat kelahiran sebesar µ1 = 0.01193 dan tingkat individu imigran sebesar µ2 = 0.02585. Tingkat individu lahir yang divaksin pada daerah tersebut sebesar σ1 = 0.7, sedangkan tingkat individu imigran yang divaksin sebesar σ2 = 0.6. Menurut Johnson [10], vaksin cacar air hanya memiliki keefektifan 99%. Dengan demikian tingkat kegagalan vaksin cacar air yaitu θ= 0.01.
Pada penerapan, ingin diketahui penyebaran penyakit apabila dengan ting-kat sanitasi maksimal atau H = 1. Diambil nilai α = 0.5, dengan demikian tingkat sanitasi dapat menurunkan tingkat rata-rata kontak dari 0.65 menjadi 0.15. Selanjutnya berdasarkan parameter yang telah diketahui, model (4.4) da-pat disajikan sebagai
commit to user
R
S
0 400
t
219 611 366 428 585 939
S R
Gambar 4.2. Jumlah individu S dan R
runan jumlah individu pada kelompok S, hal ini dikarenakan adanya individu susceptible yang tertular penyakit dan kemudian berpindah ke kelompok I. Pada awalnya tidak ada individu pada kelompok R, namun jumlah individu recovered meningkat karena adanya individu yang sembuh dari penyakit dan individu yang sukses divaksin. Jumlah individu pada kelompok R meningkat dari 0 sampai 366428 individu kemudian jumlah tersebut tetap sepanjang waktu. Hal ini ber-kebalikan dengan kelompokS yang menurun dari 585939 sampai 219611 individu kemudian jumlah tersebut tidak berubah atau tetap sepanjang waktu. Jumlah
0 24 100
t
0 100
I
commit to user
individuinfected yang tampak pada Gambar 4.3 menurun dari 100 individu sam-pai 0, kemudian jumlahnya tidak mengalami perubahan sepanjang waktu. Hal ini berarti bahwa penyakit tersebut sudah tidak menyebar lagi. Dari Gambar 4.2 dan 4.3 tampak bahwa untuk suatu waktu t jumlah individu S,I dan R akan tetap sepanjang waktu. Kondisi seperti ini disebut titik kesetimbangan.
Titik kesetimbangan merupakan suatu titik dimana tidak terjadi perubahan jumlah individu pada tiap kelompok. Pada kasus ini, hanya terdapat satu titik ke-setimbangan yaitu titik keke-setimbangan bebas penyakit pada (219611,0,366428). Tidak adanya individu pada kelompok I menunjukkan bahwa penyakit sudah tidak menyebar lagi atau bebas penyakit. Untuk tingkat sanitasi maksimal atau
H = 1, nilai eigen dari matriks Jacobian di titik kesetimbangan tersebut ada-lah (−0.28156,−0.03778). Berdasarkan Tabel 2.1 titik kesetimbangan tersebut bersifat stabil asimtotis. Selain dilihat dari nilai eigen matriks Jacobiannya, kes-tabilan di titik kesetimbangan dapat dilihat melalui perilaku trajektori di sekitar titik kesetimbangan pada bidang fase. Hal ini dilakukan untuk mengetahui ba-gaimana perilaku penyelesaian sistem disekitar titik kesetimbangan secara visual agar lebih mudah dipahami.
commit to user
tersebut stabil asimtotis maka kondisi dimana tidak ada individu yang terinfeksi akan terus berlangsung di daerah tersebut. Kondisi yang demikian sangat diha-rapkan karena penyakit tidak akan menyebar lagi.
-300 000 600 000I
-300 000
600 000
S
Gambar 4.4. Trajektori di sekitar titik kesetimbangan
Selanjutnya dilakukan simulasi pada nilaiH untuk mengetahui bagaimana pengaruh tingkat sanitasi terhadap penurunan puncak endemik. Hal tersebut dirasa penting untuk dijadikan sebagai acuan dalam mengambil tindakan pence-gahan untuk menurunkan puncak endemik. Dengan demikian diharapkan penye-baran penyakit yang terjadi akan berkurang. Simulasi pertama dilakukan pada
H = 0 atau tanpa sanitasi. Hasil simulasi menunjukkan bahwa jumlah individu infected meningkat dengan puncak endemik mencapai 6564 individu pada hari ke-31.
commit to user
dilakukan dengan menaikkan tingkat sanitasi menjadi H = 0.5. Ketika tingkat sanitasi dinaikkan menjadi 0.5, jumlah individu infected mencapai 393 individu pada hari ke-19. Hal ini berarti terjadi penurunan puncak endemik sebesar 6171 individu apabila sanitasi dinaikkan dari H = 0 sampai H = 0.5. Simulasi yang terakhir dilakukan pada H = 0.75. Jumlah individu infected maksimal menca-pai 153 individu pada hari ke-11. Dengan demikian terjadi penurunan jumlah individu infected sebesar 6411 individu.
Jumlah individu infeksi maksimum atau puncak endemik pada nilai H = 0,0.25,0.5,0.75,dan 1 disajikan pada Tabel 4.1. Berdasarkan Tabel 4.1 tampak
Tabel 4.1. Nilai puncak endemik dengan simulasi nilai H H Puncak endemik (Imaks) t (dalam hari)
bahwa semakin besar nilai H maka puncak endemik akan semakin menurun. Secara visual penurunan puncak endemik dapat dilihat pada Gambar 4.5. Pada Gambar 4.5 tampak bahwa semakin besar tingkat sanitasi, maka semakin singkat pula penyakit tersebut menyebar pada suatu wilayah.
31 150t
commit to user
Bab V
PENUTUP
5.1
Kesimpulan
Berdasarkan pembahasan dapat diambil kesimpulan sebagai berikut.
1. Model endemikSIR dengan imigrasi, vaksinasi dan sanitasi dapat dieks-presikan sebagai
2. Terdapat dua jenis titik kesetimbangan pada model SIR dengan imigrasi, vaksinasi dan sanitasi yaitu titik kesetimbangan endemik yaitu
Ee=
dan titik kesetimbangan bebas penyakit yaitu
E0 = (S0, I0, R0) =
commit to user