i
PEMODELAN MATEMATIS PENYEBARAN SARS-COV-2 YANG MELIBATKAN KELAS ASIMTOMATIK DAN KARANTINA
SERTA PENYELESAIAN NUMERISNYA DENGAN METODE RUNGE-KUTTA ORDE EMPAT
Skripsi
Diajukan Untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Matematika
Program Studi Matematika
Oleh:
Eduardus Mujiarto Sujasmin NIM: 183114016
PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI
UNIVERSITAS SANATA DHARMA YOGYAKARTA
2022
ii
MATHEMATICAL MODELING OF THE SPREAD OF SARS-COV-2 CONSIDERING ASYMPTOMATIC AND QUARANTINE CLASSES AND ITS NUMERICAL SOLUTIONS BASED ON THE FOURTH
ORDER RUNGE-KUTTA METHOD
Thesis
Presented as Partial Fulfillment of the
Requirements to Obtain the Degree of Sarjana Matematika Mathematics Study Program
Written by:
Eduardus Mujiarto Sujasmin Student Number: 183114016
MATHEMATICS STUDY PROGRAM DEPARTMENT OF MATHEMATICS FACULTY OF SCIENCE AND TECHNOLOGY
SANATA DHARMA UNIVERSITY YOGYAKARTA
2022
v
HALAMAN PERSEMBAHAN
“If you have a strong commitment to your goals and dreams, if you wake up every day with a passion to do your job, everything is possible.”
-Chantal Petitclerc-
Skripsi ini dipersembahkan untuk Tuhan Yesus Kristus, orang tua, dan keluarga tercinta.
vi
PERNYATAAN KEASLIAN KARYA
Dengan ini saya menyatakan dengan sesungguhnya bahwa skripsi yang saya tulis ini tidak memuat karya atau bagian karya orang lain kecuali yang disebutkan dalam daftar pustaka, sebagaimana layaknya karya ilmiah.
Yogyakarta, 24 Januari 2022
Eduardus Mujiarto Sujasmin
vii
LEMBAR PERNYATAAN PERSETUJUAN
PUBLIKASI KARYA ILMIAH UNTUK KEPENTINGAN AKADEMIS
Yang bertanda tangan di bawah ini, saya mahasiswa Universitas Sanata Dharma:
Nama : Eduardus Mujiarto Sujasmin NIM : 183114016
Demi kepentingan perkembangan ilmu pengetahuan, saya memberikan kepada Per- pustakaan Universitas Sanata Dharma karya ilmiah saya yang berjudul:
PEMODELAN MATEMATIS PENYEBARAN SARS-COV-2 YANG MELIBATKAN KELAS ASIMTOMATIK DAN KARANTINA
SERTA PENYELESAIAN NUMERISNYA DENGAN METODE RUNGE-KUTTA ORDE EMPAT
beserta perangkat yang diperlukan (bila ada). Dengan demikian, saya memberikan kepada Universitas Sanata Dharma untuk menyimpan, mengubah ke dalam bentuk media lain, mengelolanya dalam bentuk pangkalan data, mendistribusikan secara terbatas dan mempublikasikannya di Internet atau media lain untuk kepentingan akademis tanpa perlu meminta izin dari saya maupun memberikan royalti kepada saya selama tetap menyantumkan nama saya sebagai penulis.
Demikian pernyataan ini saya buat dengan sebenarnya.
Dibuat di Yogyakarta
Pada tanggal 24 Januari 2022 Yang menyatakan,
Eduardus Mujiarto Sujasmin
viii ABSTRAK
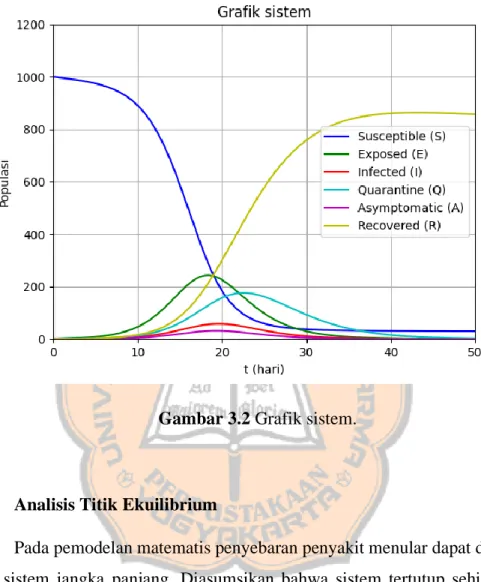
Skripsi ini memaparkan tentang pemodelan matematis penyebaran SARS- CoV-2 dengan mengembangkan model matematis yang mempertimbangkan kelas rentan (𝑆), kelas terpapar (𝐸), kelas terinfeksi (𝐼), kelas karantina atau isolasi (𝑄), kelas asimtomatik (𝐴), dan kelas sembuh (𝑅) sehingga model matematis yang dibangun berupa model 𝑆𝐸𝐼𝑄𝐴𝑅. Kelas karantina atau isolasi disiapkan untuk kelas terpapar dan kelas terinfeksi. Individu asimtomatik dapat pindah ke kelas terinfeksi setelah menunjukkan gejala pada beberapa waktu atau sembuh tanpa menjalani pengobatan. Selanjutnya akan ditentukan bilangan reproduksi. Analisis sensitivitas menunjukkan bahwa model lebih sensitif terhadap laju transmisi dari kelas terpapar ke kelas terinfeksi daripada laju transmisi dari kelas rentan ke kelas terpapar. Model disajikan dalam bentuk sistem persamaan diferensial nonlinear orde pertama dan diselesaikan secara numeris dengan metode Runge-Kutta orde empat.
Kata kunci: SARS-CoV-2, analisis sensitivitas, Runge-Kutta orde empat.
ix ABSTRACT
This thesis describes the mathematical modeling of the spread of SARS- CoV-2 by developing a mathematical model that considering the susceptible class (𝑆), exposed class (𝐸), infected class (𝐼), quarantine or isolation class (𝑄), asymp- tomatic class (𝐴), and recovered class (𝑅) so that the mathematical model built is in the form of a 𝑆𝐸𝐼𝑄𝐴𝑅 model. Quarantine or isolation classes are prepared for exposed classes and infected classes. Asymptomatic individuals may transfer to the infected class after showing symptoms for some time or recovered without undergo treatment. Next, the reproduction number will be determined. The sensitivity ana- lysis shows that the model is more sensitive to the transmission rate from the ex- posed class to the infected class rather than the transmission rate from the suscepti- ble class to the exposed class. The model is presented in the form of a first-order nonlinear differential equation system and is solved numerically using the fourth- order Runge-Kutta method.
Keywords: SARS-CoV-2, sensitivity analysis, fourth-order Runge-Kutta method.
x
KATA PENGANTAR
Puji dan syukur penulis panjatkan kepada Tuhan Yang Maha Esa sebab berkat dan kasih karunia-Nya penulis dapat menyelesaikan skripsi yang berjudul “Pemod- elan Matematis Penyebaran SARS-CoV-2 yang Melibatkan Kelas Asimtomatik dan Karantina serta Penyelesaian Numerisnya dengan Metode Runge-Kutta Orde Em- pat”. Penyusunan skripsi ini merupakan salah satu syarat untuk memperoleh gelar Sarjana Matematika pada Fakultas Sains dan Teknologi, Universitas Sanata Dharma. Penulis menyadari bahwa penulisan skripsi ini tidak lepas dari bantuan banyak pihak. Oleh karena itu, penulis ingin mengucapkan terima kasih kepada:
1. Bapak Prof. Ir. Sudi Mungkasi, S.Si., M.Math.Sc., Ph.D. selaku dosen pem- bimbing dan Dekan Fakultas Sains dan Teknologi, Universitas Sanata Dharma yang dengan sabar dan semangat membantu penulis me- nyelesaikan skripsi ini.
2. Ibu Maria V. A. Herawati, S.Si., M.Si., selaku Dosen Pembimbing Akade- mik yang membantu dan menyemangati penulis dalam menyelesaikan per- soalan selama penulis berdinamika pada Program Studi Matematika.
3. Romo Prof. Dr. Frans Susilo, SJ., Bapak Hartono, S.Si., M.Sc., Ph.D., Ibu Dr. Lusia Krismiyati Budiasih, S.Si., M.Si., Bapak Ir. Ig. Aris Dwiatmoko, M.Sc., Bapak Dr. rer. nat, Herry P. Suryawan, M.Si., dan Bapak Ricky Ad- itya, M.Sc. selaku dosen-dosen pada Program Studi Matematika yang telah memberikan begitu banyak ilmu pengetahuan kepada penulis selama menempuh pendidikan pada Program Studi Matematika.
4. Orang tua saya tercinta Bapak Yance dan mama Regina yang selalu mem- berikan begitu banyak semangat, doa, bantuan dan motivasi kepada penu- lis.
5. Saudara dan saudari saya tercinta Kakak Nardi Sujasmin, Kakak Steny Sujasmin, Kakak Yugen Sujasmin, Kakak Arni Sujasmin dan adik saya Tria Sujasmin serta Kakak Ipar saya Kakak Yuni, Kakak Engki dan Kakak Ana yang selalu memberikan senyum semangat di setiap keluh kesah saya.
6. Suster Magdalena Isa, SSpS. dan Keponakan-keponakan saya Andhika
xi
Aman, Beatrix Primajaya, Marzello Sujasmin dan Ghianna Sujasmin yang selalu memberikan semangat yang berkobar kepada penulis.
7. Sahabat-sahabat saya Charmie Wadjong, Rifqi Afuwwu, Dean Ananta, Jati Al-Karim, Vincentia Deby, Eka Yulia, Indri Belu, Jeli Agho, Monica Maya, Reni Hayon, Vion Menong, Amel Hagul, Cantika Garus, Neri Soka, Surya Andhika, dan teman-teman Pergogo yang selalu menemani di setiap keluh kesah dan curhatan penulis selama menempuh perkuliahan dari awal hingga skripsi ini selesai.
8. Teman-teman Program Studi Matematika atas kekeluargaan, kebersamaan dan kehangatan selama masa perkuliahan.
9. Semua pihak yang telah membantu penulis dalam menyelesaikan skripsi ini yang tidak dapat disebutkan satu persatu.
Penulis berharap segala bentuk cinta dan kepedulian serta bantuan yang telah penulis terima mendapat balasan dari Yang Maha Esa. Penulis menyadari bahwa skripsi ini masih jauh dari kata sempurna akan tetapi besar harapan penulis agar skripsi ini dapat bermanfaat bagi pembaca.
Yogyakarta, 24 Januari 2022 Penulis,
Eduardus Mujiarto Sujasmin
xii DAFTAR ISI
HALAMAN JUDUL………i
HALAMAN JUDUL DALAM BAHASA INGGRIS………...ii
HALAMAN PERSETUJUAN PEMBIMBING……….iii
HALAMAN PENGESAHAN……….iv
HALAMAN PERSEMBAHAN………...v
PERNYATAAN KEASLIAN KARYA………..vi
LEMBAR PERNYATAAN PERSETUJUAN PUBLIKASI KARYA ILMIAH UNTUK KEPENTINGAN AKADEMIS………...vii
ABSTRAK………viii
ABSTRACT.………...ix
KATA PENGANTAR………..x
DAFTAR ISI………..xii
BAB I PENDAHULUAN……….1
A. Latar Belakang………...…… 1
B. Rumusan Masalah………..5
C. Batasan Masalah……….5
D. Tujuan Penulisan………6
E. Manfaat Penulisan………..6
F. Metode Penelitian………...6
G. Sistematika Penulisan………6
BAB II PEMODELAN MATEMATIS………....8
A. Pengertian Model Matematis………...8
B. Persamaan Diferensial………...10
C. Topik-topik terkait………...16
BAB III PEMODELAN MATEMATIS PENYEBARAN SARS-COV-2……….38
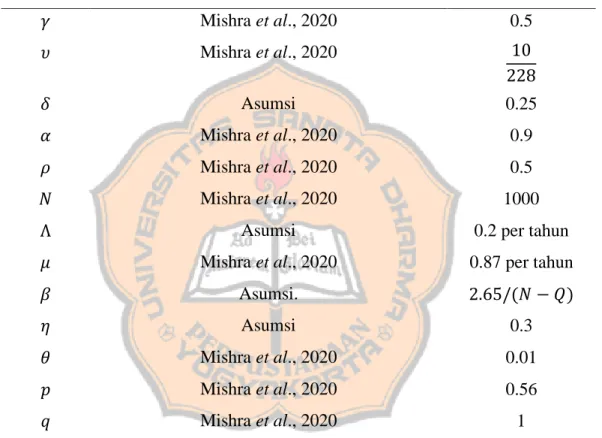
A. Asumsi-asumsi yang Digunakan………...38
xiii
B. Pembentukkan Model………...40
C. Analisis Titik Ekuilibrium………...44
BAB IV PENYELESAIAN NUMERIS MODEL MATEMATIS…...66
A. Skema Runge-Kutta Orde Empat untuk penyebaran SARS-Cov-2…66 B. Hasil Simulasi………... 69
C. Perbandingan Hasil Aproksimasi………...76
BAB V KESIMPULAN DAN SARAN……...82
A. Kesimpulan………...82
B. Saran………...83
DAFTAR PUSTAKA………...84
LAMPIRAN………...86
1 BAB I PENDAHULUAN
Pada bagian ini akan disajikan latar belakang, rumusan masalah, batasan masalah, tujuan penulisan, manfaat penulisan, metode penelitian, dan sistematika penulisan.
A. Latar Belakang
Pada bulan Desember 2019, muncul kasus pertama sebuah virus baru ber- nama Severe Acute Respiratory Syndrome Novel Coronavirus 2 (SARS-CoV-2) yang terdeteksi di Wuhan, sebuah kota di China. Salah satu varian virus SARS- CoV-2 menyebabkan penyakit Coronavirus disease 2019 atau COVID-19. Infeksi virus COVID-19 ini menunjukkan peningkatan terus menerus. Jumlah individu yang terinfeksi virus ini meningkat secara global dan memicu keadaan darurat kesehatan global. Salah satu penyebab tingginya tingkat penyebaran virus ini ada- lah proporsi yang signifikan dari individu yang mudah terkena penyakit. Sebuah studi khusus di Jepang menunjukkan 41,6% individu adalah asimtomatik yaitu orang tanpa gejala (Nishiura et al., 2020). COVID-19 merupakan salah satu jenis penyakit infeksi. Mekanisme penularan dari penginfeksi kepada yang rentan. Ham- pir semua penyakit infeksi dan penyebaran penyakit melalui rantai infeksi sudah diketahui. Namun demikian, interaksi penularan pada suatu populasi sangat kom- pleks sehingga sulit memahami dinamika penyebaran penyakit berskala besar tanpa struktur formal dari model matematis (Djafri, 2015: 1-2).
Pemodelan matematis adalah usaha untuk menggambarkan dengan seder- hana fenomena real yang terjadi di kehidupan nyata ke dalam suatu bentuk ma- tematika. Suatu model matematis dikatakan baik jika model matematis yang ter- bentuk dapat merepresentasikan atau mewakili suatu permasalahan dalam ke- hidupan nyata (Giordano et al., 2014). Penyebaran penyakit biasanya memiliki model matematis dengan konsep yang sama yaitu compartmental epidemiology (pembagian kelas) yang menggambarkan penyebaran penyakit untuk masing-mas- ing kelas (Schoenbach and Wayne, 2000). Suatu populasi akan dibagi menjadi
beberapa kelas mewakili tahapan-tahapan yang berbeda dari suatu penyakit.
Pemodelan matematis pada penyebaran penyakit infeksi telah menjadi bagian dari pengambilan keputusan kebijakan epidemiologi di banyak negara maju, termasuk Inggris, Belanda, Kanada dan Amerika Serikat. Oleh karena itu, pendekatan pemodelan menjadi sangat penting untuk pengambilan keputusan tentang program pengendalian penyakit infeksi.
Skripsi ini akan membahas tentang model matematis penyebaran SARS- CoV-2 yang sedang menjadi pandemi di berbagai negara di dunia. Pemodelan epi- demiologi berkenaan dengan pemodelan matematis dimana populasi dibagi ke da- lam kelas-kelas yang didasarkan pada status epidemiologi, misalnya yang rentan, terinfeksi dan yang sudah sembuh. Pergerakan antar kelas menjadi terinfeksi, berkembang terus, lalu pulih direpresentasikan dengan persamaan diferensial.
Model dasar dalam epidemiologi, yaitu model 𝑆𝐸𝐼𝑅, dapat digunakan untuk mem- perkirakan jumlah total populasi yang terinfeksi. Namun demikian, model ini tidak begitu akurat untuk memprediksi prevalensi penyakit COVID-19. Oleh karena itu, dalam skripsi ini akan dilibatkan kelas asimtomatik dan karantina/isolasi ke dalam model 𝑆𝐸𝐼𝑅. Model yang dibangun berupa model 𝑆𝐸𝐼𝑄𝐴𝑅, yaitu populasi yang rentan terpapar (𝑆), populasi yang terpapar (𝐸), populasi yang terinfeksi namun bersifat asimtomatik (𝐴), populasi yang terinfeksi (𝐼), populasi yang melakukan karantina/isolasi (𝑄), dan populasi yang sembuh (𝑅). Alur penyebaran SARS- CoV-2 dimulai dari (𝑆) yang merupakan populasi sehat yang mengalami penularan dan pindah ke kelas (𝐸) atau kelas terpapar. Setelah terinfeksi virus, ada individu asimtomatik (orang tanpa gejala) yang dikategorikan ke dalam kelas (𝐴). Orang yang menunjukkan gejala dipindahkan ke kelas (𝐼) yaitu kelas terinfeksi. Individu asimtomatik tidak menunjukkan adanya gejala penyakit dalam periode tertentu dan sulit mengidentifikasinya. Probabilitas dari individu terpapar menunjukkan gejala dinotasikan dengan 𝑝 dan 𝑞 adalah probabilitas individu asimtomatik menu- larkan virus. Seorang individu dari kelas asimtomatik dapat menunjukkan gejala setelah beberapa waktu dan pindah ke kelas terinfeksi (𝐼) atau beberapa individu tetap asimtomatik dan sembuh dari virus. Laju kesembuhan individu asimtomatik dinotasikan 𝛾. Orang yang terinfeksi mungkin menjalani perawatan berupa isolasi.
Pada model ini, individu tersebut akan pindah ke kelas isolasi/karantina (𝑄). Akan tetapi, beberapa individu tidak melakukan isolasi lalu sembuh dengan sendirinya dan pindah ke kelas (𝑅). Laju kesembuhan dari kelas terinfeksi dinotasikan 𝜐 dan 𝛿 notasi laju kesembuhan dari kelas karantina. Laju karantina dari kelas terinfeksi dinotasikan dengan 𝛼 dan laju transmisi dari kelas asimtomatik ke kelas terinfeksi 𝜌. Diasumsikan individu yang meninggal tidak menularkan virus dan individu yang telah sembuh tidak dapat tertular virus kembali. Oleh karena itu, kelas yang sembuh (𝑅) terdiri dari orang-orang yang mati atau sembuh dari virus dan dipisahkan dari individu yang rentan setelah mereka sembuh atau meninggal.
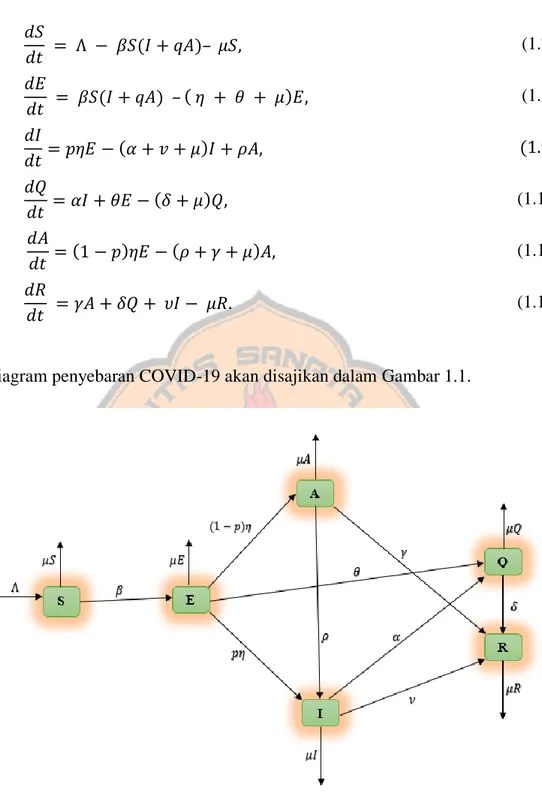
Model matematis di atas dapat ditulis sebagai sistem persamaan diferensial sebagai berikut (Mishra et al., 2020):
𝑑𝑆
𝑑𝑡 = Ʌ − 𝛽0 𝑆(𝐼 + 𝑞𝐴)
𝑁 − 𝑄 – 𝜇𝑆, (1.1)
𝑑𝐸
𝑑𝑡 = 𝛽0 𝑆(𝐼 + 𝑞𝐴)
𝑁 − 𝑄 – ( 𝜂 + 𝜃 + 𝜇)𝐸, (1.2)
𝑑𝐼
𝑑𝑡= 𝑝𝜂𝐸 − (𝛼 + 𝑣 + 𝜇)𝐼 + 𝜌𝐴, (1.3)
𝑑𝑄
𝑑𝑡 = 𝛼𝐼 + 𝜃𝐸 − (𝛿 + 𝜇)𝑄, (1.4)
𝑑𝐴
𝑑𝑡 = (1 − 𝑝)𝜂𝐸 − (𝜌 + 𝛾 + 𝜇)𝐴, (1.5)
𝑑𝑅
𝑑𝑡 = 𝛾𝐴 + 𝛿𝑄 + 𝜐𝐼 − 𝜇𝑅. (1.6) Populasi bebas dari virus sampai jumlah individu terinfeksi 𝐼(0) masuk ke dalam populasi saat 𝑡 = 0, 𝑅(0) = 0, 𝑆(0) = 𝑁, 𝑄(0) = 0, 𝐴(0) = 0 dan 𝐸(0) = 0 dimana {(𝑆, 𝐸, 𝐼, 𝑄, 𝐴, 𝑅): 𝑆 > 0, 𝐸 > 0, 𝐼 > 0, 𝑄 ≥ 0, 𝐴 ≥ 0, 𝑅 ≥ 0}. Total pop- ulasi dinotasikan dengan 𝑁 yang akan meningkat dengan laju kelahiran alami dengan notasi Ʌ dan berkurang dengan laju kematian alami dengan notasi 𝜇. Laju transmisi dari kelas rentan ke kelas terpapar dilambangkan dengan 𝛽0. Laju infeksi dinotasikan dengan 𝜂dan laju isolasi/karantina dari individu terpapar dinotasikan dengan 𝜃. Untuk menyederhanakan persamaan di atas disubstitusikan β = 𝛽0
𝑁−𝑄
dengan β adalah laju penularan per kapita sehingga persamaan (1.1 − 1.6) menjadi:
𝑑𝑆
𝑑𝑡 = Ʌ − 𝛽𝑆(𝐼 + 𝑞𝐴)– 𝜇𝑆, (1.7)
𝑑𝐸
𝑑𝑡 = 𝛽𝑆(𝐼 + 𝑞𝐴) – ( 𝜂 + 𝜃 + 𝜇)𝐸, (1.8) 𝑑𝐼
𝑑𝑡= 𝑝𝜂𝐸 − (𝛼 + 𝑣 + 𝜇)𝐼 + 𝜌𝐴, (1.9)
𝑑𝑄
𝑑𝑡 = 𝛼𝐼 + 𝜃𝐸 − (𝛿 + 𝜇)𝑄, (1.10)
𝑑𝐴
𝑑𝑡 = (1 − 𝑝)𝜂𝐸 − (𝜌 + 𝛾 + 𝜇)𝐴, (1.11)
𝑑𝑅
𝑑𝑡 = 𝛾𝐴 + 𝛿𝑄 + 𝜐𝐼 − 𝜇𝑅. (1.12)
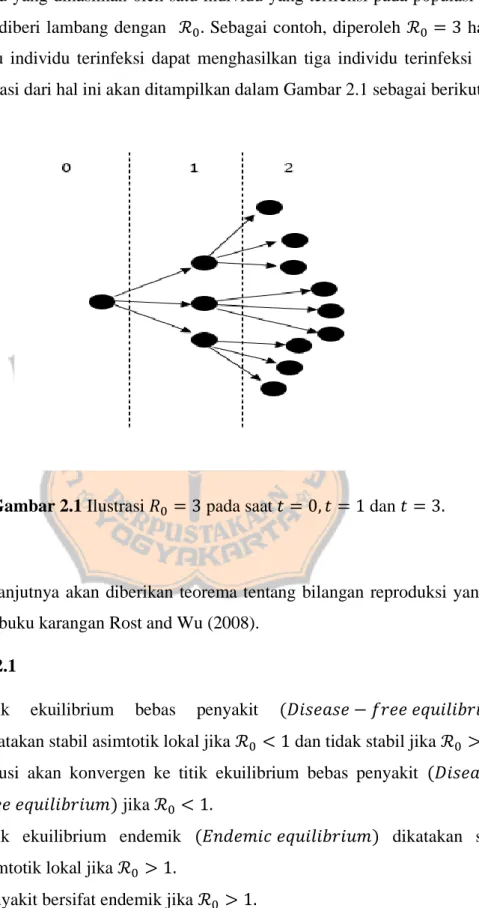
Diagram penyebaran COVID-19 akan disajikan dalam Gambar 1.1.
Gambar 1.1: Diagram penyebaran COVID-19.
Metode Runge-Kutta adalah metode penyelesaian masalah nilai awal persa- maan diferensial linear atau nonlinear dengan pendekatan iterasi numeris (Fowkes and Mahony, 1994). Metode Runge-Kutta orde empat memiliki ketelitian yang lebih tinggi dibandingkan metode Runge-Kutta orde di bawahnya.
Untuk masalah nilai awal berbentuk 𝑑𝑦
𝑑𝑥 = 𝑓(𝑡, 𝑦),
(1.9) 𝑦(𝑡0) = 𝑦0,
metode Runge-Kutta orde empat mempunyai persamaan (Burden and Faires, 2011):
𝑦𝑛+1 = 𝑦𝑛 + ℎ
6(𝑓1+ 2𝑓2+ 2𝑓3+ 𝑓4), (1.10) dengan
𝑓1 = 𝑓(𝑡𝑛, 𝑦𝑛), (1.11)
𝑓2= 𝑓 (𝑡𝑛+ℎ
2, 𝑦𝑛 +ℎ
2𝑓1), (1.12)
𝑓3= 𝑓 (𝑡𝑛+ℎ
2, 𝑦𝑛 +ℎ
2𝑓2), (1.13)
𝑓4 = 𝑓(𝑡𝑛+ ℎ, 𝑦𝑛+ ℎ𝑓3), (1.14) dengan indeks 𝑛 adalah bilangan cacah 0,1,2,3,4, …. .
B. Rumusan Masalah
Rumusan masalah yang akan dibicarakan pada skripsi ini adalah:
1. Bagaimana model matematis penyebaran virus SARS-CoV-2?
2. Bagaimana penyelesaian numeris model matematis penyebaran virus SARS- CoV-2 dengan metode Runge-Kutta orde empat?
C. Batasan Masalah
Pembahasan skripsi ini dibatasi pada masalah penyebaran virus dari manu- sia yang terinfeksi ke manusia lainnya dan penyelesaian numerisnya dengan metode Runge-Kutta orde empat.
D. Tujuan Penulisan
Berdasarkan rumusan masalah di atas, tujuan penulisan skripsi ini adalah:
1. Mendapatkan model matematis penyebaran virus SARS-CoV-2
2. Mendapatkan penyelesaian numeris model matematis penyebaran virus SARS- CoV-2 dengan metode Runge-Kutta orde empat.
E. Manfaat Penulisan
Manfaat yang diperoleh dari penulisan skripsi ini adalah penulis akan mem- peroleh model dan penyelesaian numeris dari penyebaran virus SARS-CoV-2.
Penyelesaian model tersebut diharapkan mampu menyelesaikan masalah-masalah yang berkaitan dengan penyebaran SARS-CoV-2. Hal ini dapat membantu badan kesehatan dan pemerintah untuk membuat keputusan dan kebijakan untuk memini- malisir penyebaran virus SARS-CoV-2.
F. Metode Penelitian
Metode penelitian yang digunakan dalam skripsi ini adalah metode studi kepustakaan, yaitu dengan membaca dan mempelajari buku, jurnal ilmiah dan artikel ilmiah terkait serta menyelesaikan secara numeris model matematis penyeb- aran SARS-COV2. Simulasi program menggunakan pemrograman Python.
G. Sistematika Penulisan
Sistematika penulisan skripsi ini adalah sebagai berikut:
BAB I: PENDAHULUAN A. Latar Belakang B. Rumusan Masalah C. Batasan Masalah D. Tujuan Penulisan E. Manfaat Penulisan F. Metode Penelitian
G. Sistematika Penulisan
BAB II: PEMODELAN MATEMATIS A. Pengertian Model Matematis B. Persamaan Diferensial C. Topik-topik terkait
BAB III: PEMODELAN MATEMATIS PENYEBARAN SARS-COV-2 A. Asumsi-asumsi yang digunakan
B. Pembentukan Model C. Analisis Titik Ekuilibrium
BAB IV: PENYELESAIAN NUMERIS MODEL MATEMATIS A. Skema Runge-Kutta Orde Empat untuk SARS-CoV-2 B. Hasil Simulasi
C. Perbandingan Hasil Aproksimasi BAB V: PENUTUP
A. Kesimpulan B. Saran
8 BAB II
PEMODELAN MATEMATIS
Pada bab ini akan dibahas mengenai definisi-definisi dan teorema-teorema yang menjadi landasan yang akan digunakan pada bab III. Pembahasan meliputi pengertian model matematis, persamaan diferensial dan topik-topik terkait.
Berikut akan dibahas definisi dan teorema tersebut di atas.
A. Pengertian Model Matematis
Model matematis merupakan representasi dengan sederhana fenomena real yang terjadi di kehidupan nyata ke dalam suatu bentuk matematika. Suatu model matematis dikatakan baik jika model matematis yang terbentuk dapat merepresen- tasikan atau mewakili suatu permasalahan dalam kehidupan nyata (Giordano et al., 2014).
Berikut langkah-langkah menyusun suatu model matematis menurut Giordano (2014, 62-65).
1. Mengidentifikasi suatu masalah nyata.
Langkah ini merupakan proses awal yang harus dilakukan dalam menyusun suatu model. Dari fenomena yang telah diamati dapat diidentifikasi masalah yang akan kita selesaikan secara matematis. Langkah ini membutuhkan pemahaman yang tinggi mengenai permasalahan yang akan diselesaikan secara matematis.
2. Menentukan asumsi yang sesuai untuk digunakan.
Pada langkah ini akan dipertimbangkan aspek-aspek yang turut serta mempengaruhi permasalahan yang akan diselesaikan. Pada dasarnya menetukan asumsi merupakan representasi dari proses berpikir yang akan disajikan dalam model. Oleh karena itu, asumsi akan dibagi menjadi dua bagian, yaitu:
a. Menentukan variabel
Variabel sendiri merupakan faktor-faktor yang mempengaruhi per- masalahan yang akan diselesaikan. Menentukan variabel penting yang ter- libat dalam model tentunya akan membuat model yang telah diperoleh akan merepresentasikan secara nyata permasalahan yang akan diselesaikan.
b. Menentukan hubungan antar variabel.
Suatu permasalahan pada dunia nyata sangat kompleks. Oleh karena itu, penting menentukan hubungan antar variabel agar dapat menyeder- hanakan suatu fenomena jika diperlukan.
3. Membentuk model matematis.
Setelah memiliki pemahaman mengenai permasalahan yang akan diselesaikan, menentukan variabel dan hubungan antar variabel maka langkah se- lanjutnya adalah membentuk model. Model yang akan dibentuk dapat berupa per- samaan atau sistem persamaan. Pembentukan model merupakan bagian yang paling sulit sehingga perlu dianalisis kembali asumsi-asumsi yang digunakan agar model yang dihasilkan sesuai dan realistis.
4. Menentukan solusi
Tidak semua model matematis yang telah dibentuk dapat dicari solusinya dengan mudah. Oleh karena itu dapat dilakukan penyederhanaan kembali asumsi- asumsi yang telah dibuat pada langkah dua atau kembali merumuskan masalah pada langkah satu.
5. Verifikasi model
Hal ini berhubungan dengan asumsi-asumsi yang telah dirumuskan sebe- lumnya. Model yang telah dibentuk harus menjawab permasalahan yang diidentif- ikasikan sebelumnya serta realistis dan dapat diterima oleh akal.
6. Implementasi model
Langkah selanjutnya adalah dengan memasukkan data yang dimiliki ke model yang telah dibuat. Tujuannya adalah untuk mengetahui seberapa akurat model yang telah dibentuk dalam memberi penyelesaian dan menjadi bahan per- timbangan dalam mengambil keputusan.
7. Mempertahankan model
Pada tahap ini harus ditegaskan bahwa model yang dibentuk berdasarkan asumsi-asumsi yang dibuat pada langkah dua. Permasalahan yang sama dapat dibentuk model yang berbeda karena bergantung pada asumsi-asumsi yang dibuat.
Oleh karena itu, agar model valid harus berpegang pada asumsi-asumsi yang telah dirumuskan pada langkah dua.
B. Persamaan Diferensial
Pada subbab ini akan dijelaskan mengenai definisi persamaan diferensial dan contoh persamaan diferensial dan topik-topik terkait.
1. Persamaan Diferensial
Persamaan diferensial adalah persamaan matematis yang melibatkan fungsi satu variabel atau lebih dan satu atau beberapa turunan fungsi yang tidak diketahui.
Contoh 2.2.1
𝑑𝑦
𝑑𝑡 = 𝑘𝑦 (2.2.1)
𝑑2𝑝 𝑑𝑡2 +𝑑𝑝
𝑑𝑡+ 𝑝 = 1 (2.2.2)
𝜕𝑢
𝜕𝑡 + 𝑘𝜕𝑢
𝜕𝑥 = 0 (2.2.3)
𝜕3𝑣
𝜕𝑥3+𝜕2𝑣
𝜕𝑦2+𝜕𝑣
𝜕𝑧+ 𝑣 = 0. (2.2.4)
Contoh 2.2.2
Tentukan penyelesaian persamaan diferensial biasa berikut.
𝑑𝑦
𝑑𝑡 = 𝑡 − 250 sehingga persamaan di atas dapat ditulis
𝑑𝑦 = (𝑡 − 250)𝑑𝑡 dengan mengintegralkan kedua ruas didapatkan
𝑦 =𝑡2
2 − 250𝑡 + 𝐶 dengan 𝐶 sebarang konstanta.
2. Persamaan Diferensial Biasa Definisi 2.2.2 (Ross, 1989)
Persamaan diferensial biasa adalah persamaan diferensial yang melibatkan satu atau lebih turunan fungsi yang tidak diketahui dan satu variabel bebas.
Contoh 2.2.3
Persamaan (2.2.1) dan (2.2.2) adalah contoh persamaan diferensial biasa.
Persamaan (2.2.1) adalah persamaan diferensial biasa dengan variabel bebas 𝑡 dan variabel terikat 𝑦 sedangkan persamaan (2.2.2) adalah persamaan diferensial biasa dengan variabel bebasnya 𝑡 dan variabel terikatnya 𝑝.
3. Persamaan Diferensial Parsial
Pada subbab ini akan dijelaskan mengenai definisi persamaan diferensial parsial dan contoh persamaan diferensial parsial.
Definisi 2.2.3 (Ross, 1989)
Persamaan diferensial parsial adalah persamaan diferensial yang memuat derivatif dari fungsi yang tidak diketahui dimana fungsi tersebut bergantung pada dua atau lebih variabel bebas.
Contoh 2.2.4
Persamaan (2.2.3) dan (2.2.4) adalah contoh persamaan diferensial parsial.
Persamaan (2.2.3) adalah persamaan diferensial parsial dengan variabel bebas 𝑡 dan 𝑥 serta variabel terikat 𝑦. Persamaan (2.2.4) adalah persamaan diferensial parsial dengan variabel bebas 𝑥, 𝑦 dan 𝑧 serta variabel terikat 𝑣.
4. Orde Persamaan Diferensial
Pada bagian ini akan dibahas mengenai definisi orde persamaan diferensial beserta contohnya.
Definisi 2.2.4
Orde persamaan diferensial adalah tingkat tertinggi yang muncul pada turunan fungsi yang terlibat dalam persamaan diferensial.
Contoh 2.2.5
Persamaan diferensial (2.2.1) adalah persamaan diferensial biasa orde satu.
Untuk persamaan diferensial (2.2.2) adalah persamaan diferensial biasa orde 2. Per- samaan diferensial (2.2.3) adalah persamaan diferensial parsial orde satu dan per- samaan diferensial (2.2.4) adalah persamaan diferensial parsial orde tiga.
5. Persamaan Diferensial Biasa Linear Orde ke-𝒏
Pada bagian ini akan dijelaskan definisi persamaan diferensial biasa linear orde ke-𝑛 beserta contohnya.
Definisi 2.2.5 (Ross, 1989)
Sebuah persamaan diferensial biasa linear orde ke-𝑛 dengan variabel bebas 𝑥 dan variabel terikat 𝑦 adalah persamaan yang dapat dinotasikan dalam bentuk
𝑎0(𝑥)𝑑𝑛𝑦
𝑑𝑥𝑛+ 𝑎1(𝑥)𝑑𝑛−1𝑦
𝑑𝑥𝑛−1+ ⋯ + 𝑎𝑛−1(𝑥)𝑑𝑦
𝑑𝑥+ 𝑎𝑛(𝑥)𝑦 = 𝑏(𝑥), (2.2.5)
dengan 𝑎0 tidak sama dengan nol.
Contoh 2.2.6
𝑑2𝑦
𝑑𝑥2 + 10𝑑𝑦
𝑑𝑥+ 12𝑦 = 0, (2.2.6)
𝑑3𝑦
𝑑𝑥3+ 𝑥2𝑑2𝑦
𝑑𝑥2+ 𝑥3𝑑𝑦
𝑑𝑥 = 𝑥𝑒𝑥. (2.2.7)
Contoh di atas merupakan PDB linear karena turunan variabel 𝑦 hanya memiliki satu variabel bebas 𝑥 dan tidak ada perkalian antara 𝑦 dan turunannya.
6. Persamaan Diferensial Biasa Nonlinear
Pada bagian ini akan dijelaskan definisi persamaan diferensial biasa nonlin- ear beserta contohnya.
Definisi 2.2.6 (Ross, 1989)
Persamaan diferensial biasa nonlinear adalah persamaan diferensial biasa yang bukan linear.
Contoh 2.2.7
𝑑2𝑦
𝑑𝑥2+ 10𝑑𝑦
𝑑𝑥+ 12𝑦2 = 0. (2.2.7)
Persamaan (2.2.7) adalah persamaan diferensial biasa nonlinear sebab variabel teri- kat 𝑦 mengandung pangkat dua dengan bentuk 𝑦2.
𝑥2𝑑2𝑦
𝑑𝑥2+ (𝑑𝑦 𝑑𝑥)
3
= 0. (2.2.8)
Persamaan (2.2.8) adalah persamaan diferensial biasa nonlinear terdapat perkalian antar turunan dari variabel terikat 𝑦 yang muncul dalam bentuk (𝑑𝑦
𝑑𝑥)3. 𝑑3𝑦
𝑑𝑥3+ 𝑥3𝑑2𝑦
𝑑𝑥2+ 𝑦𝑑𝑦
𝑑𝑥 = 0. (2.2.9)
Persamaan (2.2.9) adalah persamaan diferensial biasa nonlinear terdapat perkalian antara variabel terikat 𝑦 dan turunan dari variabel terikat 𝑦 yang muncul dalam bentuk 𝑦𝑑𝑦
𝑑𝑥.
7. Sistem Persamaan Diferensial Biasa Linear Orde Pertama Definisi 2.2.7 (Boyce and DiPrima, 2012)
Bentuk umum sistem persamaan diferensial biasa linear orde pertama ada- lah
𝑥1′ = 𝑝11(𝑡)𝑥1+ ⋯ + 𝑝1𝑛(𝑡)𝑥𝑛+ 𝑔1(𝑡),
(2.2.10) 𝑥2′ = 𝑝21(𝑡)𝑥1+ ⋯ + 𝑝2𝑛(𝑡)𝑥𝑛+ 𝑔2(𝑡),
⋮
𝑥𝑛′ = 𝑝𝑛1(𝑡)𝑥1+ ⋯ + 𝑝𝑛𝑛(𝑡)𝑥𝑛+ 𝑔𝑛(𝑡),
dengan fungsi-fungsinya diketahui. Bentuk di atas dapat disederhanakan sebagai berikut.
𝑥′ = 𝑷(𝑡)𝑥 + 𝑔(𝑡). (2.2.11) Dengan 𝑷(𝑡) adalah matriks 𝑛 × 𝑛 dengan elemen 𝑝11, … , 𝑝𝑛𝑛 dan 𝑔(𝑡) adalah vektor dengan elemen 𝑔1(𝑡), … , 𝑔𝑛(𝑡).
Contoh 2.2.8
Contoh dari sistem persamaan diferensial biasa linear orde pertama adalah 𝑥1′ = 6𝑥1− 4𝑥2
𝑥2′ = 8𝑥1− 8𝑥2.
8. Sistem Persamaan Diferensial Biasa Nonlinear Orde Pertama Definisi 2.2.8
Sistem persamaan diferensial biasa orde satu nonlinear, secara umum berbentuk 𝑥1′(𝑡) = 𝑓1(𝑡, 𝑥1, … , 𝑥𝑛),
(2.2.12) 𝑥2′(𝑡) = 𝑓2(𝑡, 𝑥1, … , 𝑥𝑛),
𝑥3′(𝑡) = 𝑓3(𝑡, 𝑥1, … , 𝑥𝑛),
⋮
𝑥𝑛′(𝑡) = 𝑓𝑛(𝑡, 𝑥1, … , 𝑥𝑛), dengan
𝑓𝑖(𝑡, 𝑥1, … , 𝑥𝑛), 𝑖 = 1,2,3, … , 𝑛 (2.2.13) setidaknya salah satunya adalah fungsi nonlinear terhadap 𝑥1, 𝑥2… , atau 𝑥𝑛.
Contoh 2.2.9
Contoh sistem persamaan diferensial biasa nonlinear orde pertama adalah 𝑑𝑥
𝑑𝑡 = 𝑎𝑥 − 𝑎𝑥𝑦,
(2.2.14) 𝑑𝑦
𝑑𝑡 = −𝑐𝑦 + 𝛾𝑥𝑦.
Persamaan (2.2.14) merupakan persamaan 𝐿𝑜𝑡𝑘𝑎 − 𝑉𝑜𝑙𝑡𝑒𝑟𝑟𝑎 dengan variabel bebas 𝑡, variabel terikat 𝑥 dan 𝑦 dan dan parameternya 𝑎, 𝑐 dan 𝛾. Alasan sistem persamaan (2.14) nonlinear karena melibatkan perkalian 𝑥𝑦.
C. Topik-topik Terkait
Dalam subbab ini akan dijabarkan topik-topik terkait materi yang dibahas pada bab III meliputi deret Taylor, matriks, nilai eigen dan vektor eigen, persamaan karakteristik, persamaan polinomial karakteristik, matriks Jacobian, titik ekuilib- rium dan kestabilannya, bilangan reproduksi, matriks generasi berikutnya, kriteria Routh-Hurwitz, analisis sensitivitas lokal, metode Runge-Kutta orde empat dan ma- salah nilai awal.
1. Deret Taylor
Pada bagian ini akan dijelaskan mengenai deret Taylor beserta contohnya.
Deret Taylor merupakan representasi fungsi yang terdiferensial tak hingga banyak kali yang kemudian diperluas menjadi sebuah deret (Ricardo, 2020).
Definisi 2.3.1 (Ricardo, 2020)
Diberikan fungsi 𝑓: 𝐷𝑓 ⊂ ℝ dan 𝑓: 𝐷𝑓 ⟶ ℝ yang terdiferensial sebanyak tak hingga kali pada subinterval 𝐼 ⊂ 𝐷𝑓 dengan 𝑎 adalah sebuah titik interior pada 𝐼. Fungsi 𝑓 dapat dideretkan di sekitar titik interior 𝑎 sebagai berikut:
𝑓(𝑥) = 𝑓(𝑎) + 𝑓′(𝑎)(𝑥 − 𝑎) +𝑓′′(𝑎)(𝑥 − 𝑎)2
2! +𝑓′′′(𝑎)(𝑥 − 𝑎)3 3!
+ ⋯ +𝑓𝑛(𝑎)(𝑥 − 𝑎)𝑛
𝑛! + ⋯.
(2.3.1)
Deret di atas disebut seret Taylor fungsi 𝑓 di sekitar titik 𝑎.
Contoh 2.3.1
Diberikan sebuah fungsi 𝑓(𝑥) = 𝑒𝑥 yang yang terdiferensial dengan turunan-turunan fungsi 𝑓
𝑓(𝑥) = 𝑒𝑥, 𝑓′(𝑥) = 𝑒𝑥, 𝑓′′(𝑥) = 𝑒𝑥, 𝑓′′′(𝑥) = 𝑒𝑥, … , 𝑓𝑛(𝑥) = 𝑒𝑥, sehingga untuk persekitaran 𝑎 = 0 diperoleh
𝑓(0) = 1, 𝑓′(0) = 1, 𝑓′′(0) = 1, 𝑓′′′(0) = 1, … , 𝑓𝑛(0) = 1.
Jadi deret Taylor untuk fungsi 𝑓(𝑥) = 𝑒𝑥 di sekitar titik 𝑎 = 0 adalah
𝑒𝑥= 1 + (𝑥 − 0) +(𝑥 − 0)2
2! +(𝑥 − 0)3
3! + ⋯ +(𝑥 − 0)𝑛
𝑛! + ⋯
= 1 + 𝑥 +𝑥2 2! +𝑥3
3! + ⋯ +𝑥𝑛 𝑛! + ⋯.
2. Matriks
Pada bagian ini akan dijelaskan mengenai matriks, determinan matriks dan invers matriks beserta contohnya.
Definisi 2.3.2 (Marsudi dan Marjono, 2012)
Matriks (matrix) adalah sebuah susunan (array) segi empat dari bilangan- bilangan yang disajikan dalam kurung siku (kurung). Bilangan-bilangan ini disebut entri (entry) dari matriks.
Contoh 2.3.2
[1 2
3 4] , [6 7 9], [−9 0 ]
Matriks dalam contoh 2.3.2 berturut turut adlah matriks 2 × 2, matriks 1 × 3 dan matriks 2 × 1.
Definisi 2.3.3 (Marsudi dan Marjono, 2012)
Matriks 𝐴 berukuran 𝑛 × 𝑛 adalah 𝑖𝑛𝑣𝑒𝑟𝑡𝑖𝑏𝑙𝑒 (atau 𝑛𝑜𝑛𝑠𝑖𝑛𝑔𝑢𝑙𝑎𝑟) jika ter- dapat matriks 𝐵 berukuran 𝑛 × 𝑛 sehingga 𝐴𝐵 = 𝐵𝐴 = 𝐼𝑛. Matriks 𝐵 disebut
𝑖𝑛𝑣𝑒𝑟𝑠 dari 𝐴. Matriks yang tidak mempunyai 𝑖𝑛𝑣𝑒𝑟𝑠 disebut 𝑛𝑜𝑛𝑖𝑛𝑣𝑒𝑟𝑡𝑖𝑏𝑙𝑒 (atau 𝑠𝑖𝑛𝑔𝑢𝑙𝑎𝑟).
Definisi 2.3.4 (Marsudi dan Marjono, 2012)
Jika 𝐴 = [𝑎𝑖𝑗] adalah matriks bujur sangkar order 𝑛 (𝑛 ≥ 2), maka determi- nan 𝐴 adalah jumlahan dari entri-entri dalam baris pertama 𝐴 dikalikan dengan kofaktor-kofaktornya, 𝐶𝑖𝑗. Artinya,
det(𝐴) = |𝐴| = ∑ 𝑎1𝑗𝐶1𝑗 = 𝑎11𝐶11+ 𝑎12𝐶12+ ⋯ + 𝑎1𝑛𝐶1𝑛.
𝑛
𝑗=1
(2.3.2)
Contoh 2.3.2
Tentukan determinan dari matriks
𝐴 = [
1 3 0
2 6 4
−1 0 2
]
maka dengan menghitung ekspansi kofaktor sepanjang baris pertama akan di- peroleh
𝐶11= 12, 𝐶12 = −8, 𝐶13= 6.
Dengan menggunakan definisi 2.3.2, maka diperoleh
|𝐴| = 𝑎11𝐶11+ 𝑎12𝐶12+ 𝑎13𝐶13
= 1(12) + 3(−8) + 0(6)
= 12 − 24 + 0 = −12.
3. Nilai Eigen dan Vektor Eigen
Pada bagian ini akan dijelaskan mengenai nilai eigen dan vektor eigen beserta contohnya.
Definisi 2.3.5 (Anton and Rorres, 2014)
Diberikan matriks 𝐴 berukuran 𝑛 × 𝑛 maka vektor taknol 𝒙 pada 𝑅𝑛 disebut vektor eigen dari 𝐴 jika 𝐴𝒙 adalah perkalian skalar dengan 𝒙 yaitu
𝐴𝒙 = 𝜆𝒙 (2.3.3)
untuk sebarang skalar 𝜆. Skalar 𝜆 disebut nilai eigen dari 𝐴 dan 𝒙 adalah vektor eigen yang bersesuaian dengan 𝜆.
Contoh 2.3.2 (Marsudi dan Marjono, 2012) Diberikan matriks 𝐴 = [4 −5
2 −3] , ujilah bahwa 𝒙𝟏= (5,2) dan 𝒙𝟐= (1,1) adalah vektor-vektor eigen yang bersesuaian dengan 𝜆1 = 2 dan 𝜆1 = −1.
Maka dengan mengalikan 𝒙1 dengan 𝐴 menghasilkan 𝐴𝒙1 = [4 −5
2 −3] [5
2] = 2 [5 2].
Hal ini berarti 𝜆1 = 2 adalah nilai eigen dari 𝐴 dan 𝒙𝟏 = (5,2) adalah vektor eigen yang bersesuaian dengan 𝜆1 = 2. Secara analog dengan mengalikan 𝒙𝟐 dengan 𝐴 diperoleh
𝐴𝒙2 = [4 −5 2 −3] [1
1] = −1 [1 1].
Jadi 𝜆2 = −1 adalah nilai eigen dari 𝐴 dan 𝒙𝟐= (1,1) adalah vektor eigen yang bersesuaian dengan 𝜆2 = −1.
4. Persamaan karakteristik
Pada bagian ini akan dijelaskan mengenai persamaan karakteristik beserta contohnya.
Definisi 2.3.6 (Anton and Rorres, 2014)
Bilangan real 𝜆 adalah nilai eigen dari matriks 𝐴 jika 𝜆 memenuhi persa- maan karakteristik
|𝜆𝐼 − 𝐴| = 0. (2.3.4)
Contoh 2.3.3
Diberikan matriks 𝐴 = [1 2
0 12] maka dapat kita bentuk matriks 𝜆𝐼 − 𝐴 yaitu 𝜆𝐼 − 𝐴 = [𝜆 − 1 2
0 𝜆 − 12]
Dengan mempertimbangkan persamaan (2.3.4) dapat kita tentukan persa- maan karakteristik dari matriks 𝐴 yaitu
0 = |𝜆𝐼 − 𝐴|
= (𝜆 − 1)(𝜆 − 1) − 2(0)
= (𝜆 − 1)(𝜆 − 12).
Jadi diperoleh nilai eigen 𝜆1 = 1 dan 𝜆2 = 12.
5. Persamaan polinomial karakteristik
Pada bagian ini akan dijelaskan mengenai persamaan polinomial karakteristik beserta contohnya.
Diberikan matriks 𝐴 berukuran 𝑛 × 𝑛 maka dapat kita peroleh bentuk matriks 𝜆𝐼 − 𝐴 sebagai berikut.
[
𝜆 − 𝑎11 −𝑎12 −𝑎13 ⋯ −𝑎1𝑛
−𝑎21 𝜆 − 𝑎22 −𝑎23 ⋯ −𝑎2𝑛
−𝑎31 −𝑎32 𝜆 − 𝑎33 ⋯ −𝑎3𝑛
⋮ ⋮ ⋮ ⋱ ⋮
−𝑎𝑛1 −𝑎𝑛2 −𝑎𝑛3 ⋯ 𝜆 − 𝑎𝑛𝑛]
(2.3.5)
Menurut definisi 2.3.4 tentang determinan matriks maka pangkat tertinggi yang mungkin dari determinan matriks 𝜆𝐼 − 𝐴 untuk 𝜆 adalah 𝑛 yang diperoleh dari perkalian suku pada diagonal utama. Oleh karena itu, ekspansi dari det (𝜆𝐼 − 𝐴) menghasilkan persamaan karakteristik sebagai berikut (Anton and Rorres, 2014).
𝜆𝑛+ 𝑐1𝜆𝑛−1+ ⋯ + 𝑐𝑛 = 0. (2.3.6) Diketahui bahwa koefisien dari 𝜆𝑛 adalah 1 maka polinomial
𝑝(𝜆) = 𝜆𝑛 + 𝑐1𝜆𝑛−1+ ⋯ + 𝑐𝑛 (2.3.7) disebut persamaan polinomial karakteristik dari 𝐴.
Contoh 2.3.4
Berdasarkan contoh 2.3.3 dapat diperoleh persamaan polinomial karakter- istik pangkat dua sebab (𝜆 − 1)(𝜆 − 12) = 𝜆2− 13𝜆 + 12.
6. Matriks Jacobian
Pada bagian ini akan dijelaskan mengenai matriks Jacobian beserta con- tohnya. Matriks Jacobian merupakan salah satu teknik menganalisis kestabilan dari titik ekuilibrium.
Definisi 2.3.7 (Budhi, 2001)
Matriks transformasi terhadap basis standar turunan fungsi
𝒚 = 𝒇(𝒙) = (𝑓1(𝑥1, 𝑥2, … , 𝑥𝑛), … , 𝑓𝑚(𝑥1, 𝑥2, … , 𝑥𝑛)) (2.3.8) di titik 𝒙 adalah
𝑱 =
[
𝜕𝑓1
𝜕𝑥1 ⋯ 𝜕𝑓1
𝜕𝑥𝑛
𝜕𝑓2
𝜕𝑥1 ⋯ 𝜕𝑓2
𝜕𝑥𝑛
⋮ ⋱ ⋮
𝜕𝑓𝑚
𝜕𝑥1 ⋯ 𝜕𝑓𝑚
𝜕𝑥𝑛]
(2.3.9)
adalah matriks berukuran 𝑚 × 𝑛. Matriks (2.3.9) dapat dinyatakan dengan matriks
[𝜕𝑓𝑖
𝜕𝑥𝑗]
𝑖,𝑗
(2.3.10) yang disebut matriks Jacobian.
Contoh 2.3.5
Tentukan matriks Jacobian dari matriks transformasi turunan fungsi 𝒇(𝑥1, 𝑥2) = (𝑥14 + 𝑥24, 3𝑥12𝑥2, 2𝑥1𝑥22) pada (𝑥1, 𝑥2). Maka diperoleh matriks Jacobiannya adalah
𝑱 =
[
𝜕𝑓1
𝜕𝑥1
𝜕𝑓1
𝜕𝑥2
𝜕𝑓2
𝜕𝑥1
𝜕𝑓2
𝜕𝑥2
𝜕𝑓3
𝜕𝑥1
𝜕𝑓3
𝜕𝑥2]
= [
4𝑥13 4𝑥23 6𝑥1𝑥2 3𝑥12 2𝑥22 4𝑥1𝑥2
].
7. Titik Ekuilibrium dan Kestabilannya
Pada bagian ini akan dijelaskan mengenai titik ekuilibrium dan kesta- bilannya beserta contohnya.
Diberikan suatu sistem persamaan diferensial sebagai berikut.
𝑥̇ = 𝑓(𝑥(𝑡)), (2.3.11)
Sistem (2.3.11) dikatakan stabil jika sistem tersebut mempunyai solusi konstan atau tidak mengalami perubahan sepanjang waktu.
Definisi 2.3.8 (Perko, 1991)
Titik ekuilibrium 𝑥∗ dari sistem (2.3.11) dikatakan
1. Stabil jika untuk setiap 𝜀 > 0 terdapat 𝛿 > 0 sedemikian sehingga untuk solusi 𝑥(𝑡) yang memenuhi ‖𝑥(𝑡0) − 𝑥∗‖ < 𝛿 berlaku ‖𝑥(𝑡) − 𝑥∗‖ < 𝜀,
∀𝑡 ≥ 𝑡0.
2. Stabil asimtotik lokal jika titik ekuilibrium 𝑥∗ stabil dan terdapat 𝛿1 > 0 sedemikian sehingga untuk setiap solusi 𝑥(𝑡) dari sistem yang memenuhi
‖𝑥(𝑡) − 𝑥∗‖ < 𝛿1 berlaku lim
𝑡→∞𝑥(𝑡) = 𝑥∗.
3. Tidak stabil jika titik ekuilibrium 𝑥∗ tidak memenuhi point (1).
Contoh 2.3.6
Tentukan titik ekuilibrium dari persamaan berikut:
𝑑𝑦
𝑑𝑡 = 𝑎𝑦 (1 −𝑦
𝐵) dengan 𝑎, 𝐵 > 0.
maka dengan membuat persamaan kiri sama dengan nol diperoleh 𝑎𝑦 (1 −𝑦
𝐵) = 0.
Hal ini berarti 𝑎𝑦 = 0 atau (1 −𝑦
𝐵) = 0 sehingga diperoleh titik ekuilibrium 𝑦 = 0 atau 𝑦 = 𝐵.
8. Bilangan Reproduksi
Pada bagian ini akan dipaparkan mengenai bilangan reproduksi ℛ0 beserta teorema-teorema.
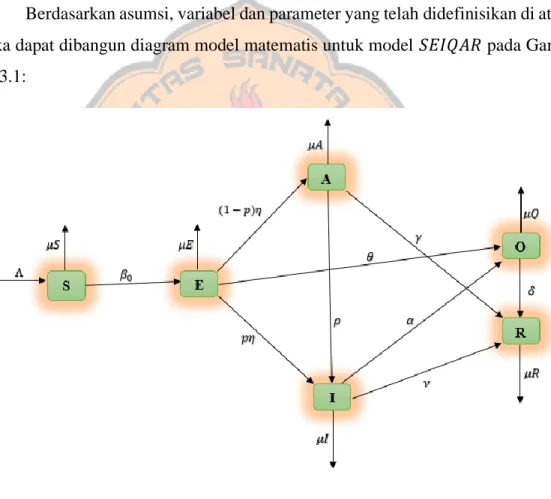
Bilangan reproduksi atau ambang batas epidemik adalah rata-rata jumlah infeksi baru yang dihasilkan oleh satu individu yang terifeksi pada populasi yang umumnya diberi lambang dengan ℛ0. Sebagai contoh, diperoleh ℛ0 = 3 hal ini berarti satu individu terinfeksi dapat menghasilkan tiga individu terinfeksi yang baru. Ilustrasi dari hal ini akan ditampilkan dalam Gambar 2.1 sebagai berikut.
Gambar 2.1 Ilustrasi 𝑅0 = 3 pada saat 𝑡 = 0, 𝑡 = 1 dan 𝑡 = 3.
Selanjutnya akan diberikan teorema tentang bilangan reproduksi yang di- ambil dari buku karangan Rost and Wu (2008).
Teorema 2.1
1. Titik ekuilibrium bebas penyakit (𝐷𝑖𝑠𝑒𝑎𝑠𝑒 − 𝑓𝑟𝑒𝑒 𝑒𝑞𝑢𝑖𝑙𝑖𝑏𝑟𝑖𝑢𝑚) dikatakan stabil asimtotik lokal jika ℛ0 < 1 dan tidak stabil jika ℛ0 > 1.
2. Solusi akan konvergen ke titik ekuilibrium bebas penyakit (𝐷𝑖𝑠𝑒𝑎𝑠𝑒 − 𝑓𝑟𝑒𝑒 𝑒𝑞𝑢𝑖𝑙𝑖𝑏𝑟𝑖𝑢𝑚) jika ℛ0 < 1.
3. Titik ekuilibrium endemik (𝐸𝑛𝑑𝑒𝑚𝑖𝑐 𝑒𝑞𝑢𝑖𝑙𝑖𝑏𝑟𝑖𝑢𝑚) dikatakan stabil asimtotik lokal jika ℛ0 > 1.
4. Penyakit bersifat endemik jika ℛ0 > 1.
Bilangan reproduksi ℛ0 dapat dicari dengan berbagai macam metode. Pada skripsi ini akan dicari bilangan reproduksi ℛ0 dengan pendekatan matriks generasi berikutnya dengan mencari nilai radius spektral atau nilai mutlak terbesar dari nilai eigen dari matriks generasi berikutnya.
8. Pendekatan Matriks Generasi Berikutnya
Pada bagian ini akan dijelaskan mengenai pendekatan matriks generasi beri- kutnya (The Next-Generation Matrix Approach) mengutip dari karangan Martcheva (2015) dalam menentukan bilangan reproduksi.
Ide pendekatan matriks generasi berikutnya adalah melihat bahwa bilangan reproduksi menandakan bahwa penularan infeksi menghasilkan keturunan (infeksi baru) dalam pengertian epidemiologi yaitu melahirkan individu baru yang terinfeksi (Martcheva, 2015). Untuk model matematis kompartemen dapat dibentuk matriks yang menunjukkan jumlah individu baru yang terinfeksi. Matriks inilah yang dise- but matriks generasi berikutnya dan pertama kali dikemukakan oleh Diekmann dan Heesterbeek tahun 1990. Selanjutnya bilangan reproduksi ℛ0 didefinisikan sebagai radius spektral dari matriks generasi berikutnya.
Teknik yang umum digunakan dalam menentukan turunan untuk matriks generasi berikutnya dari model matematis penyebaran penyakit yang melibatkan persamaan-persamaan diferensial biasa adalah pendekatan Van den Driessche and Watmough. Secara umum, pendekatan ini dilakukan dengan membagi komparte- men/kelas yang terlibat dalam model ke dalam dua kompartemen yaitu komparte- men terinfeksi dan kompartemen tidak terinfeksi (sembuh). Kompartemen terin- feksi berisi kelas-kelas di mana dalam populasinya terdapat individu yang terinfeksi bergejala maupun tidak bergejala. Kelas-kelas yang tersisa di mana dalam popu- lasinya tidak terdapat individu yang terinfeksi dimasukkan ke dalam kompartemen tidak terinfeksi (sembuh).
Langkah-langkah dalam menentukan matriks generasi berikutnya akan diu- raikan sebagai berikut.
1. Langkah pertama adalah menguraikan sistem persamaan diferensial biasa menjadi dua kompartemen yaitu kompartemen terinfeksi dan kompartemen tidak terinfeksi. Diberikan sistem persamaan diferensial biasa sebagai beri- kut:
𝑥𝑖′= 𝑓𝑖(𝑥, 𝑦), 𝑖 = 1, … , 𝑛,
(2.3.12) 𝑦𝑖′= 𝑔𝑖(𝑥, 𝑦), 𝑗 = 1, … , 𝑚
berturut-turut menyatakan kompartemen terinfeksi dan kompartemen tidak terinfeksi.
2. Langkah kedua yaitu memecah (mendekomposisi) ruas kanan pada kompartemen terinfeksi menjadi:
𝑥𝑖′=𝔉𝑖(𝑥, 𝑦)− 𝓋𝑖(𝑥, 𝑦), 𝑖 = 1, … , 𝑛,
(2.3.13) 𝑦𝑗′= 𝑔𝑗(𝑥, 𝑦), 𝑗 = 1, … , 𝑚
dengan
• 𝔉𝑖(𝑥, 𝑦) adalah laju munculnya infeksi baru pada kompartemen ke- 𝑖;
• 𝓋𝑖(𝑥, 𝑦) adalah gabungan dari laju transmisi yang tersisa yaitu ke- lahiran, kematian, perkembangan penyakit dan pemulihan.
Untuk membagi kelas-kelas yang dipertimbangkan pada model perlu di- penuhi sifat-sifat berikut.
• 𝔉𝑖(0, 𝑦) = 0 dan 𝓋𝑖(0, 𝑦) = 0 untuk setiap 𝑦 ≥ 0 dengan 𝑖 = 1, … , 𝑛. Kondisi pertama mengartikan bahwa semua infeksi yang terjadi adalah infeksi sekunder yang disebabkan oleh individu yang terinfeksi. Kondisi kedua mengisyaratkan bahwa tidak ada perpin- dahan individu rentan ke dalam kompartemen terinfeksi.
• 𝔉𝑖(𝑥, 𝑦) ≥ 0 untuk setiap 𝑥, 𝑦 ≥ 0.
• 𝓋𝑖(𝑥, 𝑦) ≤ 0 ketika 𝑥𝑖 = 0 untuk 𝑖 = 1, … , 𝑛. Setiap komponen 𝓋𝑖 menyatakan luaran dari kompartemen 𝔉𝑖(𝑥, 𝑦) dan harus mem- berikan masukan bertanda negatif jika kompartemen 𝔉𝑖(𝑥, 𝑦) kosong.
• ∑ 𝓋𝑛1 𝑖(𝑥, 𝑦) ≥ 0 untuk setiap 𝑥, 𝑦 ≥ 0. Total luaran dari semua dari kompartemen terinfeksi adalah positif.
3. Asumsikan sistem bebas penyakit
𝑦′ = 𝑔(0, 𝑦),
memiliki solusi tunggal titik ekuilibrium bebas penyakit 𝜀0 = (0, 𝑦0) sedemikian sehingga setiap solusi dengan kondisi awal berbentuk (0, 𝑦0) diperoleh (0, 𝑦0) untuk 𝑡 → ∞. Tentukan titik ekuilibrium bebas penyakit 𝜀0.
4. Tentukan matriks 𝐹 dan 𝑉 dengan komponen-komponen sebagai berikut:
𝐹 = [𝜕𝔉𝑖(0, 𝑦)
𝜕𝑥𝑗 ] dan 𝑉 [𝜕𝓋𝑖(𝑥, 𝑦)
𝜕𝑥𝑗 ]. (2.3.14) Matriks (2.3.14) diperoleh dari linearisasi dari sistem (2.3.13) di sekitar titik ekuilibrium bebas penyakit. Hal ini dapat ditunjukkan dengan
𝜕𝔉𝑖(0, 𝑦)
𝜕𝑦𝑗 = 𝜕𝓋𝑖(𝑥, 𝑦)
𝜕𝑦𝑗 = 0
untuk setiap pasang (𝑖, 𝑗). Hal ini berarti linearisasi persamaan pada kompartemen 𝑥 dihitung pada titik ekuilibrium bebas penyakit dan dipisahkan dari persamaan yang tersisa. Selanjutnya linearisasi sistem untuk kompartemen terinfeksi dapat ditulis
𝑥𝑖′= (𝐹 − 𝑉)𝑥.
5. Oleh karena itu, matriks generasi berikutnya didefinisikan sebagai 𝐾 = 𝐹𝑉−1
dan
ℛ0 = 𝜌(𝐹𝑉−1) dengan 𝜌(𝐴) adalah radius spektral dari 𝐴.
Definisi 2.3.9 (Martcheva, 2015)
Radius spektral dari matriks 𝐴 didefinisikan sebagai nilai absolut maksi- mum dari nilai eigen matriks 𝐴:
𝜌(𝐴) = sup{|𝜆|: 𝜆 ∈ 𝜎(𝐴)}, dengan 𝜎(𝐴) notasi untuk himpunan nilai eigen dari 𝐴.
9. Kriteria Routh-Hurwitz
Pada bagian ini akan diterangkan mengenai kriteria Routh-Hurwitz beserta teorema-teoremanya berdasarkan buku Martcheva (2015).
Untuk model dengan dimensi yang tinggi untuk beberapa kasus matriks Ja- cobian yang dihasilkan tidak dapat direduksi menjadi matriks 2 × 2 dan menghasilkan polinomial karakteristik berderajat tiga atau lebih. Oleh karena itu, untuk menjamin bahwa nilai eigen memiliki bagian real negatif diperlukan alat yang dapat memberikan syarat perlu dan cukup. Kondisi ini akan diberikan oleh Kriteria Routh-Hurwitz yang dinyatakan dalam teorema sebagai berikut:
Teorema 2.2 (Martcheva, 2015)
Diberikan polinomial berderajat 𝑛 dengan koefisien real konstan
𝑃(𝜆) = 𝑎0𝜆𝑛+ 𝑎1𝜆𝑛−1+ ⋯ + 𝑎𝑛−1𝜆 + 𝑎𝑛, (2.3.15) didefinisikan 𝑛 matriks Hurwitz dengan koefisien 𝑎𝑖 dari polinomial karakteristik dan 𝑎0 = 1 maka
𝐻1 = (𝑎1) 𝐻2 = (𝑎1 1
𝑎3 𝑎2) 𝐻2 = (
𝑎1 1 0
𝑎3 𝑎2 𝑎1 𝑎5 𝑎4 𝑎3
)
dan
𝐻𝑛 = (
𝑎1 1 0 0 ⋯ 0
𝑎3 𝑎2 𝑎1 1 ⋯ 0 𝑎5 𝑎4 𝑎3 𝑎2 ⋯ 0
⋮ ⋮ ⋮ ⋮ ⋯ ⋮
0 0 0 0 ⋯ 𝑎𝑛)
.
dengan 𝑎𝑗 > 0 jika 𝑗 > 𝑛. Semua akar dari polinomial karakteristik 𝑃(𝜆) bernilai negatif atau memiliki bagian real negatif jika dan hanya jika determinan dari semua matriks Hurwitz bernilai positif:
Det 𝐻𝑗 > 0, 𝑗 = 1, … , 𝑛.
Untuk 𝑛 > 2, kriteria Routh-Hurwitz akan diberikan pada Tabel 2.1 sebagai berikut:
Tabel 2.1 Kriteria Routh-Hurwitz
𝑛 Nilai koefisien Syarat tambahan
2 𝑎1 > 0, 𝑎2 > 0 −
3 𝑎1 > 0, 𝑎2 > 0, 𝑎3 > 0 𝑎1𝑎2 > 𝑎3
4 𝑎1 > 0, 𝑎2 > 0, 𝑎3 > 0, 𝑎4 > 0 𝑎1𝑎2𝑎3 > 𝑎32+ 𝑎12𝑎4 5 𝑎1 > 0, 𝑎2 > 0, 𝑎3 > 0, 𝑎4 > 0, 𝑎1𝑎2𝑎3 > 𝑎32+ 𝑎12𝑎4,
𝑎5 > 0 (𝑎1𝑎4− 𝑎5)(𝑎1𝑎2𝑎3− 𝑎32− 𝑎12𝑎4) >
𝑎5(𝑎1𝑎2− 𝑎3)2+ 𝑎1𝑎52.
Apabila persamaan (2.3.12) memiliki bagian rill negatif maka menurut Hahn (1967) 𝑎1
𝑎0 > 0,𝑎2
𝑎0 > 0, … ,𝑎𝑛
𝑎0 > 0. (2.3.16)
Contoh 2.3.7
Diberikan persamaan polinomial karakteristik berderajat tiga sebagai beri- kut.
𝑦3+ 𝑎1𝑦2+ 𝑎2𝑦 + 𝑎4 = 0.
Berdasarkan teorema 2.2 dapat dibentuk matriks Hurwitz dari persamaan po- linomial karakteristik di atas yaitu
𝐻 = (
𝑎1 1 0
𝑎3 𝑎2 𝑎1
0 0 𝑎3
).
Selanjutnya dibentuk determinan Hurwitz sebagai berikut 𝐻1 = |𝑎1| = 𝑎1
𝐻2 = |𝑎1 1
𝑎3 𝑎2| = 𝑎1𝑎2 − 𝑎3
𝐻3 = |
𝑎1 1 0
𝑎3 𝑎2 𝑎1
0 0 𝑎3
| = 𝑎3(𝑎1𝑎2− 𝑎3)
maka menurut kriteria Routh-Hurwitz agar polinomial berderajat tiga mempunyai bagian real negatif maka
𝐻1 > 0 ⇔ 𝑎1 > 0 𝐻2 > 0 ⇔ 𝑎1𝑎2 − 𝑎3 > 0 𝐻3 > 0 ⇔ 𝑎3(𝑎1𝑎2 − 𝑎3) > 0 dan
𝑎1𝑎2 > 𝑎3. Menurut persamaan (2.3.13) diperoleh
𝑎1
𝑎0 > 0 ⇔ 𝑎1 > 0 sebab 𝑎0 = 1 > 0,
𝑎2
𝑎0 > 0 ⇔ 𝑎2 > 0 sebab 𝑎0 = 1 > 0, 𝑎3
𝑎0 > 0 ⇔ 𝑎3 > 0 sebab 𝑎0 = 1 > 0.
Oleh karena itu, semua akar persamaan polinomial karakteristik (2.3.15) mempu- nyai bagian real negatif jika
i. 𝑎1, 𝑎2 > 0 dan 𝑎3 > 0 ii. 𝑎1𝑎2 > 𝑎3.
10. Analisis Sensitivitas Lokal
Pada subbab ini akan dibahas mengenai analisis sensitivitas lokal beserta contohnya.
Pada Umumnya, nilai dari suatu parameter yang terlibat dalam model ma- tematis sangat tidak pasti. Hal ini disebabkan oleh kurangnya data dan ketiadaan data. Oleh karena itu, perlu dilakukan analisis sensitivitas agar dapat ditentukan parameter yang berpengaruh pada model. Analisis sensitivitas lokal dilakukan dengan cara mengeksplorasi nilai dari satu atau lebih parameter secara bersama dan nilai parameter lainnya dipandang konstan atau tetap. Analisis sensitivitas lokal dil- akukan dengan menggunakan teknik turunan parsial.
Definisi 2.3.10 (Ndii, 2018)
Indeks sensitivitas lokal terhadap variabel 𝑉, terdiferensialkan terhadap pa- rameter 𝑝 didefinisikan sebagai berikut.
𝛾𝑝𝑉 =𝜕𝑉
𝜕𝑝×𝑝
𝑉 , (2.3.19)
dengan 𝑉 adalah variabel yang akan dianalisis dan 𝑝 adalah parameter.
Definisi 2.3.11 (Martcheva, 2015)
Tujuan dari analisis sensitivitas adalah menentukan parameter mana yang paling memberikan dampak terhadap luaran model.
Definisi 2.3.12 (Martcheva, 2015)
Suatu parameter dikatakan sensitif jika perubahan kecil pada nilai parameter tersebut menghasilkan perubahan besar dalam penyelesaian persamaan diferensial.
Contoh 2.3.9
Diberikan persamaan
𝐺 =2𝑘 + 𝑙2 𝑚 + 𝑙
dengan 𝑘, 𝑙 dan 𝑚 adalah parameter-parameter yang terlibat. Langkah dalam menentukan analisis sensitivitas adalah menurunkan variabel 𝐺 terhadap parameter yang ingin dicari. Saat mencari turunan terhadap suatu parameter maka parameter lainnya diasumsikan tetap atau konstan. Sehingga dapat kita tulis
𝛾𝑘𝐺 = 2
𝑚 + 𝑙 𝛾𝑙𝐺 = 2𝑙𝑚 + 𝑙2− 2𝑘
𝑚 + 𝑙 𝛾𝑚𝐺 = −(2𝑘 + 𝑙2) (𝑚 + 𝑙)2 . Asumsikan nilai parameter 𝑘 = 0.05, 𝑙 = 0.2 dan 𝑚 = 0.4 maka diperoleh indeks sensitivitas 𝛾𝑘𝐺 = 3.33, 𝛾𝑙𝐺 = 0.277 dan 𝛾𝑚𝐺 = −3.88.
11. Metode Runge-Kutta orde empat
Pada bagian ini akan dijelaskan mengenai metode Runge-Kutta orde empat beserta contohnya dikutip dari buku Matthews and Kurtis (2004) dan tugas akhir Agrippina (2021).
Metode Runge-Kutta adalah metode penyelesaian masalah nilai awal persa- maan diferensial linear atau nonlinear dengan pendekatan iterasi numeris (Fowkes