Simpangan, Kecepatan dan Percepatan pada Getaran Harmonis Sederhana a. Simpangan getaran harmonis
Simpangan menyatakan keadaan suatu benda setelah diganggu dari
keadaan awalnya. Persamaan simpangan menghubungkan keadaan benda
tersebut dalam tiap waktu.
Persamaan simpangan getaran harmonis sederhana dapat diperoleh dari
proyeksi gerak melingkar beraturan terhadap suatu sumbu untuk titik yang
bergerak beraturan. Hal tersebut karena pada hakikatnya gerak melingkar
beraturan merupakan gerak bolak-balik secara periodik. Tipler (1998)
menyatakan bahwa pada suatu garis lurus, Proyeksi sebuah partikel yang
bergerak dengan gerak melingkar seragam merupakan getaran harmonis
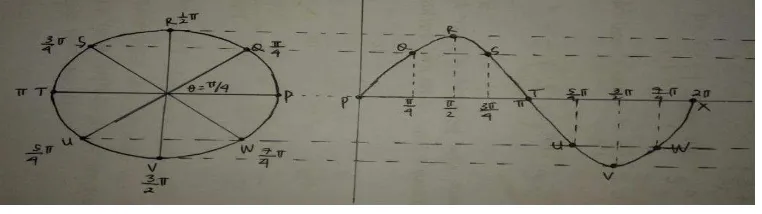
sederhana. Perhatikan gambar,
Gambar 4.1 melukiskan sebuah partikel yang bergerak melingkar
beraturan dengan kecepatan sudut �. Misalkan sebuah titik berpindah dari
posisi P ke posisi Q dalam selang waktu t, maka besar sudut yang ditempuh (�)
titik tersebut adalah:
Dengan : � = sudut yang ditempuh (rad)
� = frekuensi sudut (rad/s)
t = waktu yang ditempuh (s)
Jika diperhatikan proyeksi titik Q terhadap sumbu Y, proyeksi tersebut
mempunyai simpangan maksimum A yang disebut amplitudo sepanjang OR.
Simpangan di titik Q dapat dinyatakan sebagai berikut. Gambar 4.1
Y = r sin � = r sin �
Karena pada saat simpangan maksimum r = A, maka persamaan
simpangan di setiap titik selama bergerak melingkar beraturan dapat
dinyatakan sebagai berikut.
Dengan : Y = simpangan gerak harmonik (m)
A = amplitudo (m)
� = � = sudut fase getaran (rad)
Pada persamaan getaran harmonis sederhana akan dikenal beberapa istilah,
seperti sudut fase, fase dan beda fase. Sudut fase � menyatakan sudut terjauh
dalam waktu tertentu atau sudut yang ditempuh dalam selang waktu tertentu.
Adapun fase � merupakan kedudukan suatu benda dilihat dari arah getar dan
simpangannya pada saat tertentu. Besar fase dapat dituliskan sebagai berikut.
� = t/T = ft (tanpa satuan) Dengan : � = besar fase
T = periode (s)
f = frekuensi (Hz)
t = waktu tempuh (s)
Adapun beda fase ∆� merupakan selisih antara dua fase dalam selang
waktu tertentu (∆� = � − � ).
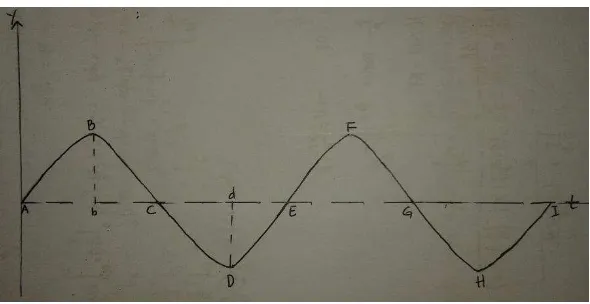
Pada gambar 4.1 di atas, titik A dan E serta titik B dan F memiliki fase
yang sama karena simpangannya sama dan arah getarnya sama. Titik A dan E
sama-sama berada di titik nπ (n = 0,1,2,3, ..) dan sama-sama akan bergetar ke
atas. Titik B dan F sama-sama berada di titik �+ � (n = 0,1,2,3, ..) dan sama-sama akan bergetar ke bawah. Syarat agar dua titik memiliki fase yang sama-sama
adalah keduanya memiliki posisi yang sama dan memiliki arah getar yang
sama. Titik A dan C serta titik B dan D memiliki fase yang berlawanan karena
arah getarnya berlawanan.
Apabila fase dan sudut fase getaran pada getaran harmonis sederhana
diperhitungkan, akan didapatkan sebuah persamaan umum getaran harmonis
sederhana yang dapat dituliskan sebagai berikut.
Dengan : Y = simpangan getaran harmonis (m)
A = amplitudo (m)
� = � = sudut fase getaran (rad)
� = sudut fase awal getaran (rad)
Selain itu dapat dinyatakan juga dalam persamaan sebagai berikut.
b. Kecepatan getaran harmonis
Kecepatan benda yang bergerak harmonis dapat diperoleh dari turunan
pertama simpangan
v = ��� = �� [� sin � + �0 ] = A �cos � + �0 � = � � � ± �
� = � � 2�� ± �
� = � � 2�� ± �
Untuk kecepatan maksimum (� �� ) dari getaran harmonis Sederhanadiperoleh :
� �� = A � dengan nilai maksimum dari cos � + �0 = 1 c. Percepatan getaran harmonis
Percepatan benda yang bergerak harmonis dapat diperoleh dari turunan
pertama kecepatan atau turunan kedua simpangan
a = ��� = �� [A �cos � + �0 ] = -A �2sin � + �0
Untuk kecepatan maksimum (� �� ) dari getaran harmonis sederhana diperoleh :