PENYUSUNAN MATRIKS RANCANGAN FRACTIONAL
FACTORIAL SPLIT-PLOT (FFSP) ORTOGONAL DUA TARAF
DENGAN MENERAPKAN ALGORITMA GENETIKA
RAEDI HERMAWAN
DEPARTEMEN STATISTIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR
BOGOR 2014
PERNYATAAN MENGENAI SKRIPSI DAN
SUMBER INFORMASI SERTA PELIMPAHAN HAK CIPTA
Dengan ini saya menyatakan bahwa skripsi berjudul Penyusunan Matriks Rancangan Fractional Factorial Split-Plot (FFSP) Ortogonal Dua Taraf dengan Menerapkan Algoritma Genetika adalah benar karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir skripsi ini.
Dengan ini saya melimpahkan hak cipta dari karya tulis saya kepada Institut Pertanian Bogor.
Bogor, Juli 2014
Raedi Hermawan
ABSTRAK
RAEDI HERMAWAN. Penyusunan Matriks Rancangan Fractional Factorial
Split-Plot (FFSP) Ortogonal Dua Taraf dengan Menerapkan Algoritma Genetika.
Dibimbing oleh AGUS MOHAMMAD SOLEH dan BAGUS SARTONO.
Dalam percobaan di dunia industri, rancangan fractional factorial split-plot (FFSP) digunakan untuk mengatasi masalah keterbatasan biaya dan kondisi yang tidak memungkinkan untuk dilakukan pengacakan secara lengkap. Namun, semakin banyak petak utama dan faktor yang dicobakan, semakin sulit dan lama waktu komputasi yang dibutuhkan untuk menyusun rancangan ini. Tulisan ini memberikan sebuah teknik alternatif penyusunan rancangan FFSP ortogonal dua taraf dengan menerapkan algoritma genetika. Teknik ini mampu memberikan matriks rancangan FFSP ortogonal yang lebih baik (pembauran lebih sedikit) dari teknik dalam literatur dengan waktu komputasi yang sangat cepat sehingga cocok digunakan untuk kasus percobaan yang besar (banyak petak utama dan faktor). Kata kunci: algoritma genetika, fractional factorial, split-plot design, rancangan
percobaan
ABSTRACT
RAEDI HERMAWAN. Application of Genetic Algorithm in Constructing Two-Level Orthogonal Fractional Factorial Split-Plot Design. Supervised by AGUS MOHAMMAD SOLEH and BAGUS SARTONO.
In industrial experiment, fractional factorial split-plot (FFSP) design is used to overcome budget limitation and situation where complete-randomization is not possible. However, more whole-plots and factors included, harder and more time needed to construct this design. This study presents a new approach in constructing two-level orthogonal FFSP design with genetic algorithm. This approach can construct orthogonal FFSP design better than other approaches on literature in very fast processing time. So, it can be used effectively in experiment that involved many whole-plots and factors.
Keywords: experimental design, fractional factorial, genetic algorithm, split-plot design
Skripsi
sebagai salah satu syarat untuk memperoleh gelar Sarjana Statistika
pada
Departemen Statistika
PENYUSUNAN MATRIKS RANCANGAN FRACTIONAL
FACTORIAL SPLIT-PLOT (FFSP) ORTOGONAL DUA TARAF
DENGAN MENERAPKAN ALGORITMA GENETIKA
RAEDI HERMAWAN
DEPARTEMEN STATISTIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR
BOGOR 2014
Judul Skripsi : Penyusunan Matriks Rancangan Fractional Factorial Split-Plot (FFSP) Ortogonal Dua Taraf dengan Menerapkan Algoritma Genetika
Nama : Raedi Hermawan NIM : G14100081
Disetujui oleh
Agus M. Soleh, SSi, MT Pembimbing I
Dr Bagus Sartono, SSi, MSi Pembimbing II
Diketahui oleh
Dr Anang Kurnia, SSi, MSi Ketua Departemen
PRAKATA
Puji dan syukur penulis panjatkan kepada Allah subhanahu wa ta’ala atas segala karunia-Nya sehingga karya ilmiah yang berjudul Penyusunan Matriks Rancangan Fractional Factorial Split-Plot (FFSP) Ortogonal Dua Taraf dengan Menerapkan Algoritma Genetika ini berhasil diselesaikan.
Terselesainya penyusunan karya ilmiah ini tentunya tidak terlepas dari bantuan, motivasi, saran, dan kerja sama dari banyak pihak. Oleh karena itu, beribu terima kasih penulis ucapkan kepada :
1. Bapak Agus M. Soleh, SSi, MT selaku ketua komisi pembimbing yang sangat sabar dan teliti dalam memberikan masukan dan nasehat kepada penulis untuk menghasilkan karya ilmiah yang terstruktur dan mudah dipahami.
2. Bapak Dr Bagus Sartono, SSi, MSi selaku anggota komisi pembimbing yang telah memberikan ide awal, bantuan pemahaman konsep, literatur serta saran sehingga penulis mampu menghasilkan karya ilmiah yang mudah dipahami.
3. Ibu Dr Ir Erfiani, MSi selaku penguji luar komisi atas saran-saran berharga yang diberikan untuk memperbaiki struktur penulisan karya ilmiah ini. 4. Teman-teman Statistika angkatan 47 atas motivasi dan doanya sehingga
penulis dapat menyelesaikan karya ilmiah ini.
5. Ayah, ibu, adik, dan seluruh keluarga besar atas motivasi, nasehat, serta doanya yang selalu ditujukan kepada penulis sehingga penulis selalu bersemangat untuk menyelesaikan karya ilmiah ini.
6. Seluruh Dosen Departemen Statistika IPB atas ilmunya yang tak ternilai sehingga penulis dapat menerapkan ilmu Statistika dengan baik dan benar. 7. Seluruh Staf Tata Usaha Departemen Statistika IPB yang selalu bersedia
direpotkan sehingga segala proses adminitrasi berjalan dengan lancar. Tak ada gading yang tak retak. Demi penyempurnaan karya ilmiah ini, saran, kritik, dan masukan sangat penulis harapkan dari para pembaca. Semoga karya ilmiah ini bermanfaat.
Bogor, Juli 2014
DAFTAR ISI
DAFTAR TABEL vi DAFTAR GAMBAR vi DAFTAR LAMPIRAN vi PENDAHULUAN 1 METODE 3Pendekatan stratum-by-stratum beserta Notasi dan Simbol 3
Data 6
Metode 7
HASIL DAN PEMBAHASAN 10
Penerapan pada rancangan 48-runs dengan 8 petak utama, 5 faktor petak utama,
dan 10 faktor anak petak 10
Penerapan pada rancangan 96-runs dengan 12 petak utama, 5 faktor petak
utama, dan 25 faktor anak petak 11
Kinerja komputasi algoritma genetika dalam penyusunan matriks rancangan
FFSP ortogonal dua taraf 13
SIMPULAN 15
DAFTAR PUSTAKA 16
LAMPIRAN 17
DAFTAR TABEL
1 Tabel ringkasan notasi dan simbol yang digunakan 4 2 Tabel ringkasan pola pembauran yang melibatkan pengaruh utama dan
pengaruh interaksi dua faktor dalam matriks rancangan FFSP 5 3 Matriks sub-rancangan petak utama (M) pada kasus rancangan 8 petak
utama 6
4 Matriks sub-rancangan petak utama (M) pada kasus rancangan 12 petak
utama 7
5 Matriks rancangan akhir (R) dari permutasi a = {1, 2, 3, 4, 5, 6, 7, 8}
tanpa algoritma genetika 11
6 Matriks rancangan akhir (R) dari permutasi a = {1, 5, 6, 2, 8, 3, 7, 4}
hasil algoritma genetika 11
7 Matriks rancangan akhir (R) dari permutasi a = {1, 2, 3, 4, 5, 6, 7, 8, 9,
10, 11, 12} hasil teknik Sartono (2012) 12
8 Matriks rancangan akhir (R) dari permutasi a = {8, 1, 4, 5, 9, 10, 11, 12,
3, 6, 2, 7} hasil algoritma genetika 13
9 Statistik waktu proses (detik) yang dibutuhkan oleh algoritma genetika hingga konvergen atau iterasi berakhir pada kasus rancangan 8 petak
utama 14
10 Statistik waktu proses (detik) yang dibutuhkan oleh algoritma genetika hingga konvergen atau iterasi berakhir pada kasus rancangan 12 petak
utama 15
DAFTAR GAMBAR
1 Diagram alir (flow chart) mekanisme algoritma genetika secara umum 7 2 Diagram kotak garis solusi terbaik yang dihasilkan: (a) pengacakan
permutasi (random assignment) dan (b) algoritma genetika dalam 100
kali ulangan 12
3 Diagram kotak garis waktu proses (detik) pencarian solusi algoritma genetika dalam 100 ulangan (kasus rancangan 8 petak utama) 14 4 Diagram kotak garis waktu proses (detik) pencarian solusi algoritma
genetika dalam 100 ulangan (kasus rancangan 12 petak utama) 15
DAFTAR LAMPIRAN
1 Matriks sub-rancangan anak petak (S) beserta penempatannya ke dalam
petak utama pada kasus rancangan 8 petak utama 17
2 Matriks assignment (B) pada kasus rancangan 8 petak utama 18 3 Matriks assignment (B) pada kasus rancangan 12 petak utama 19 4 Algoritma genetika untuk penyusunan matriks rancangan FFSP
ortogonal dua taraf pada R berbentuk fungsi ffsp.ga 21 5 128 solusi terbaik hasil evaluasi seluruh kemungkinan (8!) permutasi
1
PENDAHULUAN
Percobaan merupakan salah satu metode yang dapat dilakukan untuk menjawab pertanyaan-pertanyaan penelitian secara ilmiah. Pada awal perkembangannya, percobaan umumnya digunakan dalam bidang pertanian untuk mengidentifikasi faktor-faktor yang berpengaruh terhadap kualitas ataupun kuantitas produksi dari suatu jenis tanaman. Namun seiring perkembangan zaman, dengan semakin pesatnya pertumbuhan industri di berbagai negara, percobaan mulai banyak dilirik oleh para produsen atau perusahaan untuk mengidentifikasi faktor-faktor yang efektif dilibatkan dalam proses produksinya.
Dalam dunia industri, percobaan yang paling sering dilakukan yakni percobaan dengan perlakuan berupa kombinasi silang dari taraf faktor-faktor yang dicobakan. Percobaan ini dikenal dengan percobaan faktorial. Adapun rancangan yang pada umumnya digunakan untuk melakukan percobaan ini dinamakan rancangan faktorial biasa. Jika biaya yang diperlukan untuk menggunakan faktor-faktor yang dilibatkan besar, maka meningkatnya jumlah faktor-faktor (semakin banyak kombinasi perlakuan) yang dicobakan, biaya yang harus dikeluarkan untuk melakukan percobaan juga akan semakin besar. Hal ini tentunya merugikan produsen dari segi ekonomi sehingga rancangan faktorial biasa tidak mungkin untuk digunakan. Salah satu solusinya adalah menerapkan rancangan fractional
factorial (FF).
Rancangan FF merupakan rancangan yang hanya mencobakan sebagian dari kombinasi perlakuan lengkap. Penerapan rancangan ini tentunya akan mengurangi biaya yang harus dikeluarkan. Namun, ada resiko yang harus ditanggung atau dikorbankan akibat dari tidak dicobakannya kombinasi perlakuan lengkap. Resiko ini dikenal dengan pembauran (confounding). Pembauran merupakan isu utama dalam pemilihan atau penyusunan rancangan FF. Berdasarkan prinsip hierarchy dalam pendugaan pengaruh faktorial, rancangan FF yang baik adalah rancangan yang meminimumkan pembauran antar pengaruh-pengaruh penting. Pengaruh penting yang dimaksud adalah pengaruh utama dan pengaruh interaksi dua faktor (Sartono 2012).
Kombinasi perlakuan yang dicobakan pada rancangan FF ditempatkan secara acak lengkap pada tiap unit percobaan (run) yang digunakan. Namun pengacakan lengkap tersebut kadangkala sulit dilakukan terutama pada percobaan dalam dunia industri. Secara umum, ada dua hal yang mendasari tidak dapat dilakukannya pengacakan lengkap yakni adanya kendala teknis di lapangan atau secara teknis tidak ada masalah untuk melakukan pengacakan lengkap namun mengubah taraf faktor tertentu dari run satu ke run yang lain dikhawatirkan akan mengganggu pengaruh dari faktor yang dicobakan. Adapun solusi yang tepat digunakan untuk melakukan percobaan dengan kondisi tersebut adalah menerapkan rancangan fractional factorial split-plot (FFSP) (Winarni 2006).
Pada rancangan FFSP terdapat petak utama dan anak petak. Faktor yang sulit untuk diubah pengaturan tarafnya ditempatkan sebagai faktor petak utama dan faktor lainnya ditempatkan sebagai faktor anak petak. Petak utama merupakan kombinasi taraf dari faktor-faktor petak utama yang digunakan dan anak petak merupakan kombinasi taraf dari faktor-faktor anak petak (Winarni 2006).
2
Rancangan FF maupun FFSP biasanya digunakan dalam percobaan pendahuluan atau screening experiment untuk mengidentifikasi faktor-faktor yang berpengaruh besar (faktor-faktor yang teridentifikasi biasanya diinvestigasi lebih lanjut dalam percobaan lanjutan). Taraf faktor yang digunakan umumnya tidak banyak yakni dua atau tiga taraf untuk masing-masing faktor. Taraf-taraf tersebut dipilih sedemikian sehingga dapat mewakili pengaruh dari faktor yang bersangkutan. Dalam penelitian ini hanya akan dibahas rancangan FFSP dengan dua taraf tiap faktornya, yaitu taraf tinggi (1) dan taraf rendah (-1).
Masalah umum yang dihadapi dalam menerapkan rancangan FFSP adalah sulitnya menyusun matriks rancangan FFSP yang baik dari segi pembauran (kadar pembauran rendah) dan ketersediaan teknik penyusunannya yang masih langka untuk kasus percobaan yang melibatkan banyak faktor dan banyak petak utama. Adapun teknik penyusunan rancangan FFSP yang saat ini tersedia dalam literatur antara lain teknik yang diusulkan Huang et al. (1998), Bingham & Sitter (1999), Kowalski (2002), Bingham et al. (2004), Kulahci & Bisgaard (2005), Tichon et al. (2012), dan Sartono (2012). Diantara teknik-teknik tersebut, teknik yang paling efektif (dari segi pembauran maupun komputasi atau waktu proses) dalam menyusun rancangan FFSP dua taraf untuk percobaan yang melibatkan banyak faktor dan banyak petak utama adalah teknik Sartono (2012). Rancangan FFSP dua taraf yang dihasilkan teknik tersebut merupakan rancangan FFSP ortogonal. Keortogonalan juga menjadi fokus dalam penelitian ini karena mampu memberikan model pendugaan pengaruh utama yang terbaik secara statistik (Indahwati et al. 2013).
Sartono (2012) mengusulkan dua teknik penyusunan matriks rancangan FFSP ortogonal dua taraf yakni one-step approach untuk kasus percobaan dengan jumlah petak utama sedikit (kurang dari 10) dan two-step approach untuk kasus percobaan dengan jumlah petak utama banyak (lebih dari 10). Kedua teknik yang diusulkan tersebut menggunakan pendekatan stratum-by-stratum dengan menerapkan metode pemrograman linier integer untuk teknik one-step approach dan kombinasi pemrograman linier integer dengan variable neighborhood search (VNS) untuk teknik two-step approach. Selain itu, kedua teknik ini berusaha menimumkan pembauran antar pengaruh-pengaruh penting dengan berlandaskan konsep minimum G-aberration yang diusulkan Deng & Tang (2002).
Metode VNS yang digunakan Sartono (2012) merupakan sebuah metode optimasi yang bersifat meta-heuristik sehingga tidak ada jaminan matriks rancangan FFSP yang diperoleh memiliki kadar pembauran terendah. Oleh karena itu, improvement atau modifikasi terhadap teknik two-step approach masih diperlukan agar dapat diperoleh matriks rancangan FFSP yang lebih baik.
Tujuan dari penelitian ini adalah mengembangkan sebuah teknik pendekatan alternatif untuk menyusun matriks rancangan FFSP ortogonal dua taraf dengan memodifikasi teknik two-step approach yang diusulkan Sartono (2012). Modifikasi dilakukan dengan mengganti metode VNS dengan algoritma genetika. Teknik alternatif yang dihasilkan dari penelitian ini diharapkan mampu menghasilkan matriks rancangan FFSP ortogonal dua taraf lebih baik dalam artian memiliki kadar pembauran lebih rendah dan waktu proses yang lebih cepat (efisien dari segi komputasi) sehingga cocok digunakan untuk menyusun rancangan dari percobaan yang melibatkan lebih banyak lagi faktor dan petak utama.
3
METODE
Pendekatan stratum-by-stratum beserta Notasi dan Simbol
Pendekatan stratum-by-stratum dalam penyusunan matriks rancangan FFSP ortogonal dua taraf yang digunakan Sartono (2012) dalam teknik two-step
approach dan akan digunakan juga dalam penelitian ini digambarkan melalui
ilustrasi sebagai berikut:
Misalkan ingin disusun suatu matriks rancangan FFSP ortogonal dua taraf (R) untuk melakukan percobaan yang melibatkan b buah petak utama, n buah
runs, w faktor petak utama, dan s faktor anak petak. Dengan demikian, matriks R
yang terbentuk akan terdiri dari b buah perlakuan petak utama (kombinasi taraf faktor-faktor petak utama) dengan tiap perlakuan petak utama dipasangkan pada
n/b perlakuan anak petak (kombinasi taraf faktor-faktor anak petak) sehingga total
ada sebanyak n buah runs yang dicobakan.
Penyusunan matriks R diawali dengan menyusun rancangan secara terpisah (sub-rancangan) untuk b buah perlakuan petak utama dan n buah perlakuan anak petak. Sub-rancangan perlakuan petak utama akan dinotasikan dengan M dan sub-rancangan perlakuan anak petak dinotasikan dengan S. Adapun kedua matriks tersebut masing-masing berukuran b × w dan n × s. Penyusunan matriks M dan S dapat dilakukan mengikuti aturan rancangan reguler maupun non-reguler. Namun penyusunan tersebut harus dilakukan dengan syarat tiap faktor di dalamnya saling ortogonal. Dalam penelitian ini, matriks M dan S merupakan inputan sehingga tidak dibahas teknik penyusunannya.
Langkah berikutnya (langkah pertama atau step pertama dalam teknik
two-step approach) adalah mengelompokkan n buah perlakuan anak petak di dalam
matriks S ke dalam b kelompok (petak utama) sehingga masing-masing kelompok terdiri dari n/b buah perlakuan anak petak. Pengelompokkan dilakukan dengan syarat di dalam tiap kelompok faktor-faktor anak petak harus saling ortogonal. Aturan untuk melakukan pengelompokkan dengan syarat tersebut direpresentasikan dalam matriks B yang berukuran n × b. Adanya syarat keortogonalan faktor-faktor anak petak dalam tiap kelompok juga membatasi penggunaan teknik Sartono (2012) dan teknik alternatif hasil penelitian ini hanya untuk menyusun matriks rancangan FFSP dengan jumlah petak utama merupakan kelipatan empat dan jumlah run merupakan kelipatan dari jumlah petak utama serta menyebabkan n/b lebih dari satu. Matriks B diperoleh melalui pemrograman linier integer dengan beberapa kendala untuk menjamin persyaratan keortogonalan yang ditetapkan. Dalam penelitian ini, matriks B merupakan
inputan sehingga tidak dibahas penyusunannya. Penjelasan lengkap mengenai
penyusunan matriks B dapat dilihat pada Sartono (2012).
Langkah terakhir (step kedua dalam teknik two-step approach) yakni memasangkan b buah perlakuan petak utama (b baris dalam matriks M) ke setiap kelompok perlakuan anak petak yang terdiri dari n/b perlakuan anak petak. Pemasangan tersebut direpresentasikan oleh matriks W = BM. Metode variable
neighborhood search (VNS) digunakan oleh Sartono (2012) untuk mencari urutan
baris (permutasi) dalam matriks M yang menyebabkan kadar pembauran dalam matriks R seminimum mungkin. Adapun matriks R yang terbentuk merupakan
4
penggabungan kolom antara W dengan S sehingga R berukuran n × (w + s). Ringkasan dan beberapa tambahan dari notasi serta simbol yang digunakan dapat dilihat pada Tabel 1.
Tabel 1 Tabel ringkasan notasi dan simbol yang digunakan
Notasi Keterangan
S matriks perlakuan anak petak, yang juga merupakan matriks pengaruh utama faktor anak petak, berukuran n × s
Z matriks pengaruh interaksi dua faktor anak petak, berukuran n × s2
dengan s2 = s(s – 1)/2
M matriks perlakuan petak utama, yang juga merupakan matriks pengaruh utama faktor petak utama, berukuran b × w
Q matriks pengaruh interaksi dua faktor petak utama, berukuran b ×w2
dengan w2 = w(w – 1)/2
B matriks assignment atau pemasangan yang menunjukkan aturan pemasangan tiap perlakuan petak utama kepada n/b perlakuan anak petak. Dengan demikian, matriks ini berukuran n × b. Elemen dari
matriks ini (bij) bernilai 0 atau 1 dengan bij = 1 jika perlakuan petak
utama ke-j ditempatkan pada perlakuan anak petak ke-i dan bij = 0
jika sebaliknya. Adapun kendala tambahan untuk memperoleh matriks ini adalah sebagai berikut :
∑ untuk setiap i = 1, 2, ..., n
∑ untuk setiap j = 1, 2, ..., b
W= BM matriks perlakuan (pengaruh utama) dari faktor petak utama, berukuran n × w
V = BQ matriks pengaruh interaksi dua faktor petak utama, berukuran n × w2
dengan w2 = w(w – 1)/2
T = ( (1w)T S ) ( W (1s)T ); matriks pengaruh interaksi antara satu faktor petak utama dengan satu faktor anak petak
R= [W|S] matriks rancangan akhir berukuran n × (w + s)
Berdasarkan prinsip hierarchy, pengaruh yang dipentingkan dalam penelitian ini adalah pengaruh utama dan pengaruh interaksi dua faktor. Oleh karena itu, pola pembauran yang diamati yakni pola pembauran yang melibatkan tiga huruf (pengaruh utama dengan pengaruh interaksi dua faktor) dan empat huruf (pembauran antar pengaruh interaksi dua faktor) dengan huruf ‘W’ menunjukkan faktor petak utama dan huruf ‘S’ menunjukkan faktor anak petak. Adapun ringkasan dari pola pembaruan tersebut dapat dilihat pada Tabel 2.
5 Tabel 2 Tabel ringkasan pola pembauran yang melibatkan pengaruh utama dan
pengaruh interaksi dua faktor dalam matriks rancangan FFSP
Vektor Pola pembauran yang diukur
Pembauran antara pengaruh utama dengan pengaruh interaksi dua faktor
WWW - Pembauran antara pengaruh utama sebuah faktor petak utama (W) dengan pengaruh interaksi dua faktor petak utama (WW). WWS - Pembauran antara pengaruh utama sebuah
faktor petak utama (W) dengan pengaruh interaksi antara sebuah faktor petak utama dan sebuah faktor anak petak (WS).
- Pembauran antara pengaruh utama sebuah faktor anak petak (S) dengan pengaruh interaksi dua faktor petak utama (WW).
WSS - Pembauran antara pengaruh utama sebuah faktor petak utama (W) dengan pengaruh interaksi dua faktor anak petak (SS).
- Pembauran antara pengaruh utama sebuah faktor anak petak (S) dengan pengaruh interaksi antara sebuah faktor petak utama dan sebuah faktor anak petak (WS).
SSS - Pembauran antara pengaruh utama sebuah faktor anak petak (S) dengan pengaruh interaksi dua faktor anak petak (SS).
Pembauran antar pengaruh
interaksi dua faktor
WWWW - Pembauran antar pengaruh interaksi dua faktor petak utama (WW).
WWWS - Pembauran antara pengaruh interaksi dua faktor petak utama (WW) dengan pengaruh interaksi antara sebuah faktor petak utama dan sebuah faktor anak petak (WS).
WWSS - Pembauran antara pengaruh interaksi dua faktor petak utama (WW) dengan pengaruh interaksi dua faktor anak petak (SS).
WSSS - Pembauran antara pengaruh interaksi dua faktor anak petak (SS) dengan pengaruh interaksi antara sebuah faktor petak utama dan sebuah faktor anak petak (WS).
SSSS - Pembauran antar pengaruh interaksi dua faktor anak petak (SS).
Setiap vektor pembauran dalam Tabel 2 merupakan vektor frekuensi (confounding frequency vector atau CFV) dari beberapa nilai koefisien pembauran yang dikenal dengan characteristic. Penjelasan mengenai CFV dan
J-characteristic dapat dilihat pada Deng & Tang (2002). Matriks rancangan FFSP
yang memiliki nilai-nilai lebih kecil (minimum) dalam setiap vektor pembauran tersebut dinilai lebih baik. Oleh karena itu, penelitian ini dilakukan untuk menyusun rancangan FFSP ortogonal dua taraf yang meminimumkan kadar pembauran dalam sebanyak mungkin vektor pembauran.
6
Sartono (2012) mengelompokkan kesembilan vektor dalam Tabel 2 ke dalam tiga kategori. Kategori pertama terdiri atas WWS dan WWWS. Kategori kedua terdiri atas WWW, WWWW, SSS, dan SSSS. Kategori ketiga terdiri atas WSS, WWSS, dan WSSS. Setiap nilai dalam vektor kategori pertama dijamin bernilai 0 untuk setiap matriks rancangan FFSP yang dihasilkan melalui penelitian ini. Hal tersebut disebabkan oleh adanya syarat keortogonalan antar faktor-faktor anak petak dalam setiap petak utama. Vektor-vektor dalam kategori kedua tidak berkaitan dengan penyusunan matriks assignment (B), namun hanya berkaitan dengan pemilihan atau penyusunan matriks M dan S sehingga tidak dapat diminimumkan melalui teknik hasil penelitian ini. Dengan demikian, tugas yang dihadapi dan dikerjakan algoritma genetika melalui minimisasi fungsi fitness (fungsi tujuan) adalah meminimumkan pembauran sisanya yakni pembauran yang diukur melalui vektor dalam kategori ketiga.
Data
Data yang digunakan berupa matriks sub-rancangan petak utama (M), matriks sub-rancangan anak petak (S), dan matriks assignment (B). Matriks M dan S yang digunakan berupa kontras percobaan dua taraf yang terdiri dari unsur -1 (taraf rendah) dan 1 (taraf tinggi). Adapun matriks M, S, dan B tersebut diambil untuk kasus rancangan yang melibatkan 48-runs dengan 8 petak utama dan
96-runs dengan 12 petak utama. Matriks M yang digunakan pada kasus 8 petak
utama dan 12 petak utama masing-masing dapat dilihat pada Tabel 3 dan Tabel 4. Matriks S yang digunakan pada kasus 8 petak utama dapat dilihat pada Lampiran 1, sedangkan pada kasus 12 petak utama merupakan hasil folding-over dari matriks hadamard berlabel had.24.1 yang diunduh dari
http://neilsloane.com/hadamard/had.24.1.txt. Adapun teknik folding-over yang
digunakan mengikuti teknik pada Appendix B dalam Sartono (2012). Matriks B yang digunakan pada kasus 8 petak utama dan 12 petak utama masing-masing dapat dilihat pada Lampiran 2 dan Lampiran 3. Seluruh data yang digunakan dalam penelitian ini diperoleh dari Sartono (2012).
Tabel 3 Matriks sub-rancangan petak utama (M) pada kasus rancangan 8 petak utama W1 W2 W3 W4 W5 –1 –1 –1 –1 –1 –1 –1 –1 1 1 –1 1 1 –1 –1 –1 1 1 1 1 1 –1 1 –1 1 1 –1 1 1 –1 1 1 –1 –1 1 1 1 –1 1 –1
7 Tabel 4 Matriks sub-rancangan petak utama (M) pada kasus rancangan 12 petak
utama W1 W2 W3 W4 W5 −1 1 1 −1 1 −1 −1 −1 −1 −1 1 −1 −1 1 1 −1 1 1 1 1 −1 −1 −1 −1 1 −1 1 −1 1 −1 1 1 −1 −1 1 1 1 −1 1 −1 1 −1 1 1 1 1 −1 1 −1 −1 −1 −1 1 1 −1 1 1 1 −1 −1 Metode
Algoritma genetika merupakan sebuah metode optimasi yang bersifat meta-heuristik dan cara kerjanya mengikuti prinsip evolusi makhluk hidup. Kelebihan utamanya dibandingkan metode sejenis adalah solusi yang dihasilkan berupa list atau daftar solusi sehingga kemungkinan metode ini terjebak di solusi optimum lokal lebih kecil. Metode ini telah berhasil diaplikasikan dalam berbagai bidang terapan. Contoh aplikasi, kelebihan lain, dan kekurangannya dapat dilihat dalam Haupt R & Haupt S (2004) dan Sivanandam & Deepa (2008).
8
Beberapa istilah-istilah yang umum digunakan dalam algoritma genetika antara lain populasi, individu, gen, seleksi alam, kawin silang, dan mutasi. Karena metode ini tergolong ke dalam metode iterasi maka diperkenalkan istilah generasi untuk menyatakan populasi yang dihasilkan dari setiap iterasi. Iterasi berhenti ketika metode telah mencapai kriteria kekonvergenan atau maksimum iterasi yang ditentukan. Generasi yang dihasilkan ketika iterasi berhenti merupakan generasi terbaik yang terdapat solusi terbaik di dalamnya. Mekanisme atau tahapan algoritma genetika secara umum dapat dilihat pada Gambar 1.
Dalam penelitian ini, algoritma genetika menggantikan peran variable
neighborhood search (VNS) untuk mencari urutan baris matriks M yang mampu
menimumkan pembauran dalam matriks rancangan akhir (R). Adapun penelitian ini dilakukan melalui dua tahap yaitu:
1. Menentukan rancangan algoritma genetika yang akan digunakan. Adapun rancangan tersebut adalah sebagai berikut:
a. Gen
Gen yang digunakan berupa bilangan bulat {1, 2, ..., b} yang merepresentasikan lokasi penempatan sebuah perlakuan petak utama ke tepat sebuah petak utama yang telah ditempati n/b perlakuan anak petak. b. Individu
Individu dalam penelitian ini berperan sebagai sebuah fungsi satu-satu (one-to-one) yang memetakan seluruh perlakuan petak utama ke masing-masing petak utama. Individu ke-i merupakan gabungan dari b buah gen dan dilambangkan dengan sebuah vektor ai = {1, 2, ..., b} dengan i = 1, 2, ..., b.
c. Populasi awal
Populasi awal terdiri dari b buah individu berbeda yang diperoleh dengan menggeser posisi tiap gen ke sebelah kirinya, sehingga gen yang berada paling kiri digeser ke posisi gen paling kanan.
1 2 3 4 5 6 ... b 4 5 6 ... B 1 2 3
2 3 4 5 6 ... B 1 5 6 ... ... b 1 2 3
3 4 5 6 ... b 1 2 B ... 1 2 3 4 5 6
d. Fungsi fitness
Fungsi fitness yang digunakan yakni:
keterangan :
107; 103; 105; 101; 103; 10 –1
elemen dengan nilai tertinggi (maksimum) pada matriks D = ZT
W. penjumlahan nilai seluruh elemen pada matriks D = ZT
W. elemen dengan nilai tertinggi (maksimum) pada matriks E = ZT
V. penjumlahan nilai seluruh elemen pada matriks E = ZT
V. elemen dengan nilai tertinggi (maksimum) pada matriks F = ZT
T. penjumlahan nilai seluruh elemen pada matriks F = ZT
9 Dalam penelitian ini, fungsi fitness didefinisikan sebagai fungsi yang mengukur kadar pembauran dalam matriks rancangan FFSP. Adapun matriks D, E, dan F berturut-turut merepresentasikan pola pembauran WSS, WWSS, dan WSSS. Pemilihan konstanta , , , , , menentukan pola pembauran yang diutamakan untuk diminimumkan (pola pembauran yang diutamakan diberikan bobot atau nilai konstanta lebih besar). Pemilihan konstanta dalam penelitian ini berlandaskan konsep minimum G-aberration dengan mengikuti konstanta yang digunakan Sartono (2012).
e. Seleksi Alam
Teknik seleksi yang digunakan adalah mereduksi populasi awal dengan hanya menyisakan k buah individu dengan nilai fitness terkecil (minimum). Pada penelitian ini, digunakan k = 5.
f. Kawin Silang (Cross-Over)
Operasi kawin silang dilakukan pada setiap kombinasi pasangan k induk (hasil proses seleksi) sehingga dihasilkan individu baru dengan masing-masing individu baru diperoleh melalui rumus:
keterangan :
= individu baru yang terbentuk.
= individu ke-i (induk 1) dengan i = 1, 2, ..., k. = individu ke-j (induk 2) dengan j = 1, 2, ..., k; i j.
i =
fitnessi = nilai fitness dari individu ke-i.
fitnessj = nilai fitness dari individu ke-j.
Pada setiap individu baru yang dihasilkan kemudian dilakukan transformasi ke dalam bentuk peringkat gen dari terkecil ke terbesar. Selanjutnya, hasilnya ( individu berupa peringkat) digabungkan ke dalam populasi induk (hasil proses seleksi). Penggabungan ini bertujuan menjaga sifat induk agar tidak hilang pada populasi hasil kawin silang. g. Mutasi
Mutasi merupakan upaya pencegahan iterasi algoritma genetika berhenti pada solusi optimum lokal. Karena mutasi terjadi pada tingkat gen, maka proses diawali dengan mengacak lokasi gen-gen yang akan termutasi dengan peluang terpilihnya setiap gen menyebar Bernoulli dengan peluang sukses (gen terkena mutasi) sebesar pm. Selanjutnya, pada nilai
gen-gen terpilih ditambahkan sebuah bilangan acak yang menyebar seragam(–b, b). Setelah itu, pada setiap individu yang di dalamnya terdapat gen termutasi dilakukan transformasi ke dalam bentuk peringkat gen dari terkecil ke terbesar (seperti dalam proses kawin silang). Hasilnya, setiap individu baru yang telah di transformasi digabungkan ke dalam populasi hasil kawin silang. Pada penelitian ini, digunakan pm =
10
h. Kriteria kekonvergenan
Dalam penelitian ini digunakan kriteria kekonvergenan berupa jangkauan nilai fitness 10 solusi terbaik dalam populasi akhir tiap iterasi (setelah mutasi) sama dengan 0 (kriteria ini digunakan setelah iterasi minimal 100 kali dilakukan). Iterasi berhenti ketika kriteria terpenuhi atau mencapai maksimal jumlah iterasi yakni 1000 iterasi.
2. Menerapkan algoritma genetika pada rancangan yang melibatkan 48-runs dengan 8 petak utama dan 96-runs dengan 12 petak utama untuk mencari urutan baris matriks M (lokasi penempatan perlakuan petak utama ke dalam petak utama yang tersedia) yang dapat meminimumkan pembauran pada matriks rancangan akhir (R).
HASIL DAN PEMBAHASAN
Pengembangan algoritma genetika yang digunakan dalam penelitian ini dapat dilihat pada Lampiran 4. Jumlah petak utama merupakan faktor yang paling berpengaruh pada waktu proses pencarian permutasi baris matriks sub-rancangan petak utama (M) dalam penyusunan matriks rancangan FFSP ortogonal dua taraf. Oleh karena itu, penerapan algoritma genetika akan diilustrasikan pada rancangan yang melibatkan 8 petak utama dan 12 petak utama. Pada rancangan yang melibatkan 8 petak utama, algoritma genetika dikatakan potensial digunakan jika mampu memberikan solusi permutasi terbaik dengan nilai fitness menyamai solusi terbaik hasil evaluasi seluruh kemungkinan permutasi (Lampiran 5).
Pada rancangan yang melibatkan 12 petak utama, solusi terbaik algoritma genetika dibandingkan dengan solusi terbaik yang dihasilkan teknik Sartono (2012). Hal tersebut dilakukan karena tidak lagi memungkinkan melakukan evaluasi seluruh kemungkinan (12!) permutasi. Selain itu, solusi terbaik algoritma genetika juga dibandingkan dengan solusi hasil 100 kali pengacakan permutasi (random assignment) untuk menjamin keefektifan dan kestabilan rancangan algoritma genetika yang digunakan.
Penerapan pada rancangan 48-runs dengan 8 petak utama, 5 faktor petak utama, dan 10 faktor anak petak
Matriks rancangan akhir (R) yang diperoleh tanpa mengubah urutan baris dari matriks M (tanpa menggunakan algoritma genetika) atau dengan kata lain menerapkan permutasi a = {1, 2, 3, 4, 5, 6, 7, 8} dapat dilihat pada Tabel 5. Adapun solusi permutasi terbaik yang dihasilkan algoritma genetika tidak unik, namun solusi tersebut selalu memiliki nilai fitness menyamai solusi terbaik hasil evaluasi seluruh kemungkinan permutasi (nilai fitness = 164336141). Salah satu solusi permutasi yang diperoleh dengan algoritma genetika yakni a = {1, 5, 6, 2, 8, 3, 7, 4}. Solusi tersebut memberikan matriks R seperti pada Tabel 6.
Atas keberhasilannya menghasilkan solusi dengan nilai fitness menyamai solusi terbaik hasil evaluasi seluruh kemungkinan permutasi, maka dapat dikatakan algoritma genetika potensial digunakan dalam penyusunan matriks rancangan FFSP ortogonal dua taraf.
11 Karena tujuan utama penggunaan algoritma genetika adalah untuk menyelesaikan kasus-kasus dengan komputasi yang kompleks, maka penerapan algoritma genetika dicobakan pada kasus percobaan besar (tidak mungkin lagi dilakukan evaluasi seluruh kemungkinan permutasi) pada subab berikutnya.
Tabel 5 Matriks rancangan akhir (R) dari permutasi a = {1, 2, 3, 4, 5, 6, 7, 8} tanpa algoritma genetika
Petak Utama W1 W2 W3 W4 W5 Perlakuan Anak Petak (Baris Matriks S) 1 –1 –1 –1 –1 –1 3, 9, 17, 30, 43, 44 2 –1 –1 –1 1 1 11, 14, 21, 27, 35, 37 3 –1 1 1 –1 –1 6, 7, 20, 29, 38, 48 4 –1 1 1 1 1 5, 13, 23, 25, 34, 45 5 1 –1 1 –1 1 8, 16, 24, 28, 33, 40 6 1 –1 1 1 –1 1, 15, 22, 26, 36, 47 7 1 1 –1 –1 1 4, 10, 19, 32, 41, 42 8 1 1 –1 1 –1 2, 12, 18, 31, 39, 46
Tabel 6 Matriks rancangan akhir (R) dari permutasi a = {1, 5, 6, 2, 8, 3, 7, 4} hasil algoritma genetika
Petak Utama W1 W2 W3 W4 W5 Perlakuan Anak Petak (Baris Matriks S) 1 –1 –1 –1 –1 –1 3, 9, 17, 30, 43, 44 2 1 –1 1 –1 1 11, 14, 21, 27, 35, 37 3 1 –1 1 1 –1 6, 7, 20, 29, 38, 48 4 –1 –1 –1 1 1 5, 13, 23, 25, 34, 45 5 1 1 –1 1 –1 8, 16, 24, 28, 33, 40 6 –1 1 1 –1 –1 1, 15, 22, 26, 36, 47 7 1 1 –1 –1 1 4, 10, 19, 32, 41, 42 8 –1 1 1 1 1 2, 12, 18, 31, 39, 46
Penerapan pada rancangan 96-runs dengan 12 petak utama, 5 faktor petak utama, dan 25 faktor anak petak
Dalam kasus ini, solusi terbaik algoritma genetika dibandingkan dengan solusi terbaik yang dihasilkan teknik Sartono (2012). Hasil perbandingan tidak menjamin bahwa solusi terbaik algoritma genetika merupakan solusi terbaik
12
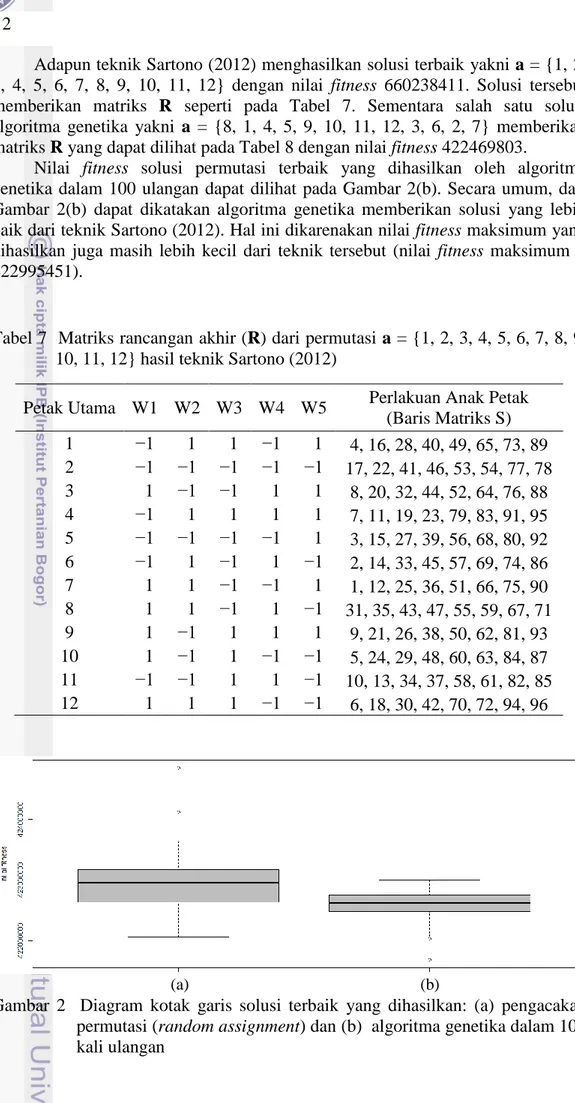
Adapun teknik Sartono (2012) menghasilkan solusi terbaik yakni a = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12} dengan nilai fitness 660238411. Solusi tersebut memberikan matriks R seperti pada Tabel 7. Sementara salah satu solusi algoritma genetika yakni a = {8, 1, 4, 5, 9, 10, 11, 12, 3, 6, 2, 7} memberikan matriks R yang dapat dilihat pada Tabel 8 dengan nilai fitness 422469803.
Nilai fitness solusi permutasi terbaik yang dihasilkan oleh algoritma genetika dalam 100 ulangan dapat dilihat pada Gambar 2(b). Secara umum, dari Gambar 2(b) dapat dikatakan algoritma genetika memberikan solusi yang lebih baik dari teknik Sartono (2012). Hal ini dikarenakan nilai fitness maksimum yang dihasilkan juga masih lebih kecil dari teknik tersebut (nilai fitness maksimum = 422995451).
Tabel 7 Matriks rancangan akhir (R) dari permutasi a = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12} hasil teknik Sartono (2012)
Petak Utama W1 W2 W3 W4 W5 Perlakuan Anak Petak (Baris Matriks S) 1 −1 1 1 −1 1 4, 16, 28, 40, 49, 65, 73, 89 2 −1 −1 −1 −1 −1 17, 22, 41, 46, 53, 54, 77, 78 3 1 −1 −1 1 1 8, 20, 32, 44, 52, 64, 76, 88 4 −1 1 1 1 1 7, 11, 19, 23, 79, 83, 91, 95 5 −1 −1 −1 −1 1 3, 15, 27, 39, 56, 68, 80, 92 6 −1 1 −1 1 −1 2, 14, 33, 45, 57, 69, 74, 86 7 1 1 −1 −1 1 1, 12, 25, 36, 51, 66, 75, 90 8 1 1 −1 1 −1 31, 35, 43, 47, 55, 59, 67, 71 9 1 −1 1 1 1 9, 21, 26, 38, 50, 62, 81, 93 10 1 −1 1 −1 −1 5, 24, 29, 48, 60, 63, 84, 87 11 −1 −1 1 1 −1 10, 13, 34, 37, 58, 61, 82, 85 12 1 1 1 −1 −1 6, 18, 30, 42, 70, 72, 94, 96 (a) (b)
Gambar 2 Diagram kotak garis solusi terbaik yang dihasilkan: (a) pengacakan permutasi (random assignment) dan (b) algoritma genetika dalam 100 kali ulangan
13 Tabel 8 Matriks rancangan akhir (R) dari permutasi a = {8, 1, 4, 5, 9, 10, 11, 12,
3, 6, 2, 7} hasil algoritma genetika
Petak Utama W1 W2 W3 W4 W5 Perlakuan Anak Petak (Baris Matriks S) 1 1 1 −1 1 −1 4, 16, 28, 40, 49, 65, 73, 89 2 −1 1 1 −1 1 17, 22, 41, 46, 53, 54, 77, 78 3 −1 1 1 1 1 8, 20, 32, 44, 52, 64, 76, 88 4 −1 −1 −1 −1 1 7, 11, 19, 23, 79, 83, 91, 95 5 1 −1 1 1 1 3, 15, 27, 39, 56, 68, 80, 92 6 1 −1 1 −1 −1 2, 14, 33, 45, 57, 69, 74, 86 7 −1 −1 1 1 −1 1, 12, 25, 36, 51, 66, 75, 90 8 1 1 1 −1 −1 31, 35, 43, 47, 55, 59, 67, 71 9 1 −1 −1 1 1 9, 21, 26, 38, 50, 62, 81, 93 10 −1 1 −1 1 −1 5, 24, 29, 48, 60, 63, 84, 87 11 −1 −1 −1 −1 −1 10, 13, 34, 37, 58, 61, 82, 85 12 1 1 −1 −1 1 6, 18, 30, 42, 70, 72, 94, 96
Selain menghasilkan solusi terbaik dengan nilai fitness lebih baik dari teknik Sartono (2012), rancangan algoritma genetika yang digunakan juga dapat dikatakan cukup stabil dalam pencarian permutasi yang meminimumkan pembauran pada matriks R. Hal ini dapat dilihat dari hasil perbandingan solusi terbaik algoritma genetika dengan solusi pengacakan permutasi (random
assignment) dalam 100 kali ulangan pada Gambar 2. Dari gambar tersebut terlihat
diagram kotak garis solusi algoritma genetika memiliki keragaman yang lebih kecil dengan solusi yang lebih baik (nilai fitness lebih kecil).
Hasil dalam kasus percobaan 12 petak utama ini menunjukkan bahwa modifikasi teknik Sartono (2012) dengan menerapkan algoritma genetika didalamnya mampu memberikan peningkatan performa yakni pembauran yang semakin dapat diminimumkan (ditunjukkan oleh nilai fitness yang lebih kecil). Dengan demikian, algoritma genetika dapat dikatakan efektif digunakan dalam penyusunan matriks rancangan FFSP ortogonal dua taraf dalam kasus percobaan besar (banyak petak utama dan banyak faktor).
Kinerja komputasi algoritma genetika dalam penyusunan matriks rancangan FFSP ortogonal dua taraf
Penerapan rancangan algoritma genetika dalam penelitian ini dilakukan pada software R 3.0.1 dengan komputer yang menggunakan prosesor 2.3 GHz, RAM 6144 MB, dan berjalan pada sistem operasi 64-bit.
Statistik waktu proses yang dibutuhkan oleh algoritma genetika dalam 100 ulangan untuk kasus rancangan yang melibatkan 8 petak utama, 5 faktor petak utama, 10 faktor anak petak, dan 48-runs disajikan pada Tabel 9 atau secara visual
14
dapat dilihat pada Gambar 3. Adapun evaluasi seluruh kemungkinan permutasi membutuhkan waktu + 15 menit. Sementara teknik Sartono (2012) membutuhkan waktu rata-rata 63.81 detik.
waktu proses (detik)
Gambar 3 Diagram kotak garis waktu proses (detik) pencarian solusi algoritma genetika dalam 100 ulangan (kasus rancangan 8 petak utama)
Tabel 9 Statistik waktu proses (detik) yang dibutuhkan oleh algoritma genetika hingga konvergen atau iterasi berakhir pada kasus rancangan 8 petak utama
Waktu Proses (detik)
Minimum Q1 (25%) Q2 (50%) Q3 (75%) Maksimum Mean
3.30 3.41 3.605 4.96 6.23 4.10
Statistik waktu proses yang dibutuhkan oleh algoritma genetika dalam 100 ulangan untuk kasus rancangan yang melibatkan 12 petak utama, 5 faktor petak utama, 25 faktor anak petak, dan 96-runs disajikan pada Tabel 10 atau secara visual dapat dilihat pada Gambar 4.
Dari hasil ini, dapat dikatakan bahwa algoritma genetika bukan hanya efektif dalam penyusunan matriks rancangan FFSP ortogonal dua taraf (R) yang baik dari segi pembauran karena terbukti juga mampu memberikan solusi dengan waktu proses yang sangat cepat sehingga sangat menghemat waktu jika digunakan dalam menyusun matriks R yang melibatkan banyak petak utama (lebih dari 12) dan banyak faktor.
15 Tabel 10 Statistik waktu proses (detik) yang dibutuhkan oleh algoritma genetika hingga konvergen atau iterasi berakhir pada kasus rancangan 12 petak utama
Waktu Proses (detik)
Minimum Q1 (25%) Q2 (50%) Q3 (75%) Maksimum Mean
26.88 37.125 38.16 39.22 44.94 37.8
waktu proses (detik)
Gambar 4 Diagram kotak garis waktu proses (detik) pencarian solusi algoritma genetika dalam 100 ulangan (kasus rancangan 12 petak utama)
SIMPULAN
Berdasarkan hasil penelitian, untuk kasus petak utama yang tidak terlalu banyak (petak utama kurang dari 10), rancangan algoritma genetika yang dibuat terbukti mampu menghasilkan permutasi baris matriks sub-rancangan petak utama (M) terbaik yang dapat meminimumkan pembauran pada matriks rancangan akhir (R), namun penerapannya tidak terlalu dirasakan karena melakukan evaluasi seluruh kemungkinan permutasi masih dapat dilakukan dalam waktu yang relatif singkat (+ 15 menit untuk kasus 8 petak utama).
Pada kasus percobaan yang besar (melibatkan petak utama lebih dari 10 dan banyak faktor) yang diilustrasikan pada percobaan yang melibatkan 12 petak utama, penerapan algoritma genetika dapat sangat dirasakan manfaatnya karena mampu menghasilkan permutasi baris matriks M yang baik sehingga semakin meminimumkan pembauran pada matriks rancangan akhir R dalam waktu proses yang sangat cepat (dibandingkan dengan teknik Sartono (2012)).
Dengan demikian, modifikasi teknik Sartono (2012) dengan mengganti metode variable neighboorbod search (VNS) dengan algoritma genetika cukup efektif dan bermanfaat dilakukan sebagai sebuah teknik pendekatan alternatif karena mampu menghasilkan matriks rancangan FFSP ortogonal dua taraf yang lebih baik dari segi pembauran maupun waktu proses (komputasi).
16
DAFTAR PUSTAKA
Bingham DR, Sitter RR. 1999. Minimum-Aberration Two-Level Fractional Factorial Split-Plot Designs. Technometrics. 41:62-70.
Bingham DR, Schoen ED, Sitter RR. 2004. Designing Fractional Factorial Split-Plot Experiments with Few Whole-Split-Plot Factors. Appl Statist. 53:325-339. Deng LY, Tang B. 2002. Design Selection and Classification for Hadamard
Matrices using Generalized Minimum Aberration Criteria. Technometrics. 44:173-184.
Haupt RL, Haupt SE. 2004. Practical Genetic Algorithms. Ed ke-2. New Jersey (US): J Wiley.
Huang P, Chen D, Voelkel JO. 1998. Minimum-Aberration Two-Level Split-Plot Designs. Technometrics. 40:314-326.
Indahwati, Anggraini Y, Sartono B. 2013. Penyusunan Rancangan Near-Orthogonal Fractional Factorial Split-Plot. Prosiding Seminar Statistika
Nasional 2013 [Internet]. Universitas Diponegoro, Jawa Timur (Indonesia).
hlm 327-338; [diunduh 20 Januari 2014]. Tersedia pada: http://eprints.undip.ac.id/40309/1/B10_Indahwati.pdf.
Kowalski SMP. 2002. 24 run Split-Plot Experiments for Robust Parameter Designs. Journal of Quality Technology. 34:399-410.
Kulahci M, Bisgaard S. 2005. The Use of Plackett-Burman Designs to Construct Split-Plot Designs. Technometrics. 47:495-501.
Sartono B. 2012. Orthogonal Experimental Designs under Complete and Restricted Randomization [disertasi]. Antwerp (BE): University of Antwerp. Sivanandam SN, Deepa SN. 2008. Introduction to Genetic Algorithms. New
York(US): Springer.
Tichon JG, Li W, Mcleod RG. 2012. Generalized Minimum Aberration Two-Level Split-Plot Designs. Journal of Statistical Planning and Inference. 142:1407-1414.
Winarni S. 2006. Kajian pada Rancangan Fractional Factorial dan Fractional Factorial Split-Plot [tesis]. Bogor (ID): Institut Pertanian Bogor.
17 Lampiran 1 Matriks sub-rancangan anak petak (S) beserta penempatannya ke
dalam petak utama pada kasus rancangan 8 petak utama
S1 S2 S3 S4 S5 S6 S7 S8 S9 S10 Ditempatkan pada petak utama ke- –1 –1 –1 –1 –1 –1 –1 –1 –1 –1 6 –1 –1 –1 –1 –1 –1 –1 1 1 1 8 –1 –1 –1 –1 –1 1 1 –1 –1 1 1 –1 –1 –1 –1 1 –1 1 –1 1 –1 7 –1 –1 –1 1 –1 –1 1 1 1 –1 4 –1 –1 –1 1 1 1 –1 –1 –1 1 3 –1 –1 1 –1 –1 –1 1 1 –1 1 3 –1 –1 1 –1 1 1 –1 1 1 –1 5 –1 –1 1 1 –1 1 –1 –1 1 –1 1 –1 –1 1 1 1 –1 –1 1 –1 1 7 –1 –1 1 1 1 1 1 –1 1 1 2 –1 –1 1 1 1 1 1 1 –1 –1 8 –1 1 –1 –1 1 1 –1 –1 1 1 4 –1 1 –1 –1 1 1 1 1 –1 –1 2 –1 1 –1 1 –1 1 –1 1 –1 –1 6 –1 1 –1 1 –1 1 1 1 1 1 5 –1 1 –1 1 1 –1 –1 1 1 –1 1 –1 1 –1 1 1 –1 1 –1 –1 1 8 –1 1 1 –1 –1 1 –1 1 –1 1 7 –1 1 1 –1 –1 1 1 –1 1 –1 3 –1 1 1 –1 1 –1 –1 –1 –1 –1 2 –1 1 1 –1 1 –1 1 1 1 1 6 –1 1 1 1 –1 –1 –1 –1 1 1 4 –1 1 1 1 –1 –1 1 –1 –1 –1 5 1 –1 –1 –1 1 1 –1 1 –1 –1 4 1 –1 –1 –1 1 1 1 1 1 1 6 1 –1 –1 1 –1 1 –1 1 1 1 2 1 –1 –1 1 –1 1 1 –1 –1 –1 5 1 –1 –1 1 1 –1 –1 –1 1 –1 3 1 –1 –1 1 1 –1 1 1 –1 1 1 1 –1 1 –1 –1 1 –1 –1 –1 1 8 1 –1 1 –1 –1 1 1 1 1 –1 7 1 –1 1 –1 1 –1 –1 –1 1 1 5 1 –1 1 –1 1 –1 1 –1 –1 –1 4 1 –1 1 1 –1 –1 –1 1 –1 –1 2 1 –1 1 1 –1 –1 1 –1 1 1 6 1 1 –1 –1 –1 –1 1 –1 1 1 2 1 1 –1 –1 –1 –1 1 1 –1 –1 3 1 1 –1 –1 –1 1 –1 –1 1 –1 8 1 1 –1 –1 1 –1 –1 1 –1 1 5 1 1 –1 1 –1 –1 –1 –1 –1 1 7 1 1 –1 1 1 1 1 –1 1 –1 7 1 1 1 –1 –1 –1 –1 1 1 –1 1 1 1 1 –1 1 1 1 –1 –1 1 1 1 1 1 1 –1 1 1 1 –1 1 4 1 1 1 1 1 –1 1 1 1 –1 8 1 1 1 1 1 1 –1 –1 –1 –1 6 1 1 1 1 1 1 –1 1 1 1 3
18
Lampiran 2 Matriks assignment (B) pada kasus rancangan 8 petak utama
Perlakuan anak petak atau baris matriks S ke-
Petak Utama ke-
1 2 3 4 5 6 7 8 1 0 0 0 0 0 1 0 0 2 0 0 0 0 0 0 0 1 3 1 0 0 0 0 0 0 0 4 0 0 0 0 0 0 1 0 5 0 0 0 1 0 0 0 0 6 0 0 1 0 0 0 0 0 7 0 0 1 0 0 0 0 0 8 0 0 0 0 1 0 0 0 9 1 0 0 0 0 0 0 0 10 0 0 0 0 0 0 1 0 11 0 1 0 0 0 0 0 0 12 0 0 0 0 0 0 0 1 13 0 0 0 1 0 0 0 0 14 0 1 0 0 0 0 0 0 15 0 0 0 0 0 1 0 0 16 0 0 0 0 1 0 0 0 17 1 0 0 0 0 0 0 0 18 0 0 0 0 0 0 0 1 19 0 0 0 0 0 0 1 0 20 0 0 1 0 0 0 0 0 21 0 1 0 0 0 0 0 0 22 0 0 0 0 0 1 0 0 23 0 0 0 1 0 0 0 0 24 0 0 0 0 1 0 0 0 25 0 0 0 1 0 0 0 0 26 0 0 0 0 0 1 0 0 27 0 1 0 0 0 0 0 0 28 0 0 0 0 1 0 0 0 29 0 0 1 0 0 0 0 0 30 1 0 0 0 0 0 0 0 31 0 0 0 0 0 0 0 1 32 0 0 0 0 0 0 1 0 33 0 0 0 0 1 0 0 0 34 0 0 0 1 0 0 0 0 35 0 1 0 0 0 0 0 0 36 0 0 0 0 0 1 0 0 37 0 1 0 0 0 0 0 0 38 0 0 1 0 0 0 0 0 39 0 0 0 0 0 0 0 1 40 0 0 0 0 1 0 0 0 41 0 0 0 0 0 0 1 0 42 0 0 0 0 0 0 1 0 43 1 0 0 0 0 0 0 0 44 1 0 0 0 0 0 0 0 45 0 0 0 1 0 0 0 0 46 0 0 0 0 0 0 0 1 47 0 0 0 0 0 1 0 0 48 0 0 1 0 0 0 0 0
19 Lampiran 3 Matriks assignment (B) pada kasus rancangan 12 petak utama
Perlakuan anak petak atau baris matriks S ke-
Petak Utama ke-
1 2 3 4 5 6 7 8 9 10 11 12 1 0 0 0 0 0 0 1 0 0 0 0 0 2 0 0 0 0 0 1 0 0 0 0 0 0 3 0 0 0 0 1 0 0 0 0 0 0 0 4 1 0 0 0 0 0 0 0 0 0 0 0 5 0 0 0 0 0 0 0 0 0 1 0 0 6 0 0 0 0 0 0 0 0 0 0 0 1 7 0 0 0 1 0 0 0 0 0 0 0 0 8 0 0 1 0 0 0 0 0 0 0 0 0 9 0 0 0 0 0 0 0 0 1 0 0 0 10 0 0 0 0 0 0 0 0 0 0 1 0 11 0 0 0 1 0 0 0 0 0 0 0 0 12 0 0 0 0 0 0 1 0 0 0 0 0 13 0 0 0 0 0 0 0 0 0 0 1 0 14 0 0 0 0 0 1 0 0 0 0 0 0 15 0 0 0 0 1 0 0 0 0 0 0 0 16 1 0 0 0 0 0 0 0 0 0 0 0 17 0 1 0 0 0 0 0 0 0 0 0 0 18 0 0 0 0 0 0 0 0 0 0 0 1 19 0 0 0 1 0 0 0 0 0 0 0 0 20 0 0 1 0 0 0 0 0 0 0 0 0 21 0 0 0 0 0 0 0 0 1 0 0 0 22 0 1 0 0 0 0 0 0 0 0 0 0 23 0 0 0 1 0 0 0 0 0 0 0 0 24 0 0 0 0 0 0 0 0 0 1 0 0 25 0 0 0 0 0 0 1 0 0 0 0 0 26 0 0 0 0 0 0 0 0 1 0 0 0 27 0 0 0 0 1 0 0 0 0 0 0 0 28 1 0 0 0 0 0 0 0 0 0 0 0 29 0 0 0 0 0 0 0 0 0 1 0 0 30 0 0 0 0 0 0 0 0 0 0 0 1 31 0 0 0 0 0 0 0 1 0 0 0 0 32 0 0 1 0 0 0 0 0 0 0 0 0 33 0 0 0 0 0 1 0 0 0 0 0 0 34 0 0 0 0 0 0 0 0 0 0 1 0 35 0 0 0 0 0 0 0 1 0 0 0 0 36 0 0 0 0 0 0 1 0 0 0 0 0 37 0 0 0 0 0 0 0 0 0 0 1 0 38 0 0 0 0 0 0 0 0 1 0 0 0 39 0 0 0 0 1 0 0 0 0 0 0 0 40 1 0 0 0 0 0 0 0 0 0 0 0 41 0 1 0 0 0 0 0 0 0 0 0 0 42 0 0 0 0 0 0 0 0 0 0 0 1 43 0 0 0 0 0 0 0 1 0 0 0 0 44 0 0 1 0 0 0 0 0 0 0 0 0 45 0 0 0 0 0 1 0 0 0 0 0 0 46 0 1 0 0 0 0 0 0 0 0 0 0 47 0 0 0 0 0 0 0 1 0 0 0 0 48 0 0 0 0 0 0 0 0 0 1 0 0 49 1 0 0 0 0 0 0 0 0 0 0 0 50 0 0 0 0 0 0 0 0 1 0 0 0 51 0 0 0 0 0 0 1 0 0 0 0 0 52 0 0 1 0 0 0 0 0 0 0 0 0
20
Lampiran 3 Matriks assignment (B) pada kasus rancangan 12 petak utama (lanjutan)
Perlakuan anak petak atau baris matriks S ke-
Petak Utama ke-
1 2 3 4 5 6 7 8 9 10 11 12 53 0 1 0 0 0 0 0 0 0 0 0 0 54 0 1 0 0 0 0 0 0 0 0 0 0 55 0 0 0 0 0 0 0 1 0 0 0 0 56 0 0 0 0 1 0 0 0 0 0 0 0 57 0 0 0 0 0 1 0 0 0 0 0 0 58 0 0 0 0 0 0 0 0 0 0 1 0 59 0 0 0 0 0 0 0 1 0 0 0 0 60 0 0 0 0 0 0 0 0 0 1 0 0 61 0 0 0 0 0 0 0 0 0 0 1 0 62 0 0 0 0 0 0 0 0 1 0 0 0 63 0 0 0 0 0 0 0 0 0 1 0 0 64 0 0 1 0 0 0 0 0 0 0 0 0 65 1 0 0 0 0 0 0 0 0 0 0 0 66 0 0 0 0 0 0 1 0 0 0 0 0 67 0 0 0 0 0 0 0 1 0 0 0 0 68 0 0 0 0 1 0 0 0 0 0 0 0 69 0 0 0 0 0 1 0 0 0 0 0 0 70 0 0 0 0 0 0 0 0 0 0 0 1 71 0 0 0 0 0 0 0 1 0 0 0 0 72 0 0 0 0 0 0 0 0 0 0 0 1 73 1 0 0 0 0 0 0 0 0 0 0 0 74 0 0 0 0 0 1 0 0 0 0 0 0 75 0 0 0 0 0 0 1 0 0 0 0 0 76 0 0 1 0 0 0 0 0 0 0 0 0 77 0 1 0 0 0 0 0 0 0 0 0 0 78 0 1 0 0 0 0 0 0 0 0 0 0 79 0 0 0 1 0 0 0 0 0 0 0 0 80 0 0 0 0 1 0 0 0 0 0 0 0 81 0 0 0 0 0 0 0 0 1 0 0 0 82 0 0 0 0 0 0 0 0 0 0 1 0 83 0 0 0 1 0 0 0 0 0 0 0 0 84 0 0 0 0 0 0 0 0 0 1 0 0 85 0 0 0 0 0 0 0 0 0 0 1 0 86 0 0 0 0 0 1 0 0 0 0 0 0 87 0 0 0 0 0 0 0 0 0 1 0 0 88 0 0 1 0 0 0 0 0 0 0 0 0 89 1 0 0 0 0 0 0 0 0 0 0 0 90 0 0 0 0 0 0 1 0 0 0 0 0 91 0 0 0 1 0 0 0 0 0 0 0 0 92 0 0 0 0 1 0 0 0 0 0 0 0 93 0 0 0 0 0 0 0 0 1 0 0 0 94 0 0 0 0 0 0 0 0 0 0 0 1 95 0 0 0 1 0 0 0 0 0 0 0 0 96 0 0 0 0 0 0 0 0 0 0 0 1
21 Lampiran 4 Algoritma genetika untuk penyusunan matriks rancangan FFSP
ortogonal dua taraf pada R berbentuk fungsi ffsp.ga fitness<-function(M,S,B,Z){ cd0<-10^7;cd1=10^3;ce0=10^5;ce1<-10;cf0<-10^3;cf1=10^-1 Q<-matrix(0,nrow(M),ncol(M)*(ncol(M)-1)/2) kolom.q<-j<-1 for (i in 1:(ncol(M)-1)) { j<-i+1 while (j <= ncol(M)) { Q[,kolom.q]<-M[,i]*M[,j] kolom.q<-kolom.q+1 j<-j+1 } } W<-B%*%M D<-abs(t(Z)%*%W) E<-abs(t(Z)%*%B%*%Q) F<-abs(t(Z)%*%(kronecker(matrix(1,1,ncol(W)),S)*kronecker(B%*%M,matrix(1,1,n col(S))))) d0<-max(D);d1<-sum(D);e0<-max(E);e1<-sum(E);f0<-max(F);f1<-sum(F) objektif<-cd0*d0+cd1*d1+ce0*e0+ce1*e1+cf0*f0+cf1*f1 } ffsp.ga<-function(M,S,B,p.mut=0.1,maxiter=1000){ Z<-matrix(0,nrow(S),ncol(S)*(ncol(S)-1)/2) kolom.z<-j<-1 for (i in 1:(ncol(S)-1)) { j<-i+1 while (j <= ncol(S)) { Z[,kolom.z]<-S[,i]*S[,j] kolom.z<-kolom.z+1 j<-j+1 } } G<-matrix(1:(nrow(M)),nrow(M),nrow(M)+1,byrow=T) for(i in 1:nrow(G)) { Mnew<-M[G[i,-ncol(G)],] G[i,ncol(G)]<-fitness(M=Mnew,S=S,B=B,Z=Z) }
for (iter in 1:maxiter) { #SELEKSI urutan<-order(G[,ncol(G)])[1:5] G<-G[urutan,] #CROSSOVER G.cross<-G for(i in 1:nrow(G)){ for(j in 1:nrow(G)) { if(i != j) { fraksi1<-G[i,ncol(G)]/(G[i,ncol(G)]+G[j,ncol(G)]) fraksi2<-G[j,ncol(G)]/(G[i,ncol(G)]+G[j,ncol(G)]) G.cross<-rbind(G.cross,rank(fraksi1*G[i,]+fraksi2*G[j,],ties.method="random")) } } }
22
Lampiran 4 Algoritma genetika untuk penyusunan matriks rancangan FFSP ortogonal dua taraf pada R berbentuk fungsi ffsp.ga (lanjutan) #MUTASI gen.mutasi<-matrix(rbinom(nrow(G.cross)*(ncol(G.cross)-1),1,0.1),nrow(G.cross),ncol(G.cross)-1) baris<-apply(gen.mutasi,1,sum) names(baris)<-1:nrow(G.cross) baris<-as.numeric(names(baris[baris!=0])) in.mutasi<-matrix(runif(nrow(G.cross)*(ncol(G.cross)-1),-ncol(M),ncol(M)),nrow(G.cross),ncol(G.cross)-1) gen.mutasi<-gen.mutasi*in.mutasi G.mutasi<-(G.cross[,-ncol(G.cross)]+gen.mutasi)[baris,] temp<-G.mutasi for(i in 1:nrow(G.mutasi)){ G.mutasi[i,]<-rank(G.mutasi[i,],ties.method="random") } G.mutasi<-rbind(G.cross,cbind(G.mutasi,9)) #HITUNG_ULANG_FITNESS for(i in 6:nrow(G.mutasi)) { Mnew<-M[G.mutasi[i,-ncol(G.mutasi)],] G.mutasi[i,ncol(G.mutasi)]<-fitness(M=Mnew,S=S,B=B,Z=Z) } G<-G.mutasi urutan<-order(G[,ncol(G)]) G<-G[urutan,] cek<-G[1,ncol(G)]-G[10,ncol(G)] if(cek==0 & iter > 100){ break } }
solusi<-G.mutasi[order(G.mutasi[,ncol(G.mutasi)])[1],-ncol(G.mutasi)] fitness_val<-G.mutasi[order(G.mutasi[,ncol(G.mutasi)])[1],ncol(G.mutasi)] if(iter==maxiter){ list(solution=solusi,fitness_value=fitness_val,note="p rocess can't reach convergen criterion in 1000 iterations, maybe the solution isn't the best") }
else{ list(solution=solusi,fitness_value=fitness_val,iteration_needed_to_ converge=iter) } } ptm<-proc.time() ffsp.ga(M=M,S=S,B=B,p.mut=0.1) proc.time()- ptm
23 Lampiran 5 128 solusi terbaik hasil evaluasi seluruh kemungkinan (8!) permutasi
pada kasus rancangan 8 petak utama
Solusi Fitness Solusi Fitness
1 2 5 6 3 7 8 4 164336141 5 1 2 6 4 7 3 8 164336141 1 2 6 5 3 8 7 4 164336141 5 1 3 7 4 6 2 8 164336141 1 2 7 8 3 5 6 4 164336141 5 2 1 6 3 7 4 8 164336141 1 2 8 7 3 6 5 4 164336141 5 2 4 7 3 6 1 8 164336141 1 3 5 7 2 6 8 4 164336141 5 3 1 7 2 6 4 8 164336141 1 3 6 8 2 5 7 4 164336141 5 3 4 6 2 7 1 8 164336141 1 3 7 5 2 8 6 4 164336141 5 4 2 7 1 6 3 8 164336141 1 3 8 6 2 7 5 4 164336141 5 4 3 6 1 7 2 8 164336141 1 5 6 2 8 3 7 4 164336141 5 6 1 2 7 3 4 8 164336141 1 5 7 3 8 2 6 4 164336141 5 6 2 1 7 4 3 8 164336141 1 6 5 2 7 3 8 4 164336141 5 6 3 4 7 1 2 8 164336141 1 6 8 3 7 2 5 4 164336141 5 6 4 3 7 2 1 8 164336141 1 7 5 3 6 2 8 4 164336141 5 7 1 3 6 2 4 8 164336141 1 7 8 2 6 3 5 4 164336141 5 7 2 4 6 1 3 8 164336141 1 8 6 3 5 2 7 4 164336141 5 7 3 1 6 4 2 8 164336141 1 8 7 2 5 3 6 4 164336141 5 7 4 2 6 3 1 8 164336141 2 1 5 6 4 7 8 3 164336141 6 1 2 5 4 8 3 7 164336141 2 1 6 5 4 8 7 3 164336141 6 1 3 8 4 5 2 7 164336141 2 1 7 8 4 5 6 3 164336141 6 2 1 5 3 8 4 7 164336141 2 1 8 7 4 6 5 3 164336141 6 2 4 8 3 5 1 7 164336141 2 4 5 7 1 6 8 3 164336141 6 3 1 8 2 5 4 7 164336141 2 4 6 8 1 5 7 3 164336141 6 3 4 5 2 8 1 7 164336141 2 4 7 5 1 8 6 3 164336141 6 4 2 8 1 5 3 7 164336141 2 4 8 6 1 7 5 3 164336141 6 4 3 5 1 8 2 7 164336141 2 5 6 1 8 4 7 3 164336141 6 5 1 2 8 3 4 7 164336141 2 5 7 4 8 1 6 3 164336141 6 5 2 1 8 4 3 7 164336141 2 6 5 1 7 4 8 3 164336141 6 5 3 4 8 1 2 7 164336141 2 6 8 4 7 1 5 3 164336141 6 5 4 3 8 2 1 7 164336141 2 7 5 4 6 1 8 3 164336141 6 8 1 3 5 2 4 7 164336141 2 7 8 1 6 4 5 3 164336141 6 8 2 4 5 1 3 7 164336141 2 8 6 4 5 1 7 3 164336141 6 8 3 1 5 4 2 7 164336141 2 8 7 1 5 4 6 3 164336141 6 8 4 2 5 3 1 7 164336141 3 1 5 7 4 6 8 2 164336141 7 1 2 8 4 5 3 6 164336141 3 1 6 8 4 5 7 2 164336141 7 1 3 5 4 8 2 6 164336141 3 1 7 5 4 8 6 2 164336141 7 2 1 8 3 5 4 6 164336141 3 1 8 6 4 7 5 2 164336141 7 2 4 5 3 8 1 6 164336141 3 4 5 6 1 7 8 2 164336141 7 3 1 5 2 8 4 6 164336141 3 4 6 5 1 8 7 2 164336141 7 3 4 8 2 5 1 6 164336141 3 4 7 8 1 5 6 2 164336141 7 4 2 5 1 8 3 6 164336141 3 4 8 7 1 6 5 2 164336141 7 4 3 8 1 5 2 6 164336141 3 5 6 4 8 1 7 2 164336141 7 5 1 3 8 2 4 6 164336141 3 5 7 1 8 4 6 2 164336141 7 5 2 4 8 1 3 6 164336141 3 6 5 4 7 1 8 2 164336141 7 5 3 1 8 4 2 6 164336141 3 6 8 1 7 4 5 2 164336141 7 5 4 2 8 3 1 6 164336141 3 7 5 1 6 4 8 2 164336141 7 8 1 2 5 3 4 6 164336141 3 7 8 4 6 1 5 2 164336141 7 8 2 1 5 4 3 6 164336141 3 8 6 1 5 4 7 2 164336141 7 8 3 4 5 1 2 6 164336141 3 8 7 4 5 1 6 2 164336141 7 8 4 3 5 2 1 6 164336141
24
Lampiran 5 128 solusi terbaik hasil evaluasi seluruh kemungkinan (8!) permutasi pada kasus rancangan 8 petak utama (lanjutan)
Solusi Fitness Solusi Fitness
4 2 5 7 3 6 8 1 164336141 8 1 2 7 4 6 3 5 164336141 4 2 6 8 3 5 7 1 164336141 8 1 3 6 4 7 2 5 164336141 4 2 7 5 3 8 6 1 164336141 8 2 1 7 3 6 4 5 164336141 4 2 8 6 3 7 5 1 164336141 8 2 4 6 3 7 1 5 164336141 4 3 5 6 2 7 8 1 164336141 8 3 1 6 2 7 4 5 164336141 4 3 6 5 2 8 7 1 164336141 8 3 4 7 2 6 1 5 164336141 4 3 7 8 2 5 6 1 164336141 8 4 2 6 1 7 3 5 164336141 4 3 8 7 2 6 5 1 164336141 8 4 3 7 1 6 2 5 164336141 4 5 6 3 8 2 7 1 164336141 8 6 1 3 7 2 4 5 164336141 4 5 7 2 8 3 6 1 164336141 8 6 2 4 7 1 3 5 164336141 4 6 5 3 7 2 8 1 164336141 8 6 3 1 7 4 2 5 164336141 4 6 8 2 7 3 5 1 164336141 8 6 4 2 7 3 1 5 164336141 4 7 5 2 6 3 8 1 164336141 8 7 1 2 6 3 4 5 164336141 4 7 8 3 6 2 5 1 164336141 8 7 2 1 6 4 3 5 164336141 4 8 6 2 5 3 7 1 164336141 8 7 3 4 6 1 2 5 164336141 4 8 7 3 5 2 6 1 164336141 8 7 4 3 6 2 1 5 164336141
25
RIWAYAT HIDUP
Penulis dilahirkan di Jakarta pada tanggal 31 Januari 1994 dari pasangan Bapak Hermayulis dan Ibu Surwita Eryani. Penulis adalah anak pertama dari dua bersaudara. Tahun 2010 penulis lulus dari SMA Insan Kamil Bogor dan pada tahun yang sama diterima sebagai mahasiswa baru jenjang Strata–1 (S1) pada Departemen Statistika, Fakultas Matematika dan Ilmu Pengetahuan Alam (FMIPA), Institut Pertanian Bogor (IPB) melalui jalur Ujian Talenta Mandiri IPB (UTMI).
Selama mengikuti perkualiahan, penulis menjadi asisten responsi Metode Statistika pada semester ganjil dan genap tahun ajaran 2012/2013, asisten praktikum Komputasi Statistika pada semester ganjil tahun ajaran 2013/2014, dan asisten praktikum Analisis Eksplorasi Data pada semester genap tahun ajaran 2013/2014. Dalam bidang organisasi, penulis pernah menjadi ketua Departemen Database Center di Himpunan Profesi Gamma Sigma Beta IPB masa kepengurusan 2012/2013. Dalam bidang kepanitiaan, penulis pernah menjadi ketua divisi khusus Kompetisi Statistika Junior (Komstat Jr) dalam rangkaian acara Pesta Sains Nasional 2013. Pada bulan Juli–Agustus 2013 penulis melaksanakan praktik lapang di PT. Ganesha Cipta Informatika, Jakarta Selatan.
Penulis juga aktif mengikuti lomba tingkat mahasiswa baik bidang akademik maupun non–akademik. Adapun beberapa prestasi yang pernah diraih antara lain sebagai semifinalis Olimpiade Nasional Statistika (ONS) 2013 di UGM, juara 4 Kompetisi Statistika Nasional (KSN) dalam rangkaian acara Statistika Ria 2013 di IPB, medali emas cabang basket putra tahun 2013 dan 2014 dalam Pekan Olahraga FMIPA di IPB, dan Most Valuable Player (MVP) atau pemain terbaik cabang basket putra tahun 2014 dalam Pekan Olahraga FMIPA di IPB.