PENDUGAAN PARAMETER DISTRIBUSI RAYLEIGH DENGAN METODE KUADRAT TERKECIL DAN METODE KEMUNGKINAN MAKSIMUM
Skripsi
Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Matematika
Program Studi Matematika
Oleh :
Skolastika Augustia Sarasvati NIM: 133114026
PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI
UNIVERSITAS SANATA DHARMA YOGYAKARTA
THE PARAMETER ESTIMATION OF RAYLEIGH DISTRIBUTION USING LEAST SQUARE METHOD AND MAXIMUM LIKELIHOOD METHOD
A Thesis
Presented as a Partial Fulfillment of the Requirements to Obtain the Degree of Sarjana Sains
Mathematics Study Program
Written by:
Skolastika Augustia Sarasvati Student Number: 133114026
MATHEMATICS STUDY PROGRAM DEPARTMENT OF MATHEMATICS FACULTY OF SCIENCE AND TECHNOLOGY
SANATA DHARMA UNIVERSITY YOGYAKARTA
v
HALAMAN PERSEMBAHAN
Karya ini saya persembahkan untuk
Tuhan Yesus Kristus dan Bunda Maria yang selalu memberkati dan memberikan kemudahan lewat orang-orang baik hati yang berada di sekelilingku terutama dalam perjuanganku menyelesaikan skripsi ini.
Kedua orangtuaku Bonaventura Saptono Arko dan Teresia Atik Solikhati
Adik-adikku, yaitu Ano, Awgia, Sekal, Zita.
Bapak Ir. Ig. Aris Dwiatmoko, M.Sc, selaku dosen pembimbing skripsi yang terbaik. Semua orang yang akan membaca skripsi saya.
viii ABSTRAK
Distribusi Rayleigh dengan parameter tunggal memiliki satu parameter yaitu parameter 𝑏. Pendugaan parameter distribusi Rayleigh dapat dilakukan dengan berbagai metode. Dalam skripsi ini dibahas pendugaan parameter distribusi Rayleigh dengan menggunakan dua metode yaitu Metode Kuadrat Terkecil (Least Square Method) dan Metode Kemungkinan Maksimum (Maximum Likelihood Method). Konsep dari Metode Kuadrat Terkecil adalah menduga parameter dengan memilih garis regresi yang terdekat dengan semua data yang meminimumkan Jumlah Kuadrat Galat (Sum of Square Error). Sedangkan, konsep dari Metode Kemungkinan Maksimum adalah menduga parameter distribusi yang memaksimumkan fungsi likelihood.
Pendugaan parameter distribusi Rayleigh diterapkan pada data tinggi gelombang terbesar tahunan di Lepas Pantai P. Kalukalukuang, Sulawesi Selatan. Rata-Rata Kuadrat Galat (Mean Square Error) dipilih sebagai kriteria pembanding kedua metode penduga. Metode yang terbaik dalam menduga parameter distribusi Rayleigh adalah metode yang memiliki Rata-Rata Kuadrat Galat yang minimum. Dari hasil penerapan pada data tinggi gelombang terbesar tahunan di Lepas Pantai P. Kalukalukuang menunjukkan bahwa Metode Kemungkinan Maksimum lebih baik dalam menduga parameter distribusi Rayleigh.
Kata kunci: distribusi Rayleigh, pendugaan parameter, Metode Kuadrat Terkecil, Metode Kemungkinan Maksimum, Rata-Rata Kuadrat Galat.
ix ABSTRACT
Rayleigh distribution with single parameter has a parameter namely parameter b. The parameter of Rayleigh distribution can be estimated using several methods. In this final assignment, writter will estimated the parameter estimation of Rayleigh distribution using two methods which are Least Square Method and Maximum Likelihood Method. In general, Least Square Method estimate the parameter by selecting the regression line that best fit among all data which minimizes the Sum of Square Error. Meanwhile the concept of Maximum Likelihood Method is to estimate the parameter distribution that maximizes the likelihood function.
The parameter estimation of Rayleigh distribution is implemented on the data of the annual biggest wave’s height in Kalukalukuang Island’s offshore, South Sulawesi. Mean Square Error is chosen as the comparasm criteria for both methods. Method which has minimum Mean Square Error is the best one. From our attempts on the annual biggest wave’s height data in Kalukalukuang Island’s offshore shows that Maximum Likelihood Method is a better method to estimate the parameter of Rayleigh distribution.
Keywords: Rayleigh distribution, parameter estimation, Least Square Method, Maximum Likelihood Method, Mean Square Error
x
KATA PENGANTAR
Puji syukur kepada Tuhan Yang Maha Kuasa atas segala berkat dan karunia-Nya sehingga penulis dapat menyelesaikan skripsi ini.
Skripsi yang berjudul “Pendugaan Parameter Distribusi Rayleigh Dengan Metode Kuadrat Terkecil Dan Kemungkinan Maksimum” ini diajukan untuk memenuhi salah satu syarat untuk memperoleh gelar sarjana Matematika pada Fakultas Sains dan Teknologi Universitas Sanata Dharma Yogyakarta. Penulis mendapat banyak dukungan dan bantuan dalam proses menyelesaikan tugas akhir ini. Oleh karena itu, dengan tulus hati penulis ingin menyampaikan terima kasih kepada:
1. Bapak Ir. Ig. Aris Dwiatmoko, M.Sc., selaku dosen pembimbing tugas akhir yang dengan penuh kesabaran telah meluangkan waktu, tenaga, dan pikiran serta memberikan masukan, arahan, bimbingan, dan nasihat kepada penulis. 2. Bapak YG. Hartono, S.Si., M.Sc., Ph.D., selaku Ketua Program Studi.
3. Ibu M. V. Any Herawati, S.Si., M.Si., selaku wakil ketua program studi Matematika dan Dosen Pembimbing Akademik yang selalu memberikan arahan yang berkaitan dengan perkuliahan.
4. Bapak Sudi Mungkasi, S.Si., M.Math.Sc., Ph.D., selaku dekan Fakultas Sains dan Teknologi.
5. Romo Prof. Dr. Frans Susilo, S.J., Bapak Dr. rer. nat. Herry P. Suryawan, S.Si., M.Si., Bapak Ir. Ig. Aris Dwiatmoko, M.Sc., Bapak YG. Hartono, S.Si., M.Sc., Ph.D., Ibu M. V. Any Herawati, S.Si., M.Sc., dan Ibu Lusia Krismiyati Budiasih, S.Si., M.Si., selaku dosen program studi matematika yang telah membagikan ilmu dan pengalaman selama masa perkuliahan.
6. Perpustakaan Universitas Sanata Dharma dan staf sekretariat Fakultas Sains dan Teknologi yang telah banyak membantu dalam proses administrasi. 7. Kedua orang tuaku yang selalu memberikan doa, semangat, dukungan, arahan,
xii DAFTAR ISI
HALAMAN PERSETUJUAN PEMBIMBING ... iii
HALAMAN PENGESAHAN ... iv
HALAMAN PERSEMBAHAN ... iv
PERNYATAAN KEASLIAN KARYA ... vi
LEMBAR PERNYATAAN PERSETUJUAN ... vii
ABSTRAK ... viii
ABSTRACT ... ix
KATA PENGANTAR ... x
DAFTAR ISI ... xii
DAFTAR TABEL ... xiv
DAFTAR GAMBAR ... xv BAB I PENDAHULUAN ... 1 A. Latar Belakang ... 1 B. Rumusan Masalah ... 2 C. Batasan Masalah ... 3 D. Tujuan Penulisan ... 3 E. Manfaat penulisan ... 3 F. Metode Penulisan... 4 G. Sistematika Penulisan ... 4
BAB IILANDASAN TEORI ... 6
A. Distribusi Probabilitas ... 6
B. Distribusi Gamma dan Sifat-sifatnya... 13
C. Momen dan Fungsi Pembangkit Momen ... 18
xiii
E. Selang Kepercayaan... 25
F. Ukuran Penduga Yang Baik ... 29
G. Metode Kuadrat Terkecil ... 31
H. Metode Kemungkinan Maksimum ... 35
I. Uji Kolmogorov-Smirnov ... 39
J. Uji Distribusi Rayleigh menggunakan Uji Kolmogorov-Smirnov ... 41
BAB III PENDUGAAN PARAMETER DISTRIBUSI RAYLEIGH DENGAN METODE KUADRAT TERKECIL DAN KEMUNGKINAN MAKSIMUM ... 44
A. Distribusi Rayleigh ... 44
B. Karakteristik Distribusi Rayleigh Satu Parameter ... 47
C. Pendugaan Parameter Distribusi Rayleigh dengan Metode Kuadrat Terkecil .. 49
D. Pendugaan Parameter Distribusi Rayleigh dengan Metode Kemungkinan Maksimum ... 51
E. Fungsi Pembangkit Momen Distribusi Rayleigh ... 53
Pendugaan Selang Distribusi Rayleigh ... 58
BAB IV PENERAPAN PENDUGAAN PARAMETER DISTRIBUSI RAYLEGH 61 A. Penerapan pendugaan Parameter Distribusi Rayleigh dengan Metode Kuadrat Terkecil (Least Squared Method) pada data tinggi gelombang terbesar tahunan di Lepas Pantai P.Kalukalukuang, Sulawesi Selatan. ... 61
B. Pendugaan parameter distribusi Rayleigh dengan menggunakan Metode Kemungkinan Maksimum ... 65
C. Uji Distribusi Rayleigh menggunakan Uji Kolmogorov-Smirnov ... 69
D. Perbandingan Pendugaan parameter distribusi Rayleigh dengan menggunakan Metode Kuadrat Terkecil dan Metode Kemungkinan Maksimum ... 71
BAB V PENUTUP ... 73
A. Kesimpulan ... 73
B. Saran ... 74
DAFTAR PUSTAKA ... 75
xiv
DAFTAR TABEL
Tabel 2.1 Data Contoh 2.10 ... 34
Tabel 2.2 Data Contoh 2.13 ... 42
Tabel 2.3 Perhitungan Uji Kolmogorov Contoh 2.13 ... 42
Tabel 4.1 Tinggi gelombang signifikan maksimum per arah per tahun di laut ... 62 Tabel 4.2 Perhitungan Uji Kolmogorov-Smirnov pada data tinggi gelombang laut. 69
xv
DAFTAR GAMBAR
Gambar 2. 1 Grafik Distribusi Gamma ... 17
Gambar 2. 2 Grafik Distribusi Chi-Square ... 18
Gambar 2. 3 Kurva Distribusi Eksponensial dengan𝑃(𝑎 ≤ 𝑈 ≤ 𝑏) = 0.90 ... 28
Gambar 2. 4 Grafik penduga Kuadrat Terkecil ... 35
Gambar 2. 5 Grafik 𝐹0(𝑥𝑖) dan 𝐹𝑛(𝑥𝑖) ... 43
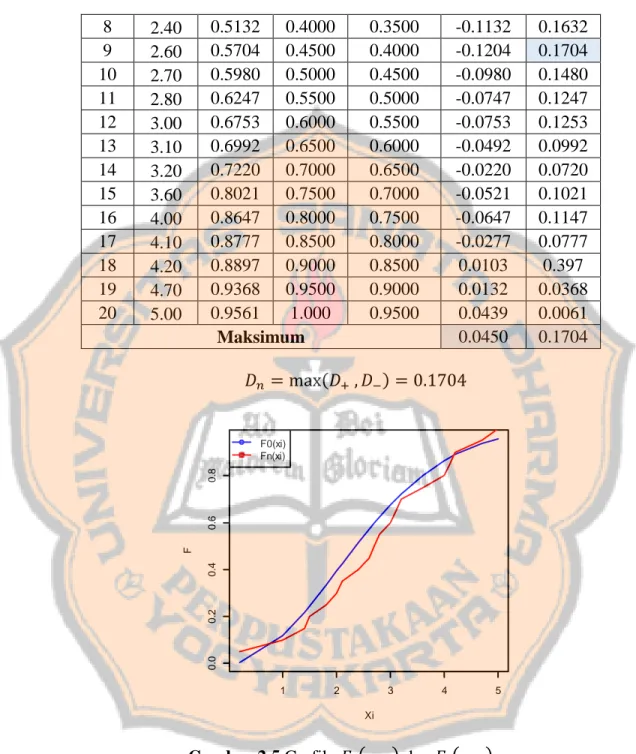
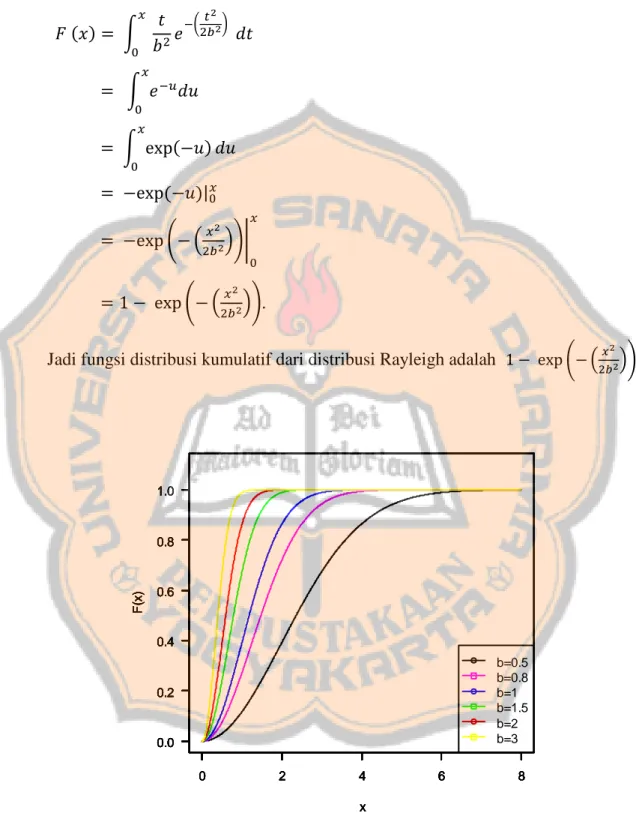
Gambar 3. 1 Grafik fungsi distribusi Rayleigh dengan nilai b = 0.5, 0.8, 1, 1.5, 2, 3. ... 45
Gambar 3. 2 Grafik fungsi distribusi kumulatif distribusi Rayleigh ... 46
Gambar 4. 1 Grafik distribusi Rayleigh dengan parameter skala b = 1.715623 ... 65
Gambar 4. 2 Grafik fungsi probabilitas distribusi Rayeligh dengan b = 1.757045 67 Gambar 4. 3 Grafik 𝐹0(𝑥𝑖) dan 𝐹𝑛(𝑥𝑖) ... 70
1 BAB I PENDAHULUAN A. Latar Belakang
Dalam teori probabilitas dan statistika, distribusi Rayleigh adalah salah satu distribusi peluang kontinu yang biasa digunakan dalam pemodelan data kelangsungan hidup. Distribusi Rayleigh diperkenalkan oleh Lord Rayleigh pada tahun 1880. Distribusi Rayleigh dikenal secara luas di bidang oseanografi dan dalam teori komunikasi untuk menggambarkan puncak sesaat kekuatan sinyal radio yang diterima. Distribusi ini juga merupakan distribusi penting dalam statistik dan diterapkan di beberapa bidang seperti kesehatan, pertanian, biologi, dan ilmu-ilmu lainnya.
Variabel acak 𝑋 dikatakan mempunyai distribusi Reyleigh dengan satu parameter 𝑏 bila fungsi densitasnya
𝑓(𝑥; 𝑏) = 𝑥 𝑏2𝑒
(−𝑥 2
2𝑏2), 𝑥 ≥ 0, 𝑏 > 0
Pendugaan parameter merupakan salah satu persoalan yang penting dalam bidang statistika. Pendugaan adalah bidang dari statistika yang berhubungan dengan menduga nilai-nilai karakteristik dari populasi (parameter) berdasarkan data yang diukur atau data empiris yang memiliki komponen acak. Pendugaan parameter adalah suatu metode untuk menduga nilai parameter populasi dengan menggunakan nilai-nilai dari sampel. Penduga dibagi menjadi dua bagian yaitu penduga titik (point estimation) dan penduga selang (interval estimation).
1. Penduga titik (Point Estimation)
Penduga titik adalah penentuan suatu nilai tunggal yang dengan sebaik-baiknya menduga parameter yang sebenarnya.
2. Penduga Selang (Interval Estimation)
Penduga selang adalah suatu penentuan selang nilai yang memiliki peluang yang besar akan memuat parameter sebenarnya.
Dalam skripsi ini, pendugaan parameter distribusi Rayleigh dilakukan dengan menggunakan dua metode yaitu Metode Kuadrat Terkecil (Least Square Method) dan Metode Kemungkinan Maksimum (Maximum Likelihood Method). Konsep dari Metode Kuadrat Terkecil adalah menduga parameter dengan memilih garis regresi yang terdekat dengan semua data yang meminimumkan Jumlah Kuadrat Galat (Sum of Square Error). Sedangkan, konsep dari Metode Kemungkinan Maksimum adalah menduga parameter distribusi yang memaksimumkan fungsi likelihood.
Selain itu, dalam skripsi ini juga akan dilakukan perbandingan Metode Kuadrat Terkecil dan Metode Kemungkinan Maksimum untuk menduga parameter distribusi Rayleigh. Untuk menentukan metode mana yang lebih baik dalam pendugaan parameter distribusi Rayleigh penulis akan menggunakan Rata-Rata Kuadrat Galat (Mean Square Error) sebagai kriteria pembanding. Rata-Rata-Rata-Rata Kuadrat Galat adalah ukuran keakuratan dari penduga. Penduga (estimator) adalah suatu aturan, yang dinyatakan dalam bentuk rumus yang memberitahukan bagaimana cara menghitung nilai suatu penduga berdasarkan pengukuran yang termuat di dalam sampel. Metode yang terbaik dalam menduga parameter distribusi Rayleigh adalah metode yang memiliki Rata-Rata Kuadrat Galat minimum.
B. Rumusan Masalah
Masalah yang akan dibicarakan pada skripsi ini adalah: 1. Bagaimana sifat-sifat distribusi Rayleigh?
2. Bagaimana pendugaan parameter distribusi Rayleigh dengan Metode Kuadrat Terkecil?
3. Bagaimana pendugaan parameter distribusi Rayleigh dengan Metode Kemungkinan Maksimum?
4. Bagaimana memilih metode terbaik dalam pendugaan parameter distribusi Rayleigh?
C. Batasan Masalah
Skripsi ini dibatasi pada masalah-masalah sebagai berikut:
1. Dalam pendugaan parameter distribusi, penulis hanya akan membahas penduga titik dan penduga selang distribusi Rayleigh dengan satu parameter. 2. Dalam pendugaan parameter distribusi, penulis hanya akan membahas
pendugaan parameter distribusi Rayleigh dengan Metode Kuadrat Terkecil dan Metode Kemungkinan Maksimum.
3. Penulis tidak membahas perluasan dari distribusi Rayleigh.
D. Tujuan Penulisan
Tujuan dari penulisan skripsi ini adalah dapat menduga parameter distribusi Rayleigh satu parameter dengan menggunakan Metode Kuadrat Terkecil dan Metode Kemungkinan Maksimum.
E. Manfaat penulisan
Manfaat yang dapat diperoleh dari penulisan skripsi ini adalah:
1. Dapat mempelajari metode untuk pendugaan parameter distribusi Rayleigh yaitu dengan Metode Kuadrat Terkecil dan Metode Kemungkinan Maksimum.
2. Dapat mengetahui seberapa baik Metode Kuadrat Terkecil dan Metode Kemungkinan Maksimum dalam pendugaan parameter distribusi Rayleigh dengan satu parameter.
F. Metode Penulisan
Metode yang digunakan penulis dalam penulisan skripsi ini adalah metode studi pustaka, yaitu dengan membaca dan mempelajari buku-buku atau jurnal-jurnal yang berkaitan dengan distribusi Rayleigh dan metode-metode yang digunakan dalam pendugaan parameter.
G. Sistematika Penulisan BAB I PENDAHULUAN A. Latar Belakang B. Rumusan Masalah C. Batasan Masalah D. Tujuan Penulisan E. Manfaat Penulisan F. Metode Penulisan G. Sistematika Penulisan BAB II LANDASAN TEORI A. Distribusi Probabilitas
B. Distribusi Gamma dan Sifat-sifatnya
C. Momen dan Fungsi Pembangkit Moment
D. Penduga Parameter E. Selang Kepercayaan
F. Ukuran Penduga Yang Baik G. Metode Kuadrat Terkecil
H. Metode Kemungkinan Maksimum
I. Uji Kolmogorov-Smirnov
J. Uji Distribusi Rayleigh menggunakan Uji Kolmogorov-Smirnov
BAB III ESTIMASI PARAMETER DISTRIBUSI RAYLEIGH DENGAN ME-TODE KUADRAT TERKECIL DAN KEMUNGKINAN MAKSIMUM A. Distribusi Rayleigh
B. Sifat-Sifat Distribusi Rayleigh
C. Pendugaan Paramater Distribusi Rayleigh dengan Metode Kuadrat Terkecil
D. Pendugaan Paramater Distribusi Rayleigh dengan Metode Kemungkinan Maksimum
BAB IV PENERAPAN PENDUGAAN PARAMETER DISTRIBUSI
RAYLEIGH BAB V PENUTUP
A. Kesimpulan B. Saran
6 BAB II
LANDASAN TEORI
Dalam proses pembuatan skripsi ini diperlukan beberapa konsep dan teori yang mendukung dalam ilmu statistika. Berikut akan dijelaskan beberapa teori yang berkaitan dengan pendugaan parameter, antara lain distribusi probabilitas, distribusi Gamma dan sifat-sifatnya, momen dan fungsi pembangkit momen, pendugaan parameter, selang kepercayaan dan sebagainya.
A. Distribusi Probabilitas
Distribusi probabilitas berkaitan erat dengan variabel random, jenis distribusi probabilitas, fungsi distribusi kumulatif dan karakteristik distribusi probabilitas yang akan dijelaskan pada subbab ini.
1. Variabel Random Definisi 2.1
Variabel random adalah fungsi yang bernilai real yang domainnya adalah ruang sampel.
Huruf kapital, misalnya 𝑋, adalah notasi untuk variabel random dan huruf kecil
𝑥, menyatakan nilainya.
Definisi 2.2
Variabel 𝑋 dikatakan diskrit jika nilai-nilainya berhingga atau tak berhingga terbilang. Jika tidak memenuhi hal tersebut maka variabel acak 𝑋 dikatakan kontinu.
Contoh:
a. Banyaknya mahasiswa matematika setiap tahun mulai dari tahun 2010. b. Banyaknya kecelakaan mobil di Kabupaten Magelang setiap bulan selama satu tahun.
2. Distribusi Probabilitas
Distribusi probabilitas dibagi atas dua macam, yaitu distribusi probabilitas diskrit yang dilambangkan dengan 𝑝(𝑥) dan distribusi probabilitas kontinu (fungsi densitas) yang dilambangkan dengan 𝑓(𝑥).
a. Distribusi Probabilitas Diskrit Definisi 2.3
Himpunan pasangan terurut (𝑥, 𝑝(𝑥)) adalah distribusi probabilitas dari variabel random diskrit 𝑋 jika
1) 0 ≤ 𝑝(𝑥) ≤ 1 untuk setiap 𝑥
2) ∑ 𝑝(𝑥) = 1𝑥 Contoh 2.1
Distribusi Geometrik
𝑝(𝑥) = 𝑝(1 − 𝑝)𝑥−1 , 𝑥 = 1, 2, 3, . . .
Akan ditunjukkan bahwa distribusi Geometrik memenuhi definisi 2.3 1) Diketahui 𝑝(𝑥) = 𝑝(1 − 𝑝)𝑥−1 untuk 𝑥 = 1, 2, 3, .. maka diperoleh
𝑝(𝑥) positif untuk setiap 𝑥. Jadi terbukti 0 ≤ 𝑝(𝑥) ≤ 1 untuk setiap 𝑥. 2) Jumlah deret tak hingga suatu deret geometri dengan 𝑎 merupakan suku pertama dan 𝑟 merupakan rasio antar suku adalah 𝑆∞=
𝑎
1− 𝑟. Dengan menggunakan jumlah deret tak hingga dari deret geometri 𝑆∞= 𝑎
1− 𝑟 maka diperoleh 𝑎 = 𝑝 dan 𝑟 = 1 − 𝑝 sehingga
∑ 𝑝(𝑥) = 𝑝
1 − (1 − 𝑝)= 1.
𝑥
b. Distribusi Probabilitas Kontinu
Dalam beberapa literatur istilah distribusi probabilitas kontinu disebut juga fungsi densitas (density function).
Definisi 2.4
Fungsi 𝑓(𝑥) adalah distribusi probabilitas untuk variabel random kontinu 𝑋, jika 1) 𝑓(𝑥) ≥ 0,untuk setiap 𝑥 ∈ 𝑅 2) ∫−∞∞ 𝑓(𝑥)𝑑𝑥 = 1 Contoh 2.2 a) Distribusi Normal 𝑓(𝑥) = 1 𝜎 √2𝜋exp [− ( 1 2𝜎2) ((𝑥 − 𝜇)2)] , −∞ < 𝑥 < ∞ Akan ditunjukkan bahwa distribusi Normal memenuhi definisi 2.4 1) Untuk setiap 𝑥 ∈ 𝑅, terbukti bahwa 𝑓(𝑥) ≥ 0.
2) ∫ 1 𝜎 √2𝜋exp [− ( 1 2𝜎2) ((𝑥 − 𝜇)2)] 𝑑𝑥 = ∞ −∞ ∫ 1 𝜎 √2𝜋 𝑒 −1 2 ( 𝑥−𝜇 𝜎 ) 2 𝑑𝑥 = 1. ∞ −∞ Misalkan 𝑚 =𝑥−𝜇 𝜎 , 𝑑𝑚 = 𝑑𝑥 𝜎 , 𝜎 𝑑𝑚 = 𝑑𝑥, misalkan 𝑄 = ∫ 1 𝜎 √2𝜋𝑒 −(1 2)𝑚 2 𝜎 𝑑𝑚 ∞ −∞ 𝑄2 = (∫ 1 √2𝜋𝑒 −(12)𝑚2 𝑑𝑚 ∞ −∞ ) (∫ 1 √2𝜋𝑒 −(12)𝑛2 𝑑𝑛 ∞ −∞ ) = 1 2𝜋 ∬ 𝑒 −(12)(𝑚2+𝑛2) 𝑑𝑚 𝑑𝑛 ∞ −∞ 0 ≤ 𝜃 ≤ 2𝜋, 0 ≤ 𝑟 ≤ ∞ 𝑚 = 𝑟 𝑐𝑜𝑠𝜃, 𝑛 = 𝑟 𝑠𝑖𝑛𝜃 𝑄2 = 1 2𝜋∫ ∫ 𝑒 −(12)(𝑟2𝑐𝑜𝑠2𝜃+ 𝑟2𝑠𝑖𝑛2𝜃)|𝐽|𝑑𝑟 𝑑𝜃 ∞ 0 2𝜋 0 |𝐽| = | 𝜕𝑚 𝜕𝜃 𝜕𝑚 𝜕𝑟 𝜕𝑛 𝜕𝜃 𝜕𝑛 𝜕𝑟 | = |−𝑟 𝑠𝑖𝑛 𝜃 cos 𝜃 𝑟 cos 𝜃 sin 𝜃| = |(−𝑟 𝑠𝑖𝑛 𝜃)(sin 𝜃) − (𝑟 cos 𝜃)(cos 𝜃)|
= |−𝑟 𝑠𝑖𝑛2𝜃 − 𝑟 𝑐𝑜𝑠2𝜃| = |−𝑟| |𝑠𝑖𝑛2𝜃 + 𝑐𝑜𝑠2𝜃| = 𝑟 𝑄2 = 1 2𝜋∫ ∫ 𝑒 −(12)𝑟2(𝑐𝑜𝑠2𝜃+ 𝑠𝑖𝑛2𝜃) 𝑟 𝑑𝑟 𝑑𝜃 ∞ 0 2𝜋 0 = 1 2𝜋∫ ∫ 𝑒 −(1 2)𝑟 2 𝑟 𝑑𝑟 𝑑𝜃 ∞ 0 2𝜋 0 Misal 𝑤 = 𝑟2, 𝑑𝑤 = 2𝑟 𝑑𝑟, 𝑑𝑤 2 = 𝑟 𝑑𝑟 = 1 2𝜋∫ [∫ 𝑒 −(12)𝑤𝑑𝑤 2 ∞ 0 ] 2𝜋 0 𝑑𝜃 = 1 2𝜋∫ 1 2 2𝜋 0 |−2 𝑒−12𝑤 | 0 ∞ 𝑑𝜃 = 1 2𝜋∫ −(0 − 1)𝑑𝜃 2𝜋 0 = 1 2𝜋∫ −(−1)𝑑𝜃 2𝜋 0 = 1 2𝜋∫ 1 𝑑𝜃 = 1 2𝜋|𝜃|0 2𝜋 2𝜋 0 = 1 2𝜋 (2𝜋 − 0) = 1 Jadi, 𝑄2 = 1 → 𝑄 = ∫ 1 𝜎 √2𝜋𝑒 −(12)𝑚2 𝜎 𝑑𝑚 ∞ −∞ = 1. b) Distribusi Eksponensial 𝑓(𝑥) = 𝜆𝑒−𝜆 𝑥, 𝜆 > 0, 𝑥 ≥ 0
Akan ditunjukkan bahwa distribusi Eksponensial memenuhi definisi 2.4 1) untuk setiap 𝑥 ∈ 𝑅, terbukti bahwa 𝑓(𝑥) ≥ 0.
2) ∫ 𝑓(𝑥) 𝑑𝑥 = ∫ 𝜆𝑒∞ −𝜆 𝑥𝑑𝑥 0 ∞ −∞ = |𝜆𝑒−𝜆 𝑥(−1 𝜆 ) |0 ∞ = − (|𝑒−𝜆 𝑥 | 0 ∞ ) = −(0 − 1) = 1.
3. Fungsi Ditribusi Kumulatif Definisi 2.5
Fungsi distribusi kumulatif (cumulative distribution function) dari sebuah va-riabel random diskrit dan kontinu 𝑋 didefinisikan sebagai berikut
𝐹(𝑥) = 𝑃(𝑋 ≤ 𝑥) = { ∑ 𝑝(𝑥) ∀𝑋≤𝑥 , jika 𝑋 diskrit ∫ 𝑓(𝑡)𝑑𝑡 𝑥 −∞ , jika 𝑋 kontinu
4. Karakteristik Distribusi Probabilitas
Distribusi probabilitas dicirikan oleh adanya konstanta mean dan variansi yang merupakan karakteristiknya.
a. Mean Definisi 2.6
Mean atau nilai harapan (expected value) dari suatu variabel random X dino-tasikan sebagai 𝜇 atau 𝐸(𝑋) didefinisikan sebagai
𝐸(𝑋) = { ∑ 𝑥𝑝(𝑥) ∀𝑥 ,jika 𝑋 diskrit ∫ 𝑥𝑓(𝑥) 𝑑𝑥 ∞ −∞ , jika 𝑋 kontinu b. Variansi Definisi 2.7
Jika 𝑋 adalah variabel random, maka variansi dari 𝑋 ditulis 𝑉(𝑋) didefini-sikan sebagai
𝑉(𝑋) = 𝐸[(𝑋 − 𝐸(𝑋))2].
Teorema 2.1
Bukti: 𝑉(𝑋) = 𝐸[(𝑋 − 𝐸(𝑋))2] = 𝐸(𝑋2− 2𝑋𝐸(𝑋) + (𝐸(𝑋))2 = 𝐸(𝑋2) − 2𝐸(𝑋)𝐸(𝑋) + (𝐸(𝑋))2 𝑉(𝑋) = 𝐸(𝑋2) − (𝐸(𝑋))2 ∎ Contoh 2.3
a) Jika 𝑥 berdistribusi Geometrik
𝑝(𝑥) = 𝑝(1 − 𝑝)𝑥−1 , 𝑥 = 1, 2, 3, . . .
Berdasarkan definisi 2.6, akan ditunjukkan mean dari distribusi Geometrik
𝐸(𝑋) = ∑ 𝑥𝑝(𝑥) ∀𝑥 = ∑ 𝑥 𝑝(1 − 𝑝)𝑥−1 ∞ 𝑥=1 = 𝑝 ∑ 𝑥(1 − 𝑝)𝑥−1 ∞ 𝑥=1 𝐸(𝑋) = 𝑝[1 + 2(1 − 𝑝) + 3(1 − 𝑝)2 + 4(1 − 𝑝)3+. . . ] (1 − 𝑝)𝐸(𝑋) = 𝑝[(1 − 𝑝) + 2(1 − 𝑝)2+ 3(1 − 𝑝)3+ 4(1 − 𝑝)4+. . . ] 𝐸(𝑋)(1 − (1 − 𝑝)) = 𝑝[1 + (1 − 𝑝) + (1 − 𝑝)2+ (1 − 𝑝)3 + (1 − 𝑝)4+. . . ].
Jumlah deret tak hingga suatu deret geometri dengan 𝑎 merupakan suku pertama dan 𝑟 merupakan rasio antar suku adalah 𝑆∞= 𝑎
1− 𝑟. Dengan menggunakan deret geometri tersebut diperoleh 𝑎 = 𝑝 dan 𝑟 = 1 − 𝑝
sehingga jumlah deret tak hingga dari 𝑝[1 + (1 − 𝑝) + (1 − 𝑝)2+ (1 − 𝑝)3+ (1 − 𝑝)4+. . . ] dapat ditulis kembali menjadi
𝐸(𝑋)𝑝 = 𝑝 1 − (1 − 𝑝) 𝐸(𝑋)𝑝 = 1.
Jadi, 𝐸(𝑋) = 1
𝑝.
Berdasarkan Teorema 2.1, akan ditunjukkan variansi dari distribusi Geometrik
Telah ditunjukkan pada contoh di atas berdasarkan definisi 2.6 bahwa
𝐸(𝑋) = 1 𝑝,
maka untuk mencari 𝑉 (𝑋) yang perlu dihitung terlebih dahulu adalah
𝐸(𝑋2) = ∑ 𝑥2𝑝(𝑥) ∀𝑥 = ∑ 𝑥2 𝑝(1 − 𝑝)𝑥−1 ∞ 𝑥=1 = 𝑝 ∑ 𝑥2(1 − 𝑝)𝑥−1 ∞ 𝑥=1 Misalkan 𝑞 = 1 − 𝑝, 𝑝 = 1 − 𝑞, ∑ 𝑥2(𝑞)𝑥−1 = 1+ 𝑞 (1− 𝑞)3 ∞ 𝑥=1 = 𝑝 ∑ 𝑥2(𝑞)𝑥−1 ∞ 𝑥=1 = 𝑝 ( 1 + 𝑞 (1 − 𝑞)3) = 𝑝 ( 1 + 1 − 𝑝 𝑝3 ) = 2 − 𝑝 𝑝2 . Jadi, variansi distribusi Geometrik adalah
𝑉(𝑋) = 𝐸(𝑋2) − [𝐸(𝑋)]2 =2 − 𝑝 𝑝2 − ( 1 𝑝) 2 = 2 − 𝑝 𝑝2 − 1 𝑝2 = 1 − 𝑝 𝑝2 .
b) Jika 𝑥 berdistribusi Normal
𝑓(𝑥) = 1
𝜎 √2𝜋exp [− ( 1
2𝜎2) ((𝑥 − 𝜇)
2)] , −∞ < 𝑥 < ∞ Berdasarkan definisi 2.6, akan ditunjukkan mean dari distribusi Normal
𝐸(𝑋) = ∫ 𝑥𝑓(𝑥) 𝑑𝑥 ∞ −∞ = 1 𝜎 √2𝜋∫ 𝑥 𝑒 −12 (𝑥−𝜇𝜎 )2 𝑑𝑥 ∞ −∞ = 1 𝜎 √2𝜋∫ 𝑥 𝑒 − 1 2𝜎2 (𝑥−𝜇)2𝑑𝑥 ∞ −∞ Misalkan 𝑦 = 𝑥 − 𝜇, 𝑑𝑦 = 𝑑𝑥, 𝑥 = 𝑦 + 𝜇 𝐸(𝑋) = 1 𝜎 √2𝜋 ∫ (𝑦 + 𝜇) 𝑒 − 1 2𝜎2 (𝑦)2𝑑𝑦 ∞ −∞ = 𝜇 + 1 𝜎 √2𝜋∫ 𝑦 𝑒 − 1 2𝜎2 (𝑦) 2 𝑑𝑦 ∞ −∞ = 𝜇.
Berdasarkan Teorema 2.1, akan ditunjukkan variansi dari distribusi Normal
𝑉(𝑋) = 𝐸[(𝑥 − 𝜇)2] = ∫ (𝑥 − 𝜇)𝑓(𝑥) 𝑑𝑥 ∞
= 1 𝜎 √2𝜋∫ (𝑥 − 𝜇)𝑒 −( 1 2𝜎2)((𝑥−𝜇)2) 𝑑𝑥 ∞ −∞ Misalkan 𝑦 = 𝑥 − 𝜇, 𝑑𝑦 = 𝑑𝑥, 𝑥 = 𝑦 + 𝜇, = 1 𝜎 √2𝜋∫ (𝑦 2)𝑒−(2𝜎12)((𝑦)2) 𝑑𝑦 ∞ −∞ Misal 𝑢 = 𝑦, 𝑑𝑢 = 𝑑𝑦, 𝑑𝑣 = 𝑦𝑒−( 1 2𝜎2)((𝑦) 2) 𝑑𝑦, 𝑣 = −𝜎2𝑒−(2𝜎21 )((𝑦)2) = 1 𝜎 √2𝜋| 𝑦 (−𝜎 2𝑒−(2𝜎12)((𝑦)2))| 0 ∞ − 1 𝜎 √2𝜋∫ −𝜎 2𝑒−(2𝜎12)(𝑦2)𝑑𝑦 ∞ −∞ = 0 + 𝜎2. 1 = 𝜎2.
Jadi, variansi dari distribusi Normal adalah 𝑉(𝑋) = 𝜎2.
B. Distribusi Gamma dan Sifat-sifatnya Definisi 2.8
Fungsi Gamma didefinisikan sebagai
𝛤(𝛼) = ∫ 𝑥𝛼−1𝑒−𝑥𝑑𝑥
∞ 0
Fungsi Gamma adalah salah satu fungsi yang penting dalam statistika karena dapat digunakan untuk menyelesaikan integral yang rumit dalam mencari fungsi pembangkit momen, variansi, rata-rata dan momen.
Teorema 2.2
Fungsi Gamma memiliki sifat
1. 𝛤(𝛼) = (𝛼 − 1)𝛤(𝛼 − 1) untuk setiap 𝛼 > 1 Bukti: Berdasarkan definisi 2.8 𝛤(𝛼) = ∫ 𝑥𝛼−1𝑒−𝑥𝑑𝑥 ∞ 0 ,
𝛤(𝛼) = 𝑢𝑣 − ∫ 𝑣 𝑑𝑢 ∞ 0 = lim 𝑏→∞[−𝑥 𝛼−1𝑒−𝑥] 0 𝑏− ∫ −(𝛼 − 1)𝑥𝛼−2𝑒−𝑥𝑑𝑥 ∞ 0 = lim 𝑏→∞[−𝑥 𝛼−1𝑒−𝑥] 0 𝑏+ (𝛼 − 1) ∫ 𝑥𝛼−2𝑒−𝑥𝑑𝑥 ∞ 0 = lim 𝑏→∞[−𝑥 𝛼−1𝑒−𝑥] 0 𝑏+ (𝛼 − 1) ∫ 𝑥(𝛼−1)−1𝑒−𝑥𝑑𝑥 ∞ 0 = lim 𝑏→∞( 𝑏𝛼−1 𝑒𝑏 ) + (𝛼 − 1)𝛤(𝛼 − 1) = − lim 𝑏→∞[ exp ((𝛼 − 1) ln 𝑏) 𝑒𝑏 ] + (𝛼 − 1)𝛤(𝛼 − 1) = − lim 𝑏→∞[exp ((𝛼 − 1) ln 𝑏 − 𝑏)] + (𝛼 − 1)𝛤(𝛼 − 1) = − lim 𝑏→∞{exp [(𝛼 − 1)𝑏 ( ln 𝑏) 𝑏 − 1)]} + (𝛼 − 1)𝛤(𝛼 − 1) = (𝛼 − 1)𝛤(𝛼 − 1).
2. 𝛤(𝑛) = (𝑛 − 1)! Dengan 𝑛 bilangan bulat positif. Bukti:
Berdasarkan sifat Gamma
𝛤(𝛼) = (𝛼 − 1)𝛤(𝛼 − 1), sehingga diperoleh 𝛤(𝑛) = (𝑛 − 1)𝛤(𝑛 − 1) = (𝑛 − 1)(𝑛 − 2)𝛤(𝑛 − 2) = (𝑛 − 1)(𝑛 − 2)(𝑛 − 3)𝛤(𝑛 − 3) = (𝑛 − 1)(𝑛 − 2)(𝑛 − 3)(𝑛 − 4) … (3)(2)(1)𝛤(1) (2.1)
Berdasarkan definisi 2.8 maka diperoleh
𝛤(1) = ∫ 𝑥1−1𝑒−𝑥𝑑𝑥 ∞
= lim 𝑝→∞∫ 𝑒 −𝑥𝑑𝑥 𝑝 0 = lim 𝑝→∞[−𝑒 −𝑥] 0 𝑝 = 1 Persamaan (2.1) menjadi 𝛤(𝑛) = (𝑛 − 1)(𝑛 − 2)(𝑛 − 3)(𝑛 − 4) … (3)(2)(1)𝛤(1) = (𝑛 − 1)!. 3. 𝛤 (1 2) = √𝜋 Bukti:
Akan dibuktikan bahwa 𝛤 (1
2) = √𝜋 Berdasarkan definisi 2.8 𝛤(𝛼) = ∫ 𝑥𝛼−1𝑒−𝑥𝑑𝑥, ∞ 0 misalkan 𝑥 = 𝑢2, 𝑑𝑥 = 2𝑢 𝑑𝑢 𝛤(𝛼) = ∫ 𝑢2𝛼−2𝑒−𝑢2 2𝑢 𝑑𝑢 ∞ 0 = 2 ∫ 𝑢2𝛼−2𝑒−𝑢2 𝑢 𝑑𝑢 ∞ 0 = 2 ∫ 𝑢2𝛼−1𝑒−𝑢2 𝑑𝑢 ∞ 0 ketika 2𝛼 − 1 = 0 maka 𝛼 =1 2, sehingga diperoleh 𝛤 (1 2) = ∫ 𝑒 −𝑢2 𝑑𝑢 ∞ 0 [𝛤 (1 2)] 2 = [𝛤 (1 2)] [𝛤 ( 1 2)] = (2 ∫ 𝑒−𝑢2 𝑑𝑢 ∞ 0 ) (2 ∫ 𝑒−𝑣2 𝑑𝑣 ∞ 0 ) = 4 ∫ ∫ 𝑒0∞ 0∞ −(𝑢2+𝑣2) 𝑑𝑢𝑑𝑣.
Integral tersebut dapat diselesaikan dengan mengubah integral kartesius menjadi integral polar. Misalkan 𝑢 = 𝑟 cos 𝜃, 𝑣 = 𝑟 sin 𝜃 maka
𝑢2+ 𝑣2 = 𝑟2𝑐𝑜𝑠2𝜃 + 𝑟2𝑠𝑖𝑛2𝜃 = 𝑟2(𝑐𝑜𝑠2𝜃 + 𝑠𝑖𝑛2𝜃) = 𝑟2 [𝛤 (1 2)] 2 = 4 ∫ ∫ 𝑒−𝑟2 𝑑𝑢 𝜋 2 0 𝑑𝑣 ∞ 0 = 4 ∫ ∫ 𝑒−𝑟2 𝑟𝑑𝑟 𝜋 2 0 𝑑𝑣 ∞ 0 = 4 (∫ 𝑑𝜃 𝜋 2 0 ) (∫ 𝑒−𝑟2 𝑟𝑑𝑟 ∞ 0 ) misalkan 𝑠 = 𝑟2, 𝑑𝑠 = 2𝑟 𝑑𝑟 = 4 (𝜋 2) (− 1 2𝑏→∞lim ∫ 𝑒 −𝑠 𝑑𝑠 𝑏 0 ) = −𝜋 lim 𝑏→∞[−𝑒 −𝑠] 0 𝑏 = −𝜋(0 − 1) = 𝜋. Definisi 2.9
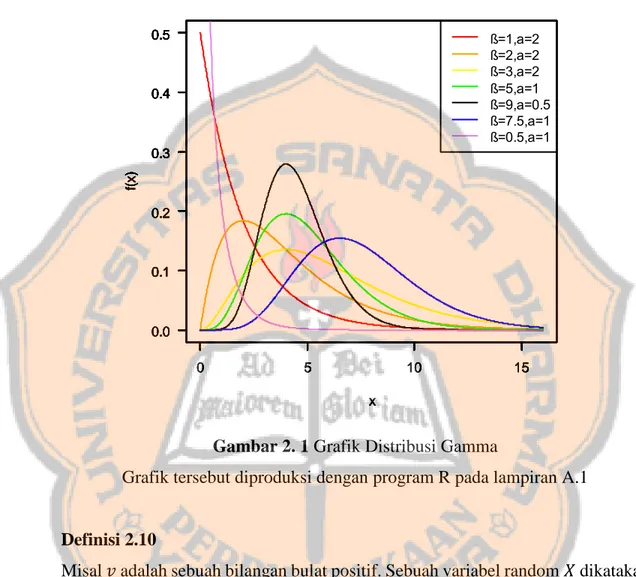
Sebuah variabel random 𝑋 dikatakan berdistribusi Gamma dengan parameter 𝛼 > 0 dan 𝛽 > 0 jika dan hanya jika fungsi densitas 𝑋 adalah
𝑓(𝑥) = {𝑥 𝛼−1𝑒−𝛽𝑥 𝛽𝛼𝛤(𝛼) , 𝑥 > 0, 𝛼 > 0, 𝛽 > 0 0, selainnya dengan 𝛤(𝛼) = ∫ 𝑥∞ 𝛼−1𝑒−𝑥𝑑𝑥 0 .
Gambar 2. 1 Grafik Distribusi Gamma
Grafik tersebut diproduksi dengan program R pada lampiran A.1
Definisi 2.10
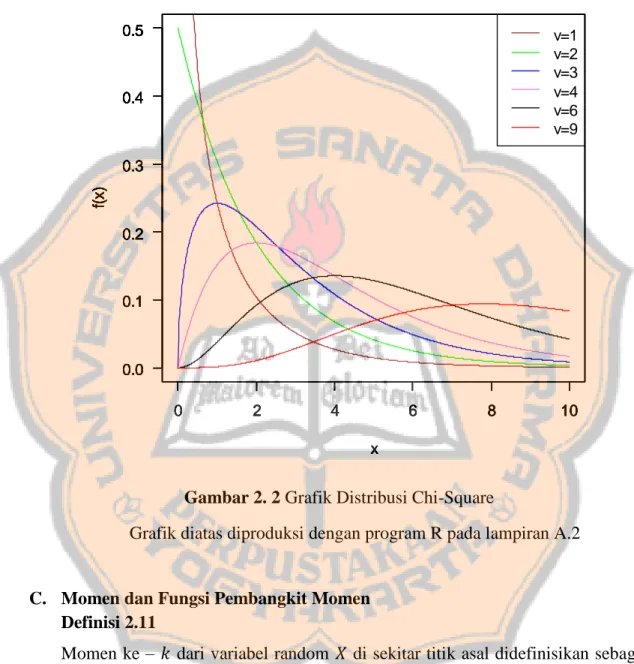
Misal 𝑣 adalah sebuah bilangan bulat positif. Sebuah variabel random 𝑋 dikatakan berdistribusi Chi-Square dengan derajat bebas 𝑣 jika dan hanya jika 𝑋 merupakan variabel random yang berdistribusi Gamma dengan parameter 𝛼 =𝑣
2 dan 𝛽 = 2. Fungsi densitasnya adalah
𝑓(𝑥) = { 𝑥 𝑣 2−1𝑒− 𝑥 2 2𝛼𝛤 (𝑣 2) , 𝑥2 > 0 0, selainnya 0 5 10 15 0.0 0.1 0.2 0.3 0.4 0.5 x f( x) 0 5 10 15 0.0 0.1 0.2 0.3 0.4 0.5 x f( x) 0 5 10 15 0.0 0.1 0.2 0.3 0.4 0.5 x f( x) 0 5 10 15 0.0 0.1 0.2 0.3 0.4 0.5 x f( x) 0 5 10 15 0.0 0.1 0.2 0.3 0.4 0.5 x f( x) 0 5 10 15 0.0 0.1 0.2 0.3 0.4 0.5 x f( x) 0 5 10 15 0.0 0.1 0.2 0.3 0.4 0.5 x f( x) ß=1,a=2 ß=2,a=2 ß=3,a=2 ß=5,a=1 ß=9,a=0.5 ß=7.5,a=1 ß=0.5,a=1
Gambar 2. 2 Grafik Distribusi Chi-Square
Grafik diatas diproduksi dengan program R pada lampiran A.2
C. Momen dan Fungsi Pembangkit Momen Definisi 2.11
Momen ke – 𝑘 dari variabel random 𝑋 di sekitar titik asal didefinisikan sebagai
𝐸(𝑋𝑘) dan dinotasikan dengan 𝜇′ 𝑘.
Contoh 2.4
Tentukan momen saat k=1 dan saat k=2. Jawab: 0 2 4 6 8 10 0.0 0.1 0.2 0.3 0.4 0.5 x f( x) 0 2 4 6 8 10 0.0 0.1 0.2 0.3 0.4 0.5 x f( x) 0 2 4 6 8 10 0.0 0.1 0.2 0.3 0.4 0.5 x f( x) 0 2 4 6 8 10 0.0 0.1 0.2 0.3 0.4 0.5 x f( x) 0 2 4 6 8 10 0.0 0.1 0.2 0.3 0.4 0.5 x f( x) 0 2 4 6 8 10 0.0 0.1 0.2 0.3 0.4 0.5 x f( x) v=1 v=2 v=3 v=4 v=6 v=9
Untuk k=1, 𝐸(𝑋) = 𝜇1′= 𝜇. Untuk k=2, 𝐸(𝑋2) = 𝜇2′. Hal ini dapat berguna saat mencari variansi, berdasarkan Teorema 2.1 𝑉(𝑋) = 𝐸(𝑋2) − (𝐸(𝑋))2
= 𝜇2′− 𝜇2.
Definisi 2.12
Fungsi pembangkit momen 𝑚(𝑡) untuk variabel random 𝑋 didefinisikan sebagai
𝑚(𝑡) = 𝐸(𝑒𝑡𝑥). Fungsi pembangkit momen dikatakan ada jika ada sebuah konstanta positif 𝑏 berhingga untuk |𝑡| ≤ 𝑏.
Definisi 2.13
Fungsi Pembangkit Momen dari variabel random 𝑋 adalah 𝐸(𝑒𝑡𝑥) dan dinyatakan dengan 𝑚𝑥(𝑡). Sehingga 𝑚𝑥(𝑡) = { ∑ 𝑒𝑡𝑥 𝑓(𝑥), ∀𝑥 jika 𝑋 diskrit ∫ 𝑒𝑡𝑥𝑓(𝑥), ∞ −∞ jika 𝑋 kontinu Contoh 2.5
1. Fungsi Pembangkit Momen distribusi Normal
𝑚𝑥(𝑡) = ∫ 𝑒𝑡𝑥𝑓(𝑥) ∞ −∞ = ∫ 𝑒𝑡(𝑥−𝜇) 1 𝜎√2𝜋𝑒 −(𝑥−𝜇)2 2𝜎2 ∞ 0 𝑑𝑥 misalkan 𝑢 = 𝑥 − 𝜇 = ∫ 𝑒𝑡𝑢 1 𝜎√2𝜋𝑒 −(𝑢)2 2𝜎2 ∞ 0 𝑑𝑥 = 1 𝜎√2𝜋∫ 𝑒 𝑡𝑢𝑒−(𝑢) 2 2𝜎2 ∞ 0 𝑑𝑥
= 1 𝜎√2𝜋∫ 𝑒 𝑡𝑢−(𝑢) 2 2𝜎2 ∞ 0 𝑑𝑥 = 1 𝜎√2𝜋∫ 𝑒 −𝑢 2 2𝜎2+ 2𝜎2𝑡𝑢 2𝜎2 ∞ 0 𝑑𝑥 = 1 𝜎√2𝜋∫ 𝑒 − 1 2𝜎2(𝑢2−2𝜎2𝑡𝑢) ∞ 0 𝑑𝑥 = 𝑒 𝑡2𝜎 2 2 𝑒𝑡2𝜎 2 2 1 𝜎√2𝜋∫ 𝑒 − 1 2𝜎2(𝑢2−2𝜎2𝑡𝑢)𝑑𝑥 ∞ 0 = 1 𝜎√2𝜋𝑒 𝑡2𝜎2 2 ∫ 𝑒−𝑡2 𝜎2 2 ∙ 𝑒− 1 2𝜎2(𝑢2−2𝜎2𝑡𝑢) ∞ 0 𝑑𝑥 = 1 𝜎√2𝜋𝑒 𝑡2𝜎 2 2 ∫ 𝑒− 1 2𝜎2(𝑢2−2𝜎2𝑡𝑢+𝜎4𝑡2) ∞ 0 𝑑𝑥 = 𝑒𝑡2𝜎 2 2 ∫ 𝑒 − 1 2𝜎2(𝑢2−2𝜎2𝑡𝑢+𝜎4𝑡2) 𝜎√2𝜋 ∞ 0 𝑑𝑥 = 𝑒𝑡2𝜎 2 2 ∫ 1 𝜎√2𝜋𝑒 −(𝑢−𝜎 2𝑡)2 2𝜎2 ∞ 0 𝑑𝑥 = 𝑒𝑡2𝜎 2 2
Jadi, fungsi pembangkit momen distribusi Normal adalah 𝑚𝑥(𝑡) = 𝑒𝑡2𝜎
2 2.
2. Fungsi Pembangkit Momen distribusi Gamma
𝑚𝑥(𝑡) = ∫ 𝑒𝑡𝑥𝑓(𝑥) ∞ −∞ = ∫ 𝑒𝑡𝑥 1 𝛽𝛼𝛤(𝛼)𝑥 𝛼−1𝑒−𝑥𝛽 ∞ 0 𝑑𝑥 = ∫ 1 𝛽𝛼𝛤(𝛼)𝑥 𝛼−1 𝑒𝑡𝑥 𝑒−𝑥𝛽 ∞ 0 𝑑𝑥 = 1 𝛽𝛼𝛤(𝛼)∫ 𝑥 𝛼−1 𝑒𝑡𝑥−𝛽𝑥 ∞ 0 𝑑𝑥
= 1 𝛽𝛼𝛤(𝛼)∫ 𝑥𝛼−1𝑒 −𝑥𝛽+𝑡𝑥 𝑑𝑥 ∞ 0 = 1 𝛽𝛼𝛤(𝛼)∫ 𝑥𝛼−1𝑒 −𝑥(𝛽1 − 𝑡) 𝑑𝑥 ∞ 0 misalkan 1 𝑠 = 1 𝛽− 𝑡 = 1 𝛽𝛼𝛤(𝛼)∫ 𝑥 𝛼−1𝑒−𝑥(1𝑠 ) 𝑑𝑥 ∞ 0 = 1 𝛽𝛼𝛤(𝛼)[𝛤(𝛼)𝑠(𝛼)] = 𝑠 𝛼 𝛽𝛼 Ingat 1 𝑠 = 1 𝛽− 𝑡 = 1−𝛽𝑡 𝛽 , maka 𝑠 = 𝛽 1−𝛽𝑡 𝑠 𝛽 = 𝛽 1 − 𝛽𝑡 𝛽 = 𝛽 1 − 𝛽𝑡∙ 1 𝛽 = 1 1 − 𝛽𝑡
Jadi, fungsi pembangkit momen distribusi Gamma adalah
𝑚𝑥(𝑡) = 𝑠𝛼 𝛽𝛼 = ( 𝑠 𝛽) 𝛼 = ( 1 1 − 𝛽𝑡) 𝛼 = (1 − 𝛽𝑡)−𝛼. Teorema 2.3
Sifat-sifat Fungsi Pembangkit Momen
1. Jika 𝑋 adalah variabel random dan 𝑐 adalah sebuah konstanta, maka
𝑚𝑐𝑋(𝑡) = 𝑚𝑋(𝑐𝑡).
2. Jika 𝑋 adalah variabel random dan 𝑐 adalah sebuah konstanta, maka
𝑚𝑋+𝑐(𝑡) = 𝑒𝑐𝑡∙ 𝑚 𝑥(𝑡).
3. Jika 𝑋 adalah variabel random dan 𝑎 & 𝑏 adalah dua buah konstanta, maka
𝑚(𝑋+𝑎) 𝑏
(𝑡) = 𝑒𝑎𝑡𝑏 ∙ 𝑚𝑥(𝑡
Bukti: 1. 𝑚𝑐𝑋(𝑡) = 𝐸(𝑒(𝑐𝑋)𝑡) = 𝐸(𝑒(𝑐𝑡)𝑋) = 𝑚𝑋(𝑐𝑡). 2. 𝑚𝑋+𝑐(𝑡) = 𝐸(𝑒(𝑋+𝑐)𝑡) = 𝐸(𝑒(𝑡𝑋)𝑒(𝑐𝑡)) = 𝑒𝑐𝑡∙ 𝑚𝑥(𝑡). 3. 𝑚(𝑋+𝑎) 𝑏 (𝑡) = 𝐸 (𝑒((𝑋+𝑎)𝑏 )𝑡) = 𝐸 (𝑒( (𝑋𝑡+𝑎𝑡) 𝑏 )) = 𝐸 (𝑒( (𝑋𝑡) 𝑏 )𝑒( (𝑎𝑡) 𝑏 )) = 𝑒 𝑎𝑡 𝑏 ∙ 𝑚𝑥(𝑡 𝑏).
Teorema 2.4 Teorema Ketunggalan
Misalkan 𝑚𝑥(𝑡) dan 𝑚𝑦(𝑡) adalah fungsi pembangkit momen dari variabel acak 𝑋 dan 𝑌. Jika kedua fungsi pembangkit momen ada dan 𝑚𝑥(𝑡) = 𝑚𝑦(𝑡) untuk semua nilai dari 𝑡, maka 𝑋 dan 𝑌 mempunyai distribusi probabilitas yang sama.
Bukti:
Julie, H. (1999). Teorema Limit Pusat Lindenberg dan Terapannya. Skripsi. Pada skripsi tersebut, teorema ketunggalan dibuktikan secara umum dengan menggunakan definisi fungsi karakteristik yaitu
𝜑𝑥(𝑡) = 𝐸(𝑒𝑖𝑡𝑥),
dengan 𝑖 adalah bilangan kompleks.
Perhatikan bahwa fungsi pembangkit momen (FPM) adalah bentuk khusus dari fungsi karakteristik, bukti dilakukan dengan menunjukan bahwa bila 𝐹 dan 𝐺
adalah fungsi distribusi kumulatif dengan fungsi karakteristik yang sama, yaitu
∫ 𝑒𝑖𝑡𝑥𝑑𝐹(𝑥) ∞ −∞ = ∫ 𝑒𝑖𝑡𝑥𝑑𝐺(𝑥) ∀𝑡 ∈ ℝ, ∞ −∞ maka 𝐹(𝑥) = 𝐺(𝑥). (Skripsi halaman 54).
Berdasarkan teorema ketunggalan terdapat korespondensi satu-satu antara fungsi pembangkit momen dengan fungsi probabilitas ∎
Teorema 2.5
Misalkan 𝑋1, 𝑋2, … , 𝑋𝑛 adalah variabel acak yang saling bebas dengan fungsi pembangkit momen 𝑚𝑋1(𝑡), 𝑚𝑋2(𝑡), … , 𝑚𝑋𝑛(𝑡). Jika 𝑈 = 𝑋1+ 𝑋2+ ⋯ + 𝑋𝑛, maka 𝑚𝑈(𝑡) = 𝑚𝑋1(𝑡) × 𝑚𝑋2(𝑡) × … × 𝑚𝑋𝑛(𝑡). Bukti: 𝑚𝑈(𝑡) = 𝐸(𝑒𝑡𝑈) = 𝐸(𝑒𝑡(𝑋1+𝑋2+⋯+𝑋𝑛)) = 𝐸(𝑒𝑡𝑋1𝑒𝑡𝑋2… 𝑒𝑡𝑋𝑛) = 𝐸(𝑒𝑡𝑋1) × 𝐸(𝑒𝑡𝑋2) × … × 𝐸(𝑒𝑡𝑋𝑛) = 𝑚𝑋1(𝑡) × 𝑚𝑋2(𝑡) × … × 𝑚𝑋𝑛(𝑡) ∎ D. Pendugaan Parameter
Pendugaan parameter adalah bidang dari statistika yang berhubungan dengan menduga nilai-nilai parameter berdasarkan data yang diukur atau data empiris yang memiliki komponen random. Pendugaan parameter adalah suatu metode untuk menduga nilai parameter populasi dengan menggunakan nilai-nilai dari sampel.
Definisi 2.15
Parameter adalah suatu konstanta yang menggambarkan (merupakan karakteristik) populasi.
Sebuah keluarga parametrik fungsi densitas adalah kumpulan fungsi densitas yang diindeks oleh suatu kuantitas yang disebut parameter.
Contoh 2.6:
1. Populasi berdistribusi Normal dengan fungsi densitasnya adalah
𝑓(𝑥) = 1
𝜎 √2𝜋exp [− ( 1
2𝜎2) ((𝑥 − 𝜇)
2)] , −∞ < 𝑥 < ∞ memiliki parameter
𝜇 dan 𝜎2, dengan 𝜇 merupakan rata-rata populasi dan 𝜎2 merupakan variansi populasi.
2. Populasi berdistribusi Eksponensial fungsi densitasnya adalah 𝑓(𝑥; 𝜆) = 𝜆𝑒−𝜆𝑥, dengan 𝜆 > 0. Maka untuk setiap 𝜆 > 0, 𝑓(𝑥; 𝜆) adalah fungsi densitas. Kumpulan dari 𝑓(𝑥; 𝜆) adalah keluarga parametrik dari fungsi densitas.
Definisi 2.16
Penduga (estimator) adalah suatu aturan, yang dinyatakan dalam suatu rumus yang digunakan untuk menghitung nilai dari pendugaan yang didasarkan atas pengukuran di dalam sampel.
Penduga dibagi menjadi dua bagian yaitu penduga titik (point estimation) dan penduga selang (interval estimation).
Definisi 2.17
Penduga Titik (Point Estimation)
Penduga titik adalah penentuan suatu nilai tunggal yang dengan sebaik-baiknya menduga parameter yang sebenarnya.
Contoh 2.7
Rata-rata sampel yang dinyatakan dalam suatu rumus
𝑥̅ =1 𝑛∑ 𝑥𝑖
𝑛
𝑖=1
Definisi 2.18
Penduga Selang (Interval Estimation)
Penduga selang adalah suatu penentuan selang nilai yang memiliki peluang yang besar akan memuat parameter sebenarnya.
E. Selang Kepercayaan
Penduga selang adalah metode yang digunakan untuk menghitung 2 nilai yang akan membentuk titik-titik batas interval. Idealnya hasil dari interval akan memiliki 2 sifat. Pertama ia akan memuat parameter 𝜃, kedua, intervalnya akan relatif sempit. Kedua titik batas dari interval merupakan fungsi dari pengukuran sampel yang akan bervariasi secara acak dari sampel yang satu dengan sampel yang lain. Jadi, panjang dan letak dari interval bersifat random. Kita tidak dapat secara pasti mengetahui letak dari parameter 𝜃, tapi kita tahu bahwa letaknya di dalam selang tersebut. Jadi tujuan kita adalah ingin menentukan interval yang relatif sempit tetapi mempunyai peluang yang besar untuk memuat parameter 𝜃.
Penduga selang sering disebut dengan Selang Kepercayaan (Confidence Interval). Titik batas atas dan titik batas bawah dari selang kepercayaan disebut juga batas atas dan batas bawah kepercayaan. Peluang bahwa selang kepercayaan akan memuat parameter 𝜃 disebut koefisien kepercayaan. Dari sudut pandang praktis, koefisien kepercayaan mengidentifikasi berapakah 𝑖 dalam sampling berulang, selang yang terbentuk akan memuat parameter 𝜃 yang menjadi sasaran. Contoh, misal koefisien kepercayannya 95% , artinya jika ada sampling sebanyak 100 kali maka 95 selang yang terbentuk akan memuat 𝜃. Jika diketahui bahwa koefisien kepercayaan yang terkait dengan penduga itu tinggi, maka dapat dipercaya bahwa setiap selang kepercayaan yang dibangun dengan menggunakan hasil dari sampel tunggal akan memuat parameter 𝜃.
Misalkan 𝜃̂𝐿 dan 𝜃̂𝑈 secara berturut-turut merupakan batas atas dan batas bawah selang kepercayaan random untuk parameter 𝜃.
Maka, jika 𝑃 (𝜃̂𝐿 ≤ 𝜃 ≤ 𝜃̂𝑈) = 1 − 𝛼 , peluang (1 − 𝛼) adalah koefisien kepercayaan. Interval random yang didefinisikan dengan [𝜃̂𝐿, 𝜃̂𝑈] disebut selang kepercayaan dua sisi.
Memungkinkan juga untuk membentuk selang kepercayaan satu sisi batas bawah yaitu
𝑃 (𝜃̂𝐿 ≤ 𝜃) = 1 − 𝛼,
selang kepercayaannya adalah [𝜃̂𝐿, ∞). Dengan cara yang sama, dapat dibentuk selang kepercayaan satu sisi batas atas yaitu
𝑃 (𝜃 ≤ 𝜃̂𝑈) = 1 − 𝛼, selang kepercayaannya adalah (−∞, 𝜃̂𝑈].
Metode yang sering digunakan untuk mencari selang kepercayaan disebut metode Pivot. Metode Pivot bergantung pada suatu nilai yang disebut kuantitas Pivot. Kuantitas Pivot memiliki 2 ciri:
1. Merupakan fungsi dari pengukuran sampel dan parameter 𝜃, dengan 𝜃 adalah kuantitas yang tidak diketahui.
2. Distribusi probabilitas dari kuantitas Pivot tidak bergantung pada parameter 𝜃.
Jika distribusi probabilitas dari kuantitas Pivot diketahui, maka logika berikut dapat digunakan untuk bentuk penduga selang. Jika 𝑌 merupakan variabel random, 𝑐 > 0 adalah konstan, dan 𝑃(𝑎 ≤ 𝑌 ≤ 𝑏) = 0.7; maka jelas bahwa
𝑃(𝑐𝑎 ≤ 𝑐𝑌 ≤ 𝑐𝑏) = 0.7. Dengan cara yang sama untuk setiap konstan 𝑑,
𝑃(𝑎 + 𝑑 ≤ 𝑌 + 𝑑 ≤ 𝑏 + 𝑑) = 0.7. Peluang kejadian 𝑃(𝑎 ≤ 𝑌 ≤ 𝑏) tidak dipengaruhi dengan perubahan skala atau translasi dari 𝑌.
Contoh 2.8
Diberikan suatu populasi, dengan variabel random Y, memiliki distribusi Eksponensial dengan mean θ. Dengan menggunakan 𝑌, buatlah selang kepercayaan bagi 𝜃 dengan koefisien kepercayaan 0.90.
Jawab:
Fungsi densitas untuk Y adalah sebagai berikut
𝑓(𝑦) = {( 1 θ) 𝑒 −𝑦θ , 𝑦 ≥ 0 0, selainnya
Dengan menggunakan metode Pivot, akan ditunjukkan bahwa U =𝑌
θ memenuhi syarat sebagai kuantitas Pivot.
F𝑢(𝑢) = 𝑃(𝑈 ≤ 𝑢) = 𝑃 (𝑌 θ ≤ 𝑢) = 𝑃(𝑌 ≤ θ𝑢) = F𝑌(θ𝑢) (2.2) F𝑌(y) = ∫ 𝑓(𝑡)𝑑𝑡 𝑦 −∞ = ∫ 1 θ 𝑦 −∞ 𝑒−θ𝑡𝑑𝑡 = 1 − 𝑒− 𝑦 θ (2.3) Dari (2.2) dan (2.3) diperoleh
F𝑌(θ𝑢) = 1 − 𝑒− 𝑢𝜃 θ = 1 − 𝑒− 𝑢 θ f𝑢(𝑢) = F𝑢′(𝑢) = F𝑌′(θ𝑢) = 𝑒−𝑢 U =𝑌
θ adalah kuantitas Pivot, karena
1. U merupakan fungsi dari pengukuran sampel dan parameter 𝜃 yang tidak diketahui.
2. f𝑢(𝑢) tidak bergantung pada 𝜃.
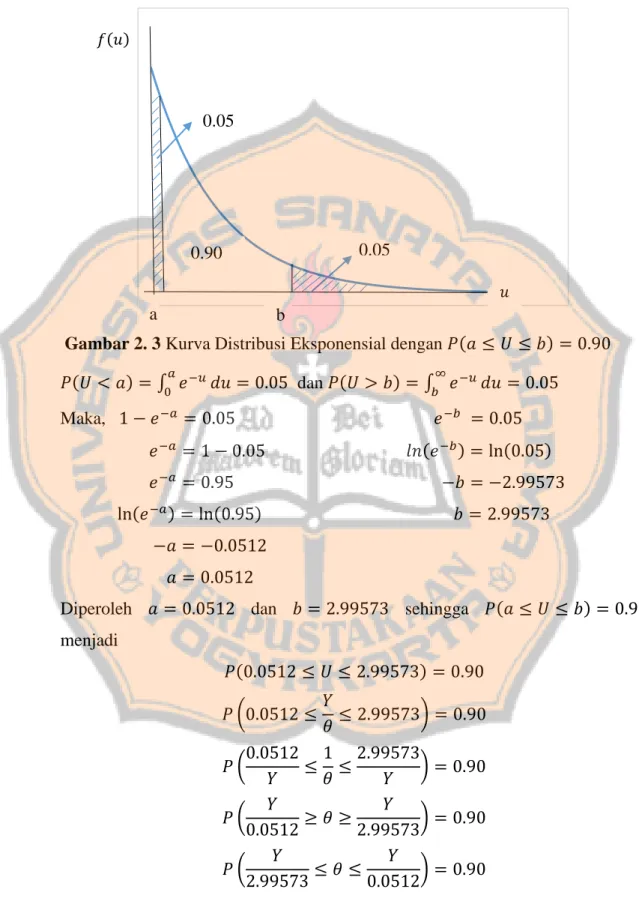
Karena akan dibuat penduga selang dengan koefisien kepercayaan sama dengan 0.90, akan dicari 𝑎 dan 𝑏 untuk 𝑃(𝑎 ≤ 𝑈 ≤ 𝑏) = 0.90
Gambar 2. 3 Kurva Distribusi Eksponensial dengan 𝑃(𝑎 ≤ 𝑈 ≤ 𝑏) = 0.90 𝑃(𝑈 < 𝑎) = ∫ 𝑒𝑎 −𝑢 0 𝑑𝑢 = 0.05 dan 𝑃(𝑈 > 𝑏) = ∫ 𝑒 −𝑢 ∞ 𝑏 𝑑𝑢 = 0.05 Maka, 1 − 𝑒−𝑎 = 0.05 𝑒−𝑏 = 0.05 𝑒−𝑎 = 1 − 0.05 𝑙𝑛(𝑒−𝑏) = ln(0.05) 𝑒−𝑎 = 0.95 −𝑏 = −2.99573 ln(𝑒−𝑎) = ln(0.95) 𝑏 = 2.99573 −𝑎 = −0.0512 𝑎 = 0.0512
Diperoleh 𝑎 = 0.0512 dan 𝑏 = 2.99573 sehingga 𝑃(𝑎 ≤ 𝑈 ≤ 𝑏) = 0.90
menjadi 𝑃(0.0512 ≤ 𝑈 ≤ 2.99573) = 0.90 𝑃 (0.0512 ≤𝑌 𝜃 ≤ 2.99573) = 0.90 𝑃 (0.0512 𝑌 ≤ 1 𝜃≤ 2.99573 𝑌 ) = 0.90 𝑃 ( 𝑌 0.0512≥ 𝜃 ≥ 𝑌 2.99573) = 0.90 𝑃 ( 𝑌 2.99573≤ 𝜃 ≤ 𝑌 0.0512) = 0.90 0.05 0.05 0.90 a b 𝑢 𝑓(𝑢)
Jadi, selang kepercayaan bagi 𝜃 dengan koefisien kepercayaan 0.90 adalah
𝑃 ( 𝑌
2.99573≤ 𝜃 ≤ 𝑌
0.0512) = 0.90.
F. Ukuran Penduga Yang Baik
Penduga yang baik adalah penduga yang mendekati nilai parameter yang sebenarnya. Ciri-ciri penduga yang baik adalah penduga yang tak bias atau memiliki bias yang sekecil mungkin.
Bias dan Rata-rata Galat dari Penduga Titik Definisi 2.19
Misalkan 𝜃̂ adalah penduga titik dari parameter 𝜃, maka 𝜃̂ adalah penduga tak bias jika E(θ̂) = θ. Jika E(θ̂) ≠ θ, maka θ̂ disebut bias.
Definisi 2.20
Bias dari penduga titik 𝜃̂ didefinisikan sebagai 𝐵(𝜃̂) = 𝐸(𝜃̂) − 𝜃.
Contoh 2.9
Diberikan 𝑦1, 𝑦2, 𝑦3, … , 𝑦𝑛 merupakan sampel random dari populasi memiliki fungsi densitas sebagai berikut
𝑓(𝑦) = {( 1 θ + 1) 𝑒 −(θ+1)𝑦 , 𝑦 > 0, 𝜃 > −1 0, selainnya
Tentukan penduga yang tak bias bagi 𝜃. Apakah 𝑌̅ merupakan penduga yang tak bias bagi 𝜃?
Jawab:
𝐸(𝑌̅) = 𝐸 (∑ 𝑌𝑖 𝑛 𝑖=1 𝑛 ) = 1 𝑛𝐸 (∑ 𝑌𝑖 𝑛 𝑖=1 ) = 1 𝑛∑ 𝐸(𝑌𝑖) = 1 𝑛𝑛(𝜃 + 1) = 𝜃 + 1. Jadi 𝑌̅ bias.
Biasnya dari 𝑌̅ adalah 1, maka
𝐸(𝑌̅) = 𝜃 + 1
𝐸(𝑌̅ − 1) = 𝜃
Jadi, 𝑌̅ − 1 adalah penduga tak bias dari 𝜃.
Definisi 2.21
Rata-rata Kuadrat Galat (Mean Square Error) dari penduga titik 𝜃̂ adalah
𝑀𝑆𝐸(𝜃̂) = 𝐸 [(𝜃̂ − 𝜃 )2].
Rata-rata Kuadrat Galat dari sebuah penduga 𝜃̂ adalah fungsi dari variansi dan biasnya. Teorema 2.6 𝑀𝑆𝐸(𝜃̂) = 𝑉(𝜃̂) + [𝐵(𝜃̂)2] Bukti: 𝑀𝑆𝐸(𝜃̂) = 𝐸 [(𝜃̂ − 𝜃)2] = 𝐸 [(𝜃̂ − 𝐸 (𝜃̂)) + (𝐸(𝜃̂) − 𝜃)2] = 𝐸 [(𝜃̂ − 𝐸 (𝜃̂))2+ 2 (𝜃̂ − 𝐸 (𝜃̂)) (𝐸(𝜃̂) − 𝜃) + (𝐸(𝜃̂) − 𝜃)2] = 𝐸 [(𝜃̂ − 𝐸 (𝜃̂))2] + 𝐸 [2 (𝜃̂ − 𝐸 (𝜃̂)) (𝐸(𝜃̂) − 𝜃)] + 𝐸 [(𝐸(𝜃̂) − 𝜃)2] = 𝑉(𝜃̂) + 2𝐸 [(𝜃̂ − 𝐸 (𝜃̂)) 𝐵(𝜃̂)] + [𝐵(𝜃̂)]2 = 𝑉(𝜃̂) + 2𝐵(𝜃̂)𝐸 [(𝜃̂ − 𝐸 (𝜃̂))] + [𝐵(𝜃̂)]2 = 𝑉(𝜃̂) + 2𝐵(𝜃̂)𝐸 (𝜃̂) − 𝐸[𝐸(𝜃̂)] + [𝐵(𝜃̂)]2
= 𝑉(𝜃̂) + 0 + [𝐵(𝜃̂)]2 = 𝑉(𝜃̂) + [𝐵(𝜃̂)]2 ∎
G. Metode Kuadrat Terkecil
Regresi linear adalah metode statistika yang digunakan untuk mengetahui hubungan antara variabel terikat (dependen;𝑌) dengan satu atau lebih variabel bebas (independen;𝑋).
Definisi 2.22
Model regresi linear sederhana didefinisikan sebagai
𝑌𝑖 = 𝛽0+ 𝛽1𝑋𝑖+ 𝑢𝑖, 𝑖 = 1,2,3, … , 𝑛
dengan 𝑌𝑖 = pengamatan ke- 𝑖 variabel dependen 𝑌
𝑋𝑖 = pengamatan ke- 𝑖 variabel independen 𝑥 𝛽0 = intersep (konstanta)
𝛽1= parameter regresi
𝑢𝑖 = galat (error) dari pengamatan ke-𝑖
Metode Kuadrat Terkecil (Least Square Method) merupakan salah satu metode yang sering digunakan untuk mendapatkan nilai-nilai penduga parameter model regresi. Misalkan (𝑥𝑖, 𝑦𝑖) pasangan sampel random berukuran 𝑛
pengamatan dari suatu populasi, berdasarkan definisi 2.22 maka persamaan garis regresinya adalah
𝑌𝑖 = 𝛽0+ 𝛽1𝑋𝑖+ 𝑢𝑖.
Metode Kuadrat Terkecil bertujuan untuk menentukan penduga dari 𝛽0 dan
𝛽1, yaitu 𝛽̂0 dan 𝛽̂1. Dengan asumsi 𝐸(𝑢𝑖) = 0 persamaan regresi akan diduga dengan
𝑌̂ = 𝛽𝑖 ̂ + 𝛽0 ̂𝑋1 𝑖.
Tujuan dari Metode Kuadrat Terkecil adalah menemukan dari 𝛽0 dan 𝛽1 yang meminimumkan Jumlah Kuadrat Galat (Sum of Square Error;SSE).
Definisi 2.23
Jumlah Kuadrat Galat (Sum of Square Error;SSE) didefinisikan sebagai berikut
𝑆𝑆𝐸 = ∑(𝑦𝑖− 𝑦̂)𝑖 2 = ∑[𝑦𝑖 − ( 𝛽̂ + 𝛽0 ̂𝑥1 𝑖)] 2 . 𝑛 𝑖=1 𝑛 𝑖=1
Jumlah Kuadrat Galat (SSE) akan memiliki nilai minimum jika nilai 𝛽̂0 dan 𝛽̂1
memenuhi persamaan 𝜕𝑆𝑆𝐸
𝜕𝛽̂0 = 0 dan 𝜕𝑆𝑆𝐸
𝜕𝛽̂1 = 0. Dengan menggunakan turunan parsial terhadap 𝛽̂0 dan 𝛽̂1, maka diperoleh
𝜕𝑆𝑆𝐸 𝜕𝛽̂0 = 𝜕( ∑𝑛𝑖=1[𝑦𝑖− ( 𝛽̂ + 𝛽0 ̂𝑥1 𝑖)]2 𝜕𝛽̂0 = 0 = − ∑ 2[𝑦𝑖− ( 𝛽̂ + 𝛽0 ̂𝑥1 𝑖)] 𝑛 𝑖=1 = 0 = −2 (∑ 𝑦𝑖 − ∑( 𝛽̂ + 𝛽0 ̂𝑥1 𝑖) 𝑛 𝑖=1 𝑛 𝑖=1 ) = 0 = (∑ 𝑦𝑖 − 𝑛𝛽̂ − 𝛽0 ̂ ∑ 𝑥1 𝑖 𝑛 𝑖=1 𝑛 𝑖=1 ) = 0 ∑ 𝑦𝑖 = 𝑛𝛽̂ + 𝛽0 ̂ ∑ 𝑥1 𝑖 𝑛 𝑖=1 𝑛 𝑖=1 (2.4) dan 𝜕𝑆𝑆𝐸 𝜕𝛽̂1 =𝜕( ∑ [𝑦𝑖− ( 𝛽̂ + 𝛽0 ̂𝑥1 𝑖)] 2 𝑛 𝑖=1 𝜕𝛽̂1 = 0 = − ∑𝑛𝑖=12[𝑦𝑖 − ( 𝛽̂ + 𝛽0 ̂𝑥1 𝑖)]𝑥𝑖 = 0 = −2(∑𝑖=1𝑛 𝑥𝑖𝑦𝑖 − 𝛽̂ ∑0 𝑖=1𝑛 𝑥𝑖 − 𝛽̂ ∑1 𝑛𝑖=1𝑥𝑖2 ) = 0 = (∑𝑖=1𝑛 𝑥𝑖𝑦𝑖 − 𝛽̂ ∑0 𝑖=1𝑛 𝑥𝑖 − 𝛽̂ ∑1 𝑛𝑖=1𝑥𝑖2 ) = 0 ∑ 𝑥𝑖𝑦𝑖 = 𝛽̂ ∑ 𝑥0 𝑖 𝑛 𝑖=1 + 𝛽̂ ∑ 𝑥1 𝑖2 𝑛 𝑖=1 𝑛 𝑖=1 (2.5)
Persamaan (2.4) dan (2.5) dapat diselesaikan dengan metode Eliminasi maka akan diperoleh 𝛽̂0 dan 𝛽̂1 sebagai berikut
𝛽1 ̂ = ∑ 𝑥𝑖 𝑛 𝑖=1 𝑦𝑖 − 1 𝑛∑𝑛𝑖=1𝑥𝑖 ∑𝑛𝑖=1𝑦𝑖 ∑𝑛 𝑥𝑖2 𝑖=1 − 1 𝑛 (∑𝑛𝑖=1𝑥𝑖)2 = ∑ (𝑌𝑖− 𝑌̅) 𝑛 𝑖=1 (𝑥𝑖 − 𝑥̅) ∑𝑛𝑖=1(𝑥𝑖 − 𝑥̅)2 (2.6) 𝛽̂ = 0 − 1 𝑛∑𝑛𝑖=1𝑥𝑖𝑦𝑖∑𝑛𝑖=1𝑥𝑖+ 1 𝑛∑𝑛𝑖=1𝑥𝑖2 ∑𝑛𝑖=1𝑦𝑖 ∑𝑛𝑖=1𝑥𝑖2− 1 𝑛 (∑𝑛𝑖=1𝑥𝑖)2 = 1 𝑛∑𝑛𝑖=1𝑥𝑖2 ∑𝑛𝑖=1𝑦𝑖− 1 𝑛∑𝑛𝑖=1𝑥𝑖𝑦𝑖∑𝑛𝑖=1𝑥𝑖 ∑𝑛 𝑥𝑖2 𝑖=1 − 1 𝑛 (∑𝑛𝑖=1𝑥𝑖)2 = 1 𝑛 ∑𝑛𝑖=1𝑦𝑖(∑𝑛𝑖=1𝑥𝑖2− 1 𝑛 (∑𝑛𝑖=1𝑥𝑖)2) − (∑𝑛𝑖=1𝑥𝑖𝑦𝑖 −1𝑛∑𝑛𝑖=1𝑥𝑖 ∑𝑛𝑖=1𝑦𝑖) ( 1 𝑛 ∑𝑛𝑖=1𝑥𝑖) ∑𝑛𝑖=1𝑥𝑖2− 1 𝑛 (∑𝑛𝑖=1𝑥𝑖)2 = 1 𝑛∑𝑛𝑖=1𝑥𝑖2 ∑𝑛𝑖=1𝑦𝑖− ( 1 𝑛2 ∑𝑛𝑖=1𝑦𝑖(∑𝑛𝑖=1𝑥𝑖)2) − 1 𝑛∑𝑛𝑖=1𝑥𝑖𝑦𝑖∑𝑛𝑖=1𝑥𝑖 + (𝑛12 ∑𝑖=1𝑛 𝑦𝑖(∑𝑛𝑖=1𝑥𝑖)2) ∑𝑛 𝑥𝑖2 𝑖=1 − 1 𝑛 (∑𝑛𝑖=1𝑥𝑖)2 = 1 𝑛 ∑ 𝑦𝑖 𝑛 𝑖=1 −∑ 𝑥𝑖 𝑛 𝑖=1 𝑦𝑖− 1 𝑛∑𝑛𝑖=1𝑥𝑖∑𝑛𝑖=1𝑦𝑖 ∑𝑛 𝑥𝑖2 𝑖=1 − 1 𝑛 (∑𝑛𝑖=1𝑥𝑖)2 (1 𝑛 ∑ 𝑥𝑖 𝑛 𝑖=1 ) = 𝑦̅ − 𝛽̂ 𝑥̅ (2.7)1
Penduga 𝛽̂0 dan 𝛽̂1 pada persamaan (2.6) dan (2.7) adalah penduga yang memiliki jumlah kuadrat galat yang paling minimum, maka 𝛽̂0 dan 𝛽̂1 adalah titik minimum.
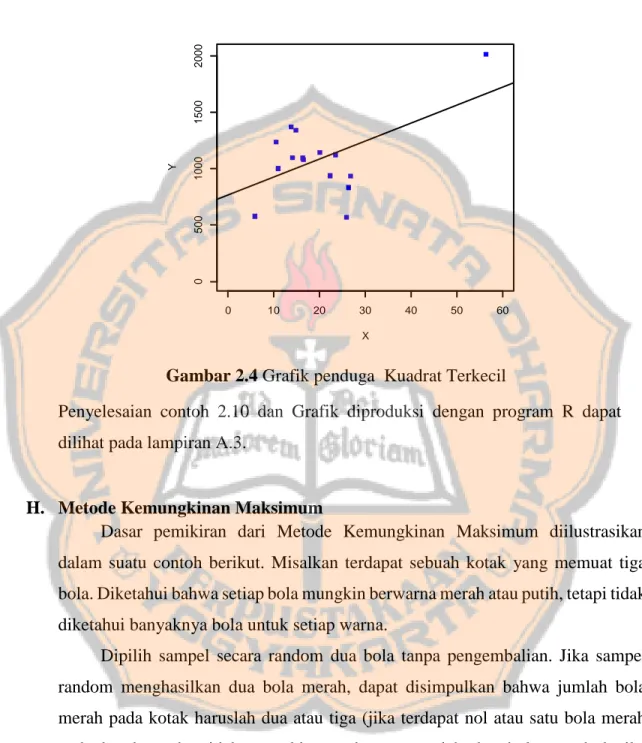
Contoh 2.10
Tentukan koefisien dari garis lurus dengan model 𝑦̂ = 𝛽𝑖 ̂ + 𝛽0 ̂𝑥1 𝑖 untuk 𝑛 = 15
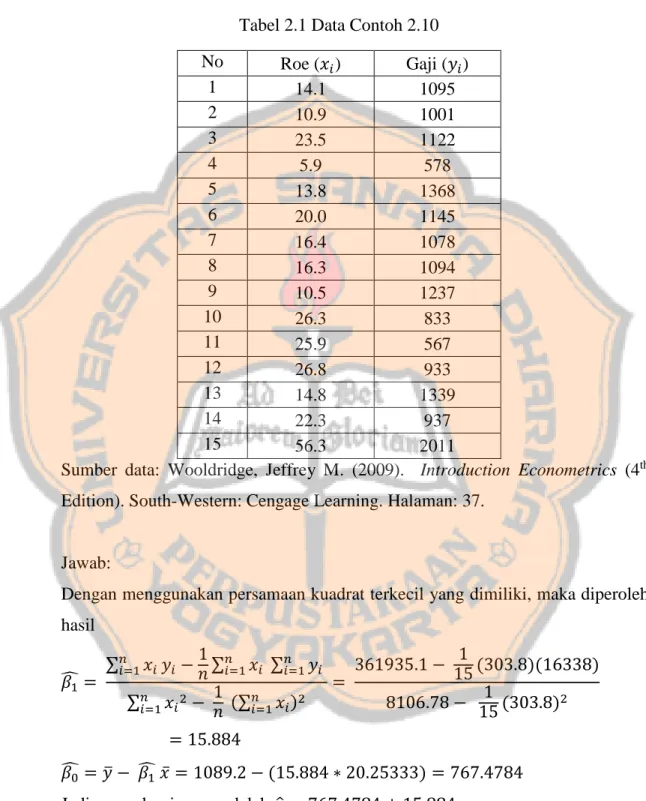
titik data yang diberikan dalam tabel di bawah ini dengan menggunakan Metode Kuadrat Terkecil.
Tabel 2.1 Data Contoh 2.10 No Roe (𝑥𝑖) Gaji (𝑦𝑖) 1 14.1 1095 2 10.9 1001 3 23.5 1122 4 5.9 578 5 13.8 1368 6 20.0 1145 7 16.4 1078 8 16.3 1094 9 10.5 1237 10 26.3 833 11 25.9 567 12 26.8 933 13 14.8 1339 14 22.3 937 15 56.3 2011
Sumber data: Wooldridge, Jeffrey M. (2009). Introduction Econometrics (4th Edition). South-Western: Cengage Learning. Halaman: 37.
Jawab:
Dengan menggunakan persamaan kuadrat terkecil yang dimiliki, maka diperoleh hasil 𝛽1 ̂ = ∑ 𝑥𝑖 𝑛 𝑖=1 𝑦𝑖 − 1 𝑛∑𝑛𝑖=1𝑥𝑖 ∑𝑛𝑖=1𝑦𝑖 ∑𝑛 𝑥𝑖2 𝑖=1 − 1 𝑛 (∑𝑛𝑖=1𝑥𝑖)2 = 361935.1 − 1 15(303.8)(16338) 8106.78 − 151 (303.8)2 = 15.884 𝛽̂ = 𝑦̅ − 𝛽0 ̂ 𝑥̅ = 1089.2 − (15.884 ∗ 20.25333) = 767.47841
Gambar 2.4 Grafik penduga Kuadrat Terkecil
Penyelesaian contoh 2.10 dan Grafik diproduksi dengan program R dapat dilihat pada lampiran A.3.
H. Metode Kemungkinan Maksimum
Dasar pemikiran dari Metode Kemungkinan Maksimum diilustrasikan dalam suatu contoh berikut. Misalkan terdapat sebuah kotak yang memuat tiga bola. Diketahui bahwa setiap bola mungkin berwarna merah atau putih, tetapi tidak diketahui banyaknya bola untuk setiap warna.
Dipilih sampel secara random dua bola tanpa pengembalian. Jika sampel random menghasilkan dua bola merah, dapat disimpulkan bahwa jumlah bola merah pada kotak haruslah dua atau tiga (jika terdapat nol atau satu bola merah pada kotak, maka tidak mungkin untuk memperoleh dua bola merah ketika mengambil sampel tanpa pengembalian). Jika terdapat dua bola merah dan satu bola putih pada kotak, peluang terpilihnya dua bola merah secara random adalah
0 10 20 30 40 50 60 0 500 1000 1500 2000 X Y
(22)(10) (32) =
1 3
Jika terdapat tiga bola merah di dalam kotak, peluang terpilihnya tiga bola merah secara random adalah
(32) (32)= 1
Oleh karena itu dipilih tiga sebagai perkiraan jumlah bola merah di dalam kotak, karena perkiraan ini memaksimumkan peluang dari sampel yang diamati. Tentu saja, ada kemungkinan bahwa kotak hanya berisi dua bola merah, tetapi hasil yang diamati memberikan kepercayaan lebih bahwa ada tiga bola merah di dalam kotak.
Contoh ini mengilustrasikan suatu metode untuk menemukan suatu penduga yang dapat diaplikasikan di berbagai situasi. Metode ini disebut Metode Kemungkinan Maksimum (Maximum Likelihood Method).
Definisi 2.24
Misalkan 𝑥1, 𝑥2, . . . , 𝑥𝑛 adalah variabel random kontinu berukuran 𝑛 dengan fungsi densitas 𝑓(𝑥; 𝜃) dan 𝜃 adalah parameter yang tidak diketahui. Fungsi likelihood dari sampel random adalah fungsi densitas bersama dari 𝑛 variabel random dan merupakan fungsi dari parameter yang tidak diketahui. Fungsi likelihood
dinotasikan dengan 𝐿 (𝑥|𝜃) dan didefinisikan sebagai 𝐿 (𝑥|𝜃) =
∏𝑛𝑖=1𝑓(𝑥𝑖; 𝜃), dengan 𝑓(𝑥𝑖; 𝜃) adalah notasi fungsi probabilitas dari 𝑥𝑖 dengan parameter 𝜃.
Definisi 2.25
Bila fungsi kemungkinan 𝐿 (𝜃) bergantung pada 𝑘 buah parameter yaitu
𝜃1, 𝜃2, . . . , 𝜃𝑘 maka tujuan dari Metode Kemungkinan Maksimum adalah
𝐿 (𝑥1, 𝑥2, . . . , 𝑥𝑛 |𝜃1, 𝜃2, . . . , 𝜃𝑘 ) atau ekuivalen dengan memaksimumkan fungsi log-likelihood 𝑙(𝑥|𝜃) dengan 𝑙 = ln 𝐿 (𝑥|𝜃).
Nilai parameter 𝜃 dapat diperoleh dengan memaksimumkan fungsi log-likelihood. Hal tersebut dapat diperoleh dengan mencari turunan parsial pertama dari fungsi log-likelihood-nya terhadap setiap parameternya. Sehingga, MLE 𝜃̂
merupakan penyelesaian persamaan 𝜕𝐿
𝜕𝜃= 𝜃. Misalkan terdapat 𝑘 parameter yang tidak diketahui, maka pendugaan 𝜃𝑖 dengan Metode Kemungkinan Maksimum
𝜕𝐿
𝜕𝜃𝑖 = 0 dengan 𝑙 =ln(𝜃1, 𝜃2, . . . , 𝜃𝑘
) dan 𝑖 = 1,2,3, … , 𝑘.
Contoh 2.11
Misalkan 𝑥1, 𝑥2, . . . , 𝑥𝑛 adalah sampel random berdistribusi Normal dengan rata-rata 𝜇 dan variansi 𝜎2. Tentukan 𝜇̂ dan 𝜎̂2 dengan menggunakan Metode Kemungkinan Maksimum.
Jawab:
𝑥1, 𝑥2, . . . , 𝑥𝑛 adalah variabel random kontinu berdistribusi Normal dengan rata-rata 𝜇 dan variansi 𝜎2 maka fungsi probabilitas densitasnya didefinisikan sebagai berikut
𝑓(𝑥) = 1
𝜎 √2𝜋exp [− ( 1
2𝜎2) ((𝑥𝑛− 𝜇)2)], − ∞ < 𝑥 < ∞ Berdasarkan definisi 2.24 maka diperoleh
𝐿 (𝜇|𝜎2) = ∏ 𝑓(𝑥𝑖; 𝜇, 𝜎2) 𝑛 𝑖=1 = 𝑓(𝑥1, 𝑥2, . . . , 𝑥𝑛 ; 𝜇, 𝜎2) = 𝑓(𝑥1|𝜇, 𝜎2) × 𝑓(𝑥 2|𝜇, 𝜎2) × … × 𝑓(𝑥𝑛|𝜇, 𝜎2) = [ 1 𝜎 √2𝜋exp (− ( 1 2𝜎2) ((𝑥1− 𝜇)2))] × … × 1 𝜎 √2𝜋exp (− ( 1 2𝜎2) ((𝑥𝑛− 𝜇)2))
= ( 1 𝜎2 2𝜋) 𝑛 2 exp [− ( 1 2𝜎2) ∑(𝑥𝑖− 𝜇) 2 𝑛 𝑖=1 ]
Fungsi log-likelihood dari persamaan di atas adalah
ln[𝐿 (𝜇|𝜎2)] = ln {( 1 𝜎2 2𝜋) 𝑛 2 exp [− ( 1 2𝜎2) ∑(𝑥𝑖 − 𝜇)2 𝑛 𝑖=1 ]} =𝑛 2[ln ( 1 𝜎2 2𝜋)] − 1 2𝜎2 ∑(𝑥𝑖− 𝜇)2 𝑛 𝑖=1 =𝑛 2ln 𝜎 2−𝑛 2ln 2𝜋 − 1 2𝜎2 ∑(𝑥𝑖 − 𝜇)2 𝑛 𝑖=1
Penduga Kemungkinan Maksimum dari 𝜇 dan 𝜎2 adalah penduga yang memaksimumkan ln[𝐿 (𝜇|𝜎2)], dengan mencari nilai turunan parsial terhadap 𝜇 dan 𝜎2, maka diperoleh
∂ln[𝐿 (𝜇|𝜎2)] 𝜕𝜇 = 1 𝜎2 ∑(𝑥𝑖− 𝜇) 𝑛 𝑖=1 (2.6) ∂ln[𝐿 (𝜇|𝜎2)] 𝜕𝜎2 = − 𝑛 2𝜎2 + 1 2𝜎4 ∑(𝑥𝑖− 𝜇) 2 𝑛 𝑖=1 (2.7)
Jika persamaan (2.6) diselesaikan maka akan diperoleh
1 𝜎2 ∑(𝑥𝑖 − 𝜇) 𝑛 𝑖=1 = 0 ∑(𝑥𝑖− 𝜇) 𝑛 𝑖=1 = 0 ∑ 𝑥𝑖 − 𝑛𝜇 𝑛 𝑖=1 = 0 𝜇̂ = ∑ 𝑥𝑖 𝑛 𝑖=1 𝑛 = 𝑥̅
dan jika persamaan (2.7) diselesaikan maka akan diperoleh − 𝑛 2𝜎2+ 1 2𝜎4 ∑(𝑥𝑖− 𝜇)2 𝑛 𝑖=1 = 0 1 2𝜎4 ∑(𝑥𝑖 − 𝜇)2 𝑛 𝑖=1 = 𝑛 2𝜎2 1 𝜎2 ∑(𝑥𝑖 − 𝜇) 2 𝑛 𝑖=1 = 𝑛 𝜎̂ =2 1 𝑛∑(𝑥𝑖 − 𝜇) 2 𝑛 𝑖=1
Dengan substitusi hasil dari persamaan (2.6) yaitu 𝜇 = 𝑥̅ maka hasil dari persamaan (2.7) menjadi 𝜎2 = 1
𝑛∑ (𝑥𝑖− 𝑥̅) 2. 𝑛
𝑖=1 Jadi, penduga kemungkinan
maksimum untuk 𝜇̂ dan 𝜎̂2 adalah 𝜇̂ = 𝑥̅ dan 𝜎̂ =2 1
𝑛∑ (𝑥𝑖 − 𝑥̅) 2. 𝑛
𝑖=1
I. Uji Kolmogorov-Smirnov
Hal yang sangat penting dalam prosedur statistik adalah menentukan distribusi yang mendasari suatu kumpulan data. Uji kecocokan (goodness of fit test) biasanya mengkaji sebuah variabel random dari beberapa distribusi yang tidak diketahui, yaitu suatu fungsi tertentu. Pada dasarnya uji ini mencakup perhitungan distribusi frekuensi kumulatif yang akan terjadi dibawah distribusi teoritisnya.
Misalkan variabel random 𝑥1, 𝑥2, … , 𝑥𝑛 berasal dari distribusi yang tidak diketahui 𝐹(𝑥), dan dimisalkan 𝑥(1) < 𝑥(2) < . . < 𝑥(𝑛) adalah statistik terurut, akan diuji hipotesis bahwa 𝐹(𝑥) adalah sama dengan suatu distribusi tertentu
Definisi 2.26
Misalkan 𝑥1, 𝑥2, … , 𝑥𝑛 adalah variabel random. Fungsi distribusi empiris 𝐹𝑛(𝑥) didefinisikan sebagai 𝐹𝑛(𝑥) = 1 𝑛∑ 1(𝑥𝑖 ≤ 𝑥) 𝑛 𝑖=1 Contoh 2.12
Diberikan 10 sampel random yang memuat 𝑥1= 0.621, 𝑥2 = 0.503, 𝑥3 = 0.203, 𝑥4 = 0.477, 𝑥5 = 0.710, 𝑥6 = 0.581, 𝑥7 = 0.329, 𝑥8 = 0.480, 𝑥9 = 0.554, 𝑥10 = 0.382.
Berdasarkan definisi 2.26 fungsi distribusi empirisnya adalah
𝐹𝑛(𝑥(𝑖)) = 1
𝑛∑ 1(𝑥𝑖 ≤ 𝑥(𝑖))
𝑛
𝑖=1
Dengan 𝑥(𝑖) adalah statistik terurut dari 𝑥𝑖, 𝑖=1,2,3,4,5,6,7,8,9,10. Maka akan diperoleh
𝑥(𝑖) 0.203 0.329 0.382 0.477 0.480 0.503 0.554 0.581 0.621 0.71
𝐹𝑛(𝑥(𝑖)) 0.10 0.20 0.30 0.40 0.50 0.60 0.70 0.80 0.90 1.00
Definisi 2.27
Statistik Uji Kolmogorov-Smirnov 𝐷𝑛 didefinisikan sebagai
𝐷𝑛 = 𝑚𝑎𝑘𝑠 (𝐷+, 𝐷−)
𝐷+ = 𝑚𝑎𝑘𝑠 (𝐹𝑛(𝑥) − 𝐹0(𝑥(𝑖))) 𝐷− = 𝑚𝑎𝑘𝑠 (𝐹0(𝑥(𝑖)) − 𝐹𝑛−1(𝑥𝑖)) Dengan 𝑖 = 1,2, … , 𝑛.
Hipotesis uji Kolmogorov-Smirnov adalah
Untuk setiap 𝑥 dengan 𝐹0(𝑥) adalah fungsi distribusi kumulatif yang diketahui, dan
𝐻1: 𝐹(𝑥) ≠ 𝐹0(𝑥)
Jika 𝐷𝑛 ≥ 𝐷𝛼(𝑛) yang diberikan oleh tabel Kolmogorov-Smirnov, maka 𝐻0
ditolak pada tingkat signifikansi 𝛼. 𝐷𝛼(𝑛) adalah nilai kritis Kolmogorov-Smirnov pada tingkat 𝛼 dan ukuran sampel 𝑛. Tabel 𝐷𝛼(𝑛) dapat dilihat pada lampiran A.4.
J. Uji Distribusi Rayleigh menggunakan Uji Kolmogorov-Smirnov
Uji Kolmogorov-Smirnov dapat juga digunakan untuk menguji apakah data berdistribusi Rayleigh atau tidak. Uji distribusi Rayleigh dengan Kolmogorov-Smirnov dilakukan setelah pendugaan parameter distribusi Rayleigh.
Langkah-langkah uji Kolmogorov-Smirnov untuk distribusi Rayleigh adalah sebagai berikut
1. 𝐻0 = data berdistribusi Rayleigh 2. 𝐻1= data tidak berdistribusi Rayleigh 3. Tentukan tingkat signifikansi 𝛼
4. Statistik Uji: 𝐷𝑛 = max(𝐷+ , 𝐷−)
5. Wilayah kritis
𝐻0 ditolak jika 𝐷𝑛 ≥ 𝐷𝛼(𝑛)
6. a) Data diurutkan dari yang terkecil sampai yang terbesar
b) Hitunglah 𝐹0(𝑥) berdasarkan fungsi distribusi kumulatif dari distribusi Rayleigh
c) Berdasarkan definisi 2.26 hitunglah fungsi distribusi empiris 𝐹𝑛(𝑥)
d) Berdasarkan definisi 2.27 hitunglah nilai 𝐷+ dan 𝐷− dan tentukan maksimum dari 𝐷𝑛 = max(𝐷+ , 𝐷−)
Contoh 2.13
Ujilah apakah data berikut berdistribusi Rayleigh dengan parameter skala 𝑏 = 2
Tabel 2.2 Data Contoh 2.13
No 1 2 3 4 5 6 7 8 9 10
𝑥𝑖 2 0.2 1 1.8 2.7 5 3.6 1.4 4.7 1.5
No 11 12 13 14 15 16 17 18 19 20
𝑥𝑖 4.2 3 2.1 2.4 3.1 4 2.8 3.2 4.1 2.6
Jawab:
1. 𝐻0 = data berdistribusi Rayleigh dengan parameter skala 𝑏 = 2
2. 𝐻1 = data tidak berdistribusi Rayleigh 3. Tingkat signifikansi 𝛼 = 0.05
4. Statistik Uji: 𝐷𝑛 = max(𝐷+ , 𝐷−)
5. Wilayah kritis
𝐻0 ditolak jika 𝐷𝑛 ≥ 𝐷𝛼(𝑛) = 0.29408
6. a) Data diurutkan dari yang terkecil sampai yang terbesar
b) Akan dihitung 𝐹0(𝑥) berdasarkan definisi fungsi distribusi kumulatif dari distribusi Rayleigh, yaitu 𝐹(𝑥) = 1 − exp (− (2𝑏𝑥22))
c) Akan dihitung fungsi distribusi empiris 𝐹𝑛(𝑥) berdasarkan definisi 2.26 d) Akan dihitung nilai 𝐷+ dan 𝐷− berdasarkan definisi 2.27 dan menentukan
maksimum dari 𝐷𝑛 = max(𝐷+ , 𝐷−)
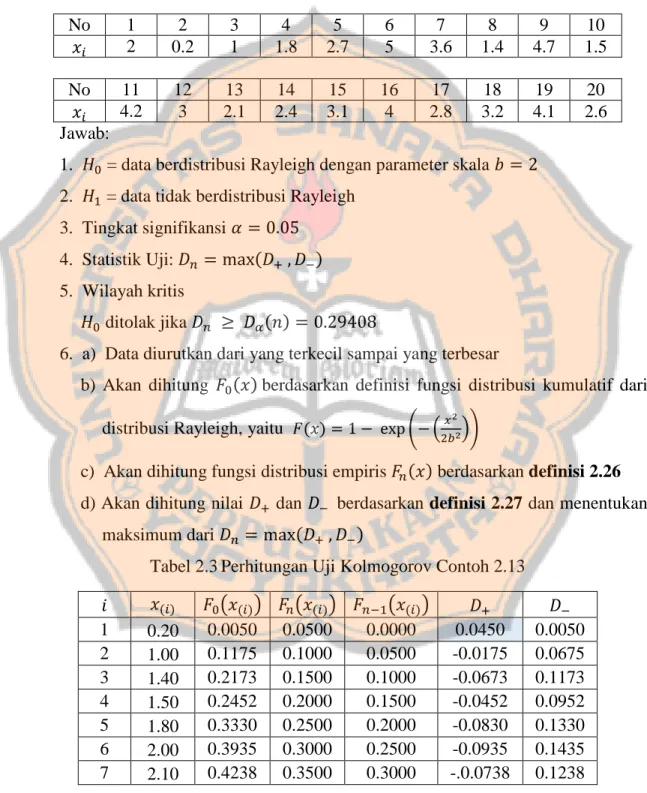
Tabel 2.3Perhitungan Uji Kolmogorov Contoh 2.13
𝑖 𝑥(𝑖) 𝐹0(𝑥(𝑖)) 𝐹𝑛(𝑥(𝑖)) 𝐹𝑛−1(𝑥(𝑖)) 𝐷+ 𝐷− 1 0.20 0.0050 0.0500 0.0000 0.0450 0.0050 2 1.00 0.1175 0.1000 0.0500 -0.0175 0.0675 3 1.40 0.2173 0.1500 0.1000 -0.0673 0.1173 4 1.50 0.2452 0.2000 0.1500 -0.0452 0.0952 5 1.80 0.3330 0.2500 0.2000 -0.0830 0.1330 6 2.00 0.3935 0.3000 0.2500 -0.0935 0.1435 7 2.10 0.4238 0.3500 0.3000 -.0.0738 0.1238
8 2.40 0.5132 0.4000 0.3500 -0.1132 0.1632 9 2.60 0.5704 0.4500 0.4000 -0.1204 0.1704 10 2.70 0.5980 0.5000 0.4500 -0.0980 0.1480 11 2.80 0.6247 0.5500 0.5000 -0.0747 0.1247 12 3.00 0.6753 0.6000 0.5500 -0.0753 0.1253 13 3.10 0.6992 0.6500 0.6000 -0.0492 0.0992 14 3.20 0.7220 0.7000 0.6500 -0.0220 0.0720 15 3.60 0.8021 0.7500 0.7000 -0.0521 0.1021 16 4.00 0.8647 0.8000 0.7500 -0.0647 0.1147 17 4.10 0.8777 0.8500 0.8000 -0.0277 0.0777 18 4.20 0.8897 0.9000 0.8500 0.0103 0.397 19 4.70 0.9368 0.9500 0.9000 0.0132 0.0368 20 5.00 0.9561 1.000 0.9500 0.0439 0.0061 Maksimum 0.0450 0.1704
Gambar 2.5 Grafik 𝐹0(𝑥(𝑖)) dan 𝐹𝑛(𝑥(𝑖))
Grafik tersebut diproduksi dengan program R pada lampiran A.5. 7. Kesimpulan
𝐻0 diterima sebab 𝐷𝑛 = 0.0.18949 ≤ 𝐷𝛼(𝑛) = 0.29408, maka data di atas berdistribusi Rayleigh dengan parameter skala 𝑏 = 2.
1 2 3 4 5 0 .0 0 .2 0 .4 0 .6 0 .8 Xi F F0(xi) Fn(xi) 𝐷𝑛 = max(𝐷+ , 𝐷−) = 0.1704
44 BAB III
PENDUGAAN PARAMETER DISTRIBUSI RAYLEIGH DENGAN METODE KUADRAT TERKECIL DAN KEMUNGKINAN MAKSIMUM
A. Distribusi Rayleigh Definisi 3.1
Variabel random 𝑋 dikatakan mempunyai distribusi Rayleigh dengan satu parameter bila fungsi probabilitasnya
𝑓(𝑥; 𝑏)={ 𝑥 𝑏2𝑒 (−𝑥2 2𝑏2), 𝑥 ≥ 0, 𝑏 > 0 0, selainnya
dengan 𝑏 adalah parameter skala (scale parameter).
Berdasarkan definisi 2.4, akan ditunjukkan bahwa fungsi probabilitas distribusi Rayleigh merupakan fungsi densitas.
1) 𝑓(𝑥, 𝑏) ≥ 0,untuk setiap 𝑥 ∈ 𝑅
Jelas bahwa 𝑓(𝑥) ≥ 0 untuk setiap 𝑥 ∈ 𝑅. 2) ∫−∞∞ 𝑓(𝑥, 𝑏)𝑑𝑥 = 1
Selanjutnya akan ditunjukkan bahwa ∫−∞∞ 𝑓(𝑥)𝑑𝑥 = 1
Misalkan 𝑢 = (𝑥2 2𝑏2) maka 𝑑𝑢 = 1 𝑏2𝑥 𝑑𝑥 ∫ 𝑓(𝑥) ∞ 0 𝑑𝑥 = ∫ 𝑥 𝑏2𝑒 −(𝑥2 2𝑏2) ∞ 0 𝑑𝑥 = lim 𝑐→∞∫ 𝑒 −𝑢𝑑𝑢 𝑐 0 = lim 𝑐→∞−𝑒 −𝑢| 0 𝑐 = lim 𝑐→∞ − 𝑒 −𝑐+ 𝑒0 = 1.