Vektor dalam Ruang-Tiga

Vektor dalam

Ruang-Tiga

Indikator Pencapaian Hasil Belajar

Mahasiswa menunjukkan kemampuan dalam :

1. Menentukan letak titik dalam sistem koordinat Cartesius

2. Menentukan jarak, persamaan bola dan titik tengah pada ruang dimensi tiga 3. Menggambar permukaan pada ruang dimensi tiga

Materi Ajar

Koordinat Kartesius dalam Ruang Tiga Dimensi

Untuk menyatakan lokasi titik pada ruang, tempatkan tiga garis riil berpotongan saling tegak lurus dengan titik 0 ( nol ) berimpit di satu titik O. Titik tersebut dinamakan

titik asal dan ketiga garis tersebut masing-masing dinamakan sumbu koordinat ( sumbu- x , sumbu-y dan sumbu- z ).

Biasanya sumbu- x dan sumbu-y ditempatkan horizontal dan sumbu- z vertikal.

Arah sumbu- z biasanya ditentukan dengan aturan tangan kanan, jika jari-jari tangan kanan mengelilingi sumbu- z dalam arah putaran 0

90 berlawanan jarum jam dari

sumbu-x positif ke sumbu-ypositif maka ibu jari menunjukkan arah positif dari sumbu- z

Ketiga sumbu koordinat menentukan tiga bidang koordinat xy, xz dan yz yang membagi ruang menjadi delapan oktan.

Setiap titik P di ruang berkaitan dengan triple (x,y,z) yang masing-masing

komponennya mengukur jarak berarah terhadap bidang-bidang koordinat.

Sebagai contoh titik-titik ( 2,-3,4 ) dan ( -3,2,-5 ) di gambarkan pada sistem koordinat sebagai berikut :

Latihan :

1. Gambarkan titik yang koordinatnya (2,0,3) , (-3,4,5 ), (0,4,0) dan (-2,-6,-1) 2. Apa yang istimewa pada koordinat titik di bidang yz ? Sumbu-z ?

Jarak, persamaan bola dan titik tengah

Tinjau dua titik P₁(x₁,y₁,z₁)dan P₂(x₂,y₂,z₂), dengan x₁ x₂,y₁  y₂,z₁ z₂.

Pandang kedua titik tersebut sebagai titik sudut – titik sudut dari sebuah balok genjang yang sisi-sisinya sejajar bidang koordinat, seperti ilustrasi berikut :

Perhatikan ,

Jadi jarak antara dua titik P1(x1,y1,z1)dan P2(x2,y2,z2) dalam ruang dengan ( )

,

, _{1 2 1 2}

2

1 x y y z z

x    dapat ditentukan dengan :

Permukaan bola adalah tempat kedudukan titik-titik pada ruang dimensi tiga yang berjarak sama dari suatu titik tetap.

Jika (x,y,z)adalah titik pada permukaan bola dengan pusat (h,k,l) dan jari-jari r ,

maka :

persamaan dinamakan persamaan standar bola. Jika persamaan diuraikan kita akan peroleh persamaan dalam bentuk

Tapi perlu diingat bahwa sebaliknya persamaan dalam bentuk tersebut grafiknya tidak selalu berbentuk bola, bisa jadi berupa titik atau himpunan kosong.

Titik tengah dari dua titik yang diketahui adalah adalah titik yang jaraknya sama terhadap kedua titik

Selanjutnya titik tengah dari dua titik P₁(x₁,y₁,z₁)dan P₂(x₂,y₂,z₂) _{dapat ditentukan} dengan ) , , ( _{2 2 2} 2 x y z P ) , , ( _{1 1 1} 1 x y z P ) , , (m₁ m₂ m₃

Latihan :

1. Cari pusat dan jari-jari dari persamaan bola x2 +y2 +z2 +3x−4z+1=0

2. Tentukan persamaan bola yang diameternya adalah ruas garis yang menghubungkan titik (-1,2,3) dan (5,-2,7)

Menggambar grafik permukaan di ruang dimensi tiga

Dalam banyak kasus suatu bidang berpotongan dengan bidang-bidang kordinat . Jadi pertama kita cari terlebih dahulu kurva perpotongannya dengan bidang-bidang koordinat yang dinamakan jejak. Dengan sedikit keartistikan , kita dapat menggunakan jejak tersebut untuk menggambar grafik. Cara yang analog kita terapkan untuk menggambar grafik dari permukaan-permukaan yang lain. Jika permukaan tidak berpotongan dengan bidang koordinat, carilah penampang – yakni perpotongan permukaan dengan bidang yang secara khusus dipilih ( biasanya bidang yang sejajar dengan bidang koordinat )

a) Bidang

Persamaan dalam bentuk linier

merupakan persamaan bidang dalam ruang dimensi tiga. Latihan :

Buat sketsa bidang yang persamaannya diberikan sebagai berikut : 1. x+3y−z =6

2. x+ y3 =8

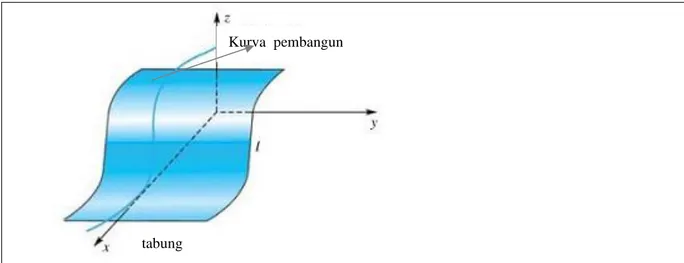
b) Tabung

Mestinya anda sudah sangat mengenal permukaan yang berbentuk tabung tegak. Sekarang kita akan membicarakan pengertian tabung dalam pengertian yang lebih luas. Misal C suatu kurva dan l adalah garis yang memotong C tapi tidak sebidang dengan C . Semua garis yang sejajar dengan l dan memotong C akan membentuk permukaan yang disebut sebagai tabung. Kurva C dinamakan kurva pembangun.

Dalam ruang dimensi tiga tabung muncul jika kita menggambar persamaan yang diberikan dalam dua variabel

Latihan :

Buat sketsa grafik permukaan yang persamaannya diberikan sebagai 1. y2 + z2 =15

2. 2x2 − z16 2 =0

c) Permukaan Kuadrik

Gambar permukaan dalam ruang dimensi tiga yang persamaannya berderajat dua dinamakan permukaan kuadrik. Bentuk umum persamaan berderajat dua dalam ruang dimensi tiga diberikan sebagai

Dapat ditunjukkan bahwa persamaan tersebut melalui rotasi atau translasi sumbu koordinat dapat direduksi menjadi

atau

Permukaan kuadrik (i) dan (ii) simetri terhadap bidang-bidang koordinat dan titik asal sehingga disebut sebagai permukaan kuadrik sentral.

Berikut adalah nama dan sketsa dari enam tipe permukaan kuadrik : Kurva pembangun

Latihan :

Koordinat Tabung dan Koordinat Bola

Koordinat Cartesius adalah salah satu cara yang dapat dipakai untuk menunjukkan posisi titik pada ruang dimensi tiga. Ada dua koordinat lain yang juga digunakan di kalkulus , yaitu kordinat tabung (r,,z)dan koordianat bola (,,). Ketiga koordinat

tersebut diilustrasikan seperti pada gambar berikut ,

r0,0 2  0,0 2,0

Jika benda pejal atau permukaan memiliki suatu sumbu simetri, biasanya akan lebih baik jika kita menempatkan sumbu simetrinya pada sumbu- z dan menggunakan koordinat tabung. Sebagai contoh tabung dengan alas berbentuk lingkaran dan bidang yang memuat sumbu- z , seperti yang ditunjukkan pada gambar berikut

Latihan

1. Cari koordinat Cartesius dari titik yang koordinat tabungnya       5 , 3 2 , 4 

2. Tentukan dalam koordinat tabung persamaan permukaan yang persamaannya dalam koordinat Cartesius x2 +y2 =2x

3. Tentukan dalam koordinat Cartesius persamaan permukaan yang persamaannya dalam koordinat tabung 2 + z4 2 =16

r

Jika suatu benda pejal atau permukaan simetris terhadap suatu titik, kita dapat menempatkannya pada koordinat bola. Sebagai contoh bola dengan pusat titik asal memiliki persamaan  =0 dan kerucut dengan titik puncak titik asal memiliki persamaan = , seperti yang ditunjukkan oleh gambar berikut ₀

Hubungan antara koordinat Cartesius dengan koordinat bola dinyatakan dalam persamaan

Latihan

1. Cari koordinat Cartesius dari titik yang koordinat bolanya       3 2 , 3 , 8  

2. Tentukan dalam koordinat Cartesius persamaan permukaan yang persamaannya dalam koordinat bola  =2cos

3. Tentukan dalam koordinat bola persamaan permukaan yang persamaannya dalam koordinat Cartesius 2 2 y x z = +

Vektor dalam Ruang Dimensi Tiga

Indikator Pencapaian Hasil Belajar

Mahasiswa menunjukkan kemampuan dalam :

1. Menjelaskan representasi vektor secara geometris dan aljabar dalam ruang dimensi tiga

2. Menentukan syarat dua vektor saling tegak lurus dan sejajar berdasarkan sifat hasil kali titik dan hasil kali silang

3. Menentukan vektor proyeksi dan proyeksi skalar 4. Menentukan persamaan bidang

5. Menentukan jarak antara titik dan bidang

6. Mencari volume balok genjang yang ditentukan oleh tiga vektor yang diketahui Materi Ajar

Vektor dalam Ruang Dimensi Tiga

Istilah vektor digunakan untuk menunjukkan besaran yang memiliki besar dan arah. Vektor biasanya direpresentasikan dengan anak panah atau ruas garis berarah. Panjang vektor menunjukkan besar vektor dan arah anak panah menunjukkan arah vektor.

Kita menuliskan vektor dengan huruf yang ditebalkan (u) atau dengan meletakkan anak panah di atasnya (→u ) . Jika titik pangkal vektor u adalah A dan titik ujungnya adalah

B, maka ditulis u= AB. Dua vektor u dan v dikatakan sama, ditulis u = v , jika besar dan arah kedua vektor sama. Vektor 0 adalah vektor yang besarnya 0 dan tidak memiliki arah yang spesifik. Besar atau panjang vektor dinotasikan dengan u

Operasi pada Vektor

Jumlah dua vektor dapat ditentukan dengan menggunakan aturan segitiga atau jajar genjang , ilustrasinya dapat dilihat seperti berikut ini

Selanjutnya dapat ditunjukkan bahwa operasi penjumlahan vektor memiliki sifat-sifat berikut :

Vektor uk adalah vektor yang besarnya adalah k kali besar vektor u dan arahnya sama dengan arah vektor u jika k 0atau berwanan arah dengan arah vektor u jika

0 

k . Gambar berikut adalah ilustrasi untuk operasi dengan skalar :

Khususnya, vektor v− ( dibaca negatif dari v ) adalah vektor yang besarnya sama dengan vektor u , tapi berlawanan arah dengan arah vektor u . Selanjutnya operasi pengurangan didefinisikan sebagai :

dan kita punyai u+(−u)=(−u)+u=0

Pendekatan Aljabar Vektor

Vektor u=u1,u2,u3  dalam ruang dimensi tiga direpresentasikan dengan anak panah yang titik pangkalnya berada di titik asal dan titik ujungnya adalah suatu titik yang koordinatnya (u1,u2,u3), gambar berikut adalah ilustrasi untuk hal tersebut :

Dua vektor u=u1,u2,u3  dan v=v1,v2,v3  dikatakan sama jika 3 3 2 2 1 1 v ,u v ,u v

u = = = . Vektor nol didefinisikan sebagai 0=0,0,0. Selanjutnya jika k

skalar dan u=u1,u2,u3  didefinisikan :

 = = k ku1,ku2,ku3 ku u  − − − = − = −u ( 1)u u₁, u₂, u₃ dan jika u=u1,u2,u3  dan v=v1,v2,v3 , maka :

Vektor-vekor i=1,0,0, j=0,1,0 dan k =0,0,1 adalah vektor basis di ruang

dimensi tiga. Ketiga vektor tersebut bebas linier dan setiap vektor u=u1,u2,u3  dapat dinyatakan sebagai kombinasi linier dari i, j dan k, yakni :

Besar suatu vektor u=u1,u2,u3  menunjukkan panjang ruas garis titik asal ke titik yang koordinatnya (u₁,u₂,u₃)dapat ditentukan dengan

Vektor yang panjangnya satu disebut vektor satuan Latihan

1. Misal u=1,0,1 dan v=−5,0,0. Tentukan u + , v u −v, u dan −3v 2. Cari vektor satuan yang arahnya sama dengan vektor v=2i+3j+4k

Selanjutnya menggunakan interpretasi aljabar dari vektor , aturan berikut dapat dibuktikan

Teorema

Untuk sebarang vektor u,v dan w dan konstanta a dan b , berlaku

Hasil Kali Titik

Jika u=u1,u2,u3 dan v=v1,v2,v3  , hasil kali titik atau hasil kali skalar dari u dan v didefinisikan sebagai u v=u₁v₁+u₂v₂ +u₃v₃. Dari pendefinisian tersebut sifat-sifat hasil kali titik yang berikut dapat dibuktikan

Teorema

Untuk sebarang vektor u,v dan w dan konstanta c , berlaku

Teorema berikut berkaitan dengan tafsiran geometris dari hasil kali titik

Teorema

Jika  adalah sudut vektor u,vmaka

Teorema

Dua vektor u,vadalah tegak lurus jika dan hanya jika u.v=0

Vektor-vektor yang tegak lurus disebut ortogonal Latihan

1. Misal u=0,1,1, v=2,−1,1 dan w=6,−3,3. Hitung :

2. Cari besarnya sudut-sudut pada suatu segitiga ABC , jika A(4,3), B( −1, 1)dan

Proyeksi

Misal u dan v vektor dan  sudut antara kedua vektor tersebut. Asumsikan dulu 2

/

0  . Misal w adalah vektor yang arahnya sama dengan v dan w = u cos.

Karena w searah dengan v , kita dapat tuliskan w=cv untuk suatu skalar c0. Jadi

Jika /2  , kita mendefinisikan w sebagai vektor yang arahnya berlawanan dengan v dan w =−u cos.

Karena w berlawanan arah dengan v , kita dapat tuliskan w=−cv untuk suatu skalar 0



Vektor w dinamakan vektor proyeksi dari u pada v , dinotasikan dengan prvu, jadi

sementara , u cos dinamakan proyeksi skalar dari u pada v .

Latihan :

Tentukan vektor proyeksi dan proyeksi skalar dari u pada v , jika u=−i+5 +j 3k dan k

j i

v =− + −

Sudut dan Cosinus Arah

Sudut antara vektor a dengan vektor basis i,jdan kdinamakan sudut arah dari a dan dinotasikan dengan , dan  .

Tapi terkadang kita bekerja dengan cosinus arah. Misal a=a1,a2,a3 , maka cosinus arah dari a didefinisikan dengan :

Perhatikan bahwa :

Jadi vektor cos,cos,cos  adalah vektor satuan yang arahnya sama dengan vektor

Latihan :

1. Cari sudut arah dari vektor a=4i−5j+3k

2. Cari suatu vektor yang panjangnya 5 satuan dngan 

32 =  dan  100 =  sebagai dua dari ketiga sudut arahnya.

Bidang

Salah satu cara untuk mendeskripsikan bidang adalah dengan menggunakan vektor. Misal n= A,B,C0 vektor tetap dan P₁(x₁,y₁,z₁) titik tetap. Himpunan semua

titik P(x,y,z) yang memenuhi P₁Pn=0 adalah bidang yang tegak lurus terhadap vektor n dan memuat titik P1.

Tulis vektor PP₁ dalam bentuk komponen

maka P₁Pn=0ekivalen dengan

Persamaan tersebut ( dengan A,B,C tidak semuanya nol ) dinamakan bentuk baku dari persamaan bidang. Jika tanda kurung dibuka, maka akan diperoleh persamaan linier

Ini berarti setiap bidang memiliki persamaan linier.

Misal (x₁,y₁,z₁) suatu titik tetap yang memenuhi persamaan linier, maka

Ambil sebarang tititk (x,y,z)yang memenuhi persamaan linier, maka

Dengan mengurangkan kedua persamaan kita peroleh

Dengan demikian sebaliknya berlaku bahwa setiap persamaan linier merepresentasikan suatu bidang.

Latihan :

1. Cari persamaan bidang yang melalui titik (5,1,−2) dan tegak lurus vektor n= 2,4,3 . Cari sudut antara bidang ini dengan bidang yang persamaannya diberikan sebagai

5 7 4

3x− y+ z =

2. Tunjukkan bahwa jarak antara bidang Ax+By+Cz= Ddengan titik (x₀,y₀,z₀) dapat ditentukan dengan menggunakan rumus

3. Cari jarak antara dua bidang sejajar 3x−4y+5z =9 dan 3x−4y+5z =4

Hasil Kali Silang

Hasil kali silang u v dari u= u1,u2,u3 dan v= v1,v2,v3 didefinisikan sebagai

Untuk lebih memudahkan, hasil kali silang tersebut sering dituliskan dalam bentuk determinan seperti berikut

Dapat ditunjukkan bahwa pada hasil kali silang berlaku sifat anti komutatif ,

Latihan :

Misal u= 1,−2,−1 dan v= −2,4,1 . Hitung u v danv u dengan menggunakan definisi.

Tafsiran geometris dari hasil kali silang , diberikan oleh teorema berikut .

Teorema

Jika u,vadalah vektor dan  adalah sudut diantara keduanya , maka :

1. u(uv)=0 dan u(uv)=0, yakni u v tegak lurus terhadap u dan v 2. u,vdan u v membentuk sistem tangan kanan

Kita memperoleh teorema berikut sebagai akibat dari teorema di atas.

Teorema

Dua vektor u dan v sejajar jika dan hanya jika uv=0 Latihan :

1. Cari persamaan bidang yang memuat tiga titik P₁(1,−2,3), P₂(4,1,−2)dan P3(−2,−3,0) 2. Tunjukkan bahwa luas jajar genjang dengan vektor a dan b sebagai sisi yang

berdampingan adalah a b

3. Tunjukkan bahwa volume dari balok genjang yang ditentukan vektor-vektor a , b dan c adalah

Selanjutnya dengan menuliskan vektor dalam komponen, dapat ditunjukkan teorema berikut berlaku

Teorema

Jika u , v dan w vektor-vektor dalam ruang dimensi tiga dan k adalah skalar, maka berlaku :

Dengan menggunakan sifat di atas dan hasil kali silang vektor-vektor basis berikut

perhitungan hasil kali silang bisa dilakukan tanpa harus menggunakan definisi Latihan :

Fungsi Bernilai Vektor

Indikator Pencapaian Hasil Belajar

Mahasiswa menunjukkan kemampuan dalam : 1. Menjelaskan pengertian fungsi bernilai vektor 2. Menentukan limit fungsi bernilai vektor 3. Menentukan turunan fungsi bernilai vektor 4. Menentukan integral fungsi bernilai vektor

5. Menentukan kecepatan dan percepatan gerakan sepanjang kurva lintasan 6. Menentukan persamaan garis pada ruang dimensi tiga

7. Menentukan persamaan garis singgung kurva pada ruang dimensi tiga 8. Menentukan kelengkungan dan komponen percepatan

Materi Ajar

Ingat kembali bahwa fungsi adalah aturan yang mengaitkan setiap t anggota suatu himpunan ( daerah asal ) dengan suatu nilai f(t) yang tunggal pada himpunan yang

kedua. Himpunan dari semua nilai yang diperoleh disebut daerah hasil dari fungsi.

Sejauh ini yang kita bicarakan adalah fungsi bernilai riil dari peubah riil, yakni daerah asal dan daerah hasilnya adalah himpunan bagian dari himpunan bilangan riil. Sebagai contoh 2

) (t t

f = yang mengaitkan setiap bilangan riil t dengan bilangan riil 2

t .

Sekarang kita akan membicarakan suatu fungsi yang daerah asalnya adalah himpunan bagian dari bilangan riil dan daerah hasilnya adalah himpunan vektor

Fungsi bernilai vektor Fdari variabel riil t mengaitkan setiap t anggota suatu himpunan bagian dari himpunan bilangan riil dengan tepat satu vektor F(t).

dengan f ,g dan h fungsi variabel riil bernilai riil. Sebagai cotoh

Biasanya fungsi bernilai vektor dituliskan dengan huruf tebal untuk membedakan fungsi bernilai vektor dengan fungsi bernilai riil.

Kalkulus Fungsi Bernilai Vektor Secara intuitif F =L

→ ( )

lim t

c

t berarti bahwa vektor F(t) mendekati Lketika t

mendekati c . Dengan kata lain vektor F(t)−Lmendekati 0 ketika t → c

Definisi

Mengatakan bahwa F =L → ( )

lim t

c

t berarti bahwa untuk setiap  0( berapapun kecilnya ),

h terdapat suatu  0 sedemikian sehingga F )(t − L  jika 0 t−c  , yakni

   −   −  t c F(t) L 0 Teorema

Misal F(t)= f(t)i+g(t)j+h(t)k, maka Fmemiliki limit di c jika dan hanya jika f ,gdan h

memiliki limit di c , dan

Selanjutnya fungsi Fdikatakan kontinu pada c jika lim (t) (c) c

t→ F =F dan akibat dari

teorema di atas, maka Fkontinu pada c jika dan hanya jika f ,gdan h kontinu di c

dan jika F(t)= f(t)i+g(t)j+h(t)i, maka

Latihan :

Jika F(t)=(t2 +1)i+etj+2k, cari F' t( ), F"(t) dan sudut antara F'(0)dan F"(0)

Berikut adalah aturan pencarian turunan pada fungsi peubah riil bernilai vektor

Teorema

Jika Fdan G adalah fungsi bernilai vektor dapat diturunkan, p fungsi bernilai riil dapat

diturunkan dan c adalah skalar , maka :

Karena turunan dari fungsi bernilai vektor dapat ditentukan dengan menghitung turunan dari komponen-komponennya maka suatu yang masuk akal jika kemudian integralnya juga dapat ditentukan dengan menghitung integral dari komponennya, yakni jika F(t)= f(t)i+g(t)j+h(t)k,

Latihan :

Gerak Sepanjang Kurva Lintasan

Kita akan menggunakan teori tentang fungsi bernilai vektor yang telah kita bicarakan sebelumnya untuk mempelajari gerakan titik pada ruang. Misal t mengukur waktu dan misal koordinat titik P diberikan secara geometri sebagai x = f(t), y = g(t)

dan z =h(t), maka vektor r(t)= f(t)i+g(t)j+h(t)k diasumsikan memancar dari titik asal dan disebut sebagi vektor posisi dari titik P. Seraya t bergerak , ujung r(t)

menelusuri lintasan gerakan dari titik P. Lintasan tersebut berbentuk kurva dan kita

menamakan gerakan titik tersebut sebagai gerak sepanjang kurva lintasan.

Analog dengan gerak lurus , kita mendefinisikan kecepatan v(t) sebagai :

yakni v(t)=r'(t) dan percepatan a(t)=v'(t). Interpretasi geometrinya, vektor

kecepatan menentukan arah garis singgung dan percepatan secara mengarah ke dalam lengkungan kurva seperti yang diilustrasikan berikut ini :

Jika r(t)adalah vektor posisi dari suatu titik, maka panjang lintasan dari t =ake b

Akumulasi dari panjang busur dari t =ake sebarang t diberikan oleh

Berdasarkan Teorema Dasar Kalkulus, kita punyai

Selanjutnya laju dari suatu objek didefinisikan sebagai :

Latihan :

Posisi suatu titik ditentukan secara parametrik oleh persamaan x=cost,y=sint, t z =

.

a. Buat sketsa kurva tersebut

b. Tentukan kecepatan , percepatan dan laju dari gerak sepanjang kurva Garis dan garis singgung di ruang dimensi tiga

Kurva yang paling sederhana adalah garis. Suatu garis ditentukan oleh suatu titik 0

P dan suatu vektor tetap v=ai+bj+ckdisebut vektor arah dari garis. Garis dilihat sebagai himpunan semua titik P demikian sehingga PP₀ sejajar dengan v , yakni

Jika r =OPdan r₀ =OP₀ adalah vektor posisi dari P dan P , sehingga 0 P0P=r −r0 sehingga persamaan garis dapat ditulis sebagai

Jika ditulis r= x,y,z dan r₀ = x₀,y₀,z₀ , dengan menyamakan komponen dari persamaan di atas, kita peroleh

Persamaan tersebut dinamakan persamaan parametrik garis yang melalui titik )

, , ( 0 0 0 0 x y z

P dan sejajar v= a ,,b c . Vektor v= a ,,b c disebut vektor arah dan bilangan

b

a, dan c disebut bilangan arah dari garis. Bilangan arah tidak tunggal, karena jika a,b

dan c bilangan arah maka ka,kb dan kc juga bilangan arah.

Latihan :

Cari persamaan parametrik garis yang melalui titik-titik ( −3, 2,4) dan (5,6,−2)

Jika kita menyelesaikan persamaan parametrik untuk t ( asumsikan a ,,b c tidak

semuanya nol ) dan dengan menyamakan hasil tersebut kita memperoleh persamaan simetrik untuk garis yang melalui titik (x0,y0,z0)dengan bilangan arah a,b dan c

Ini adalah irisan dari dua persamaan bidang

Latihan :

1. Tentukan persamaan simetrik dari garis yang sejajar dengan vektor 4 −, 3,2 dan melalui titik (2,5,−1)

2. Cari persamaan simetrik dari perpotongan dua bidang 2x−y−5z=−14 dan bidang 28

4 5

4x+ y+ z=

3. Cari persamaan parametrik dari garis yang melalui titik ( −1, 2,3) dan tegak lurus pada

sumbu- x dan garis

5 1 3 2 4 y z x = − − = − Misal

adalah vektor posisi yang menentukan kurva di ruang dimensi tiga. Garis singgung dari kurva memiliki vektor arah

Latihan :

1. Cari persamaan parametrik dan persamaan simetrik dari garis singgung kurva

pada titik       3 8 , 2 , 2 P

2. Cari persamaan bidang yang tegak lurus terhadap kurva

Kelengkungan

Kelengkungan secara natural bisa kita lihat sebagai ukuran seberapa tajam kurva melengkung. Garis lurus tentu saja kelengkungannya sama dengan nol dan semakin tajam kurva melengkung maka semakin besar kelengkungannya.

Misal r(t)= f(t)i+g(t)j+h(t)k _{menyatakan posisi suatu objek pada saat t.} Asumsikan r' t( )kontinu dan tidak pernah sama dengan vektor nol. Hal ini menjamin

bahwa s(t) bertambah jika t bertambah. Ukuran kelengkungan akan menunjukkan

seberapa cepat vektor singgung berubah. Tapi nantinya kita akan bekerja dengan vektor singgung satuan.

Tinjau laju perubahan vektor singgung satuan seperti yang dilustrasikan sebagai berikut.

Ketika objek bergerak dari titik A ke titik B , perubahan sangat sedikit atau panjang

) ( ) (t t Tt

T + − kecil , sedangkan ketika objek bergerak dari C ke D perubahan lebih banyak atau panjang T(t+t)−T(t)lebih besar. Kelengkungan didefinisikan sebagai

besarnya laju perubahan vektor satuan terhadap panjang lintasan s , yakni

Selanjutnya kita bisa menuliskan ,

Latihan :

Cari kelengkungan helix acosti+ sinb tj+ctk pada sebarang titik Komponen percepatan

Misal r(t) vektor posisi dan T(t) adalah vektor singgung satuan dari gerak

sepanjang suatu kurva. Mengingat T(t) vektor satuan, maka kita punyai

untuk semua t . Selanjutnya turunkan kedua ruas terhadap t , diperoleh

Dari kesamaan di atas kita bisa simpulkan bahwa

Ini mengatakan pada kita bahwa T(t) dan T' t( )saling tegak lurus untuk semua t . Secara

umum vektor T' t( )bukan vektor satuan , selanjutnya kita definisikan vektor normal

satuan

Selanjutnya kita akan menyatakan percepatan dalam vektor singgung satuan dan vektor dan vektor normal satuan. Secara lebih spesifik kita akan mencari komponen tangensial aT dan

komponen a sedemikian sehingga N

Karena a = v', T' = T'N dan dt ds  = ' T

Sehingga komponen tangensial dan komponen normal dapat ditentukan dengan

Selanjutnya kita akan menyatakan komponen tangensial dan komponen normal menggunakan vektor posisi r . Perhatikan yang berikut ini ,

Dengan demikian kelengkungan juga bisa dinyatakan menggunakan vektor posisi, Latihan : Pada titik       3 1 , 1 ,