Pelabelan Selimut H-Ajaib Super Pada Kelas Graf Ilalang dan Hasil Koronasi Dua Graf JURNAL

commit to user

H

−

SUPERMAGIC COVERINGS ON SHRUBS GRAPH AND ON

THE CORONA OF TWO GRAPHS

Risala Ulfatimah, Mania Roswitha, Tri Atmojo Kusmayadi

Department of Mathematics

Faculty of Mathematics and Natural Sciences Sebelas Maret University

Abstract. _{A finite simple graph G admits an H-covering if every edge of E(G)}

be-longs to a subgraph of G isomorphic to H. We said the graph G = (V, E) that

ad-mits H-covering to be H-magic if there exists bijection function f : V(G)∪E(G) →

1,2, . . . ,|V(G) +E(G)|, such that for each subgraphH′ _of

Gisomorphic to H, f(H′_{) =}

∑

v∈V′f(v) +

∑

e∈E′f(e) = m(f) is constant. Furthermore, iff(V) = 1,2, . . . ,|V(G)|

thenGis calledH-supermagic. In this research we definedS₂,₂-supermagic covering on

shrub graph ˇS(m₁, m₂, . . . , mn), moth-supermagic covering onWn⊙Km for evenn≥4

and for primen≥5, and fish-supermagic covering onLm⊙Pn form, n≥2.

Keywords: S2,2-supermagic covering, moth-supermagic covering, fish-supermagic covering, shrub graphS(mˇ 1, m2, . . . , mn),Wn⊙Km graph,Lm⊙Pn graph

1.

Introduction

Gallian [2] defined a graph labeling as an assignment of integers to the vertices

or edges, or both, subject to certain condition. Graph labeling was first introduced

in the late 1960s. Magic labeling is a type of graph labeling that the most often to

be studied.

In 2005 Guti´errez and Llad´o [5] generalized the concept of an edge-magic

total labeling into an

H

-magic covering as follows. Let

G

= (

V, E

) be a finite

simple graph that admits

H

-covering. A bijection function

f

:

V

(

G

)

∪

E

(

G

)

→

1

,

2

, . . . ,

|

V

(

G

) +

E

(

G

)

|

is called

H

-magic labeling of

G

, for every subgraph

H

′

=

(

V

′

, E

′

) of

G

isomorphic to

H, f

(

H

′

) =

∑

v∈V′

f

(

v

)+

∑

e∈E′

f

(

e

) =

m

(

f

) is constant.

Graph

G

is called

H

-supermagic if

f

(

V

(

G

)) = 1

,

2

, . . . ,

|

V

(

G

)

|

. In [5], it is proved

that a complete bipartite graph

K

n,n

is

K

1,n

-magic for

n

≥

1.

Selvagopal and Jeyanthi in Gallian [2] proved that for a positive integer

n

,

the

k

-polygonal snake of length

n

is

C

4

-supermagic; for

m

≥

2

, n

= 3

,

or

n >

4,

C

n

×

P

m

is

C

4

-supermagic;

P

2

×

P

n

and

P

3

×

P

n

are

C

4

-supermagic for all

n

≥

2.

Roswitha et al. [9] proved

H

-magic covering on some classes of graphs. In this

research we investigate that a shrub graph ˇ

S

(

m

1

, m

2

, . . . , m

n

) admits a double star

S

2,2

-supermagic labeling,

W

n

⊙

K

m

admits a moth-supermagic labeling, and

L

m

⊙

P

n

admits a fish-supermagic labeling.

2.

Main Results

commit to user

Let

k

∈

N

and

Y

be a multiset that contains positive integers.

Y

is said to

be

k

−

balanced if there exists

k

subsets of

Y

, say

Y

1

, Y

2

, . . . , Y

k

, such that for every

i

∈

[

i, k

]

,

|

Y

i

|

=

|Y_k|

, σY

i

=

σY_k

∈

N

, and

⊎

k_i=1

Y

i

=

Y

, then

Y

i

is called a balanced

subset of

Y

.

Lemma 2.1.

(Roswitha and Baskoro [8])

Let

x

and

y

be non-negative integers. Let

X

= [

x

+ 1

, x

(

y

+ 1)]

with

|

X

|

=

xy

and

Y

= [

x

(

y

+ 2)

,

2

x

(

y

+ 1)

−

1]

where

|

Y

|

=

xy

.

Then, the multiset

K

=

X

⊎

Y

is

xy

-balanced with all its subsets are

2

-sets.

Proof.

For every

j

∈

[1

, xy

], define

K

j

=

{

a

j

, b

j

}

, where

aj= x+j,

bj= 2x(y+ 1)−j.

Then,

∑

K

j

= (2

y

+ 3) for each

j

∈

[1

, xy

], and so

K

is

xy

-balanced with all its

subsets are 2-sets.

2.2.

(

k, δ

)-anti balanced multiset.

Inayah [3] defined (

k, δ

)-anti balanced

mul-tiset as follows. Let

k, δ

∈

N

and

X

be a set containing the elements of positive

integers. A multiset

X

is said to be (

k, δ

)-anti balanced if there exists

k

subsets from

X

, say

X

1

, X

2

, . . . , X

k

such that for every

i

∈

[1

, k

],

|

X

i

|

=

|X_k|

,

⊎

k

i=1

X

i

=

X

, and

for

i

∈

[1

, k

−

1],

∑

X

i+1

−

∑

X

i

=

δ

. Here, we give several lemmas on (

k, δ

)-anti

balanced multiset.

Lemma 2.2.

Let

x, y, z

and

k

be non-negative integers,

k

≥

2. Let

R

= [

x, x

+

⌊

k

2

⌋

]

⊎

[

x

+ 1

, x

+

⌊

k

2

⌋

]

⊎

[

y, y

+

⌊

k−1

2

⌋

]

⊎

[

y, y

+

⌊

k−1

2

⌋ −

1]

⊎

[

z, z

+

k

−

1], then

R

is

(

k,

2)-anti balanced.

Proof.

For every

j

∈

[1

, k

] we define the multisets

R

j

=

{

x

+

⌊

j₂

⌋

, y

+

⌊

j−₂1

⌋

, z

+(

j

−

1)

}

.

It is obvious that for each

j

∈

[1

, k

]

,

|

R

j

|

= 3

, R

j

⊂

R

, and

⊎

k_j=1

R

j

=

R

. Since

∑

R

j

=

x

+

y

+

z

+

⌊

2j₂−1

⌋

+

j

−

1 for every

j

∈

[1

, k

], then

∑

R

j+1

−

∑

R

j

= 2,

R

is (

k,

2)-anti balanced.

Lemma 2.3.

Let

x

and

k

be non-negative integers,

k

≥

2. Let

Y

= [

x, x

+

k

]

⊎

[

x

+

1

, x

+

k

−

1], then

Y

is (

k,

2)-anti balanced.

Proof.

For every

j

∈

[1

, k

] we define the mutisets

Y

j

=

{

x

+

j

−

1

, x

+

j

}

. Now we have

for every

j

∈

[1

, k

]

,

|

Y

j

|

= 2

, Y

j

⊂

Y

and

⊎

k

j=1

Y

j

=

Y

. Since

∑

Y

j

= 2(

x

+

k

−

j

) + 1

for every

j

∈

[1

, k

], then

∑

Y

j+1

−

∑

Y

j

= 2,

Y

is (

k,

2)-anti balanced.

Here we provide two examples of those lemmas as follows.

(1) Let

R

= [2

,

4]

⊎

[3

,

4]

⊎

[3

,

5]

⊎

[3

,

4]

⊎

[4

,

8]

, x

= 2

, y

= 3

, z

= 4

,

and

k

= 5. By

applying Lemma 2.2, we have 5-subsets of

R

as follows.

R

1

=

{

2

,

3

,

4

}

, R

2

=

commit to user

that Σ

R

1

= 9

,

Σ

R

2

= 11

,

Σ

R

3

= 13

,

Σ

R

4

= 15

,

and Σ

R

5

= 17 for every

i

∈

[1

,

5]. Therefore

R

is (5

,

2)-anti balanced.

(2) Let

Y

= [3

,

6]

⊎

[4

,

5]

, x

= 3 and

k

= 3. According to Lemma 2.3, we have

3-subsets of

Y

as follows.

Y

1

=

{

3

,

4

}

, Y

2

=

{

4

,

5

}

,

and

Y

3

=

{

5

,

6

}

. Hence

Σ

Y

1

= 7

,

Σ

Y

2

= 9

,

and Σ

Y

3

= 11 for every

i

∈

[1

,

3]. Therefore

Y

is (3

,

2)-anti

balanced.

2.3.

S

2,2

-supermagic Labeling on Shrubs Graphs.

Maryati [6] defined a shrub

graph ˇ

S

(

m

1

, m

2

, . . . , m

n

) as a graph that obtained from a star graph

K

1,n

for

n

≥

2

with central vertex

c

, and adding some vertices and edges so that for every

i

∈

[1

, n

]

, v

i

is related with the new

m

i

≥

1 vertices. The double star

S

(

n, m

) is the

graph consisting of the union of two stars

K

1,n

and

K

1,m

together with a line joining

their centers (Grossman [4]).

Theorem 2.1.

Any shrub graph

S

ˇ

(

m

1

, m

2

, . . . , m

n

)

is

S

2,2

-supermagic for any

in-teger

n

and

m

i

≥

2

, i

∈

[1

, n

]

.

Proof.

Let

G

be a shrub graph ˇ

S

(

m

1

, m

2

, . . . , m

n

) for any integer

n

and

m

1

, m

2

, . . . ,

m

n

≥

2. Then

|

V

(

G

)

|

=

m

1

+

m

2

+

. . .

+

m

n

+

n

+1 and

|

E

(

G

)

|

=

m

1

+

m

2

+

. . .

+

m

n

+

n

.

Let

A

= [1

,

2(

n

+

m

1

+

m

2

+

. . .

+

m

n

) + 1]. Partition

A

into 3 sets,

A

=

K

∪

X

,

with

X

=

L

⊎

M

where

K

=

{

1

}

, L

= [2

, n

+ 1 +

m

1

+

. . .

+

m

n

]

, M

= [

n

+ 2 +

m

1

+

. . .

+

m

n

,

2

n

+ 1 + 2(

m

1

+

. . .

+

m

n

)]. Let

f

be a total labeling of

G

and

s

(

f

)

be the supermagic sum in every subgraph

H

of

G

that is isomorphic to double star

S

2,2

. Now we define a total labeling

f

on

G

as follows. Label the center vertex

with 1. Apply Lemma 2.1 to partition

X

into

{

X

i

, x

≤

i

≤

y

}

with

x

= 1 and

y

=

n

+

m

1

+

m

2

+

. . .

+

m

n

. We obtain that

X

is

n

+

m

1

+

m

2

+

. . .

+

m

n

-balanced

with all its subsets are 2-sets and

∑

X

i

= 2(

n

+

m

1

+

m

2

+

. . .

+

m

n

) + 3. Use the

smaller labels in every

X

i

for the vertices. Thus, the sum of labels of each double

star

S

2,2

is

s

(

f

) = 10(

n

+

m

1

+

m

2

+

. . .

+

m

n

) + 16. Hence, the shrubs graph is

S

2,2

-supermagic.

2.4.

Moth-Supermagic Labeling on

W

n

⊙

K

m

.

W

n

⊙

K

m

graph is obtained by

taking one copy of

W

n

and

n

+ 1 copies of

K

m

and then joining by a line the

i

’th

vertex of

W

n

to every vertex in the

i

’th copy of

K

m

. The definition of a moth graph

is

K

1

+

{

P

3

∪

2

K

1

}

(Menon [7]).

Theorem 2.2.

For even

n

≥

4

and for prime

n

≥

5

,

W

n

⊙

K

m

graph is a

moth-supermagic.

Proof.

Let

G

be

W

n

⊙

K

m

. Let

V

(

C

n

) =

{

v

1

, v

2

, v

3

, . . . , v

n

}

, V

(

K

m

) =

{

u

1

, u

2

, u

3

, . . . ,

u

m(n+1)

}

,

and

v

0

be the central vertex of

G

. We obtain that

V

(

G

) =

V

(

C

n

)

∪

V

(

K

m

)

∪

commit to user

v

0

v

m+1

, . . . , v

0

v

2m

, . . . , v

n

u

nm+1

, . . . , v

(n+1)m

}

. Let

L

i

=

{

v

i

, v

i

v

0

}

for

i

∈

[1

, n

]

, M

j

=

{

u

j

, u

j

v

0

}

for

j

∈

[1

, m

] and

N

ik

=

{

u

k

, u

k

v

i

}

for

k

∈

[

m

+ 1

,

(

n

+ 1)

m

] and

i

∈

[1

, n

].

Let

f

be a total labeling of

G

and

s

(

f

) be the supermagic sum in every subgraph

H

of

G

that is isomorphic to moth graph. The supermagic sum is obtained by the

formula

s

(

f

) =

f

(

L

i

) +

f

(

L

i+1

) +

f

(

L

i+2

)

f

(

v

i

v

i+1

) +

f

(

v

i+1

v

i+2

) + 2

f

(

N

ik

/M

j

) +

f

(

v

0

) (2.1)

Furthermore, we divide the proof into two cases according to the values of

n

.

Case 1

.

n

is even (

n

≥

4).

The total labeling

f

of

G

is defined as follows.

(1) Label each vertex of

G

other than central vertex by

f

(

v

i

) =

{

i+1

2

+ 1

,

for

i

odd;

i

∈

[1

, n

]

2n+4−i

2

,

for

i

even;

i

∈

[1

, n

].

(2) Label each edge of

G

as follows

f

(

v

0

v

i

) =











5(

n

+ 1) +

n

2

,

for

i

= 2

5(

n

+ 1) +

i−2

2

,

for

i

even;

i

∈

[4

, n

]

6(

n

+ 1)

−

i+1

2

,

for

i

odd;

i

∈

[1

, n

]

and

f

(

v

i

v

i+1

) =











6(

n

+ 1) +

n

2

,

for

i

= 2

7(

n

+ 1)

−

i

2

,

for

i

even;

i

∈

[4

, n

]

6(

n

+ 1) +

i−1

2

,

for

i

odd;

i

∈

[1

, n

].

Thus,

f

(

v

0

) = 1

, f

(

L

n

) = 6(

n

+ 1)

, f

(

L

1

) = 6(

n

+ 1) + 1

, f

(

L

2

) = 6(

n

+

1) +

n

2

, f

(

v

n

v

1

) = 7(

n

+ 1)

−

n₂

,

and

f

(

v

1

v

2

) = 6(

n

+ 1). From Lemma 2.1 with

X

= [

x

+ 2

,

3(

x

+ 1)] and

Y

= [3

y

+ 1

,

5

y

]

, x

=

n, y

=

n

+ 1 we obtain that

f

(

N

ik

) = 6(

n

+ 1) + 1. Let

s

(

f

) be a constant sum in every subgraph moth graph

of

G

. By Equation (2.1) we have

s

(

f

) = 43(

n

+ 1) + 4

Hence,

W

n

⊙

K

m

for

n

even is a moth-supermagic.

Case 2

.

n

is prime (

n

≥

5).

The total labeling

f

of

G

is defined as follows.

(1) Label each vertex of

G

other than central vertex by

f(vi) =

{

2, untuki= 1

2 +⌊i

commit to user

Forn mod 3 = 2

f(vi) =

{

n+i+5

3 , fori∈ {2,5,8, . . . , n}

⌊2n+i

3 ⌋+ 2, fori∈ {3,6,9, . . . , n−2}.

Forn mod 3 = 1

f(vi) =

{

2n+i+5

3 , fori∈ {2,5,8, . . . , n−2}

n+i+5

3 , fori∈ {3,6,9, . . . , n−1}.

(2) Label each edge of

G

as follows

f(v0vi) =



  

  

5(n+ 1) + 1, fori=n−2

f(v0v₍2i+n+3 2 )modn

+ 1, fori̸=n−2, i̸= n−3

2 ;i∈[1, n]

f(v0v₍2i+n+3

2 )

+ 1, fori= n−3 2 .

f(vivi+1) = 6(n+ 1) + i−

n₋3 2

2 , fori∈ {n−23,n−23 + 2,n−23 + 2 + 2, . . . , n−1}

For (

n−3

2

) is even.

f(vivi+1) = {

6(n+ 1) +⌈n+2i+2

4 ⌉, foriodd; i∈[1, n]

6(n+ 1) +⌈3n₄+2⌉+₂i, forieven,n >7;i∈[2,n−₂7].

For (

n−3

2

) is odd.

f(vivi+1) = {

6(n+ 1) +⌈3n+2₄ i⌉, foriodd, n >5; i∈[1,n−₂3],

6(n+ 1) +⌈n+2i

4 ⌉, forieven; i∈[2, n].

For

f

(

v

0

) = 1. By Lemma 2.1 with

X

= [

x

+2

,

3(

x

+1)] and

Y

= [3

y

+1

,

5

y

]

, x

=

n, y

=

n

+ 1 we obtain that

f

(

N

ik

) = 6(

n

+ 1) + 1. Let

s

(

f

) be a constant sum in

every subgraph moth graph of

G

. By Equation (2.1) we have

s

(

f

) = 42(

n

+ 1) + (

n

−

3) + 8

Hence,

W

n

⊙

K

m

when

n

prime is a moth-supermagic. This completes the proof

of the theorem.

2.5.

Fish-Supermagic Labeling on

L

m

⊙

P

n

.

L

m

⊙

P

n

graph is obtained by taking

one copy of

L

m

and 2(

m

+ 1) copies of

P

n

and then joining by a line the

i

’th vertex

of

L

m

to every vertex in the

i

’th copy of

P

n

.

Theorem 2.3.

Any

L

m

⊙

P

n

graph for

m, n

≥

2

is fish-supermagic.

Proof.

Let

G

be the

L

m

⊙

P

n

graph for any integer

m, n

≥

2

.

Then

|

V

(

G

)

|

= 2(

m

+

1)(

n

+1) and

|

E

(

G

)

|

= 2(

m

+1)(2

n

−

1)+3

m

+1. Let

A

= [1

,

2(

m

+1)(3

n

−

1)+5

m

+3]

.

commit to user

Let

A

= [1

,

2(

m

+ 1)(3

n

−

1) + 5

m

+ 3]

.

Partition

A

into 4 sets,

A

=

V

⊎

W

⊎

X

⊎

Y

,

where

V

= [1

,

2

n

(

m

+ 1)]

, W

= [(

m

+ 1)(2

n

+ 3)

,

(

m

+ 1)(4

n

+ 3)

−

1]

, X

= [(

m

+

1)(4

n

+ 3)

,

(

m

+ 1)(4

n

+ 3) +

n

−

2]

⊎

[(

m

+ 1)(4

n

+ 3) +

n,

(

m

+ 1)(4

n

+ 3) + (2

n

−

2)]

⊎

. . .

⊎

[(

m

+ 1)(4

n

+ 3) + (2

m

+ 1)

n,

(

m

+ 1)(4

n

+ 3) + 2

n

(

m

+ 1)

−

2]

,

and

Y

= [2

n

(

m

+ 1) + 1

,

2(

n

+ 1)(

m

+ 1) +

m

]

⊎

{

(

m

+ 1)(4

n

+ 3) + (

n

−

1)

,

(

m

+ 1)(4

n

+

3) + (

n

−

1) +

n,

(

m

+ 1)(4

n

+ 3) + (

n

−

1) + 2

n, . . . ,

(

m

+ 1)(4

n

+ 3) + (

n

−

1) + 2

mn

}

.

Let

f

be a total labeling of

G

and

s

(

f

) be the supermagic sum in every subgraph

H

of

G

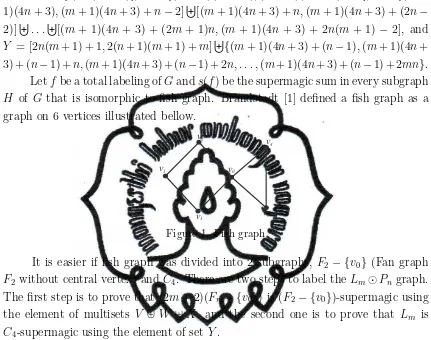
that is isomorphic to fish graph. Brandstadt [1] defined a fish graph as a

graph on 6 vertices illustrated bellow.

v5

v₃

v₄

v0

v₂

v₁

Figure 1. Fish graph

It is easier if fish graph was divided into 2 subgraphs,

F

2

− {

v

0

}

(Fan graph

F

2

without central vertex) and

C

4

. There are two steps to label the

L

m

⊙

P

n

graph.

The first step is to prove that (2

m

+ 2)(

F

n

− {

v

0

}

) is (

F

2

− {

v

0

}

)-supermagic using

the element of multisets

V

⊎

W

⊎

X

, and the second one is to prove that

L

m

is

C

4

-supermagic using the element of set

Y

.

Step 1.

The first step is to prove that (2

m

+ 2)(

F

n

− {

v

0

}

) is (

F

2

− {

v

0

}

)-supermagic

using the element of multisets

V

⊎

W

⊎

X

. Furthermore we divide into two cases.

Case 1.

n

= 2.

For

n

= 2, the number of (

F

2

− {

v

0

}

) subgraphs on graph

G

is 2

m

+ 2 as shown

in Figure 2.

u₁ f₁ v₁

e_{1 g} 1

u₂ f2 v₂

e_{2 g} 2

u_i f_i v_i

[image:6.595.94.525.164.504.2]

e_{i g} i

Figure 2. F2− {v0} subgraph on Lm⊙P2

Now, we prove that (2

m

+ 2)(

F

2

− {

v

0

}

) on

L

m

⊙

P

2

is (

F

2

− {

v

0

}

)-supermagic

using the element of multisets

V

⊎

W

⊎

X

. Let

H

be (2

m

+ 2)(

F

2

− {

v

0

}

). We have

V

(

H

) =

{

u

i

, v

i

: 1

≤

i

≤

2(

m

+ 1)

}

and

E

(

H

) =

{

e

i

∪

f

i

∪

g

i

: 1

≤

i

≤

2(

m

+ 1)

}

.

Let

f

be the total labeling of

H

and

s

(

f

) be the supermagic sum in every

F

2

− {

v

0

}

subgraph on (2

m

+ 2)(

F

2

− {

v

0

}

). The total labeling of

H

for every 1

≤

i

≤

2(

m

+ 1)

commit to user

f(x) = 

      

      

i, ifx=vi,

2(m+ 1) +i, ifx=ui,

(m+ 1)(4n+ 3) + 1−2i, ifx=ei,

(m+ 1)(4n+ 3) + 2(i−1), ifx=fi,

(m+ 1)(4n+ 3)−2i, ifx=gi.

For every 1

≤

i

≤

2(

m

+ 1), let (

F

2

− {

v

0

}

)

i

be the subgraph of

L

m

⊙

P

2

with

V

((

F

2

− {

v

0

}

)

i

) =

{

u

i

, v

i

}

and

E

((

F

2

− {

v

0

}

)

i

) =

{

e

i

, f

i

, g

i

}

. It can be checked that

for every 1

≤

i

≤

2(

m

+ 1)

,

∑

f

((

F

2

− {

v

0

}

)

i

) = 3(

m

+ 1)(4

n

+ 3) + 2(

m

+ 1)

−

1.

Hence (2

m

+ 2)(

F

2

− {

v

0

}

) is (

F

2

− {

v

0

}

)-supermagic.

Case 2.

n >

2.

Now we prove that (2

m

+2)(

F

n

−{

v

0

}

) is (

F

2

−{

v

0

}

)-supermagic using the element

of multisets

V

⊎

W

⊎

X

. Let

f

be the total labeling of (2

m

+ 2)(

F

n

− {

v

0

}

) and

s

(

f

)

be the supermagic sum in every

F

2

− {

v

0

}

of (2

m

+ 2)(

F

n

− {

v

0

}

). The total labeling

of (

F

n

− {

v

0

}

)

i

for every 1

≤

i

≤

2(

m

+ 1) will be executed within two steps. Firstly,

we label the subgraph of (

F

n

− {

v

0

}

)

i

called

P

ni

, then we label the edges besides on

P

i

n

that are incident with the vertices of

P

ni

.

Lemma 2.2 is applied for every

i

of

P

i

n

where 1

≤

i

≤

2(

m

+ 1) with

x

i

=

1 + (

i

−

1)

⌈

n

2

⌉

, y

i

= 2(

m

+ 1)

⌈

n

2

⌉

+ (

i

−

1)

⌊

n

2

⌋

+ 1

, z

i

= (

m

+ 1)(4

n

+ 3) +

n

(

i

−

1)

,

and

k

=

n

−

1 using the element of

V

⊎

X

. We have

V

⊎

X

in every

P

i

is (

k,

2)-anti

balanced. Next, by applying Lemma 2.3 we label the edges besides on

P

i

n

that are

incident with the vertices of

P

i

n

using the element of

W

with

x

= (

m

+1)(4

n

+3)

−

ni

and

k

=

n

, starting from the edge that incident with a vertex

v

n

until the edge

that incident with a vertex

v

1

in every

P

ni

. Now we have that

W

for every

i

∈

[1

,

2(

m

+1)] is (

k,

2)-anti balanced. This implies that multiset

V

⊎

W

⊎

X

is 2

k

(

m

+1)-balanced. Hence (2

m

+ 2)(

F

n

− {

v

0

}

) of

L

m

⊙

P

n

is (

F

2

− {

v

0

}

)-supermagic with

∑

f

((

F

2

− {

v

0

}

)

i

) = (

m

+ 1)(12

n

+ 2

⌈

n₂

⌉

+ 2) + 7

m

+ 6. We conclude that for

n

≥

2

,

(2

m

+ 2)(

F

n

− {

v

0

}

) is (

F

2

− {

v

0

}

)-supermagic.

Step 2.

The next step is to prove that

L

m

is

C

4

-supermagic using the element of

set

Y

. Let

L

m

∼

=

P

m

×

P

2

be a graph with

V

(

L

m

) =

{

u

i

, v

i

: 1

≤

i

≤

m

+ 1

}

and

E

(

L

m

) =

{

u

i

v

i

: 1

≤

i

≤

m

+ 1

} ∪ {

u

i

u

i+1

, v

i

v

i+1

: 1

≤

i

≤

m

}

. Let

f

be a total

labeling of

V

(

L

m

)

∪

E

(

L

m

) using the element of set

Y

. The total labeling of

L

m

is

defined as follows.

Label each vertex of

L

m

as follows.

f(ui) = (m+ 1)(2n+ 1)−(i−1), fori∈[1, m+ 1].

f(vi) =

{

(m+ 1)(2n+ 1) + i+1₂ , foriodd, i∈[1, m+ 1],

(m+ 1)(2n+ 1) +⌈m+1

commit to user

Next, label each edge of

L

m

for every

i

∈

[1

, m

] as follows.

f(uiui+1) = (m+ 1)(4n+ 3)−1 +ni

f(vivi+1) = (m+ 1)(2n+ 2) +i

For every

i

∈

[1

, m

+ 1], label each edge of

L

m

as follows.

For

m

odd.

f(uivi) =

{

(m+ 1)(4n+ 3) +n(m+ 1) +mn−1−n(i−1

2 ), foriodd, (m+ 1)(4n+ 3) +n(m₂+1) +mn−1−n(i−₂2), forieven.

For

m

even.

f(uivi) =

{

(m+ 1)(4n+ 3) +n(m+2

2 ) +mn−1−n(i−21), fori odd, (m+ 1)(4n+ 3) +n(m+ 1) +mn−1−n(i−2

2 ), fori even

For every 1

≤

i

≤

m

,

C

i

4

be the subgraph of

L

m

⊙

P

n

with

V

(

C

4i

) =

{

u

i

, u

i+1

, v

i

, v

i+1

}

and

E

(

C

4i

) =

{

u

i

u

i+1

, v

i

v

i+1

, u

i

v

i

, u

i+1

v

i+1

}

. It can be checked that

for every 1

≤

i

≤

m,

∑

f

(

C

i

4

) = (

m

+1)(22

n

+14)+

n

(2+

⌈

m2+1

⌉

)+

⌈

m+1

2

⌉

+

m

(3

n

+1).

Hence

L

m

is

C

4

-supermagic.

It has been proved that (2

m

+ 2)(

F

n

− {

v

0

}

) is (

F

2

− {

v

0

}

)-supermagic and

L

m

is

C

4

-supermagic. Hence,

L

m

⊙

P

n

is fish-supermagic with its supermagic sum is

s

(

f

) = (

m

+1)[(12

n

+2+2

⌈

n

2

⌉

)+(22

n

+14)]+

n

(2+

⌈

m+1 2

⌉

)+

⌈

m+1

2

⌉

+

m

(3

n

+8)+6.

References

[1] Brandstadt, A. and J.P. Spinrad,Graph Classes: A Survey, Philadelphia, PA: SIAM, 1987.

[2] Gallian, J. A.,A Dynamic Survey of Graph Labeling, The Electronic Journal of Combinatorics.

17_{(2014), 1-384 #DS6.}

[3] Inayah, N., Pelabelan (a, d)−H−Anti Ajaib pada Beberapa Kelas Graf, Disertasi, Institut

Teknologi Bandung, Bandung, 2013.

[4] Grossman, J.W., F. Harary, and M.Klawe,Generalized Ramsey Theory for Graphs, x: Double

Stars, Discrete Mathematics28_{(1979), 247-254.}

[5] Guti´errez, A. and A. Llad´o ,Magic Coverings, J. Combin. Math. Combin. Comput55_(2005),

43-56.

[6] Maryati, T.K.,Karakteristik Graf H-Ajaib dan Graf H-Ajaib Super, Disertasi, Institut

Teknologi Bandung, Bandung, 2011.

[7] Menon, M.K.,Studies on Some Graph Operators and Related Topics, Thesis, Department of

Mathematics, Cochin University of Science and Technology, Cochin, 2009.

[8] Roswitha, M. and E. T. Baskoro,H-Magic Covering on Some Classes of Graphs, American

Institute of Physics Conference Proceedings on ICREM5 ,1450_{(2012), 135-138.}

[9] Roswitha, M., E.T.Baskoro, T.K.Maryati, N.A.Kurdhi, and I.Susanti, Further Results on