Peramalan dengan model arch.

ABSTRAK

ABSTRACT

PERAMALAN DENGAN MODEL ARCH

SKRIPSI

Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Sains (S.Si)

Program Studi Matematika

Oleh:

SUHARTINI

NIM : 003114038

PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

UNIVERSITAS SANATA DHARMA YOGYAKARTA

MOTTO

™

Serahkanlah perbuatanmu kepada Tuhan, maka terlaksanalah segala

rencanamu. (Amsal 16:3).

™

Do not dwell in the past, do not dream of the future, concentrate the mind on the

present moment. ( Budha )

™

Our greatest glory is not in never falling, but in rising every time we fall. (Budha).

Dengan penuh kasih karya ini kupersembahkan untuk :

Bapak dan Ibukku,

Mas Arno, mas Ardi, mbak yanti, wandi,

“bee”, all family,

ABSTRAK

ABSTRACT

KATA PENGANTAR

Puji dan syukur kepada Hati kudus Tuhan Yesus dan bunda Maria, karena berkat karunia dan rahmatnya yang telah mereka berikan penulis dapat menyele-saikan skripsi ini.

Banyak hambatan dan kesulitan yang ditemui penulis dalam menyusun dan menulis skripsi ini. Namun, berkat bantuan dan dorongan dari berbagai pihak, baik langsung maupun tidak langsung, akhirnya skripsi ini dapat terselesaikan. Oleh karena itu penulis ingin mengucapkan terima kasih kepada :

1. Ibu Ch. Enny Murwaningtyas, S.Si, M.Si , selaku dosen pembimbing yang telah meluangkan waktu, pikiran, memimjamkan buku, serta kesabaran membimbing penulis dalam menyusun skripsi ini.

2. Bapak YG. Hartono, S.Si, M.Sc, selaku ketua program studi mate-matika FMIPA USD Yogyakarta.

3. Ibu Mv. Any Herawati, S.Si, M.Si, selaku dosen pembimbing akademik.

4. Bapak Ir. Ig. Aris Dwiatmoko, M.Sc dan Ibu Lusia Krismiyati Budi-asih, S.Si, M.Si, selaku dosen penguji yang telah memberikan masu-kan-masukan dan koreksi.

5. Bapak dan ibu dosen FMIPA yang telah memberikan ilmu yang ber-guna kepada penulis selama dibangku kuliah.

7. Mas Tukijo yang telah memberikan pelayanan administrasi dalam urusan-urusan perkuliahan kepada penulis.

8. Kedua orangtuaku yang tak henti-hentinya memberikan dukungan baik moral, spiritual, maupun materi sehingga penulis dapat menye-lesaikan skripsi ini.

9. Kakak-kakakku, mas Ardi, mas Arno dan adiku yang selalu mem-berikan dukungan, doa, bantuan materi serta kesabarnya selama ini. 10.Keluarga mbak Yanti dan keponakan-keponakanku Angela, Jepin

yang selalu memberi semangat, doa, bantuan materi.

11.Teman-temanku Sumi, Vin, Dora, Dewi, Deni, Veri (’01), Anjrah, Heri (Ndoet), yang selalu setia menemani, memberikan semangat dan mendengarkan curhatku.

Penulis menyadari bahwa skripsi ini masih jauh dari sempurna, oleh karena itu penulis membuka diri untuk menerima kritik serta saran yang bermanfaat bagi kesempurnaan skripsi ini. Penulis berharap semoga skripsi ini memberikan man-faat dan berguna bagi semua pihak.

Yogyakarta, 22 Februari 2007

DAFTAR ISI

Halaman

HALAMAN JUDUL... i

HALAMAN PERSETUJUAN PEMBIMBING ... ii

HALAMAN PENGESAHAN... iii

HALAMAN PERSEMBAHAN ... iv

PERNYATAAN KEASLIAN KARYA ... v

ABSTRAK ... vi

ABSTRACT... vii

KATA PENGANTAR ... viii

DAFTAR ISI... x

BAB I PENDAHULUAN... 1

A. Latar Belakang Masalah... 1

B. Rumusan Masalah ... 2

C. Tujuan Penulisan... 2

D. Pembatasan Masalah ... 2

E. Manfaat Penulisan... 3

F. Metode Penulisan ... 3

G. Sistematika Penulisan ... 3

BAB II LANDASAN TEORI... 5

A. Konsep Dasar Runtun Waktu... 11

B. Fungsi Autokovariansi dan Fungsi Autokorelasi... 15

D. Autoregresi (AR)... 19

BAB III MODEL ARCH... 32

A. ARCH... 32

B. Pengujian Adanya Efek ARCH Dalam Data Runtun Waktu 41 C. Fungsi Kelihood ARCH... 47

BAB IV PENERAPAN MODEL ARCH PADA DATA HARGA SAHAM COMPOSITE INDEX... 53

A. Identifikasi Model ARCH ... 53

B. Uji Efek ARCH ... 57

C. Pembentukan Model Akhir ... 58

BAB V PENUTUP... 60

A. Simpulan ... 60

B. Saran... 60

DAFTAR PUSTAKA ... 61

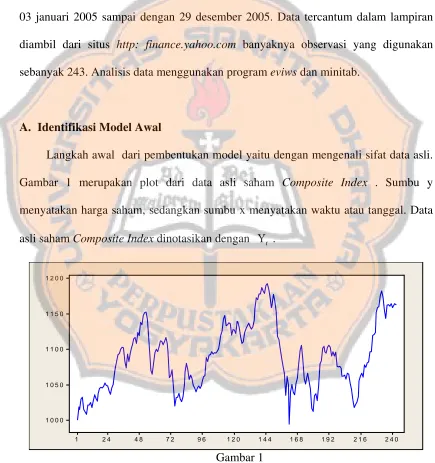
LAMPIRAN... LAMPIRAN 1 Data Harga Saham Composite Index dari tanggal 03 Januari 2005 sampai 29 Desem-ber 2005... 62

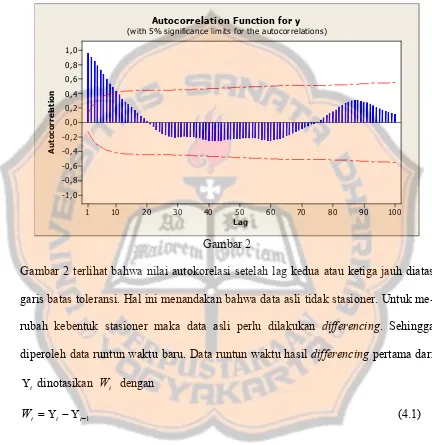
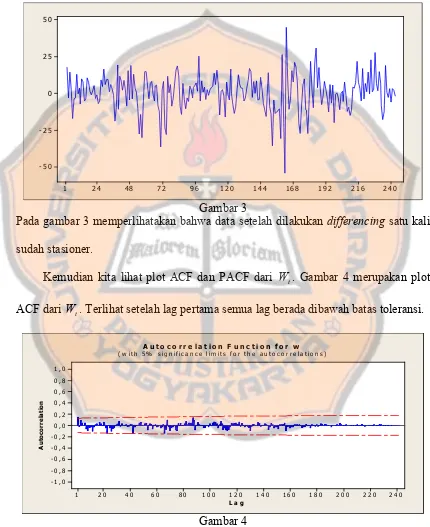
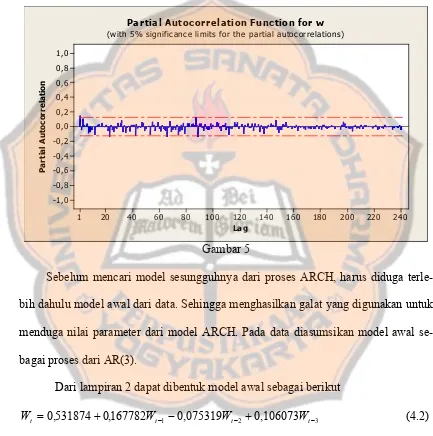
LAMPIRAN 2 Hasil Analisa Data yang Telah Didifferenc-ing Satu Kali dengan Menggunakan AR (3) .. 66

LAMPIRAN 3 Hasil Analisa Data yang Telah Didifferenc-ing Satu Kali dengan Menggunakan AR (1) .. 67

BAB I

PENDAHULUAN

A. Latar Belakang Masalah

Pada kenyataannya data runtun waktu tidak semuanya memiliki variansi

kon-stan. Model Autoregresif (AR) merupakan model yang menganggap bahwa data

run-tun waktu memiliki variansi yang konstan. Variansi merupakan variabel dalam

statistik yang menggambarkan seberapa jauh perubahan data terhadap nilai

rata-ratanya. Persamaan umum AR adalah

t k t k t

t =β +β Υ + +β Υ +ε

Υ _{0 1 −1} K ₋ dengan :

Υ_t = deret waktu tunggal

=

Υt₋i deret waktu tunggal yang ketinggalan i perioda

(

i=1,2,3,K,k

)

β = parameter

ε = galat

Bila variansi galat berubah terhadap waktu maka keadaan ini disebut

heteroskedastisitas. Untuk itulah Robert F. Engle pada tahun 1982 menawarkan

model ARCH (Autoregressive Conditional Heteroscedastic). Model ARCH

Bentuk model ARCH adalah

t t t =v h

ε dengan

∑

∞

= −

+ =

1 2 0

i

i t i t

h α α ε dan v_t berdistribusi normal standar.

Peramalan dengan model ARCH dapat kita lakukan cukup dengan adanya data

runtun waktu tunggal. Peramalan dengan model ini tidak perlu memandang

aspek-aspek lain yang dapat mempengaruhi perubahan data runtun waktu.

B. Rumusan Masalah

Pokok bahasan yang akan dibahas dalam tulisan ini dapat dirumuskan sebagai

berikut:

1. Apa yang dimaksud dengan model ARCH?

2. Bagaimana penerapan model ARCH dalam peramalan dengan

menggunakan data runtun waktu?

C. Tujuan Penulisan

Untuk menjelaskan dan membahas kegunaan model ARCH dalam peramalan

data runtun waktu serta landasan teori yang mendukungnya.

D. Pembatasan Masalah

Dalam tulisan ini peramalan dengan model ARCH hanya akan membahas

2. Uji efek ARCH menggunakan pengganda langrange (langrange

multiplier).

3. Estimasi model ARCH menggunakan maksimum likelihood distibusi

normal.

4. Pembuktian distribusi khi-kuadrat tidak dibuktikan.

E. Manfaat Penulisan

Manfaat yang akan diperoleh setelah mempelajari topik ini adalah untuk

semakin memahami dan menguasai penggunaan model ARCH dalam peramalan

khususnya peramalan dengan menggunakan data runtun waktu.

F. Metode Penulisan

Metode yang digunakan dalam penulisan ini menggunakan metode kepustakaan

dan data diolah menggunakan software Eviws dan Minitab.

G. Sistematika Penulisan

BAB I : menjelaskan tentang latar belakang masalah, rumusan masalah, tujuan

penu-lisan, manfaat penupenu-lisan, sistematika penulisan.

BAB II : menjelaskan tentang konsep dasar runtun waktu, fungsi autokovariansi dan

BAB III : menjelaskan tentang model ARCH, ARCH, pengujian adanya efek ARCH

dalam data runtun waktu, fungsi likelihood ARCH.

BAB IV : menjelaskan Penerapan Model ARCH Pada Data Harga Saham Composite

BAB II

LANDASAN TEORI

Dalam peramalan dikenal adanya model deret berkala dan model regresi. Pada

jenis model deret berkala, penduga masa depan dilakukan berdasarkan nilai masa lalu

dari suatu variabel atau kesalahan masa lalu. Sedangkan model regresi

mengasumsikan bahwa faktor yang diramalkan menunjukkan suatu hubungan

sebab-akibat dengan satu atau lebih variabel bebas (variabel independen).

Suatu model regresi yang memiliki satu variabel bebas disebut model regresi

sederhana atau model regresi linear klasik. Model regresi linear klasik dapat

dinyatakan sebagai berikut:

(2.1)

1

0 i i i =β +β Χ +ε

Υ

dengan:

stokastik gangguan

unsur parameter

) independen (variabel

bebas variabel

dependen) (variabel

bebas tak variabel

= =

= Χ

= Υ

ε β

Model tersebut memiliki beberapa asumsi yaitu:

Asumsi 1:

Asumsi 2:

Tidak adanya autokorelasi atau tidak terdapat korelasi diantara unsur gangguan

sto-kastik, yaitu

(

)

(

(

( )

)

(

( )

)

)

(

)

(

)

(

)

( )

0

0 0

,

= Ε =

− −

Ε =

Ε − Ε

− Ε =

j i

j i

j j i i j

i Kov

ε ε

ε ε

ε ε ε ε ε

ε

dengan i dan j adalah indeks untuk dua pengamatan yang berbeda.

Asumsi 3:

Varian ε_i adalah suatu bilangan konstan positif yang sama dengan σ2 dengan kata

lain asumsi ini menyatakan homoskedastisitas atau variansi sama, yaitu:

( )

(

( )

)

( )

2 2

2

σ ε

ε ε ε

= Ε =

Ε − Ε =

i

i i i

Var

Penyimpangan dari asumsi 3 disebut sebagai heteroskedastisitas (variansi yang tidak

konstan), yaitu:

( )

2

i i Var ε =σ

Asumsi 4:

Untuk menaksir parameterβ digunakan metode kuadrat terkecil biasa ( method of ordinary least squares (OLS) ). Langkah –langkahnya sebagai beriku :

Persamaan (2.1) dapat ditulis menjadi

(2.2) ˆ

ˆ ˆ

1 0

i i

i i i

ε

ε β

β

+ Υ =

+ Χ + = Υ

dengan Υˆ_i merupakan nilai taksiran Υ_i. Secara alternatif persamaan (2.2) dapat

din-yatakan sebagai berikut

(2.3) ˆ

ˆ

ˆ

1

0 i

i i i i

Χ − − Υ =

Υ − Υ =

β β ε

yang menunjukkan bahwa ε_i (galat) hanyalah perbedaan antara nilai Υ sebenarnya

dengan yang ditaksir. Untuk sampel berukuran N pasang observasi jumlah kuadrat

galatnya dapat dinyatakan sebagai berikut

(

)

(

ˆ ˆ

)

(2.4)

ˆ

2 1 0

2 2

∑

∑

∑

Χ − − Υ =

Υ − Υ =

i i

i i i

β β ε

Bila persamaan (2.4) diturunkan terhadap βˆ₀ maka diperoleh persamaan

(

)

(

)

(2.5) 0 ˆ

ˆ 2

ˆ 0 1

0 2

∑

∑

_{=− Υ − − Χ =}

∂ ∂

i i

i _{β β}

β ε

Bila persamaan (2.4) diturunkan terhadap βˆ₁ maka diperoleh persamaan

(

)

(

)

(2.6) 0 ˆ

ˆ 2

ˆ 0 1

0 2

∑

∑

_{=− Υ − − Χ Χ =}

∂ ∂

i i i

i _{β β}

Persamaan (2.5) dapat ditulis menjadi (2.7) ˆ ˆ 1 0

∑

∑

Υ_i =Nβ +β Χ_i

Persamaan (2.6) dapat ditulis menjadi

(2.8) ˆ ˆ 2 1

0

∑

∑

∑

Υ_iΧ_i =β Χ_i+β Χ_i

Dari persamaan (2.7) dan (2.8) diperoleh

(

)

(2.9) ˆ 2 2 1

∑

∑

∑

∑ ∑

Χ − Χ Υ Χ − Υ Χ = i i i i i i N N β

(

)

(2.10) ˆ 2 2 2 0

∑

∑

∑ ∑

∑ ∑

Χ − Χ Υ Χ Χ − Υ Χ = i i i i i i i N β

Selain menaksir parameter β kita tentukan koefisien determinasi R2. Koefisien

determinasi merupakan ukuran ikhtisar yang menyatakan seberapa baik garis regresi

sampel mencocokkan data. Bila persamaan (2.2) kedua sisi dikurangi Υ maka

per-samaannya menjadi (2.11) ˆ i i

i −Υ =Υ −Υ+ε

Υ

Kemudian persamaan (2.11) kedua sisi dikuadratkan sehingga persamaannya menjadi

(

)

2

(

ˆ

)

2 2

(

ˆ

)

∑

2 (2.12)

∑

Υ_i −Υ =

∑

Υ_i −Υ +

∑

Υ_i −Υε_i + ε_i

Karena persamaan (2.5)

∑

ε_i =0 dan persamaan (2.6)

∑

ε_iΧ_i =0 maka

Sehingga persamaan (2.12) menjadi

(

)

2

(

ˆ

)

2

∑

2 (2.14)

∑

Υ_i −Υ =

∑

Υ_i −Υ +

ε

_i

dengan

(

)

∑

Υ −Υ 2

i = jumlah kuadrat total ( total sum of squares (TSS) )

(

)

∑

Υ −Υ 2

ˆ

i = jumlah kuadrat yang dijelaskan ( explined sum of squares (ESS) )

∑

2

i

ε = jumlah kuadrat galat/residual ( residual sum of squares (RSS) )

Definisi 2.1:

Koefisien determinasi R2 didefinisikan sebagai

(

)

(

)

∑

∑

Υ − Υ

Υ − Υ =

= ₂

2

2 ˆ

i i TSS

ESS R

Teorema 2.1

Bila

(

)

(

)

∑

∑

Υ −Υ

Υ − Υ

= ₂

2

2 ˆ

i i N

TR dengan T merupakan banyaknya observasi maka

sta-sistik uji TR2 akan berdistribusi khi-kuadrat.

Bukti :

( )

(

)

2 2

1 ˆ

ˆ _S

n Var

i

i ₋ =

Υ − Υ =

Υ

∑

sedangkan

( )

(

)

2 2

σ

= Υ − Υ = Υ

∑

N Var

i

i

akibatnya

(

)

(

)

(

)

(

)

₂2

2 2

2 2 2

1

1

ˆ

σ σ

S n

N S n N

N TR

i i

− =

− =

Υ − Υ

Υ − Υ =

∑

∑

Jadi terbukti bahwa TR2 berdistribusi χ2 dengan derajat bebas n-1. ■

Sedangkan model regresi yang memiliki lebih dari satu variabel bebas disebut

mode regresi linear berganda. Model regresi linear berganda dapat dinyatakan sebagai

berikut:

(2.15) ...

2 2 1 1

0 i i k ki i

i =β +β Χ +β Χ + +β Χ +ε

Υ

dengan:

parameter bebas variabel

bebas tak variabel

= = Χ

= Υ

1,2,3,...) (i

i, -ke observasi i

stokastik gangguan

unsur

= =

=

ε

Model tersebut memiliki asumsi yang sama dengan asumsi pada model regresi linear

klasik. Sedangkan untuk menaksir parameter β juga menggunakan metode OLS.

A. Konsep Dasar Runtun Waktu

Suatu runtun waktu (deret waktu/deret berkala) adalah sekumpulan observasi

yang berurutan dalam waktu tertentu. Suatu runtun waktu dinotasikan dengan Υ_t

dengan t menunjuk pada perioda waktu yang berturutan. Bila t adalah bilangan asli

maka Υ_t merupakan runtun waktu diskrit. Bila t sembarang bilangan real maka Υ_t

merupakan runtun waktu kontinu.

Dilihat dari sejarah nilai observasi, runtun waktu dapat dibedakan atas runtun

waktu deterministik dan runtun waktu stokastik. Runtun waktu deterministik adalah

runtun waktu dengan nilai observasi mendatang dapat dihitung atau diramalkan

se-cara pasti melalui suatu fungsi berdasarkan nilai observasi yang lampau. Sedangkan

runtun waktu stokastik adalah runtun waktu yang nilai observasi mendatang hanya

menunjukkan struktur probabilistik yang digambarkan melalui fungsi tertentu

ber-dasarkan observasi yang lampau. Contoh runtun waktu deterministik Υ_t =cos

(

2πft

)

dengan Υ_t merupakan nilai observasi pada saat t. Sedangkan f merupakan

fre-kuensi yang nilainya dapat ditentukan dengan

N

panga-matan). Contoh runtun waktu stokastik adalah ada Nobservasi yang nilainya dapat

ditentukan sebagai Υ₁,Υ₂,Υ₃,K,Υ_n dengan Υ₁,Υ₂,Υ₃,K,Υ_n merupakan variabel-variabel random yang memiliki fungsi probabilitas.

Suatu runtun waktu disebut stasioner bila

a. Ε

( )

Υ_t =konstan untuk setiapt

b. Var

( )

Υ_t =konstan untuk setiapt

c. Kov

(

Υ_t,Υ_t−k

)

=konstan untuk setiaptdan Kov

(

Υ_t,Υ_t−k

)

dependen terhadap

lag k

Dengan demikian, suatu runtun waktu dikatakan stasioner bila rata-rata,

variansi, dan kovariansinya tetap konstan sepanjang waktu. Sedangkan runtun waktu

dikatakan tidak stasioner bila runtun waktu tersebut gagal memenuhi satu bagian atau

lebih dari syarat tersebut. Untuk mencapai asumsi stasioneritas, data yang belum

stasioner harus diubah menjadi stasioner. Hal itu dapat diatasi melalui metode

pembedaan (differencing).

Misal diketahui deret angka sebagai berikut : 2,4,6,8,K,20 yang mengandung

trend linear dan tidak bersifat acak. Dengan mengurangkan nilai-nilai yang berurutan

, 4-2, 6-4, 8-6, ... ,20-18, kita akan mendapatkan nilai-nilai pembedaan pertama (first

differeneces) yang merupakan deret angka 2,2,2,...,2 dan deret ini jelas stasioner. Jadi untuk mendapatkan kestasioneran dapat dibuat deret baru yang terdiri dari perbedaan

angka antara periode yang berturut-turut:

(2.16)

1

−

Υ − Υ =

Deret baru Υ′_t, akan mempunyai n−1 buah nilai dan akan stasioner apabila trend

dari data awal Υ_t adalah linear (pada orde pertama).

Apabila autokorelasi dari data yang dibedakan pertama tidak mendekati nol

sesudah lag kedua atau ketiga, berarti data belum bisa dikatakan stasioner. Oleh

karena itu perlu dilakukan pembedaan lagi dari data pembedaan pertama sebagai

berikut:

(2.17)Υ ′′_t =Υ′_t −Υ′_t−1

t

Υ ′′ dinyatakan sebagai deret pembedaan orde kedua (second order differences).

Deret ini akan mempunyai n−2 buah nilai. Dengan mensubstitusikan (2.16) ke

dalam (2.17) akan diperoleh:

(

) (

)

2 1

2 1 1

2 _{− −}

− − −

Υ + Υ − Υ = Υ ′′

Υ − Υ − Υ − Υ = Υ ′′

t t t t

t t t

t t

Barisan

{ }

ε_t merupakan proses white noise bila untuk setiap periode waktu t

maka berlaku

I. Ε

( )

ε_t =0untuk setiapt

II. Ε

( )

ε_t2 =σ2 untuk setiapt

Teorema 2.2

Bila ε_t white noise maka ε_t stasioner.

Bukti:

Pertama karena Ε

( )

ε_t =0 dan 0 suatu konstanta maka syarat pertama stasioner

dipenuhi.

Kedua karena Ε

( )

ε_t =0 dan Ε

( )

ε_t2 =σ2 maka

( )

(

( )

)

(

)

( )

2 2

2 2

0

σ ε ε

ε ε ε

= Ε =

− Ε =

Ε − Ε =

t t

t t t

Var

Yang berarti syarat kedua stasioner dipenuhi.

Ketiga karena Ε

( )

ε_t =0untuk setiapt dan Ε

(

ε_tε_s

)

=0untuk setiapt≠s maka

(

)

(

(

( )

)

(

( )

)

)

(

)(

)

(

)

(

)

0

0 0

,

= Ε =

− −

Ε =

Ε − Ε

− Ε =

− −

− −

−

k t t

k t t

k t k t t t k

t t Kov

ε ε

ε ε

ε ε

ε ε ε

ε

Yang berarti syarat ketiga stasioner dipenuhi.

Jadi terbukti bahwa ε_t stasioner. ■

B. Fungsi Autokovariansi dan Fungsi Autokorelasi (ACF)

Definisi 2.2:

Autokovariansi antara Υ_t dan Υ_t−kdidefinisikan sebagai

(

_t, _{t k}

)

(

(

_t

( )

_t

)

(

_{t k}

(

_{t k}

)

)

)

_k (2.18)

Kov Υ Υ₋ =Ε Υ −Ε Υ Υ₋ −Ε Υ₋ =γ

Teorema 2.3

Bila Υ_t runtun waktu stasioner maka γ₀ =Var

( )

Υ_t dan γ_k =γ_−k. Bukti:

(

)

( )

(

)

(

( )

)

(

)

( )

(

)

( )

t t t

t t

t t

t t

Var Kov

Υ =

Υ Ε − Υ Ε =

Υ Ε − Υ Υ Ε − Υ Ε =

Υ Υ =

,

2 0

γ

dengan mengingat syarat ketiga stasioner sehingga

(

)

(

,

)

,

k t t

k t t k

Kov Kov

+ −

Υ Υ =

Υ Υ =

γ

=γ_−k ■

Fungsi autokovariansi merupakan plot dari γ_k terhadap lag k.

Fungsi korelasi digunakan untuk mengetahui sejauh mana hubungan antara satu

merupakan perkembangan lebih lanjut dari fungsi korelasi. Fungsi autokorelasi

digunakan untuk mengetahui apakah suatu data pada waktu tertentu dipengaruhi oleh

data pada waktu sebelumnya dan juga digunakan untuk mengetahui apakah suatu data

stasioner atau tidak stasioner. Stasioneritas sangat diperlukan karena untuk

mempermudah melakukan peramalan.

Definisi 2.3 :

Didalam runtun waktu korelasi antara Υ_t dan Υ_t−k disebut autokorelasi bila

(

)

(

)

( ) (

)

( )

(

)

(

(

)

)

(

)

( )

(

)

(

)

(

(

(

)

)

)

(2.19)

, ,

2 2

k t k

t t

t

k t k

t t t

k t t

k t t k

t t

Var Var

Kov Korr

− −

− −

− − −

Υ Ε − Υ Ε Υ Ε − Υ Ε

Υ Ε − Υ Υ Ε − Υ Ε =

Υ Υ

Υ Υ =

Υ Υ

Karena syarat kedua stasioner dan sifat pertama autokovariansi persamaan (2.19)

menjadi

(

)

(

(

( )

)

(

(

)

)

)

( )

(

)

(2.20)

,

0

2

k k

t t

k t k

t t t

k t t Korr

ρ γ γ

= =

Υ Ε − Υ Ε

Υ Ε − Υ Υ Ε − Υ Ε = Υ

Υ − −

Teorema 2.4

Bila Υ_t runtun waktu stasioner maka ρ₀ =1 dan ρ_k =ρ_−k.

Bukti:

1

0 0 0 =_γ =

γ ρ

Menggunakan Teorema 2.3 maka diperoleh

0

0 γ

γ γ γ

ρ k k k

− =

=

= ρ_−k ■

Fungsi autokorelasi merupakan plot dari ρ_k terhadap lag k.

Dalam praktek kita bisa menggunakan autokorelasi sampel, dengan

mengasumsikan Υ_t stasioner sehingga Υ =Υt =Υt−1 dan Var

( )

Υ_t =Var

(

Υ_t−k

)

sebagai berikut:

(

)

( ) (

)

(

)(

)

(

)

1 1

,

1

2 1

− Υ − Υ

−    



 _{Υ −Υ Υ −Υ}

=

Υ Υ

Υ Υ =

∑

∑

= +

= −

− −

n n Var

Var Kov

n

t t n

k t

k t t

k t t

k t t k

(

)(

)

(

)

(2.21)

1

2 1

∑

∑

= +

= −

Υ − Υ

Υ − Υ Υ − Υ = _n

t t n

k t

k t t

k ρ

C. Fungsi Autokorelasi Parsial (PACF)

Fungsi autokorelasi parsial (PACF) digunakan untuk menunjukkan keeratan

hubungan antara Υ_t dan Υ_t−k.

Definisi 2.4 :

Autokorelasi parsial didefinisikan sebagai berikut:

( ) ( )

(2.22)

k k kk

Μ Η =

φ

dengan Μ_{( )k} dan Η_{( )k} adalah matriks autokorelasi k×k, yaitu

( )

     

 

     

 

= Μ

− − −

− − −

1 1

1 1

3 2 1

3 1

2

2 1

1

1 2

1

L M M M M M

L L L

k k k

k k k

k

ρ ρ ρ

ρ ρ

ρ

ρ ρ

ρ

ρ ρ

ρ

Sedangkan Η_{( )k} adalah Μ_{( )k} yang kolom terakhirnya diganti

   

 

   

 

k ρ ρ ρ

M

2 1

dapat ditulis

( )                 = Η − −

− k k k

k k ρ ρ ρ ρ ρ ρ ρ ρ ρ ρ ρ ρ ρ L M M M M M L L L 3 2 1 3 1 2 2 1 1 1 2 1 1 1 1

Untuk memperoleh φ_kkdengan k =1,2,3,K digunakan aturan Cramer akan diperoleh

2 1 2 2 2 2 1 3 2 1 2 1 3 1 2 2 1 3 1 2 1 1 2 1 3 1 2 2 1 1 1 33 2 1 2 1 2 1 1 2 1 1 22 1 11 2 2 1 2 1 1 1 1 1 , 3 1 1 1 1 , 2 , 1 ρ ρ ρ ρ ρ ρ ρ ρ ρ ρ ρ ρ ρ ρ ρ ρ ρ ρ ρ ρ ρ ρ ρ ρ ρ φ ρ ρ ρ ρ ρ ρ ρ ρ φ ρ φ − − + − − + + = = = − − = = = = = k k k

D. Autoregresif (AR)

Model Autoregresif memiliki persamaan umum sebagai berikut:

(2.23) ... 2 2 1 1

0 t t k t k t

t =φ +φ Υ +φ Υ + +φ Υ +ε

Υ _{− − −}

Persamaan (2.23) juga merupakan persamaan regresi, tetapi berbeda dengan

persamaan (2.15). Pada persamaan (2.15) variabel-variabel sebelah kanan merupakan

faktor-faktor bebas yang lain, sedangkan pada persamaan (2.23) variabel-variabel

Asumsi-asumsi pada persamaan regresi juga berlaku pada persamaan tersebut denganε_t

merupakan white noise.

Bila persamaan (2.23) variabel sebelah kanan hanya dipengaruhi oleh nilai

sebelumnya dari variabel tak bebas Υ_t yang ketinggalan satu perioda maka

persamaannya disebut autoregresif orde satu (AR (1)). Persamaan AR (1) adalah

(2.24) 1 1

0 t t

t =φ +φ Υ +ε

Υ ₋

Bila Υ_t diketahui maka akan diperoleh

(

)

(

)

2 _{0 1 1 2} 1 1 0 2 1 0 1 0 1 0 2 1 1 0 2 1 0 1 0 1 1 ε ε φ φ φ φ ε ε φ φ φ φ ε φ φ ε φ φ + + Υ + + = + + Υ + + = + Υ + = Υ + Υ + = Υ

(

)

(

)

(

)

M 1 1 3 2 1 1 2 1 0 3 1 2 1 1 0 3 2 1 1 2 1 0 3 1 2 1 0 1 0 0 3 2 1 1 0 2 1 1 0 1 0 3 2 1 0 3 ε ε φ ε φ φ φ φ φ ε ε φ ε φ φ φ φ φ φ φ ε ε ε φ φ φ φ φ φ ε φ φ + + + Υ + + + = + + + Υ + + + = + + + Υ + + + = + Υ + = Υ

(

)

( )

( ) ( ) n (n n)

n n n n n n n n n n n n n n − − − − − − − − − − − − − + + + + + Υ + + + + + = Υ ε φ ε φ ε φ ε φ φ φ φ φ φ 1 3 3 1 2 2 1 1 1 1 0 1 1 1 2 1 1 0 1 K K

Sehingga untuk setiap 0t〉 akan didapatkan

(2.25) 1 0 1 0 1 1 0 1

0

∑

∑

− = − − = + Υ + = Υ t i i t i t t i i

Nilai harapan Υ_t pada persamaan (2.25) dapat dicari dengan mengingat syarat

pertama white noise adalah

( )

(

)

(2.26) 0 1 1 0 1 0 1 0 1 0 1 1 0 1 0 1 0 1 0 1 1 0 1 0 Υ + =       Ε + Υ Ε +       Ε =       _{+ Υ +} Ε = Υ Ε

∑

∑

∑

∑

∑

− = − = − − = − = − − = t t i i t i i t i t t i i t i i t i t t i i t φ φ φ ε φ φ φ φ ε φ φ φ φ

Sedangkan nilai harapan dari Υ_t−k dengan mengingat syarat pertama white noise

adalah

(

)

(

)

(2.27) 0 1 1 0 1 0 1 0 1 0 1 1 0 1 0 1 0 1 0 1 0 1 1 0 Υ + =       Ε + Υ Ε +       Ε =       _{+ Υ +} Ε = Υ Ε − − − = − − = − − − − − = − − = − − = − − − −

∑

∑

∑

∑

∑

k t k t i i k t i i k t i k t k t i i k t i k t i i k t i k t i k t φ φ φ ε φ φ φ φ ε φ φ φ φ

Persamaan (2.26) dan (2.27) keduanya dependen terhadap waktu. Karena

( )

Υt ≠Ε

(

Υt−k

)

Ε maka

{ }

Υ_t tidak stasioner.

Teorema 2.5

bila φ₁〈1 maka

II. ₀

(

1 _{1 1}2 ₁3 ...

)

1 0

1

0

∑

= + + + +

− − = φ φ φ φ φ φ t k

i i konvergen ke 1 1 φ φ − o (2.29) Bukti:

I. Karena φ₁〈1 maka lim ₁− =0

∞ →

k t t φ

II. Karena ₀

(

1 _{1 1}2 ₁3 ...

)

1 0

1

0

∑

= + + + +

− − = φ φ φ φ φ φ t k

i i

merupakan deret geometri yang

konvergen dengan a=φ₀dan r=φ₁ maka

1 0 1 1 φ φ − = −r a ■

Jadi untuk

(

t→∞

)

dan φ₁〈1,

( )

(2.30) 1 lim lim 0 1 1 0 1 0 1 0 1 1 0 1 0

∑

∑

∑

∞ = − − = − − = ∞ → ∞ → + − =       _{+ Υ +} = Υ i i t i t i i t i t t i i t t t ε φ φ φ ε φ φ φ φ

Nilai harapan Υ_t dengan menggunakan persamaan (2.30) dan mengingat syarat

pertama white noise adalah

Terlihat bahwa rata-rata dari Υ_t berhingga dan independen terhadap waktu. Jadi

( ) (

)

untuk semua .

1 ₁ 0 _t k t t _φ φ − = Υ Ε = Υ Ε ₋

Nilai variansiΥ_t dengan menggunakan persamaan (2.30), (2.31) dan mengingat

syarat kedua white noise adalah

( )

(

( )

)

( )

( )

( )

(2.32) 1 ... ... 1 1 2 1 2 2 4 1 2 2 1 2 2 2 4 1 2 1 2 1 2 2 0 1 2 1 0 0 1 1 0 2 φ σ σ φ σ φ σ ε φ ε φ ε ε φ φ φ ε φ φ φ − = + + + = + Ε + Ε + Ε =       Ε =       − − + − Ε = Υ Ε − Υ Ε = Υ − − ∞ = − ∞ = −

∑

∑

t t t i i t i i i t i t t t Var

yang juga berhingga dan independen terhadap waktu.

Nilai kovariansiΥ_t dengan mengingat persamaan (2.30), syarat kedua white noise dan

persamaan (2.31) adalah

(

)

(

(

)

(

))

( )

(

)

(

)

(

K

)

K K K + Ε + Ε + Ε = + + + + + + + + + + + Ε = Υ Υ − − + − − + − − − + − − − − − − − − + − − − − 2 2 4 1 2 1 2 1 2 1 1 2 1 1 2 1 2 2 1 1 1 1 1 1 1 2 2 1 1 1 , k t k k t k k t k k t k k t k k t k t k t k t k k t k t t t k t t Kov ε φ ε φ ε φ ε φ ε φ ε φ ε φ ε ε φ ε φ ε φ ε φ ε

(

)

(2.33) 1 1 2 1 1 2 4 1 2 1 1 2 φ φ σ φ φ φ σ − = + + + = k k _K

Ternyata nilai kovariansinya berhingga dan tidak berubah terhadap waktu. Jadi bila

nilai limit (2.30) digunakan maka deret

{ }

Υ_t akan menjadi stasioner.

Fungsi Autokorelasi (ACF) untuk AR (1) dapat dicari dengan menggunakan

persamaan (2.32) dan (2.33) sebagai berikut

Bila .0〈φ₁〈1makaρ_k〉0untuk semuak Bila −1〈φ₁〈0 maka ρ_k akan berubah tanda

dari negatif ke positif untuk semua k ≥1.

Fungsi Autokorelasi Parsial (PACF) untuk AR (1)

Untuk

, 1

=

k φ₁₁ =ρ₁ =φ₁

, 2

=

k 0

1

1 ₁2

2 1 2 1 2 1

2 1 2

22 =

− − = −

− =

φ φ φ ρ

ρ ρ φ

Karena AR (1) persamaannya hanya berhubungan dengan Υ_t−1 maka untuk k≥2

nilai φ_kk bernilai nol. Secara umum dapat ditulis menjadi

  

≥ =

2 untuk 0

1 untuk

1

k k kk

φ φ

Pada proses ini autokorelasi parsial bernilai tidak nol pada lag pertama, yang juga

merupakan order dari proses, tetapi bernilai nol untuk lag yang lain.

Bila persamaan (2.23) variabel sebelah kanan hanya dipengaruhi oleh nilai

sebelumnya dari variabel tak bebas Υ_t yang ketinggalan p perioda maka

persamaannya disebut autoregresif orde p (AR (p)). Persamaan AR (p) adalah

(2.34)

1

0 t i t

p

i i

t =φ + φ Υ +ε

Υ ₋

Nilai harapanΥ_t persamaan (2.34) dengan mengingat syarat pertama white noise adalah

( )

( )

( )

t 1 0 1 0 ε φ φ ε φ φ Ε +       Υ Ε + Ε =       + Υ + Ε = Υ Ε

∑

∑

= − = − p i i t i t p i i t i t (2.35) 1 0

∑

= − Υ + = p i i t i φ φ

sedangkan nilai harapan Υ_t−k adalah

(

)

( )

( )

(2.36) 1 0 k t 1 0 1 0

∑

∑

∑

= − − − = − − − = − − − Υ + = Ε +       Υ Ε + Ε =       + Υ + Ε = Υ Ε p i i k t i p i i k t i k t p i i k t i k t φ φ ε φ φ ε φ φ

Persamaan (2.35) dan (2.36) keduanya dependen terhadap waktu. Karena

( ) (

Υ_t ≠Ε Υ_t−_k

)

Ε maka

{ }

Υ_t tidak stasioner.

Persamaan (2.34) dapat ditulis menjadi

0 1 t p i i t i

t − φ Υ =φ +ε

Υ

∑

= − (2.37) 0 2 2 1

1 t t p t p t

t −φ Υ −φ Υ − −φ Υ =φ +ε

Υ _{− −} K ₋

Apabila persamaan (2.37) ditulis dalam bentuk operator pergeseran mundur dengan

i t t i

t p i i i t t p i i i t t t p p t t t B B B B B ε φ φ ε φ φ ε φ φ φ φ + =       Υ + = Υ       − Υ + = Υ − − Υ − Υ − Υ

∑

∑

= = 0 1 t 0 1 0 2 2 1 -1 K (2.38) 1 -1 1 0 1 0 t

∑

∑

= = − + = Υ _p i i t p i i

iB φ B

ε

φ φ

dengan 1

1 ≠

∑

= p i i iB φ .

Nilai harapan Υ_t persamaam (2.38) dengan mengingat syarat pertama white noise

Nilai variansi Υ_t persamaam (2.38) dengan mengingat syarat kedua white noise adalah

( )

(

( )

)

2 1 0 1 1 0 2 1 1 1             − − − + − Ε = Υ Ε − Υ Ε = Υ

∑

∑

∑

= = = p i i i p i i i t p i i i t t t B B B Var φ φ φ ε φ φ (2.40) 1 1 2 1 2 2 1 2       − =                     − Ε =

∑

∑

= = p i i i p i i i t B B φ σ φ ε

Nilai kovariansi

(

Υ_t,Υ_t−k

)

dengan mengingat syarat ketiga white noise adalah

(

t t k

)

(

(

t

( )

t

)

(

t k

(

t k

)

)

)

Kov Υ ,Υ₋ =Ε Υ −Ε Υ Υ₋ −Ε Υ₋

(

)

                        −             − Ε = Υ Υ

∑

∑

= − = − _p i i i k t p i i i t k t t B B Kov 1 1 1 1 , φ ε φ ε (2.41) 0 1 ₂ 1 =                     − Ε =

∑

= − p i i i k t t B φ ε ε

Jadi autoregresi orde p merupakan runtun waktu yang stasioner.

Bila persamaan (2.34) dikalikan Υ_t−k dengan k〉0 maka persamaannya menjadi

(2.42) 1 1

0 t k t t k p t p t k t t k

k t

tΥ− = Υ− + Υ−Υ− + + Υ− Υ− + Υ−

Υ φ φ K φ ε

dan dengan mengambil nilai harapannya diperoleh

(

ΥtΥt−k

)

= 0Ε

(

Υt−k

)

+ 1Ε

(

Υt−1Υt−k

)

+ + pΕ

(

Υt−pΥt−k

)

+Ε

(

tΥt−k

)

(2.43)

Ε φ φ K φ ε

Persamaan (2.43) menurut definisi 2.2 dan dengan menggunakan persamaan (2.39)

serta syarat ketiga white noise dapat ditulis menjadi

(2.44) 1 1 1 1 2 0 p k p k p i i i k B − − = + + + − =

∑

φ φγ φ γ φ γ K

Bila persamaan (2.44) dibagi γ₀ maka diperoleh fungsi autokorelasi AR (p) sebagai

Persamaan (2.45) merupakan persamaan yule-walker. 2 1 1 2 1 2 0 1 1 1 2 1 2 1 2 0 1 1 1 1 1, k untuk φ ρ φ φ σ φ φ ρ ρ φ ρ φ φ σ φ φ ρ − + + +                   − = + + + +       − = = − = − =

∑

∑

p p p i i i p p p i i i B B K K M K ₂ 2 1 1 2 1 2 0 2 1 2,

k = + + + + ₋

      − =

=

∑

_{p p}

p i i iB ρ φ φ ρ φ σ φ φ ρ p p p p i i i p B

p φ ρ φ ρ φ

σ φ φ ρ + + + +     − = =

∑

= _{− −} K 2 2 1 1 2 1 2 0 1 , k

Fungsi Autokorelasi Parsial (PACF) untuk AR (p)

1 1

1

1 1

,

3 2 1

2 1

1

1 2

1

3 2 1

2 1

1

1 2

1

L M L M M M

L L L

M M M M M

L L

− − −

− − −

− −

= =

p p p

p p p p

p p pp p

k

ρ ρ ρ

ρ ρ

ρ

ρ ρ

ρ

ρ ρ

ρ ρ

ρ ρ

ρ

ρ ρ

ρ

φ

. untuk ,

0 k p

kk = 〉

φ

Autokorelasi parsial akan nol setelah lag p atau kurva akan terputus setelah suku

BAB III

MODEL ARCH

A. ARCH

Autoregressive Conditional Heteroscedastic (ARCH) merupakan model

autoregresif dalam keadaan variansi tidak konstan. Masalah yang dihadapi ketika

berhadapan dengan data runtun waktu adalah masalah variabilitas, yang menentukan

seberapa cepat data berubah menurut waktu. Variabilitas menjadi bagian sangat

penting ketika sebuah sistem lebih bersifat stokastik dari pada deterministik. Dalam

sistem stokastik sendiri juga masih dibedakan antara data runtun waktu dengan

variabilitas konstan atau variabilitas tidak konstan. Suatu besaran yang dapat

mengukur variabilitas adalah variansi. Variansi mengukur harapan seberapa besar

nilai suatu data runtun waktu berbeda terhadap rata-rata data keseluruhan.

Engle (1982) menunjukkan bahwa model runtun waktu, rata-rata dan

variansinya dapat dicari secara bersamaan. Dengan manunjukkan bahwa ramalan

bersyarat lenih unggul dari pada yang tidak bersyarat. Sebagai contoh, kita miliki

AR(1)

(3.1)

1 1

0 t t t =φ +φ Υ +ε

Υ ₋

dan ingin meramalkan Υt₊₁ yaitu ramalan satu langkah kedepan. Ramalan bersyarat

(

Υ+1 Υ

) (

=Ε 0 + 1Υ + +1

)

Ε _{t t} φ φ _t ε_t

( ) (

) ( )

(3.2) 1 0 1 1 0 t t t Υ + = Ε + Υ Ε + Ε = ₊ φ φ ε φ φ

Sedangkan bila digunakan ramalan tak bersyarat dengan memperhatikan persamaan

(2.16) maka nilai harapan adalah

( )

(3.3)

1 ₁ 0 1 _φ φ − = Υ Ε _t+

Bila kita gunakan rata-rata bersyarat (3.2) untuk mencari nilai variansi bersyarat, akan

diperoleh

(

)

[

(

)

]

[

]

[

]

( )

2 1 2 1 0 1 1 0 2 1 0 1 2 1 1 1 + + + + + + Ε = Υ − − + Υ + Ε = Υ − − Υ Ε = Υ Υ Ε − Υ Ε = Υ Υ t t t t t t t t t t t Var ε φ φ ε φ φ φ φ

karena Ε

( )

ε_t =0 maka

( ) ( )

(

( )

)

( )

(3.4) 2 1 2 1 2 1 2 1 σ ε ε ε ε = = Ε − Ε = Ε + + + + t t t t Var

Sedangkan bila digunakan ramalan tak bersyarat dengan memperhatikan persamaan

(2.11) maka variansi tidak bersyarat dari

( )

(3.5)

1 ₁2

2

1 _φ

σ

− = Υ_t+

Bila 1 1

1 maka 1 0

2 1

1〈 ₋ ≥

〈

φ

φ sehingga ramalan tidak bersyarat mempunyai variansi

yang lebih besar, dengan alasan inilah ramalan bersyarat lebih digemari. Bila

variansi bersyarat Υ_t dependen terhadap waktu maka disebut heteroskedastisitas.

Suatu pendekatan menggambarkan kuadrat dari ε_t dapat ditulis dalam proses

AR (1) sebagai berikut

(3.6)

2 1 1 0 2

t t t =α +α ε − +u ε

Dengan u_t merupakan white noise baru,α₀〉0 dan α₁ ≥0.

Persamaan (3.6) merupakan pesamaan Autoregressive Conditional

Heteroscedastic orde 1 (ARCH (1)). Sebagai alternatif persamaan (3.6), dapat dinyatakan dalam bentuk multiplikatif yang diusulkan Engle (1982) sebagai berikut

(3.7)

t t t =v h ε

dengan h_t =α₀ +α₁ε_t2₋₁ dan v_t berdisribusi normal standar. Bila persamaan (3.7)

kedua sisi dikuadratkan dan ε_t2 menggunakan persamaan (3.6) maka persamaannya

menjadi

(

2 1

)

2

− =

+ =

t t t

t t t t

v h u

u h v h

Berikut ini beberapa sifat yang dimiliki oleh model ARCH (1):

a. Nilai harapan ε_t sama dengan nol.

Sifat tersebut dapat dibuktikan dengan menggunakan persamaan (3.9), sehingga akan

diperoleh nilai harapan galat sebagai berikut

( )

(

)

( )

(

)

(

)

0 0 2 1 1 0 2 1 1 0 2 1 1 0 t = + Ε = + Ε Ε = + Ε = Ε − − − t t t t t v v ε α α ε α α ε α α ε

b. Bila α₁〈1 maka galat

( )

ε_t mempunyai variansi tidak bersyarat yang konstan.

Sifat tersebut dapat dibuktikan dengan

( )

(

( )

)

2

t t t

Var ε =Εε −Εε

( )

2

=Εε_t

( )(

)

(

)

( ) (

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

2

)

( )

(

)

1 0 3 1 2 1 1 0 3 1 0 2 1 0 1 0 0 1 1 α α α α α α α α α α α α α ε − = + + + + = + + + + = K K t Var

Jadi variansi tidak bersyarat dari ε_t bersifat homoskedastik.

c. Galat

( )

ε_t mempunyai variansi bersyarat yang tidak konstan.

Sifat tersebut dapat dibuktikan dengan

(

)

(

)

(

(

)

)

(

)

0

2 ₁ 2 1 1 2 1 − Ε = Ε − Ε = − − − − t t t t t t t t Var ε ε ε ε ε ε ε ε

(

)

_    ₊ Ε

= 2₋ 2 1 1 0

v_t α α ε_t

(

)

(

)

( ) (

)

( )

( )

t t t t t t t t t t h v v v v v = + = Ε + Ε = Ε + Ε = + Ε = − − − − 2 1 1 0 2 2 1 1 2 0 2 1 1 2 0 2 2 1 1 0 2 ε α α ε α α ε α α ε α α

Jadi variansi bersyarat dari ε_t bersifat heteroskedastisitas.

d. Galat

{ }

ε_t tidak berkorelasi

Sifat tersebut dapat dibuktikan dengan

(

)

[

(

( )

)

(

( )

)

]

(

t t k

)

(

)

(

)

( ) ( )

(

(

)(

)

)

0

. ,

2 1 1 0 2

1 1 0

2 1 1 0 2

1 1 0

=

+ +

Ε Ε Ε =

+ +

Ε =

− − −

−

− − −

− −

k t t

k t t

k t k

t t t

k t t

v v

v v

kov

ε α α ε α α

ε α α ε

α α ε

ε

Jadi

(

)

(

)

( ) ( )

( ) ( )

0

0

, ,

= = =

− − − −

k t t

k t t

k t t k

t t

Var Var

Var Var

kov korr

ε ε

ε ε

ε ε ε

ε

Karena nilai korelasi nol berarti

{ }

ε_t tidak berkorelasi.

Bila pada persamaan (3.6) kuadrat dari ε_t ditulis dalam proses AR (q) maka

persamaannya menjadi

(3.8)

2 2

2 2 2

1 1 0 2

t q t q t

t

t =α +α ε − +α ε − + +α ε − +u

ε K

Dengan u_t merupakan white noise,α₀〉0 dan α_i ≥0 untuk i=1,2,K,q Bila

0

3 2

1 =α =α = =αq =

α K maka variabel galat terestimasi menjadi α₀. Sebaliknya

apabila hal ini tidak terjadi variansi bersyarat Υ_t akan membesar menurut proses

autoregresi pada (3.8).

Persamaan (3.8) merupakan pesamaan Autoregressive Conditional

(3.9) t t t =v h ε

dengan h_t =α₀ +α₁ε_t2₋₁ +K+α_qε_t2_−q dan v_t berdisribusi normal standar Berikut ini beberapa sifat yang dimiliki oleh model ARCH (q):

a. Nilai harapan ε_t sama dengan nol.

Sifat tersebut dapat dibuktikan dengan menggunakan persamaan (3.9), sehingga akan

diperoleh nilai harapan galat sebagai berikut

( )

( )

0 0 2 1 0 2 1 0 2 1 0 t =         + Ε =         + Ε Ε =         + Ε = Ε − = − = − =

∑

∑

∑

i t q i i i t q i i t i t q i i t v v ε α α ε α α ε α α ε

b. Galat

( )

ε_t mempunyai variansi tidak bersyarat yang konstan.

Sifat tersebut dapat dibuktikan dengan

( )

(

( )

)

2

t t t

Var ε =Εε −Εε

( )

(

)

(

)

(

)

(

(

)

)

(

2

)

1 0 2 2 2 1 0 2 1 1 0 2 2 1 1 0 1 − − − − − − − + + + + + Ε = + + + Ε = q t q q t q t t q t q t t v v Var ε α α α ε α α α α ε α ε α α ε K K

(

)

(

)

(

)

(

(

)

(

))

(

)

(

)

(

)

(

)

(

)

(

)

q q q q q q q q t q t q t q q t q t q q t q t t t t t t q t q q t q t q q t q t t t q t q t q q t q t t t v v v v v v v v v v v v v v v v v v v α α α α α α α α α α α α α α α α α α α α α α α ε α α α β α ε α α α α α ε α α α α α ε α α α α α ε α α α ε α α α α − − − = + + + + + + + + + = + + + + + + + + + = + + + + + + + Ε = + + + + + + Ε = + + + + + Ε = − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − K K K K K K K K K K 1 0 3 2 3 1 2 1 1 0 3 0 2 0 0 3 1 0 2 1 0 1 0 0 2 2 2 1 2 2 2 1 2 2 0 2 0 2 3 2 2 2 1 3 1 2 2 2 1 2 1 0 2 1 0 0 2 2 0 2 1 2 2 2 1 0 2 3 1 0 2 2 2 1 1 0 0 2 1 2 2 2 0 2 2 2 1 2 1 2 1 1 0 0 1 1

Jadi variansi tak bersyarat dari ε_t bersifat homoskedastik.

c. Galat

( )

ε_t mempunyai variansi bersyarat yang tidak konstan.

Sifat tersebut dapat dibuktikan dengan

(

)

( )

2

( )

2 1

2 0

1, , t i t

q i i t q t t

t v v

Var = Ε + ₋Ε

= − − ε α

∑

α ε ε ε K t i t q i i h = + = ₋ =

∑

2 1

0 α ε

α

Jadi variansi bersyarat dari ε_t bersifat heteroskedastisitas.

d. Galat

{ }

ε_t tidak berkorelasi

Sifat tersebut dapat dibuktikan dengan

(

)

[

(

( )

)

(

( )

)

]

(

)

( ) ( )

0 . , 2 1 0 2 1 0 2 1 0 2 1 0 =               +       + Ε Ε Ε =         + + Ε = Ε = Ε − Ε − Ε = − − = − = − − − = − − = − − − −

∑

∑

∑

∑

i k t q i i i t q i i k t t i k t q i i k t i t q i i t k t t k t k t t t k t t v v v v kov ε α α ε α α ε α α ε α α ε ε ε ε ε ε ε ε Jadi

(

)

(

)

( ) ( )

( ) ( )

0 0 , , = = = − − − − k t t k t t k t t k t t Var Var Var Var kov korr ε ε ε ε ε ε ε ε

B. Pengujian Adanya Efek ARCH Dalam Data Runtun Waktu

Data runtun waktu dalam kenyataannya tidak semua mempunyai efek ARCH.

Untuk mengetahui ada atau tidaknya efek ARCH dalam data runtun waktu dapat diuji

dengan uji Pengganda Langrange.

Langkah-langkah dalam uji Pengganda langrange sebagai berikut:

1. Tentukan persamaan rata-rata yang paling sesuai untuk data runtun waktu yang

ingin dianalisis. Dari persamaan tersebut akan diperoleh kuadrat galat

{ }

2

t ε .

2. Regresikan kuadrat galat

{ }

ε_t2 pada konstanta dan qlag terhadap dirinya sendiri.

(3.10)

2 2

2 2 2

1 1 0 2

q t q t

t

t =α +α ε − +α ε − + +α ε −

ε K

3. Hitung koefisien determinasi

( )

_R2 _{dari persamaan (3.10).}

4. Dilakukan uji hipotesis seperti dibawah ini:

. , , 4 , 3 , 2 , 1 , 0 satu rdapat sedikit te paling

). lag hingga ARCH

efek ada tidak ( 0

k 1

2 1 0 0

q k

q q

K K

= ≠ =

Η

= = = = = = Η

α α α

α α

Digunakan statistik uji TR2 dengan T menyatakan banyaknya galat pada

langkah satu. Dibawah hipotesis nol statistik uji TR2 akan berdistribusi 2

q χ .

Hipotesis nol ditolak bila nilai TR2 lebih besar dari χ_q2 maka terdapat efek

Contoh 3.1

Pada data dibawah ini periksalah apakah ada efek ARCH pada data dengan

menggunakan uji Langrange Multiplier .

t Υt

1 30

2 20

3 45

4 35

5 30

6 60

7 40

8 50

9 45

10 65

Penyelesaiannya

1. Untuk memperoleh kuadrat galat digunakan persamaan model AR (1)

t t t =β +β Υ +ε

t Υt Υt−1 ΥtΥt−1

2 1

−

Υ_t

1 30 - 0 0

2 20 30 600 900

3 45 20 900 400

4 35 45 1575 2025

5 30 35 1050 1225

6 60 30 1800 900

7 40 60 2400 3600

8 50 40 2000 1600

9 45 50 2250 2500

10 65 45 2925 2025

∑

Υ_t =420

∑

Υ_t−1 =355

∑

Υ_tΥ_t−1 =15.500

∑

Υ_t2₋₁ =15.175

Nilai β dapat diduga dengan

(

)

(

) ( )( )

(

) ( )

229349 ,

0

355 175

. 15 10

420 355 500

. 15 10

ˆ

2 2 1 2

1

1 1

1

=

− − =

Υ − Υ

Υ Υ − Υ Υ =

∑

∑

∑

∑ ∑

− −

− −

t t

t t t

t n n β

(

)

85811 , 33

10 355 229349 ,

0 10 420

ˆ

ˆ 1

1 0

= − =

Υ −

Υ

=

∑

∑

− n n

t

t _β

β

1 1

1 0

ˆ 22935 , 0 85811 , 33

ˆ ˆ ˆ ˆ

− −

Υ +

=

Υ + = Υ

t t

t β β

Nilai galat dapat dihitung dengan

t t t =Υ −Υˆ ε

t Υt Υt−1 Υˆt εt

2

t ε

1 30 33,85811 -3,85811 14,88501

2 20 30 40,73861 -20,73861 430,08994

3 45 20 38,44511 6,55489 42,96658

4 35 45 44,17886 -9,17886 84,25147

5 30 35 41,88536 -11,88536 141,26178

6 60 30 40,73861 19,26139 371,00114

7 40 60 47,61911 -7,61911 58,05084

8 50 40 43,03211 6,96789 48,55149

9 45 50 45,32561 -0,32561 0,10602

2. Regresi kuadrat galat

{ }

ε_t2 dalam persamaan ε_t2 =α₀ +α₁ε_t2₋₁

t εt2

2 1

− t

ε 2

1 2

− t tε

ε 4

1

− t ε

1 14,88501 - - -

2 430,08994 14,88501 6401,89432 221,56361

3 42,96658 430,08994 18.479,49527 18.4977,36056

4 84,25147 42,96658 3.619,99781 1.846,12725

5 141,26178 84,25147 11.901,51294 7.098,31035

6 371,00114 141,26178 52.408,28295 19.954,89115

7 58,05084 371,00114 21.536,92705 137.641,84939

8 48,55149 58,05084 2.818,45470 3.369,89970

9 0,10602 48,55149 5,14752 2.357,24728

10 433,51987 0,10602 45,96259 0,01124

∑

ε_t2 =1.624,68416

∑

ε_t2₋₁ =1.191,16429

∑

ε_t2ε_t2₋₁ =117.217,67516

∑

ε_t4₋₁ =357.467,26052

Nilai α dapat diduga dengan

(

)

(

) (

)(

)

(

) (

)

35397 , 0

16429 , 191 . 1 26052 , 467 . 357 10

16429 , 191 . 1 68416 , 624 . 1 67516 , 217 . 117 10

ˆ

2 2

2 1 4

1

2 1 2 2

2 1 1

− =

− − =

− − =

∑

∑

∑

∑ ∑

− −

− −

t t

t t t

t n n

ε ε

ε ε ε

(

)

63208 , 204

10 16429 , 191 . 1 35397 , 0 10

68416 , 624 . 1

ˆ ˆ

2 1 1

2 0

=

− =

−

=

∑

∑

− n n

t

t _α ε

ε α

2 1 2

1 1 0 2

ˆ 35397 , 0 63208 , 204

ˆ ˆ ˆ ˆ

− −

− =

+ =

t t

t

ε ε

α α ε

46842 , 162 10

68416 , 1624

2

2 _{= = =}

∑