PENGGUNAAN PEMODELAN UNTUK MENINGKATKAN
KEMAMPUAN MEMAHAMI KONSEP GEOMETRI BANGUN
DATAR DENGAN PENDEKATAN PMRI KELAS V-C SD
NEGERI UNGARAN 1 YOGYAKARTA
SKRIPSI
Diajukan Untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Pendidikan Program Studi Pendidikan Guru Sekolah Dasar
Oleh:
Lidia Rosita Dianningsih NIM. 101134166
PROGRAM STUDI PENDIDIKAN GURU SEKOLAH DASAR JURUSAN ILMU PENDIDIKAN
FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN UNIVERSITAS SANATA DHARMA
i
PENGGUNAAN PEMODELAN UNTUK MENINGKATKAN
KEMAMPUAN MEMAHAMI KONSEP GEOMETRI BANGUN
DATAR DENGAN PENDEKATAN PMRI KELAS V-C SD
NEGERI UNGARAN 1 YOGYAKARTA
SKRIPSI
Diajukan Untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Pendidikan Program Studi Pendidikan Guru Sekolah Dasar
Oleh:
Lidia Rosita Dianningsih
NIM. 101134166
PROGRAM STUDI PENDIDIKAN GURU SEKOLAH DASAR JURUSAN ILMU PENDIDIKAN
FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN UNIVERSITAS SANATA DHARMA
iv
Skripsi ini dipersembahkan untuk:
Tuhan YME
Bapak dan Ibu tercinta
Keluargaku tersayang
Kekasih hatiku
Teman-
teman seperjuanganku PGSD ‘10 Kelas E
Dan tentunya
ALMAMATERKU
v
Mimpi harus kita perjuangkan dengan sungguh-sungguh,
bukan orang lain yang akan memperjuangkannya,
namun diri kita sendiri yang harus terus berjuang sampai mimpi-mimpi itu menjadi
nyata
Tidak ada manusia sempurna,
namun kita bisa membuat hidup kita sempurna
vi
Saya menyatakan dengan sesungguhnya bahwa skripsi yang saya tulis ini tidak memuat
karya atau bagian orang lain, kecuali yang telah disebutkan dalam kutipan dan daftar pustaka,
sebagaimana layaknya karya ilmiah.
Yogyakarta, 23 Juli 2014
vii
PUBLIKASI KARYA ILMIAH UNTUK KEPENTINGAN AKADEMIS
Yang bertanda tangan di bawah ini, saya mahasiswa Universitas Sanata Dharma:
Nama : Lidia Rosita Dianningsih
Nomor Mahasiswa : 101134166
Demi pengembangan ilmu pengetahuan, saya memberikan kepada perpustakaan Universitas
Sanata Dharma karya ilmiah saya yang berjudul:
PENGGUNAAN PEMODELAN UNTUK MENINGKATKAN KEMAMPUAN
MEMAHAMI KONSEP GEOMETRI BANGUN DATAR DENGAN PENDEKATAN PMRI KELAS V-C SD NEGERI UNGARAN 1 YOGYAKARTA
Beserta perangkat yang diperlukan. Dengan demikian saya memberikan kepada Perpustakaan
Universitas Sanata Dharma hak untuk menyimpan, mengalihkan dalam bentuk media lain,
mengelolanya dalam bentuk pangkalan data, mendistribusikan secara terbatas dan
mempublikasikannya di internet atau media lain untuk kepentingan akademis tanpa perlu
meminta ijin dari saya maupun memberikan royalty kepada saya selama mencantumkan nama saya sebagai penulis.
Demikian pernyataan ini saya buat dengan sebenarnya.
Dibuat di Yogyakarta
Pada Tanggal 23 Juli 2014
Yang menyatakan,
viii
Dianningsih, Lidia Rosita. (2014). Penggunaan Pemodelan untuk Meningkatkan Kemampuan Memahami Konsep Geometri Bangun Datar dengan Pendekatan PMRI Kelas V-C SD Negeri Ungaran 1 Yogyakarta. Skripsi. Yogyakarta: Program Studi Pendidikan Guru Sekolah Dasar, Fakultas Keguruan dan Ilmu Pendidikan, Universitas Sanata Dharma.
Penelitian ini bertujuan untuk mengetahui peningkatan kemampuan memahami konsep geometri bangun datar siswa dengan menggunakan pendekatan PMRI karakteristik pemodelan pada siswa kelas V-C SDN Ungaran 1 Yogyakarta tahun ajaran 2013/2014. Penelitian ini merupakan Penelitian Tindakan Kelas (PTK). Subjek penelitian ini adalah siswa kelas V-C semester genap SDN Ungaran 1 Yogyakarta yang berjumlah 30 siswa. Objek penelitiannya adalah kemampuan memahami konsep geometri bangun datar. Peneliti melaksanakan penelitian dalam dua siklus. Setiap siklus terdiri atas perencanaan, pelaksanaan, observasi, dan refleksi. Teknik pengumpulan data pada penelitian ini menggunakan tes kemampuan memahami bangun datar, kuesioner respon siswa, observasi pembelajaran, dan wawancara dengan guru kelas V-C. Data hasil tes kemampuan memahami bangun datar dianalisis dengan cara menghitung banyaknya siswa yang memperoleh nilai di atas Kriteria Ketuntasan Minimal (KKM) untuk setiap indikator kemampuan memahami.
Hasil penelitian menunjukkan adanya peningkatan kemampuan memahami konsep geometri bangun datar dengan menggunakan pemodelan dalam pendekatan PMRI. Indikator memberikan contoh suatu konsep mengalami peningkatan dari kondisi awal sebesar 70% menjadi 86,2%. Indikator menggambarkan konsep dengan suatu model mengalami peningkatan dari kondisi awal 70% menjadi 89,6%. Indikator mengubah suatu bentuk ke bentuk lain mengalami peningkatan dari kondisi awal 70% menjadi 100%. Indikator membandingkan beberapa bentuk dalam sebuah konsep mengalami peningkatan dari kondisi awal 70% menjadi 93,1%. Indikator menyatakan ulang suatu konsep mengalami peningkatan dari kondisi awal 70% menjadi 100%. Data ini menunjukkan hasil peningkatan kemampuan memahami dari kondisi awal ke kondisi akhir siklus.
ix
Dianningsih, Lidia Rosita. (2014). Use of Modeling to Improve Understanding the Geometrical Concept Using PMRI Approach in Class V-C of SD Negeri Ungaran 1 Yogyakarta. Thesis. Yogyakarta: Elementary School Teacher Education Program, The Faculty of Teacher Training and Education, University of Sanata Dharma.
This study purposed to determine the increase in the ability to understand the concept of geometrical using modeling by PMRI approach to students in grade V-C SDN Unggaran 1 Yogyakarta academic year 2013/2014. This research was a Classroom Action Research (CAR). The subjects were 30 students of grade V-C in semester two at SDN Unggaran 1 Yogyakarta. The research object was the ability to understand the concept of geometrical. Researcher conducted the research in two cycles. Each cycle consisted of planning, implementation, observation, and reflection. Data collection techniques in this study used a test's ability to understand the geometrical, student response questionnaires, observational learning, and interviews with teachers of V-C class. Ability to understand the test results data of geometrical were analyzed by calculating the number of students scoring above a minimum completeness criteria (KKM) for each indicator's ability to understand.
The results showed an increase in the ability to understand the concept of geometrical using the modeling in PMRI approach. Giving an example of a concept indicator the initial conditions increased from 70% to 86,2%. Illustrating the concept with a model indicator the initial conditions from 70% to 89,6%. Transforming a form to another indicator the initial conditions from 70% to 100%. Comparing several forms in a concept indicator the initial conditions from 70% to 93,1%. Declaring reexamined a concept indicator the initial conditions from 70% to 100%. The data shows the results of the ability to understand improvement of the initial conditions and the end of cycle.
x
Puji syukur peneliti panjatkan kepada Tuhan YME yang telah melimpahkan
rahmat, taufik, dan hidayah-Nya, sehingga peneliti dapat menyelesaikan penyusunan
skripsi yang berjudul “Penggunaan Pemodelan untuk Meningkatkan Kemampuan
Memahami Konsep Geometri Bangun Datar dengan Pendekatan PMRI di SD Negeri
Ungaran 1 Yogyakarta” ini dengan lancar tanpa halangan suatu apapun. Skripsi ini
disusun sebagai salah satu syarat untuk memperoleh gelar Sarjana Pendidikan Guru
Sekolah Dasar, Fakultas Keguruan dan Ilmu Pendidikan, Universitas Sanata Dharma,
Yogyakarta.
Peneliti menyadari bahwa dalam penyusunan skripsi ini tidak lepas dari
adanya kerjasama, bimbingan, dan bantuan dari berbagai pihak. Peneliti tidak
mungkin dapat menyelesaikan skripsi ini tanpa adanya bantuan, bimbingan, serta
dukungan tersebut. Oleh karena itu, pada kesempatan ini ijinkan peneliti untuk
menyampaikan ucapan terimakasih kepada semua pihak yang telah memberikan
bantuan, bimbingan, serta dukungannya kepada peneliti dalam proses penelitian dan
penyusunan skripsi ini, baik secara langsung maupun tidak langsung.
Ucapan terimakasih ini peneliti sampaikan kepada:
1. Rohandi, Ph.D. selaku Dekan FKIP yang telah memberikan ijin
dilaksanakannya penelitian ini,
2. Gregorius Ari Nugrahanta, S.J., S.S., BST., M.A. selaku Kaprodi PGSD yang
telah memberikan ijin sehingga penelitian ini dapat terlaksana dengan lancar,
3. Dra. Haniek Sri Pratini, M.Pd. selaku dosen pembimbing I yang telah
membimbing peneliti dengan penuh kesabaran sehingga skripsi ini dapat
selesai dengan baik,
4. Christiyanti Aprinastuti, S.Si., M.Pd. selaku dosen pembimbing II yang selalu
memberikan bimbingan dan masukan dalam penyusunan skripsi ini sehingga
xi
banyak masukan kepada peneliti untuk memperbaiki skripsi ini,
6. Para validator yang telah melakukan validasi instrumen yang dibutuhkan
dalam penelitian ini sehingga penelitian ini dapat berjalan dengan lancar,
7. Kuswandi, S.Pd. selaku Kepala SD Negeri Ungaran 1 Yogyakarta yang telah
memberikan ijin untuk melaksanakan penelitian di SD Negeri Ungaran 1
Yogyakarta,
8. Supriyanti, S.Pd. selaku wali kelas V-C yang telah bersedia membantu
pelaksanaan penelitian di kelas V-C,
9. Zeny Nurahmawati, S.H. selaku wali kelas V-B yang telah mengijinkan untuk
dilaksanakannya uji validitas di kelas V-B,
10.Seluruh siswa kelas V-C SD Negeri Ungaran 1 Yogyakarta tahun ajaran
2013/2014 yang telah bersedia menjadi subjek penelitian ini,
11.Kedua orangtuaku (Bapak Markus Ngadeno dan Ibu Susana Watri) yang
selalu mendoakan tanpa henti, kakakku Maria Puji Setianingsih yang selalu
menjadi teman berbagi cerita, keponakanku Dian dan Fajar yang selalu
memberikan tawa riangnya, serta Bulek Sriwati yang selalu memberikan
dukungan. Keluargaku tercinta yang selalu mendoakan, mendukung, dan
menyemangati peneliti sehingga skripsi ini dapat segera terselesaikan dengan
baik,
12.Kekasihku sahabatku Dwi Kuncoro Jati yang selalu mendoakan, membantu,
mendukung, menasihati, memarahi, memberikan semangat dalam
penyelesaian skripsi ini, serta tidak pernah lelah mendengarkan dan menerima
keluh kesah, emosi, marah, kecewa peneliti dalam melaksanakan penelitian
dan penyusunan skripsi ini. Thankyou honey,
13.Sahabatku (Shintia, Wulan, dan Puput) yang selalu membantu dengan tulus
dalam setiap kesempatan, teman seperjuangan satu payung (Ida dan Avi) yang
memacu peneliti untuk segera menyelesaikan skripsi ini, teman-temanku PPL
xii penyusunan skripsi ini,
14.Kakak kosku (Mbak Ita) yang sudah membantu keterbatasan peneliti dalam
penyusunan skripsi ini,
15.Semua pihak yang tidak dapat penulis sebutkan satu persatu, yang telah
membantu selama proses penelitian dan penyusunan skripsi ini.
Peneliti menyadari bahwa skripsi ini masih jauh dari sempurna. Oleh karena
itu, peneliti megharapkan kritik dan saran yang membangun untuk menyempurnakan
skripsi ini. Semoga skripsi ini bermanfaat bagi semua pihak yang membacanya.
Yogyakarta, 23 Juli 2014
Peneliti,
xiii
HALAMAN JUDUL ... i
HALAMAN PERSETUJUAN PEMBIMBING ... ii
HALAMAN PENGESAHAN ... iii
HALAMAN PERSEMBAHAN ... iv
HALAMAN MOTTO ... v
PERNYATAAN KEASLIAN KARYA ... vi
PERNYATAAN PERSETUJUAN PUBLIKASI ... vii
ABSTRAK ... viii
ABSTRACT ... ix
KATA PENGANTAR ... x
DAFTAR ISI ... xiii
DAFTAR GAMBAR ... xv
DAFTAR TABEL ... xvi
DAFTAR LAMPIRAN ... xviii
BAB I PENDAHULUAN ... 1
A. Latar Belakang Masalah ... 1
B. Pembatasan Masalah ... 6
C. Rumusan Masalah ... 7
D. Tujuan Penelitian... 7
E. Manfaat Penelitian ... 7
F. Definisi Operasional ... 8
BAB II TINJAUAN PUSTAKA ... 11
A. Kajian Teori... 11
B. Penelitian yang Relevan ... 28
C. Kerangka Berpikir ... 30
xiv
BAB III METODE PENELITIAN ... 33
A. Jenis Penelitian ... 33
B. Setting Penelitian ... 34
C. Rencana Tindakan ... 35
D. Indikator Keberhasilan dan Pengukurannya ... 43
E. Teknik Pengumpulan Data ... 44
F. Instrumen Penelitian ... 46
G. Validitas, Reliabilitas, dan Indeks Kesukaran ... 52
H. Teknik Analisis Data ... 57
BAB IV HASIL PENELITIAN, ANALISIS, DAN PEMBAHASAN ... 62
A. Hasil Penelitian ... 62
B. Pembahasan ... 123
C. Keterbatasan dalam Penelitian ... 129
BAB V KESIMPULAN DAN SARAN ... 130
A. Kesimpulan ... 130
B. Saran ... 131
Daftar Pustaka ... 132
xv
Gambar 2.1 Diagram Penelitian yang Relevan ... 30
xvi
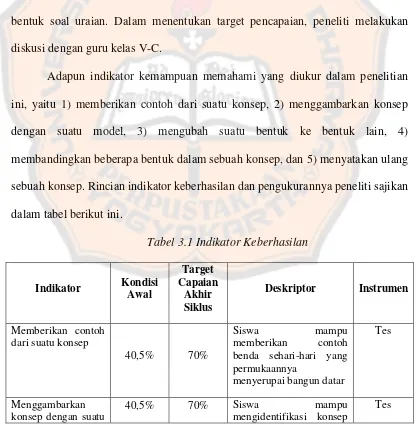
Tabel 3.1 Indikator keberhasilan ... 43
Tabel 3.2 Kisi-kisi Instrumen Tes Siklus I dan II ... 47
Tabel 3.3 Kisi-kisi Observasi Penggunaan Masalah Kontekstual ... 48
Tabel 3.4 Kisi-kisi Observasi Penggunaan Model ... 49
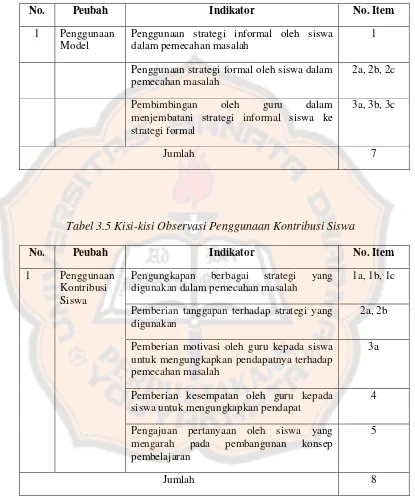
Tabel 3.5 Kisi-kisi Observasi Penggunaan Kontribusi Siswa ... 49
Tabel 3.6 Kisi-kisi Observasi Interaktivitas ... 50
Tabel 3.7 Kisi-kisi Observasi Intertwining dalam Pembelajaran... 50
Tabel 3.8 Kisi-kisi Instrumen Kuesioner Respon Siswa ... 51
Tabel 3.9 Kisi-kisi Instrumen Pengumpulan Wawancara ... 51
Tabel 3.10 Kriteria Reliabilitas ... 54
Tabel 3.11 Kualifikasi Indeks Kesukaran ... 56
Tabel 3.12 Kategori Sikap Siswa Menurut Skala Likert... 60
Tabel 4.1 Hasil tes kemampuan memahami pada indikator memberikan contoh dari suatu konsep ... 71
Tabel 4.2 Hasil tes kemampuan memahami pada indikator menggambarkan konsep dengan suatu model ... 73
Tabel 4.3 Hasil tes kemampuan memahami pada indikator mengubah suatu bentuk ke bentuk lain ... 74
Tabel 4.4 Hasil tes kemampuan memahami pada indikator membandingkan beberapa bentuk dalam sebuah konsep ... 75
Tabel 4.5 Hasil tes kemampuan memahami pada indikator menyatakan ulang sebuah konsep... 77
Tabel 4.6 Hasil kuesioner respon siswa mengenai penggunaan intertwining 78 Tabel 4.7 Hasil kuesioner respon siswa mengenai penggunaan interaktivitas siswa ... 79
Tabel 4.8 Hasil kuesioner respon siswa mengenai penggunaan pemodelan .. 80
Tabel 4.9 Hasil kuesioner respon siswa mengenai penggunaan kontribusi siswa ... 81
xvii
Tabel 4.12 Hasil observasi penggunaan model ... 85
Tabel 4.13 Hasil observasi penggunaan kontribusi siswa ... 86
Tabel 4.14 Hasil observasi interaktivitas siswa ... 88
Tabel 4.15 Hasil observasi penggunaan intertwining ... 90
Tabel 4.16 Hasil wawancara dengan guru matematika ... 91
Tabel 4.17 Hasil tes kemampuan memahami pada indikator memberikan contoh dari suatu konsep ... 102
Tabel 4.18 Hasil tes kemampuan memahami pada indikator menggambarkan konsep dengan suatu model ... 103
Tabel 4.19 Hasil tes kemampuan memahami pada indikator mengubah suatu bentuk ke bentuk lain ... 104
Tabel 4.20 Hasil tes kemampuan memahami pada indikator membandingkan beberapa bentuk dalam sebuah konsep ... 105
Tabel 4.21 Hasil tes kemampuan memahami pada indikator menyatakan ulang sebuah konsep... 106
Tabel 4.22 Hasil kuesioner respon siswa mengenai penggunaan intertwining 108 Tabel 4.23 Hasil kuesioner respon siswa mengenai penggunaan interaktivitas siswa ... 109
Tabel 4.24 Hasil kuesioner respon siswa mengenai penggunaan pemodelan .. 110
Tabel 4.25 Hasil kuesioner respon siswa mengenai penggunaan kontribusi siswa ... 111
Tabel 4.26 Hasil kuesioner respon siswa mengenai penggunaan masalah kontekstual ... 112
Tabel 4.27 Hasil observasi penggunaan konteks ... 113
Tabel 4.28 Hasil observasi penggunaan model ... 115
Tabel 4.29 Hasil observasi penggunaan kontribusi siswa ... 116
Tabel 4.30 Hasil observasi interaktivitas siswa ... 118
Tabel 4.31 Observasi penggunaan intertwining ... 119
Tabel 4.32 Hasil wawancara dengan guru matematika ... 121
xviii
Lampiran 1 : Validasi Ahli ... (2)
1. Validasi instrumen tes ... (3)
2. Validasi instrumen kueasioner ... (8)
3. Validasi instrumen wawancara ... (10)
4. Validasi perangkat pembelajaran ... (16)
Lampiran 2 : Uji Coba Validitas dan Reliabilitas ... (19)
1. Instrumen Uji Coba Tes Kemampuan Memahami... (20)
2. Hasil Pengisian Uji Coba Tes Kemampuan Memahami ... (27)
3. Perhitungan Validitas dan Reliabilitas Uji Coba Tes Kemampuan Memahami ... (33)
4. Rincian Hasil Validitas Uji Coba Tes Kemampuan Memahami ... (39)
Lampiran 3 : Tes, Observasi, Kuesioner, Wawancara ... (41)
1. Instrumen Tes Kemampuan Memahami ... (42)
2. Hasil Pengisian Tes Kemampuan Memahami ... (49)
3. Instrumen Kuesioner ... (57)
4. Hasil Pengisian Lembar Kuesioner ... (60)
5. Instrumen Observasi... (66)
6. Hasil Pengisian Lembar Observasi ... (72)
7. Instrumen Wawancara ... (112)
8. Verbatim Hasil Wawancara ... (113)
Lampiran 4 : Silabus dan RPP ... (117)
1. Silabus Siklus 1 ... (118)
2. RPP Siklus I ... (123)
3. Silabus Siklus II ... (158)
4. RPP Siklus II ... (163)
Lampiran 5 : Dokumentasi dan Surat-surat ... (188)
1. Foto-foto ... (189)
2. Surat Penelitian ... (190)
1
BAB I
PENDAHULUAN
A. LATAR BELAKANG
Sekolah Dasar (SD) merupakan salah satu lembaga formal penyelenggara
pendidikan yang berada di bawah naungan Departemen Pendidikan Nasional
dengan tugas untuk mengemban misi dasar dalam memberikan konstribusi untuk
mencapai tujuan pendidikan nasional (Amin, 2004: 1). Pendidikan tersebut
dilaksanakan melalui proses belajar mengajar yang dilakukan sesuai dengan
kurikulum sekolah. Melalui pengajaran yang dilaksanakan di sekolah, siswa SD
yang sedang berada pada tahap perkembangan operasional konkret dapat
memperoleh bekal ilmu pengetahuan dasar dan keterampilan dasar yang dapat
menjadi persiapan untuk proses belajar pada jenjang pendidikan yang lebih tinggi.
Bekal ilmu pengetahuan dan keterampilan dasar siswa diperoleh dari berbagai
macam mata pelajaran yang terdapat di SD, salah satunya adalah matematika.
Menurut Fowler (dalam Muslich, 2009: 221), matematika merupakan mata
pelajaran yang bersifat abstrak sehingga dituntut kemampuan guru untuk dapat
mengupayakan metode yang tepat sesuai dengan tingkat perkembangan mental
siswa. Berdasarkan pendapat tersebut, diketahui bahwa karakteristik matematika
adalah mempunyai objek yang bersifat abstrak.
Menurut Rosser (dalam Sagala, 2003: 73), konsep adalah suatu abstraksi
yang mewakili satu kelas objek-objek, kejadian-kejadian, kegiatan-kegiatan, atau
hubungan-hubungan yang mempunyai atribut-atribut yang sama. Kemampuan
kurang berbakat matematika atau kurang mampu dalam mempelajari matematika,
sering mengalami kesulitan menangkap dan memahami konsep yang benar dalam
proses belajar, sehingga proses belajar mengajar tidak dapat berlangsung dengan
baik. Oleh sebab itu, pelaksanaan proses pembelajaran harus sesuai dengan
perkembangan dalam dunia pendidikan sekarang ini serta harus dapat menerapkan
pendekatan proses pembelajaran yang relevan dengan paradigma pendidikan saat
ini, yang lebih mengaktifkan siswa. Sehingga, hasil belajar yang diperoleh siswa
akan memuaskan serta pemahaman konsep siswa akan meningkat.
Peneliti melaksanakan observasi pembelajaran Matematika di kelas V-C
SDN Ungaran 1 Yogyakarta pada tanggal 4 Desember 2013 dengan pembelajaran
mengenai materi bangun datar. Berdasarkan hasil observasi, terlihat bahwa
sebagian siswa menyimak dan memperhatikan guru pada saat pembelajaran
dimulai. Pembelajaran yang berlangsung cenderung didominasi oleh guru dengan
menggunakan metode ceramah, sehingga ketika pertengahan proses pembelajaran
siswa mulai tidak fokus belajar. Sebagian besar siswa tidak ramai di kelas, namun
terlihat melakukan kesibukan sendiri yang tidak berkaitan dengan pelajaran
Matematika yang sedang diikuti. Walaupun guru berusaha menggunakan media
pembelajaran, namun siswa masih terlihat pasif dengan media yang digunakan.
Ketika guru menunjukkan cara mengerjakan soal di depan kelas, siswa terlihat
mendengarkan. Namun, ketika siswa diminta mengerjakan beberapa soal, siswa
masih mengalami kesulitan untuk mengerjakannya. Siswa yang kesulitan
mengerjakan soal tidak langsung bertanya kepada guru, namun hanya diam saja
dilakukan, terlihat bahwa siswa masih kurang aktif mengikuti pembelajaran.
Pembelajaran yang berlangsung masih fokus kepada guru, sehingga siswa belum
memperoleh kesempatan untuk mengembangkan pengetahuan mereka sendiri
berdasarkan media yang digunakan dalam pembelajaran. Hal ini menyebabkan
siswa tidak bersemangat mengikuti pembelajaran dan siswa kurang mampu
memahami materi yang dipelajari.
Selain melakukan observasi, peneliti juga melakukan wawancara dengan
guru kelas V-C di SDN Ungaran 1 Yogyakarta. Berdasarkan hasil wawancara
tersebut, dapat diketahui bahwa sebagian besar siswa di kelas V-C masih
mengalami kesulitan untuk memahami materi pelajaran yang diberikan. Sebagian
siswa masih kesulitan untuk memahami materi walaupun guru sudah berusaha
memberikan penjelasan kepada siswa, serta menyediakan media pembelajaran
untuk memudahkan siswa dalam belajar. Namun media yang ada kurang efektif
dalam pembelajaran, karena siswa yang kesulitan memahami materi cenderung
menggunakan media pembelajaran sebagai mainan di dalam kelas. Selain itu,
siswa masih terlihat pasif dalam mengikuti pembelajaran di dalam kelas. Hal ini
tentu menjadi salah satu masalah yang dihadapi guru kelas V-C di SDN Ungaran
1 Yogyakarta. Guru merasa sudah kehabisan ide untuk membuat siswa mudah
memahami materi Matematika.
Berdasarkan hasil penilaian siswa di kelas V-C SDN Ungaran 1
Yogyakarta semester dua tahun pelajaran 2012/2013, dari 37 siswa kelas V-C ada
22 siswa yang masih mendapatkan nilai ulangan harian di bawah KKM, yaitu 72.
Perolehan nilai ulangan harian tersebut dapat menggambarkan kemampuan
memahami siswa, karena setelah materi pelajaran selesai diberikan, maka
dilaksanakan ulangan harian untuk melihat seberapa besar tingkat kemampuan
memahami siswa terhadap materi pelajaran tersebut. Oleh karena itu, peneliti
melaksanakan penelitian di SDN Ungaran 1 Yogyakarta dengan menerapkan
pendekatan PMRI untuk meningkatkan kemampuan memahami siswa terhadap
materi pelajaran yang dipelajari.
Pendidikan Matematika Realistik Indonesia (PMRI) merupakan
pendekatan pembelajaran yang sesuai dengan paradigma pendidikan saat ini.
PMRI menginginkan adanya perubahan dalam paradigma pembelajaran, yaitu dari
paradigma mengajar menjadi paradigma belajar (Marpaung, 2004). PMRI
merupakan salah satu pendekatan pembelajaran yang relatif baru, sehingga belum
semua kalangan dalam dunia pendidikan mengenal pendekatan tersebut. Namun
untuk saat ini, sudah banyak seminar-seminar yang dilakukan oleh pemerintah
untuk lebih mengenalkan PMRI pada para pendidik, sehingga PMRI sudah mulai
diterapkan dalam dunia pendidikan untuk mendukung proses pembelajaran
matematika.
Melalui pendekatan PMRI, siswa tidak hanya dilatih untuk membangun
pengetahuannya sendiri tetapi siswa juga dilatih untuk mengetahui seberapa jauh
tingkat pemahaman siswa terhadap materi yang diperoleh dalam setiap proses
pembelajaran yang diikuti. Selain itu, PMRI menekankan untuk membawa
matematika pada pengajaran bermakna dengan mengaitkannya dalam kehidupan
suatu situasi yang dapat dibayangkan oleh siswa atau menggambarkan situasi
dalam dunia nyata.
Pendekatan PMRI memiliki lima karakteristik menurut De Lange
(Zulkardi, 2005: 14), yaitu 1) The use of context (menggunakan masalah kontekstual), 2) The use of models (menggunakan berbagai model), 3) Student contributions (kontribusi siswa), 4) Interactivity (interaktivitas), dan 5) Intertwining (keterkaitan). Dalam penelitian ini, peneliti memfokuskan penelitian pada karakteristik yang kedua, yaitu The use of models (menggunakan berbagai model/ pemodelan). Pemilihan karakteristik ini mengacu pada hasil observasi dan
wawancara yang telah dilakukan, yang menjelaskan bahwa siswa masih kurang
aktif mengikuti pembelajaran, serta siswa belum memperoleh kesempatan untuk
mengembangkan sendiri pengetahuan yang diperoleh. Hal ini sejalan dengan
karakteristik tersebut yang lebih menekankan pada pengembangan sendiri model
matematika oleh siswa. PMRI dimulai dengan suatu hal yang nyata dan dekat
dengan siswa, oleh karena itu siswa dapat mengembangkan sendiri model
matematika yang mereka peroleh. Melalui pengembangan sendiri model-model
matematika oleh siswa, maka siswa dapat menambah pemahamannya terhadap
materi matematika.
Penelitian ini menerapkan pendekatan PMRI karakteristik pemodelan
dalam pembelajaran Matematika untuk materi geometri bangun datar kelas V
SDN Ungaran 1. Pengambilan materi geometri bangun datar ini dilandasi dengan
alasan, karena siswa masih belum mampu memahami konsep geometri bangun
siswa dan sering dijumpai siswa. Penerapan PMRI karakteristik pemodelan dalam
materi geometri bangun datar dapat memberikan kesempatan bagi siswa untuk
mengembangkan sendiri model-model yang diperoleh, sehingga kemampuan
memahami konsep geometri bangun datar dapat meningkat.
Berdasarkan permasalahan-permasalahan yang telah diungkapkan di atas,
penelitian ini berjudul ”Penggunaan Pemodelan untuk Meningkatkan Kemampuan
Memahami Konsep Geometri Bangun Datar dengan Pendekatan PMRI Kelas V-C
SD Negeri Ungaran 1 Yogyakarta”.
B. PEMBATASAN MASALAH
Agar permasalahan dalam penelitian ini tidak meluas dan menyimpang
dari sasaran yang diharapkan, maka peneliti membatasi permasalahan pada hal-hal
berikut:
1. Peningkatan yang dimaksud yaitu adanya peningkatan pemahaman konsep
geometri bangun datar dalam pembelajaran matematika siswa kelas V-C SD
Negeri Ungaran 1 Yogyakarta tahun pelajaran 2013/2014.
2. Pemahaman siswa terhadap konsep geometri bangun datar dapat dilihat dari
hasil tes kemampuan memahami yang memiliki lima indikator pemahaman
konsep dalam proses pembelajaran dengan menggunakan pendekatan PMRI.
3. Peningkatan pemahaman konsep geometri bangun datar pada standar
kompetensi “Memahami sifat-sifat bangun dan hubungan antar bangun”,
“Menyelesaikan masalah yang berkaitan dengan bangun datar dan bangun
ruang sederhana”.
C. RUMUSAN MASALAH
Berdasarkan hal-hal yang telah diuraikan di atas, maka permasalahan yang
timbul adalah: “Bagaimana penerapan pendekatan PMRI karakteristik Pemodelan
dalam pembelajaran Matematika dapat meningkatkan kemampuan memahami
konsep geometri bangun datar siswa kelas V-C SD Negeri Ungaran 1 Yogyakarta
pada tahun ajaran 2013/2014?”.
D. TUJUAN PENELITIAN
Tujuan dari pelaksanaan penelitian ini yaitu meningkatkan kemampuan
memahami konsep geometri bangun datar siswa kelas V-C SD Negeri Ungaran 1
Yogyakarta pada tahun ajaran 2013/2014 dalam proses pembelajaran matematika
dengan menerapan pendekatan PMRI Pemodelan.
E. MANFAAT PENELITIAN
Hasil dari penelitian ini diharapkan dapat memberikan manfaat, antara
lain:
1. Manfaat Praktis
a. Bagi sekolah tempat penelitian, sebagai bahan pertimbangan untuk
meningkatkan dan menyempurnakan program pengajaran matematika di
b. Bagi guru mata pelajaran, sebagai informasi dan acuan untuk
meningkatkan kualitas pengajaran dalam proses pembelajaran matematika.
c. Bagi peneliti, sebagai pengalaman langsung dalam pelaksanaan
pembelajaran dengan menerapkan pendekatan yang realistik untuk siswa.
2. Manfaat Teoritis
a. Bagi program studi, sebagai gambaran pelaksanaan pembelajaran dengan
pendekatan PMRI Pemodelan di Sekolah Dasar.
b. Bagi peneliti lanjutan, sebagai bahan acuan untuk penelitian selanjutnya
yang relevan.
c. Bagi dunia pendidikan, sebagai sumbangan peneliti untuk
mensosialisasikan PMRI pada masyarakat.
F. DEFINISI OPERASIONAL
1. Pemahaman konsep. Siswa dikatakan mampu memahami apabila siswa
mampu memberikan contoh dari suatu konsep, menggambarkan konsep
dengan suatu model, mengubah suatu bentuk ke bentuk lain, membandingkan
beberapa bentuk dalam sebuah konsep, dan menyatakan ulang sebuah
konsep.Pemahaman konsep adalah kemampuan siswa yang berupa
penguasaan sejumlah materi pelajaran, tetapi mampu mengungkapkan kembali
dalam bentuk lain yang mudah dimengerti, memberikan intepretasi data dan
mampu mengaplikasi konsep yang sesuai denan struktur kognitif yang
2. Konsep geometri adalah salah satu struktur matematika yang memuat banyak
konsep mengenai penyajian abstraksi dari pengalaman visual dan spasial yang
sering digunakan dalam kehidupan sehari-hari.
3. Karakteristik siswa SD yang berada dalam tahap operasional konkret memiliki
ciri khusus, yaitu siswa memiliki kemampuan berpikir logis dengan
menggunakan benda-benda konkret, serta mampu untuk memanipulasi
gambaran yang ada di dalam dirinya.
4. Pembelajaran matematika adalah pembelajaran yang bersifat abstrak, yang
diajarkan secara bertahap dengan menggunakan metode spiral, serta
menggunakan penyampaian pembelajaran yang bermakna, sehingga siswa
lebih cepat untuk memahami.
5. Pendekatan PMRI adalah sebuah pendekatan dalam proses pembelajaran
matematika yang menekankan bagaimana siswa menemukan konsep atau
prosedur dalam matematika melalui masalah kontekstual yang dipahami siswa
untuk memperlancar pembelajaran matematika.
6. Prinsip PMRI yang diterapkan dalam penelitian ini adalah prinsip aktivitas,
prinsip realitas, prinsip berjenjang, prinsip jalinan, prinsip interaksi, dan
prinsip bimbingan.
7. Karakteristik PMRI yang diterapkan dalam penelitian ini adalah penggunaan
masalah kontektual, penggunaan berbagai model, penggunaan kontribusi
siswa, interaktivitas, dan keterkaitan.
8. Pendekatan PMRI pemodelan dalam penelitian ini adalah jembatan yang
disempurnakan sendiri oleh siswa menjadi bentuk pengetahuan formal dengan
bimbingan guru.
9. Langkah-langkah PMRI yang diterapkan dalam penelitian ini adalah
mengkondisikan siswa untuk belajar, mengajukan masalah kontekstual,
membimbing siswa untuk menyelesaikan masalah kontekstual, meminta siswa
menyajikan penyelesaian masalah, membandingkan dan mendiskusikan
11
BAB II
TINJAUAN PUSTAKA
Tinjauan pustaka pada bab ini terdiri dari kajian teori, penelitian yang
relevan, kerangka berpikir, dan hipotesis tindakan. Kajian teori menjelaskan
mengenai berbagai pengertian yang dikaji oleh peneliti.
A. KAJIAN TEORI
1. Pemahaman Konsep
Sanjaya (2009) mengemukakan bahwa pemahaman konsep adalah
kemampuan siswa yang berupa penguasaan sejumlah materi pelajaran, tetapi
mampu mengungkapkan kembali dalam bentuk lain yang mudah dimengerti,
memberikan intepretasi data dan mampu mengaplikasi konsep yang sesuai dengan
struktur kognitif yang dimilikinya. Indikator pemahaman konsep menurut Sanjaya
(2009) adalah:
a. Mampu menerangkan secara verbal mengenai apa yang telah dicapainya
b. Mampu menyajikan situasi matematika ke dalam berbagai cara serta
mengetahui perbedaan
c. Mampu mengklasifikasikan objek-objek berdasarkan dipenuhi atau
tidaknya persyaratan yang membentuk konsep tersebut
d. Mampu menerapkan hubungan antara konsep dan prosedur
f. Mampu menerapkan konsep secara alogaritma
g. Mampu mengembangkan konsep yang telah dipelajari
Sedangkan indikator pemahaman konsep menurut Kurikulum 2006 (dalam
Kesumawati, 2010), yaitu:
a. Menyatakan ulang sebuah konsep
b. Mengklasifikasikan objek-objek menurut sifat-sifat tertentu (sesuai dengan
konsepnya)
c. Memberikan contoh dan non contoh dari konsep
d. Menyajikan konsep dalam berbagai bentuk representasi matematis
e. Mengembangkan syarat perlu atau syarat cukup suatu konsep
f. Menggunakan, memanfaatkan, dan memilih prosedur atau operasi tertentu
g. Mengaplikasikan konsep atau alogaritma pemecahan masalah.
Hasil belajar adalah kemampuan-kemampuan yang dimiliki siswa setelah
ia menerima pengalaman belajarnya. Untuk mengevaluasi hasil belajar siswa yang
diharapkan, diperlukan tujuan yang bersifat operasional yaitu tujuan berupa
tingkah laku yang dapat dikerjakan dan diukur. Tujuan berkaitan dengan sifat
secara operasional dan tujuan pembelajaran khusus (Subiyanto, 1986: 46).
Benyamin Bloom mengklasifikasikan kemampuan hasil belajar ke dalam tiga
kategori, yaitu:
a. Ranah kognitif, meliputi kemampuan menyatakan kembali konsep atau
b. Ranah afektif, berkenaan dengan sikap dan nilai yang terdiri atas aspek
penerimaan, tanggapan, penilaian, pengelolaan, dan penghayatan
(karakterisasi).
c. Ranah psikomotorik, mencakup kemampuan yang berupa keterampilan
fisik (motorik) yang terdiri dari gerakan refleks, keterampilan gerakan
dasar, kemampuan perseptual, ketepatan, keterampilan kompleks, serta
ekspresif dan interperatif.
Taksonomi tujuan pembelajaran dalam kawasan kognitif menurut Bloom
terdiri atas enam tingkatan yaitu (1) Pengetahuan, (2) Pemahaman, (3) Penerapan,
(4) Analisis, (5) Sintesis, dan (6) Evaluasi.
Pemahaman adalah kemampuan untuk memahami segala pengetahuan
yang diajarkan seperti kemampuan mengungkapkan dengan struktur kalimat lain,
membandingkan, menafsirkan, dan sebagainya. Kemampuan memahami dapat
juga disebut dengan istilah “mengerti”. Kemampuan-kemampuan yang tergolong
dalam taksonomi ini, mulai dari yang terendah sampai yang tertinggi ialah:
a) Translasi, yaitu kemampuan untuk mengubah simbol tertentu menjadi simbol
lain tanpa perubahan makna.
b) Interpretasi, yaitu kemampuan untuk menjelaskan makna yang terdapat di
dalam simbol, baik simbol verbal maupun non verbal.
c) Ekstrapolasi, yaitu kemampuan untuk melihat kecenderungan atau arah atau
kelanjutan dari suatu temuan.
Berdasarkan penjelasan dari para ahli di atas, dapat disimpulkan bahwa
dari suatu konsep, menggambarkan konsep dengan suatu model, mengubah suatu
bentuk ke bentuk lain, membandingkan beberapa bentuk dalam sebuah konsep,
dan menyatakan ulang sebuah konsep.
2. Konsep Geometri Bangun Datar
Travers dkk (1987: 6) menyatakan bahwa: “Geometry is the study of the relationships among points, lines, angles, surfaces, and solids”. Geometri adalah ilmu yang membahas tentang hubungan antara titik, garis, sudut, bidang dan
bangun-bangun ruang.
Geometri menempati posisi khusus dalam kurikulum matematika, karena
banyaknya konsep-konsep yang termuat di dalamnya. Dari sudut pandang
psikologi, geometri merupakan penyajian abstraksi dari pengalaman visual dan
spasial, misalnya bidang, pola, pengukuran dan pemetaan. Sedangkan dari sudut
pandang matematik, geometri menyediakan pendekatan-pendekatan untuk
pemecahan masalah, misalnya gambar-gambar, diagram, sistem koordinat, vektor,
dan transformasi. Geometri juga merupakan lingkungan untuk mempelajari
struktur matematika (Burger & Shaughnessy, 1993:140). Hal ini berarti bahwa
geometri merupakan suatu lingkup materi yang memberikan kesempatan kepada
siswa untuk mempelajari struktur matematika. Dengan mempelajari struktur
matematika, siswa akan terlatih untuk berpikir logis, sistematis, dan kritis, yang
sangat membantu dalam mengembangkan pengetahuan siswa.
Alders (1961, dalam Intan & Bagus, 2012: 2) menyatakan bahwa
hubungannya antara yang satu dengan yang lain”. Ada dua macam geometri, yaitu geometri datar dan geometri ruang. Geometri bidang (geometri datar atau
geometri dimensi dua) membicarakan bangun-bangun datar, sedangkan geometri
ruang membicarakan bangun-bangun ruang dan bangun-bangun datar yang
merupakan bagian dari bangun ruang. Suatu bangun disebut bangun datar apabila
keseluruhan bangun itu terletak pada satu bidang. Suatu bangun disebut bangun
ruang apabila titik-titik yang membentuk bangun itu tidak semuanya terletak pada
satu bidang yang sama.
Geometri digunakan oleh setiap orang dalam kehidupan sehari-hari.
Ilmuwan, arsitek, artis, insinyur, dan pengembang perumahan adalah sebagian
kecil contoh profesi yang menggunakan geometri secara reguler. Dalam
kehidupan sehari-hari, geometri digunakan untuk mendesain rumah, taman, atau
dekorasi (Van de Walle, 1990:269). Usiskin (1987:26-27) mengemukakan bahwa
geometri adalah (1) cabang matematika yang mempelajari pola-pola visual, (2)
cabang matematika yang menghubungkan matematika dengan dunia fisik atau
dunia nyata, (3) suatu cara penyajian fenomena yang tidak tampak atau tidak
bersifat fisik, dan (4) suatu contoh sistem matematika.
Tujuan pembelajaran geometri adalah agar siswa memperoleh rasa percaya
diri mengenai kemampuan matematikanya, menjadi pemecah masalah yang baik,
dapat berkomunikasi secara matematik, dan dapat bernalar secara matematik
(Bobango, 1992:148). Sedangkan Budiarto (2000:439) menyatakan bahwa tujuan
pembelajaran geometri adalah untuk mengembangkan kemampuan berpikir logis,
materi yang lain, dan dapat membaca serta menginterpretasikan argumen-argumen
matematik.
Berdasarkan pengertian para ahli diatas, maka konsep geometri bangun
datar adalah salah satu cabang matematika yang mempelajari titik, garis, dan
sudut, yang terletak pada satu bidang.
3. Karakteristik Siswa SD
Menurut Piaget (Budiningsih, 2004), proses belajar seseorang akan
mengikuti pola dan tahap-tahap perkembangan sesuai dengan umurnya. Pola dan
tahap-tahap tersebut bersifat hirarkis, artinya harus dilalui berdasarkan urutan
tertentu dan seseorang tidak dapat belajar sesuatu yan berada di luar tahap
perkembangan kognitifnya. Piaget membagi tahap-tahap perkembangan kognitif
menjadi empat tahap, yaitu:
a. Tahap sensorimotor (usia 0 – 2 tahun), pada tahap ini bayi mengorganisasikan skema tindakan fisiknya seperti menghisap,
menggenggam, dan memukul untuk menghadapi dunia yang ada di
hadapannya.
b. Tahap preoperasional (usia 2 – 7/8 tahun), pada tahap ini seorang anak belajar berpikir menggunakan simbol-simbol dan pencitraan batiniah,
namun pikiran anak masih tidak sistematis dan tidak logis.
namun hanya ketika anak dapat mengacu kepada objek-objek atau
aktivitas konkret.
d. Tahap operasional formal (usia 11/12 tahun – 18 tahun), pada tahap ini seorang anak dapat mengembangkan kemampuan untuk berpikir sistematis
menurut rancangan yang murni abstrak dan hipotesis.
Siswa SD yang berada pada tahap operasional konkret memiliki beberapa
ciri pokok, diantaranya: (1) Anak sudah mulai menggunakan aturan-aturan yang
jelas dan logis, yang ditandai dengan adanya reversible dan kekekalan, (2) Anak telah memiliki kecakapan berpikir logis, akan tetapi hanya dengan benda-benda
yang bersifat konkret, (3) Anak dapat memanipulasi objek atau gambaran yang
ada di dalam dirinya, (4) Anak dapat menangani sistem klasifikasi, (5) Anak
sudah tidak perlu coba-coba dan membuat kesalahan, karena anak sudah dapat
berpikir dengan menggunakan model “kemungkinan” dalam melakukan kegiatan tertentu.
Dalam penelitian ini, karakteristik siswa SD yang berada dalam tahap
operasional konkret memiliki ciri khusus, yaitu siswa memiliki kemampuan
berpikir logis dengan menggunakan benda-benda konkret, serta mampu untuk
memanipulasi gambaran yang ada di dalam dirinya.
4. Pembelajaran Matematika
Siswa SD yang berada pada umur 7/8 tahun sampai umur 11/12 tahun,
Kemampuan yang tampak dalam fase ini adalah kemampuan dalam proses
berpikir untuk mengoperasikan kaidah-kaidah logika, meskipun masih terikat
dengan objek yang bersifat konkret (Heruman, 2008). Siswa SD masih terikat
dengan objek yang ditangkap dengan pancaindra, sehingga sangat diharapkan
dalam pembelajaran matematika yang bersifat abstrak, siswa lebih banyak
menggunakan media belajar sebagai alat bantu, dan penggunaan alat peraga.
Penggunaan media belajar dan alat peraga dapat memperjelas apa yang
disampaikan oleh guru, sehingga siswa lebih cepat memahaminya. Suwangsih dan
Tiurlina (2006) menyatakan ciri-ciri pembelajaran matematika SD yaitu:
1) Pembelajaran matematika menggunakan metode spiral
Pendekatan spiral dalam pembelajaran matematika merupakan pendekatan
di mana pembelajaran konsep atau suatu topik matematika selalu mengaitkan
atau menghubungkan dengan topik sebelumnya, topik sebelumnya merupakan
prasyarat untuk topik baru, topik baru merupakan pendalaman dan perluasan
dari topik sebelumnya. Konsep yang diberikan dimulai dengan benda-benda
konkret kemudian konsep itu diajarkan kembali dengan bentuk pemahaman
yang lebih abstrak dengan menggunakan notasi yang lebih umum digunakan
dalam matematika.
2) Pembelajaran matematika bertahap
Materi pelajaran matematika diajarkan secara bertahap yaitu dimulai dari
konsep-konsep yang sederhana, menuju konsep yang lebih sulit, selain
pembelajaran matematika dimulai dari yang konkret, ke semi konkret, dan
3) Pembelajaran matematika menggunakan metode induktif
Matematika merupakan ilmu deduktif. Namun karena sesuai tahap
perkembangan siswa maka pada pembelajaran matematika di SD digunakan
pendekatan induktif.
4) Pembelajaran matematika menganut kebenaran konsistensi
Kebenaran matematika merupakan kebenaran yang konsisten artinya
pertentangan antara kebenaran yang satu dengan kebenaran yang lainnya.
Suatu pernyataan dianggap benar jika didasarkan kepada
pernyataan-pernyataan sebelumnya yang telah diterima kebenarannya. Meskipun di SD
pembelajaran matematika dilakukan dengan cara induktif tetapi pada jenjang
selanjutnya generalisasi suatu konsep harus secara deduktif.
5) Pembelajaran matematika hendaknya bermakna
Pembelajaran matematika secara bermakna merupakan cara mengajarkan
materi pelajaran yang mengutamakan pengertian dari pada hafalan. Dalam
belajar bermakna, aturan-aturan dan dalil-dalil tidak diberikan dalam bentuk
jadi, tetapi sebaliknya aturan-aturan dan dalil-dalil ditemukan oleh siswa
melalui contoh-contoh secara induktif di SD, kemudian dibuktikan secara
deduktif pada jenjang selanjutnya.
Berdasarkan pengertian dan ciri-ciri di atas, maka pembelajaran
matematika adalah pembelajaran yang bersifat abstrak, yang diajarkan secara
bertahap dengan menggunakan metode spiral, serta menggunakan penyampaian
5. Pendekatan PMRI
Pendidikan Matematika Realistik Indonesia (PMRI) merupakan salah satu
pendekatan dalam pendidikan matematika yang telah dikembangkan di Belanda
selama kurang lebih 35 tahun yang lalu. PMRI merupakan hasil pengembangan
pembelajaran matematika yang berasal dari pandangan Freudenthal tentang
matematika, yaitu matematika merupakan aktivitas manusia, dan banyak
berhubungan dengan realita. Ini berarti matematika harus dekat dengan anak dan
relevan dengan situasi anak sehari-hari.
Menurut Freudenthal (1973), pembelajaran matematika harus dipandang
sebagai proses. Materi matematika yang disajikan kepada siswa harus berupa
suatu "proses" bukan sebagai barang 'jadi' yang siap "disuapkan" kepada siswa
(Yuwono, 2001). PMRI adalah pendekatan pembelajaran matematika yang
menekankan bagaimana siswa menemukan konsep-konsep atau prosedur-prosedur
dalam matematika melalui masalah-masalah kontekstual. Soedjadi (2001)
mengemukakan bahwa pembelajaran matematika dengan pendekatan realistik
pada dasarnya adalah pemanfaatan realita dan lingkungan yang dipahami peserta
didik untuk memperlancar proses pembelajaran matematika sehingga dapat
mencapai tujuan pendidikan matematika secara lebih baik daripada masa yang
lalu. Realita merupakan hal-hal yang nyata atau konkret yang dapat diamati atau
dipahami siswa lewat membayangkan. Sedangkan yang dimaksud dengan
lingkungan adalah lingkungan tempat peserta didik berada baik lingkungan
Berdasarkan pengertian para ahli di atas, pendekatan PMRI adalah sebuah
pendekatan dalam proses pembelajaran matematika yang menekankan bagaimana
siswa menemukan konsep atau prosedur dalam matematika melalui masalah
kontekstual yang dipahami siswa untuk memperlancar pembelajaran matematika.
6. Prinsip dan Karakteristik PMRI
Prinsip PMRI menurut Heuvel-Panhuizen (1996) dalam Kemendiknas
(2010: 10) adalah sebagai berikut:
a. Prinsip aktivitas, yaitu matematika adalah aktivitas manusia. Pembelajar harus
aktif baik secara mental maupun fisik dalam pembelajaran matematika.
b. Prinsip realitas, yaitu pembelajaran seyogianya dimulai dengan
masalah-masalah yang relistik atau dapat dibayangkan oleh siswa. Masalah realistik
lebih menarik bagi siswa daripada masalah-masalah matematis formal tanpa
makna.
c. Prinsip berjenjang, artinya dalam belajar matemtika siswa melewati berbagai
jenjang pemahaman, yaitu dari mampu menemukan solusi suatu masalah
kontekstual atau relistik secara informal, melalui skematisasi memperoleh
pengetahuan tentang hal-hal yang mendasar sampai mampu menemukan
solusi suatu masalah matematis secara formal.
d. Prinsip jalinan, artinya berbagai aspek atau topik dalam matematika jangan
dipandang dan dipelajari sebagai bagian-bagian yang terpisah, tetapi terjalin
satu sama lain sehingga siswa dapat melihat hubungan antara materi-materi itu
e. Prinsip interaksi, yaitu matematika dipandang sebagai aktivitas sosial. Siswa
perlu dan harus diberikan kesempatan menyampaikan strateginya dalam
menyelesaikan suatu masalah kepada yang lain untuk ditanggapi, dan
menyimak apa yang ditemukan orang lain dan strateginya menemukan itu
serta menanggapinya.
f. Prinsip bimbingan, yaitu siswa perlu diberi kesempatan untuk menemukan
kembali (reinvention) pengetahuan matematika terbimbing.
Sejalan dengan pendapat ahli di atas, maka prinsip PMRI yang diterapkan
dalam penelitian ini adalah prinsip aktivitas, prinsip realitas, prinsip berjenjang,
prinsip jalinan, prinsip interaksi, dan prinsip bimbingan.
Karakteristik PMRI menurut de Lange dalam Zulkardi (2005: 14) ada
lima, yaitu:
1) The use of context (menggunakan masalah kontekstual), masalah kontekstual berfungsi untuk memanfaatkan realitas sebagai sumber aplikasi matematika.
Selain itu juga untuk melatih kemampuan siswa khususnya dalam menerapkan
matematika pada situasi nyata.
2) The use of models (menggunakan berbagai model), istilah model berkaitan dengan model matematika yang merupakan jembatan bagi siswa dari situasi
informal ke formal.
3) Student contributions (kontribusi siswa), menggunakan kontribusi siswa dimana siswa diberi kesempatan untuk mengembangkan strategi-strategi
pengkontribusian prosedur pemecahan, dengan bimbingan guru diharapkan
siswa bisa menemukan.
4) Interactivity (interaktivitas), interaksi antara siswa dengan siswa, siswa dengan guru serta siswa dengan perangkat pembelajaran juga harus ada dalam
pembelajaran. Bentuk-bentuk interaksi misalnya diskusi, penjelasan,
persetujuan, pertanyaan, dan sebagainya digunakan untuk mencapai bentuk
pengetahuan matematika formal dari bentuk-bentuk pengetahuan matematika
informal yang ditentukan sendiri oleh siswa.
5) Intertwining (keterkaitan), struktur dan konsep matematika saling berkaitan, biasanya pembahasan suatu topik (unit pelajaran) harus dieksplorasi untuk
mendukung terjadinya proses pembelajaran yang lebih bermakna.
Sedangkan menurut Treffers (1987) dalam Wijaya (2013: 21-23)
karakteristik PMRI, yaitu 1) penggunaan konteks, 2) penggunaan model untuk
matematisasi progresif, 3) pemanfaatan hasil konstruksi siswa, 4) interaktivitas,
dan 5) keterkaitan. Konteks atau permasalahan realistik digunakan sebagai titik
awal pembelajaran matematika, melalui penggunaan konteks siswa dilibatkan
secara aktif untuk melakukan kegiatan eksplorasi permasalahan. Penggunaan
model berfungsi sebagai jembatan (bridge) dari pengetahuan matematika tingkat konkrit menuju pengetahuan matematika tingkat formal. Hasil konstruksi siswa
menunjukkan pengembangan aktivitas dan kreativitas siswa. Dalam interaktivitas,
belajar bukan hanya suatu proses individu namun juga proses sosial. PMRI juga
mengandung karakteristik keterkaitan, artinya konsep-konsep dalam matematika
Berdasarkan pendapat para ahli di atas, karakteristik PMRI yang
diterapkan dalam penelitian ini adalah penggunaan masalah kontektual,
penggunaan berbagai model, penggunaan kontribusi siswa, interaktivitas, dan
keterkaitan.
7. Pendekatan PMRI Karakteristik Pemodelan
Dalam karakteristik ini, siswa diberi kesempatan untuk menjalani proses
yang disebut matematisasi yang biasanya dimulai dari matematisasi horizontal
lalu dilanjutkan matematisasi vertikal. Dalam proses matematisasi tersebut,
digunakan model of (model of situation) yang dikembangkan menjadi model for (model for formal mathematics). Dalam model of, pengetahuan yang dikembangkan masih dalam bentuk pengetahuan informal yang kemudian akan
dikembangkan dan disempurnakan sendiri oleh siswa menjadi bentuk matematika
formal dalam bentuk model for dengan bimbingan guru. Keberagaman jenis model yang digunakan dapat bergeser dari model konkret, semi konkret, semi
abstrak, sampai kemodel abstrak, merupakan ciri dari terjadinya proses
matematisasi yang berangkat dari situasi yang pada awalnya tidak terstruktur,
general, dan formal.
Penggunaan berbagai model of situation untuk menuju pada matematika formal merupakan sesuatu yang esensial. Hal ini berarti bahwa model dapat
dipandang sebagai suatu alat atau jembatan (Gravemeijer, 1994) yang
menghubungkan bagian konkret ataupun informal dengan bagian abstrak atau
Berdasarkan pendapat ahli di atas, pendekatan PMRI pemodelan dalam
penelitian ini adalah jembatan yang menghubungkan pengetahuan informal siswa
yang dikembangkan dan disempurnakan sendiri oleh siswa menjadi bentuk
pengetahuan formal dengan bimbingan guru.
8. Langkah–Langkah PMRI
Menurut Amin (2004), langkah-Langkah dalam kegiatan PMRI adalah
sebagai berikut.
1) Mengkondisikan siswa untuk belajar. Guru mengkondisikan siswa untuk belajar dengan menyampaikan tujuan pelajaran yang ingin dicapai,
memotivasi siswa, mengingatkan materi prasyarat yang harus dimiliki siswa,
dan mempersiapkan kelengkapan belajar/ alat peraga yang diperlukan dalam
pembelajaran.
2) Mengajukan masalah kontekstual. Guru selalu mengawali pembelajaran dengan pengajuan masalah kontekstual. Masalah kontekstual tersebut sebagai
pemicu terjadinya penemuan kembali (re-invention) matematika oleh siswa. Masalah kontekstual yang diajukan oleh guru hendaknya masalah yang
divergen. Masalah tersebut juga memberi peluang untuk memunculkan berbagai strategi pemecahan masalah. Karakteristik PMRI yang tergolong
pada langkah ini adalah menggunakan masalah kontekstual yang diangkat
sebagai masalah awal dalam pembelajaran untuk menuju ke matematika
formal sampai ke pembentukan konsep.
petunjuk seperlunya terhadap bagian-bagian situasi dan kondisi masalah (soal)
yang belum dipahami siswa. Dengan demikian terdapat kesatuan pemahaman
terhadap masalah kontekstual. Guru juga dapat meminta siswa untuk
menjelaskan atau mendiskripsikan masalah kontekstual dengan bahasa mereka
sendiri. Karakteristik PMRI yang tergolong pada langkah ini adalah
karakteristik keempat, yaitu adanya interaksi antara guru dengan siswa, dan
siswa dengan siswa.
4) Meminta siswa menyajikan penyelesaian atau selesaian masalah. Siswa secara individu atau kelompok menyelesaikan masalah kontekstual yang
disajikan oleh guru dengan cara mereka sendiri, sehingga sangat mungkin
terjadi perbedaan dalam penyelesaian masalah antara siswa yang satu dengan
yang lain. Guru mengamati dan memotivasi siswa memperoleh penyelesaian
soal. Misalnya, "bagaimana kamu tahu?", "bagaimana kamu
mendapatkanya?", "mengapa kamu berfikir demikian?". Pada tahap ini siswa
dibimbing untuk dilakukan "re-invention" atau menemukan kembali ide/ konsep/ definisi matematika. Pada langkah ini siswa diarahkan menggunakan
model-model, gambar, simbol-simbol atau skema-skema yang dikembangkan
oleh siswa sendiri sesuai dengan pengetahuan yang dimiliknya untuk
memudahkan mereka menyelesaikan masalah. Guru tidak perlu memberi tahu
penyelesaian masalah (soal), sebelum siswa memperoleh penyelesaian sendiri.
Karakteristik PMRI yang tergolong pada langkah ini adalah karakteristik
kedua dan ketiga, yaitu menggunakan model dan menggunakan produksi dan
5) Membandingkan dan mendiskusikan penyelesaian atau selesaian masalah. Guru memberikan waktu dan kesempatan kepada siswa untuk
membandingkan dan mendiskusikan jawaban soal secara berkelompok, untuk
selanjutnya dibandingkan (memeriksa, memperbaiki) dan didiskusikan dalam
kelas. Kemudian guru sebagai fasilitator dan moderator mengarahkan siswa
berdiskusi dan membimbing siswa sehingga diperoleh jawaban yang benar.
Pada tahap ini akan tampak penggunaan ide atau kotribusi siswa, sebagai
upaya untuk mengaktifkan siswa melalui optimalisasi interaksi antara siswa
dengan siswa, siswa dengan guru dan siswa dengan sarana prasarana.
Karakteristik yang tergolong pada langkah ini adalah karakteristik ketiga dan
keempat, yaitu mengunakan produksi dan kontruksi oleh siswa dan interaksi.
6) Bernegosiasi. Berdasarkan hasil diskusi kelompok atau diskusi kelas yang telah dilakukan, guru mengarahkan siswa untuk menarik kesimpulan tentang
suatu konsep/ teorema/ prinsip matematika yang terkait dengan masalah
kontekstual yang baru diselesaikan. Karakteristik PMRI yang tergolong pada
langkah ini adalah karakteristik keempat yaitu terdapat interaksi antara siswa
dengan guru dan siswa dengan siswa lain.
Sejalan dengan langkah-langkah PMRI di atas, maka langkah-langkah
PMRI yang diterapkan dalam penelitian ini adalah mengkondisikan siswa untuk
belajar, mengajukan masalah kontekstual, membimbing siswa untuk
menyelesaikan masalah kontekstual, meminta siswa menyajikan penyelesaian
masalah, membandingkan dan mendiskusikan penyelesaian masalah, dan
B. PENELITIAN YANG RELEVAN
Penelitian mengenai penerapan pendekatan PMRI dalam pembelajaran
matematika bukanlah penelitian yang pertama kali dilakukan. Beberapa penelitian
mengenai pendekatan PMRI telah dilakukan sebelumnya, meskipun dalam
pembahasan yang berbeda. Berikut ini beberapa penelitian, yang telah dilakukan
oleh beberapa peneliti yang relevan dengan penelitian ini.
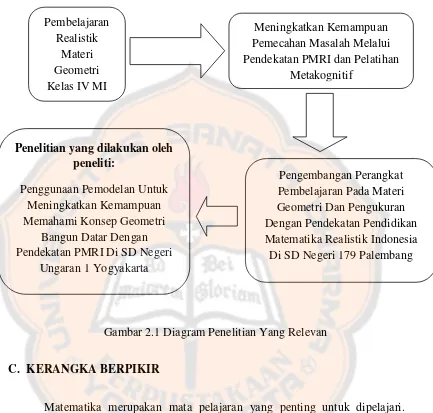
Penelitian yang dilakukan oleh Fuadiah, Zulkardi, Hiltrimartin dengan
judul “Pengembangan Perangkat Pembelajaran Pada Materi Geometri Dan Pengukuran Dengan Pendekatan Pendidikan Matematika Realistik Indonesia Di
SD Negeri 179 Palembang”. Dari hasil penelitian dan pembahasan dapat disimpulkan bahwa hasil analisis data observasi aktivitas siswa mencapai skor
rata-rata 6,47 dan berada pada kategori sangat tinggi. Sedangkan untuk hasil
analisis data tes yang dilakukan menggunakan buku siswa, mencapai skor
rata-rata 90,70 dengan kategori sangat baik.
Penelitian yang dilakukan oleh Danoebroto dengan judul “Meningkatkan Kemampuan Pemecahan Masalah Melalui Pendekatan PMRI dan Pelatihan
Metakognitif”. Dari hasil penelitian dan pembahasan dapat disimpulkan bahwa rata-rata pretes PMRI mencapai 17,55 dan rata-rata postes PMRI mencapai 22,91,
yang menunjukkan adanya peningkatan kemampuan siswa dalam memecahkan
masalah.
bahwa ketuntasan secara klasikal tergolong efektif. Aktivitas siswa dalam
pembelajaran efektif, dan rata-rata aktivitas guru dalam proses pembelajaran
sangat efektif.
Apabila penelitian ini dibandingkan dengan penelitian relevan lainnya,
maka penelitian ini merupakan sebuah penelitian yang dilakukan untuk
melengkapi penelitian yang sudah ada. Jika penelitian-penelitian yang sebelumnya
mengenai pengembangan perangkat pembelajaran, peningkatan kemampuan
pemecahan masalah, dan pembelajaran geometri, maka penelitian ini merupakan
penelitian untuk melihat kemampuan memahami siswa dalam materi geometri
bangun datar. Penelitian ini bertujuan untuk meningkatkan kemampuan
memahami konsep geometri bangun datar siswa kelas V-C SD Negeri Ungaran 1
Yogyakarta pada tahun ajaran 2013/2014 dengan menerapkan pendekatan PMRI
karakteristik pemodelan dalam pembelajaran matematika. Dengan kata lain,
bahwa penelitian ini merupakan penelitian lanjutan dari penelitian yang telah
dilaksanakan sebelumnya.
Desain diagram penelitian yang relevan pada penelitian ini dapat dilihat
Gambar 2.1 Diagram Penelitian Yang Relevan
C. KERANGKA BERPIKIR
Matematika merupakan mata pelajaran yang penting untuk dipelajari.
Materi pelajaran yang ada dalam matematika dapat diterapkan dalam kehidupan
sehari-hari. Oleh karena itu, siswa hendaknya memiliki kemampuan memahami
konsep yang baik dan tepat, serta cara berpikir abstrak yang tepat dalam
mempelajari materi pelajaran matematika, misalnya dalam materi bangun datar.
Dalam mempelajari materi tersebut, diperlukan proses pembelajaran yang menarik
sehingga dapat membantu siswa untuk memahami konsep dengan tepat.
Pengembangan Perangkat Pembelajaran Pada Materi Geometri Dan Pengukuran Dengan Pendekatan Pendidikan Matematika Realistik Indonesia Di SD Negeri 179 Palembang Pembelajaran
Realistik Materi Geometri Kelas IV MI
Penelitian yang dilakukan oleh peneliti:
Penggunaan Pemodelan Untuk Meningkatkan Kemampuan Memahami Konsep Geometri
Bangun Datar Dengan Pendekatan PMRI Di SD Negeri
Ungaran 1 Yogyakarta
Meningkatkan Kemampuan Pemecahan Masalah Melalui Pendekatan PMRI dan Pelatihan
Pembelajaran yang hanya dilakukan secara konvensional dengan metode
ceramah akan membuat siswa merasa bosan dalam mengikuti pembelajaran.
Proses pembelajaran yang ada di kelas kurang menarik sehingga siswa cenderung
ramai sendiri dan tidak memperhatikan penjelasan guru. Siswa cenderung
menerima materi yang diberikan guru dan menyelesaikan suatu masalah dengan
cara yang diberikan guru tanpa ada upaya untuk menyelesaikannya dengan cara
sendiri. Hal ini mengakibatkan kemampuan memahami konsep yang baik dan
tepat kurang dimiliki oleh siswa.
Berdasarkan permasalahan tersebut, peneliti melakukan penelitian dengan
menerapkan pendekatan PMRI dalam proses pembelajaran matematika.
Pendekatan PMRI merupakan sebuah strategi pembelajaran kontekstual yang
dekat dengan kehidupan siswa. Dalam pembelajaran PMRI memandang
matematika sebagai sebuah aktivitas manusia yang bermakna bagi siswa, dan
disesuaikan dengan kondisi kehidupan masyarakat Indonesia.
Penerapan pendekatan PMRI ini diharapkan dapat menjadikan
pembelajaran matematika menjadi lebih menarik dan menyenangkan bagi siswa.
Selain itu, melalui penerapan pendekatan PMRI ini diharapkan dapat membantu
siswa untuk meningkatkan kemampuan memahami konsep geometri bangun datar
D. HIPOTESIS TINDAKAN
Berdasarkan beberapa fakta dan kajian teori yang telah dilakukan,
hipotesis penelitian ini adalah penerapan pendekatan PMRI karakteristik
pemodelan dalam pembelajaran matematika dapat meningkatkan kemampuan
memahami konsep geometri bangun datar siswa kelas V-C SD Negeri Ungaran 1
Yogyakarta tahun ajaran 2013/2014, dengan langkah-langkah: mengkondisikan
siswa untuk belajar, mengajukan masalah kontekstual, membimbing siswa untuk
menyelesaikan masalah kontekstual, meminta siswa menyajikan penyelesaian
masalah kontekstual, membandingkan dan mendiskusikan penyelesaian masalah
33
BAB III
METODE PENELITIAN
Pada bagian ini, peneliti memaparkan mengenai jenis penelitian, setting
penelitian, rencana penelitian, persiapan, rencana setiap siklus, instrumen
penelitian, teknik pengumpulan data, teknik analisis data, dan indikator
keberhasilan.
A. JENIS PENELITIAN
Penelitian ini merupakan Penelitian Tindakan Kelas (PTK). Dalam
penelitian ini, peneliti menggunakan model penelitian yang dikemukakan oleh
Kemmis dan Mc. Taggart, yang terdiri dari empat tahap dan merupakan satu
siklus. Keempat tahap ini yaitu perencanaan, tindakan, observasi, dan refleksi.
Berikut ini merupakan bagan model penelitian menurut Kemmis dan Mc. Taggart:
Gambar 3.1 Model PTK oleh Kemmis & Mc. Taggart
Refleksi
Refleksi Tindakan
Tindakan
Observasi SIKLUS II Perencanaan
Observasi SIKLUS I Perencanaan
Dalam model penelitian Kemmis dan Mc. Taggart, terdapat pembagian
siklus pada setiap pelaksanaan di kelas. Jika rancangan kegiatan pada siklus I
belum berhasil, maka peneliti dapat melanjutkan siklus II dengan pertimbangan
perbaikan atau peningkatan tindakan pada siklus I. Jika rancangan kegiatan pada
siklus II belum berhasil juga, maka peneliti melanjutkan siklus selanjutnya dengan
pertimbangan perbaikan tindakan pada siklus I dan siklus II. Penelitian akan tetap
dilanjutkan ke siklus selanjutnya apabila hasil yang diperoleh belum memenuhi
target capaian akhir siklus yang telah ditentukan di awal penelitian.
B. SETTING PENELITIAN
1. Tempat Penelitian
Penelitian dilakukan di SD Negeri Ungaran I Yogyakarta yang terletak di
Jalan Serma Taruna Ramli No. 03 Kotabaru, Yogyakarta. Peneliti memilih SDN
Ungaran 1 Yogyakarta sebagai tempat penelitian karena berdasarkan observasi
yang dilakukan, guru di SDN Ungaran 1 Yogyakarta belum sepenuhnya
menerapkan pendekatan PMRI dalam pembelajaran matematika. Oleh karena itu,
peneliti menerapkan pendekatan PMRI dalam pembelajaran matematika untuk
meningkatkan kemampuan memahami konsep geometri bangun datar, terutama
untuk siswa Kelas V-C SDN Ungaran 1 Yogyakarta.
2. Subjek Penelitian
Siswa kelas V-C SDN Ungaran I Yogyakarta tahun ajaran 2013/2014 yang
3. Objek Penelitian
Objek dalam penelitian ini adalah kemampuan memahami konsep geometri
bangun datar siswa kelas V-C SDN Ungaran 1 Yogyakarta tahun ajaran
2013/2014 melalui penerapan pendekatan PMRI.
C. RENCANA TINDAKAN
1. Persiapan
Sebelum melaksanakan penelitian ini, peneliti melakukan beberapa
persiapan diantaranya, yaitu:
a. Menyiapkan surat izin dari Universitas Sanata Dharma untuk
melaksanakan penelitian di SDN Ungaran 1 Yogyakarta.
b. Meminta izin serta menyerahkan surat izin kepada Kepala SDN Ungaran 1
Yogyakarta untuk melaksanakan penelitian.
c. Melakukan observasi kegiatan pembelajaran Matematika di kelas V-C
SDN Ungaran 1 Yogyakarta dan mewawancarai guru kelas V-C.
d. Mengidentifikasi masalah pembelajaran Matematika yang ada di kelas
V-C.
e. Merumuskan masalah.
f. Menyusun rencana tindakan tiap siklus.
g. Menyusun silabus, RPP, kisi-kisi soal, instrumen penilaian, serta
instrumen penelitian.