t - 5 I b I b - 1 Latnpiran 1. Bidang Cartesius untuk b.,, b3, b,,..., b12 Diperoleh T (f,g, h) = - Diperoleh T (f, g, h) = 1 Diperoleh ~*~(j,g,hj = 1

Latnpiran 1. Bidang Cartesius untuk b.,, b3, b,, ..., b12

I

b

I b - 1 Diperoleh T ( f ,g, h ) = - Lo,,' 112 1 312 2 512 2 b2

- - -

Diperoleh T ( f ,

g ,

h ) = 1 L , - I + I L4-I LI,-I Diperoleh ~ * ~ ( j , g , h j = 1 . I Lo,, 112 1 312 2 512

t

- 5 Diperoleh T ( f , g , h j z - 2 L J . / L , I I Lo, 1 L1,-1 5 Diperoleh Tb7 ( j , g , h ) = - 2 LII, a 112 1 312 2 512 Diperoleli Tb4 ( 7 ,

g,

hj

= 2

Diperoleh

Tb"(f.g,h)

= 2 1 Diperoleh

~ ~ ( f , g , h )

=

-

2 3 Diperoleh

T b k 2 ( f , g ,

h )

= - 2 5 Diperoleh T h o

(f.

g , h )

>

5

Lampiran 2. Diagram alir algoritma untuk menentukan

R&

-

Tentukan matriks

angora

Dk

Tidak

Untuk matriks yang bernila sama diambil salah satu saj

$.

Tentukan anggota

Hk,

Rk,

Ek

Ya Ak=Aa, Ak = min ET(s(k)) r(k)e& Selesai

Lampiran 3. Tahap-tahap algoritma untnk menentukan R$

Tahap inisialisasi : Ao=47/48 cia1 s(1) = [[l)2[;j,[;i)3[! 1

~ ] 7 [ - ~ ] * [ ~ ] 3 [ ~ ~ ) 7 [ ~ 1 ) ]

,

* Tahap 1: Diketahui k = l sehingga s(k) = s(1). Banyaknya matriks s(1) adalah 2 * ' = ~ ~ = 8 ,

yaitu:

sfl)=[~),[~),[~l),[~~),[j],[~],[j~),[~l)]

1 -1 -1 -1

,

Karena k = l maka jelas bal~wa Dl =s(l). Dari kedelapau matriks itu

akan

ditentukan yang menjadi anggota HI ,RI,

dan

El. Karena matriks bernilai sama dengan

d i d [:jnntnk &;roses selanjutnya. Begitu pula mat&

maka bisa diarnbil matriks

.

Untuk s(l)= 1

[:I

; artinya pemain I, pemain 11, &II pemain 111 melanjntkan arah sebelumnya

. .

pada t=1/2. T(cI,s(l)) menyatakau waktu pertemuan peltama kali dari dua pemain yang berdekatan dengan posisi awal pa& cl (0,1,2,+, 1. +) untnk [0,1/2]

dan

dilanjutkan dengan

s(1) untuk [112,1]. Apabila digambarkan pada bidang Cartesius diperolel~ l~asil sebagai berikut:

Karena pada waktu t=l

,

permainan belum berakhir, maka diperoleh T(cl,sl(l))=m. Dengall cara yang sama untuk ke-23 kasus yang lain diperoleh:

24

.

makadiperoleh hasil ~ T * ( c ~ , s ( l ) ) = 21

,

sehingga

i=l

Dari hasil ini, diperoleh bahwa ET'(~(I))<A,, Apabila T(c,s(l)) digambarkan pada bidang Cartesius diperoleh hasil :

sehingga T(c,s(l))= m. Hal ini menghasilkan maksCec T(c,s(I)) =a, sehingga M(s(l))=O. / I \

Karena ET'(s(1)) 410 dan M(s(l))=O

,

maka s(1) = 1 mempakan anggota HI . Dengan

I-J

cara perhitungan yang sama seperti

[:]

1 dan

[IJ,

maka untuk dua matriks yang lain diperoleh :

-

1 E HI dan - 1 E R,. Pada tahap ini El tidak mempunyai anggota.

I-lj

.

,

I-lj

.

,

Karena El himpunan kosong, maka A1=A0=47/48. Pada tahap ini ada dua matriks anggota ( 1 ) 1 1 )

1 dan -1 sehingga HI bukan himpunan kosong. Akibatnya proses

-"

1-

J

1-

J

ditemskax pada tahap berikutnya untuk k=2.

Tahap 2:Diketahui k=2 selungga s(k) = s(2). Pada tahap 2 ini, matriks s(2) yang diproses adalah anggota

Dz

yaitu matriks anggota HI dengan tambahan satu kolom matriks s(1). Pada tahap

Lampiran 4. Pembuktian Lema 2 dan Leilia 5

Bukti Lema 2:

Misalkan pemain terdekat dengan peinain i adalah pemain r dan s, dengan MS. Diasumsikan bahwa pemain i menggunakan strategi

J

dan mengikuti lintasan Ll,,(.), sehigkan pemain r dan s n~enggunakan strategi g dan h dan mengikuti lintasan

Lp(.)

dan Lo,&), dengan

fi

y €{+I; -1). Bukti

dibagi menjadi kemungkinan-kemungkinan berikut:

Kemunglunan 1: Satu agen pemain i bertemu dengan agen pemain r pada

fi,~

sedangkan agen lain pemain i tidak bertemu dengan agen peinain manapun pa& tPl,

Kemunglunan 2: Satu agen pemain i bertemu dengan agen penlain r pada tj,~, sedan- agen lain pemain i bertemu agen pemain s pada

t,,).

Kemungkinan 3: Hanya satu agen pemain i yang bertemu dengan agen kedna pemain r dan s pada $+I, sedangkan agen pemain i yang lain tidak bertemu dengan agen pemain manapun.

Kejadian dimana satu agen pemain i memenuhi kemungkinan 3 sedangkan agen pemain i lainnya bertemu agen pemain lain tak mungkin terjadi. Hal ini karena jika kemungkinan 3 berlaku, maka :

af($+d

+ 1 = .Bg($+3 + 2 = yh ($+I) yang berakibat -aJ($+J + 1 =

-.Bgft,,J

= -yh

($+3

+ 2

sehi~igga diperoleh

-a

f ($+I)

+ 1

# -,13g($+I)

+

2

clan

-a J($+))

+

1 t -yh ($+I). Oleh karena itu lintasan pada Ll,., tidak berpotongan dengan lintasan agen-agen pemain lain pada

ti,).

Kemungkinan dimana agen pemain i bertemu dengan agen kedua pemain r ( atau s

,

tapi bukan kednanya), &pat diperlakukan dengan cara

yang

sama seperti kemungkinan 1. Unmk keperluan pembuktian lema, maka tanpa mengurangi keumuman &pat diasumsikan bahwa satu agen pemain i yang dibahas adatall agen yang mengikuti lintasan strategi L1,1(1).

Kemungkinan 1:

Misalkan

1

J($+I) - J(tJ

1

<

$+I

-

4,

maka $-$+~<fl$+~)

-f$<

$+I

-

$.

Perhatihi bahwa jika penlain i bertemu deiigan pemain r di $+I, maka

Lzpt$+l)=fl$+l) + 1 ( 6 )

sehingga

LZptt)- J(t)

-

1 > 0, Vf<lj+~. Akibatnya, &pat dituliskan strategi baru : t - t j

+

J(tj) u n t u k t ~ [ t ~ , t ~ + , ] r ( t ) = J(t) selainnya, sehingga &,(tj+1)-7(t,+,)-1= &p(f+l)-f+l + t j - J ( t j ) - l

<

&p(tj+I)- t,+~ + tj + t j + ~ -tj - J(tj+1)-1 = 0

-

Karena L2P(.)

dan

f

(.)

kontinu yang berakibat bahwa terdapat

q+,

E (t, .tj+,) sedemikian sehingga

= [L2@ @,+1)-L2fl

)I

= l ( k f t j + l ) + 2 ) - (&(T+l) + 211 = ] k ( t j + I I-&(<+,

11

= l ~ { g ( t , + ~ ) - a < + , )>I

=\PI

[ g ( t j + , ) - g K + l ) [ = Ig(t,+l)-g(<+l)[ karenap = +l

5 Itj+,

-<.+lI

karenag E P

-

-

-

tj+1

-

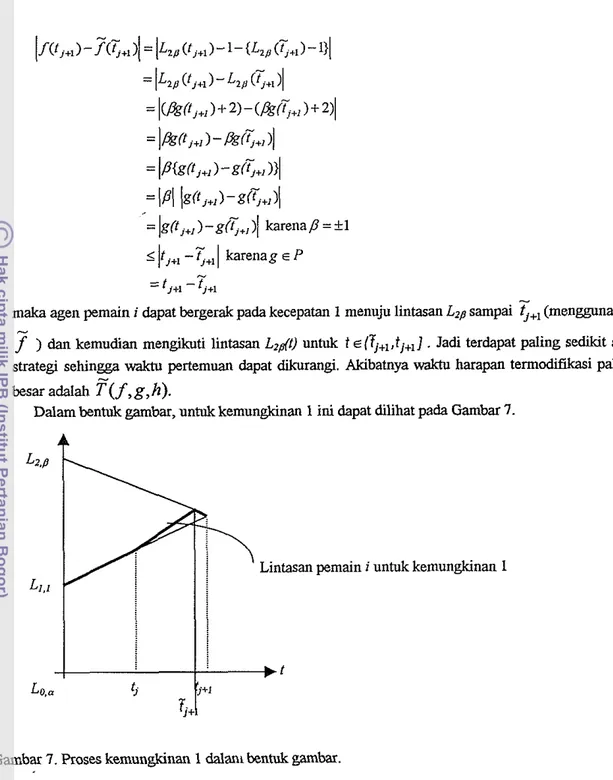
f j + l

maka agen pemain i &pat bergerak pada kecepatan 1 menuju lintasan Lz8 sampai

<+,

(menggunakan

-

f

) clan kemudian mengikuti lintasan L2dt) untuk t E ( T ~ + , , ~ ~ + ~ ]

.

Jadi terdapat paling sedikit satu strategi sehingga waktu pertemuan &pat dikurangi. Akibatnya waktu harapan termodifikasi paling besar adalah

T"(

f

,g,h).

Dalam bentuk gambat, untuk kemungkinan 1 ini &pat dilihat pa& Gambar 7.

4

Gambar 7. koses kemungkinan 1 dalanl bentuk gambar

Kemungkinan 2:

Karena pertemuan antara agen-agen tejadi pertamald pada waktu $+I

,

maka L2/Xt) -J(t)-1 > 0

dan

L d t )

+

f(t) -1

<

0

,

untuk semua t

<

t j t l .

Misalkan V(tj+,)

-flvl<

5+1

-ti.

dan

t

-

t j

+

J ( t j ) untuk t E [t,, t j U ] selainnya

maka dillasilkan : ~ , ~ ( t ) - f " ( t ) - l > 0 dan

{

~ o ~ ( t ) + ? ( t ) - l < o

~ 2(fj+l , )-7(tj+l)- 1 < 0, Lor (fj+,)+ 7(fj+,)

>

0.

-

Karena Lzd.), LO&.) dan

f

()

kontinu yang menmbatkan terdapat <+j,i,+l E (tj,tj+j)

.

sedemikian sehinga

L,, (q+,) =

+

1 L,, (ij+,) = -7(ij+,)

+

1.

Misalkan f' = maks(i;+,

,Fit,),

maka

\f(t,+,)-7(t.)\ =lf(tj+,)-t. + t j

-JV,)l

= I f ( t j + , ) - f ( f j ) - t . + f j l <Ij+,-t, -t

-

+ t j

I

-t-1

= t .

-t J+l Jadi

1

f(tl+,)-7(t*4 < t l i l - t ' ,

maka satu agen pemain

_-

i dapat bergerak pada kecepatan 1 menuju lintasan Lzp sampai

t j , (menggunakan

7

) dan kemudian mengikuti lintasan Lzdt) untuk t E ( ~ + l , t , + l ] , sedangkan satn

agen yang lain bergerak menuju lintasan LO,, sampai

i1+,

dan kemudian mengikuti lintasan Lo,#)

untuk

t ~(i,+~,t,+,]. Jadi terdapat paling sedikit satn strategi sehingga waktu pertemuan dapat dikurangi. Akibatnya waMu harapan temodifikasi paling besar adalah

T"(

f

,g,h).

Karena pertemuan antara satu agen pemain i dengan agen pemain r dan s terjadi pertamakali pa& waktuIi,~.maka

L z d f ) -/It)-1

>

0 dan L d t ) -/It)-1

<

0 , untuk semua 1

<

$+,.

Misalkan

Ifl$+~)

-flII,l< $1

- r/,

dan

t - t , + j ( t , ) untuk t c [ t j , t j + , ]

f ( t ) selainnya

maka dihasilkan :

-

Karena Lzd.), L d . ) dan

f

()

kontinu yang mengahbatkan terdapat

T+,

E (t,. t,,) dengan

<+,

<

t ,

-

1 1 2 3 m T ( f ; g , h ) = - ( a , x - + a , x - + a , x - + a m x-) 24 2 2 2 2 1 1 2 3 m = - ( 1 2 x - + 6 x - + 5 x - + - ) 24 2 2 2 2 1 39 m =-(-+-) 24 2 2 1 = -(39+m). 48

Berdasarkan Lema 1, maka diperoleh: 47

1 47

- ( 3 9 + m ) < -

48 48

m

<

8,