BAB 2 LANDASAN TEORI

(1)

BAB 2

LANDASAN TEORI

2.1 Persediaan

2.1.1 Definisi Persediaan

Persediaan adalah stok bahan yang digunakan untuk memudahkan produksi atau untuk memuaskan permintaan pelanggan. Secara khusus persediaan meliputi bahan baku, barang dalam proses dan barang jadi (Schroeder, 2000, P. 304). Persediaan juga bisa berarti penyimpanan sumber daya yang digunakan untuk memenuhi kebutuhan saat ini atau di masa mendatang (Heizer and Barry, 1996, P. 574). Persediaan meliputi persediaan bahan mentah, barang dalam proses, barang jadi, dan bahan-bahan pembantu atau bahan pelengkap (Ebert, 1996, P. 453). Persediaan adalah bahan atau barang yang disimpan yang akan digunakan untuk memenuhi tujuan tertentu, misalnya untuk proses produksi perakitan, untuk dijual kembali, untuk suku cadang dari suatu peralatan atau mesin (Herjanto, 1999, P. 219).

2.1.2 Fungsi Pengendali Persediaan

Persediaan mempunyai beberapa fungsi (Herjanto, 1999, P. 220), antara lain:

1. Menghilangkan resiko keterlambatan pengiriman bahan baku atau barang yang dibutuhkan perusahaan.

(2)

2. Menghilangkan resiko jika bahan yang dipesan tidak baik atau barang yang dibutuhkan perusahaan.

3. Menghilangkan resiko terhadap kenaikan barang atau inflasi.

4. Untuk menyimpan bahan baku yang dihasilkan secara musiman sehingga perusahaan tidak akan mengalami kesulitan jika bahan itu tidak tersedia di pasaran.

5. Mendapatkan keuntungan dari pembelian berdasarkan pemotongan kuantitas (quantity discounts).

6. Memberikan pelayanan kepada pelanggan dengan tersedianya barang yang diperlukan

2.2 Model Optimalisasi

Optimalisasi adalah sarana untuk mengekspresikan, dalam model matematika, hasil dari penyelesaian suatu masalah dengan cara terbaik (Nash dan Sofer, 1996, P. 3). Hal ini dapat diartikan sebagai menjalankan bisnis untuk memaksimalkan keuntungan dan efisiensi serta meminimalkan kerugian, biaya atau resiko. Keinginan untuk memecahkan masalah dengan model optimalisasi secara umum digunakan pada hampir semua bidang aplikasi.

Model optimalisasi telah digunakan selama berabad-abad. Pada masa sekarang ini menjadi sangat cocok jika ingin mengembangkan bisnis menjadi semakin besar dan rumit. Para insinyur pun menjadi semakin ambisius. Dalam banyak keadaan, tidak lagi mungkin untuk membuat keputusan tanpa bantuan model optimalisasi. Sebagai contoh, dalam sebuah kerjasama multinasional yang

(3)

besar, persentase kecil suatu perkembangan dalam proses operasi mungkin meningkatkan penambahan keuntungan hingga jutaan dollar.

Untuk model yang besar, dengan segala kerumitan yang ada, akan sedikit bermasalah jika tidak dapat diselesaikan. Beberapa dekade terakhir telah menjadi saksi pengembangan yang sangat mengejutkan dalam hardware dan software komputer, dan kemajuan ini telah membuat model optimalisasi menjadi alat yang umum dipakai dalam bisnis, ilmu pengetahuan, dan perusahaan. Sekarang ini, sangat mungkin untuk menyelesaikan permasalahan dengan ribuan atau bahkan jutaan peubah.

2.2.1 Sistem Persamaan Linear Simultan

Sistem persamaan linear adalah pusat dari hampir semua algoritma optimalisasi, dan bagian dari model optimalisasi yang luas (Nash dan Sofer, 1996, P. 4).

Sistem persamaan linear simultan timbul hampir di setiap cabang matematika, dalam beberapa hal, persamaan ini timbul langsung dari perumusan awal dari suatu permasalahan. Di dalam hal lain, penyelesaian dari persamaan merupakan salah satu bagian dari penyelesaian beberapa macam permasalahan lain.

Dalam aljabar, terdapat dua macam metode dalam menyelesaikan sistem persamaan linear simultan, yaitu: eliminasi dan determinan. Dalam menyelesaikan sistem persamaan linear simultan dengan tiga peubah, metode determinan mempunyai kelebihan dibandingkan dengan metode eliminasi.

(4)

Tetapi dalam menyelesaikan sistem persamaan linear simultan dengan peubah yang lebih banyak, metode determinan menjadi sangat tidak praktis. Hal ini dikarenakan dalam menyelesaikan persamaan simultan dengan n peubah, diperlukan (n – 1)(n + 1)! perkalian. Sehingga untuk menyelesaikan suatu persamaan simultan dengan sepuluh peubah dengan menggunakan metode determinan, diperlukan 359.251.200 perkalian.

Kurva merupakan pendekatan terbaik dari suatu himpunan data percobaan yang berkaitan dengan penyelesaian suatu sistem persamaan simultan. Penyelesaian satu set n persamaan dengan n peubah. Jika setiap suku dari setiap persamaan mengandung hanya satu peubah, dan setiap peubahnya berpangkat satu, maka persamaan tersebut disebut sistem persamaan linear. Apabila menggunakan dua peubah, grafik persaman linear yang terjadi berupa garis lurus. Apabila menggunakan tiga peubah, grafik persaman linear yang terjadi berupa sebuah bidang. Sedangkan jika menggunakan lebih dari tiga peubah, maka grafik yang terjadi disebut sebagai hyperplane. Jawaban yang dicari dari sistem persamaan linear simultan adalah satu himpunan nilai dari n peubah, yang apabila nilai-nilai tersebut disubtitusikan ke persamaan linear sebanyak n, maka diperoleh kesamaan pada semua sistem persamaan linear secara simultan.

Sistem persamaan linear simultan belum tentu mempunyai jawaban. Suatu sistem persamaan linear simultan sembarang dapat mempunyai jawaban, tetapi juga tidak mustahil jika tidak mempunyai jawaban. Terdapat tiga kemungkinan jawaban dari sistem persamaan linear simultan sembarang, yaitu:

(5)

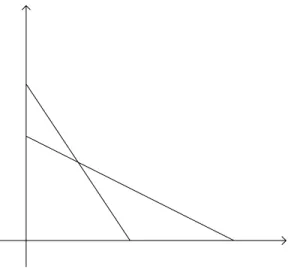
a. Sistem mempunyai jawaban yang unik. Contohnya:

3 x + 2 y = 6

x + 2 y = 4 (2.1)

Jawaban yang memenuhi persamaan (2.1) adalah x = 1 dan y = 1,5. Tidak ada pasangan lain dari nilai x dan y yang dapat memenuhi persamaan (2.1). Sistem semacam ini yang menjadi tujuan utama dari pencarian suatu jawaban. Persamaan (2.1) dapat digambarkan diagram Cartesian dua dimensi, seperti pada gambar 2.1. Pada gambar 2.1, dapat dilihat bahwa kedua garis berpotongan hanya pada satu titik. Koordinat titik tersebut merupakan jawaban yang dicari dan yang dapat memenuhi sistem persamaan linear simultan (2.1).

(6)

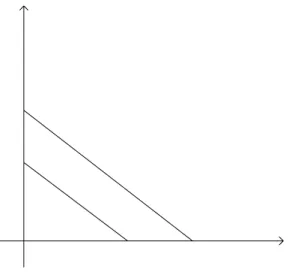
b. Sistem tidak mempunyai jawaban. Contohnya: 3 x + 4 y = 10

6 x + 8 y = 12 (2.2)

Sistem persamaan linear simultan (2.2) tidak akan memiliki jawaban. Grafik persamaan (2.2) dapat dilihat pada gambar 2.2. Dapat dilihat terdapat dua garis yang sejajar. Kedua garis tersebut tidak akan saling berpotongan ataupun bersinggungan, sehingga persamaan (2.2) tidak akan mempunyai jawaban.

Gambar 2.2 Sistem persamaan linear simultan yang tidak mempunyai jawaban

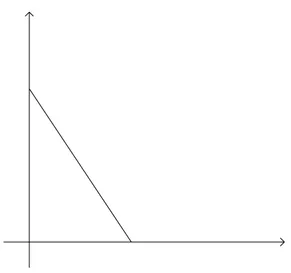
c. Sistem mempunyai jumlah jawaban yang tak berhingga. Contohnya:

3 x + 2 y = 6

6 x + 4 y = 12 (2.3)

Sistem persamaan linear simultan (2.3) mempunyai banyak jawaban yang dapat memenuhi persamaan tersebut, seperti: x = 2, y = 0 ; x = 0, y = 3 ; x = 1, y = 1,5 ; dan seterusnya.

(7)

Gambar 2.3 Sistem persamaan linear simultan yang mempunyai jumlah jawab tak berhingga

Sistem persamaan garis yang sejajar dan sistem persamaan garis yang bersinggungan dikatakan singular. Sistem merupakan singular atau tidak, terkadang dapat diketahui dari perumusan suatu persoalan. Jika informasi tersebut tidak ada, maka tergantung dari metode penyelesaiannya untuk mengetahui suatu sistem adalah singular atau tidak, atau dapat juga melakukan pengujian eksplisit untuk mengetahui kemungkinannya.

Suatu pengujian dapat dilakukan dengan cara menghitung determinan dari koefisien suatu sistem. Jika hasil perhitungan determinan tersebut adalah nol, maka sistem tersebut merupakan singular. Kekurangan dari pengujian tersebut adalah usaha menghitung determinan hampir sama dengan usaha menyelesaikan persamaan.

Dari sudut pandang matematika, presisi tak terhingga dari suatu sistem memiliki dua kemungkinan, yaitu: singular atau tidak. Dari sudut pandang

(8)

perhitungan praktis, hampir semua sistem merupakan singular, yang memberikan jawaban yang mempunyai keandalan kecil.

Pada umumnya, terdapat dua macam teknik numerik untuk menyelesaikan sistem persamaan linear simultan, yaitu: metode langsung yang berhingga dan metode tak langsung yang tak berhingga. Metode langsung pada prinsipnya (dengan mengabaikan galat pembulatan) akan memberikan jawab eksak, bila operasi matematika berhingga jumlahnya. Sedangkan metode tak langsung, pada prinsipnya membutuhkan suatu operasi matematika yang tak berhingga banyaknya untuk memberikan jawab eksak. Dengan kata lain metode tak langsung mempunyai galat pembulatan, sedangkan metode langsung tidak mempunyai galat pembulatan.

Dalam sistem dengan kondisi buruk, galat pembulatan dalam metode langsung akan menghasilkan jawaban yang tidak berarti. Sedangkan metode tak langsung walaupun secara teoritik ada galat pemotongannnya, metode ini mungkin lebih baik karena galat pembulatan metode ini tidak mengumpul.

2.2.2 Metode Numerik

Metode numerik adalah salah satu alternatif pencarian jawaban dalam permasalahan matematika yang tidak dapat diselesaikan secara analisis. Tujuan dari metode ini adalah mencari metode yang terbaik untuk memperoleh jawaban yang berguna dari persoalan matematika dan untuk menarik informasi yang berguna dari berbagai jawaban yang dapat diperoleh.

(9)

Dalam mengerjakan metode numerik terdapat beberapa cara pendekatan (Djojodihardjo, 2000, P. 2), yaitu:

a. Pendekatan atau penyederhanaan perumusan persoalan sehingga dapat dipecahkan secara eksak.

b. Mengusahakan diperolehnya jawab pendekatan dari persoalan yang perumusannya eksak.

c. Gabungan dari kedua cara pemecahan diatas.

Pada umumnya, metode numerik tidak mengutamakan diperolehnya jawaban yang eksak (tepat), tetapi mengusahakan perumusan metode yang menghasilkan jawaban pendekatan yang memiliki selisih sebesar suatu nilai yang ditentukan berdasarkan kesepakatan dari jawab eksak.

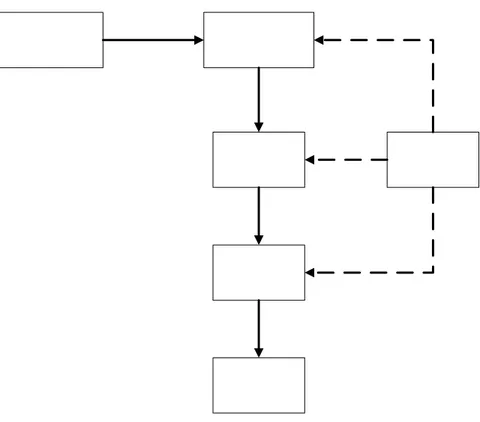
Proses pemecahan persoalan pada umumnya berlangsung dalam tiga tahap (Djojodihardjo, 2000, P. 2), yaitu:

a. Perumusan secara tepat dari model matematik dan model numerik yang berkaitan.

b. Penyusunan metode untuk memecahkan persoalan numerik. c. Penerapan metode untuk menghitung jawaban yang dicari.

(10)

Gambar 2.4 Proses pemecahan persoalan dalam metode numerik

2.2.3 Cramer’s Rule

Cramer’s rule adalah suatu rumusan untuk menyelesaikan sistem persamaan linear simultan berdasarkan determinan. Rumusan ini dinamakan oleh Gabriel Cramer (1704-1752), seorang matematikawan berkebangsaan Swiss.

2.2.3.1 Cramer’s Rule untuk dua persamaan dengan dua peubah

Cramer’s rule menyatakan bahwa penyelesaian untuk ax + by = e dan cx + dy = f didapat dari perhitungan determinan.

(11)

d c b a f c e a y d c b a d f b e x= _L = (2.4)

Berikut ini merupakan bukti dari teorema (2.4) berdasarkan metode perkalian cross vektor.

Ketika kita menemukan sistem persamaan linear simultan seperti :

⎩ ⎨ ⎧ = + = + f dy cx e by ax (2.5)

Kita dapat menemukan x dan y dengan menggunakan determinan berikut : 0 , ≠ = = = D f c e a D d f b e D d c b a D x y D D y D D x= x = y c d a b c f a e y d c b a d f b e x= = (2.6)

Determinan ini merupakan aturan dari Cramer.

Produk alternatif _⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ∧ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ d b c a

adalah area parallelogram yang dihasilkan

dari vektor _⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ c a dan _⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ d b . . 0 . _⎟⎟= ⎠ ⎞ ⎜⎜ ⎝ ⎛ ∧ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ∧ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ c a c a bc ad d b c a (2.7)

(12)

Kemudian gunakan produk alternatif untuk menemukan sistem persamaan linear simulatan (2.5).

⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⇔ f e d b y c a x (2.8)

Persamaan (2.8) dikalikan dengan vektor _⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ d b

. Selain itu, persamaan

(2.8) juga dikalikan dengan vektor _⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ c a

, sehingga terdapat dua persamaan yang

baru: ⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ∧ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ∧ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ∧ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ∧ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ∧ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ∧ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⇒ c a f e c a d b y c a c a x d b f e d b d b y d b c a x (2.9)

Persamaan (2.9) dihitung dengan mempertimbangkan syarat (2.7) :

⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ∧ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ∧ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ∧ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ∧ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⇒ c a f e c a d b y d b f e d b c a x (2.10) ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ∧ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ∧ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ∧ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ∧ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = ∴ c a d b c a f e y d b c a d b f e x , (2.11)

Hasil (2.11) dapat diekspresikan menjadi determinan seperti berikut:

c d a b c f a e y d c b a d f b e x= = (2.12)

(13)

2.2.3.2 Cramer’s Rule untuk tiga persamaan dengan tiga peubah Terdapat sistem persamaan linear simultan:

⎪ ⎩ ⎪ ⎨ ⎧ = + + = + + = + + 3 3 3 3 2 2 2 2 1 1 1 1 d z c y b x a d z c y b x a d z c y b x a (2.13)

Persamaan (2.13) mempunyai determinan:

3 3 3 2 2 2 1 1 1 c b a c b a c b a D≡ (2.14)

Kemudian kalikan D dengan x, gunakan sifat determinan mengenai perkalian determinan dengan suatu konstanta, nilainya ekuivalen dengan perkalian pada setiap input dalam suatu kolom dengan konstanta tersebut. Sehingga: 3 3 3 2 2 2 1 1 1 3 3 3 2 2 2 1 1 1

c

b

x

a

c

b

x

a

c

b

x

a

c

b

a

c

b

a

c

b

a

x

=

_(2.15)

Sifat determinan yang lain mengijinkan kita untuk menambahkan suatu konstanta dikalikan dengan suatu kolom ke suatu kolom dan mendapatkan determinan yang sama, maka tambahkan y dikalikan kolom 2 dan z dikalikan kolom 3 ke kolom 1 : 3 3 3 2 2 2 1 1 1 3 3 3 3 3 2 2 2 2 2 1 1 1 1 1

c

b

d

c

b

d

c

b

d

c

b

z

c

y

b

x

a

c

b

z

c

y

b

x

a

c

b

z

c

y

b

x

a

xD

=

+

=

_(2.16)

Jika d = 0, maka persamaan (2.16) akan menghasilkan xD = 0, sehingga sistem persamaan linear simultan tersebut mempunyai jawaban yang tidak dapat

(14)

diturunkan (contohnya, (0,0,0)) hanya jika D = 0. Jika d≠0 dan D = 0, maka persamaan tidak mempunyai jawaban unik. Sebaliknya jika d≠0 dan D≠0, maka jawaban yang diperoleh adalah:

D c b d c b d c b d x 3 3 3 2 2 2 1 1 1 = (2.17)

Dengan perhitungan yang hampir sama, maka diperoleh:

D c d a c d a c d a y 3 3 3 2 2 2 1 1 1 = (2.18) D d b a d b a d b a z 3 3 3 2 2 2 1 1 1 = (2.19)

2.2.3.3 Cramer’s Rule untuk n persamaan dengan n peubah Terdapat sistem persamaan linear simultan:

⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ n n nn n n n d d x x a a a a a a M M M L O L M M 1 1 1 2 12 1 11 (2.20) dengan determinan: nn n n n a a a a a a D _M L O L M M 1 2 12 1 11 ≡ (2.21)

(15)

Jika d = 0, maka persamaan akan mempunyai jawaban yang tidak dapat diturunkan hanya jika D = 0. Jika d≠0 dan D = 0, maka persamaan tidak mempunyai jawaban unik. Selain itu (d≠0 dan D≠0), hitung:

nn k n n k n n n k k k a a d a a a a d a a D L L M O M M M O M L L ) 1 ( ) 1 ( 1 1 ) 1 ( 1 1 ) 1 ( 1 11 + − + − ≡ (2.22)

Kemudian hitung xk =Dk /D untuk 1≤k ≤n.

2.2.4 Gauss-Jacobi Method

Metode Gauss-Jacobi adalah salah satu metode menyelesaikan persamaan matriks pada matriks yang tidak mempunyai nilai nol pada diagonal utamanya (Bronshtein dan Semendyayev, 1997, P. 892). Setiap elemen diagonal dihitung, dan nilai pendekatan tersebut dimasukkan. Proses tersebut diiterasi hingga mencapai konvergen. Metode ini dinamakan oleh Carl Gustav Jacob Jacobi (1804-1851), seorang matematikawan berkebangsaan Jerman.

Metode Gauss-Jacobi dapat dengan mudah didapat dengan cara memeriksa satu per satu dari n persamaan dalam sistem persamaan linear simultan Ax = b. Dalam persamaan ke-i:

n i b x a i n j j ij , 1, , 1 K = =

∑

= (2.23)

Kemudian menghitung nilai x dengan menganggap nilai x awal telah i ditentukan:

(16)

ii n i j j k j ij i k i a x a b x

∑

≠ = + − = 1 ) ( ) 1 ( (2.24)

Rumus tersebut yang disebut metode Gauss-Jacobi.

Matriks yang dapat dikerjakan dengan metode Gauss-Jacobi harus merupakan matriks dominan diagonal.

Dalam kondisi matriks, definisi dari metode Gauss-Jacobi dapat diekspresikan sebagai: b D x U L D x(k+1) = −1( + ) (k) + −1 (2.25) ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = − − nn n n a a a a D 0 0 0 0 0 0 0 0 0 0 0 0 1 , 1 22 11 L L M M O M M L L ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − − − − − − = − − − 0 0 0 0 0 0 0 0 0 0 1 , 2 1 2 , 1 1 , 1 21 n n n n n n a a a a a a L L L M M O M M L L ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − − − − − − = − − − 0 0 0 0 0 0 0 0 0 0 , 1 2 1 , 2 1 1 , 1 12 L L M M O M M L L n n n n n n a a a a a a U

Dimana matriks D, -L, dan -U masing-masing mewakili diagonal utama, diagonal segitiga bawah, dan diagonal segitiga atas dari suatu matriks A dengan persamaan Ax = b dan jumlah iterasi sebanyak k.

(17)

Rumusan (2.24) diiterasikan hingga mencapai keadaan konvergen. Cara untuk menentukan keadaan konvergen metode Gauss-Jacobi adalah jika semua nilai x_i(k+1) dikurang x_i(k) mencapai selisih yang telah ditentukan.

Mengurangi x_i(k+1) dengan x_i(k), menghasilkan:

n i e a a e n i j j k j ij ii k i , 1, , 1 1 ) ( ) 1 ( K = − =

∑

≠ = + (2.26)

Dengan ek =x−x(k). Dalam bentuk matriks: 0 , ) ( ) 1 ( + = ≥ k Me e k k (2.27) ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − = − − − − 0 0 0 0 1 , 1 1 , 1 , 1 22 2 22 21 11 1 11 12 nn n n nn n n n n n n n a a a a a a a a a a a a a a M L M O M L (2.28) Dari (2.24), diperoleh: 0 , ) 0 ( ) ( = ≥ k e M e k k (2.29)

Untuk nilai x(0) yang telah ditentukan, kita mendapatkan x(m) →x jika dan hanya jika:

( )

M <1

r_σ (2.30)

Hal ini dapat dipenuhi jika M <1 untuk beberapa aturan operator matriks.

(18)

Kasus 1 : M _∞ <1. Hal ini berarti: n i a a _ii n i j j ij , 1, , 1 K = <

∑

≠ = (2.31)

Dapat dikatakan bahwa matriks A pada persamaan (2.23) merupakan dominan secara diagonal. Dalam kasus ini:

0 , ) ( ) 1 ( ≤ − ≥ − ∞ ∞ ∞ + k x x M x x k k (2.32) Kasus 2 : 1 1 <

M . Hal ini berarti:

n j a a n i ii ij , , 1 , 1 1 K = <

∑

= (2.33)

Dalam kasus ini:

0 , 1 ) ( 1 1 ) 1 ( ≤ − ≥ − + k x x M x x k k (2.34)

2.2.5 Conjugate Gradient Method

Dalam matematika, metode Conjugate Gradient merupakan suatu algoritma untuk solusi numerik dari beberapa sistem khusus persamaan linier yang mempunyai matriks yang simetris dan nilai elemennya positif berhingga. Metode Conjugate Gradient merupakan suatu metode iterasi. Metode ini dikembangkan pada tahun 1952 oleh Hestenes dan Stiefel.

Metode Conjugate Gradient digunakan untuk menyelesaikan masalah minimalisasi kuadratik:

( )

T T n R x b x Qx x x f = − , ∈ 2 1 (2.35)

(19)

Atau secara ekuivalen untuk menyelesaikan sistem persamaan linier 0

= − b

Qx , dimana Q merupakan matriks positif berhingga simetris n×n dan b merupakan vector n. Algoritma ini membutuhkan iterasi, dimulai dari nilai awal

0

x yang telah ditentukan (umumnya nilai x₀ yang dipakai adalah 0).

Berikut ini merupakan langkah-langkah dalam algoritma Conjugate Gradient:

1. Ditentukan k =0 dan tentukan nilai awal x(0).

2. g(0) =∇f(x(0)). (2.36)

Jika 0g(0) = , maka iterasi berhenti. Selain itu, (0) (0) g d =− . (2.37) 3. ₍ ₎ ₍ ₎ ) ( ) ( k T k k T k k Qd d d g − = α . (2.38) 4. x(k+1) = x(k) +α_kd(k). (2.39) 5. g(k+1) =∇f(x(k+1)). (2.40)

Jika 0g(k+1) = , maka iterasi berhenti. Selain itu, lanjutkan ke langkah berikutnya. 6. ₍ ₎ ₍ ₎ ) ( ) 1 ( k T k k T k k Qd d Qd g + = β . (2.41) 7. ( 1) ( 1) k (k) k k d g d + =− + +β . (2.42) 8. k = k+1.

(20)

2.3 Penelitian Relevan

Penelitian-penelitian yang pernah dilakukan peneliti lain dan berhubungan dengan penelitian yang terkait dengan penulisan skripsi ini adalah sebagai berikut:

• An Introduction To The Conjugate Gradient Method Without The Agonizing

Pain Edition 1 4 1

, 1994, Jonathan Richard Shewchuk. Membahas Conjugate Gradient Method secara mendetail.

• On The Modified Conjugate Gradient Method In Cloth Simulation, 1998, Uri M. Ascher, Eddy Boxerman. Menggunakan algoritma Modified Preconditioned Conjugate Gradient (MPCG) untuk simulasi pembuatan pakaian.