PENGGUNAAN NILAI EIGEN DAN VEKTOR EIGEN UNTUK MENENTUKAN MODEL GENOTIP KETURUNAN YANG TERTAUT KROMOSOM X

(1)

15

PENGGUNAAN NILAI EIGEN DAN VEKTOR EIGEN UNTUK

MENENTUKAN MODEL GENOTIP KETURUNAN

YANG TERTAUT KROMOSOM X

Havid Syafwan

*1

_,

_Nurwati

2

Jurusan Manajemen Informatika, Amik Royal, Kisaran

e-mail:

*1

_{havid_syafwan@yahoo.com, nurwati@yahoo.com}

Abstrak

Untuk menentukan genotip keturunan yang tertaut kromosom X dari suatu populasi makhluk hidup dapat dibentuk modelnya. Dengan mengasumsikan bahwa keturunan tersebut dikawinkan dengan jenis genotip yang sama dan dengan peluang yang sama. Pada penelitian ini akan ditentukan genotip keturunan yang tertaut kromosom X dengan menggunakan MATLAB 6.1 untuk mencari nilai eigen dan vektor eigen. Jadi model yang digunakan untuk memprediksikan kemungkinan genotip keturunan yang tertaut kromosom X dapat digunakan.

Kata kunci : distribusi genotip, nilai eigen, vektor eigen, diagonalisasi matriks

1. PENDAHULUAN

Setiap makhluk hidup memiliki sifat-sifat seperti induknya. Sifat-sifat tersebut tidak saja mengenai kejiwaan, tetapi juga mengenai bentuk dan kemampuan yang berbeda-beda. Inilah sifat-sifat yang dimiliki keturunan yang dibawa dari induknya.

Sifat keturunan tersebut terdapat di dalam genotip yang merupakan bentuk atau susunan genetis suatu karakter yang dikandung suatu individu. Pengendali faktor pembawa sifat keturunan pada makhluk hidup itu disebut dengan gen yang terdapat dalam kromosom, sedangkan pasangan gen itu akan membentuk alel. Jika pasangan dua alel pada suatu individu persis sama berarti simbolnya persis sama disebut homozigot, sedangkan jika pasangan kedua alel pada suatu individu tidak sama berarti simbolnya berbeda disebut heterozigot. Adakalanya pada dua atau lebih gen menempati kromosom yang sama dan tidak dapat memisahkan diri secara bebas (harus memisah bersama-sama). Peristiwa terbentuknya gen ini disebut tautan atau linkage. Istilah “yang tertaut kromosom X” digunakan karena gen-gen seperti itu dijumpai pada kromosom X [4].

Ilmu yang mempelajari tentang sifat-sifat keturunan dari suatu makhluk hidup itu disebut dengan ilmu genetika (dalam bahasa Yunani gen artinya jadi). Seperti halnya dengan ilmu-ilmu lainnya, genetika pada mulanya hanya merupakan genetika empiris, yaitu genetika yang didasarkan atas pengalaman sehari-hari atas observasi yang dilakukan oleh khalayak dengan cara yang tidak sistematis. Barulah pada tahun 1866 genetika diselidiki secara sistematis oleh seorang pendeta yang bernama Gregor Johann Mendel (1822-1884) di kota Brunn-Austria. Namun, hasil percobaan itu baru muncul lagi pada awal abad 19 [4].

Mendel menemukan pertama kali bahwa sifat pada tanaman mengikuti sejumlah perhitungan matematika yang sederhana dikenal dengan “Hukum Pewarisan Mendel”. Setelah itu barulah genetika

berkembang menjadi genetika molekuler, genetika sel, dan genetika kwantitatif [4].

Oleh sebab itu, matematika yang merupakan salah satu ilmu yang sangat berkaitan dengan ilmu genetika ini dapat menentukan jenis genotip keturunan yang tertaut kromosom X dengan menggunakan nilai eigen dan vektor eigen yang merupakan bagian dari materi aljabar linier [3].

2. METODE PENELITIAN 2.1 Matriks

Bentuk matriks banyak digunakan dalam menyelesaikan persoalan pada aplikasi aljabar linier, termasuk dalam menentukan model genotip keturunan melalui nilai eigen dan vektor eigen, yaitu dengan cara merubah hasil pemasangan genotip keturunan tersebut ke dalam bentuk matriks.

Definisi 2.1.1

Matriks adalah sebuah susunan segiempat siku-siku dari bilangan-bilangan. Bilangan-bilangan dalam susunan tersebut dinamakan entri dalam matriks. Ukuran sebuah matriks ditentukan oleh banyaknya baris dan kolom. Untuk matriks M yang berukuran r

x s dapat ditulis sebagai berikut :

 

ij _rxs rs s s r r m m m m m m m m m m M                      2 1 2 22 12 1 21 11 dengan

i



1 

,

2 ,

,

r

dan

j



1 

,

2 ,

,

s

Elemen matriks M dinyatakan dengan huruf kecil dan diberi dua indeks. Elemen yang terletak pada baris ke-i dan kolom ke-j dari matriks M dinyatakan dengan mij. Matriks yang mempunyai satu baris saja disebut matriks baris dan yang mempunyai satu kolom saja disebut matriks kolom.

(2)

16 Matriks bujursangkar adalah matiks yang jumlah

baris dan kolomnya sama (r = s) dan dikatakan berukuran r atau berukuran s.

Definisi 2.1.2

Suatu matriks bujursangkar yang semua entrinya yang tidak terletak pada diagonal utama adalah nol disebut matriks diagonal (diagonal matrix). Suatu matriks diagonal umum D yang berukuran n x n, dapat ditulis sebagai :

             n d d d D        0 0 0 0 0 0 2 1

2.2 Ruang Vektor dan Subruang Vektor Definisi 2.2.1

Suatu subhimpunan W dari suatu ruang vektor V disebut subruang (subspace) dari V jika W itu sendiri merupakan suatu ruang vektor di bawah penjumlahan dan perkalian skalar yang didefinisikan pada V.

Definisi 2.2.2

Jika W adalah suatu himpunan yang terdiri dari satu atau lebih vektor dari suatu ruang vektor V, maka W adalah suatu subruang dari V, jika dan hanya jika syarat-syarat berikut terpenuhi :

a. Jika u dan v adalah vektor-vektor pada W, maka u

+ v berada pada W

b. Jika k adalah skalar sebarang dan u adalah vektor sebarang pada W, maka ku berada pada W.

Definisi 2.2.3

Jika

M

x



0

adalah suatu sistem linier

homogen yang terdiri dari m persamaan dengan n faktor yang tidak diketahui, maka himpunan vektor solusi adalah subruang dari Rn_.

2.3 Nilai Eigen dan Vektor Eigen

Dari pemasangan genotip dapat ditentukan kemungkinan jenis genotip keturunannya dengan merubah hasil pemasangan genotip ke dalam bentuk matriks. Nilai eigen dan vektor eigen adalah salah satu cara dalam aljabar linier yang dapat digunakan untuk menentukan jenis genotip keturunan untuk generasi selanjutnya.

Definisi 2.3.1

Jika M adalah sebuah matriks n x n, maka sebuah vektor taknol

x

pada Rn_{disebut vektor eigen} (eigenvector) dari M jika

M

x

adalah sebuah kelipatan skalar dari

x

, yaitu :

x

M





untuk skalar sebarang



. Skalar



disebut nilai eigen (eigenvalue) dari M, dan

x

disebut sebagai vektor eigen dari M yang terkait dengan



.

Definisi 2.3.2

Jika M adalah sebuah matriks n x n dan



adalah sebuah bilangan riel, maka pernyataan-pernyataan berikut ini adalah ekuivalen

(a)



adalah sebuah nilai eigen dari M

(b) Sistem persamaan

(



I



M

)

x



0

memiliki

solusi taktrivial

(c) Terdapat sebuah vektor taknol

x

pada Rn sedemikian _{rupa sehingga}

_M

_x





_x

(d)



adalah sebuah solusi dari persamaan karakteristik

det(



I



M

)



0

Definsi 2.3.3

Jika

v

₁

,

v

₂

,



,

v

_kadalah vektor eigen dari matriks M yang terkait dengan nilai-nilai eigen yang berbeda



₁

,



₂

,



,



_k, maka



v

₁

,

v

₂

,



v

_k



adalah suatu himpunan bebas linier.

2.4. Diagonalisasi Definisi 2.4.1

Sebuah matriks bujursangkar M dikatakan dapat didiagonalisasi (diagonalizable) jika terdapat sebuah matriks P yang dapat dibalik sedemikian rupa sehingga P-1_{MP adalah sebuah matriks diagonal.} Matriks P dikatakan mendiagonalisasi (diagonalize)

M.

Definisi 2.4.2

Jika M adalah sebuah matriks n x n, maka kedua pernyataan berikut ini adalah ekuivalen

a. M dapat didiagonalisasi

b. M memiliki n vektor eigen yang bebas linier

1. HASIL DAN PEMBAHASAN 3.1 Menentukan Genotip Asal [3]

Permasalahan yang dibatasi pada penelitian ini adalah pada keturunan yang tertaut kromosom X. Dalam jenis keturunan ini, jenis jantan hanya memiliki satu gen yaitu A atau a dan yang betina memiliki dua gen yaitu AA, Aa, ataupun aa. Penurunan dari gen-gen tersebut adalah keturunan jantan menerima salah satu gen pembawa sifat dari induk betinanya dengan kemungkinan yang sama, dan keturunan betina menerima gen pembawa sifat satu-satunya dari induk jantannya dan salah satu lagi di antara kedua gen pembawa sifat induk betinanya dengan kemungkinan yang sama.

Akan dipelajari sebuah program perkembangbiakan yang berkaitan dengan penurunan yang tertaut kromosom X ini. Pertama, dimulai dengan satu induk jantan dan satu induk betina, dipilih dua dari keturunannya secara acak, satu untuk setiap jenis kelamin, dan kawinkan kedua keturunan itu. Pilihlah dua dari keturunan yang dihasilkan dan kawinkanlah kedua keturunan ini kembali, dan

(3)

17 demikian seterusnya. Perkawinan seperti ini biasanya

dilakukan pada hewan.

3.2 Menentukan Kemungkinan Hasil Setiap Pemasangan Genotip

Apabila genotip induk jantan adalah A atau a dipasangkan dengan genotip induk betina yaitu AA,

Aa, atau aa yaitu :

Induk Jantan x Betina

genotip A atau a AA, Aa, atau aa

Dari pemasangan induk jantan dan induk betina tersebut, maka akan menghasilkan keturunan pertamanya sebagai berikut :

1. Apabila A genotip jantan yang dilambangkan dengan genotip pertama (genotip I) dipasangkan dengan AA genotip betina yang dilambangkan dengan genotip kedua (genotip II), maka diagram pohon kemungkinan genotip hasilnya adalah :

Dari diagram pohon di atas dapat dilihat bahwa keturunannya 100% mempunyai genotip AA, yang artinya peluang keturunan genotip jantan A adalah 1 dan peluang keturunan genotip betina AA adalah 1. 2. Apabila A genotip jantan yang dilambangkan

dengan genotip pertama (genotip I) dipasangkan dengan Aa genotip betina yang dilambangkan dengan genotip kedua (genotip II), maka diagram pohon kemungkinan genotip hasilnya adalah :

Dari diagram pohon di atas dapat dilihat bahwa keturunannya 50% mempunyai genotip AA dan 50% lagi mempunyai genotip Aa, yang artinya peluang keturunan genotip jantan A adalah ½ dan genotip jantan a adalah ½, sedangkan peluang keturunan genotip betina AA adalah ½ dan genotip Aa adalah ½. Dan begitu seterusnya sampai dengan a genotip jantan yang dilambangkan dengan genotip pertama (genotip I) dipasangkan dengan aa genotip betina yang dilambangkan dengan genotip kedua (genotip II)

Dari semua diagram pohon tersebut dapat diketahui jenis keturunan pertama dari pemasangan genotip asal dan peluang jenis keturunanya.

Pemasangan genotip keturunan pertama jantan dan betina dengan genotip asal dapat dibuat dalam bentuk tabel dibawah ini

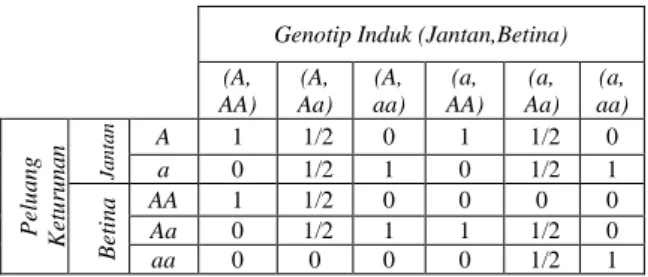
Tabel 1. Peluang Genotip Keturunan Pertama Jantan

dan Betina terhadap Genotip Induk

Dari Tabel 1, dapat diketahui pasangan genotip keturunan pertama jantan dan betina yang tertaut kromosom X, yaitu :

(A, AA), (A, Aa), (A, aa), (a, AA), (a, Aa), (a, aa)

Untuk menentukan peluang pasangan keturunan yang tertaut kromosom X ke-n, maka akan dikawinkankan masing-masing dari keenam pasangan keturunan pertama yang tertaut kromosom

X tersebut dengan jenis genotip yang sama, sehingga

diperoleh :

1. Pasangan keturunan pertama yang tertaut kromosom X jenis (A, AA)

Apabila A genotip jantan yang dilambangkan dengan genotip pertama (genotip I) dipasangkan dengan AA genotip betina yang dilambangkan dengan genotip kedua (genotip II), maka diagram pohon kemungkinan genotip hasilnya adalah :

Dari diagram pohon di atas dapat dilihat bahwa keturunannya 100% mempunyai genotip AA, yang artinya peluang keturunan genotip jantan A adalah 1 dan peluang keturunan genotip betina AA adalah 1. Maka pasangan keturunan yang tertaut kromosom X selanjutnya hanya berjenis (A, AA). Dan begitu seterusnya untuk pasangan keturunan yang berjenis lainnya.

Sehingga dari penjelasan tersebut, dapat dilihat peluang pasangan genotip keturunan pertamanya terhadap genotip berikutnya dalam bentuk tabel di bawah ini :

Tabel 2. Peluang Pasangan Genotip Keturunan

Pertama yang Tertaut Kromosom X terhadap Genotip Keturunan Berikutnya

Genotip Keturunan Pertama (A, AA) (A, Aa) (A, aa) (a, AA) (a, Aa) (a, aa) Pe lu a n g G en o ti p K et u r u n a n Be ri k u tn ya (A, AA) 1 1/4 0 0 0 0

Genotip Induk (Jantan,Betina) (A, AA) (A, Aa) (A, aa) (a, AA) (a, Aa) (a, aa) Pe lu a n g K et u ru n a n Jantan A 1 1/2 0 1 1/2 0 a 0 1/2 1 0 1/2 1 Be ti n a AA 1 1/2 0 0 0 0 Aa 0 1/2 1 1 1/2 0 aa 0 0 0 0 1/2 1 A (genotip I)

A AA (genotip II1) A AA (genotip II2) A (genotip I) A AA (genotip II1)

a

Aa

(genotip II2)

A

(genotip I) A AA (genotip II1) A AA (genotip II2)

(4)

18 (A, Aa) 0 1/4 0 1 1/4 0 (A, aa) 0 0 0 0 1/4 0 (a, AA) 0 1/4 0 0 0 0 (a, Aa) 0 1/4 1 0 1/4 0 (a, aa) 0 0 0 0 1/4 1 Jumlah 1 1 1 1 1 1

Pasangan keturunan yang tertaut kromosom X dalam tiap generasi yang berurutan mempunyai kemungkinan-kemungkinan tertentu untuk menjadi salah satu dari keenam jenis genotip ini. Untuk menghitung kemungkinan tersebut, untuk n = 0, 1, 2, ... , maka dibuat :

an = kemungkinan pasangan keturunan yang tertaut kromosom X yang dikawinkan dalam generasi ke-n adalah jenis (A, AA)

bn = kemungkinan pasangan keturunan yang tertaut kromosom X yang dikawinkan dalam generasi ke-n adalah jenis (A, Aa)

cn = kemungkinan pasangan keturunan yang tertaut kromosom X yang dikawinkan dalam generasi ke-n adalah jenis (A, aa)

dn = kemungkinan pasangan keturunan yang tertaut kromosom X yang dikawinkan dalam generasi ke-n adalah jenis (a, AA)

en = kemungkinan pasangan keturunan yang tertaut kromosom X yang dikawinkan dalam generasi ke-n adalah jenis (a, Aa)

fn = kemungkinan pasangan keturunan yang tertaut kromosom X yang dikawinkan dalam generasi ke-n adalah jenis (a, aa)

Dari Tabel 3.2 dapat ditentukan distribusi genotip untuk tiap generasi dari distribusi genotip pada generasi sebelumnya dengan persamaan-persamaan sebagai berikut :

an = an-1 + ¼ bn-1 bn = ¼ bn-1 + dn-1 + ¼ en-1 cn = ¼ en-1 n = 1, 2, ... (3.2.1) dn = ¼ bn-1 en = ¼ bn-1 + cn-1 + en-1 fn = ¼ en-1 + fn-1

Persamaan (3.2.1) dapat ditulis dalam bentuk notasi matriks sebagai berikut :

                                                                   1 1 1 1 1 1 4 1 4 1 4 1 4 1 4 1 4 1 4 1 4 1 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 n n n n n n n n n n n n f e d c b a f e d c b a _..(3.2.2) dengan syarat :

a

_n



b

_n



c

_n



d

_n



e

_n



f

_n



1

, untuk n = 0, 1, 2, ... n n n n n n

b

c

d

e

f

a

,

adalah genotip ke-n

3.3 Menentukan Jenis Genotip yang Terjadi dengan Menggunakan Nilai Eigen dan Vektor Eigen

Seperti yang telah dijelaskan dalam pembatasan masalah, maka penulis akan meneliti pemasangan

genotip keturunan untuk generasi ke-n dengan melihat hasil perkawinan keturunan pertama yang sejenis. Dari Tabel 3.2 pemasangan genotip keturunan pertama yang tertaut kromosom X dapat ditulis dalam bentuk persamaan berikut :

) 0 ( ) 1 (

Mx

x



... (3.3.1) dapat ditulis dalam bentuk notasi matriks sebagai berikut :                                                              0 0 0 0 0 0 4 1 4 1 4 1 4 1 4 1 4 1 4 1 4 1 1 1 1 1 1 1 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 f e d c b a f e d c b a ... (3.3.2)

dengan :

a

₀

,

b

₀

,

c

₀

,

d

₀

,

e

₀

,

f

₀ adalah genotip asal

Apabila persamaan (3.3.1) dilanjutkan, maka diperoleh : ) 0 ( ) 1 (

Mx

x



) 0 ( ) 2 ( ) 0 ( ) 1 ( ) 2 (

x

M

MMx

Mx

x



) 0 ( ) 3 ( ) 2 ( ) 3 (

x

M

Mx

x



) 0 ( ) 4 ( ) 3 ( ) 4 (

x

M

Mx

x





) 0 ( ) ( ) (

x

M

x

n



n , n = 1, 2, .... ... (3.3.3) Jika dapat menentukan sebuah persamaan eksplisit untuk M(n)_{, maka dapat digunakan} persamaan (3.3.3) untuk memperoleh sebuah persamaan eksplisit untuk x(n)_{. Untuk menentukan} persamaan eksplisit untuk M(n)_{, maka langkah} pertama yang harus dilakukan adalah mendiagonalisasi M. Dalam hal ini, tentukan terlebih dahulu sebuah matriks P yang dapat dibalik, invers dari matriks P,dan sebuah matriks diagonal D sedemikian rupa sehingga:

M = PDP-1

Dengan diagonalisasi semacam ini, maka akan diperoleh : M(n)_{= PD}(n)_P-1_, _{untuk n = 1, 2,... ...(3.3.4)} di mana                                           n n n n n n n n D 6 5 4 3 2 1 6 5 4 3 2 1 ) ( 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0            

Untuk mendapatkan matriks P, maka dicari nilai eigen dan vektor eigen dari matriks M.

Karena mencari nilai eigen ini cukup rumit untuk ukuran matriks 6 x 6, maka digunakan program

(5)

19 nilai eigennya, sehingga didapat nilai-nilai eigen dari

matriks M sebagai berikut :

1





,



₂



1

,



₃



0 .

809

,



₄



0 .

5

,

5 .

0

5







,



₆





0 .

309

... (3.3.5) Akan ditentukan vektor eigen dari masing-masing nilai eigen yang diperoleh pada persamaan (3.3.5) yang merupakan vektor solusi dari ruang solusi...(3.3.6)

Untuk memudahkan perhitungan, maka bilangan pecahan diubah menjadi bilangan desimal, sehingga diperoleh ruang solusi umum sebagai berikut :















































































0

1

25 .

0

25 .

0

1

25 .

0

25 .

0

25 .

0

25 .

0

1

0

25 .

0

25 .

0

1

6 5 4 3 2 1 6 5 4 3 2 1

x

S



... ...(3.3.7)

Kemudian dicari vektor eigen untuk M dengan cara mensubstitusikan masing-masing nilai eigen



1



1

,

1

2





,



₃



0 .

809

,



₄



0 .

5

,



₅





0 .

5

,

309 .

0

6







, sehingga diperoleh:

P





x

1

x

2

x

3

x

4

x

5

x

6



=                                 191 . 0 1 1 308 . 1 1 0 1 6 2 1 0 0 809 . 0 3 1 309 . 0 0 0 809 . 0 3 1 309 . 0 0 0 1 6 2 1 0 0 191 . 0 1 1 308 . 1 0 1

Setelah diperoleh matriks P, maka akan ditentukan matriks P-1_{. Dengan bantuan program}

MATLAB 6.1, maka diperoleh matriks P-1 _sebagai berikut :                             0 138 . 0 447 . 0 447 . 0 138 . 0 0 0 042 . 0 083 . 0 083 . 0 042 . 0 0 0 125 . 0 25 . 0 25 . 0 125 . 0 0 0 362 . 0 447 . 0 447 . 0 362 . 0 0 1 666 . 0 333 . 0 666 . 0 333 . 0 0 0 333 . 0 666 . 0 333 . 0 666 . 0 1 1 P

dan matriks D(n)_{dari nilai-nilai eigen matriks M} adalah :                        n n n n n D 309 . 0 0 0 0 0 0 0 5 . 0 0 0 0 0 0 0 5 . 0 0 0 0 0 0 0 809 . 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 ) (

Dari uraian entri-entri matriks M(n)_{tersebut, maka} barulah dapat dicari model genotip keturunan yang tertaut kromosom X untuk generasi ke-n dengan menyelesaikan persamaan , yaitu :

) 0 ( ) ( ) (

x

M

x

n



n , n = 1, 2, ... dalam bentuk matriks dapat ditulis :

                                                             0 0 0 0 0 0 66 65 64 63 62 61 56 55 54 53 52 51 46 45 44 43 42 41 36 35 34 33 32 31 26 25 24 23 22 21 16 15 14 13 12 11 f e d c b a e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e f e d c b a n n n n n n ... ... (3.3.8) atau dapat juga ditulis :

                                                                       0 66 0 65 0 64 0 63 0 62 0 61 0 56 0 55 0 54 0 53 0 52 0 51 0 46 0 45 0 44 0 43 0 42 0 41 0 36 0 35 0 34 0 33 0 32 0 31 0 26 0 25 0 24 0 23 0 22 0 21 0 16 0 15 0 14 0 13 0 12 0 11 f e e e d e c e b e a e f e e e d e c e b e a e f e e e d e c e b e a e f e e e d e c e b e a e f e e e d e c e b e a e f e e e d e c e b e a e f e d c b a n n n n n n ... ... (3.3.9)

Diperoleh bentuk linier dari persamaan (3.3.9), yaitu : 0 16 0 15 0 14 0 13 0 12 0 11

a

e

b

e

c

e

d

e

f

e

a

_n





an = a0 + [0.666 - 0.473(0.809)n - 0.125(0.5)n - 0.042(-0.5)n _- _{0.026(-0.309)}n_] _b 0 +[0.333 - 0.585(0.809)n_{+ 0.25(0.5)}n_{- 0.083(-0.5)}n₊ 0.085(-0.309)n_{] co}_{+[0.666 - 0.585(0.809)}n_{- 0.25(0.5)}n₊ 0.083(-0.5)n_{+ 0.085(-0.309)}n_{] d0} _{+ [0.333 -} 0.473(0.809)n_{+ 0.125(0.5)}n_{+ 0.042(-0.5)}n_- 0.026(-0.309)n_{] e0} 0 26 0 25 0 24 0 23 0 22 0 21

a

e

b

e

c

e

d

e

f

e

b

_n





bn = [0.362(0.809)n + 0.25(0.5)n + 0.252(-0.5)n + 0.138(-0.309)n_{] b0}_{+[0.447(0.809)}n_{- 0.5(0.5)}n₊ 0.498(-0.5)n_{- 0.447(-0.309)}n_{] c0}_{+[0.447(0.809)}n₊ 0.5(0.5)n_{- 0.498(-0.5)}n_{- 0.447(-0.309)}n_{] d0} +[0.362(0.809)n_{- 0.25(0.5)}n_{- 0.252(-0.5)}n₊ 0.138(-0.309)n_{] e} 0 0 36 0 35 0 34 0 33 0 32 0 31

a

e

b

e

c

e

d

e

f

e

c

_n





cn = [0.112(0.809)n - 0.125(0.5)n + 0.126(-0.5)n - 0.112(-0.309)n_{] b0}_{+[0.138(0.809)}n_{+ 0.25(0.5)}n₊

(6)

20 0.249(-0.5)n_{+ 0.362(-0.309)}n_{] c0}_{+[0.138(0.809)}n_- 0.25(0.5)n_{- 0.249(-0.5)}n_{+ 0.362(-0.309)}n_{] d0} +[0.112(0.809)n_{+ 0.125(0.5)}n_{- 0.126(-0.5)}n_- 0.112(-0.309)n_{] e0} 0 46 0 45 0 44 0 43 0 42 0 41

a

e

b

e

c

e

d

e

f

e

d

_n





dn = [0.112(0.809)n_{+ 0.125(0.5)}n_{- 0.126(-0.5)}n_- 0.112(-0.309)n_{] b0} _{+[0.138(0.809)}n_{- 0.25(0.5)}n_- 0.249(-0.5)n_{+ 0.362(-0.309)}n_{] c0}_{+[0.138(0.809)}n₊ 0.25(0.5)n_{+ 0.249(-0.5)}n_{+ 0.362(-0.309)}n_{] d0} +[0.112(0.809)n_{- 0.125(0.5)}n_{+ 0.126(-0.5)}n_- 0.112(-0.309)n_{] e0} 0 56 0 55 0 54 0 53 0 52 0 51

a

e

b

e

c

e

d

e

f

e

_n





en = [0.362(0.809)n_{- 0.25(0.5)}n_{- 0.252(-0.5)}n₊ 0.138(-0.309)n_{] b0} _{+ [0.447(0.809)}n_{+ 0.5(0.5)}n_- 0.498(-0.5)n_{- 0.447(-0.309)}n_{] c0}_{+[0.447(0.809)}n_- 0.5(0.5)n_{+ 0.498(-0.5)}n_{- 0.447(-0.309)}n_{] d0} +[0.362(0.809)n_{+ 0.25(0.5)}n_{+ 0.252(-0.5)}n₊ 0.138(-0.309)n_{] e0} 0 66 0 65 0 64 0 63 0 62 0 61

a

e

b

e

c

e

d

e

f

e

f

_n





fn = [0.333 - 0.473(0.809)n_{+ 0.125(0.5)}n₊ 0.042(-0.5)n_{- 0.026(-0.309)}n_{] b0}_{+ [0.666 - 0.585(0.809)}n_- 0.25(0.5)n_{+ 0.083(-0.5)}n_{+ 0.085(-0.309)}n_{] c0}₊ [0.333 - 0.585(0.809)n_{+ 0.25(0.5)}n_{- 0.083(-0.5)}n₊ 0.085(-0.309)n_{] d0 + [0.666 - 0.473(0.809)}n_- 0.125(0.5)n_{- 0.042(-0.5)}n_{- 0.026(-0.309)}n_{] e0 + f0} 4. KESIMPULAN

Dari penelitian ini dapat diambil kesimpulan sebagai berikut :

1. Untuk menentukan model genotip keturunan

ke-n yake-ng tertaut kromosom X dapat dicari deke-ngake-n

mengetahui genotip keturunan pertama yang tertaut kromosom X terlebih dahulu.

2. Model genotip keturunan ke-n yang tertaut kromosom X dapat ditentukan dengan menggunakan nilai eigen dan vektor eigen dan dengan bantuan MATLAB 6.1 untuk menghitung nilainya didapat nilai eigennya sbg :

1





,



2



1

,



3



0 .

809

,



4



0 .

5

,

5 .

0

5







,



₆





0 .

309

dan vektor eigennya :



x

1

x

2

x

3

x

4

x

5

x

6



P



=















191 .

0

1

308 .

1

0

1

6

2

1

0

809 .

0

3

1

309 .

0

809 .

0

3

1

309 .

0

1

6

2

1

0

191 .

0

1

308 .

1

0

1

5. SARAN

Berdasarkan hasil penelitian yang dilakukan, maka penulis memberikan saran-saran sebagai berikut :

1. Untuk penelitian lebih lanjut, untuk jenis genotip keturunan ke – n pada kasus kromosom uang lain

2. Untuk penelitian lebih lanjut menggunakan metode lain dalam mendapatkan model genotip keturunan berikutnya.

6. UCAPAN TERIMA KASIH

Penulis mengucapkan terima kasih kepada semua pihak maupun instansi yang sudah membantu secara moril ataupun materil erhadap penelitian ini, semoga penelitian ini bermanfaat bagi yang membutuhkannya.

7. DAFTAR PUSTAKA

Anton, H. 1987. Aljabar linear Elementer. Alih Bahasa : Pantur Silaban, I Nyoman Susila. Erlangga, Jakarta.

Anton, H. dan Rorres, C. 2004. Aljabar linear

Elementer Versi Aplikasi jilid 1. Alih Bahasa :

Refina Idriasari, Irzam harmein. Erlangga, Jakarta.

Anton, H. dan Rorres, C. 2004. Aljabar linear

Elementer Versi Aplikasi jilid 2. Alih Bahasa :

Refina Idriasari, Irzam harmein. Erlangga, Jakarta.

Dwidjoseputro, D. 1977. Pengantar Genetika. Bhratara, Jakarta.

Hanselman, D. dan Littlefield, B. 2000. Matlab

bahasa Komputasi Teknis. Alih Bahasa :