Metode Matematika Untuk Geofisika, Edisi 1, Th. 2009

(1)

Metode Matematika untuk Geofisika

Supriyanto Suparno

( Website: http://supriyanto.fisika.ui.ac.id ) ( Email: supri@fisika.ui.ac.id atau supri92@gmail.com )

Edisi I

Revisi terakhir tgl: 2 Desember 2009

(2)

(3)

(4)

Ketekunan adalah jalan yang terpercaya untuk mengantarkan kita menuju kesuksesan

(5)

Kata Pengantar

Ini adalah buku ke-empat yang saya tulis dalam 2 tahun terakhir, semenjak saya kembali ke Indonesia. Namun isi-nya masih tidak terlepas dari dunia komputasi dan analisis numerik sebagaimana buku-buku karya saya sebelumnya. Kali ini, saya menulis buku untuk mem-berikan catatan kuliah Metode Matematika untuk Geofisika di Departemen Fisika, FMIPA-UI. Di dalam buku ini, algoritma numerik ditulis ke dalam bahasa pemrograman Matlab.

Akhirnya saya ingin mengucapkan rasa terima kasih yang tak terhingga kepada Dede Djuhana yang telah berkenan memberikan format LA_{TEX-nya sehingga tampilan tulisan pada} buku ini benar-benar layaknya sebuah buku yang siap dicetak. Tak lupa, saya pun sepatutnya berterima kasih kepada seluruh rekan diskusi yaitu para mahasiswa yang telah mengambil mata kuliah Metode Matematika untuk Geofisika PTA 2008/2009 program Pasca Sarjana Ilmu Fisika di Departemen Fisika, FMIPA, Universitas Indonesia.

Walaupun buku ini masih jauh dari sempurna, namun semoga ia dapat salah satu mata air ilmu pengetahuan anak bangsa. Saya izinkan anda meng-copy dan menggunakan buku ini selama itu ditujukan untuk belajar dan bukan untuk tujuan komersial. Bagi yang ingin berdiskusi, memberikan masukan, kritikan dan saran, silakan dikirimkan ke email saya yang tercantum di halaman depan buku ini.

Depok, 14 November 2008 Supriyanto Suparno

(6)

(7)

Daftar Isi

Lembar Persembahan i

Kata Pengantar iii

Daftar Isi iii

Daftar Gambar vi

Daftar Tabel vii

1 Matrik dan Komputasi 1

1.1 Pengenalan matrik . . . 1

1.2 Inisialisasi matrik dalam memori komputer . . . 2

1.3 Macam-macam matrik . . . 3

1.3.1 Matrik transpose . . . 3

1.3.2 Matrik bujursangkar . . . 3

1.3.3 Matrik simetrik . . . 3

1.3.4 Matrik diagonal . . . 3

1.3.5 Matrik identitas . . . 4

1.3.6 Matrik upper-triangular . . . 4

1.3.7 Matrik lower-triangular . . . 4

1.3.8 Matrik tridiagonal . . . 4

1.3.9 Matrik diagonal dominan . . . 5

1.3.10 Matrikpositive-definite . . . 5

1.3.11 Vektor-baris dan vektor-kolom . . . 6

1.4 Operasi matematika . . . 6

1.4.1 Penjumlahan matrik . . . 6

1.4.2 Komputasi penjumlahan matrik . . . 7

1.4.3 Perkalian matrik . . . 9

1.4.4 Komputasi perkalian matrik . . . 12

1.4.5 Perkalian matrik dan vektor-kolom . . . 13

1.4.6 Komputasi perkalian matrik dan vektor-kolom . . . 14

1.5 Penutup . . . 15

1.6 Latihan . . . 15

2 Formulasi Masalah Inversi 17 2.1 Klasifikasi masalah inversi . . . 17

2.2 Inversi Model Garis . . . 17

(8)

vi

2.3 Inversi Model Parabola . . . 22

2.4 Inversi Model Bidang . . . 25

2.5 Contoh aplikasi . . . 27

2.5.1 Menghitung gravitasi di planet X . . . 27

2.6 Kesimpulan . . . 31

Daftar Pustaka 33

(9)

Daftar Gambar

2.1 Data observasi perubahan temperatur terhadap kedalaman dari permukaan tanah 18 2.2 Grafik data pengukuran gerak batu . . . 28 2.3 Grafik hasil inversi parabola . . . 31

(10)

(11)

Daftar Tabel

2.1 Data temperatur bawah permukaan tanah terhadap kedalaman . . . 18 2.2 Data temperatur bawah permukaan tanah terhadap kedalaman . . . 22 2.3 Data ketinggian terhadap waktu dari planet X . . . 27

(12)

(13)

Bab 1

Matrik dan Komputasi

✍Objektif :

⊲ Mengenalkan matrik dan jenis-jenis matrik.

⊲ Mengenalkan operasi penjumlahan dan perkalian matrik.

⊲ Mendeklarasikan elemen-elemen matrik ke dalam memori komputer.

⊲ Membuat script operasi matrik.

1.1 Pengenalan matrik

Notasi suatu matrik berukurannxm ditulis dengan huruf besar dan dicetak tebal, misalnya

An×m. Hurufnmenyatakan jumlah baris, dan hurufmjumlah kolom. Suatu matrik tersusun

dari elemen-elemen yang dinyatakan dengan huruf kecil diikuti angka-angka indeks, misalnya

aij, dimana indeksi menunjukan posisi baris ke-idan indeksj menentukan posisi kolom ke-j.

A= (aij) = 

    

a11 a12 . . . a1_m

a21 a22 . . . a2_m ..

. ... ...

an1 a_n2 . . . a_nm 

    

(1.1)

Contoh 1: MatrikA2_×3

A=

"

3 8 5 6 4 7

#

dimana masing-masing elemennya adalaha11 = 3, a12 = 8, a13 = 5, a21 = 6, a22 = 4, dan

a23= 7.

Contoh 2: MatrikB3_×2

B=



 

1 3 5 9 2 4



 

(14)

2 BAB 1. MATRIK DAN KOMPUTASI

dimana masing-masing elemennya adalahb11 = 1, b12 = 3, b21 = 5, b22 = 9, b31 = 2, dan

b32= 4.

1.2 Inisialisasi matrik dalam memori komputer

Dalam bahasa pemrograman Matlab, cara mengisi memori komputer dengan elemen-elemen matrikA2×3, sesuai dengan Contoh 1 adalah

1 clear all

2 clc

3

4 A(1,1) = 3;

5 A(1,2) = 8;

6 A(1,3) = 5;

7 A(2,1) = 6;

8 A(2,2) = 4;

9 A(2,3) = 7;

10 A

Sedangkan untuk matrikB3×2, sesuai Contoh 2 adalah

1 clear all

2 clc

3

4 B(1,1) = 1;

5 B(1,2) = 3;

6 B(2,1) = 5;

7 B(2,2) = 9;

8 B(3,1) = 2;

9 B(3,2) = 4;

10 B

Ini bukan satu-satunya cara menginisialisasi suatu matrik, disamping itu, ada juga cara lain yang relatif lebih mudah. Misalnya untuk matrik A dan matrik B bisa ditulis sebagai berikut

1 clear all

2 clc

3

4 A=[ 3 8 5

5 6 4 7 ];

6

7 B=[ 1 3

8 5 9

9 2 4 ];

atau

1 clear all

2 clc

3

4 A=[ 3 8 5 ; 6 4 7 ];

(15)

1.3. MACAM-MACAM MATRIK 3

1.3 Macam-macam matrik

1.3.1 Matrik transpose

Operasi transpose terhadap suatu matrik akan menukar elemen-elemen dalam satu kolom menjadi elemen-elemen dalam satu baris; demikian pula sebaliknya. Notasi matrik tranpose adalahAT.

Contoh 3: Operasi transpose terhadap matrikA

A=

1.3.2 Matrik bujursangkar

Matrik bujursangkar adalah matrik yang jumlah baris dan jumlah kolomnya sama.

Contoh 4: Matrik bujursangkar berukuran 3x3 atau sering juga disebut matrik bujursangkar orde 3

1.3.3 Matrik simetrik

Matrik simetrik adalah matrik bujursangkar yang elemen-elemen matrikAbernilai sama den-gan matrik transpose-nya (AT).

Contoh 5: Matrik simetrik

A=

1.3.4 Matrik diagonal

Matrik diagonal adalah matrik bujursangkar yang seluruh elemen-nya bernilai 0 (nol), kecuali elemen-elemen diagonalnya.

Contoh 6: Matrik diagonal orde 3

(16)

1.3.5 Matrik identitas

Matrik identitas adalah matrik bujursangkar yang semua elemen-nya bernilai 0 (nol), kecuali elemen-elemen diagonal yang seluruhnya bernilai 1.

Contoh 7: Matrik identitas orde 3

I=



 

1 0 0 0 1 0 0 0 1



 

1.3.6 Matrik upper-triangular

Matrik upper-tringular adalah matrik bujursangkar yang seluruh elemen dibawah elemen di-agonal bernilai 0 (nol).

Contoh 8: Matrik upper-triangular

A=



    

3 6 2 1 0 4 1 5 0 0 8 7 0 0 0 9



    

1.3.7 Matrik lower-triangular

Matrik lower-tringular adalah matrik bujursangkar yang seluruh elemen diatas elemen diago-nal bernilai 0 (nol).

Contoh 9: Matrik lower-triangular

A=



    

12 0 0 0

32 −2 0 0

8 7 11 0

−5 10 6 9



    

1.3.8 Matrik tridiagonal

Matrik tridiagonal adalah matrik bujursangkar yang seluruh elemen bukan 0 (nol) berada dis-ekitar elemen diagonal, sementara elemen lainnya bernilai 0 (nol).

Contoh 10: Matrik tridiagonal

A=



    

3 6 0 0

2 −4 1 0

0 5 8 −7

0 0 3 9



(17)

1.3. MACAM-MACAM MATRIK 5

1.3.9 Matrik diagonal dominan

Matrik diagonal dominan adalah matrik bujursangkar yang memenuhi

|aii|> n X

j=1_,j₆=_i

|aij| (1.2)

dimanai=1,2,3,..n. Coba perhatikan matrik-matrik berikut ini

A= matrikAdisebut matrik diagonal dominan. Sekarang perhatikan elemen diagonal matrikB,

|6|<|4|+| −3|,| −2|<|4|+|0|, dan|1|<| −3|+|0|. Dengan demikian, matrikBbukan matrik diagonal dominan.

1.3.10 Matrikpositive-definite

Suatu matrik dikatakanpositive-definitebila matrik tersebut simetrik dan memenuhi

xtAx>0 (1.3)

Contoh 11: Diketahui matrik simetrik berikut

A=

untuk menguji apakah matrikAbersifatpositive-definite, maka

xtAx = hx1 x2 x3

Dari sini dapat disimpulkan bahwa matrikAbersifatpositive-definite, karena memenuhi

(18)

kecuali jikax1=x2=x3=0.

1.3.11 Vektor-baris dan vektor-kolom

Notasi vektor biasanya dinyatakan dengan huruf kecil dan dicetak tebal. Suatu matrik dina-makan vektor-baris berukuran m, bila hanya memiliki satu baris danm kolom, yang diny-atakan sebagai berikut

a=ha11 a12 . . . a1m i

=ha1 a2 . . . am i

(1.4)

Sedangkan suatu matrik dinamakan vektor-kolom berukurann, bila hanya memiliki satu kolom dannbaris, yang dinyatakan sebagai berikut

a=

1.4 Operasi matematika

1.4.1 Penjumlahan matrik

Operasi penjumlahan pada dua buah matrik hanya bisa dilakukan bila kedua matrik tersebut berukuran sama. Misalnya matrikC2×3

C=

"

9 5 3 7 2 1

#

dijumlahkan dengan matrikA2_×3, lalu hasilnya (misalnya) dinamakan matrikD2_×3

D=A+C

(19)

1.4. OPERASI MATEMATIKA 7

Dijabarkan satu persatu sebagai berikut

d11=a11+c11

d12=a12+c12

d13=a13+c13 (1.6)

d21=a21+c21

d22=a22+c22

d23=a23+c23

Dari sini dapat diturunkan sebuah rumus umum penjumlahan dua buah matrik

dij =aij+cij (1.7)

dimanai=1,2 danj=1,2,3.

1.4.2 Komputasi penjumlahan matrik

Berdasarkan contoh operasi penjumlahan di atas, indeksj pada persamaan (1.7) lebih cepat berubah dibanding indeksisebagaimana ditulis pada persamaan (1.6),

d11=a11+c11

d12=a12+c12

d13=a13+c13

Jelas terlihat, ketika indeks i masih bernilai 1, indeks j sudah berubah dari nilai 1 sampai 3. Hal ini membawa konsekuensi pada scriptpemrograman, dimana looping untuk indeks j

harus diletakkan di dalamloopingindeksi. Pokoknya yanglooping-nya paling cepat harus diletakkan paling dalam; sebaliknya, looping paling luar adalah looping yang indeksnya paling jarang berubah.

Dalam matlab, algoritma penjumlahan dua matrik ditulis sebagai berikut:

1 for i=1:2

2 for j=1:3

3 D(i,j)=A(i,j)+C(i,j);

4 end

5 end

Sedangkan dalam Fortran77, operasi penjumlahan antara matrik ditulis sebagai berikut:A2_×3 danC2×3adalah

1 do i=1,2

2 do j=1,3

3 D(i,j)=A(i,j)+C(i,j)

4 end do

(20)

Perhatikan kedua script di atas! Penulisan indeksiharus didahulukan daripada indeksj. Perlu dicatat bahwa ukuran matrik tidak terbatas hanya 2x3. Tentu saja anda bisa men-gubah ukurannya sesuai dengan keperluan atau kebutuhan anda. Jika ukuran matrik diny-atakan secara umum sebagainxm, dimananadalah jumlah baris danmadalah jumlah kolom, maka bentuk pernyataan komputasinya dalam matlab menjadi

1 for i=1:n

2 for j=1:m

3 D(i,j)=A(i,j)+C(i,j);

4 end

5 end

sedangkan dalam Fortran77

1 do i=1,n

2 do j=1,m

3 D(i,j)=A(i,j)+C(i,j)

4 end do

5 end do

Sekarang, mari kita lengkapi dengan contoh sebagai berikut: diketahui matrikA2×3

A=

"

3 8 5 6 4 7

#

dan matrikC2_×3

C=

"

9 5 3 7 2 1

#

Program untuk menjumlahkan kedua matrik tersebut dalam matlab adalah:

1 clear all

2 clc

3

4 A(1,1) = 3;

5 A(1,2) = 8;

6 A(1,3) = 5;

7 A(2,1) = 6;

8 A(2,2) = 4;

9 A(2,3) = 7;

10 C(1,1) = 9;

11 C(1,2) = 5;

12 C(1,3) = 3;

13 C(2,1) = 7;

14 C(2,2) = 2;

15 C(2,3) = 1;

16 n=2

17 m=3

18 for i=1:n

19 for j=1:m

20 D(i,j)=A(i,j)+C(i,j);

21 end

(21)

sedangkan dalam Fortran77

1 A(1,1) = 3

2 A(1,2) = 8

3 A(1,3) = 5

4 A(2,1) = 6

5 A(2,2) = 4

6 A(2,3) = 7

7 C(1,1) = 9

8 C(1,2) = 5

9 C(1,3) = 3

10 C(2,1) = 7

11 C(2,2) = 2

12 C(2,3) = 1

13 n=2

14 m=3

15 do i=1,n

16 do j=1,m

17 D(i,j)=A(i,j)+C(i,j)

18 end do

19 end do

1.4.3 Perkalian matrik

Operasi perkalian dua buah matrik hanya bisa dilakukan bila jumlah kolom matrik pertama sama dengan jumlah baris matrik kedua. Jadi kedua matrik tersebut tidak harus berukuran sama seperti pada penjumlahan dua matrik. Misalnya matrikA2×3 dikalikan dengan matrik

B3_×2, lalu hasilnya (misalnya) dinamakan matrikE2_×2

E2×2 =A2×3.B3×2

E =

"

3 8 5 6 4 7

# 

 

1 3 5 9 2 4



 

=

"

3.1 + 8.5 + 5.2 3.3 + 8.9 + 5.4 6.1 + 4.5 + 7.2 6.3 + 4.9 + 7.4

#

=

"

53 101

40 82

#

Tanpa mempedulikan nilai elemen-elemen masing-masing matrik, operasi perkalian antara matrikA2_×3 danB3_×2, bisa juga dinyatakan dalam indeks masing-masing dari kedua matrik tersebut, yaitu

"

e11 e12

e21 e22 #

=

"

a11.b11+a12.b21+a13.b31 a11.b12+a12.b22+a13.b32

(22)

Bila dijabarkan, maka elemen-elemen matrikE2_×2adalah

e11=a11.b11+a12.b21+a13.b31 (1.8)

e12=a11.b12+a12.b22+a13.b32 (1.9)

e21=a21.b11+a22.b21+a23.b31 (1.10)

e22=a21.b12+a22.b22+a23.b32 (1.11)

Sejenak, mari kita amati perubahan pasangan angka-angka indeks yang mengiringi elemene,

adanbpada persamaan (1.8) sampai persamaan (1.11). Perhatikan perubahan angka indeks pertama pada elemeneseperti berikut ini

e1..=..

e2_..=..

Pola perubahan yang sama akan kita dapati pada angka indeks pertama dari elemena

e1_..=a1_...b_...+a1_...b_...+a1_...b_...

e2_..=a2_...b_...+a2_...b_...+a2_...b_...

e2..=a2...b...+a2...b...+a2...b...

Dengan demikian kita bisa mencantumkan huruf i sebagai pengganti angka-angka indeks yang polanya sama

ei.. =ai...b...+ai...b...+ai...b...

dimanaibergerak mulai dari angka 1 hingga angka 2, atau kita nyatakani=1,2. Selanjutnya, masih dari persamaan (1.8) sampai persamaan (1.11), marilah kita perhatikan perubahan angka indeks masih pada elemenedan elemenb,

ei1 =a_i...b_..1+a_i...b_..1+a_i...b_..1

ei2 =a_i...b_..2+a_i...b_..2+a_i...b_..2

ei1 =ai...b..1+ai...b..1+ai...b..1

(23)

Dengan demikian kita bisa mencantumkan huruf j sebagai pengganti angka-angka indeks yang polanya sama

eij =ai...b..j+ai...b..j+ai...b..j

dimanajbergerak mulai dari angka 1 hingga angka 2, atau kita nyatakanj=1,2. Selanjutnya, masih dari persamaan (1.8) sampai persamaan (1.11), mari kita perhatikan perubahan angka indeks masih pada elemenadan elemenb, dimana kita akan dapati pola sebagai berikut

eij =ai1.b1_j +a_i2.b2_j+a_i3.b3_j

eij =ai1.b1j +ai2.b2j+ai3.b3j

Dan kita bisa mencantumkan huruf k sebagai pengganti angka-angka indeks yang polanya sama, dimanakbergerak mulai dari angka 1 hingga angka 3, atau kita nyatakank=1,2,3.

eij =aik.bkj+aik.bkj+aik.bkj

Kemudian secara sederhana dapat ditulis sebagai berikut

eij =aik.bkj+aik.bkj+aik.bkj (1.12)

Selanjutnya dapat ditulis pula formula berikut

eij = 3 X

k=1

aikbkj (1.13)

dimanai=1,2;j=1,2; dank=1,2,3.

Berdasarkan contoh ini, maka secara umum bila ada matrikAn×myang dikalikan dengan ma-trikBm×p, akan didapatkan matrikEn×pdimana elemen-elemen matrikEmemenuhi

eij = m X

k=1

aikbkj (1.14)

(24)

1.4.4 Komputasi perkalian matrik

Komputasi operasi perkalian antara matrikA2×3danB3×2dilakukan melalui 2 tahap;pertama adalah memberikan nilai 0 (nol) pada elemen-elemen matrikE2_×2dengan cara (dalam matlab)

1 for i=1:2

2 for j=1:2

3 E(i,j)=0.0;

4 end

5 end

dalam Fortran77

1 do i=1,2

2 do j=1,2

3 E(i,j)=0.0

4 end do

5 end do

keduaadalah menghitung perkalian matrik dengan cara (dalam matlab)

1 for i=1:2

2 for j=1:2

3 for k=1:3

4 E(i,j)=E(i,j)+A(i,k)*B(k,j);

5 end

6 end

7 end

dalam Fortran77

1 do i=1,2

2 do j=1,2

3 do k=1,3

4 E(i,j)=E(i,j)+A(i,k)*B(k,j)

5 end do

6 end do

7 end do

(25)

Tentu saja anda bisa mengubah ukurannya sesuai dengan keperluan atau kebutuhan anda. Jika ukuran matrikAdinyatakan secara umum sebagainxmdan matrikBberukuranmxp, maka bentuk pernyataan komputasinya dalam Matlab menjadi

1 for i=1:n

2 for j=1:p

3 E(i,j)=0.0;

4 end

5 end

6 for i=1:n

7 for j=1:p

8 for k=1:m

9 E(i,j)=E(i,j)+A(i,k)*B(k,j);

10 end

11 end

12 end

dalam Fortran77

1 do i=1,n

2 do j=1,p

3 E(i,j)=0.0

4 end do

5 end do

6 do i=1,n

7 do j=1,p

8 do k=1,m

9 E(i,j)=E(i,j)+A(i,k)*B(k,j)

10 end do

11 end do

12 end do

dimana akan diperoleh hasil berupa matrikEyang berukurannxp.

1.4.5 Perkalian matrik dan vektor-kolom

Operasi perkalian antara matrik dan vektor-kolom sebenarnya sama saja dengan perkalian an-tara dua matrik. Hanya saja ukuran vektor-kolom boleh dibilang spesial yaitumx1, dimana

mmerupakan jumlah baris sementara jumlah kolomnya hanya satu. Misalnya matrik A, pa-da contoh 1, dikalikan dengan vektor-kolom x yang berukuran3 x 1 atau disingkat dengan mengatakan vektor-kolomxberukuran3, lalu hasilnya (misalnya) dinamakan vektor-kolomy

(26)

y =

"

3 8 5 6 4 7

# 

 

2 3 4



 

=

"

3.2 + 8.3 + 5.4 6.2 + 4.3 + 7.4

#

=

"

50 52

#

Sekali lagi, tanpa mempedulikan nilai elemen-elemen masing-masing, operasi perkalian antara matrikAdan vektor-kolomx, bisa juga dinyatakan dalam indeksnya masing-masing, yaitu

"

y1

y2 #

=

"

a11.x1+a12.x2+a13.x3

a21.x1+a22.x2+a23.x3 #

Bila dijabarkan, maka elemen-elemen vektor-kolomyadalah

y1 =a11.x1+a12.x2+a13.x3

y2 =a21.x1+a22.x2+a23.x3

kemudian secara sederhana dapat diwakili oleh rumus berikut

yi= 3 X

j=1

aijxj

dimanai=1,2.

Berdasarkan contoh tersebut, secara umum bila ada matrikAberukurannxmyang dikalikan dengan vektor-kolomxberukuranm, maka akan didapatkan vektor-kolomyberukurannx1

dimana elemen-elemen vektor-kolomymemenuhi

yi= m X

j=1

aijxj (1.15)

dengani=1,2,. . . ,n.

1.4.6 Komputasi perkalian matrik dan vektor-kolom

Sama seperti perkalian dua matrik, komputasi untuk operasi perkalian antara matrikA beruku-rannxmdan vektor-kolomxberukuranmdilakukan melalui 2 tahap; pertama adalah mem-berikan nilai 0 (nol) pada elemen-elemen vektor-kolomyyang berukurann. Lalu tahap kedua adalah melakukan proses perkalian. Kedua tahapan ini digabung jadi satu dalam program berikut ini

1 for i=1:n

(27)

1.5. PENUTUP 15

3 end

4 for i=1:n

5 for j=1:m

6 b(i,1)=b(i,1)+A(i,j)*x(j,1);

7 end

8 end

dan dalam Fortran

1 do i=1,n

2 b(i,1)=0.0

3 end do

4 do i=1,n

5 do j=1,m

6 b(i,1)=b(i,1)+A(i,j)*x(j,1)

7 end do

8 end do

1.5 Penutup

Demikianlah catatan singkat dan sederhana mengenai jenis-jenis matrik dasar yang seringkali dijumpai dalam pengolahan data fisika secara numerik. Semuanya akan dijadikan acuan atau referensi pada pembahasan topik-topik numerik yang akan datang.

1.6 Latihan

Diketahui matrikA, matrikB, dan vektorxsebagai berikut

A=



    

1 3 −6 −2

5 9 7 5.6

2 4 8 −1

2.3 1.4 0.8 −2.3



    

B=



    

8 1 4 21

3 10 5 0.1

7 −2 9 −5

2.7 −12 −8.9 5.7



    

x=



    

0.4178 −2.9587

56.3069 8.1



    

1. Buatlah script untuk menyelesaikan penjumlahan matrikAdan matrikB.

2. Buatlah script untuk menyelesaikan perkalian matrikAdan matrikB.

3. Buatlah script untuk menyelesaikan perkalian matrikAdan vektorx.

(28)

(29)

Bab 2

Formulasi Masalah Inversi

2.1 Klasifikasi masalah inversi

Dalam masalah inversi, kita selalu berhubungan dengan parameter model (M) dan data (N); yang mana jumlah dari masing-masing akan menentukan klasifikasi permasalahan inversi dan cara penyelesaiannya. Bila jumlah model parameter lebih sedikit dibandingkan data observasi (M < N), maka permasalahan inversi ini disebutoverdetermined. Umumnya masalah ini dis-elesaikan menggunakan pencocokan (best fit ) terhadap data observasi. Dalam kondisi yang lain dimana jumlah parameter yang ingin dicari (M) lebih banyak dari pada jumlah datanya (N), maka masalah inversi ini disebut underdetermined. Dalam kasus ini terdapat sekian banyak model yang dapat sesuai kondisi datanya. Inilah yang disebut dengan masalah non-uniqness. Bagaimana cara untuk mendapatkan model yang paling mendekati kondisi bawah permukaan? Menurut Meju, 1994 persoalan ini bisa diselesaikan dengan model yang param-eternya berbentuk fungsi kontinyu terhadap posisi. Kasus yang terakhir adalah ketika jumlah data sama atau hampir sama dengan jumlah parameter. Ini disebutevendetermined. Pada ka-sus ini model yang paling sederhana dapat diperoleh menggunakan metode inversi langsung. Pada bab ini, saya mencoba menyajikan dasar teknik inversi yang diaplikasikan pada mod-el garis, modmod-el parabola dan modmod-el bidang. Uraian aplikasi tersebut diawali dari ketersediaan data observasi, lalu sejumlah parameter model (unknown parameter) mesti dicari dengan teknik inversi. Mari kita mulai dari model garis.

2.2 Inversi Model Garis

Secara teori, variasi temperatur bawah permukaan akan semakin meningkat ketika temper-atur tersebut diukur semakin kedalam permukaan bumi. Misalnya telah dilakukan sebanyak sepuluh kali (N = 10) pengukuran temperatur (Ti) pada kedalaman yang berbeda beda (zi) sebagaimana ditunjukan datanya pada Tabel 2.1.

(30)

18 BAB 2. FORMULASI MASALAH INVERSI

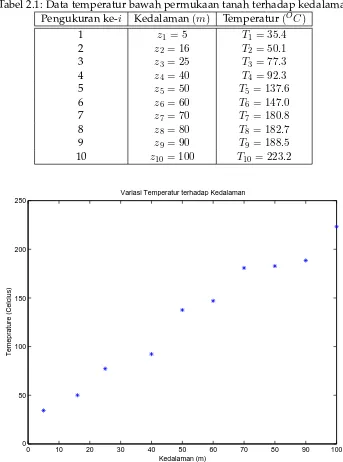
Tabel 2.1: Data temperatur bawah permukaan tanah terhadap kedalaman Pengukuran ke-i Kedalaman(m) Temperatur(O_C₎

1 z1 = 5 T1 = 35.4 2 z2 = 16 T2 = 50.1 3 z3 = 25 T3 = 77.3 4 z4 = 40 T4 = 92.3

5 z5 = 50 T5 = 137.6

6 z6 = 60 T6 = 147.0

7 z7 = 70 T7 = 180.8

8 z8 = 80 T8 = 182.7

9 z9 = 90 T9 = 188.5

10 z10= 100 T10= 223.2

0 10 20 30 40 50 60 70 80 90 100 0

50 100 150 200 250

Kedalaman (m)

Temeprature (Celcius)

Variasi Temperatur terhadap Kedalaman

Gambar 2.1: Data observasi perubahan temperatur terhadap kedalaman dari permukaan tanah

Source code untuk menggambar grafik tersebut dalam Matlab adalah

1 clear all

2 clc

3 % Data observasi

4 z = [5 16 25 40 50 60 70 80 90 100];

5 T = [34.4 50.1 77.3 92.3 137.6 147.0 180.8 182.7 188.5 223.2];

6

7 % Menampilkan grafik

8 plot ( z, T, ’b*’ )

9 xlabel(’Kedalaman (meter)’);

10 ylabel(’Temeprature (Celcius)’);

(31)

2.2. INVERSI MODEL GARIS 19

Lalu kita berasumsi bahwa variasi temperatur terhadap kedalaman ditentukan oleh rumus berikut ini:

m1+m2z_i=T_i (2.1)

dimana m1 dan m2 adalah konstanta-konstanta yang akan dicari. Rumus di atas disebut

model matematika. Sedangkanm1 danm2disebutparameter modelatau biasa juga disebut

unknown parameter. Pada model matematika di atas terdapat dua buah parameter model,

(M = 2). Sementara jumlah data observasi ada empat, (N = 10), yaitu nilai-nilai kedala-man, zi, dan temperatur, Ti. Berdasarkan model tersebut, kita bisa menyatakan temperatur dan kedalaman masing-masing sebagai berikut:

m1+m2z1 =T1

Semua persamaan tersebut dapat dinyatakan dalam operasi matrik berikut ini:



Lalu ditulis secara singkat

Gm=d (2.3)

(32)

menda-20 BAB 2. FORMULASI MASALAH INVERSI

patkan nilaim1danm2pada vektor kolomm? Manipulasi1berikut ini bisa menjawabnya

GTGm₌_GTd _(2.4)

dimanaT disini maksudnya adalah tanda transpos matrik. Selanjutnya, untuk mendapatkan elemen-elemenm, diperlukan langkah-langkah perhitungan berikut ini:

GTGm ₌ _GTd

[GTG]−1GTGm _{= [}_GT_G_]−1_GTd

m _{= [}_GT_G_]−1_GTd _(2.5)

1. Tentukan transpos dari matrik kernel, yaituGT

G=

2. Lakukan perkalian matriksGT_G

GTG=

(33)

2.2. INVERSI MODEL GARIS 21

3. Kemudian tentukan pulaGT_d

GTd₌

4. Dengan menggunakan hasil dari langkah 2 dan langkah 3, maka persamaan (2.4) dapat dinyatakan sebagai

Berdasarkan data observasi pada tabel di atas, diperoleh

m _{= [}_GT_G_]−1_GTd

Perintah di Matlab untuk menghitung elemen-elemen m, yaitu

m=inv(G’*G)*G’*d

Secara lebih lengkap, source code Matlab untuk melakukan inversi data observasi adalah Source-code Matlab untuk perhitungan inversi data observasi tersebut adalah:

1 clear all

2 clc

3 % Data observasi

4 z = [5 16 25 40 50 60 70 80 90 100];

5 T = [34.4 50.1 77.3 92.3 137.6 147.0 180.8 182.7 188.5 223.2];

6

(34)

8 G = [1 z(1) ;

9 1 z(2) ;

10 1 z(3) ;

11 1 z(4) ;

12 1 z(5) ;

13 1 z(6) ;

14 1 z(7) ;

15 1 z(8) ;

16 1 z(9) ;

17 1 z(10) ];

18

19 % Perhitungan inversi

20 m = inv(G’*G)*G’*T’

Demikianlah contoh aplikasi teknik inversi untuk menyelesaikan persoalan model garis. Anda bisa mengaplikasikan pada kasus lain, dengan syarat kasus yang anda tangani memiliki bentuk model yang sama dengan yang telah dikerjakan pada catatan ini, yaitu model garis:

y=m1+m2x. Selanjutnya mari kita pelajari inversi model parabola.

2.3 Inversi Model Parabola

Kembali kita ambil contoh variasi temperatur terhadap kedalaman dengan sedikit modifikasi data. Misalnya telah dilakukan sebanyak delapan kali (N = 8) pengukuran temperatur(Ti) pada kedalaman yang berbeda beda(zi). Tabel pengukuran yang diperoleh adalah: Lalu

ki-Tabel 2.2: Data temperatur bawah permukaan tanah terhadap kedalaman Pengukuran ke-i Kedalaman(m) Temperatur(O_C₎

1 z1 = 5 T1= 21,75 2 z2 = 8 T2= 22,68 3 z3 = 14 T3= 25,62 4 z4 = 21 T4= 30,87 5 z5 = 30 T5 = 40,5 6 z6 = 36 T6= 48,72 7 z7 = 45 T7= 63,75

8 z8 = 60 T8= 96

ta berasumsi bahwa variasi temperatur terhadap kedalaman memenuhi model matematika berikut ini:

m1+m2zi+m3z 2

i =Ti (2.8)

(35)

2.3. INVERSI MODEL PARABOLA 23

jumlah data observasi):

m1+m2z1+m3z



Gm₌d _(2.10)

dimanadadalah data yang dinyatakan dalam vektor kolom,madalah model parameter, juga dinyatakan dalam vektor kolom, danGdisebutmatrik kernel. Lantas bagaimana cara menda-patkan nilaim1,m2danm3pada vektor kolomm? Manipulasi berikut ini bisa menjawabnya

GtGm₌_Gtd _(2.11)

(36)

1. Tentukan transpos dari matrik kernel, yaituGt

G=

3. Kemudian tentukan pulaGt_d

Gtd₌

4. Sekarang persamaan (2.16) dapat dinyatakan sebagai

(37)

2.4. INVERSI MODEL BIDANG 25

Berdasarkan data observasi pada tabel di atas, diperoleh



 

8 219 8547

219 8547 393423

8547 393423 19787859



Program Matlab telah menyediakan sebuah baris perintah untuk menghitung elemen-elemen m, yaitu

Sehingga operasi matriks di atas akan menghasilkan nilaim1 = 21,m2 = 0,05danm3 =

0,02.

Demikianlah contoh aplikasi teknik inversi untuk menyelesaikan persoalan model parabola. Anda bisa mengaplikasikan pada kasus lain, dengan syarat kasus yang anda tangani memiliki bentuk model yang sama dengan yang telah dikerjakan pada catatan ini, yaitu model garis:

y = m1 +m2x+ +m3x 2

. Selanjutnya mari kita pelajari inversi model bidang atau model 2-dimensi (2-D).

2.4 Inversi Model Bidang

Dalam catatan ini saya belum sempat mencari contoh data observasi yang sesuai untuk model dimensi. Maka, saya ingin langsung saja mengajukan sebuah model matematika untuk 2-dimensi berikut ini:

m1+m2x_i+m3y_i =d_i (2.14)

dimanam1,m2danm3merupakanunknown parameteryang akan dicari. Adapun yang berlaku sebagai data adalah d1, d2, d3, ..., di. Berdasarkan model matematika tersebut, kita bisa ny-atakan

(38)

Gm₌d _(2.15)

dimana d adalah data yang dinyatakan dalam vektor kolom, m adalah unknown parameter, juga dinyatakan dalam vektor kolom, dan Gdisebutmatrik kernel. Lantas bagaimana cara mendapatkan nilaim1,m2danm3pada vektor kolomm? Sama seperti sebelumnya, kita harus membuat persamaan matriks berikut ini

GtGm₌_Gtd _(2.16)

dimanatdisini maksudnya adalah tanda transpos matrik. Selanjutnya, untuk mendapatkan elemen-elemenm, diperlukan langkah-langkah perhitungan berikut ini:

1. Tentukan transpos dari matrik kernel, yaituGt

G=

3. Kemudian tentukan pulaGt_d

Gtd₌

4. Sekarang, persamaan (2.16) dapat dinyatakan sebagai

(39)

2.5. CONTOH APLIKASI 27

5. Sampai disini, jika tersedia data observasi, maka anda tinggal memasukan data tersebut ke dalam persamaan di atas, sehingga nilai elemen-elemen m dapat dihitung dengan perintah matlab

Langkah-langkah selanjutnya akan sama persis dengan catatan sebelumnya (model lin-eardanmodel parabola)

Anda bisa mengaplikasikan data pengukuran yang anda miliki, dengan syarat kasus yang anda tangani memiliki bentukmodelyang sama dengan yang telah dikerjakan pada catatan ini, yaitu memiliki tiga buah model parameter yang tidak diketahui dalam bentuk persamaan bidang (atau 2-dimensi):d=m1+m2x+m3y.

2.5 Contoh aplikasi

2.5.1 Menghitung gravitasi di planet X

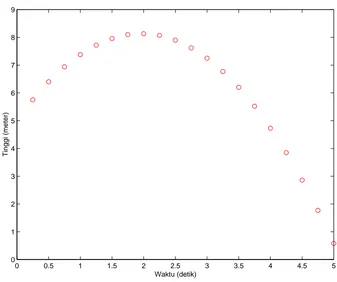
Seorang astronot tiba di suatu planet yang tidak dikenal. Setibanya disana, ia segera mengelu-arkan kamera otomatis, lalu melakukan ekperimen kinematika yaitu dengan melempar batu vertikal ke atas. Hasil foto-foto yang terekam dalam kamera otomatis adalah sebagai berikut Plot data pengukuran waktu vs ketinggian diperlihatkan pada Gambar 2.2. Anda diminta

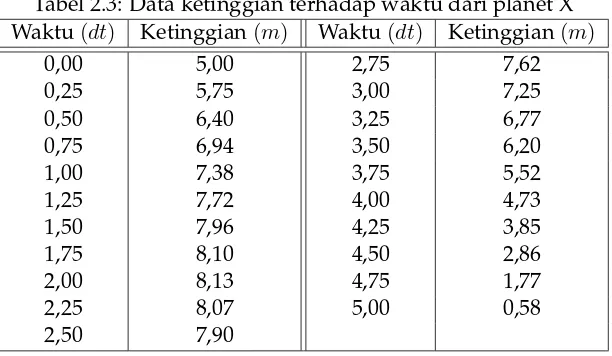
un-Tabel 2.3: Data ketinggian terhadap waktu dari planet X Waktu(dt) Ketinggian(m) Waktu(dt) Ketinggian(m)

0,00 5,00 2,75 7,62

0,25 5,75 3,00 7,25

0,50 6,40 3,25 6,77

0,75 6,94 3,50 6,20

1,00 7,38 3,75 5,52

1,25 7,72 4,00 4,73

1,50 7,96 4,25 3,85

1,75 8,10 4,50 2,86

2,00 8,13 4,75 1,77

2,25 8,07 5,00 0,58

2,50 7,90

tuk membantu proses pengolahan data sehingga diperoleh nilai konstanta gravitasi di planet tersebut dan kecepatan awal batu. Jelas, ini adalah persoalan inversi, yaitu mencari unkown parameter (konstanta gravitasi dan kecepatan awal batu) dari data observasi (hasil foto gerak sebuah batu).

(40)

0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5 0

1 2 3 4 5 6 7 8 9

Waktu (detik)

Tinggi (meter)

Gambar 2.2: Grafik data pengukuran gerak batu

tentang Gerak-Lurus-Berubah-Beraturan (GLBB), yang formulasinya seperti ini

ho+vot−

1 2gt

2

=h

Berdasarkan tabel data observasi, ketinggian pada saatt= 0adalah5m. Itu artinyaho = 5m. Sehingga model matematika (formulasi GLBB) dapat dimodifikasi sedikit menjadi

vot−

1 2gt

2

=h−ho (2.18)

Selanjut, didefinisikanm1danm2sebagai berikut

m1=v_o m2 =−

1

2g (2.19)

sehingga persamaan model GLBB menjadi

m1ti+m2t 2

i =hi−5 (2.20)

dimanaimenunjukkan data ke-i.

(41)

2.5. CONTOH APLIKASI 29

memasukan data observasi kedalam model matematika (persamaan (2.20))

m1t1+m2t



Operasi matrik di atas memenuhi persamaan matrik

Gm₌d

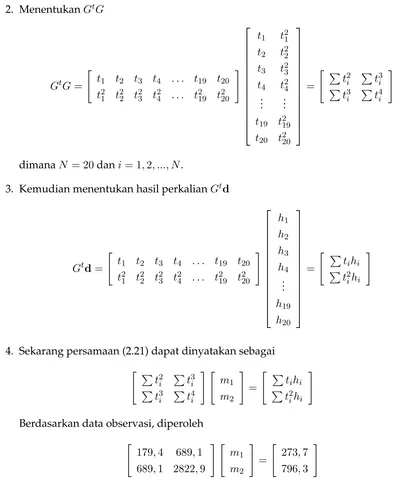
Seperti yang sudah dipelajari pada bab ini, penyelesaian masalah inversi dimulai dari pros-es manipulasi persamaan matrik sehingga perkalian antaraGt _dan_G _{menghasilkan matriks} bujursangkar

GtGm₌_Gtd _(2.21)

Selanjutnya, untuk mendapatkanm1danm2, prosedur inversi dilakukan satu-per-satu

1. Menentukan transpos matrik kernel, yaituGt

(42)

3. Kemudian menentukan hasil perkalianGt_d

Gtd₌

4. Sekarang persamaan (2.21) dapat dinyatakan sebagai

" _P

Berdasarkan data observasi, diperoleh

"

Hasil operasi matriks ini dapat diselesaikan dengan satu baris statemen di matlab yaitu

Hasil inversinya adalah nilai kecepatan awal yaitu saat batu dilempar ke atas adalah sebesar

m1 =vo = 3,2009 m/dt. Adapun percepatan gravitasi diperoleh dari m2 dimana m2 =− 1 2g= -0,8169; maka disimpulkan nilaigadalah sebesar 1,6338m/dt2

.

(43)

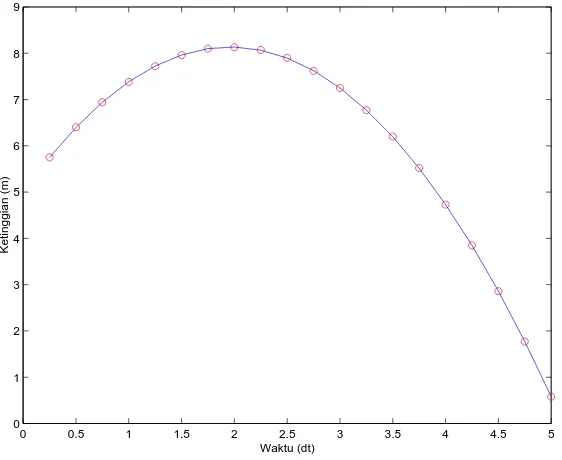
2.6. KESIMPULAN 31

0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5 0

1 2 3 4 5 6 7 8 9

Waktu (dt)

Ketinggian (m)

Gambar 2.3: Grafik hasil inversi parabola

2.6 Kesimpulan

(44)

(45)

Daftar Pustaka

[1] Burden, R.L. and Faires, J.D., (2001), Numerical Analysis, Seventh Edition, Brooks/Cole, Thomson Learning Academic Resource Center.

[2] Haliday and Resnick, (2001),Fundamental of Physics, Brooks/Cole, Thomson Learning Aca-demic Resource Center.

(46)

(47)

Indeks

Positive-definite, 5

Transpose, 3 Tridiagonal, 4

Vektor-baris, 6 Vektor-kolom, 6