berikan bimbingan dan arahan serta motivasi kepada penulis dalam penulisan tesis ini.
Dr. Mardiningsih, M.Si selaku Pembimbing Kedua yang telah banyak mem-berikan bimbingan dan arahan serta motivasi kepada penulis dalam penulisan tesis ini.
Seluruh Staf Pengajarpada Program Studi Magister Matematika FMIPA USU yang telah banyak memberikan ilmu pengetahuan selama masa perkuliahan. Kak Misiani, S.Siselaku Staf Administrasi Program Studi Magister Matematika FMIPA USU yang telah banyak memberikan pelayanan yang baik kepada penulis selama mengikuti perkuliahan. Seluruh rekan-rekan Mahasiswa Program Studi Magister Matematika FMIPA USU tahun 2013 genap (Bang Julham (Ayah), Kak Aida, Kak Mei, Kak Ayu, Amora, Kristin, Nina) yang telah memberikan bantu-an moril dbantu-an dorongbantu-an kepada penulis dalam penulisbantu-an tesis ini. Semua pihak yang telah banyak membantu, baik langsung maupun tidak langsung yang tidak dapat penulis sebutkan namanya satu persatu, hanya Tuhan yang mampu mem-berikan balasan terbaik. Mudah-mudahan tesis ini dapat memberi sumbangan yang berharga bagi perkembangan dunia ilmu dan bermanfaat bagi orang banyak. Penulis menyadari bahwa tesis ini masih jauh dari sempurna, untuk itu penulis mengharapkan kritik saran untuk penyempurnaan tesis ini. Semoga tesis ini dapat bermanfaat bagi pembaca dan pihak-pihak lain yang memerlukannya. Terima kasih.
Medan, 16 Desember 2015 Penulis,
RIWAYAT HIDUP
DAFTAR ISI
Halaman
PERNYATAAN i
ABSTRAK ii
ABSTRACT iii
KATA PENGANTAR iv
RIWAYAT HIDUP vi
DAFTAR ISI vii
DAFTAR GAMBAR x
BAB 1 PENDAHULUAN 1
1.1 Latar Belakang 1
1.2 Perumusan Masalah 3
1.3 Tujuan Penelitian 3
1.4 Manfaat Penelitian 3
1.5 Metode Penelitian 4
BAB 2 TINJAUAN PUSTAKA 5
2.1 Graf 5
2.1.1 Jenis-jenis Graf 7
2.2 Pohon dan Hutan 13
2.3 Pohon Merentang (Spanning Tree) 15
BAB 3 ANALISA GRAF KORDAL 18
3.1 Graf Kordal sebagai Irisan Graf 19
3.3 Pewarnaan Graf (Colouring Graph) 24 BAB 4 MENENTUKAN REPRESENTASI POHON DARI GRAF KORDAL
BIPARTISI 26
4.1 Analisa Algoritma 27
4.2 Representasi Pohon dari Graf Kordal Bipartisi 32
BAB 5 KESIMPULAN DAN SARAN 38
5.1 Kesimpulan 38
5.2 Saran 38
DAFTAR GAMBAR
Nomor Judul Halaman
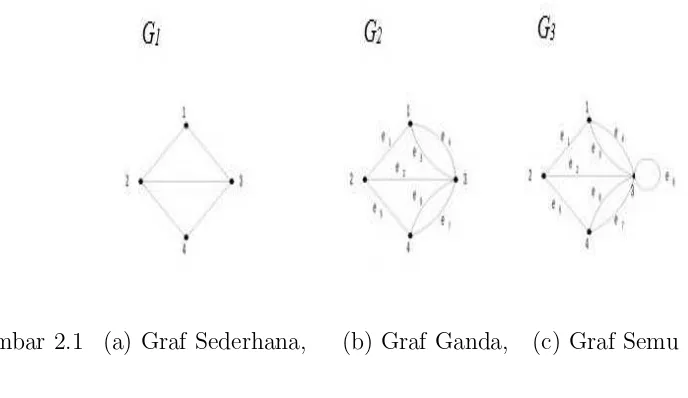
2.1 (a) Graf Sederhana, (b) Graf Ganda, (c) Graf Semu 6
2.2 Graf berhingga 8
2.3 Graf tak berhingga 8
2.4 Graf berarah 9
2.5 Graf lengkapKn,1≤n ≤6 9
2.6 Graf lingkar Cn,3≤n ≤68 10
2.7 Graf teratur derajat 0, 1, dan 2 10
2.8 Dua graf 3-bipartisi 10
2.9 Tiga gambar dari graf bipartisi K3,3 =K32 11
2.10 Graf bipartitG(V1, V2) 12
2.11 Graf tak-berarah tidak terhubung 12
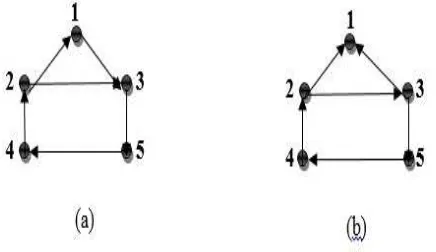
2.12 (a) Graf berarah terhubung kuat, (b) Graf berarah terhubung lemah 13
2.13 Graf Pohon 14
2.14 Graf lengkapG dan empat buah pohon merentangnya, T1, T2, T3, T4 16 2.15 Graf yang menyatakan jaringan jalur rel kereta api. Bobot pada setiap
sisi menyatakan panjang rel kereta api (×100m) (b). Pohon merentang
yang mempunyai jumlah jarak minimum 17
3.1 Graf kordal (sumber, Wikipedia) 18
3.2 Graf kordal dan dua representasi pohon (Sumber, Mckee dan Mcmorris,
3.3 Clique pada graf 20 3.4 Perfect elimination bipartite graphyang tidak mengandung kordal.
(Sum-ber: Golumbic, 1978) 22
3.5 Graf C6,3K2, C8 24
4.1 (a) Graf kordalGdan (b) Representasi pohon dari graf kordal (Sumber:
F ˜ANIC ˜A GAVRIL, 1974) 27
4.2 Irisan graf subpohon dari pohon adalah graf kordal. 32
4.3 Graf Kordal Bipartisi 34
4.4 Graf Kordal Bipartisi dengan Colouring Graph pada clique 34
4.5 Hasil bipartisi dari Clique 35
4.6 Representasi pohon dari graf kordal bipartisi 35
4.7 Pembagian Clique dengan Colouring Graph 36
BAB 1 PENDAHULUAN
1.1 Latar Belakang
Matematika sebagai ilmu dasar telah memberikan kemajuan yang begitu banyak dalam berbagai bidang. Teori graf merupakan salah satu cabang mate-matika yang turut memberikan andil dalam kemajuan tersebut. Teori graf ini sebenarnya telah dikenal lebih dari 250 tahun yang silam. Teori graf lahir pada tahun 1736 melalui tulisan euler yang berisi tentang upaya pemecahan masalah jembatan konisberg yang sangat terkenal di Eropa. Kurang lebih seratus tahun setelah lahirnya tulisan Euler tersebut tidak ada perkembangan yang sangat berarti berkenaan dengan teori graf. Tahun 1847, Kirchoff (1824-1887) berhasil mengem-bangkan teori pohon (Theory of trees) yang digunakan dalam persoalan jaringan listrik. Sepuluh tahun kemudian Cayley (1821-1895) juga menggunakan konsep po-hon untuk menjelaskan permasalahan kimia yaitu hidrokarbon. Hal yang penting untuk dibicarakan sehubungan dengan teori graf adalah apa yang dikemukakan oleh Hamilton (1805-1865). Tahun 1859 berhasil menemukan suatu permainan yang kemudian dijualnya ke pabrik mainan di Dublin. Permainan tersebut dari kayu berbentukdodecahedronberaturan yakni berupa sebuah pentagon beraturan dan tiap pojoknya dibentuk oleh tiga sisi berbeda. Tiap pojok dari em dedaca-hedron tersebut dipasangkan dengan sebuah kota terkenal seperti London, New York, Paris, dan lain-lain. Masalah dalam permainan ini adalah kita diminta un-tuk mencari suatu rute melalui sisi-sisi dari dodecahedron sehingga tiap kota dari 20 kota yang ada dapat dilalui tepat satu kali.
2
graf tersebut. Istilah ini juga digunakan dalam teori graf, dimana sebuah chord lingkaran dari graf lingkaran adalah sisi yang tidak terletak di lingkaran namun titik akhir darichordtersebut ada pada graf lingkaran (Mckee dan Mcmorris, 2006: 19). Meskipun telah ada kegiatan yang cukup selama 1960-an, tidak sampai 1970 graf kordal telah dikarakteristikkan dalam irisan graf. Irisan graf adalah graf/pola yang mewakili irisan dari titik ataupun garis yang terdapat pada himpunan keluar-ga suatu graf. Setiap graf dapat direpresentasikan sebakeluar-gai irisan graf. Irisan graf bertujuan mengelompokkan setiap himpunan yang memiliki kesamaan dalam suatu keadaan sehingga membentuk pola yang tercipta dari hasil kesamaan (irisan) itu sendiri. Kesamaan dalam suatu keadaan tersebutlah yang menjadikan irisan graf banyak digunakan untuk menyajikan permasalahan-permasalahan di dunia nya-ta. Selanjutnya, permasalahan tersebut akan dipecahkan dan diperoleh solusinya dengan cara matematis.
Nancy et al., (2006) berhasil mengembangkan graf kordal dengan merepre-sentasikan graf kordal menjadi graf pohon. Sebuah graf Gdalam keluarga [△, d, t] (Catatan: △, d, t adalah derajat titik di grafG), jika terdapat pohon dengan dera-jat maksimum△dan subpohon yang bersesuaian ke titik-titik diGsehingga setiap subpohon yang mempunyai derajat yang paling maksimumd dan dua titik dari G dikatakan bertetangga jika dan hanya jika subpohon yang bersesuaian kepada yang memiliki setidaknyat umum titik.
3
Dalam penelitian ini penulis akan meneliti representasi pohon dari graf kordal bipartisi dengan cara mengembangkan model yang terlebih dahulu diperkenalkan oleh F ˜ANIC ˜A GAVRIL. Penelitian ini terinspirasi dari tulisan N. Eaton et al ”Tree Representation of Graph” dan tulisan Jiang Huang ”Representation Characteri-zations of Chordal Bipartite Graph” yang pada dasarnya merupakan kombinasi dari keduanya. Hasil dari penelitian ini adalah representasi pohon yang diperoleh melalui pengembangan model oleh F ˜ANIC ˜A GAVRIL dari graf kordal bipartisi.
1.2 Perumusan Masalah
Graf kordal adalah graf yang mengandung lingkaran (Cycle) dengan panjang lingkaran lebih besar atau sama dengan 4 (empat). Seiring semakin berkembangnya teori graf, Nancyet al., pada tahun 2006 menemukan cara bagaimana merepresen-tasikan graf kordal menjadi graf pohon. Graf pohon merupakan graf yang tidak mengandung lingkaran (Cycle). Jelaslah bahwa graf kordal bertolak belakang de-ngan graf pohon. Namun Nancy et al., mampu membuktikannya. Huang pada tahun 2006 memperluas pengetahuan dengan membuat sebuah tulisan yang mem-bahas karateristik dari graf kordal bipatisi. Berkaitan dengan hal-hal tersebut, peneliti akan membahas representasi pohon dari graf kordal bipartisi dengan me-ngembangkan algoritma yang terlebih dahulu telah diperkenalkan oleh F ˜ANIC ˜A GAVRIL.
1.3 Tujuan Penelitian
Tujuan dari penelitian ini adalah merepresentasikan pohon dari graf kordal bipartisi dengan mengembangkan algoritma yang terlebih dahulu telah diperke-nalkan oleh F ˜ANIC ˜A GAVRIL.
1.4 Manfaat Penelitian
4
1.5 Metode Penelitian
Penelitian yang dilakukan merupakan studi literatur dan kepustakaan untuk memberikan pemahaman tentang representasi pohon dari graf. Berikut adalah langkah-langkah yang akan dilakukan:
1. Mengumpulkan informasi dari literatur-literatur mengenai representasi po-hon dari graf terutama graf kordal;
2. Mengumpulkan informasi dari referensi beberapa buku dan jurnal mengenai teori graf, Dimulai dengan penjelasan definisi pengertian graf, jenis-jenis graf, graf khusus yaitu graf pohon dan graf kordal;
3. Mengumpulkan informasi dari referensi beberapa buku dan jurnal mengenai graf kordal bipartisi. Dimulai dengan penjelasan defenisi graf kordal bipar-tisi, sifat-sifat graf kordal biparbipar-tisi, serta pembuktian beberapa teorema yang berhubungan dengan graf kordal bipartisi;
4. Mengembangkan representasi pohon dari graf kordal menjadi representasi pohon dari graf kordal bipartisi.
(a) Memaparkan persoalan secara konseptual yang disertakan pembuktian-nya;
(b) Memaparkan karakter-karakter khusus yang berkaitan dengan graf ko-rdal bipartisi;
(c) Menganalisa algoritma yang akan dikembangkan untuk merepresentasikan pohon dari graf kordal bipartisi;
(d) Menyusun cara kerja dan langkah-langkah representasi graf kordal bi-partisi menjadi graf pohon;
BAB 2
TINJAUAN PUSTAKA
Teori graf banyak digunakan dalam menyelesaikan permasalahan yang timbul di dunia nyata. Penggunaan graf dianggap bisa memodelkan masalah yang ada. Hal ini menimbulkan ketertarikan untuk menggali dan meneliti lebih banyak lagi tentang graf. Pada dasarnya graf memiliki banyak hal yang bisa diteliti, seperti halnya graf-graf khusus yang berkaitan dengan titik, sisi, dan derajatnya. Salah satu graf khusus yang akan dibahas pada penelitian ini adalah graf kordal. Mckee dan Mcmorris secara khusus membahas graf kordal dalam bukunya yang berjudul Intersection Graph Teory(1999). Dalam bukunya tersebut dibahas mengenai ciri-ciri dan karakteristik dari graf kordal beserta aplikasinya.
2.1 Graf
Bahan utama yang digunakan pada pembahasan berikut diambil dari Rein-hard Diestel (2010) kecuali disebutkan berbeda.
Graf didefenisikan sebagai pasangan himpunan (V, E) ditulis dengan notasi G= (V, E), dimanaV adalah himpunan tak kosong dari simpul-simpul danE ada-lah himpunan sisi yang menghubungkan sepasang simpul. Himpunan simpul dari graf G ditulis dengan V(G) = {v1, v2, v3, . . . , vn}, sedangkan himpunan sisi dari grafG dinyatakan dengan E(G) ={e1, e2, e3, . . . , en} atau sisi yang menghubung-kan simpulvi dengan simpul vj dapat dinyatakan dengan pasangan (vi, vj). Pada
umumnya untuk menggambarkan sebuah graf terdiri atas dot sebagai titik (vertex) dan gabungan dari 2 (dua) titik adalah garis (edge). Suatu graf G dikatakan ter-hubung jika untuk setiap simpul dari graf G terdapat jalur yang menghubungkan kedua simpul tersebut. Jalur pada grafGadalah perjalanan yang melewati semua simpul yang berbeda-beda. Perjalanan pada suatu graf G adalah barisan simpul dan ruas berganti-ganti. v1, e1, v2, e2, v3, e3, . . . , vn, en.
6
1. Graf G didefinisikan sebagai pemasangan himpunan (V, E) yang dalam hal ini: V ={v1, v2, . . . , vn} adalah himpunan tidak kosong dari titik-titik (ver-tices atau node) dan E = {e1, e2, . . . , en} adalah himpunan sisi (edges atau arcs) yang menghubungkan sepasang titik;
2. HimpunanV tidak boleh kosong, sedangkan himpunanEboleh kosong. Jadi, sebuah graf dimungkinkan tidak mempunyai sisi satu pun, tetapi titiknya harus ada, minimal satu. Graf yang hanya mempunyai satu titik tanpa sisi dinamakan graf trivial.
Titik pada graf dapat dinomori dengan huruf, seperti a, b, c, . . . , v, w, . . . , dengan bilangan asli 1,2,3, . . . , atau gabungan keduanya. Sedangkan sisi yang menghubungkan titik v1 dinyatakan dengan pasangan (vi, vj) atau dengan
lam-bange1, e2, . . .. Dengan kata lain, jika e adalah sisi yang menghubungkan titik vi,
maka e dapat ditulis sebagai e= (vi, vj).
Secara geometri graf digambarkan sebagai sekumpulan titik di dalam bidang dwimatra yang dihubungkan dengan sekumpulan garis (sisi).
7
2.1.1 Jenis-jenis Graf
Graf dapat dikelompokkan menjadi beberapa kategori (jenis) bergantung pa-da sudut panpa-dang pengelompokannya. Pengelompokkan graf pa-dapat dipanpa-dang berdasarkan ada tidaknya sisi ganda atau sisi gelang, berdasarkan jumlah titik, atau berdasarkan orientasi arah pada sisi.
Berdasarkan ada tidaknya gelang atau sisi ganda pada suatu graf. Sehingga secara umum graf dapat digolongkan menjadi 2 (dua) jenis:
1. Simple Graph
Graf yang tidak mengandung gelang maupun sisi-ganda dinamakan graf seder-hana. Pada graf sederhana, sisi adalah pasangan tak-terurut. Jadi menuliskan sisi (u, v) sama saja dengan (v, u). Graf sederhana G = (V, E) terdiri dari himpunan tidak kosong simpul-simpul dan E adalah himpunan pasangan tak-terurut yang berbeda disebut sisi;
2. Unsimple Graph
Graf yang mengandung sisi ganda atau gelang dinamakan graf tak-sederhana. Ada 2 (dua) macam graf tak-sederhana, yaitu graf ganda dan graf semu. Graf ganda adalah graf yang mengandung sisi ganda. G2pada Gambar 2.1 adalah graf ganda. Sisi ganda yang menghubungkan sepasang simpul bisa lebih dari dua buah. Sisi ganda dapat diasosiasikan sebagai pasangan tak-terurut yang sama (Rinaldi Munir, 2010: 357). Graf semu adalah graf yang mengandung gelang. G3 adalah graf semu (meskipun memiliki sisi ganda sekalipun). Graf semu lebih umum daripada graf ganda, karena sisi pada graf semu dapat terhubung ke dirinya sendiri.
8
Berdasarkan jumlah titik pada suatu graf, graf digolongkan menjadi 2 (dua) jenis:
1. Limited Graph
Graf berhingga adalah graf yang memiliki jumlah titikn yang berhingga.
Gambar 2.2 Graf berhingga
2. Unlimited Graph
Graf tak-berhingga adalah graf yang memiliki jumlah titik yang tak-berhingga.
Gambar 2.3 Graf tak berhingga
Berdasarkan orientasi arah pada sisi, secara umum graf dapat dibedakan atas 2 (dua) jenis:
1. Undirected Graph
9
2. Directed graph atau Digraph
Graf yang setiap sisinya diberikan orientasi arah disebut sebagai graf berarah. Pada graf berarah, (u, v) dan (v, u) menyatakan dua buah busur yang berbe-da, dengan kata lain (u, v)6= (v, u). Titik u dinamakan titik asal dan titikv dinamakan titik terminal.
Gambar 2.4 Graf berarah
Ada beberapa graf khusus yang dijumpai pada banyak aplikasi. Beberapa di antaranya adalah:
1. Complete Graph
Graf lengkap adalah graf sederhana yang setiap titiknya mempunyai sisi ke semua titik lainnya. Graf lengkap dengann buah titik dilambangkan dengan Kn. Setiap titik pada Kn berderajat n−1.
Gambar 2.5 Graf lengkap Kn,1≤n ≤6
2. Cyclic Graph
Graf lingkaran adalah graf sederhana yang setiap titiknya berderajat 2 (dua). Graf lingkaran dengann titik dilambangkan dengan Cn adalah v1, v2, . . . , vn,
sehingga sisi-sisinya adalah (v1, v2),(v2, v3), . . . ,(vn−1, vn), dan (vn, v1).
10
Gambar 2.6 Graf lingkarCn,3≤n ≤68
3. Regular Graph
Graf teratur adalah graf yang memiliki derajat yang sama. Jika derajat setiap titik adalahr, maka graf disebut sebagai graf teratur derajatr. Graf lengkap Kn dan graf lingkar Cn juga termaksud ke dalam graf teratur.
Gambar 2.7 Graf teratur derajat 0, 1, dan 2
4. Bipartie Graph
Jika r ≥ 2 adalah bilangan bulat. Graf G = (V, E) disebut r-partite jika V menambahkan partisi kedalam kelas r sehingga setiap sisi mempunyai titik akhir di kelas yang berbeda: titik di kelas partisi yang sama tidak harus bertetangga sebagai ganti 2-partisi.
Sebuah graf r-partite yang mana setiap 2 titik dari kelas partisi berbeda yang saling bertetangga disebut lengkap: grafr-partitelengkap untuk semua r yang bersamaan adalah graf lengkap multipartite.
11
GrafG yang himpunan titiknya dapat dikelompokkan menjadi 2 (dua) him-punan bagian V1 dan V2, sedemikian sehingga setiap sisi di dalam G meng-hubungkan sebuah titik diV1 ke sebuah titik diV2 disebut graf bipartit dan dinyatakan sebagai G(V1, V2). Dengan kata lain, setiap pasangan titik di V1 (demikian pula dengan titik-titik diV2) tidak bertetangga. Jika setiap titik diV1 bertetangga dengan semua titik di V2, maka G(V1, V2) disebut sebagai graf bipartit lengkap, dilambangkan denganKm,n. Jumlah sisi pada bipartit
lengkap adalah mn.
Teorema 2.1.1 Asratian et al.,(1998)) Sebuah graf G adalah graf bipartisi jika dan hanya jika G tidak mempunyai cycle ganjil.
Bukti: AndaikanGadalah sebuah graf bipastisi dengan partisi (V1, V2) dan C = v0v1v2, .vkv0 adalah sebuah cycle di G. tanpa menghilangkan
keumu-mannya asumsikanv0 ∈V1. Maka, karenaGgraf bipartisi,v1haruslah sebuah titik di subset V2. Tentu harus punya v2i ∈V1 dan v2i+1 ∈ V2. Karena itu k haruslah ganjil, danC adalah cycle genap.
Graf r-partite lengkap K¯n1 ∗. . .∗K¯nr dinotasikan oleh K
n1,...,nr ; jika n1 =
. . . = nr =: s. Dengan mempertimbangkan Ksr·Ksr adalah graf lengkap
r-partite yang mana setiap kelas partisi mengandung tepat s titik. Graf dari
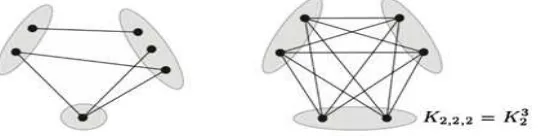
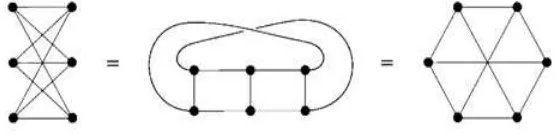
Gambar 2.9 Tiga gambar dari graf bipartisiK3,3 =K32
bagianK1,ndisebutstars; titik di kelas partisi singleton dariK1,nadalahstars
centre. Jelaslah bahwa sebuah graf bipartisi tidak dapat mengandung sebuah odd cycle, panjang lingkaranodd. Pada kenyataannya graf dikarakteristikkan oleh sifat berikut:
12
Bukti: jika G = (V, E) menjadi sebuah graf tanpa odd cycle, dapat ditun-jukkan bahwa G bipartisi. Jelaslah bahwa sebuah graf adalah bipartisi jika semua komponen adalah biparitisi atau trivial dan graf G terhubung.
Gambar 2.10 Graf bipartitG(V1, V2)
5. Connected
Keterhubungan dua buah titik adalah penting di dalam graf. Jika dua buah titik u dan titik v dikatakan terhubung, maka terdapat lintasan dari u dan v. Jika 2 (dua) buah titik terhubung, maka pasti titik yang pertama dapat dicapai dari titik yang ke dua.
Jika setiap pasang titik di dalam graf terhubung, maka graf tersebut dikatakan graf terhubung. Secara formal, definisi graf terhubung menurut Rinaldi Mu-nir (2010: 372) adalah sebagai berikut: Graf tak-berarah G disebut graf terhubung untuk setiap pasang titiku dan v dalam himpunan V dan terda-pat lintasan dariu ke v. Jika tidak ada keterhubungan antara titiku dan v, maka Gdisebut graf tak-terhubung.
13
Graf yang hanya terdiri atas satu titik saja (tidak ada sisi) tetap dikatakan terhubung, karena titik tunggalnya terhubung dengan dirinya sendiri juga dikatakan graf terhubung. Jika graf tak berarahnya terhubung (graf tak-berarah dariGdiperoleh dengan menghilangkan arahnya), maka graf berarah Gdikatakan terhubung.
Keterhubungan 2 (dua) buah titik pada graf berarah dibedakan menjadi ter-hubung kuat dan terter-hubung lemah. Dua titiku dan v pada graf berarah G disebut terhubung kuat karena terdapat lintasan berarah dariukev, dan ju-ga sebaliknya lintasan berarah darivkeu. Jikaudanvtidak terhubung kuat tetapi tetap terhubung pada graf tak-berarahnya, makaudanvdikatakan ter-hubung lemah. Ke dua pernyataan tersebut (terter-hubung kuat dan terter-hubung lemah) melahirkan definisi graf terhubung kuat: Graf berarahGdisebut graf terhubung kuat apabila untuk setiap pasang titik sembarang vi dan vj di G
terhubung kuat. Jika tidak, maka Gdisebut graf terhubung lemah.
Gambar 2.12 (a) Graf berarah terhubung kuat, (b) Graf berarah terhubung lemah
2.2 Pohon dan Hutan
14
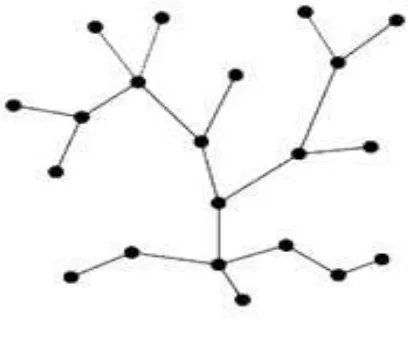
Gambar 2.13 Graf Pohon
Pohon adalah tipe graf sederhana yang tidak biasa. Seperti yang akan dije-laskan, pohon memiliki sifat-sifat yang relatif bagus sehingga pada kenyataannya setiap dua simpul yang terhubung membentuk sisi akan menghasilkan lintasan yang unik.
Daftar teorema berikut adalah beberapa sifat sederhana dari pohon.
Teorema 2.2.1 Jika T adalah graf dengan n titik, maka pernyataan berikut akan ekuivalen.
i T adalah pohon
ii T tidak mengandung lingkaran dan mempunyai n−1 sisi. iii T terhubung dan mempunyai n−1 sisi.
iv T terhubung dan setiap sisi adalah sebuah lintasan/jembatan.
v Dua titik dari T terhubung oleh tepat satu jalur.
vi T tidak mengadung lingkaran, tetapi penambahan setiap sisi baru akan men-ciptakan tepat satu lingkaran.
15
(i)→(ii), karenaT tidak mengandung lingkaran, maka penghapusan beberapa sisi harus memutuskan T ke dalam 2 (dua) graf yang masing-masing adalah pohon. Berdasarkan induksinya, jumlah sisi di setiap 2 (dua) pohon adalah kurang satu dari jumlah titik. Sehingga dapat disimpulkan bahwa total keseluruhan jumlah sisi pada pohon T adalah n−1.
(ii)→(iii) jikaT tidak terhubung, maka setiap komponenT adalah graf terhubung dengan tanpa lingkaran dan karenanya pada bagian sebelumnya jumlah titik di setiap komponen melebihi jumlah sisi yaitu 1. Total jumlah titik dari graf T melebihi total jumlah sisi sedikitnya 2. Ini berlawanan dengan kenyataan bahwa T mempunyain−1 sisi.
(iii)→(iv) penghapusan beberapa hasil sisi dari graf denganntitik dann−2 sisi. (iv) → (v) karena T terhubung, setiap pasang titik terhubung oleh paling sedikit satu lintasan. Jika diberikan pasangan titik terhubung oleh 2 (dua) lintasan, maka mereka akan memiliki lingkaran. Ini berlawanan dengan kenyataan bahwa setiap sisi adalah jembatan.
(v) → (vi) jika T mengandung sebuah lingkaran, maka ada 2 (dua) titik da-lam lingkaran yang akan terhubung dengan kurang lebih 2 (dua) lintasan, ini berlawanan dengan pernyataan (v). Jika sebuah sisi e ditambahkan ke T, ma-ka titik yang bertetangga dengan e telah terhubung di T dan akan membentuk sebuah lingkaran.
(vi) → (i) Diperkirakan bahwa T tidak terhubung. Jika ditambahkan ke T ga-bungan beberapa titik yang menghasilkan sisi dari komponen titik yang lain, maka tidak akan ada lingkaran yang terbentuk.
2.3 Pohon Merentang (Spanning Tree)
16
semua sirkuit diGhilang, makaGmenjadi sebuah pohonT yang dinamakan pohon merentang (spanning tree). Disebut pohon merentang karena semua simpul pada pohon T sama dengan simpul semua simpul pada graf G, dan sisi-sisi pada pohon T ⊆ sisi-sisi pada graf G. dengan kata lain, V1 =V dan E1 ⊆E.
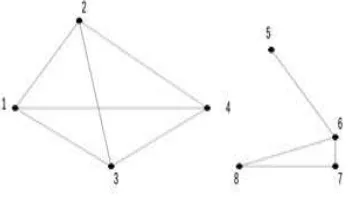
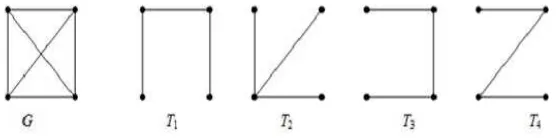
Aplikasi pohon merentang misalnya pada pemeliharaan jalan raya. Misalkan pada gambar 2.14 di bawah ini, adalah peta jaringan jalan raya yang menghu-bungkan empat buah kota. Karena dana pemeliharaan yang terbatas, pemerintah daerah mempertimbangkan hanya memelihara jalan-jalan sesedikit mungkin se-demikian sehingga keempat kota masih tetap terhubung satu sama lain. Pohon merentang juga memainkan peranan penting dalam jaringan komputer.
Gambar 2.14 Graf lengkapGdan empat buah pohon merentangnya,T1, T2, T3, T4
Harus diingat bahwa pohon merentang didefenisikan hanya untuk graf ter-hubung, karena pohon selalu terhubung. Pada graf tak terhubung dengan n buah simpul tidak akan dapat menemukan upagraf terhubung dengan n buah simpul. Tiap komponen dari graf tak terhubung mempunyai satu buah pohon merentang. Dengan demikian, graf tak-terhubung dengan k komponen mempunyai hutan me-rentang (spanning tree) yang terdiri dari k buah pohon merentang. Sisi pada pohon merentang disebut cabang (branch) adalah sisi dari graf semula, sedangkan tali hubung (chordatau link)dari pohon adalah sisi dari graf yang tidak terdapat di dalam pohon merentang.
17
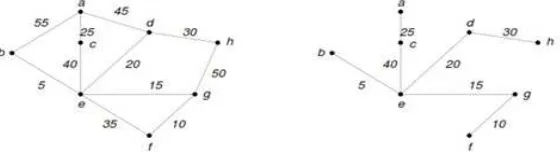
membangun jalur rel kereta api yang menghubungkan sejumlah kota seperti gam-bar 2.3. Membangun rel kereta api membutuhkan biaya yang tidak sedikit. Oleh karena itu, dibutuhkan perencanaan terbaik dengan menentukan jarak minimum untuk menghubungkan dua kota.
Gambar 2.15 Graf yang menyatakan jaringan jalur rel kereta api. Bobot pada setiap sisi menyatakan panjang rel kereta api (× 100m) (b). Pohon merentang yang mempunyai jumlah jarak minimum