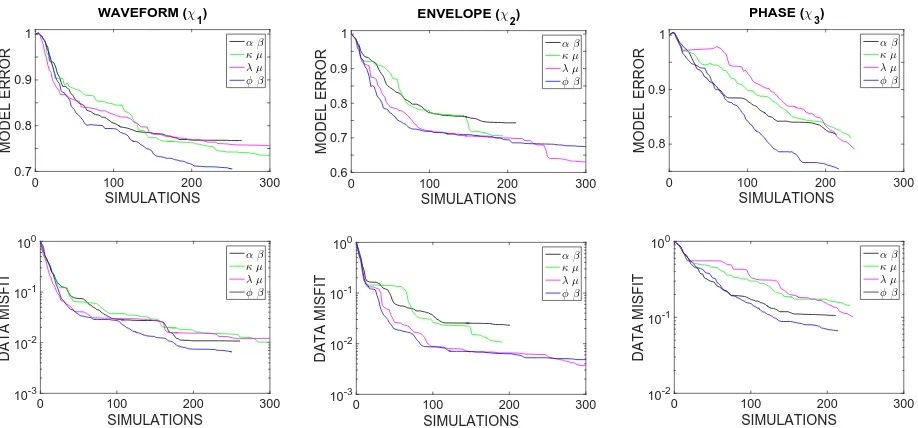
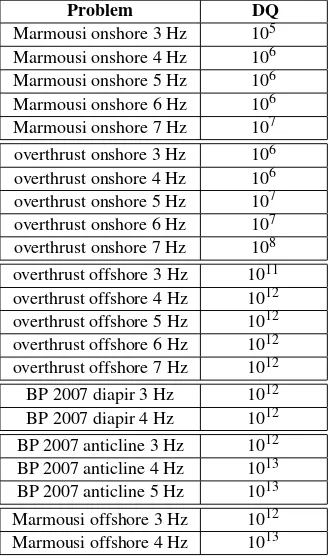
On the choice of material parameters for
Teks penuh
Gambar
Dokumen terkait
Hal tersebut disebabkan karena zeolit merupakan mineral yang mempunyai sifat hidrofobik yang baik, selain itu zeolit mempunyai sifat adsorbsi yang baik sehingga dapat
Berkata An-Naqqaasy : Ayat ini menjadi hujjah terhadap orang yang berkata : "Sesungguhnya kadi boleh memisahkan di antara suami isteri sekiranya si suami itu miskin
DINAS SOSIAL PROVINSI SULAWESI BARAT Pengadaan Saranan dan Prasarana Pendukung Usaha Bagi Keluarga Miskin Pengadaan Barang Alat Pertukangan Kayu. JB: Barang/jasa
Kepada peserta yang keberatan terhadap hasil pengumuman ini dapat mengajukan sanggah melalui Aplikasi pada sistem SPSE sesuai jadwal dalam SPSE.. Tanggal 27
Hasil belajar siswa dalam proses kegiatan pembelajaran melalui metode diskusi Perolehan hasil LKS pada awal tindakan siklus I adalah dengan nilai rata-rata nilai indiviu yaitu
[r]
Brand Image Kawasan Maribaya Sebagai Objek Wisata Berwawasan Lingkungan (Ekowisata) Universitas Pendidikan Indonesia | repository.upi.edu..
Nurmaida (2015) meneliti tentang Pengaruh Current Ratio, Debt to Equity Ratio, Growth, Collaterzible Assets, Return on Equity terhadap Dividend Payout Ratio (DPR) pada Perusahaan