SIMULASI NUMERIK
Pada bab ini akan dibahas analisis model penyebaran penyakit flu burung untuk ka-sus adanya pertumbuhan dan kematian alami serta kaka-sus tidak adanya pertumbuhan dan kematian alami secara numerik menggunakan MATLAB 6.5.1. Hal ini dimak-sudkan untuk membandingkan kedua model sehingga diketahui pengaruh adanya faktor pertumbuhan dan kematian alami pada model. Selain itu, akan dilakukan simulasi terhadap model untuk beberapa nilai parameter λ, ξ, dan γ sebagai pa-rameter penentu terjadinya gelombang berjalan pada penyebaran flu burung. Dalam simulasi numerik ini, penulis menggunakan metode MacCormack untuk me-nyelesaikan model permasalahan yang berupa sistem persamaan diferensial parsial secara numerik. Model yang diselesaikan adalah sistem persamaan diferensial parsial yang tak berdimensi. Hal ini dimaksudkan agar hasil yang diperoleh bisa diinterpre-tasikan secara umum, tidak hanya untuk suatu data dengan satuan tertentu saja.
4.1
Kasus I
Pandang sistem persamaan diferensial parsial tak berdimensi ∂S ∂t = −IS + ∂2S ∂x2, ∂I ∂t = −λI +IS+ ∂2I ∂x2. 34
Di titik interior persamaan akan didiskritisasikan dengan metode MacCormack. Metode ini merupakan metode eksplisit, 2 tahap, dengan tingkat akurasiO(∆x2,∆t3).
Selanjutnya, akan dilakukan penyesuaian untuk titik-titik di batas kiri dan kanan. Terakhir, model akan disimulasikan dengan nilai parameter yang bervariasi.
Diskritisasi model di titik interior sebagai berikut: 1. Tahap predictor
Notasikan Sn
i ≡ S(xi, tn). Pada tahap ini akan diprediksi nilai Sin+1 jika
diketahui nilaiSn
i dan Sin+1.
Ekspansi Taylor untuk Sin+1 di sekitar Sn
i adalah
Sin+1 =Sn
i +St|ni∆t+O(∆t
2). (4.1.1)
Mengingat St = −IS + Sxx, dengan penerapan center difference bagi Sxx
dilanjutkan dengan substitusi ke dalam (4.1.1) menghasilkan persamaan beda Sin+1 =Sin+ (−IinSin+S
n
i+1−2Sin+Sin−1
∆x2 )∆t, (4.1.2)
dengan tingkat akurasiO(∆x2,∆t2).
Dengan melakukan langkah diskritisasi yang sama terhadap persamaan ∂I
∂t =−λI +IS+ ∂2I
∂x2,
diperoleh persamaan beda
Iin+1 =Iin+ (−λIin+IinSin+ I
n
i+1−2Iin+Iin−1
∆x2 )∆t, (4.1.3)
dengan tingkat akurasiO(∆x2,∆t2).
2. Tahap corrector
Pada tahap ini nilai Sin+1 yang telah didapat dari tahap predictor, dikoreksi lagi dengan tingkat akurasi yang lebih tinggi yaituO(∆x2,∆t3). Sama halnya
di sekitar Sn
i . Namun, perbedaannya terletak pada suku St|ni. Pada tahap
corrector yang digunakan adalah nilai rata-rata dariSt|ni saat indeks waktun
dan n+ 1 yaitu St|ni+St|
n+1
i
2 .
Pandang ekspansi Taylor untukSin+1 di sekitarSn
i sebagai berikut
Sin+1 =Sin+St|ni∆t+Stt|ni
∆t2
2! +O(∆t
3). (4.1.4)
GunakanForward Time untuk mendiskritisasi sukuStt|ni pada ekspansi Taylor
(4.1.4):
Stt|ni =
St|ni+1−St|ni
∆t . (4.1.5)
Substitusi (4.1.5) ke (4.1.4) menghasilkan ekspansi Taylor untukSin+1 di seki-tarSn
i pada tahap ini sebagai berikut
Sin+1=Sin+ ∆t 2 (St|
n
i +St|ni+1) +O(∆t3).
Perhatikan bahwa persamaan di atas mempunyai akurasi dengan orde 3. Ber-dasarkanSt =−IS+Sxx,maka dengan mensubstitusikannya ke dalam ekspansi
Taylor di atas menghasilkan persamaan beda Sin+1 = Sin+ ∆t 2 −IinSin+S n i+1−2Sin+Sin−1 ∆x2 +∆t 2 −I n+1 i Sin+1+ Sin+1+1−2Sin+1+Sin−+11 ∆x2 ! , (4.1.6) dengan tingkat akurasiO(∆x2,∆t3).
Analog denganS, diskritisasi terhadapI menghasilkan persamaan beda Iin+1 = Iin+∆t 2 −λIin+IinSin+ I n i+1−2Iin+Iin−1 ∆x2 +∆t 2 −λI n+1 i +Iin+1Sin+1+ Iin+1+1−2Iin+1+Iin−+11 ∆x2 ! ,(4.1.7) dengan tingkat akurasiO(∆x2,∆t3).
Jadi, untuk titik interior diterapkan persamaan beda (4.1.2) & (4.1.3) pada tahap
Untuk penyesuaian di titik-titik batas kiri dan kanan, digunakan persamaan gelom-bang yang masing-masing berjalan ke kiri dan ke kanan. Hal ini dilakukan agar gelombang hasil simulasi terus berjalan ke luar batas pengamatan sesuai dengan keadaan sebenarnya. Pendekatan Forward Time Forward Space di batas kiri meng-hasilkan persamaan beda:
S1n+1 = (1−C)S1n+CS2n, I1n+1 = (1−C)I1n+CI2n,
dan pendekatan Forward Time Backward Space di batas kanan menghasilkan per-samaan beda:
SN xn+1 = (1−C)SN xn +CSN xn −1,
IN xn+1 = (1−C)IN xn +CIN xn −1, denganC = c∆∆xt, dan cadalah kecepatan gelombang.
4.2
Kasus II
Langkah diskritisasi untuk kasus II analog dengan kasus I. Perbedaannya hanya terletak pada penambahan suku ξS pada persamaan diferensial parsial bagi S dan mengganti parameter λ dengan γ pada persamaan diferensial parsial bagi I, diper-oleh persamaan beda: Tahap predictor:
Sin+1 = Sin+ ξSin−IinSin+ Sn i+1−2Sin+Sin−1 ∆x2 ∆t, Iin+1 = Iin+ (−γIin+IinSin+ In i+1−2Iin+Iin−1 ∆x2 )∆t,
Tahap corrector: Sin+1 = Sin+∆t 2 ξSin−IinSin+S n i+1−2Sin+Sin−1 ∆x2 +∆t 2 ξS n+1 i −Iin+1Sin+1+ Sin+1+1−2Sin+1+Sin−+11 ∆x2 ! , Iin+1 = Iin+∆t 2 −γIin+IinSin+I n i+1−2Iin+Iin−1 ∆x2 +∆t 2 −γI n+1 i +Iin+1Sin+1+ Iin+1+1−2Iin+1+Iin−+11 ∆x2 ! ,
dengan tingkat akurasiO(∆x2,∆t3).
Untuk simulasi, pada kasus I dipilih nilai parameter λ = 0.51 dan λ = 1.2. Pada
kasus II dengan memilih nilai γ yang tetap yaitu 0.5, dipilih nilai ξ yang berbeda yaitu ξ=−0.6 dan ξ = 0.01. Saat awal pengamatan, sumber epidemi (ayam sakit) ada di tengah-tengah domain pengamatan sebanyak 10 % dari banyaknya populasi ayam sehat saat awal pengamatan, sehingga diperoleh hasil simulasi sebagai berikut:
1
Pemilihan nilai parameter ini didasarkan pada nilai threshold number untuk penyakit influenza, yaitu 1/λ≈2.
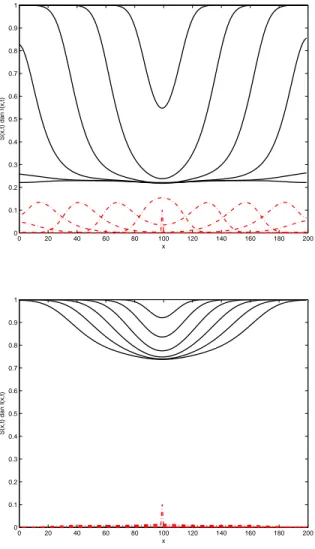
0 20 40 60 80 100 120 140 160 180 200 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 x S(x,t) dan I(x,t) 0 20 40 60 80 100 120 140 160 180 200 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 x S(x,t) dan I(x,t)
Gambar 4.1: Kasus I: Kurva-kurvaS(x, t) (hitam) danI(x, t) (merah) terhadap posisixuntuk beberapa waktu pengamatan 0 =t0< t1< ... < tn= 60.1 dengan nilai parameterλ= 0.5 (atas),
danλ= 1.2 (bawah).
Dapat dilihat ketika λ = 0.5, jumlah ayam yang sakit di suatu tempat bertam-bah seiring dengan bertambertam-bahnya waktu. Selanjutnya, infeksi tersebut menyebar ke sekitarnya, dalam hal ini ke kiri dan ke kanan. Populasi ayam sakit di daerah dengan jarak yang sama terhadap daerah pusat wabah mencapai nilai maksimum yang sama. Dapat dilihat dari Gambar 4.1 atas, bahwa penyebaran penyakit mem-punyai bentuk yang tetap. Inilah yang dimaksudkan dengan ”gelombang berjalan” pada penyebaran penyakit, atau gelombang epizootic penyebaran penyakit flu bu-rung. Untuk nilai λ < 1 lainnya, diperoleh hasil yang serupa, penyebaran infeksi
mengikuti gelombang berjalan. Namun, ketika dipilih nilai λ = 1.2, hasil simulasi menunjukkan bahwa infeksi tetap menyebar ke sekitarnya. Namun, dapat dilihat bahwa pola penyebarannya tidak mengikuti pola gelombang berjalan. Hasil simulasi ini menunjukkan secara visual makna dari pentingnya nilai λ.
Berdasarkan studi awal pada Subbab 3.2, ξ < 0 menjadi syarat perlu terjadinya
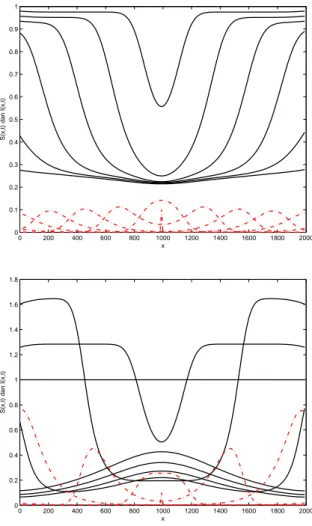
0 200 400 600 800 1000 1200 1400 1600 1800 2000 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 x S(x,t) dan I(x,t) 0 200 400 600 800 1000 1200 1400 1600 1800 2000 0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 x S(x,t) dan I(x,t)
Gambar 4.2: Kasus II: Kurva-kurvaS(x, t) (hitam) danI(x, t) (merah) terhadap posisixuntuk beberapa waktu pengamatan 0 = t0 < t1 < ... < tn = 60.1 dengan nilai parameterγ = 1.01/2,
ξ=−0.01/4 (atas), danγ= 1.01/2,ξ= 0.01/4 (bawah).
gelombang berjalan pada penyebaran penyakit. Ketika dipilih nilai ξ = −0.01/4 pada simulasi, terlihat dari Gambar 4.2 atas, infeksi menyebar ke kanan dan kiri sumber infeksi seiring dengan bertambahnya waktu. Sekilas tampak bahwa infeksi menyebar dengan bentuk yang tetap. Tetapi, jika diamati dengan lebih seksama,
banyaknya ayam sakit maksimum berkurang seiring dengan bertambahnya waktu. Jadi, penyebaran penyakit tidak mengikuti pola gelombang berjalan.
Alasan pemilihan parameter γ = 1.01/2, ξ = −0.01/4 adalah sebagai berikut. Mengingat γ =λ+b/rS0, dan ξ= (c−b)/rS0 maka pemilihan nilaiγ yang sedikit
lebih dari 1/2 danξ =−0.01/4 bisa diartikan: tidak ada kelahiran alami namun ada kematian alami dengan faktor yang relatif kecil. Hal ini dapat menjelaskan bahwa jumlah total ayam berkurang seiring dengan bertambahnya waktu.
Ketika dipilih nilai ξ = 0.01/4, positif, tampak jelas bahwa infeksi menyebar ke sekitarnya dengan tidak mengikuti pola gelombang berjalan. Hal ini sesuai dengan hasil analitis di Subbab 3.2. Bisa dilihat bahwa seiring dengan bertambahnya waktu, banyak ayam sakit semakin bertambah dengan cukup signifikan.
Berdasarkan simulasi, pemilihan nilai ξ = −0.01/4 dan ξ = 0.01/4 tidak meng-hasilkan penyebaran penyakit yang mengikuti pola gelombang berjalan. Hal ini masih sesuai dengan hasil studi analitis pada Subbab 3.2 yang menyatakan bahwa ξ < 0 merupakan syarat perlu terjadinya gelombang berjalan pada penyebaran pe-nyakit. Jika ξ >0, maka penyebaran infeksi pasti tidak mengikuti pola gelombang berjalan. Jikaξ < 0, maka belum tentu infeksi menyebar mengikuti pola gelombang berjalan. Sejauh ini penulis belum menemukan batasan nilai ξ yang bisa meng-hasilkan penyebaran infeksi berupa gelombang berjalan.
5.2
Saran
Dalam karya tulis ilmiah ini belum dilakukan analisis lebih lanjut mengenai hu-bungan antara kesetimbangan solusi gelombang berjalan pada model untuk kasus II dengan kondisi fisisnya. Hal ini disebabkan adanya ketidaksesuaian hasil yang diper-oleh dengan kondisi fisis. Oleh karena itu, penulis menyarankan untuk dilakukan kajian lebih lanjut mengenai hal ini. Penulis juga menyarankan untuk dilakukan pencarian syarat cukup terjadinya gelombang berjalan pada penyebaran penyakit. Selain itu, perlu dilakukan simulasi lebih lanjut terhadap model dengan berdasarkan data real yang akurat.
[1] Murray, J.D. 1993. Mathematical Biology, 2nd Edition. New York:
Springer-Verlag.
[2] Mattheij, Robert, Jaap Molenaar. 2002. Ordinary Differential Equations in Theory and Practice. Philadelphia: SIAM (Society for Industrial and Applied Mathematic).
[3] Brauer, Fred, Carlos Castillo-Chavez. 2000. Mathematical Models in Popula-tion Biology and Epidemiology. Ithaca, N.Y., U.S.A.: Springer.
[4] Edwards, C.H., JR David E. Penney. 1993.Elementary Differential Equations with Boundary Value Problem, third edition. New Jersey: Prentice-Hall. [5] http://id.wikipedia.org/wiki/W abah
[6] http://id.wikipedia.org/wiki/Kejadian Luar Biasa
[7] http : //www.tempointeraktif.com/hg/ekbis/2004/02/03/brk,20040203 − 08, id.html [8] http : //www.tempointeraktif.com/hg/ekbis/2004/01/30/brk,20040130 − 39, id.html [9] http://www.tempointeraktif.com/hg/nasional/2004/01/30/brk,20040130− 04, id.html 44
Program MATLAB
Program Model Penyebaran Flu Burung Tanpa Pertumbuhan
dan Kematian Alami
nilai λ <1 % SPD: SI + difusi pd 0 ¡ x ¡ L % sy awal: S(x,0)=1; I(x,0)=0 clear all format long Nt=700 Nx=200 dt=0.1 dx=0.5 lambda=0.5
%kecepatan minimum gelombang berjalan c=2*sqrt(1-lambda) %sy awal S(1:Nx,1)=1 I(1:Nx,1)=0 p=0.1; 45
I(Nx/2,1)=p; for n=1:(Nt-1)
%persamaan beda model untuk batas kiri
Sp(1,n+1)=S(1,n)-dt*I(1,n)*S(1,n)+dt*(S(3,n)-2*S(2,n)+S(1,n))/dx/dx;
Ip(1,n+1)=I(1,n)+dt*I(1,n)*S(1,n)-lambda*dt*I(1,n)+dt*(I(3,n)-2*I(2,n)+I(1,n))/dx/dx; %persamaan beda model untuk grid di tengah tahappredictor
for i=2:(Nx-1)
Sp(i,n+1)=S(i,n)-dt*I(i,n)*S(i,n)+dt*(S(i+1,n)-2*S(i,n)+S(i-1,n))/dx/dx;
Ip(i,n+1)=I(i,n)+dt*I(i,n)*S(i,n)-lambda*dt*I(i,n)+dt*(I(i+1,n)-2*I(i,n)+I(i-1,n))/dx/dx; end
%persamaan beda model untuk batas kanan
Sp(Nx,n+1)=S(Nx,n)-dt*I(Nx,n)*S(Nx,n)+dt*(S(Nx,n)-2*S(Nx-1,n)+S(Nx-2,n))/dx/dx; Ip(Nx,n+1)=I(Nx,n)+dt*I(Nx,n)*S(Nx,n)-lambda*dt*I(Nx,n)+dt*(I(Nx,n)-2*I(Nx-1,n)+I(Nx-2,n))/dx/dx;
%persamaan beda gelombang untuk batas kiri S(1,n+1)=(1-c)*S(1,n)-c*S(2,n);
I(1,n+1)=(1-c)*I(1,n)-c*I(2,n);
%persamaan beda model di grid tengah tahapcorrector
for i=2:(Nx-1) S(i,n+1)=S(i,n)+(dt/2)*(-I(i,n)*S(i,n)-Ip(i,n+1)*Sp(i,n+1)) +(1/2)*(dt/dx/dx)*(S(i+1,n)-2*S(i,n)+S(i-1,n)+Sp(i+1,n+1)-2*Sp(i,n+1)+Sp(i-1,n+1)); I(i,n+1)=I(i,n)+(dt/2)*(I(i,n)*S(i,n)-lambda*I(i,n)+Ip(i,n+1)*Sp(i,n+1)-lambda*Ip(i,n+1)) +(1/2)*(dt/dx/dx)*(I(i+1,n)-2*I(i,n)+I(i-1,n)+Ip(i+1,n+1)-2*Ip(i,n+1)+Ip(i-1,n+1)); end
%persamaan beda gelombang untuk batas kanan S(Nx,n+1)=(1-c)*S(Nx,n)+c*S(Nx-1,n);
I(Nx,n+1)=(1-c)*I(Nx,n)+c*I(Nx-1,n); end %plot S(x,t) figure(1) plot(S) %plot I(x,t) figure(2) plot(I)
%inisiasi untuk plot S(x,t) dan I(x,t) untuk waktu tertentu shift =0.5; banyakplot=7; pengali=100; for j = 1:banyakplot for i= 1:Nx xplot(i,j) = (i-1) * 2*dx; Splot(i,j) = S(i,(j-1)*pengali+1); Iplot(i,j) = I(i,(j-1)*pengali+1); end end
% Plot S(x,t) dan I(x,t) terhadap x figure(3)
plot(xplot,Splot,’-’,’Color’,’black’,’LineWidth’,1.5) hold on
plot(xplot,Iplot,’-.’,’Color’,’red’,’LineWidth’,1.5) hold off
% inisiasi untuk plot S(x,t) dan I(x,t) untuk posisi tertentu shift =0.5;
banyakplot=10; pengali=10; for j = 1:Nt for i= 1:banyakplot tplot(i,j) = (j-1) *dt; Splot1(i,j) = S((i-1)*pengali+1,j); Iplot1(i,j) = I((i-1)*pengali+1,j); end end
% plot S(x,t) dan I(x,t) terhadap t figure(4)
plot(tplot,Splot1,’-’,’Color’,’black’,’LineWidth’,1.5) hold on
plot(tplot,Iplot1,’-.’,’Color’,’red’,’LineWidth’,1.5) hold off
catatan: program simulasi matlab untuk kasus λ > 1 diperoleh dengan mengubah nilai lambda menjadi >1
Program Model Penyebaran Flu Burung Dengan
Pertum-buhan dan Kematian Alami
% SPD: SI + difusi pd 0 ¡ x ¡ L % sy awal: S(x,0)=1; I(x,0)=0 clear all format long Nt=700 Nx=200 dt=0.1
dx=0.5 ksi=-0.01/4 gama=1.01/2
% kecepatan minimum gelombang berjalan c=2*sqrt(sqrt(-ksi*gama)) %syarat awal S(1:Nx,1)=1; I(1:Nx,1)=0; p=0.1; I(Nx/2,1)=p; for n=1:(Nt-1)
% persamaan beda model di batas kiri
Sp(1,n+1)=S(1,n)+dt*ksi*S(1,n)-dt*I(1,n)*S(1,n)+dt*(S(3,n)-2*S(2,n)+S(1,n))/dx/dx; Ip(1,n+1)=I(1,n)+dt*I(1,n)*S(1,n)-gama*dt*I(1,n)+dt*(I(3,n)-2*I(2,n)+I(1,n))/dx/dx; % persamaan beda model di grid tengah untuk tahappredictor
for i=2:(Nx-1)
Sp(i,n+1)=S(i,n)+dt*ksi*S(i,n)-dt*I(i,n)*S(i,n)+dt*(S(i+1,n)-2*S(i,n)+S(i-1,n))/dx/dx; Ip(i,n+1)=I(i,n)+dt*I(i,n)*S(i,n)-gama*dt*I(i,n)+dt*(I(i+1,n)-2*I(i,n)+I(i-1,n))/dx/dx; end
% persamaan beda model di batas kanan
Sp(Nx,n+1)=S(Nx,n)+dt*ksi*S(Nx,n)-dt*I(Nx,n)*S(Nx,n) +dt*(S(Nx,n)-2*S(Nx-1,n)+S(Nx-2,n))/dx/dx;
Ip(Nx,n+1)=I(Nx,n)+dt*I(Nx,n)*S(Nx,n)-gama*dt*I(Nx,n) +dt*(I(Nx,n)-2*I(Nx-1,n)+I(Nx-2,n))/dx/dx;
% persamaan beda gelombang di batas kiri S(1,n+1)=(1-c)*S(1,n)+c*S(2,n);
I(1,n+1)=(1-c)*I(1,n)+c*I(2,n);
% persamaan beda model di grid tengah untuk tahapcorrector
for i=2:(Nx-1) S(i,n+1)=S(i,n)+(dt/2)*(ksi*S(i,n)-I(i,n)*S(i,n)+ksi*Sp(i,n+1)-Ip(i,n+1)*Sp(i,n+1)) +(1/2)*(dt/dx/dx)*(S(i+1,n)-2*S(i,n)+S(i-1,n)+Sp(i+1,n+1)-2*Sp(i,n+1)+Sp(i-1,n+1)); I(i,n+1)=I(i,n)+(dt/2)*(I(i,n)*S(i,n)-gama*I(i,n)+Ip(i,n+1)*Sp(i,n+1)-gama*Ip(i,n+1)) +(1/2)*(dt/dx/dx)*(I(i+1,n)-2*I(i,n)+I(i-1,n)+Ip(i+1,n+1)-2*Ip(i,n+1)+Ip(i-1,n+1)); end
% persamaan beda gelombang di batas kanan S(Nx,n+1)=(1-c)*S(Nx,n)+c*S(Nx-1,n); I(Nx,n+1)=(1-c)*I(Nx,n)+c*I(Nx-1,n); end % plot S(x,t) figure(1) plot(S) % plot I(x,t) figure(2) plot(I)
% inisiasi untuk plot S(x,t) dan I(x,t) untuk waktu tertentu shift =0.5; banyakplot=7; pengali=100; for j = 1:banyakplot for i= 1:Nx xplot(i,j) = (i-1) * 20*dx; Splot(i,j) = S(i,(j-1)*pengali+1); Iplot(i,j) = I(i,(j-1)*pengali+1);
end end
% plot S(x,t) dan I(x,t) terhadap x figure(3)
plot(xplot,Splot,’-’,’Color’,’black’,’LineWidth’,1.5) hold on
plot(xplot,Iplot,’-.’,’Color’,’red’,’LineWidth’,1.5) hold off
% inisiasi untuk plot S(x,t) dan I(x,t) untuk posisi tertentu shift =0.5; banyakplot=10; pengali=10; for j = 1:Nt for i= 1:banyakplot tplot(i,j) = (j-1) *dt; Splot1(i,j) = S((i-1)*pengali+1,j); Iplot1(i,j) = I((i-1)*pengali+1,j); end end
% plot S(x,t) dan I(x,t) terhadap t figure(4)
plot(tplot,Splot1,’-’,’Color’,’black’,’LineWidth’,1.5) hold on
plot(tplot,Iplot1,’-.’,’Color’,’red’,’LineWidth’,1.5) hold off
catatan: program simulasi matlab untuk kasusξγ > 0 diperoleh dengan mengubah nilai ksi menjadi >0