Geometri Metrik - USD Repository

Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Sains

Program Studi Matematika

Oleh:

Monica Lili Megawati NIM: 043114015

PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI

UNIVERSITAS SANATA DHARMA YOGYAKARTA

ii

Presented as Partial Fulfillment of the Requirements To Obtain the SARJANA SAINS Degree

In Mathematics

By:

Monica Lili Megawati Student Number: 043114015

MATHEMATICS STUDY PROGRAM MATHEMATICS DEPARTMENT SCIENCE AND TECHNOLOGY FACULTY

SANATA DHARMA UNIVERSITY YOGYAKARTA

vii ABSTRAK

viii ABSTRACT

Abstract Geometry is a set of points and lines that meet a certain axiom. The Abstract Geometry is an Incidence Geometry if it meets an axiom system that contains the uniqueness of lines. Metric Geometry is a concept of Abstract Geometry that unifies the previous geometry concepts like Euclidean Geometry and Non Euclidean Geometry that use the axiom system. The concept used in Metric Geometry is a distance concept. The ”distance” is the function that determines the number d

(

P,Q

)

for every pair of points P, . This thesis will discuss three models of the Metric Q

x

KATA PENGANTAR

Puji dan syukur kepada Tuhan Yang Maha Esa yang telah memberikan berkat dan rahmat-Nya sehingga penulis dapat menyelesaikan skripsi ini.

Berkat dukungan dan bantuan dari banyak pihak, akhirnya skripsi ini dapat terselesaikan. Oleh karena itu penulis menyampaikan terima kasih kepada:

1. Bapak Herry Pribawanto Suryawan, S.Si.,M.Si. selaku dosen pembimbing yang telah memberikan pengarahan dan bimbingan selama penyusunan skripsi ini. 2. Bapak Yosef Agung Cahyanta, S.T.,M.T. selaku Dekan Fakultas Sains dan

Teknologi yang telah mendukung penulis selama penyusunan skripsi ini.

3. Ibu Lusia Krismiyati Budiasih, S.Si.,M.Si. selaku Kaprodi Matematika dan Dosen Pembimbing Akademik angkatan 2004 yang telah memberikan nasehat, saran dan dukungan kepada penulis.

4. Bapak dan Ibu dosen yang telah memberikan bekal ilmu kepada penulis.

5. Bapak Tukijo dan Ibu Linda yang telah memberikan pelayanan administrasi kepada penulis selama masa perkuliahan.

6. Perpustakaan Universitas Sanata Dharma dan staf yang telah menyediakan fasilitas dan memberikan kemudahan kepada penulis selama masa perkuliahan. 7. Kedua orang tuaku tercinta: Bapak Andreas Leonardus Pardiyo dan Ibu Maria

xi

8. Kedua kakakku tersayang, FX. Budi Ari Wibowo dan Paulus Janu Rahprobo, adikku tersayang Agatha Viti Anggraini, serta kekasihku tercinta Yulius Libralvo Junischrisye, dan semua keluarga besar yang telah memberikan doa dan dukungan kepada penulis.

9. Teman-teman angkatan 2004: Nancy Hartono, Theodora, Fransiska, Eni, Retno, Ratna, Dwi, Lina, dan Yohanes, serta Ridwan Rahadiyanto dan Septi juga bapak-ibu kost dan teman-teman Majus Community yang telah memberikan semangat, saran dan nasehat kepada penulis.

10. Teman-teman KKN: Devita, Dewi, Silvia, Dita, Lilik, Lusia, Lucky, Hardian, dan Udjo, juga Estiningsih yang telah memberikan semangat, saran, dan nasehat kepada penulis.

Penulis juga menyampaikan terima kasih kepada semua pihak yang telah membantu penulis dalam penyusunan skripsi ini yang tidak dapat disebutkan satu-persatu di sini.

Yogyakarta, Februari 2009

xii DAFTAR ISI

Halaman

HALAMAN JUDUL ... i

HALAMAN JUDUL DALAM BAHASA INGGRIS ... ii

HALAMAN PERSETUJUAN PEMBIMBING ... iii

HALAMAN PENGESAHAN ... iv

HALAMAN PERSEMBAHAN ... v

HALAMAN PERNYATAAN KEASLIAN KARYA... vi

HALAMAN ABSTRAK ... vii

HALAMAN ABSTRACT ... viii

LEMBAR PERNYATAAN PERSETUJUAN PUBLIKASI KARYA ILMIAH UNTUK KEPENTINGAN AKADEMIS ... ix

KATA PENGANTAR ... x

DAFTAR ISI... xii

BAB I PENDAHULUAN... 1

1.1 Latar Belakang Masalah ... 1

1.2 Rumusan Masalah ... 3

1.3 Batasan Masalah ... 4

1.4 Tujuan Penulisan... 4

1.5 Metode Penulisan... 4

xiii

1.7 Sistematika Penulisan ... 4

BAB II HIMPUNAN, RELASI EKUIVALENSI, DAN FUNGSI ... 7

2.1 Aksioma dan Model ... 7

2.2 Himpunan dan Relasi Ekuivalensi ... 8

2.3 Fungsi... 15

BAB III GEOMETRI ABSTRAK DAN GEOMETRI INSIDENSI ... 25

3.1 Geometri Abstrak... 25

3.2 Geometri Insidensi ... 38

BAB IV GEOMETRI METRIK ... 48

4.1 Geometri Metrik... 48

4.2 Sistem Koordinat Khusus ... 75

4.3 Keantaraan di dalam Geometri Metrik... 80

BAB V PENUTUP ... 101

5.1 Kesimpulan ... 101

5.2 Saran ... 102

1.1Latar Belakang Masalah

dasar-dasar geometri aksiomatik, serta masih ada beberapa tokoh lain. Pada masa Euclides (abad 3 SM) geometri sudah berbentuk sebagai cabang ilmu tersendiri dan mendapatkan wajah sebagai ilmu yang abstrak dalam bentuk sistem deduktif/aksiomatik, dilandasi oleh logika Yunani. Pada waktunya dahulu Euclides berhasil menyusun geometri sebagai sistem aksiomatik material, kini timbul sistem aksiomatik yang formal. Ini ditandai dengan timbulnya manifold dengan unsur yang tidak harus berupa titik geometris (Plucker 1829) dan juga ruang abstrak (Frechet 1906), sedemikian sehingga geometri menjadi semakin abstrak.

Ada dua pendekatan mendasar dalam Geometri Abstrak. Pendekatan pertama disebut pendekatan sintetik, yang digunakan oleh Euclides dalam bukunya yang berjudul Elements (sekitar 300 SM) dan dilengkapi oleh seorang matematikawan Jerman David Hilbert (1862-1943) dalam bukunya yang berjudul

Grundlagen der Geometrie. Pendekatan kedua disebut pendekatan metrik, yang ditemukan oleh seorang matematikawan Amerika yang bernama George David Birkhoff (1884-1944) dalam makalahnya “A Set of Postulates for Plane Geometry Based on Scale and Protractor” [1932]. Dalam pendekatan ini, konsep mengenai jarak dan pengukuran sudut ditambahkan untuk geometri insidensi untuk mendapatkan ide dasar mengenai keantaraan, segmen garis, kongruensi, dan lain sebagainya.

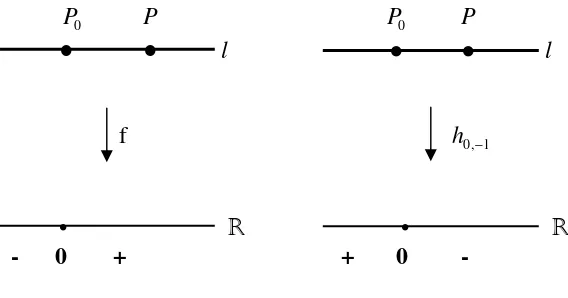
d(P, Q) untuk setiap pasangan titik P, Q. Hal itu mestinya tidak berarti apakah kita ukur dari P ke Q atau dari Q ke P (ditulis d(P, Q)). Selanjutnya, jarak antara dua titik adalah nol dapat terjadi ketika kedua titik itu sama.

Pada keseluruhannya dalam skripsi ini penulis akan mengilustrasikan berbagai macam aksioma, definisi-definisi, dan teorema-teorema dengan model-model dari Bidang Kartesian yang umum dikenal hingga separuh dari bagian atas Bidang Poincarè, dan Bidang Taxicab. Penulis berharap bahwa melalui sebuah gambaran dengan contoh, pembaca akan memperoleh pemikiran nyata dan intuisi untuk geometri non-Euklides. Ada tiga model yang utama dari geometri dengan pendekatan metrik yang akan muncul, yaitu Bidang Euklidean , Bidang Poincarè , dan Bidang Taxicab . Serta akan dibahas pula sifat keantaraan di dalam Geometri Metrik.

1.2Rumusan Masalah

Berdasar atas uraian yang dikemukakan dalam latar belakang, pokok permasalahan dalam skripsi ini dapat dirumuskan sebagai berikut:

1. Apa yang dimaksud dengan Geometri Abstrak, Geometri Insidensi, dan Geometri Metrik?

2. Apa saja model-model yang muncul dari setiap Geometri di atas? 3. Apa sifat dari masing-masing Geometri?

1.3Batasan Masalah

1. Geometri Abstrak yang dibahas hanya dalam pendekatan metrik saja.

2. Dalam penulisan skripsi ini yang dibahas hanya definisi dari Geometri Abstrak, Insidensi dan Metrik, serta model-model yang muncul di dalamnya dan sifat keantaraan dalam Geometri Metrik.

1.4Tujuan Penulisan

Penulisan skripsi ini bertujuan untuk mempelajari Geometri dengan pendekatan metrik serta mempelajari model-model yang muncul di dalamnya.

1.5Metode Penulisan

Metode yang digunakan dalam penulisan skripsi ini adalah dengan menggunakan metode studi pustaka.

1.6Manfaat Penulisan

Manfaat dari penulisan skripsi ini adalah untuk mengetahui definisi dari Geometri Metrik serta untuk mengetahui model-model yang muncul di dalam Geometri Metrik.

1.1Latar Belakang Masalah 1.2Rumusan Masalah 1.3Batasan Masalah 1.4Tujuan Penulisan 1.5Metode Penulisan 1.6Manfaat Penulisan 1.7Sistematika Penulisan

BAB II HIMPUNAN, RELASI EKUIVALENSI DAN FUNGSI 2.1 Aksioma dan Model

2.2 Himpunan dan Relasi Ekuivalensi 2.3 Fungsi

BAB III GEOMETRI ABSTRAK DAN GEOMETRI INSIDENSI 3.1 Geometri Abstrak

3.2 Geometri Insidensi

BAB IV GEOMETRI METRIK 4.1 Geometri Metrik

4.2 Sistem Koordinat Khusus

BAB II

HIMPUNAN, RELASI EKUIVALENSI, DAN FUNGSI

2.1Aksioma dan Model

Studi tentang geometri diawali dengan dua konsep dasar, yaitu pengertian tentang titik dan garis. Pengertian tersebut kemudian dihubungkan dengan kumpulan aksioma, atau prinsip utama. Sebagai contoh, ketika kita mendiskusikan tentang awal munculnya geometri, prinsip utama yang mungkin kita asumsikan yaitu jika A dan B adalah dua titik yang berbeda maka ada tepat satu garis yang dapat ditarik melalui titik A dan B.

Aksioma-aksioma dinyatakan sebagai “kebenaran dasar”. Aksioma adalah pernyataan dari sifat yang sangat diperlukan untuk dipelajari tetapi tidak dibuktikan. Aksioma-aksioma yang demikian akan “terbukti dengan sendirinya”. Pandangan modernnya bahwa aksioma adalah sebuah pernyataan tentang sifat yang sangat berguna. Pemilihan aksioma ditentukan oleh tiga prinsip dasar. Pertama, aksioma harus “layak” atau “menarik”. Kedua, aksioma akan berguna dan berperan penting untuk bermacam-macam teorema dan bermacam struktur matematika. Ketiga, aksioma harus konsisten. Sistem aksioma adalah sistem yang didasarkan pada penalaran deduktif. Sistem deduktif terdiri dari empat komponen, antara lain :

3. Hal-hal yang terdefinisi ( defined terms ) 4. Teorema

Terdapat beberapa sifat sistem aksioma :

1. Konsisten yang artinya tidak ada dua pernyataan ( dua aksioma, aksioma dengan teorema, atau dua teorema yang bertentangan satu sama lain ).

2. Independen artinya jika sebuah aksioma tidak dapat dibuktikan / diturunkan dari aksioma yang lain.

3. Lengkap artinya jika tidak mungkin menambahkan sebuah aksioma yang konsisten dan independen ke dalam sistem tersebut.

Setiap model dalam geometri ditentukan dari pemberian sebuah himpunan yang anggotanya disebut “titik” dan kumpulan himpunan bagian dari himpunan ini yang disebut “garis”. Jika kita menggunakan beberapa model khusus, maka model-model tersebut harus memenuhi aksioma-aksioma yang ada.

2.2Himpunan dan Relasi Ekuivalensi

dengan kita menulis a∉S yang berarti bahwa a tidak berada dalam S, yaitu a

bukan anggota dari S.

Definisi 2.2.1

a) Himpunan T adalah himpunan bagian dari S, ditulis T⊂S, jika setiap anggota

T juga merupakan anggota S.

b) Himpunan T dikatakan sama dengan himpunan S, ditulis T=S, jika setiap anggota T berada di S, dan setiap anggota S berada di T. Karena itu T=S jika dan hanya jika T⊂S dan S ⊂T.

c) Himpunan kosong adalah himpunan yang tidak memiliki anggota dan diberi lambang φ.

Notasi T = { x ∈ S | … } berarti bahwa anggota T merupakan anggota dari S yang memenuhi sifat setelah tanda “|”.

Definisi 2.2.2

a) Gabungan dari dua himpunan A dan B adalah himpunan

A∪B = { x | x ∈A atau x ∈B }. b) Irisan dari dua himpunan A dan B adalah himpunan

c) Selisih dari himpunan A dan B adalah himpunan

A-B = { x | x ∈ A dan x∉B }.

Di bawah ini akan diberikan contoh agar dapat lebih memahami definisi di atas. Ingat bahwa untuk menunjukkan dua himpunan S dan T sama dilakukan dengan menunjukkan bahwa S ⊂T dan T ⊂S.

Contoh 2.2.1

Akan ditunjukkan bahwa A∩

(

B∪C

) (

= A∩B

) (

∪ A∩C

)

Penyelesaian :

Pertama kita tunjukkan bahwa A∩

(

B∪C

) (

⊂ A∩B

) (

∪ A∩C

)

. Misalkan

(

B C

)

A

x∈ ∩ ∪ , maka x∈A dan x∈

(

B∪C

)

. Karena x∈

(

B∪C

)

maka x∈B

atau x∈C (atau di keduanya). Jika x∈B maka x∈

(

A∩B

)

. Jika x∈C maka

(

A C

)

x∈ ∩ . Hal ini berarti x∈

(

A∩B

) (

∪ A∩C

)

. Jadi

(

B C

) (

A B

) (

A C

)

A∩ ∪ ⊂ ∩ ∪ ∩ .

Kemudian kita tunjukkan bahwa

(

A∩B

) (

∪ A∩C

)

⊂ A∩

(

B∪C

)

. Misalkan

(

A B

) (

A C

)

x∈ ∩ ∪ ∩ . Jika x∈

(

A∩B

)

maka x∈A dan x∈B. Karena itu

(

B C

)

x∈ ∪ dan x∈A∩

(

B∪C

)

. Demikian juga, jika x∈

(

A∩C

)

maka x∈A

dan x∈C. Karena itu, x∈

(

B∪C

)

dan x∈A∩

(

B∪C

)

. Dalam salah satu hal,

(

B C

)

A

Karena A∩

(

B∪C

) (

⊂ A∩B

) (

∪ A∩C

)

dan

(

A∩B

) (

∪ A∩C

)

⊂ A∩

(

B∪C

)

, jadi kita dapatkan A∩

(

B∪C

) (

= A∩B

) (

∪ A∩C

)

.

Definisi 2.2.3

Misalkan A dan B adalah himpunan. Sebuah pasangan terurut adalah simbol

(

a,b

)

di mana a∈A dan b∈B. Dua pasangan terurut

(

a,b

)

dan

(

c,d

)

dikatakan sama jika a=c dan b=d. Hasilkali Kartesius dari A dan B adalah himpunan

=

×B

A {(a,b)|a∈A dan b∈B}.

Catatan bahwa R2 =R×R. Sebagai contoh grafik pertidaksamaan x< y

dalam 2

R memuat semua pasangan terurut

(

_,

)

2

R b

a ∈ sedemikian sehingga

b a< .

Definisi 2.2.4

Sebuah relasi biner R pada himpunan S adalah himpunan bagian dari S×S. Jika

( )

s,t ∈R maka kita katakan bahwa s berelasi dengan t.

Kita seringkali menggunakan simbol untuk relasi seperti ~

||, , ,

, ≡ ≈ atau

membuat pernyataan tentang “relasi ~” dan menulis pernyataannya seperti “a ~ b”. Jika dua anggota a, b tidak berelasi, maka kita tulis a ~/ b.

Gagasan mengenai relasi bergantung pada pasangan terurut. Untuk beberapa relasi khusus urutan tidaklah penting – relasi bersifat simetris. Catatan bahwa jika ~ adalah sebuah relasi pada S dan a∈S, maka di dalamnya mungkin tidak ada anggota b dengan a~b. Sebagai contoh, jika S adalah himpunan bilangan bulat positif, dan jika relasinya “>” ( lebih besar dari ) maka tidak ada

S

b∈ dengan 1>b. Dalam hal ini 1 tidak berelasi dengan apapun.

Definisi 2.2.5

Sebuah relasi biner “~” pada S adalah relasi ekuivalensi jika untuk setiap

S c b

a, , ∈ berlaku : i. a~a ( refleksif )

ii. Jika a~b maka b~a ( simetris )

iii. Jika a~b dan b~ , maka c a~c ( transitif )

Contoh 2.2.2

Misalkan adalah himpunan semua bilangan bulat dan didefinisikan a~b jika

b

Untuk mengatakan bahwa a−b habis dibagi 2 artinya bahwa ada bilangan bulat k sedemikian sehingga a−b=2k. Jadi a~b jika dan hanya jika ada k∈Z

sehingga a−b=2k.

i. Misalkan a∈Z , maka a−a=0=2.0 sehingga a~a dan “~” refleksif. ii. Misalkan a,b∈Z dan a~b, maka ada k∈Z dengan a−b=2.k. Ini berarti

bahwa b−a =2.(−k). Karena −k∈Z , kita peroleh b~a. Jadi “~” bersifat simetris.

iii. Jika a~b dan b~ maka ada bilangan c k₁∈Z dan k₂∈Z dengan ,

. 2k₁ b

a− = dan b−c=2.k₂. Dengan menjumlahkan kedua persamaan kita peroleh a−c=2

(

k₁+k₂

)

, dengan k₁+k₂∈Z dan kemudian a~c. Jadi “~” bersifat transitif.

Oleh karena itu “~” adalah relasi ekuivalensi.

Definisi 2.2.6

Jika a dan b adalah bilangan bulat maka a ekuivalen dengan b modulo n jika

kn b

a− = untuk suatu bilangan bulat k. Ditulis a≡b

( )

n dan artinya bahwa a−b

Definisi 2.2.7

Jika “~” adalah relasi ekuivalensi pada himpunan S dan s∈S, maka kelas ekuivalensi s adalah himpunan bagian dari S dengan definisi

[ ]

s =

{

x∈S|x~s

} {

= x∈S|s~ x

}

.

Contoh 2.2.3

Dalam Contoh 2.2.2 kelas ekuivalensi dari 3 adalah himpunan bilangan bulat ganjil, dan kelas ekuivalensi dari 2 adalah himpunan bilangan bulat genap. Catatan pada kasus ini adalah jika x,y∈Z maka

[ ] [ ]

x = y atau

[ ] [ ]

x ∩ y =

φ

.

Teorema 2.2.1

Jika “~” adalah relasi ekuivalensi pada S dan jika s,t∈S maka

[ ] [ ]

s ∩ t =

φ

atau

[ ] [ ]

s = t .

Bukti :

Kita akan menunjukkan bahwa jika pernyataan pertama tidak benar

(

[ ] [ ]

s ∩ t ≠

φ

)

, maka pernyataan kedua benar. Asumsikan bahwa

[ ] [ ]

s ∩ t ≠

φ

, maka ada

[ ] [ ]

s t

x∈ ∩ . Karena itu x∈

[ ]

s dan x∈

[ ]

t . Jadi x~s dan x~t. Dari simetri s~x, dan maka dari transitif s~x dan x~t berakibat bahwa s~t. Kita gunakan ini untuk

Misalkan y∈

[ ]

s , maka y~s dan, karena s~t, kita juga mempunyai y~t dari sifat transitif. Jadi y∈

[ ]

t . Karena itu

[ ] [ ]

s ⊂ t . Sama halnya t~s, dapat kita tunjukkan

[ ] [ ]

t ⊂ s . Karena itu

[ ] [ ]

s = t .

2.3Fungsi

Pada subbab ini kita akan membicarakan fungsi dan bijeksi. Di sini kita akan terus menggunakan R untuk menotasikan himpunan semua bilangan real dan

Z untuk himpunan semua bilangan bulat.

Definisi 2.3.1

Jika S dan T adalah himpunan, maka sebuah fungsi f : S →T adalah sebuah himpunan bagian f ⊂S×T sehingga untuk setiap s∈S ada tepat satu t∈T

dengan

( )

s,t ∈ f . Elemen tunggal t ini biasanya dinotasikan f(s). Himpunan S

disebut daerah asal (domain) dari f dan T disebut daerah hasil (range) dari f.

Contoh 2.3.1

Misalkan f : R →R dengan persamaan f(x) = x2. Misalkan g : Z→R dengan persamaan g(x) = x2. Catat bahwa f tidak sama dengan g – masing-masing memiliki daerah asal yang berbeda. Sekarang misalkan R+ =

{

x∈R|x≥0

}

dan misalkan +

→R

R

h: dengan persamaan

( )

2

x x

Definisi 2.3.2

Jika f :S →T adalah sebuah fungsi maka peta f adalah

( )

{ | ( )

Im f = t∈T t = f s untuk suatu s∈S}.

Im(f ) memuat elemen dari T yang benar-benar “dipetakan” oleh f. Tentu saja, Im(f)⊂ daerah hasil (f ), tetapi himpunannya tidak harus sama.

Definisi 2.3.3

Fungsi f :S →T adalah surjektif jika untuk setiap t∈T ada s∈S dengan

( )

s t

f = .

Sebuah elemen mungkin dapat dioperasikan lebih dari sekali, yaitu mungkin ada beberapa s∈S sehingga f

( )

s =t. Hal ini umum digunakan untuk menyatakan bahwa sebuah fungsi adalah “pada” sebagai ganti dari “surjektif”.

Contoh 2.3.2

Akan ditunjukkan bahwa f : R R oleh

( )

3 1

− = x x

f adalah surjektif sedangkan

g : R R oleh

( )

2 1

− = x x

g tidak surjektif.

Untuk menunjukkan bahwa f adalah surjektif kita harus memperlihatkan bahwa untuk setiap t∈daerah hasil

( )

f = R ada s∈daerah asal

( )

f sehingga f

( )

s =t, yaitu kita harus menunjukkan bahwa persamaan

t

mempunyai penyelesaian untuk setiap nilai t. Karena setiap bilangan real mempunyai akar pangkat tiga, kita tuliskan 3 ₁

+

= t

s . Maka

( )

s

(

t

)

t t f = 3 +1 3 −1= +1−1=

Karena itu f adalah surjektif.

Untuk menunjukkan bahwa g tidak surjektif kita hanya perlu menentukan satu nilai t sehingga persamaan

t

s2 −1= _{. . . ( 2 )}

tidak mempunyai penyelesaian. Misalkan t = - 2. maka penyelesaian dari persamaan ( 2 ) harus memenuhi

1 2

1 2

2

− = −

=

− atau s

s

untuk sembarang bilangan real s. Karena itu g tidak surjektif.

Contoh 2.3.2 mengilustrasikan bagaimana kita mencoba membuktikan sebuah fungsi surjektif. Konsep mengenai sebuah fungsi yang surjektif memberi kita penjelasan apakah sebuah persamaan mempunyai penyelesaian atau tidak. Gagasan penting lain adalah dugaan mengenai fungsi injektif, yang terkait banyaknya penyelesaian untuk sebuah persamaan.

Definisi 2.3.4

Fungsi f :S →T adalah injektif jika untuk setiap s₁,s₂∈S dengan

( )

s1 f

( )

s2

Hal ini merupakan cara umum untuk menggunakan terminologi “satu-satu” untuk arti injektif. Cara lain untuk mendefinisikan fungsi injektif adalah : f

injektif jika s₁ ≠s₂ berakibat f

( )

s₁ ≠ f

( )

s₂ .

Contoh 2.3.3

Akan ditunjukkan bahwa + +

→

 R

R

h: oleh

( )

2

x x

h = adalah injektif.

Asumsikan bahwa h

( )

s₁ =h

( )

s₂ yaitu s₁2 =s₂2. Kemudian dengan menarik akar kuadrat kita peroleh s₁ =±s₂. Karena elemen dari R2 tidak negatif, keduanya dari s₁ dan s₂harus lebih besar dari atau sama dengan nol. Karena itu s₁ ≠−s₂ (kecuali jika keduanya adalah 0) dan kemudian s₁ =s₂. Jadi h adalah injektif.

Kata “injektif “ dan “surjektif” adalah kata sifat. Jika kita mempunyai sebuah kata benda maka ini adalah umum untuk mengatakan “injeksi” untuk “fungsi injektif” dan “surjeksi” untuk “fungsi surjektif”.

Definisi 2.3.5

Contoh 2.3.3 adalah bijeksi. Istilah lain untuk bijeksi adalah korespondensi satu-satu.

Definisi 2.3.6

Jika diberikan fungsi-fungsi f :S →T, g:U →V , dan Im

( )

f ⊂U , maka komposisi dari f dan g adalah fungsi g f :S →V yang diperoleh dari

(

g f

)( )

s =g

(

f

( )

s

)

untuk setiap s∈S.

Catat bahwa daerah asal g harus memuat peta dari f dalam komposisi f

dan g agar terdefinisi.

Teorema 2.3.1

Jika f :S →T dan g:T →V keduanya adalah surjeksi maka g f juga merupakan sebuah surjeksi.

Bukti :

Ambil sebarang v∈V. Kita harus menunjukkan bahwa ada s∈S sehingga

(

g f

)( )

s =v. Karena g adalah surjektif, ada t∈T sehingga g

( )

t =v. Karena f

adalah surjektif ada s∈S dengan f

( )

s =t. Sekarang berlaku

(

g f

)( )

s =g

(

f

( )

s

)

= g

( )

t =v.

Teorema 2.3.2

Jika f :S →T dan g:T →V keduanya adalah injeksi maka g f :S →V

adalah sebuah injeksi. Bukti :

Akan dibuktikan : g f :S →V adalah sebuah injeksi. Definisi dari dua fungsi yang injektif :

Untuk setiap x₁,x₂ ∈ daerah asal (f )

(

jika

(

g f

)( ) (

x₁ = g f

)( )

x₂ ,makax₁=x₂

)

Asumsikan :

(

g f

)( ) (

x₁ = g f

)( )

x₂ .

Untuk sebarang x₁,x₂ berada di daerah asal (f ), maka

( )

(

f x1

)

g

(

f

( )

x2

)

g = , sehingga

( )

x1 f

( )

x2

f = ( g adalah injeksi ). Jadi, x₁ =x₂ ( f adalah injeksi )

Jadi terbukti bahwa g f adalah sebuah injeksi, jika f dan g keduanya adalah

injeksi.

Teorema 2.3.3

Jika f :S →T dan g:T →V keduanya adalah bijeksi maka g f :S →V

adalah sebuah bijeksi. Bukti :

Jika f :S →T adalah bijeksi maka untuk setiap t∈T terdapat dengan tunggal

S

s∈ dengan f

( )

s =t. Hal ini mengijinkan kita untuk mengatakan bahwa untuk setiap t∈T berkorespondensi dengan tepat satu s∈S.

Definisi 2.3.7

Jika f :S →T adalah sebuah bijeksi, maka invers dari f adalah fungsi g:T →S

yang didefinisikan oleh

g

( )

t =s, di mana s adalah elemen tunggal dari S dengan f

( )

s =t . . . ( 3 ) Fungsi g sering dinotasikan dengan −1

f .

Jika f adalah fungsi logaritma natural yang diberikan oleh f

( )

s =ln

( )

s , maka invers dari f adalah fungsi eksponensial g yang diberikan oleh

( )

t

e t

g =

karena eln( )x =s.

Definisi 2.3.8

Jika S adalah sebuah himpunan, maka fungsi identitas ids:S →S diberikan oleh

Teorema 2.3.4

Jika f :S→T, maka f adalah bijeksi jika dan hanya jika g f =id_S dan

T

id g

f = untuk suatu fungsi g:T →S. Lebih jelas, pada kasus ini invers dari f

adalah g. Bukti :

Pertama kita akan menunjukkan bahwa jika ada sebuah fungsi g:T →S dengan

T

id g

f = dan g f =idS maka f adalah bijeksi dan g adalah inversnya.

Asumsikan bahwa ada fungsi g:T →S dengan f g =idT dan g f =idS. Jika

T

t∈ maka g

( )

t ∈S dan f

(

g

( )

t

)

=id_T

( )

t =t. Oleh karena itu t∈Im

( )

f dan f

adalah surjeksi. Jika f

( )

s₁ = f

( )

s₂ untuk s₁,s₂ ∈S, maka

( )

(

f s1

)

g

(

f

( )

s2

)

atau id

( )

s1 id

( )

s2 atau s1 s2

g = S = S = . Jadi f adalah injeksi dan

karenanya adalah sebuah bijeksi. Akhirnya jika t = f(s) maka

( )

t g

(

f

( )

s

)

id

( )

s s

g = = S = . Jadi g adalah invers dari f.

Kemudian kita akan menunjukkan bahwa jika f adalah sebuah bijeksi maka ada fungsi g:T →S dengan f g =idT dan g f =idS. Karena f adalah bijeksi

yang mempunyai invers. Sebut saja invers ini g:T →S. Maka g

( )

t =s apabila

( )

s t

f = .

Dalam kasus tertentu, jika t∈T maka

( )

(

g t

)

f

( )

s t

kemudian bahwa f g =idT. Juga jika s∈T misalkan t = f

( )

s . Maka dari

persamaan ( 3 ), g

( )

t =s Kemudian

( )

(

f s

)

s

g = untuk semua s∈S

Jadi g f =idS.

Contoh 2.3.4

Misalkan diberikan himpunan P+ =

{

t∈R|t >0

}

dan fungsi +

→P

R

f : dengan

( )

s

e s

f = . Akan ditentukan f −1:P+ →R_.

Persamaan (3) menyebutkan bahwa kita harus menemukan sebuah fungsi

R P f

g = −1_: + → _{dengan sifat bahwa}

( )

s t

g = apabila kapan saja es =t. Fungsi ini adalah g

( )

t =lnt.

Karena

t

elnt = dan lnes =s.

Teorema 2.3.4 memberi bukti bahwa penyelesaian kita benar.

Teorema 2.3.5

Jika f :S →T dan h:T →V adalah bijeksi maka

(

)

−1 −1 −1

= f h

f

h .

Bukti :

Akan dibuktikan :

(

h f

)

(

h f

)

=ids

(

h f

) (

h f

)

=idT

−1

Jika f :S →T maka f−1 =T →S

Jika h:T →V maka h−1 =V →T

Kemudian kita amati

(

h f

)

(

h f

)

=ids

−1

Juga,

(

f−1 h−1

)

(

h f

)

= f −1

[

h−1

(

h f

)

]

( komposisi bersifat asosiatif )

(

)

[

h h f

]

f−1 −1

= ( komposisi bersifat asosiatif )

[

id f

]

f T

1

−

=

(

h−1 h=id_T

)

f f−1

=

(

id_T f = f

)

S

id

=

Dengan demikian kita mempunyai

(

h f

)

−1

(

h f

)

=

(

f −1 h−1

)

(

h f

)

Jadi kita peroleh bahwa

(

)

−1 −1 −1

= f h

f h

Jadi terbukti bahwa

(

)

−1 −1 −1

= f h

f

BAB III

GEOMETRI ABSTRAK DAN GEOMETRI INSIDENSI

Pada bab ini kita akan mendefinisikan pengertian geometri abstrak dan geometri insidensi. Ini dilakukan dengan memberikan sekumpulan aksioma yang harus terpenuhi. Setelah definisi-definisi dibuat, akan diberikan sejumlah contoh yang akan disajikan sebagai model-model untuk geometri-geometri tersebut. Dua dari model-model tersebut adalah Bidang Kartesian dan Bidang Poincarè yang akan seterusnya digunakan dalam skripsi ini.

Model-model geometri yang akan digunakan adalah Bidang Kartesian dan Bidang Poincare. Pada pembahasan sebelumnya, geometri adalah himpunan yang terdiri dari titik dan himpunan yang terdiri dari garis bersama dengan hubungan antara titik dan garis.

3.1 Geometri Abstrak Definisi 3.1.1

Geometri abstrak terdiri dari himpunan yang anggota-anggotanya disebut titik, bersama dengan sebuah koleksi dari himpunan bagian tak kosong dari , yang disebut garis, sehingga :

i. Untuk setiap dua titik A,B∈ ada sebuah garis l ∈ dengan A∈l dan .

ii. Setiap garis mempunyai sekurang-kurangnya dua titik.

Jika adalah sebuah geometri abstrak dengan P∈ , l∈ dan

l

P∈ , kita katakan bahwa P terletak pada garis l, atau bahwa l melalui P. Jadi aksioma pertama dari geometri abstrak berbunyi : “setiap pasang titik terletak pada suatu garis.”

Proposisi 3.1.1

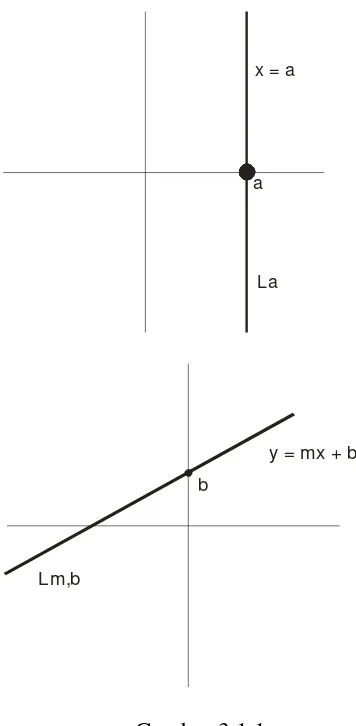
Misalkan = 2 = {( x, y ) | x, y ∈ Kita definisikan himpunan dari “garis-garis” sebagai berikut. Garis vertikal adalah sebarang himpunan bagian 2 yang berbentuk

La = {( x, y ) ∈ 2 | x = a }

dimana a adalah bilangan real yang tetap. Garis tak vertikal adalah sebarang himpunan bagian 2 yang berbentuk

Lm,,b = {( x, y ) ∈ 2 | y = mx + b }

dimana m dan b adalah bilangan real yang tetap. Misalkan E adalah himpunan semua garis-garis vertikal dan tak vertikal. Maka = { 2, E } adalah sebuah geometri abstrak.

Kita harus menunjukkan bahwa jika P=

(

x₁,y₁

)

dan Q=

(

x₂,y₂

)

adalah dua titik yang berbeda dari 2 maka ada l∈ E memuat keduanya. Ini dilakukan dengan memperhatikan dua kasus.

Kasus 1. Jika x₁ =x₂ misalkan a=x₁ = x₂. Kemudian P dan Q keduanya termuat di l =L_a∈ E.

Kasus 2. Jika x₁ ≠ x₂ akan dicari m dan b sehingga P, Q ∈ Lm,,b. Dimotivasi oleh ide tentang “kemiringan / gradien” dari sebuah garis, kita mendefinisikan m dan b

memuat persamaan :

1 2

1 2

x x

y y m

− −

= dan b= y₂ −mx₂.

Dapat ditunjukkan bahwa y₂ =mx₂ +b dan karena titik P juga berada di Lm,,b maka didapat y₁ =mx₁ +b, kemudian bahwa P dan Q keduanya termuat dalam

∈ =Lmb

l _, E.

x = a

a

La

y = mx + b

b

Lm,b

Gambar 3.1.1

Definisi 3.1.2

Model = { 2, E }disebut Bidang Kartesian ( notasi La dan Lm,b akan

digunakan untuk melambangkan garis di Bidang Kartesian ).

aksioma pertama mengenai geometri. Nama Kartesian digunakan untuk menghormati matematikawan dan Filsuf Prancis Renè Descartès ( 1956 – 1650 ), orang yang merevolusionerkan ide mengenai koordinat pada bidang. Pembuktian kita bahwa memenuhi aksioma yang sangat bergantung pada penggunaan koordinat. Descartès juga menetapkan beberapa ketentuan dalam aljabar, seperti menggunakan x, y, z untuk nilai yang tidak diketahui dan a, b, c untuk nilai yang diketahui, serta memperkenalkan notasi eksponensial n

x .

Proposisi 3.1.2

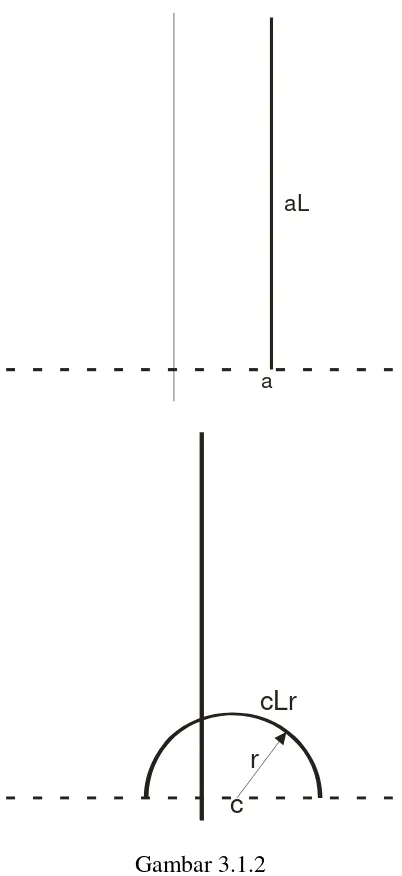
Misalkan = = {( x, y ) ∈ 2 | y > 0 }. Sebagaimana kasus dalam bidang Kartesian, akan dideskripsikan dua jenis garis. Garis tipe I adalah sebarang himpunan bagian dari yang berbentuk

=

L

a {(x, y)∈ x = a}

dimana a adalah sebuah bilangan real yang tetap. Garis tipe II adalah sebarang himpunan bagian dari yang berbentuk

=

r

cL {(x, y)∈ | ( x – c )

2

+ y2 = r2 }

dimana c dan r adalah bilangan real yang tetap dengan r > 0. (Lihat gambar 3.1.2) Misalkan H merupakan himpunan semua garis tipe I dan tipe II. Maka

Misalkan P=

(

x₁,y₁

)

dan Q=

(

x₂,y₂

)

merupakan dua titik berbeda dalam maka y₁ >0 dan y₂ >0.

Kasus 1. Jika x₁ =x₂ maka P dan Q keduanya termuat dalam l=_aL∈ H dimana

2

1 x

x

a= = .

Kasus 2. Jika x₁ ≠ x₂, didefinisikan c dan r sebagai berikut

(

2 1

)

2 1 2 2 2 1 2 2

2 x x x x y y c − − + − =

(

)

2.

1 2

1 c y

x

r= − +

Dengan _cL_r ={(x, y)∈ | ( x – c )2 + y2 = r2 } akan dibuktikan P dan Q berada di dengan memasukkan P dan Q ke dalam persamaan :

( x – c )2 + y2 = r2

1. Akan diperlihatkan titik P=

(

x₁,y₁

)

berada di :

(

)

2 2

1 2

1 c y r

x − + = , kemudian kita masukkan nilai c dan r, dan diperoleh persamaan :

(

)

(

)

2 2 1 2 1 2 2 1 2 2 2 1 2 2 1 2 1 2 1 2 2 1 2 2 2 1 2 2 1

2

2

−

+

−

+

−

−

=

+

−

−

+

−

−

y

x

x

x

x

y

y

x

y

x

x

x

x

y

y

x

(

)

(

)

2 1 2 1 2 2 1 2 2 2 1 2 2 1 2 1 2 1 2 2 1 2 2 2 1 2 2 1

2

2

x

x

y

x

x

y

y

x

y

x

x

x

x

y

y

x

+

−

−

+

−

−

=

+

−

−

+

−

−

Ini berarti bahwa titik P=

(

x₁,y₁

)

berada di

2. Akan diperlihatkan titik Q=

(

x₂,y₂

)

berada di :

(

)

2 2

2 2

2 c y r

x − + = , kemudian kita masukkan nilai c dan r, dan diperoleh persamaan :

(

)

(

)

2 2 1 2 1 2 2 1 2 2 2 1 2 2 1 2 2 2 1 2 2 1 2 2 2 1 2 2 2 2

2 − +

− + − − = + − − + − − y x x x x y y x y x x x x y y x

Jika ruas kanan dikuadratkan maka diperoleh :

(

)

(

)

2 1 2 1 2 2 1 2 2 2 1 2 2 1 2 2 2 1 2 2 1 2 2 2 1 2 2 2

2

2

x

x

y

x

x

y

y

x

y

x

x

x

x

y

y

x

+

−

−

+

−

−

=

+

−

−

+

−

−

(

)

(

)

2 1 2 1 2 2 2 2 1 2 1 2 2 2 1 2 2 2 1 2 2 1 2 2 2 1 2 1 2 2 2 2 2 2 y x x y y x x x x y x x x x y y x x + − − + − − = + − − − + +

Mudah diperiksa bahwa kesamaan ini benar. Jadi kita dapatkan 2 1 2

2 y

y = . Ini berarti titik Q=

(

x₂,y₂

)

berada di .

Misalkan y₁,y₂∈ . Ada

(

a,y₁

)

dan

(

a,y₂

)

∈ . Jadi

(

a,y₁

)

dan

(

a,y₂

)

berada di garis x=a.

Misalkan x₁,x₂,y₁,y₂∈ da

(

x₁,y₁

)

∈ dan

(

x₂,y₂

)

∈ , dan

(

x₁,y₁

)

dan

(

x2,y2

)

berada di garis

(

)

2 2 2 r y c

Jadi terbukti bahwa titik P=

(

x₁,y₁

)

dan Q=

(

x₂,y₂

)

keduanya berada di . Dapat diperiksa bahwa setiap garis mempunyai paling sedikit dua titik. Dengan demikian H} adalah geometri abstrak.

aL

a

c

r

cLr

Proposisi 3.1.3

Misalkan { 1, 1 } dan { 2, 2 } adalah geometri abstrak. Jika = 1∩ 2 dan

= ₁∩ 2 maka akan dibuktikan bahwa { , } adalah geometri abstrak.

Bukti :

Ambil sembarang dua titik P, Q ∈ , maka ada l∈ yang memuat P dan Q.

Jika P, Q ∈ maka P, Q ∈ ₁∩ 2. Jika P, Q ∈ 1∩ 2, maka P, Q ∈ 1 dan

P,Q∈ 2.

Diketahui { 1, 1 } adalah geometri abstrak. Jika P, Q ∈ 1 maka ada l1∈ 1

dengan P, Q ∈l₁ dan setiap l₁ mempunyai sekurang-kurangnya dua titik.

Diketahui { 2, 2 } adalah geometri abstrak. Jika P, Q ∈ 2 maka ada l2∈ 2

dengan P, Q ∈l2 dan setiap l2 mempunyai sekurang-kurangnya dua titik.

Jadi, jika P, Q ∈ ₁∩ 2 maka ada l ∈ dengan P, Q ∈l = l1∩l2.

Jadi jika l1 dan l2 mempunyai sekurang-kurangnya dua titik, maka l = l1∩l2

mempunyai sekurang-kurangnya dua titik.

Jadi, terbukti bahwa { , } adalah geometri abstrak.

Definisi 3.1.3

Model H } disebut Bidang Poincarè. ( Notasi aL dan cLr hanya

Berikut ini akan diberikan contoh untuk mencari garis Poincarè dengan menggunakan Proposisi 3.1.2.

Contoh 3.1.1

Akan dicari garis Poincarè yang melalui titik (1, 2) dan (3, 4).

Penyelesaian :

Diketahui : bidang Poincarè H}

Garis tipe II : _cL_r ={(x, y)∈ | ( x – c )2 + y2 = r2 } Keduanya terletak pada garis tipe II:

i. (1−c)2 +22 =r2

2 2

4 1

2c r

c − + + =

2

2 _{2 5}

r c

c − + = (*)

ii. (3−c)2+42 =r2

2 2

16 9

6c r

c − + + =

2

2 _{6 25}

r c

c − + = (**)

Dari persamaan (*) dan (**) diperoleh: 5

=

c dan r=2 5.

Jadi garis Poincarè yang melalui titik (1, 2) dan (3, 4) adalah ∈

={( , )

5 2

5L x y |( 5) 20}

2 2

= +

− y

disebut Bidang Poincarè untuk menghormati matematikawan Prancis Henri Poincarè (1854–1912) yang pertama kali menggunakannya. Huruf , , dan H digunakan untuk mengingatkan kita pada kata “hiperbolik”. Suatu ketika kita telah menambahkan struktur lain untuk yang akan menjadi sebuah model yang akan kita sebut geometri hiperbolik.

Pada model yang diberikan dalam Proposisi 3.1.1 dan 3.1.2 jelas bahwa melalui sembarang dua titik ada dengan tunggal sebuah garis yang melaluinya. Hal ini tidak benar untuk semua geometri abstrak. Contoh ini akan mempunyai himpunan bagian tertentu dari 3 = {(x, y, z )| x, y, z ∈ sebagai himpunan dari titik,

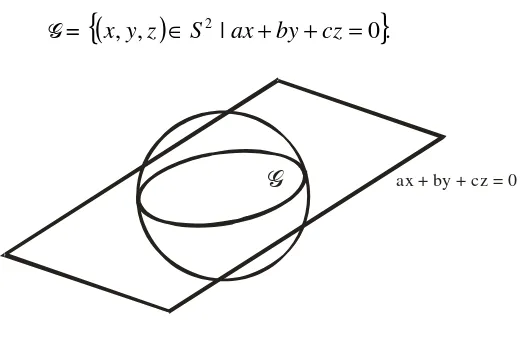
Definisi 3.1.4

Luasan Bola dalam 3 adalah

S 2 = {( x, y, z )∈ 3 | x2 +y2 +z2 =1 }. Sebuah bidang dalam 3 adalah himpunan yang berbentuk

{( x, y, z )∈ 3 | ax + by + cz = d }

dimana a, b, c, d adalah bilangan real tertentu, dan tidak semua dari a, b, c

adalah nol.

Definisi 3.1.5

Sebuah lingkaran besar, dari luasan bola S 2 adalah perpotongan dari S 2

dengan sebuah bidang yang melalui titik asal. Jadi adalah lingkaran besar jika ada a, b, c∈ , tidak semuanya nol, dengan

=

{

(

, ,

)

2 | 0

}

.

= + +

∈S ax by cz

z y x

ax + by + cz = 0

Gambar 3.1.3

Proposisi 3.1.4

Misalkan = S 2 dan misalkan R merupakan himpunan dari lingkaran besar pada S 2. Maka { S 2, R } adalah geometri abstrak.

Bukti :

Kita harus menunjukkan bahwa jika

(

)

2 1 1

1,y ,z S

x

P= ∈ dan

(

)

2

2 2

2,y ,z S

x

Q= ∈

maka ada sebuah lingkaran besar dengan P∈ dan Q∈ . Kemudian kita harus mencari bilangan real a, b, c ( tidak semua nol ) sehingga

0

1 1

1 +by +cz =

Pandang dua persamaan di atas sebagai dua persamaan dalam a, b, c yang ketiganya tidak diketahui. Karena sistem persamaan linear homogen dengan dua persamaan dalam tiga koefisien yang tidak diketahui selalu mempunyai sebuah penyelesaian yang tak nol, kita selalu dapat menemukan a, b, dan c sebagai penyelesaian persamaan di atas. Maka ada sebuah lingkaran besar dengan

∈

P dan Q∈ Terakhir setiap lingkaran besar mempunyai paling sedikit dua

titik.

Definisi 3.1.6

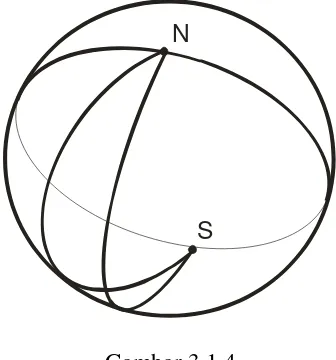
Lingkaran Riemann adalah sebuah geometri abstrak = { S 2, R }.

Catat bahwa “jelas secara geometri” dan terbukti di atas bahwa ada dua titik di S 2 yang terletak dalam sebuah lingkaran besar. Namun demikian,tidak seperti dua contoh berikutnya dua titik dalam S 2 mungkin mempunyai lebih dari satu lingkaran besar yang memuatnya. Perhatikan kutub utara dan selatan N dan S

seperti dalam gambar 3.1.4. Ada lingkaran besar yang tak terbatas jumlahnya dari

N ke S. Ketunggalan garis yang memuat dua titik merupakan sebuah konsep penting untuk mendefinisikan geometri insidensi.

N

S N

S

Gambar 3.1.4

3.2 Geometri Insidensi Definisi 3.2.1

Geometri abstrak { } disebut geometri insidensi jika

Catatan. Jika { }adalah sebuah geometri insidensi dan P,Q∈ , maka garis

tunggal l yang memuat P dan Q akan ditulis sebagai l = PQ.

Definisi 3.2.2

Sebuah himpunan titik adalah segaris ( kolinier ) jika ada satu garis l sehingga

l

⊂ Himpunan tak kolinier jika bukan sebuah himpunan kolinier.

Kadang-kadang kita akan menyebutkan bahwa ”A, B, dan C adalah kolinier” sebagai ganti mengatakan ”{A,B,C} adalah sebuah himpunan kolinier”. Penggunaan notasi ini membuatnya lebih mudah untuk menyatakan beberapa hasil. Aksioma ii dari Definisi 3.2.1 di atas dapat dinyatakan ulang sebagai

ii’ Ada sebuah himpunan dari tiga titik yang tak kolinier.

Walaupun Lingkaran Riemann bukan merupakan geometri insidensi, tetapi Bidang Kartesian dan Bidang Poincarè keduanya adalah geometri insidensi, seperti yang akan kita lihat sekarang.

Proposisi 3.2.1

Kita harus menunjukkan bahwa dua titik berbeda menentukan secara tunggal sebuah garis Kartesian. Misalkan P=

(

x₁,y₁

)

dan Q=

(

x₂,y₂

)

dengan P≠Q. Kita akan mengasumsikan bahwa P, Q terletak pada dua garis berbeda dan pada akhirnya diperoleh kontradiksi

Kasus 1. Misalkan P, Q berada di La dan La’ dengan a≠a'. Maka a=x1 = x2 dan

2 1

' x x

a= = kemudian bahwa a=a’ , merupakan kontradiksi.

Kasus 2. Jika P, Q berada di La dan Lm,b, maka P=

(

a,y1

)

dan Q=

(

a,y2

)

,

karena keduanya berada di Lm,b kita juga memiliki b

ma b mx

y₁ = ₁+ = + dan y₂ =mx₂ +b=ma+b. (3-1) Dengan begitu y₁ = y₂, yang kontradiksi dengan

(

a,y₁

)

=P≠Q=

(

a,y₂

)

.

Kasus 3. Misalkan bahwa P, Q berada di Lm,b dan Ln,c dan bahwa Lm,b≠ Ln,c. Maka

b mx

y₁ = ₁+ y₂ =mx₂ +b. (3-2) Dari kasus 2, P, Q tidak berada di sebuah garis vertikal jadi x₁ ≠ x₂. Oleh karena itu dari (3-2) kita dapat mencari nilai m :

1 2

1 2

x x

y y m

− −

= . (3-3)

Dari nilai m kita peroleh nilai b :

1

1 mx

y

1 2

1 2

x x

y y n

− −

= , c= y₁−nx₁.

Tapi ini berakibat m = n dan b = c ini kontradiksi dengan Lm,b≠ Ln,c.

Dengan begitu dalam semua kasus, asumsi bahwa P, Q berada dalam dua garis berbeda mengantar ke sebuah kontradiksi, yang berarti bahwa P, Q berada dalam satu garis tunggal. Di dalam Bidang Kartesian, ada paling sedikit tiga titik yang takkolinier. Misalnya titik (-1,0), (0,2), dan (1,-3). Oleh karena itu adalah sebuah geometri insidensi.

Proposisi 3.2.2

Bidang Poincare adalah sebuah geometri insidensi. Bukti :

Misalkan P,Q∈ dengan P≠Q. Jika P dan Q berada pada dua garis tipe I _aL

dan a'L maka kita dapat menunjukkan bahwa a=a' seperti dalam Proposisi

3.1.4. Jadi P dan Q tidak dapat tidak berada pada dua garis tipe I yang berbeda. Misalkan jika P dan Q terletak pada aL dan cLr maka P dan Q adalah titik yang

sama. Misalkan P=

(

x₁,y₁

)

dan Q=

(

x₂,y₂

)

.

Diketahui P terletak pada aL, maka x1 =a dan Q juga terletak pada aL, maka

a

x₂ = . Jadi x₁ =x₂.

(

)

2 2 1 2

1 c y r

x − + = (3-5)

Diketahui Q juga terletak pada cLr, maka

(

)

2 2

2 2

2 c y r

x − + = (3-6)

Padahal x₁=x₂, maka persamaan (3-5) menjadi

(

)

2 2

1 2

2 c y r

x − + = (3-7)

Dari persamaan (3-6) dan (3-7)

(

)

(

)

2

1 2 2 2 2 2 2

2 c y r x c y

x − + = = − +

(

)

(

)

2

1 2 2 2 2 2

2 c y x c y

x − + = − +

y₂2 = y₁2

y₂ = y₁

Padahal y₁ ≥0, maka y₁ tidak mungkin negatif. Jadi, nilai yang mungkin untuk

1

2 y

y = . Karena x₁ =x₂ dan y₂ = y₁, maka P = Q. Kontradiksi. Karena P dan Q

adalah titik yang berbeda, jadi P dan Q tidak dapat terletak pada aL dan cLr

secara bersamaan.

Kita akan membuktikan bahwa jikaP=

(

x₁,y₁

)

dan Q=

(

x₂,y₂

)

berada di _cL_r

dan dLs maka cLr=dLs. Kita akan menunjukkan bahwa c = d dan r = s. oleh

karena itu P dan Q berada di _cL_r,

(

)

2 2

1 2

1 c y r

x − + = dan

(

)

2 2.

2 2

2 c y r

Dengan mengurangkan kedua persamaan, kita peroleh

(

)

(

)

2

1 2 2 2 2 2

1 c x c y y

x − − − = − atau

2 1 2 2 2 2 2 1 2

1 2cx x 2cx y y

x − − + = − .

Dengan menyelesaikan untuk c :

(

2 1

)

2 1 2 2 2 1 2 2

2 x x x x y y c − − + − =

Sebuah perhitungan yang serupa dengan pembuktian proposisi 3.1.2 dengan menggunakan fakta bahwa P dan Q berada di _dL_s akan menghasilkan

(

2 1

)

2 1 2 2 2 1 2 2

2 x x x x y y d − − + − =

sehingga c = d. Karenanya

(

x c

)

y

(

x d

)

y s r= ₁− 2 + ₁2 = ₁ − 2 + ₁2 =

kita lihat bahwa r = s dan kemudian cLr=dLs.

Ada tiga titik (1,2), (-2,0), dan (-1,3)∈ yang tidak terletak pada satu garis. Dengan demikian adalah sebuah geometri insidensi.

Contoh 3.2.1

P

Q

R

Diketahui P terletak pada satu garis dengan R dan P juga terletak pada satu garis dengan Q.

Akan dibuktikan:

i. Setiap dua titik berbeda pada yang terletak pada satu garis tunggal. ii. Ada tiga titik pada yang tidak semuanya terletak pada satu garis. Bukti :

i. Diketahui titik P, Q, R∈ dengan P terletak satu garis dengan R, dan P juga terletak satu garis dengan Q, ini berarti juga bahwa Q terletak satu garis dengan R. Jadi terbukti bahwa setiap dua titik berbeda pada yang terletak pada satu garis tunggal.

ii. Diketahui garis PQ, PR, QR∈ , jelas PQ tidak memuat R, PR tidak memuat

Q dan QR tidak memuat P. Jadi terbukti bahwa ada tiga titik berbeda pada yang tidak semuanya terletak pada satu garis.

Jadi, terbukti bahwa { } adalah geometri insidensi.

Teorema 3.2.1

Bukti :

Asumsikan bahwa P≠Q,P∈l₁∩l₂, dan Q∈l₁∩l₂. Karena P dan Q berada di

1 1,PQ l

l = . Bagaimanapun juga, P dan Q juga berada di l₂ sehingga PQ=l₂.

Jadi l₁ =l₂.

Definisi 3.2.3

Jika l₁ dan l₂adalah garis-garis dalam sebuah geometri abstrak maka l₁ sejajar dengan l₂ ditulis l₁||l₂ jika l₁ =l₂ atau l₁∩l₂ =Ø.

Akibat 3.2.1

Dalam sebuah geometri insidensi, dua garis sejajar atau berpotongan tepat di satu titik.

Contoh 3.2.2

Akan dicari garis yang sejajar dengan garis i. tak vertikal L_3,−1 di Bidang Kartesian.

ii. tipe II ₃L₁ di Bidang Poincarè.

Penyelesaian:

i. Garis tak vertikal di Bidang Kartesian Lm,b yang sejajar dengan L3,−1 adalah

∈

ii. Garis tipe II di Bidang Poincarè cLr yang sejajar dengan 3L1 adalah ∈

k L_k,

3

Proposisi 3.2.3

Misalkan { } adalah geometri abstrak. Jika l₁ dan l₂ adalah garis-garis di kita tulis l₁ ~l₂ jika l₁ sejajar dengan l₂. Maka “~” adalah relasi ekuivalensi. Bukti :

Akan dibuktikan bahwa “~” adalah relasi ekuivalensi.

Jika “~” relasi ekuivalensi, maka “~” harus refleksif, simetris, dan transitif.

i. Jika l₁∈ , maka dari Definisi 3.2.3 l₁ sejajar dengan l₁. Karena l₁ sejajar dengan l₁, maka l₁~l₁. Jadi ”~” refleksif.

ii. Jika l₁,l₂∈ , maka dari Definisi 3.2.3 l₁ sejajar dengan l₂. Jika l₁ sejajar dengan l₂, maka l₁∩l₂ =

φ

atau l₁ =l₂. Karena l₁ =l₂, maka l₂ =l₁ dan

φ

=

∩ ₁

2 l

l . Dengan demikian l₂ sejajar dengan l₁. Sehingga l₂ ~l₁. Jadi “~” simetris.

Karena l₁ =l₂ dan l₂ =l₃ maka l₁=l₃. Sehingga l₁∩l₃ =

φ

. Dan l₁ ~l₃. Jadi “~” transitif.

BAB IV

GEOMETRI METRIK

4.1Geometri Metrik

Ada dua pendekatan mendasar dari geometri. Pertama, disebut pendekatan sintetik, yang digunakan oleh Euclid dalam bukunya yang berjudul Elements

(sekitar 300 SM) dan dilengkapi oleh seorang matematikawan Jerman David Hilbert (1862-1943) dalam bukunya yang berjudul Grundlagen der Geometrie. Hilbert, pada tahun yang sama dengan Poincarè berkarya dalam beberapa daerah matematika dan mempengaruhi matematika modern. Ia menempatkan beberapa topik matematika dengan tempat berpijak aksioma yang kuat. Dalam pidatonya untuk Kongres Internasional Matematika pada tahun 1900 ia mengusulkan sebuah rangkaian dari tujuhbelas pertanyaan yang ia rasa berperan penting dalam masalah teoritis pada masanya.

menggunakan aksioma. Birkhoff juga diingat untuk pekerjaannya dalam relativitas, persamaan diferensial, dan sistem dinamik.

Pendekatan ketiga, diperjuangkan oleh Felix Klein (1849-1925), memiliki pendekatan yang sangat berbeda, yaitu menggunakan aljabar abstrak, dan lebih maju dari yang lain karena mempergunakan teori grup. Klein merasa bahwa geometri harus dipelajari dari sudut pandang grup yang beraksi pada sebuah himpunan.

Kita menggunakan pendekatan metrik karena konsep tentang jarak adalah seperti suatu yang alami. “Jarak” adalah fungsi yang menentukan sebuah bilangan

d(P, Q) untuk setiap pasangan titik P, Q. Hal itu mestinya tidak bergantung apakah kita ukur dari P ke Q atau dari Q ke P (ditulis d(P, Q)). Selanjutnya, jarak antara dua titik adalah nol hanya terjadi ketika kedua titik itu sama.

Definisi 4.1.1

Sebuah Fungsi Jarak pada himpunan adalah sebuah fungsi d : × sehingga untuk semua P, Q∈ berlaku

i. d

(

P,Q

)

≥0;

ii. d

(

P,Q

)

=0 jika dan hanya jika P = Q ; dan iii. d

(

P,Q

)

=d

(

Q,P

)

.

Definisi 4.1.2

Misalkan = 2, P=

(

x₁,y₁

)

dan Q=

(

x₂,y₂

)

. Jarak Euklidean dE diberikan

oleh

(

)

(

)

(

)

2

2 1 2 2 1

,Q x x y y

P

d_E = − + − .

Proposisi 4.1.1

Jarak Euklidean dEdiberikan oleh

(

)

(

)

(

)

2

2 1 2 2 1

,Q x x y y

P

dE = − + −

adalah fungsi jarak pada 2. Bukti :

Misalkan P=

(

x₁,y₁

)

dan Q=

(

x₂,y₂

)

∈ 2, sebuah fungsi jarak dE harus memenuhi tiga aksioma.

i. d_E

(

P,Q

)

=

(

x₁−x₂

)

2 +

(

y₁ −y₂

)

2

Selalu bernilai ≥0, karena semua bilangan apabila dikuadratkan selalu bernilai tak negatif.

Jadi d_E

(

P,Q

)

≥0 terpenuhi. ii. Jika d_E

(

P,Q

)

=0, maka

(

x₁−x₂

)

2+

(

y₁−y₂

)

2 =0

(

x₁−x₂

)

2 ≥0 dan

(

y₁−y₂

)

2 ≥0

(

x₁−x₂

)

2 =0 dan

(

y₁−y₂

)

2 =0

0

2 1−x =

x y₁−y₂ =0 sehingga,

2

1 x

x = dan y₁= y₂. Jadi, P = Q.

Jika P = Q, maka

(

)

(

)

(

)

2

2 2 2 2 2

,Q x x y y

P

d_E = − + −

= 0+0=0

Jadi, dE

(

P,Q

)

=0 jika dan hanya jika P = Q, terpenuhi.

iii. d_E

(

P,Q

)

=

(

x₁−x₂

)

2 +

(

y₁ −y₂

)

2

=

(

( )(

−1 x₁−x₂

)

2

)

+

(

( )(

−1 y₁−y₂

)

2

)

=

(

−x₁+x₂

)

2 +

(

−y₁+y₂

)

2

=

(

x₂−x₁

)

2 +

(

y₂−y₁

)

2 =dE

(

Q,P

)

Jadi, dE

(

P,Q

)

=dE

(

Q,P

)

terpenuhi.

Untuk memberikan contoh yang masuk akal bagi sebuah fungsi jarak dalam Bidang Poincarè memerlukan lebih banyak pemikiran. Misalkan P dan Q

termuat dalam garis tipe I. Perkiraan jarak yang tepat antara P=

(

a,y₁

)

dan

(

a,y2

)

Q= menjadi y₁ −y₂ . Bagaimanapun juga, hal ini tidak mudah karena ini berarti bahwa seperti y₂ cenderung mendekati nol (dan kemudian Q ke arah x-absis atau “tepi”) jarak dari P ke Q cenderung ke y₁ yang merupakan bilangan berhingga. Hal ini akan menjadi “lebih baik” jika “tepi” bukan merupakan sebuah jarak yang berhingga. Satu cara untuk menghindarinya adalah menggunakan skala logaritma dan disebut sebagai jarak dari

(

a,y₁

)

ke

(

a,y₂

)

yaitu

( )

−

( )

= 2 1 2

1 ln ln

ln

y y y

y . ( Catat bahwa → →∞

2 1 2 0,ln

y y

y . ) Hal ini memberi

beberapa per