PENGGUNAAN SOFTWARE MATLAB
UNTUK ANALISA STRUKTUR
Ramses Hutahaean Jurusan Teknik Sipil, Universitas Yapis
Jl.Dr Sam Ratulangi, Dok 5, Jayapura
ramses_yh@yahoo.com
Abstrak
Perkembangan teknologi komputasi banyak digunakan dalam dunia rekayasa teknik, dalam tulisan ini akan dijelaskan penggunaan perangkat lunak MATLAB yang digunakan untuk simulasi terjadinya resonansi pada suatu struktur, dimana fenomena resonansi adalah fenomena yang harus dihindari karena akan mengakibatkan kerusakan struktur mesin atau bangunan. Dengan simulasi terjadinya resonansi kita akan dapat mengetahui parameter parameter dinamik yang harus di pilih, yaitu berupa nilai massa, redaman dan kekakuan yang tepat agar tidak terjadi resonansi.
Kata kunci : Resonansi, Matlab, Parameter dinamik.
1. Pendahuluan
Berkembangkan teknologi komputer saat ini, sangat membantu analisa perhitungan teknik, yang dilakukan pada struktur bangunan, automotive, pesawat terbang dan lain lain. Pada tulisan ini penulis akan menjabarkan penggunaan software MATLAB sebagai software yang digunakan untuk analisa perilaku dinamik suatu struktur, software yang ada saat ini adalah software yang langsung dapat digunakan oleh praktisi, seperti ANSYS, STAAD PRO, PRO MECHANICA dan lain lain, namun software software tersebut tidak praktis jika digunakan untuk menjelaskan perilaku dinamik suatu struktur. Pada tulisan ini penulis akan mendemonstrasikan perilaku dinamik sederhana, dengan menggunakan sistem pegas, massa dan peredam.
1. Pemodelan Struktur Sederhana
Kita akan memodelkan suatu struktur sederhana yang terdiri dari massa, pegas dan peredam, model yang ditunjukan berupa sistem dengan dua derajat kebebasan, seperti ditunjukan pada gambar 1.
Gambar 1
2.1 PERSAMAAN GERAK
Persamaan gerak sistim dengan dua derajat kebebasan suatu sistim yang diperlihatkan pada gambar 2 dapat kita turunkan dengan menerapkan hukum Newton kedua.
Gambar 2
Kita asumsikan bahwa redaman adalah redaman viskus dan perpindahan x1(t) dan x2(t) diukur dari
posisi keseimbangan statik. Dengan menjumlahkan gaya gaya dinamik yang bekerja pada tiap-tiap massa, diperoleh :
Persamaan tersebut kita susun kembali menjadi ;
2
204
Dimana F1(t) dan F2(t) adalah gaya eksitasi terhadap
massa 1 dan massa 2, dari persamaan (1) kita ketahui bahwa kedua persamaan tersebut terkopel, karena pada persamaan yang berisi m1 terdapat suku
yang berisi x1 dan x2, hal yang sama juga terjadi
pada persamaan yang berisi m2. Suku kopel pada
persamaan pertama adalah
c
x
2
kx
2
. Hal yang serupa suku kopel pada persamaan pertama adalah
c
x
1
kx
1
. Dengan kata lain, gerak masssa 1, x1(t) dipengaruhi oleh gerak massa 2,x2(t) dan sebaliknya.
Dalam bentuk matriks persamaan 1 kita susun kembali menjadi :
0 0
2 Atau
dimana [M] adalah matriks massa, [C] adalah matriks redaman ,[K] adalah matriks kekakuan, {x} adalah matriks perpindahan dan {F(t)} adalah matriks gaya eksitasi.
1.2Kurva Fungsi Respon Frekwensi
Merupakan fungsi respon suatu titik terhadap gaya atau eksitasi di titik tertentu, karena
,
dan
Maka respon sistem adalah
3 Dimana dalam fungsi respon frekwensi gaya merupakan satuan.
1.3 MENENTUKAN FREKWENSI NATURAL
Kita dapat mencari frekwensi natural dengan menggunakan metoda elemen hingga, kita mengabaikan faktor redaman, dalam hal ini matriks
kita abaikan, sehingga persamaan gerak menjadi 0 4 Dimana adalah matriks massa struktur dan adalah matriks kekakuan struktur. Solusi homogen untuk persamaan 3 adalah
5 Dimana adalah amplitudo dari perpindahan nodal, dengan mensubstitusikan persamaan 5 pada persamaan 4, diperoleh 0 6 Atau 0 7 Dimana 8 Persamaan 7 atau persamaan 8 dinamakan persamaan eigen. Untuk memperoleh nilai eigen tersebut, harus terpenuhi kondisi
| | 0 9
Dari persamaan 9 akan diperoleh nilai eigen , , , … , , dimana adalah jumlah derajat kebebasan struktur.
2.3 RESPON SISTEM DENGAN MENGGUNAKAN METODE RUNGE KUTTA
Cara lain untuk mendapatkan respon dari struktur secara teoritis dan dengan hasil yang akurat adalah dengan menggunakan metoda integrasi numerik Runge-Kutta.
Fungsi dari metode ini adalah menyelesaikan persamaan diferensial tingkat satu. Untuk persamaan dinamik dengan persamaan diferensial tingkat dua, persamaan tersebut dirubah menjadi persamaan diferensial tingkat satu.
Sistem dinamik dengan satu derajat kebebasan memiliki persamaan diferensial tingkat dua sebagai berikut :
9 Kemudian persamaan gerak tersebut disederhanakan menjadi :
1
, , 10 dari persamaan tersebut diketahui bahwa percepatan
merupakan fungsi terhadap , , . Dengan menentukan , maka
, , atau
, ,
Kedua suku x dan y disekitar xi dan yi dapat
dinyatakan dalam deret taylor. Dengan mengambil pertambahan waktu h = t, didapat :
2 ⋯
2 ⋯
11
Dengan menggunakan deret dari persamaan (11), dapat diambil turunan pertama sebagai rata-rata kemiringan, sehingga turunan yang lebih tinggi dapat dihilangkan, sehingga diperoleh
12
Dengan menggunakan metoda simpson, rata kemiringan dalam interval h menjadi :
1
6 4
1
6 4
13
Metoda Runge-Kutta menggunakan persamaan(13) dan mengubah bagian tengah dari persamaan tersebut menjadi 2 bagian , sehingga kita memiliki
205
empat parameter. Keempat parameter dapat dihitung dengan menggunakan persamaan berikut :
Dari persamaan (14) terlihat bahwa empat nilai Yi dibagi enam merupakan rata-rata kemiringan
dx/dt , dan empat nilai Fi dibagi enam merupakan
rata-rata kemiringan dy/dt. Dengan kondisi awal :
0 0 0 0 0 y x t x x t x Substitusi kondisi awal pada persamaan (14) akan menghasilkan respon struktur sebagai fungsi waktu untuk setiap interval h atau (∆t) dapat dihitung dengan menggunakan persamaan :
n
n
n
n
4 3 2 1 n n 4 3 2 1 n n t kx t x c t f m 1 t x F F 2 F 2 F h 6 1 t x h t x Y Y 2 Y 2 Y h 6 1 t x h t x (15) dengan
tn ytn x t h 2. Listing Pemrograman MATLAB Untuk
Respon Sistem suatu Struktur
Berikut ini akan ditunjukan listing pemrograman MATLAB untuk sistem dua derajat kebebasan, berikut dengan animasinya.
%Program Animasi ini menggunakan metode Runge Kutta
disp '
****************************************** ************************'
disp ' * PROGRAM ANIMASI TWO DEGREE OF FREEDOM *'
disp ' * Oleh : Ramses Y Hutahaean *' disp ' ***********************************' clf clear n=input('Jumlah data ? '); t=0.0; dt=0.001;
ff2=input(' Amplitudo gaya pada massa 2( N ) ? '); ff=[0;ff2];
ww=input(' frekwensi getar ? '); sc=input(' Skala animasi ? ');
M=[10 0;0 10];K=[9000 -4000;-4000 4000]; C=0.002.*K; x10=input('Simpangan awal m1 ? '); v10=input('Kecepatan awal m1 ? '); x20=input('Simpangan awal m2 ? '); v20=input('Kecepatan awal m2 ? '); x=[x10;x20]./1000; v=[v10;v20]./1000; for i = 1:n; t1=t; x1=x; v1=v; f1=inv(M)*([0;ff2*sin(ww.*t1)]-C*v1-K*x1); % t2=t+dt/2; x2=x+v1.*dt/2; v2=v+f1*dt/2; f2=inv(M)*(sin(ww.*t2).*ff-C*v2-K*x2); % t3=t+dt/2; x3=x+v2.*dt/2; v3=v+f2.*dt/2; f3=inv(M)*(sin(ww.*t3).*ff-C*v3-K*x3); t4=t+dt; x4=x+v3.*dt; v4=v+f3.*dt; f4=inv(M)*(sin(ww.*t4).*ff-C*v4-K*x4); t=t+dt; v=v+dt/6.*(f1+2.*f2+2.*f3+f4); x=x+dt/6.*(v1+2.*v2+2.*v3+v4); tt(i)=t; vv1(i)=v(1,1); vv2(i)=v(2,1); xx1(i)=x(1,1); xx2(i)=x(2,1); dx(i)=0.08*sin(ww*t); dy(i)=-0.025*cos(ww*t); ffk(i)=ff2*sin(ww*t); end pegas1=[ ... 0.00 0.25 0.10 0.25 0.20 0.275 0.30 0.225 0.40 0.275 0.50 0.225 0.60 0.275 0.70 0.25 1.00 0.25];% panjang pegas 1 pegas2=pegas1; xyBox1=[ ...
206
0.00 0.25 0.00 0.20 0.00 0.30 0.3 0.30 0.3 0.20 0.00 0.20 0.3 0.20 0.3 0.25]; xyBox2=[ ... 1.30 0.25 1.30 0.20 1.30 0.30 1.6 0.30 1.6 0.20 1.30 0.20]; aa=[max(xx1);max(xx2)]; am=max(aa); L=1; xr1=xx1/L; xr2=(xx2-xx1)/L; X1=[xyBox1(:,1)]+1;Y1=[xyBox1(:,2)]; X2=[xyBox2(:,1)]+1;Y2=[xyBox2(:,2)]; ddx=1.15;ddy=0.25; p=length(xx1); for j=1:p tk(j)=tt(j); fk(j)=ffk(j); yyk1(j)=xx1(j);yyk2(j)=xx2(j); psx1=pegas1(:,1)*(1+xr1(j)); psx2=pegas2(:,1)*(1+xr2(j))+(0.3+max(psx1)).*one s(size(psx1)); psy1=pegas1(:,2); psy2=psy1; cx1=X1+sc*xx1(j); cx2=X2+sc*xx2(j); xp1=[psx1;cx1]; xp2=[psx2;cx2]; yp1=[psy1;Y1]; yp2=[psy2;Y2]; ux=[max(xp2)-0.15+dx(j)]; uy=[0.25+dy(j)]; pxt=[0;0;0;xp1;xp2]; pyt=[0.2;0.3;0.25;yp1;yp2]; if ff2==0 subplot(211) h=plot(tk,yyk1,'k-',tk,yyk2,'r-.','EraseMode','background'); set(h,'lineWidth',1.2);
axis([0 n*dt -1.1*am 1.1*am]) title('Response ') if j==p grid end subplot(212) h=plot(pxt,pyt,'k-','EraseMode','background'); set(h,'lineWidth',3); axis([0 4 0.1 .32]) axis off drawnow else subplot(311) h=plot(tk,fk,'k-','EraseMode','background'); set(h,'lineWidth',1); axis([0 n*dt -1.1*ff2 1.1*ff2]) title('Unbalance Force ') subplot(312) h=plot(tk,yyk1,'k-',tk,yyk2,'r-.','EraseMode','background'); set(h,'lineWidth',1);
axis([0 n*dt -1.1*am 1.1*am]) title('Response ') subplot(313) h=plot(pxt,pyt,'k-',ux-dx(j),0.25,'bo',ux,uy,'ro','EraseMode','background'); % set(h,'lineWidth',3); axis([0 4 0.1 .32]) axis off drawnow % pause(0.01) end end 3. Simulasi
Dari hasil menjalankan bahasa pemrograman MATLAB, diperoleh kurva fungsi respon frekwensi, dengan data data sebagai berikut
1.5 0
0 1 ; 900300 600300 ; 0.005
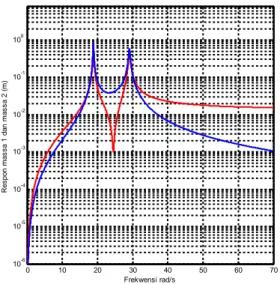
Pada gambar 3, ditunjukan kurva respon frekwensi, dimana puncak kurva terjadi pada frekwensi 18.85 rad/s dan pada frekwensi 29.07 rad/s.
Tahap pertama kita menggunakan frekwensi getar 15 rad/s, dimana frekwensi natural sistem adalah
18.85 / dan 29.07 / .
Gambar 3 Kurva fungsi respon frekwensi
Hasil simulasi dengan frekwensi getar 15 rad/s ditunjukan pada gambar 4
Gambar 4 Animasi pada frekwensi 15 rad/s
Hasil simulasi dengan frekwensi getar 18 rad/s ditunjukan pada gambar 5
Gambar 5 Animasi pada frekwensi 18 rad/s
Hasil simulasi dengan frekwensi getar 29.8 rad/s ditunjukan pada gambar 6
Gambar 6 Animasi pada frekwensi 29.8 rad/s Pada animasi yang ditunjukan pada gambar 4 dan gambar 5, bahwa arah getaran massa 1 dan massa 2 adalah sama, pada saat massa 1 bergerak kekiri maka massa 2 juga bergerak ke kiri. Sedangkan jika massa 1 bergerak ke kanan, maka massa 2 juga bergerak kekanan, hal ini terjadi pada mode 1.
Pada animasi yang ditunjukan gambar 6, ditunjukan bahwa gerakan massa 1 berlawanan dengan arah massa 2, hal ini menunjukan mode kedua.
4. Kesimpulan
Bahasa pemrograman MATLAB dapat digunakan untuk menganalisa perilaku struktur.
Berdasarkan pengalaman penulis, Bahasa pemrograman MATLAB telah digunakan untuk melakukan condition monitoring suatu sistem permesinan, dan kemudian menentukan waktu yang tepat untuk melakukan perbaikan.
Bahasa pemrograman MATLAB juga digunakan untuk penerapan transformasi Fourier.
Daftar Pustaka:
1. Clough, W Ray, Penzien Joseph, ‘Dynamics Of
Structures ‘, Mc Graw Hill, International
Edition. 1993
2. Dimaragonas D Andrew, Haddad Sam,’
Vibration For Engineers’, Prentice Hall,
Englewood, 1992.
3. Hanselman, Duane, Little, Field ,’Student
edition of MATLAB ‘, Prentice Hall,1997
4. Hutahaean, Ramses ,’ Getaran Mekanik ‘ ,
Penerbit ANDI, Yogyakarta, 2010
5. Hutahaean, Ramses,’ Teknik Kontrol
Automatik ’. Penerbit ANDI Yogyakarta, 2015
6. Knight, Andrew,’ Basics of MATLAB and
beyond’. Chapman and Hall/CRC, 2000.
7.
Rao, Singiresu, “ Mechanical Vibration ‘Prentice Hall, 5th Edition, 2011.
0 10 20 30 40 50 60 70 10-6 10-5 10-4 10-3 10-2 10-1 100 R e s pon m a s s a 1 da n m a s s a 2 ( m ) Frekwensi rad/s 17.5 18 18.5 19 19.5 20 -4 -2 0 2 4 Unbalance Force 17.5 18 18.5 19 19.5 20 -0.02 0 0.02 Response 22.5 23 23.5 24 24.5 25 -5 0 5 Unbalance Force 22.5 23 23.5 24 24.5 25 -0.2 -0.1 0 0.1 0.2 Response 22.5 23 23.5 24 24.5 25 -10 0 10 Unbalance Force 22.5 23 23.5 24 24.5 25 -0.2 0 0.2 Response