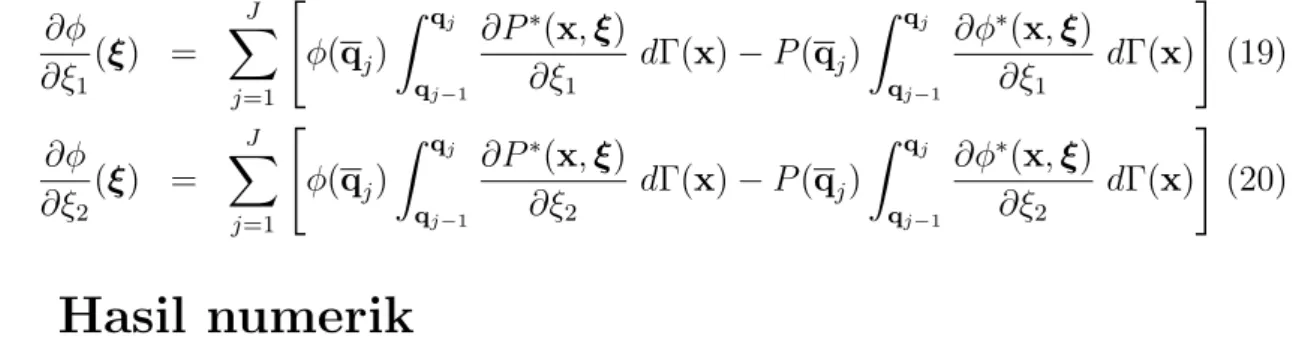Metode Elemen Batas (MEB) untuk Model
Perambatan Gelombang
∗
Moh. Ivan Azis
†September 13, 2011
Abstrak
Metode Elemen Batas untuk masalah perambatan gelombang akustik (har-monis) berhasil diturunkan pada tulisan ini. Sistem yang diperhatikan terpakai untuk media yang anisotropik.
Daftar Isi
1 Pendahuluan 1
2 Masalah Nilai Batas 2
3 Solusi fundamental 2
4 Persamaan integral batas 3
5 Diskritisasi 4
6 Hasil numerik 7
7 Konklusi 10
1
Pendahuluan
Tulisan ini mendiskusikan pembentukan MEB untuk solusi numerik masalah nilai batas yang dibangun oleh persamaan berbentuk
λij
∂2ϕ ∂xi∂xj
+ k2ϕ = 0, untuk i, j = 1, 2 (1)
∗Dipublikasikan pada Jurnal Fisika FUSI Jurusan Fisika FMIPA Unhas, Vol. 6, Nomor 8, 2002, Halaman 64 - 70
†Dosen Jurusan Matematika Fak. MIPA Unhas, Makassar Indonesia. Email:mohivanazis@ hotmail.com
dimana kofisien λij dan k konstan, dan matriks kofisien [λij] merupakan matriks
bi-langan real definit positif dan simetris. Juga, pada (1) penjumlahan untuk index yang berulang (jumlahan dari 1 sampai 2) diberlakukan, sehingga secara eksplisit (1) dapat dituliskan sebagai λ11 ∂2ϕ ∂x2 1 + 2λ12 ∂2ϕ ∂x1∂x2 + λ22 ∂2ϕ ∂x2 2 + k2ϕ = 0
Bila λ11 = λ22 = 1 dan λ12 = 0 maka persamaan (1) adalah persamaan Helmholtz
yang merupakan persamaan pembangun untuk model perambatan gelombang harmonis waktu (time-harmonic waves) dalam media isotropik, yaitu gelombang kontinyu pada suatu frekuensi tetap, dimana ϕ melambangkan potensial kecepatan (velocity potential) dan k adalah bilangan gelombang (wave number) (lihat misalnya Wu [4]).
2
Masalah Nilai Batas
Dengan merujuk pada sistim kordinat Cartesian Ox1x2 solusi dari (1) dicari dimana
solusi tersebut valid dalam daerah Ω di R2 dengan batas Γ yang terdiri dari sejumlah berhingga kurva mulus bagian demi bagian. Pada Γ salah satu dari ϕ(x) atau
P (x) = λij
∂ϕ(x) ∂xi
nj(x)
diberikan, dimana x = (x1, x2), n = (n1, n2) melambangkan vektor normal satuan
mengarah ke luar di batas Γ. Metode solusi yang dipakai akan bekerja dengan cara menurunkan suatu persamaan integral batas, yang relevan untuk persamaan differensial (1), darimana nilai numerik ϕ dan P dapat ditentukan untuk semua titik dalam daerah Ω.
3
Solusi fundamental
Persamaan integral batas yang disebutkan pada Pasal 2 melibatkan suatu fungsi solusi fundamental ϕ∗ yang didefinisikan sebagai
λij
∂2ϕ∗ ∂xi∂xj
+ k2ϕ∗ = δ(x− ξ) (2) dimana ξ = (ξ1, ξ2) dan δ adalah fungsi delta Dirac. Solusi fundamental ϕ∗ ini dapat
dituliskan sebagai berikut (lihat Azis [2] untuk penurunan ϕ∗)
ϕ∗(x, ξ) = ℜ ( ıK 4 H (2) 0 (ωR) ) (3)
dimanaℜ melambangkan bagian real dari bilangan (kompleks) argumen ı = √−1 K = ρ/D¨ D = [λ11+ λ12(ρ + ρ) + λ22ρρ]/2 ω = |k|/√D R = √(x1+ ˙ρx2− ξ1− ˙ρξ2)2+ ( ¨ρx2− ¨ρξ2)2 ˙
ρ dan ¨ρ berturut-turut merupakan bagian real dan imajiner positif dari akar kompleks ρ dari persamaan kuadrat
λ11+ 2λ12ρ + λ22ρ2 = 0
dan H0(2) adalah fungsi Hankel jenis kedua orde nol, serta tanda bar (¯.) melambangkan operasi konjugat untuk bilangan kompleks.
Selain ϕ∗ kita juga memerlukan fungsi P∗, yang didefinisikan sebagai
P∗(x, ξ)≡ λij
∂ϕ∗(x, ξ)
∂xi
nj(x)
untuk evaluasi persamaan integral batas tersebut di atas. Fungsi P∗ ini dapat dit-uliskan sebagai P∗ =ℜ ( −ıKω 4 λij ∂R ∂xi nj H (2) 1 (ωR) ) (4)
dimana H1(2) adalah fungsi Hankel jenis kedua orde satu, dan ∂xi∂R diberikan oleh
∂R ∂x1 = 1 R(x1+ ˙ρx2 − ξ1− ˙ρξ2) ∂R ∂x2 = 1 R[ ˙ρ(x1+ ˙ρx2− ξ1− ˙ρξ2) + ¨ρ(¨ρx2− ¨ρξ2)]
Perlu dicatat bahwa P∗ memiliki titik singular pada x = ξ.
4
Persamaan integral batas
Bila (1) diperkalikan dengan ϕ∗ lalu diintegralkan, maka ∫ Ω λij ∂2ϕ ∂xi∂xj ϕ∗dΩ + ∫ Ω k2ϕϕ∗dΩ = 0 (5)
Dengan menggunakan Teorema Divergensi Gauss pada integral pertama dalam per-samaan (5) kita akan memperoleh
∫ Γ λij ∂ϕ ∂xi njϕ∗dΓ− ∫ Ω λij ∂ϕ ∂xi ∂ϕ∗ ∂xj dΩ + ∫ Ω k2ϕϕ∗dΩ = 0 (6)
Penggunaan Teorema Divergensi Gauss sekali lagi pada integral kedua dalam per-samaan (6) akan menghasilkan
∫ Γ ( λij ∂ϕ ∂xi njϕ∗ − ϕ λij ∂ϕ∗ ∂xi nj ) dΓ + ∫ Ω ( λij ∂2ϕ∗ ∂xi∂xj + k2ϕ∗ ) ϕ dΩ = 0 atau ∫ Ω ( λij ∂2ϕ∗ ∂xi∂xj + k2ϕ∗ ) ϕ dΩ =− ∫ Γ (P ϕ∗− P∗ϕ) dΓ (7)
Sebagai salah satu sifat dari fungsi delta Dirac, persamaan berikut berlaku ∫
Ω
ϕ(x) δ(x− ξ) dΩ(x) = η(ξ) ϕ(ξ) (8)
dimana η = 12 bila ξ berada pada batas domain Γ dan Γ mempunyai kemiringan yang berubah secara kontinyu pada ξ, η = 1 bila ξ berada di dalam domain Ω, η = 0 bila ξ berada di luar domain Ω.
Substitusi persamaan (2) ke dalam persamaan (7) dan penggunaan persamaan (8) memberikan
η(ξ) ϕ(ξ) =
∫
Γ
[P∗(x, ξ) ϕ(x)− P (x) ϕ∗(x, ξ)] dΓ(x) (9) Persamaan (9) dapat digunakan untuk menentukan solusi ϕ dan P di setiap titik x di batas Γ dan di dalam domain Ω. Dan kalkulasi solusi ini sepenuhnya hanya memer-lukan kalkulasi integral batas pada ruas kanan persamaan (9). Tetapi secara umum integral batas ini tidak mudah dikalkulasi secara analitik, karena bentuk geometri dari Γ tidak beraturan atau kelakuan dari fungsi ϕ dan P sangat bervariasi. Untuk itu, nilai integral batas ini lalu diapproksimasi dengan cara memenggal-menggal batas domain Γ menjadi segmen-segmen kecil berupa garis lurus dan kelakuan dari fungsi ϕ dan P pada setiap segmen juga didekati dengan mengasumsikan bahwa fungsi-fungsi ini kon-stan, atau bervariasi secara linear, kuadratik dan seterusnya. Lalu integral dihitung untuk setiap segmen dan kemudian menjumlahkannya. Dengan kata lain batas domain Γ diapproksimasi oleh suatu poligon yang jumlah sisinya diambil sebanyak mungkin sehingga nilai pendekatan akurat dapat diperoleh.
5
Diskritisasi
Misalkan batas domain Γ didekati oleh suatu poligon dengan sejumlah J sisi, sehingga Γ terdiri atas segmen-segmen garis lurus Γj ≡ [qj−1, qj], j = 1, 2, . . . , J dimana qj−1
dan qj adalah titik-titik ujung awal dan akhir dari segmen Γj, maka persamaan (9)
dapat ditulis sebagai
η(ξ) ϕ(ξ) = J ∑ j=1 ∫ Γj [P∗(x, ξ) ϕ(x)− P (x) ϕ∗(x, ξ)] dΓ(x) (10) Selanjutnya, bila kita mengasumsikan bahwa pada setiap segmen Γj nilai ϕ dan P
dari segmen tertentu Γj, maka persamaan (10) dapat ditulis sebagai η(ξ) ϕ(ξ) = J ∑ j=1 [ ϕ(qj) ∫ qj qj−1 P∗(x, ξ) dΓ(x)− P (qj) ∫ qj qj−1 ϕ∗(x, ξ) dΓ(x) ] (11)
Hasil penelitian telah menunjukkan bahwa pengambilan nilai ϕ dan P pada titik-tengah
qj untuk setiap segmen Γj menghasilkan keakuratan maksimal.
Sebagaimana disebutkan pada Pasal 2, pada suatu segmen Γj hanya salah satu dari
ϕ dan P diketahui. Bila nilai ϕ(qj) diberikan maka nilai P (qj) menjadi unknown di Γj. Sebaliknya, bila pada segmen Γj nilai P (qj) diberikan maka nilai ϕ(qj) menjadi
unknown.
Untuk penentuan nilai unknown di batas domain Γ, hanya ada dua kemungkinan pengambilan posisi titik ξ, yakni diletakkan di batas domain Γ (yang mengimplikasikan bahwa η = 1
2) atau di luar domain Ω (mengimplikasikan η = 0). Kita tidak dapat
meletakkan ξ di dalam domain Ω (untuk mana η = 1) untuk penentuan nilai unknown di batas domain Γ, kecuali bila kita mempunyai informasi tambahan mengenai nilai ϕ di titik dalam ξ ini. Sementara itu, peletakan titik ξ di luar domain Ω akan menghindari titik singular dari P di x = ξ dan hal ini tentu akan memiliki advantage untuk hasil evaluasi integral. Dan telah ada beberapa kajian di dalam beberapa paper yang telah terpublish, yang memakai analisis peletakan titik ξ di luar domain Ω. Umumnya kajian-kajian ini telah berhasil menentukan jarak ideal dari titik ξ ke batas domain Γ untuk tingkat keakuratan yang cukup bagus. Namun penentuan jarak optimal ini masih sebatas cara coba-coba (trial and error), dan belum dilandasi oleh dan belum dibuktikan keabsahannya secara analitik matematik.
Untuk itu, pada tulisan ini kita akan memposisikan titik ξ pada batas domain Γ. Sehingga untuk penentuan nilai unknown di batas domain Γ, nilai ϕ(ξ) pada ruas kiri (11) akan mengambil nilai ϕ(ql) dan η(ξ) = 12. Persamaan (11) kemudian dapat dituliskan sebagai 1 2 ϕ(ql) = J ∑ j=1 [ ϕ(qj) ∫ qj qj−1 P∗(x, ql) dΓ(x)− P (qj) ∫ qj qj−1 ϕ∗(x, ql) dΓ(x) ] (12)
untuk l = 1, 2, . . . , J . Persamaan ini dapat dituliskan dalam bentuk matriks
−1 2 ϕl+ J ∑ j=1 b Hlj ϕj = J ∑ j=1 Glj Pj (13) dimana ϕj = ϕ(qj), Pj = P (qj), dan b Hlj = ∫ qj qj−1 P∗(x, ql) dΓ(x) (14) Glj = ∫ qj qj−1 ϕ∗(x, ql) dΓ(x) (15)
Evaluasi integral pada persamaan (14) dan (15) dapat dilakukan secara analitik maupun numerik. Tentunya evaluasi analitik (eksak) akan memberikan hasil yang
lebih memuaskan (akurat) daripada evaluasi numerik (pendekatan). Namun perlu diperhatikan bahwa untuk j = l selang integral dalam (14) memuat titik singular ql dari integran P∗(x, ql). Untuk itu nilai prinsipal Cauchy (Cauchy principal value) dari integral ini biasanya diambil untuk evaluasi analitik. Di lain hal, dangan evaluasi numerik dari kedua integral ini, strategi pemilihan metode kuadratur (pengintegralan numerik) sangatlah penting, sebab terdapat beberapa metode kuadratur yang meli-batkan dan ada pula yang tidak melimeli-batkan (misalnya aturan trapezoidal) kalkulasi nilai fungsi integran pada titik tengah dari selang integral. Dan metode kuadratur yang terakhir inilah yang dikehendaki. Pada tulisan ini, untuk hasil numerik dari se-tiap contoh masalah yang akan dibicarakan pada Pasal 6, evaluasi integral dilakukan secara numerik dengan menggunakan aturan trapezoidal termodifikasi enam titik (lihat Abramowitz and Stegun [1]).
Nilai fungsi-fungsi Hankel H0(2) dan H1(2) yang terlibat dalam solusi fundamen-tal ϕ∗ dan P∗ dihitung dengan menggunakan pendekatan polinomial fungsinya (lihat Abramowitz and Stegun [1]).
Lebih kompak, persamaan (13) dapat ditulis sebagai
J ∑ j=1 Hlj ϕj = J ∑ j=1 Glj Pj (16) dimana Hlj = { b Hlj bila l ̸= j b Hlj − 12 bila l = j
Persamaan matriks (16) dapat diurutkan ulang dengan meletakkan unknown di ruas kiri dan known-nya di ruas kanan, dalam bentuk
AX = B (17)
dimana X adalah vektor unknown ϕ dan/atau P . Persamaan ini merupakan suatu sistem persamaan aljabar linear dengan J persamaan dan J unknown. Penyelesian sistem persamaan aljabar linear (17) dapat dilakukan dengan berbagai metode, antara lain dengan metode eliminasi Gauss. Namun, pada tulisan ini, untuk hasil numerik dari setiap contoh masalah yang akan dibicarakan pada Pasal 6, solusi sistem per-samaan aljabar linear (17) ditentukan dengan menggunakan metode gradien konjugat (lihat Coleman [3]), yang secara empiris telah diketahui lebih stabil ketimbang metode
eliminasi Gauss.
Solusi dari persamaan (17) ini dapat ditentukan untuk unknown ϕ dan P di batas domain Γ. Sekali nilai ϕ dan P pada batas domain Γ telah diketahui, maka kita bisa menentukan nilai ϕ dan P pada sebarang titik dalam ξ dengan menggunakan persamaan (11), yakni ϕ(ξ) = J ∑ j=1 [ ϕ(qj) ∫ qj qj−1 P∗(x, ξ) dΓ(x)− P (qj) ∫ qj qj−1 ϕ∗(x, ξ) dΓ(x) ] (18)
Selain itu dapat pula ditentukan nilai turunan ∂ϕ/∂ξ1 dan ∂ϕ/∂ξ2 melalui persamaan berikut ∂ϕ ∂ξ1 (ξ) = J ∑ j=1 [ ϕ(qj) ∫ qj qj−1 ∂P∗(x, ξ) ∂ξ1 dΓ(x)− P (qj) ∫ qj qj−1 ∂ϕ∗(x, ξ) ∂ξ1 dΓ(x) ] (19) ∂ϕ ∂ξ2 (ξ) = J ∑ j=1 [ ϕ(qj) ∫ qj qj−1 ∂P∗(x, ξ) ∂ξ2 dΓ(x)− P (qj) ∫ qj qj−1 ∂ϕ∗(x, ξ) ∂ξ2 dΓ(x) ] (20)
6
Hasil numerik
Pada pasal ini beberapa contoh masalah nilai batas yang dibangun oleh persamaan (1) akan diselesaikan secara numerik.
Contoh 1 : Masalah Uji
Perhatikan solusi analitik untuk (1) berikut
ϕ = sin βx2 (21)
dimana β = k/√λ22. Geometri medium dan syarat batas dari masalahnya adalah
(lihat Gambar 1)
P, yang dapat dihitung dari (21), diketahui pada AB, BC dan CD, ϕ, seperti diberikan oleh (21), diketahui pada AD.
Kofisien λij dan k2 adalah
λ11 = 1, λ12= 0.5, λ22= 0.5,
k2 = 0.5.
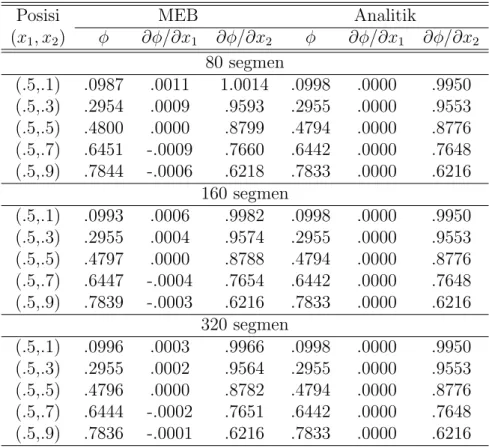
Tabel 1 memperlihatkan perbandingan antara solusi MEB dan solusi analitik. Da-pat diamati bahwa solusi MEB konvergen ke solusi analitik sejalan dengan meningkat-nya jumlah segmen dari 80, 160 dan 320. Hasil ini sesuai dengan yang diharapkan, dengan alasan bahwa semakin kecil selang integral yang digunakan maka semakin aku-rat pendekatan integrasi numerik yang akan diperoleh.
Contoh 2
Perhatikan masalah nilai batas seperti diperlihatkan dalam Gambar 2. Kofisien λij
dan k2 adalah
λ11 = 0.5, λ12 = 0.2, λ22= 0.3,
k2 = 0.1.
Tidak tersedia solusi analitik sederhana untuk contoh masalah ini. Justifikasi solusi MEB dilakukan dengan cara mengamati kekonvergenannya.
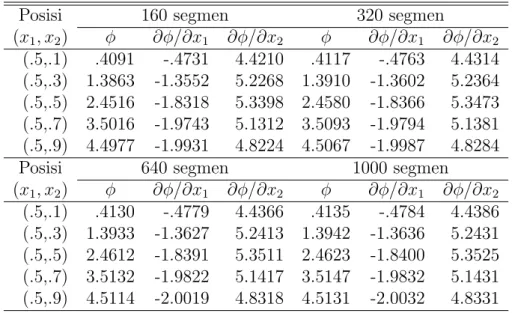
Tabel 2 memperlihatkan solusi MEB dengan menggunakan 160, 320, 640 dan 1000 segmen. Dari tabel ini dapat diamati bahwa solusi MEB ini konvergen ke suatu solusi tertentu dengan penambahan jumlah segmen.
-6 x1 x2 D(0, 1) A(0, 0) B(1, 0) C(1, 1)
Gambar 1: Geometri dari masalah uji
Tabel 1: Solusi MEB dan analitik untuk Contoh 1 Posisi MEB Analitik
(x1, x2) ϕ ∂ϕ/∂x1 ∂ϕ/∂x2 ϕ ∂ϕ/∂x1 ∂ϕ/∂x2 80 segmen (.5,.1) .0987 .0011 1.0014 .0998 .0000 .9950 (.5,.3) .2954 .0009 .9593 .2955 .0000 .9553 (.5,.5) .4800 .0000 .8799 .4794 .0000 .8776 (.5,.7) .6451 -.0009 .7660 .6442 .0000 .7648 (.5,.9) .7844 -.0006 .6218 .7833 .0000 .6216 160 segmen (.5,.1) .0993 .0006 .9982 .0998 .0000 .9950 (.5,.3) .2955 .0004 .9574 .2955 .0000 .9553 (.5,.5) .4797 .0000 .8788 .4794 .0000 .8776 (.5,.7) .6447 -.0004 .7654 .6442 .0000 .7648 (.5,.9) .7839 -.0003 .6216 .7833 .0000 .6216 320 segmen (.5,.1) .0996 .0003 .9966 .0998 .0000 .9950 (.5,.3) .2955 .0002 .9564 .2955 .0000 .9553 (.5,.5) .4796 .0000 .8782 .4794 .0000 .8776 (.5,.7) .6444 -.0002 .7651 .6442 .0000 .7648 (.5,.9) .7836 -.0001 .6216 .7833 .0000 .6216
-6 x1 x2 D(0, 1) P = 0 A(0, 0) ϕ = 0 B(1, 0) P = 0 C(1, 1) P = 1
Gambar 2: Geometri untuk Contoh 2
Tabel 2: Solusi MEB untuk Contoh 2 Posisi 160 segmen 320 segmen
(x1, x2) ϕ ∂ϕ/∂x1 ∂ϕ/∂x2 ϕ ∂ϕ/∂x1 ∂ϕ/∂x2 (.5,.1) .4091 -.4731 4.4210 .4117 -.4763 4.4314 (.5,.3) 1.3863 -1.3552 5.2268 1.3910 -1.3602 5.2364 (.5,.5) 2.4516 -1.8318 5.3398 2.4580 -1.8366 5.3473 (.5,.7) 3.5016 -1.9743 5.1312 3.5093 -1.9794 5.1381 (.5,.9) 4.4977 -1.9931 4.8224 4.5067 -1.9987 4.8284 Posisi 640 segmen 1000 segmen
(x1, x2) ϕ ∂ϕ/∂x1 ∂ϕ/∂x2 ϕ ∂ϕ/∂x1 ∂ϕ/∂x2 (.5,.1) .4130 -.4779 4.4366 .4135 -.4784 4.4386 (.5,.3) 1.3933 -1.3627 5.2413 1.3942 -1.3636 5.2431 (.5,.5) 2.4612 -1.8391 5.3511 2.4623 -1.8400 5.3525 (.5,.7) 3.5132 -1.9822 5.1417 3.5147 -1.9832 5.1431 (.5,.9) 4.5114 -2.0019 4.8318 4.5131 -2.0032 4.8331
7
Konklusi
Suatu MEB untuk solusi masalah nilai batas untuk model perambatan gelombang dalam suatu medium anisotropik telah ditemukan. MEB ini secara umum cukup mu-dah untuk diimplementasikan untuk memperoleh solusi numerik untuk masalah ter-tentu. Hasil numerik yang diperoleh dengan menggunakan MEB ini mengindikasikan bahwa MEB ini dapat menghasilkan solusi numerik yang cukup akurat. Evaluasi inte-gral secara analitik, penerapan proses refinement untuk penyelesaian sistim persamaan aljabar linear, dan strategi peletakan titik ξ di luar domain Ω akan memberikan hasil yang lebih akurat.
References
[1] Abramowitz, M. and Stegun, A. Handbook of Mathematical Functions, Dover, New York, 1970.
[2] Azis, M. I. (2001). On the boundary integral equation method for the solution of
some problems for inhomogeneous media (PhD Thesis), Department of Applied
Mathematics, University of Adelaide.
[3] Coleman, C. J. University of Wollonggong, Australia.
[4] Wu, T. W. (editor) Boundary Element Acoustics Fundamentals and Computer