3.
PRINSIP ENERGI DAN MOMENTUM DALAM ALIRAN
SALURAN TERBUKA
ENERGI DALAM ALIRAN SALURAN TERBUKA
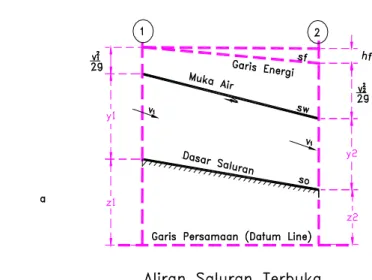
Gambar 3.1. Aliran Dalam Saluran Terbuka
Garis energi : garis yang menyatakan ketinggian dari jumlah tinggi aliran. Kemiringan garis energi = gradien energi (energy gradien) = sf
Kemiringan muka air = sw Kemiringan dasar saluran = so
Untuk aliran seragam (uniform flow), sf = sw = so (dasar saluran sejajar muka air dan sejajar kemiringan garis energi).
Jumlah tinggi energi pada penampang 1 di hulu akan sama dengan jumlah tinggi energi pada penampang 2 di hilir, hal ini dinyatakan dengan :
hf g v y z g v y z + + = + + + 2 2 2 2 2 2 1 1 1 1 α α
Jika α1= α2=1 dan hf=0 maka persamaan di atas menjadi :
tan 2 2 2 2 2 1 1 1 kons g v y z g v y z + + = + + = (1)
Persamaan di atas dikenal sebagai persamaan Bernoulli.
Pusat Pengembangan Bahan Ajar - UMB Ir. Agus Suroso MT
ENERGI SPESIFIK
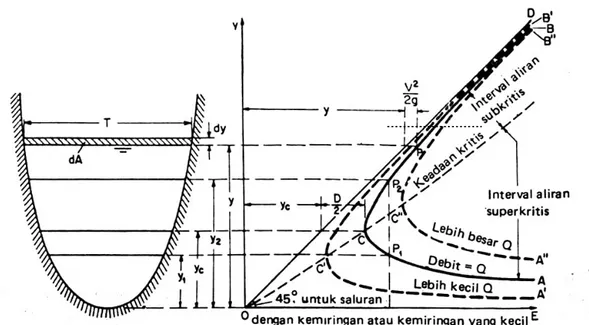
Gambar 3.2. Kurva Energi Spesifik Dalam Saluran Terbuka
Untuk saluran dengan kemiringan dasar kecil dan α=1 ( koefisien energi =1), Energi Spesifik adalah jumlah kedalaman air ditambah tinggi kecepatan, atau :
g v y E 2 2 + = atau 2 2 2gA Q y E= + (2)
Kurva energi spesifik untuk harga E tertentu mempunyai 2 kemungkinan kedalaman yaitu y1 dan y2.
Jika persamaan (2) diturunkan terhadap y (didiferensialkan) dengan Q konstan, maka:
dy dA gA Q dy dE 3 2 1−
= mengingat bahwa dA=A.dy atau T dy dA = maka : T gA Q dy dE . 1 3 2 − = atau T gA v dy dE . 1 2 − = Mengingat bahwa T A D= maka: gD v dy dE 2 1− =
KRITERIA ALIRAN KRITIS
Pada kondisi aliran kritis, energi spesifik adalah minimum atau =0
dy dE
sehingga persamaan di atas menjadi :
0 1 2 = − = gD v dy dE atau 1=gDv2 atau D g v = 2 atau 2vg2 =D2
Pusat Pengembangan Bahan Ajar - UMB Ir. Agus Suroso MT
(Ini berarti pada kondisi aliran kritis, tinggi kecepatan sama dengan dri kedalaman hidrauliknya.)
bisa juga persamaan di atas menjadi : T gA Q dy dE . 1 3 2 − = T gA Q . 1 0 3 2 − = atau 3 2 . . 1 A g T Q = (3) atau 1 vg..AT 2 = atau 1 gv.D 2 =
Bilangan Froude F dinyatakan sebagai F = gDv pada kondisi kritis, nilai F=1. Kriteria aliran kritis adalah sebagai berikut :
- Aliran sejajar atau berubah lambat laun.
- Kemiringan saluran adalah kecil.
- Koefisien energi dianggap sama dengan 1. Kedalaman Kritis Untuk Penampang Saluran Segi empat :
Pada kondisi kritis berlaku persamaan 1 . . 3 2 = A g T Q Atau 1 ) . .( . 3 3 2 = c y B g B Q , jika q B Q =
(debit per satuan lebar)
maka: 1 ) . .( . 3 2 2 = c y B g Q atau 1 . . 3 2 = c y g q atau 3 2 . c y g q = sehingga : g q yc 2 3 = (4)
Pada kondisi kritis, E=Ec dan y=yc sehingga :
g v y E c c c 2 2 + =
Pusat Pengembangan Bahan Ajar - UMB Ir. Agus Suroso MT
MEKANIKA FLUIDA DAN HIDROLIKA B
g y q y c c 2 ) / ( 2 + = 2 2 2 c c gy q y + =
diketahui sebelumnya bahwa :
c c v y B Av Q = =( . ). c c v y B Q . = c c v y q = . atau c c v y q = 2 2 2 c c gy q y + = 2 2 2 c c gy q y + = g q y y c c 2 2 2 1 +
= ingat bahwa : q2 = g.yc3 atau 3 2 c y g q = 3 2 2 1 c c c y y y + = 2 3 2 c c c y y y + = 2 c c y y + = c y 5 . 1 =
Kedalaman Kritis Untuk Penampang Saluran Segi empat : Pada kondisi kritis berlaku persamaan
1 . . 3 2 = A g T Q
Sebelumnya didata dulu unsure-unsur geometris dari penampang trapezium seperti :
2 my By A= + my B T = +2 sehingga : 1 ) .( ) 2 .( 3 2 2 = + + my By g my B Q (5)
Pusat Pengembangan Bahan Ajar - UMB Ir. Agus Suroso MT
dalam hal ini y adalah kedalaman kritis (yc), sehingga untuk mendapatkan nilai yc
dilakukan dengan cara coba-coba (trial and error). Contoh Soal :
Suatu saluran berpenampang trapezium spt gambar, debit yang mengalir Q=6 m3/dt. Pertanyaan :
a. Berapakah kedalaman kritisnya (yc)? b. Berapakah penampang kritisnya (Ac)? c. Berapakah kecepatan kritisnya (vc)?
d. Jika kedalaman aliran yang terjadi (y) sama dengan 1.10 m, bagaimana kondisi alirannya?
e. Gambarkan kurva energi spesifiknya dan berapakah energi spesifik minimumnya. Jawab :
A=By+my2 = 2y+0.5y2
P=B+2yw(1+m2) = 2+2yw(1+0.5)
T=B+2my = 2+2(0.5)y = 2+y
a. Aliran berada dalam kondisi kritis jika : 1 . . 3 2 = A g T Q , sehingga:
Table perhitungan untuk mencari yc
y (2+y) (2y+0.5y2)3 A/B Keterangan
(A) (B)
1 (2+1)=3 {2(1)+0.5(1)2}3=15.625 3/15.625=0.705 ≠ 0.273 2 (2+2)=4 {2(2)+0.5(2)2}3=216 4/216=0.019 ≠ 0.273 0.9 (2+0.9)=2.9 {2(0.9)+0.5(0.9)2}3=10.72 2.9/10.72=0.271 ≠ 0.273
0.273 Ada diantara ini 0.8 (2+0.8)=2.8 {2(0.8)+0.5(0.8)2}3=7.078 2.8/7.078=0.396 ≠ 0.273
Harga yc yang dicari berada diantara 0.9 dan 0.8, untuk itu dicari dengan interpolasi linier seperti berikut:
Pusat Pengembangan Bahan Ajar - UMB Ir. Agus Suroso MT
MEKANIKA FLUIDA DAN HIDROLIKA
m=0.5 B=2 m yc 1 62(2+Y) 9.81(2Y+0.5Y2)3 = 1 (2+Y) (2Y+0.5Y2)3 = 9.81 36 (2+Y) (2Y+0.5Y2)3 =0.273
y yang dicari dalam soal ini adalah ykritis (yc). Diselesaikan dengan cara coba-coba menggunakan tabel perhitungan.
0.9 0.271 yc 0.273 0.8 0.396
Yc =
Yc = 0.898 m
b. Ac = 2 yc + 0.5 yc2 = 2 (0.898) + 0.5 (0.898)2 = 2.20 m2
c. Vc = Q/Ac = 6 / 2.20 = 2.73 m/dt
d. Jika y = 1.10 m, maka : y > yc (0.898) kondisi aliran sub kritis. Bisa juga dicek dgn bilangan Froude : F =
Untuk y = 1.10 m , A = 2 (1.1)+ 0.5(1.1)2 = 2.905 m2
T= 2 + 2 (0.5) (1.10) = 3.10 m D = A/T = 2.805/3.10 = 0.905 m
V = Q/A = 6/2.805 = 2.14 m/dt v < v kritis aliran sub kritis. F =
Karena F < 1, maka aliran tergolong sub kritis. e. Energi spesifik E = y + A = 2 y + 0.5 y2 y A A2 Q2/(2gA2) E = y + Q2/(2gA2) 0.2 0.42 0.18 10.40 10.60 0.4 0.88 0.77 2.37 2.77 0.6 1.38 1.90 0.96 1.56 0.8 1.92 3.69 0.49 1.29 1.0 2.5 6.25 0.294 1.294 1.2 3.12 9.73 0.188 1.388 1.4 3.78 14.29 0.128 1.528
Pusat Pengembangan Bahan Ajar - UMB Ir. Agus Suroso MT
MEKANIKA FLUIDA DAN HIDROLIKA 0.273 - 0.271 yc - 0.9 = 0.396 - 0.2710.8 - 0.9 0.002 yc - 0.9 = -1.25 - 0.002 1.25 + 0.9 V √(gD) V √(gD) 2.14 √(9.81 (0.905) = = 0.718 V2 2g = y + Q 2 2gA2
Hubungan y ~ Energi Spesifik
0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2 2.2 2.4 2.6 2.8 3 Energi Spesifik y
Gejala Lokal (Local Phenomenon)
Perubahan dari kondisi aliran sub kritis ke aliran super kritis atau dari super kritis ke sub kritis pada jarak yang pendek dikenal sebagai gejala local (local phenomenon). Gejala local yang sering dijumpai adalah :
- Penurunan Hidraulik (hydraulic drop) berupa loncatan bebas (free overfall)
- Loncatan Hydraulic (Hydraulic jump)
Penurunan Hidraulik (hydraulic drop)
Contoh Penurunan hidraulik salah satunya adalah Loncatan bebas (free overfall) seperti diungkapkan pada gambar berikut :
Pusat Pengembangan Bahan Ajar - UMB Ir. Agus Suroso MT
MEKANIKA FLUIDA DAN HIDROLIKA
E min=1.286 yc=0.832
Gambar 3.3. Loncatan Bebas ditafsirkan dari lengkung energi spesifik Sumber : Hidrolika Saluran Terbuka
Beberapa hal mengenai loncatan bebas (free overfall):
- Terjadi akibat dasar saluran tiba-tiba terputus (terjadi terjunan).
- Aliran berubah dari kondisi sub kritis menjadi super kritis dalam jarak pendek.
- Pada saluran dengan kemiringan kecil, kedalaman kritisnya adalah 1.4 kali kedalaman di tepi (yc =1.4yo).
- Letak kedalaman kritis berada 3 yc hingga 4 yc dari tepi terjunan.
Loncatan hidraulik (Hydraulic jump)
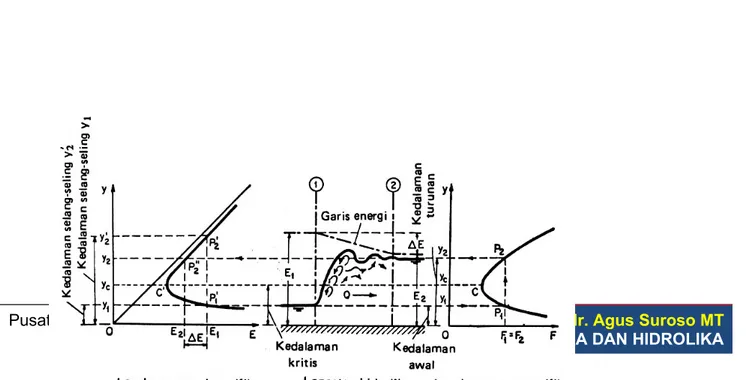
Beberapa hal mengenai loncatan hidraulik (Hydraulic jump):
- Aliran berubah dari kondisi super kritis menjadi sub kritis dalam jarak pendek.
- Kedalaman aliran sebelum loncatan dinamakan sebagai kedalaman awal (initial depth) y1.
- Kedalaman aliran sesudah loncatan dinamakan sebagai kedalaman turunan (sequent depth) y2.
- Kedalaman awal (initial depth) dan kedalaman turunan (sequent depth tidak sama dengan kedalaman selang-seling (alternate depth).
Pusat Pengembangan Bahan Ajar - UMB Ir. Agus Suroso MT
Gambar 3.4. Penafsiran loncatan hidrolik dari lengkung energi dan gaya spesifik Sumber : Hidrolika Saluran Terbuka
Contoh soal :
Saluran dengan penampang segi empat, lebar menyempit dari 3 m ke 2.4 m sepanjang 15 m. Debit Q yang mengalir 2.83 m3/dt, kedalaman aliran di hulu 1.5 m, gesekan di daerah penyempitan diabaikan dan tanpa terjadi penurunan hidraulik.
Pertanyaan :
a. Berapa energi spesifik total yang terjadi? b. Berapa kedalaman air di daerah penyempitan? c. Bagaimana kondisi aliran?
Jawab :
Pusat Pengembangan Bahan Ajar - UMB Ir. Agus Suroso MT
MEKANIKA FLUIDA DAN HIDROLIKA 2.4 m 3 m 15 m Tampak atas E=1.52 0.02 Y ? 0.035 Pot. memanjang = y + Q2 2gA2
a. Energi spesifik total E
= 1.5 + = 1.52 m
(Energi spesifik ini dianggap konstan sepanjang tempat penyempitan karena kehilangan energi diabaikan. Sehingga garis energi berupa garis lurus). b. Kedalaman selang seling (alternate depth) dihitung dengan persamaan :
E = y + 1.52 = y +
untuk lebar B = 3 m, maka akan didapat 2 nilai y : y1 = 0.184 m kedalaman selang-seling
y2 = 1.50 m kedalaman aliran
untuk lebar B = 2.4 m, maka akan didapat 2 nilai y : y1 = 0.234 m kedalaman selang-seling
y2 = 1.485 m kedalaman aliran ( kedlm. di penyempitan)
c. Bilangan Froude di hulu F =
= 0.16 F < 1 , kondisi aliran sub kritis. Bilangan Froude di hilir F =
= 0.21 F < 1 , kondisi aliran sub kritis
Jika direncanakan muka air hilir terjadi penurunan hidraulik lambat laun pada daerah penyempitan, maka :
d. Berapa kedalaman kritisnya ? e. Berapa kecepatan kritisnya?
f. Berapa lebar penampang kritisnya (B) ?
Pusat Pengembangan Bahan Ajar - UMB Ir. Agus Suroso MT
MEKANIKA FLUIDA DAN HIDROLIKA Q2 2gA2 2.832 2(9.81)(B.y)2 2.83/(3x1.5) √(9.81 (1.5) 2.83/(2.4x1.485) √(9.81 (1.485) 2.4 m 3 m 15 m Tampak atas B ? 2.832 2. (9.81)(1.5 x 3)2
Jawab :
d. Pada kondisi aliran kritis energi spesifik Ec dan kedalaman kritis adalah yc, Ec = yc + (vc2/2g) = yc + {(q/yc)2/2g} = yc + q2/(2gy c2) = yc + (1/2yc2) (q2/g) = yc + (1/2yc2). yc3 = yc + (1/2yc) = 1.5 yC yc = Ec/1.5 =1.52/1.5 = 1.01 m
e. Pada kondisi aliran kritis, F = 1 F = vc/√(gyc) = 1 maka vc = √(gyc)
kecepatan kritis vc = √(9.81x 1.01) = 3.15 m/dt
f. Lebar penampang kritis B :
Bc = Q / (yc vc) = 2.83 / ( 1.01 x 3.15) = 0.89 m
Kecepatan di hilir v = Q/A = 2.83 /(2.4 x 0.234 ) = 5. 04 m/dt.
Kondisi aliran di hilir F = v / (g yc) = 5.04/√(9.81 x 0.234) = 3.33 > 1,
Karena F >1, maka kondisi aliran subkritis.
MOMENTUM DALAM ALIRAN SALURAN TERBUKA
Pusat Pengembangan Bahan Ajar - UMB Ir. Agus Suroso MT
MEKANIKA FLUIDA DAN HIDROLIKA Q = A v
= B (yc vc)
Q/B = ycvC
q = yc vc
α
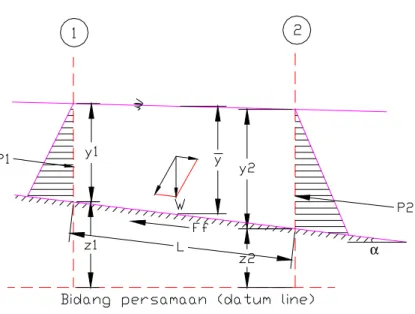
Gambar 3.5. Penerapan Dalil Momentum Pada saluran Terbuka Sumber : Hidrolika Saluran Terbuka
Perubahan momentum per satuan waktu pada aliran diantara penampang (1) dan penampang (2) adalah : (Persamaan Momentum)
Qw/g (β2 v2 – β1 v1 ) = P1 - P2 + Wsinα -Ff
P1 dan P2 = resultan tekanan yang bekerja di sepanjang bidang kontak antara air dan saluran.
W = berat air yang terdapat di antara penampang (1) dan (2). Ff = jumlah gaya luar dari gesekan dan tahanan yang bekerja di
sepanjang bidang kontak antara air dan dasar saluran. w = berat satuan air.
β = koefisien momentum Q = debit aliran
v = kecapatan aliran rata-rata P1 = ½ w b y12
P1 = ½ w b y22
Ff = whf’bỹ
Dengan memasukkan besaran di atas, persamaan momentum bias ditulis sebagai : z1 + y1 + β1 (v12/2g) = z2 + y2 + β2 (v22/2g) +hf’
Pusat Pengembangan Bahan Ajar - UMB Ir. Agus Suroso MT
MEKANIKA FLUIDA DAN HIDROLIKA Q = ½(v1+v2)bỹ
W = wbỹL