Institut Teknologi Sepuluh Nopember Surabaya PERS. DIFERENSIAL

Institut Teknologi Sepuluh Nopember Surabaya

PERS. DIFERENSIAL

Aulia Siti Aisjah Teknik Fisika ITS

Pengantar

Materi

Contoh Soal

Latihan

Asesmen

Ringkasan

Definisi

: Persamaan diferensial mengandung fungsi yang belum diketahui Beserta turunannya. 3 2 + = x dx dy 0 3 2 2 = + + ay dx dy dx y d 3 6 4 3 3 = +       + y dx dy dx y d Contoh:.

y variabel dependent dan x variabel

independent, dan contoh di atas merupakan kelas Persamaan Diferensial Biasa.

1 . 2 . 3 .

Persamaan Diferensial Parsial

Contoh: 0 2 2 2 2 =   +   y u x u 0 4 4 4 4 =   +   t u x u t u t u x u   −   =   2 2 2 2

u variabel dependent dan independent, dan contoh di atas merupakan persamaan diferensial parsial.

u variabel dependent dan x dan t variabel-variabel independent

1.

2.

Orde dari Persamaan Diferensial

Orde dari persamaan diferensial adalah orde dari turunan tertinggi. Persamaan Diferensial 3 2 + = x dx dy 0 9 3 2 2 = + + y dx dy dx y d 3 6 4 3 3 = +       + y dx dy dx y d 1 2 3 ORDE

Derajat Turunan

Persamaan Diferensial Derajat Turunan

0 3 2 2 = + + ay dx dy dx y d 3 6 4 3 3 = +       + y dx dy dx y d 0 3 5 3 2 2 = +       +       dx dy dx y d 2 3 2

Persamaan Diferensial Linier

Persamaan diferensial adalah linier, jika

1. variabel dependent tunggal (tidak ada perkalian antara variabel dependent),

2. koefisien tidak bergantung dari variabel dependent.

Example: 3 6 4 3 3 = +       + y dx dy dx y d

non - linier karena dalam term keduaterdapat perkalian.

. 0 9 3 2 2 = + + y dx dy dx y d Contoh: linier. 1. 2.

Example: 3 2 2 2 x dx dy y dx y d x + =

non – liniear karena dalam term kedua, koefisien bergantung y.

3.

Example:

non – linier karena sbb; y dx dy sin = − + − = ! 3 sin 3 y y

y adalah non – linier

Persamaan Diferensial Orde 1

2. Bentuk diferensial:

(

1

.

+

x

)

dy

−

ydx

=

0

. 0 ) , , ( = dx dy y x f ) , (x y f dx dy = 3. Bentuk umum: atau 1. Bentuk turunan:

( )

a

( )

x y g

( )

x dx dy x a₁ + ₀ =

Persamaan diferensial biasa orde -n

1. Dengan koefisien konstan.

( )

x g y a dx dy a dx y d a dx y d a dx y d a n n n n n n + − + + + + = − − ₂ 1 0 2 2 1 1 1 ....

2. Dengan koefisien variabel

( )

( )

( )

( )

a

( )

x y g

( )

x dx dy x a dx y d x a dx y d x a dx dy x a _n n n n + + + + + = − − ₂ 1 0 2 2 1 1 ...

Penyelesaian PD secara

Analitis

y=3x+c, adalah penyelesaian dari persamaan diferensial orde 1 dengan c₁ konstanta sembarang. Nilai c₁ bergantung dari kondisi

batas sehingga solusi tersebut merupakan solusi umum.

3 = dx dy Contoh Contoh ( ) ( )  = sin  = −cos + y x y x C  = +   = 2 + +  = 3 + + + 1 1 2 6 ex 3 ex ex y x y x C y x C x C

Amati bahwa penyelesaian dari orde 1 mempunyai 1 parameter, sementara pada

Kelas-Kelas Penyelesaian

9yy ' 4+ x = 0 ( + ) =  + =



9yy ' 4x dx C1



9 ( ) '( )y x y x dx



4xdx C1 + = = 2 2 1

Ini menghasilkan dengan .

4 9 18 C y x C C Contoh Solusi

Solusi berada pada kelas elips.





+ 2 =  2 + 2 =  2 + 2 = 1 1 1 9 9 2 2 9 4 2 2 y ydy x C x C y x C

Amati bahwa pada setiap titik (x₀,y₀), ada solusi unik dari persamaan di atas dimana kurvanya melewati titik yang ditentukan tersebut.

Penyelesaian berasal dari

2 1x c c y = + 0 2 2 = dx y d

1. Untuk kelas garis lurus

persamaan diferensialnya adalah

.

2. Untuk kelas-kelas kurva

2

2

x

ce

y = persamaan diferensialnya adalah xy

dx dy = A. B. x x

e

c

e

c

y

=

₁ 2

+

₂ −3

persamaan diferensialnya adalah ₂ 6 0

2 = − + y dx dy dx y d

Aplikasi di dalam Ilmu Fisika

1. Gerak jatuh bebas

g dt s d _{= −} 2 2

dimana s adalah jarak atau tinggi dan g percepatan gravitasi.

2. Gerak pegas ky dt y d m ₂ = − 2

Dimana y adalah posisi, m adalah massa dan k konstanta pegas

3. RLC – circuit, Hukum kedua Kirchoff

E q c dt dq R dt q d L ₂ + + 1 = 2 q muatan kapacitor, L induktansi, c kapasitansi. R resistansi E tegangan

Aplikasi

dy

y

dt

=



1.Newton’s Law of Cooling

(

)

s T T dt dT _{=  −} dimana dt dT

adalah laju pendinginan,

s

T

T − adalah perbedaan suhu antara liquid ‘T’

dan lingkungan Ts

2. Pertumbuhan dan peluruhan

Tugas 1 – minggu ke 9:

CP: Mampu menjelaskan beberapa aplikasi bentuk PD dalam permasalahan bidang sains dan Teknik

1. Searching dalam bidang keilmuan Teknik Fisika, untuk aplikasi dari

beberapa model PD, dengan melalui www.sciencedirect atau yang lain, yang menunjukkan sumber terpercaya bahwa PD diaplikasikan, minimal 5 buah jurnal.

2. Tuliskan ulang bentuk PD yang ada di dalam 5 jurnal tersebut, dan

identifikasi masing-masing dari PD, merupakan bentuk PD linier / non liner dan berapa orde PD.

3. Tugas diketik di dalam word, beri identitas Anda.

Institut Teknologi Sepuluh Nopember Surabaya

PERS. DIFERENSIAL

Aulia Siti Aisjah Teknik Fisika ITS

Pengantar

Materi

Contoh Soal

Latihan

Asesmen

Ringkasan

Metode Numerik

Penyelsaian PD

Persamaan Diferensial Separable

Persamaan diferensial separable dapat didefinisikan sebagai perkalian antara fungsi x dan fungsi y.

( ) ( )

dy g x h y dx =  Contoh: 2 2 dy xy dx =

Kalikan kedua sisi dengan dx dan bagi kedua sisi dengan y2 untuk memisahkan variable - variabel nya (Syarat y2 bukan nol) 2 2 dy x dx y = 2 2 y dy− = x dx

( )

0 h y 

2 2 dy xy dx = 2 2 dy x dx y = 2 2 y dy− = x dx 2 2 y dy− = x dx





1 2 1 2 y− C x C − + = + 2 1 x C y − = + 2 1 y x C − = + 2 1 y x C = − + → Gabungan konstanta integrasi

C x y xdx ydy y x dx dy + = = =





2 2

Solusi Umum Persamaan Diferensial

Contoh

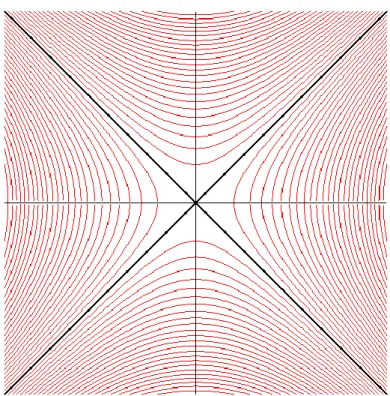
Gambar disamping adalah visualisasi dari solusi persamaan diferensial di atas. Garis lurus

y = x and y = -x

adalah solusi khusus. Solusi yang unik melalui setiap titik yang

berbeda. Adapun solusi khusus

Kondisi Awal

• Di dalam persoalan fisis, kita perlu untuk menentukan solusi khusus yang memenuhi kondisi awal y(x₀)=y₀. Masalah solusi persamaan diferensial yang memenuhi kondisi awal disebut initial-value problem (IVP).

• Contoh: Tentukan solusi y2 _{= x}2 _{+ C yang memenuhi}

kondisi awal y(0) = 2. 22 _{= 0}2 _{+ C}

C = 4

Contoh:

(

₂

)

2 2 1 x dy x y e dx = + 2 2 1 2 1 x dy x e dx y = +

x dan y dapat dipisah (separable)

2 2 1 2 1 x dy x e dx y = +





u = x2 2 du = x dx 2 1 1 u dy e du y = +





1 1 2 tan− y C+ = eu + C 2 1 1 2 tan− y + C = ex + C tan−1 y = ex2 +C →

Contoh:

(

₂

)

2 2 1 x dy x y e dx = + 2 1

tan− y = ex +C Dihasilkan y sebagai fungsi implisit dari x.

Dalam kasus di atas, kita dapat menentukan y sebagai fungsi

eksplisit dari x dengan melakukan

operasi tangen pada kedua sisi.

(

)

(

2

)

1

tan tan− y = tan ex + C

(

2

)

tan x

y = e + C

Sebuah populasi secara normal meningkat secara

proporsional terhadap jumlahnya sekarang. Contoh lain yang meningkat atau menurun secara proporsional

dengan jumlahnya diantaranya peluruhan radioaktif dan peningkatan uang dalam rekening bank berbunga.

Jika laju perubahannya proporsional dengan jumlah saat ini, maka perubahannya dapat diekspresikan sbb:

dy

ky

dt

=

→

dy

ky

dt

=

1

dy

k dt

y

=

1

dy

k dt

y

=





ln y

= +

kt

C

Persamaan di samping menunjukkan bahwa perubahannya (ruas kiri) proporsional terhadap jumlah saat ini (ruas kanan).

Bagi kedua sisi dengan y.

Integralkan kedua sisi.

→

ln y kt C

e

=

e

+

C kt

Populasi dalam kenyataannya tidaklah meningkat selamanya. Ada faktor batasan dalam makanan maupun ruang untuk hidup (habitat) Sehingga ada keadaan populasi maksimum, atau carrying capacity, M. Model yang lebih realistis adalah model pertumbuhan logistik dimana laju pertumbuhan proporsional dengan ukuran populasi saat ini (y) dan jumlah dimana y turun dari ukuran maksimum (M-y). Sehingga model tersebut menjadi: ) (M y ky dt dy _{= −}

Model Pertumbuhan Logistik

Dengan solusi sebagai berikut (verify yourself): 0 0 0 0 , dengan (0) ( ) kMt y M y y y y M y e− = = + −

Metode Numerik dalam Peny. PD, didasarkan dari penyelesaian integrasi numerik. Beberapa metode yang ada:

1. Integrasi dengan metode Trapesium

2. Integrasi dengan metode Simpson 1/3; 3/8 dst Dll

Tugas 2:

Cari metode numerik di dalam penyelesaian Integrasi secara numerik selain yang disebutkan dalam 2 di atas, Tuliskan tahapan dalam metode tersebut dalam word

Upload tugas 2, ini paling lambat 12 April 2019, jam 24.00