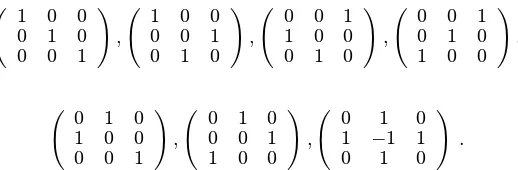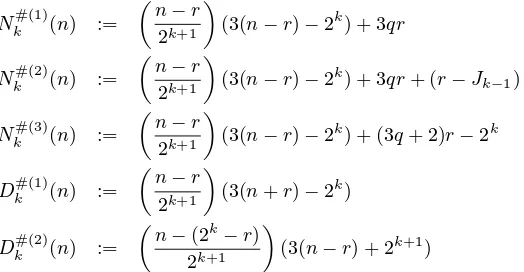23 11
Article 00.2.3
Journal of Integer Sequences, Vol. 3 (2000),
23 6 1 47
Jacobsthal Numbers and Alternating Sign Matrices
Darrin D. Frey and James A. Sellers
Department of Science and Mathematics
Cedarville College
Cedarville, OH 45314
Email addresses:
[email protected]
and
[email protected]
Abstract
Let A(n) denote the number of n×n alternating sign matrices and Jm the mth Jacobsthal number. It is known that
A(n) =
n−1
Y
ℓ=0
(3ℓ+ 1)! (n+ℓ)!.
The values ofA(n)are in general highly composite. The goal of this paper is to prove thatA(n)is odd if and only if nis a Jacobsthal number, thus showing thatA(n)is odd infinitely often.
2000Mathematics Subject Classification: 05A10, 15A15
Keywords: alternating sign matrices, Jacobsthal numbers
1 Introduction
In this paper we relate two seemingly unrelated areas of mathematics: alternating sign matrices and Jacob-sthal numbers. We begin with a brief discussion of alternating sign matrices.
An n×nalternating sign matrix is ann×n matrix of 1s, 0s and−1s such that
• the sum of the entries in each row and column is 1, and
• the signs of the nonzero entries in every row and column alternate.
Alternating sign matrices include permutation matrices, in which each row and column contains only one nonzero entry, a 1.
1 0 0
The determination of a closed formula for A(n) was undertaken by a variety of mathematicians over the last 25 years or so. David Bressoud’s text [1] chronicles these endeavors and discusses the underlying mathematics in a very readable way. See also the survey article [2] by Bressoud and Propp.
As noted in [1], a formula forA(n) is given by
It is clear from this that, for most values ofn,A(n) will be highly composite. The following table shows the first few values ofA(n) (sequenceA005130in [8]). Other sequences related to alternating sign matrices can also be found in [8].
9 911835460 22
·5·172·193·23
10 129534272700 22
·3·52·7·17·193·232
11 31095744852375 32
·53·7·192·233·29·31
12 12611311859677500 22
·33·54·19·233·292·312
13 8639383518297652500 22
·35·54·232·293·313·37
14 9995541355448167482000 24
·35·53·23·294·314·372
15 19529076234661277104897200 24
·33·52·294·315·373·41·43
16 64427185703425689356896743840 25
·32·5·11·293·315·374·412·432
17 358869201916137601447486156417296 24
·3·72·11·292·314·375·413·433·47
18 3374860639258750562269514491522925456 24
·73·13·29·313·376·414·434·472
19 53580350833984348888878646149709092313244 22
·73·132·312·376·415·435·473·53
20 1436038934715538200913155682637051204376827212 22
·74·132·31·375·416·436·474·532
21 64971294999808427895847904380524143538858551437757 75
·13·374·416·437·475·533·59·61
22 4962007838317808727469503296608693231827094217799731304 23
·3·76·373·415·437·476·534·592·612
Table 1: Values ofA(n)
Examination of this table and further computer calculations reveals that the first few values of n for whichA(n) is odd are
1,3,5,11,21,43,85,171.
These appear to be the well–knownJacobsthal numbers{Jn}(sequenceA001045in [8]). They are defined
by the recurrence
with initial valuesJ0= 1 andJ1= 1.
This sequence has a rich history, especially in view of its relationship to the Fibonacci numbers. For examples of recent work involving the Jacobsthal numbers, see [3], [4], [5] and [6].
The goal of this paper is to prove that this is no coincidence: for a positive integern,A(n) is odd if and only ifnis a Jacobsthal number.
2 The Necessary Machinery
To show thatA(Jm) is odd for each positive integerm, we will show that the number of factors of 2 in the
prime decomposition ofA(Jm) is zero. To accomplish this, we develop formulas for the number of factors of
2 in
N(n) =
n−1
Y
ℓ=0
(3ℓ+ 1)! and D(n) =
n−1
Y
ℓ=0
(n+ℓ)!.
Once we prove that the number of factors of 2 is the same forN(Jm) andD(Jm), but not the same forN(n)
andD(n) ifnis not a Jacobsthal number, we will have our result.
We will make frequent use of the following lemma. For a proof, see for example [7, Theorem 2.29].
Lemma 2.1. The number of factors of a primepinN!is equal to
X
k≥1
N pk
.
It follows that the number of factors of 2 inN(n) is
N#(n) =
n−1
X
ℓ=0
X
k≥1
3ℓ+ 1
2k
=X
k≥1
Nk#(n)
where
Nk#(n) =
n−1
X
ℓ=0
3ℓ+ 1
2k
. (3)
Similarly, the number of factors of 2 inD(n) is given by
D#(n) =
n−1
X
ℓ=0
X
k≥1
n+ℓ
2k
=X
k≥1
Dk#(n)
where
Dk#(n) =
n−1
X
ℓ=0
n+ℓ
2k
. (4)
For use below we note that the recurrence for the Jacobsthal numbers implies the following explicit formula (cf. [9]).
Theorem 2.2. ThemthJacobsthal numberJ
m is given by
Jm=
2m+1+ (−1)m
3 Formulas forNk#(n) and D # k(n)
Lemma 3.1. The smallest value ofℓ for which
3ℓ+ 1
and no smaller value ofℓyieldsmsince the numerators differ by multiples of three. Ifm≡1 (mod 3) andℓ=m−1
and no smaller value ofℓyieldsm. Ifm≡2 (mod 3) andℓ=m−2
and no smaller value ofℓyieldsm.
Lemma 3.3. For any positive integer k,
Proof. To analyze the sum
= 2kq
k is the smallest value ofℓfor which
The second expression intail(n) is clearly equal to 3qr+r−Jk−1. For the third expression, we have
3qJk−1+ (3q+ 1)(Jk−Jk−1) + (3q+ 2)(r−Jk) = 3qr+Jk−Jk−1+ 2r−2Jk
Theorem 3.5. Let n= 2k
Proof. We may write
D#k(n) =
In both sums,
Hence in this case
2n−1
X
ℓ=0
ℓ 2k
= 2k[1 + 2 +· · ·+ 2q] + (2s−1 + 1)(2q+ 1)
= (2q+ 1)(n+r−2k).
So in this case
D#k(n) =
n−1
X
ℓ=0
n+ℓ
2k
=
2n−1
X
ℓ=0
ℓ 2k
−
n−1
X
ℓ=0
ℓ 2k
= (2q+ 1)(n+r−2k)−
q
n+r−2k
2
=
n+r−2k
2k+1
(3(n−r) + 2k+1).
The reader will note that in the statement of the theorem we have separated the cases according as 0 ≤ r ≤2k−1 and 2k−1 < r < 2k, whereas in the proof the cases are 0 < r ≤2k−1 and 2k−1 < r ≤ 2k.
However, these are equivalent since n−0
2k+1(3(n+ 0)−2
k) =n−(2 k−2k)
2k+1 (3(n−2
k) + 2k+1).
4 A(Jm) is odd
Now that we have closed formulas forNk#(n) andD#k(n) we can proceed to prove thatA(Jm) is odd for all
Jacobsthal numbersJm.
Theorem 4.1. For all positive integersm,A(Jm) is odd.
Proof. The proof simply involves substituting Jm into (6) and (8) and showing that Nk#(Jm) = D#k(Jm)
for all k. This implies that N#(Jm) =D#(Jm), and so the number of factors of 2 in A(Jm) is zero. Our
theorem is then proved.
We break the proof into two cases, based on whether the parity ofkis equal to the parity ofm.
• Case 1: The parity ofmequals the parity ofk. Then
2k(J
m−k−1) +Jk = 2k
2m−k+1+ (−1)m−k
3 −1
+2
k+1+ (−1)k
3
= 2
m+1+ 2k−3·2k+ 2k+1+ (−1)k
3 since (−1)
m−k= 1
= 2
m+1+ (−1)m
3 since (−1)
k = (−1)m
= Jm
Thus, in the notation of Theorems3.4and 3.5,q=Jm−k−1 andr=Jk. We now calculateNk#(Jm)
= 1 2k+1
2m+1+ (−1)m
3 −
2k+ (−1)k−1
3 3
2m+1+ (−1)m
3 −
2k+ (−1)k−1
3
−2k
+ 3
2m−k+1+ (−1)m−k
3
2k+ (−1)k−1
3
= 1
3·2k+1 2
m+1−2k
2m+1−2·2k
+1 3((2
m−k+1−1)(2k
+ (−1)k−1)) since (−1)m= (−1)k−1 and (−1)m−k=−1
= 1 3(2
2m−k+1−2m+1−2m
+ 2k+ 2m+1−2k+ 2m−k+1(−1)k−1+ (−1)k
)
= 1 3(2
2m−k+1−2m
+ 2m−k+1(−1)k−1+ (−1)k
)
after much simplification. Again we find thatNk#(Jm) =D#k(Jm).
Now we calculateD#k(Jm), recalling that 0< r <2k−1.
D#k(Jm) =
(Jm−Jk−1)
2k+1 (3(Jm+Jk−1)−2 k)
= 1
2k+1
2m+1+ (−1)m
3 −
2k+ (−1)k−1
3 3
2m+1+ (−1)m
3 +
2k+ (−1)k−1
3
−2k
= 1
3·2k+1(2
m+1−2k)(2m+1+ 2(−1)k−1) since (−1)m= (−1)k−1
= 1 3(2
2m−k+1−2m+ 2m−k+1(−1)k−1+ (−1)k)
after simplification. Again we find thatNk#(Jm) =Dk#(Jm).
This completes the proof thatA(Jm) is odd for all Jacobsthal numbersJm.
5 The Converse
We now prove the converse to Theorem4.1. That is, we will prove thatA(n) is even ifnis not a Jacobsthal number. As a guide in how to proceed, we include a table of values forNk#(n) andD
#
k(n) for small values
n N#
In order to prove the first assertion (that Nk#(n)≥ D#k(n)), we separate the functions defined by the cases in equations (6) and (8) into individual functions denoted byNk#(1)(n), Nk#(2)(n), . . . , D#(2)k (n). That for some j ∈ {1,2} depending on the value of r. Note that not all combinations of i and j are possible (for example, there is no value ofn such thati= 1 andj = 2). In Lemmas5.1through5.4 we show that Nk#(i)(n) ≥ Dk#(j)(n) for all possible combinations of i and j (that correspond to some integer n) which implies thatNk#(n)≥D#k(n) for all positive integersn.
Lemma 5.1. For all integers nandk,Nk#(1)(n) =D#(1)k (n).
=
n−r
2k+1 3(n−r)−2 k
+ 3qr
2 q
since n−r 2k+1 =
q 2
=
n−r 2k+1
(3n+ 3r−2k)
= D#(1)k (n).
Lemma 5.2. For all integers kand all integersnsuch that r > Jk−1 (in the notation of Theorem3.4),
Nk#(2)(n)> Dk#(1)(n).
Proof.
Nk#(2)(n) =
n−r 2k+1
(3(n−r)−2k) + 3qr+ (r−
Jk−1)
>
n−r 2k+1
(3(n−r)−2k) + 3qr since
r > Jk−1
= Nk#(1)(n)
= Dk#(1)(n) by Lemma5.1.
This proves our result.
Lemma 5.3. For all integers kand all integersnsuch that r≤Jk (in the notation of Theorem 3.4),
Nk#(2)(n)≥Dk#(2)(n).
Proof. We see that r ≤Jk = 2k −Jk−1 by Lemma 3.2. Thus, 2kq+r ≤2k(q+ 1)−Jk−1. This implies
n≤2k(q+ 1)−J
k−1, so 2n−2k(q+ 1)≤n−Jk−1. Hence,
Nk#(2)(n) =
n−r 2k+1
(3(n−r)−2k) + 3qr+ (r−Jk−1)
= q 2(3(2
kq)−2k) + 3q(n−2kq) +
n−2k
q−Jk−1
= q2(−3(2k−1)) +q(−3(2k−1) + 3n) +
n−Jk−1
≥ q2(−3(2k−1)) +q(−3(2k−1) + 3n) + 2n−2k(q+ 1) by the above argument
= 2n−2
k−2kq
2k+1 (3(2 k
q) + 2k+1)
= D#(2)k (n).
Proof.
Nk#(3)(n) =
n−r
2k+1
(3(n−r)−2k) + (3q+ 2)r−2k
= q 2
(3(2kq)−2k) + 3q(n−2kq) + 2(n−2kq)−2k
= n−2
k+n−2kq
2k+ 1 (3(2
kq) + 2k+1)
= D#(2)k (n).
Remark 5.5. To summarize, Lemmas 5.1through 5.4tell us that for any positive integern,
Nk#(n)≥D#k(n).
For Propositions5.6through5.9we make the assumption thatJℓ< n < Jℓ+1 for some positive integerℓ.
Proposition 5.6. For ℓandn, as given above, Nℓ#+1(n) =n−Jℓ.
Proof. By Lemma3.1,
n−1
X
i=0
3i+ 1
2ℓ+1
= 0×(Jℓ) + 1×((n−1)−(Jℓ−1))
= n−Jℓ.
Proposition 5.7. Dk#(n) = 0 ifn <2k−1. In particular, D#
ℓ+1(n) = 0 ifn <2 ℓ.
Proof. Ifn <2k then, in the notation of Theorem3.5,n=randq= 0, so by Theorem3.5,D#
k(n) = 0.
Proposition 5.8. Dℓ#+1(n) = 2(n−2ℓ) if2ℓ≤n < J ℓ+1.
Proof. If 2ℓ≤n < J
ℓ+1 then, in the notation of Theorem3.5,q= 0 andr=n. Sincen≥2ℓ, we are in the
second case of Theorem3.5so
Dℓ#+1(n) = n−2
ℓ+1+n
2ℓ+2 (0 + 2
ℓ+2) = 2(n−2ℓ).
Proposition 5.9. For nandℓ as given above,2(n−2ℓ)< n−J ℓ.
Proof. We begin by showing thatJℓ+1−2ℓ= 2ℓ−Jℓ. We have
Jℓ+1−2ℓ =
2ℓ+2+ (−1)ℓ+1
3 −2
ℓ
= 2ℓ−2
ℓ+1+ (−1)ℓ
and hence
2(n−2ℓ) = n−2ℓ+n−2ℓ
< n−2ℓ+
Jℓ+1−2ℓ
= n−2ℓ+ 2ℓ−Jℓ from the above argument
= n−Jℓ
so we have our result.
We are now ready to prove our theorem.
Theorem 5.10. A(n) is even ifn is not a Jacobsthal number.
Proof. Our goal is to show that there is somek such that Nk#(n) is strictly greater than Dk#(n) since, by Remark5.5, we have shown thatNk#(n)≥D#k(n) for all positive integerskandn.
Given n, not a Jacobsthal number, there exists a positive integer ℓ such that Jℓ < n < Jℓ+1. Then
Nℓ#+1(n) =n−Jℓby Proposition5.6, and sincen > Jℓ,Nℓ#+1(n)>0. On the other hand, by Proposition5.7,
if n < 2ℓ, then D#
ℓ+1(n) = 0. If 2ℓ ≤ n < Jℓ+1, then by Proposition5.8, D#ℓ+1(n) = 2(n−2ℓ) which is
strictly less thann−Jℓ=Nℓ#+1(n) by Proposition5.9. Hence, in every case,N #
ℓ+1(n) is strictly greater than
Dℓ#+1(n) so there is at least one factor of two inA(n) and we have our result.
6 A Closing Remark
We close by noting that we can prove a stronger result than Theorem5.10. IfJℓ< n < Jℓ+1, then
Nℓ#+1(n)−D#ℓ+1(n) =
n−Jℓ if Jℓ< n≤2ℓ
Jℓ+1−n if 2ℓ≤n < Jℓ+1
by Propositions5.6,5.7,5.8and Lemma 3.2.
Letord2(n) be the highest power of 2 that dividesn. By Remark5.5,Nk#(n)−D #
k(n)≥0 for allnand
for allk, so that
ord2(A(n))≥
n−Jℓ if Jℓ< n≤2ℓ
Jℓ+1−n if 2ℓ≤n < Jℓ+1 ,
which strengthens Theorem5.10.
Finally, we see that ord2(A(2ℓ)) = Jℓ−1 since, for all k < ℓ+ 1, Nk#(2 ℓ) =
Nk#(1)(2 ℓ) =
D#(1)k (2 ℓ) =
Dk#(2ℓ), and 2ℓ−J
ℓ =Jℓ+1−2ℓ =Jℓ−1. So, for example, we know that A(210) is divisible by 2J9, which
equals 2341, and thatA(210) is not divisible by 2342.
7 Acknowledgements
The authors gratefully acknowledge the excellent technical help of Robert Schumacher in the preparation of this document.
References
[2] D. M. Bressoud and J. Propp, How the Alternating Sign Matrix Conjecture Was Solved,Notices of the American Mathematical Society,46(6) (1999), 637-646.
[3] A. F. Horadam, Jacobsthal Representation Numbers, Fibonacci Quarterly,34(1) (1996), 40-53.
[4] A. F. Horadam, Jacobsthal Representation Polynomials,Fibonacci Quarterly,35(2) (1997), 137-148.
[5] A. F. Horadam, Rodriques’ Formulas for Jacobsthal-Type Polynomials, Fibonacci Quarterly, 35 (4) (1997), 361-370.
[6] A. F. Horadam and P. Filipponi, Derivative Sequences of Jacobsthal and Jacobsthal-Lucas Polynomials,
Fibonacci Quarterly,35(4) (1997), 352-357.
[7] C. T. Long, “Elementary Introduction to Number Theory”, 3rd edition, Waveland Press, Inc., Prospect Heights, IL, 1995.
[8] N. J. A. Sloane, The On-Line Encyclopedia of Integer Sequences. Published electronically at
http://www.research.att.com/∼njas/sequences/.
[9] A. Tucker, “Applied Combinatorics”, 3rd edition, John Wiley & Sons, 1995.
(Concerned with sequencesA001045,A001859andA005130.)
Received Jan. 13, 2000; published in Journal of Integer Sequences June 1, 2000.