Konsep dan aplikasi metode elemen hingga

• •

•

•

KONSEP DAM APLIKASI

METODE

ELEMEN HINCi.CA

No. Ki

^{ass _ ...}

. ?.-:.1

^..

:. . .l:±L.COO k

^·

I o.

�J1d11k.�J.�. T

_gl

.�.�-:.�3.J- H , d . ah ·/�.

_i ···--·--·--

.. ^.

D

^{ll r I}

.

^...... ·-···-···--·-^'

·.

•

•

KONSEP DAN APLIKASI

ME TO DE

ELEMEN HINCiCiA

Robert

D.

Cook

Departemen of Eng�neering Mechanics University of Wisconsin - Madison

PENERJEMAH

Ir. Bambang Suryoatmono,· M.Sc Fakultas Teknik Jurusan Sipil Universitas Katolik Parahyangan

PENERBIT PT ERESCO BANDUNG 1990

,

Copyright C 1981 by John Wiley & ^{Sons Inc} All Right Reserved

Authorized translation from English language Edition published -Oy John Wiley

& Sons lr,ic

TK.03.01.90

Judul Asli: CONC�PTS AND APPLICATIONS OF FlNITE ELEMENT ANALYSIS

Second Edition - Robert D. Cook Hak terjemahan dalam bahasa Indonesia pada Penerbit PT ^Eresco

KONSEP DAN APLIKASI METODE ELEMEN HINGGA Penerjemah : Ir. Barn bang Suryoatmono, M.Sc.

Fakultas Teknik Jurusan Sipil Univers�tas Katolik Parahyangan Editor : Tjun Surjaman

Disain Sampul : Mustaghfirin Cetakan Pertama 1990

,,,

Diterbitkan oleh PT ERESCO. Anggota IKAPI Hak Cipta dilindungi undang-undang; Tidak diperke­

Jlankan memperbanyak penerbitan ini dalam bentuk apa pun tanpa izin tertulis dari penerbit

,

sol us me di elem stru�

masa perh sama

Te or cuku sarja yang men:

din a teru1 perh dan haru term PenE anali buk1 kom

•

PEN GANT AR

Pada umumnya metode elemen hingga dapat digunakan untuk memperoleh suatu solusi numerik. Banyak masalah dalam analisis tegangan, transfer panas, aliran Ouida, medan listrik, dan sebagainya, yang telah diselesaikan dengan menggunakan metocffi elemen hingga. Buku ini bertitik berat pada masalah analisis tegangan dan mekanika struktur. Analisis tegangan dibahas karena mudah untuk dimengerti, sedangkan masalah-masalah lainnya dapat dipelajari lebih lanjut karerta formulasi dan prosedur perhitungan elemen hingga untuk berbagai masalah aplikasi kurang Jebih adalah sama.

Buku ini adalah pendahuluan dan lebih condong ke masalah aplikasi praktek.

Teori-teori disajikan sebagaimana yang diperlukan. Buku ini mengandung

.bahan yang

cukup untuk disajikan dalam dua semester. Dengan mempelajari buku ini, seorang sarjana teknik akan dapat belajar menggunakan elemen hingga secara efektif. Untuk yang akan bekerja lebih lanjut, di dalam ini juga dapat diperoleh pengertian fisik mengenai elemen hingga.

Latar belakang buku ini adalah sebagai berikut. Kuliah-kuliah mengenai statika, dinamika, dan mekanika bahan harus telah dikuasai. Materna'tfka juga diperlukan terutama diferensiasi dan integrasi sinus, cosinus, dan polinomial. Penulis menekankan perlunya dikuasai juga pengetahuan mengenai operasi matriks, transposisi, diferensiasi, dan arti inversi (P,rosedur perhitungan inversi tidak begitu diperlukan). Mahasiswa harus terbiasa dengan pemrograman komputer, khususnya dengan bahasa Fortran, termasuk juga penggunaan subrutin, blok COMMON. dan penyimpananfi/e ke disket.

Pengetahuan lain - se p erti teori elastisitas ; pelat dan cangkang, metoda-metoda energi, analisis numerik - tidak harus, tetapi sebaiknya dikuasai. Kadang·kadang di dalam buku ini disinggung juga mengenai perigetahuan terse but, akan tetapi biasanya hanya konsep dasarnya.

Berikut ini dicantumkan penjelasan mengenai isi dan orientasi buku ini.

Pembahasannya meliputi analisis kontinum, bukan metode khusus untuk struktur rangka. Akan tetapi untuk memberikan penjelasan yang sederhana tetapi berguna, dibahas juga elemen rangka batang

(truss)

dan balok.

Ditekankan pada analisis statik Jinier.

Elemen yang dibahas secara rinci didasarkan pada medan .perpindahan yang di­

asumsikan (assumed displacement fields}. Elemen ini tidak dib.atasi pada bentuk yang khusus, juga tidak mempunyai kontinuitas nodal yang berlebil\an. Dari berbagai elemen yang ada, hanya beberapa yang dibahas secara rinci, yaitu ter­

utama yang berjenis isoparametr

�

.

. Untuk memperlihatkan Jangkah-langkah proses tertentu, diberikan pengkodean

dengan bahasa Fortran, apaqila dirasakan mudah, berguna, dan tidak terlalu panjang. Pengkodean ini bis� saja bu�an merupakan yang paling mutakhir atau.

paling efisien. Program dalam bentuk lengkap dapat diperoleh dari berbagai sumber Jain.

Topik-topiknya ditekankan pada masalah yang benar-benar berguna, dan telah terpecahkan dengan baik pada saat

^ini.

Topik-topik yang cepat beruban terhadap

1 I

waktu, seperti pembahasan mengenai program komputer yang sedang terkenal.

tidak ad.a dalam buku ini.

Ada beberapa perubahan dari edisi pertama ke edisi kedua ini. Sebagian topik edisi pertama yang tidak sesuai dengan maksud dan orientasi buku ini sudah ditiada·

kan. Beberapa topik baru ditambahkan apabila mema'ng sesuai (lihat Bab

14. 17.

^dan

18).

Pada buku ini juga ditambahkan contoh-contoh numerik. Yang tidak banyak berubah adalah susunan bab juga paragraf/kalimat-kalimatnya. Beberapa tambahai1 lain adalah yang diperoleh penulis dari berbagai literatur terakhir, clan dari komentar para mahasiswa, dan sesama pengajar yang pernah menggunakan buku ini. Ditambah·

kan pula beberapa pekerjaan rum ah, yang jawabannya diberikari pad a bagian belakang buku ini. Soal-soalnya dipilih yang dapat memberikan prinsip dan prosedur yang telah dijelaskan pada bab yang bersangkutan. Sebagian besar dari soal-soal tersebut tidak memerlukan perhitungan dengan komputer maupun perhitungan numerik yang rumit.

Keberhasilan dalam pemanfaatan met ode elemen hingga akan sangat tcrgan tung pada program komputer yang dibuat. Para mahasiswa pada kuliah semester pertama akan mengatakan bahwa tugas pemrograman merupakan alat belajar yang sangat baik.

Mahasiswa tersebut lebih senang menulis dan mencoba pro!:!ram sederhana tctapi lengkap, bukan ·membuat subrutin-subrutin saja. Elcmen-elcmen contoh dan kondisi·

nya masing-masing yang merupakan dasar pemrograman dicantumkan di sini. Sebagai contoh, kuadratur Gauss untuk pembentukan kekakuan elemen diberikan di dalam buku' ini. Untuk m�asiswa yang bukan dari bidang mekanika struktur, di sini dibahas juga beberapa masalah nonstruktural.

I. Elemen balok standar, dua derajat bebas (degree offreedom. d.o.f) tiap titik.

2. Seperti ad

(I)

tetapi dengan tambahan derajat be bas internal.

3.

Balok geser yang terletak di atas fundasi elastis, satu Jerajat bebas tiap titik.

(Lihat Gambar

9.5.2.

Untuk balok, tinjau saja w dan energi yang disimpan oleh . 'Yxy

)

^.

4.

Balok yang terbentuk oleh elemen pelat isoparametrik (Gambar

9.5.1

^atau

9.5.2).

5.

Elemen batang tak prismatis (tapered bar element), clua clerajat bebas pacla titik dan satu tak bertitik.

6.

Disk datar yang tebalnya konstan atau pun .berubah. clengan elemen lingkaran

i!

dan beban torsional saja.

f

7.

Sama dengan ad 6 tetapi ditambah clengan derajat bebas tak bertitik (nodeless d.o.f).

8.

Sama dengan ad 6, tetapi dengan beban radial saja.

9.

Sama dengan ad

6,

tetapi ada fundasi elastis, clan hanya dapat mempunyai ke­

kakuan geser melintang, clan behan lateral.

I 0.

Sama clengan ad 5 tetapi dengan meninjau aksi torsional saja.

11.

Rangka bidang(planeframe), tiga derajat bebas per titik .

...12. Sama dengan ad

11,

tetapi menggunakan elemen dari ad

4.

,

13.

Elemen segi empat, satu derajat bebas pada tiap ujung, untuk pe'rsamaan harmonis (Iapis sabun, aliran fluida, dan sebagainya).

14.

Aplikasi Persamaan

4.10.4

untuk,balok tak prismatis yang dibebani gaya aksial.

vi

,

Tu gas dapat superp masala dan bE sederh:

dapat serba ; dalam

Pe bertan:

baik, c

dari b karena hal bal which.

penjel�

yang c pen get cepat ^c

<enal.

topik tiada-

7.

dan an yak

bah an

1entar 11bah­

akang : telah tidak rn1it.

ntung

·rt a ma

I

baik.

tctapi

)nuisi­

ebagai dalam ibahas

<.

I

litik.

n olch 9.5.2).

1a titik gkaran

Jdeless

yai ke-

rmonis sial.

Tugas pemrograman juga dapat dibcrikan pada kuliah semester ke dua. Tugas •yang dapat saja diherikan misalnya komponcn dcrct h:>urier dari suatu pembebanan, dan superposisi masing-masing solusinya. Con toh-contoh yang diberikan di sini !fleliputi masalah tegangan bidang, termasuk untuk dacrah lingkaran, dengan elemen melingkar dan beban asimctris, juga analisis jalur hingga

(finite strip)

pada pelat yang ditumpu ,, sederhana. Tugas lain seperti masalah frekuensi alami getaran a tau respons dinamis juga dapat diberikan. Kemungkinan lainnya, adalah tugas pembuatan program komputer serba guna, yang disertai penggambaran intcraktif, yang diperlukan oleh mahasiswa dalam memecahkan masalah clemen hingga.

Penulis sangat berterima kasih kepada mahasiswa-mahasiswa yang telah banyak bertanya schingga penulis menjadi terbi�sa untuk menjelaskan dengan cara yang lebih baik. dan dapat memberikan pekcrjann u1mah yang lebih sempurna. Sebagian besar dari buku ini herasal dari makalah-makalah

(paper)

yang telah pernah diterbitkan, karena itu penulis juga sangat mcnghargai kerja para penulis makalah tersebut. Dalam hal bahasa, penulis pernah mengalami kebingungan dalarn penggunaan kata

that

dan which. Kepada editor dari penerbit

Willey

penulis mengucapkan terima kasih atas penjelasan mcngenai perbedaan kedua kata terse but. Buku

The Elements of Style

yang ditulis oleh Strunk dan White telah banyak membantu pen�lis. Kepada keenam pengetik, terutama Pat KJitzke, penulis mcngucapkan terima kllsih atas kerja yang.

cepat dan berkualitas.

Robert D. Cook

PENGANTAR DAFTAR ISl NOTASI

BAB 1 PENDAHULUAN

1.1

Metode Elemen Hingga

D AFT A R ISi

1.2

Beberapa Matriks dan Persamaan yang Penting

1.3

Teori Elastisitas _../

1.4

Hubungan Regangan-Peralihan "'

{[)

Hubungan Tegangan-Regangan ^V

1.6

Pengaruh Temperatur, Tegangan, dan Regangan Awai

1.7

Mencari Informasi Tambahan

1.8

Kemajuan Komputer Soal-soal

. ,

BAB ₂ METODE KEKAKUAN DAN RANGKA DATANG BIDANG

2.1

Pendahuluan·

2.2

Persamaan Kekakuan Struktur

2.3

Sifat-sifat [kl. Solusi Anu

2.4

Persamaan Kekakuan Elemen

J

2.5

Penyusunan Matriks Kekakuan Struktur

J

2.6

Pembentukan Persamaan Keseimbagan ^V

2.7

Penomoran Titik yang dapat Menghasilkan Matriks Jalur

2.8

Penomoran Kembali Titik-titik secara otomatis

2.9

Kondisi Batas Peralihan

2.10

Reaksi Tumpuan dan Perhitungan Tegangan

2.11

Solusi Persamaan dengan Eliminasi Gauss

2.12

Algoritma Solusi Gauss dan Choleski

2.13

Catatan Mengenai Berbagai Cara Pemecahan dan Persamaan

2.14

Pemecahan Persamaan Tidak Langsung

2.15

Rangkuman

2.16

Beberapa Masalah Nonstruktural yang Berkaitan Soal-soal

BAB 3 ENERGI POTENSIAL DAN METODE RAYLEIGH-RITZ

Q 3.1 .2

Q .3

Pendahuluan

Energi Potensial Total "

Beberapa Derajat Bebas. Manipulasi Matriks ^\,/

Halaman

"

v

ix 1

4 10 4 15 12 19 16 20 21 22 25 25 25 28 29·

31 34 37 . 41

40

45

46

49 53 54 56 58 60 65 65 65 67

ix

��

Persamaan-persamaan untuk Energi Potensial Total

70 6.4

3.5

Metode Rayleght-Ritz

74 6.5

3.6

Komentar pada �etode Rayleigh-Ritz

77 6.6

3.7

Bentuk Elemen Hingga pada Metode Rayleigh-Ritz

78

I 6.7

3.8

Rangkuman Kesimpulan

83 6.8

Soal-soal

84 6.9

6.10

BAB4 ELEMEN-ELEMEN YANG DIDASARKAN AT AS MEDAN PERALIHAN

J 6.11

TERASUMSI

88 6.12

4.1

Pendahuluan

88 I 6.13

4.2

lnterpolasi

88

^Soal-sc

4.3

Rumus untuk Matriks Elemen

92

4.4

Matriks untuk Elemen Rangka Batang (Truss) dan Rangka (Frame)

98

^BAB7

4.5

Segitiga Regangan Konstan

100 7.1

4.6

Elemen Segitiga Linler

103 7.2

4.7

Keseimbangan dan Keserasian pada Solusi

105 7.3

4.8

. Persyaratan Konvergensi. Uji Patch .

106 7.4

4.9

Persyaratan lain untuk Konvergensi dan Kekekalan

108 7.5

@

Perhitungan Tegangan

1 12 7.6

4. 11

Titik Simpul Pojok, Titik Tepi, Biaya dan Pendimensian

1 16 7.7

4. 12

Elemen Hingga versus Beda Hingga

1 17 I 7.8

4.13

Metode Solusi Batas

1 18 I 7.9

Soal-soal

1 2 1 I 7. 10

7.1 1

BABS FORMULASI ISOPARAMETRIK

128 7.12

5.1

Elemen lsoparametrik

128 7.13

5.2

Contoh-coi:1toh pada l Dimensi

129 7.14

5.3

Elemen Isoparametrik Linier Bidang

131 7.15

5.4

Ringkasan Gauss Quadrature

134

^Soal-so

5.5

Subrutin Komputer untuk Elemen Linier

137

I

^BABS

5.6

Elemen Bidang Lagrange

140

_•

I

•

5.7

lsoparametrik Padat (masif)

142 8. 1

5.8

Beban Titik Si.mpul dari Traksi �ermukaan dan Gaya Benda

144 ( 8.2

5.9

Kesahihan Elemen Isoparametrik

147 8.3

5.10

Orde Quadrature yang Jayak

150 8.4

5. 11

Cata tan Mengenai Perhitungan Tegangan

153 8.5

5.12

Catatan Kesimpulan. Contoh-contoh. Berbagai error

155 8.6

Soal-soal

159

_(-,

8.7

So al-so:

,, BAB 6 TRANSFORMASI KOORDINAT

165

_BAB9

6. 1

Pendahuluan

165 9. 1

6.2 6.3.

Transformasi Tegangan, Regangan, dan Besaran Material Transformasi Kekakuan dalam

2

_Dimensi

168 165 9.2 9.3

x

70 74 77 78 83 84

HAN

88 88 88 92 98 100 103 lOS 106 108 112 1 16 117 1 18 12 1

128 128 129 131 134 137 140 142 144 147 ISO IS3

!SS IS9

16S 16S 16S 168

f l

6.4

Transformasi untuk Tumpuan yang miring

170

6.S

Transformasi pada Ruang. Matriks [T] y.ang tidak Persegi Panjang

171 6.6

Penggabungan Antara Elemen yang tidak sama ^J

72 6.7

Penghubung Kaku. Elemen Kaku. Sendi Ekstra

17S 6.8

Kendala (Constraints) dan Persamaan Transformasi ^J

77,,

6.9

Kendala dan Pengali Lagrange

180

6.10

Kendala dan Fungsi Penal ti

18 1

6.11

Penggunaan Simetri Suktur

183

6.12

Simetri Siklik

18S

6. 13

Pelaksanaan Substruktur

187

Soal-soal

189

BAB 7 TOPIK MENGENAI FORMULASI ELEMEN DAN PENGGUNAANNY A J

99 7. I

Kernel Elastis dan Elem en Um um

7.2

Titik Simpul di dalam Elemen. Kondensasi

7 .3

Derajat Bebas tak Bertitik Simpul. Formulasi Global-Lokal

7.4

Algoritma Kondensasi dan Persamaan.Kendala

7 .S

Turunan Lebih Tinggi sebagai Derajat Bebas Titik Simpul

7 .6

Geser Parasitik pada Elemen Linier

7.7

Elemen QM6. Elemen tak Serasi

7 .8

Elemen Membran Terpilin (Warped Membrane Element)

7. 9

Elemen Segitiga dan Koordinat Lu as

7. IO

Segitiga Kuadratik. lntegrasi Numerik

7 .1 1

Pilihan Lain dalam Formulasi Elemen

7 .12

Penurunan Derajat Elemen

7.

J

3

Pemodelan. Pola Jaring dan Pembagian Derajat

7 .14

Elemen-elemen yang Berbentuk Khusus a tau yang Tak Hingga

7.

l

S

Mekanika Fracture. Singularitas Elem en

Soal-soal

BAB

8

BENDA PUTAR

8.1

Pendahuluan

8.2

Formulasi Pembebanan Simetris Aksial

8.3

Catatan Mengenai Deret Fourier

8.4

Behan Umum. Pendahuluan

8.S

Pembebanan Umum. Matriks Elemen

8.6

Pembebanan Umum dan Besaran Umum

8.7

Catatan Kesimpulan

So a I-so al

BAB9 LENTU�PELAT DATAR

9. 1

9.2 9.3

Perilaku "Pelat dan Cangkang Elem en Hingga dan J alur Hingga Elemen Pelat Isoparametrik

199 201 203 206 208 210 211 216 217 221 226 227 230 233 23S 240

249 249 249 2S2 2SS 2S8 260 262 263

267 267 271 277

xi

. ,

9.4

Elemen Pelat Isoparametrik (lanjutan)

9.5

Elemen Isoparametrik untuk Pelat Tipis dan Pelat Tebal

9.6

Kasus Uji untuk Pelat Terlentur

Soal-soal

BAB 10 CANGKANG

10.1

Pendahuluan

10.2

Elemen Datar

10.3

Gerak Benda Tegar

10.4

Pilihan Teori Cangkang dan Medan Peralihan

10.5

Elemen Cangkang lsoparametrik

10.6

Elemen Cangkang lsoparametrik (lanjutan)

10.7

Uji Kasus Elemen Cangkang

10.8

Cangkang Tipis Putar

10.9

Cangkang Tipis Putar (Lanjutan)

10.10

Kesirnpulan Tentang.Cangkang Tipis Putar

10.11

Elemen Cangkang'Putar lsoparametrik Soal-soal

BAB 11 ELEMEN HINGGA PADA DINAMIKA DAN GETARAN

11.1

Pendahuluan

11,2

Matriks Massa dan Redaman. Persamaan Dinamika

11.3

Matriks Massa, Konsisten dan Diagonal

11.4

Frekuensi Alami. Masalah Nilai Eigen

11.5

Kondens�si untuk Mereduksi Jumlah Derajat Bebas

11.6

Teknik-teknik Solusi untuk Masalah Eigen

11.7

Respons Dinamik. Metode Ragam

11.8

Respohs Dinamik. Integrasi Langsung

11.9

Respons Dlnamik. Catatan Tentang Metode-metode

10.10

Bermacam-macam Persoalan Dinamik

Soal-soal

BAB 12 TEKUK DAN PENG AR UH LAIN. GAY A MEMBRAN

12.1

Pendahuluan

12.2

Matriks Kekakuan Teg�ngan untuk Batang, Balok, dan Pelat

12.3

. Perumusan Lebih Umum

12.4

Beban Kritis (masalah Nilai Eigen)

12 � )

Bifurkasi^, Ketaksempurnaan, Titik Batas, dan Nonlinieritas Soal-soal

,,

BAB 13 PENGENALAN PADA PERSOALAN NONLINlER

!i)

Pendahuluan. Nonlinieritas Geometri

13.2

Formulasi

Updated Lagrangian

xii

280

284 j 13.3

288 13.4

290 13.5

13.6 296 J 13.7 13.8

296 13.9

297 199 tt 13.1 1 13.10

301 13.12

303 13.13

307 13.14

309

_Soal-so

3 12

315 l

^{BAB 1·}

316

317 14.

_l

320

I

14.2

14.3

327 14.4

14.5

327 l 14.6

327 14.7

329

_I

14.8

333 14.9

336

340

_{BAB 1:}

343

345 15.

_l

348 15.2

350 15.3

351 15 .4

15.5

357

\.

15.6

'

15.7

357 15.8

359 15.9

363 15.10

367

... So al-so

37 1

373

_{BAB 1}

378 16. l

l6})

378 16.3

�80 16.4

16.5

280

284 13.3

Algoritma Solusi. Newton-Raphson

382

288 13.4

Interpretasi Algoritma Solusi

384

290 13.5

Formulasi Lagrangian Total

387

13.6

Algoritma Solusi Lain. lterasi Langsung

389

296 13.7

_Persoalan joint, gap, dan kontak

39 Y

296 13.8

Kabel, Membran, dan Cangkang

394

297 13.9

Nonlinieritas Material. Teori lnkremental

395

13. 10

Teori Deformasi. Solusi Iterasi Langsung

399

199 13. 1

_I Algoritma untuk Plastisitas lnkremental

402

301 13.12

Aksi Lentur dengan Nonlinieritas Material

406

303 13.13

Hal-ha! Jain tentang Nonlinieritas Material

408

307 13.14

Memilih Metode Solusi

·410

309

_Soal-soal

41 1

3 12

3 15

_BAB

14

PENGUASAAN PADA DATA, PROGRAM, DAN PEMROGRAMAN

421

316

3 17 14. 1

Pendahuluan

421

320 14.2

Dokumentasi ^{. ,}

421

14.3

Pembentukan Jaring ^..

422

327 14.4

Grafik Komputer 425

14.5

Kesalahan Fatal dan Perangkap Kesalahan

425

327 14.6

Catatan Tentang Program Besar dan Kecil

427

327 14.7

Rekomendasi Pemrograman

421:

329 14.8

Alokasi Tempat Penyimpanan Dinamik

43U

333 14.9

Biaya-biaya

432

336

340

_{BAB 15} MENDETEKSI DAN MENGHINDARI KESULITAN NUME�IK

434 343

345 15.1

Pendahuluan

484

348 15 .2

Uji Nilai Eigen pada Elemen-elemen

435

350 15.3

Uji Kualitas Elemen

436

35 1 15.4

Kesalahan ldealisasi. Laju Konvergensi

437

15.5

Kondisi Buruk. Kesalahan Pemotongan dan Pembulatan

441

357 15.6

Bilangan Kondisi

443

15.7

Pengurutan Persamaan

446

357 15.8

Kerusakan pada Koefisien Diagonal

447

359 15.9

Persamaan Residu dan Iteratif

448

363 15.10

Kesimpulan

450

367

So al-so al

45 1

371

373

_{BAB 16} BERMACAM TOPIK DALAM MEKANIKA STRUKTUR

454

378 16.

_l Metode Keseimbangan, Campuran, dan Hibrid

454

�

Balok Lurus dan Balok Lengkung

456

378 16.3

Fondasi Elastis

457

180 16.4

Konstruksi lnkremental

459

16.5

Reanalisis Setelah Modifikasi Struktur

459

xiii

16:6 Media Inkompresibel 461

16.7 lnteraksi Struktur-Fluida 462

So al-so al 464

BAB 17 PENGENALAN PADA PERPINDAHAN PANAS DAN PERSOALAN

NONSTRUKTURAL LAINNY A 470

17 .1 Formulasi untuk Perpindahan Panas dan Persoalan Lainnya 17 .2 Persamaan-persamaan untuk Konduksi Panas dalam Bidang 17 .3 Formulasi Elemen Hingga

17.4 Benda Pejal Urn um dan- Benda Pu tar 17.5 Persoalan Termal Transien

17 .6 Beberapa So al Pen ting Pada Perpindahan Panas 17 .7 Persamaan Kuasi-Harmonik

17 .8 Aplikasi pada Aliran Fluida dua Dimensi

17 .9 Persamaan Gelombang. Ragam Akustik dalam Rongga Soal-soal

BAB 18 PENGANTAR METODE RESIDU BERBOBOT

·18. l Alasan-alasan Menggunakan Metode Residu Berbobot

18.2 Beberapa Metode Residu Berbobot.

18.3 Contoh Numerik

18 .4 Met ode Elem en Hingga Oalerkin

18.5 Aplikasi Metode Gauss pada Dua Dimensi 18.6 lntegrasi Sebagian

18.7 Metode Kolokasi Kuadrat Terkecil

18.8 Metode Elemen Hingga Galerkin. Formulasi Campuran 18.9 Penerapan Galerkin pada Persamaan Kuasi Harmonik Soal-soal

Apendiks A Matriks kekakuan Kolom -Balok Bidang Apendiks B Contoh Jaring Elemen Hingga

Daftar ^Pustaka Jawaban Soal-soal Indeks

/

,­

,,

xiv

470 471 473 475 476 478 479 481 483 485

489 489 489 491 495 497 499

SOI

503 505 506

511 513 519 550 571

NOTA

ill I

_Beriku1

pada b dcfinisi punyai digunal SIM BO

{ }

[ 1-1

( J

^T

. [ 1-1

.anp aa

SIM BO A

[A]

{a(

B

...

[BJ, [E Ca C(K)

[CJ

D d.o.f.

• {D}

{d}

461 462 464

470 470 471 473 475 476 478 479 481 483 485

489 489 489 491 495 497 499 50 1 503 505 506

5 11 513 519 550 57 1

•

NOTASI

13erikut ini dicantumkan daftar simbol-simbol utama. Notasi yang digunakan hanya pada bagian tertentu dan modifikasinya (sepcrti dengan penambahan subskrip) di­

definisikan pada bagian di mana digunakan. Begitu pola simbol-simbol yang mem-,..

punyai arti yang berbeda untuk konteks tcrtentu didefinisikan di mana simbol tersebut digunakan. Matriks dicantumkan dengan cetak tebal.

SIMBOLrSIMBOL MATEMATIKA

Matriks segi empat atau bujuf sangkar Matriks diagonal

Vektor baris

Vektor kolom.

Catatan: { u

v } ^=:

{ u

v}

Invers matriks

Transpos matriks (berlaku juga untuk matriks bar1s dan matriks kolom Transpos invers;

( ) - T

^=:

(( l -1

t ^{T =:} (

( ) Tr

^1.

Cata tan.

Tanda kurung biasa maupun kurung siku dapat diabaikan dari suatu sub- matriks dan dari matriks bagian dari perkalian matriks yang dikurung.

turunan waktu; sebagai contoh, it= du/dt,

u

⁼

d2 u/dt2•

turunan parsial terhadap 'variabel di sebelah tanda ini; sebagai contoh

W,x

⁼

3wf3x, W,xy

⁼

32 wf3x3y

Amplitudo; sebagai contoh, ^u _=ii sin wt. (Banyak lagi arti-arti lainnya).

anp anp a_np

Menunjukkan - -. ^. . ^-

3a1 3a2 aa/1

^{yang mana}

np

^merupakan

fungsi skalar dengan parameter a ^1,

a2, a3, ... , a11•

SIMBOLrSIMBOL LATIN

A

[A) {i

B

[B], [B0]

C(K)

Cu

[C]

D

d.o.f.

{D}

{d}

Lu as

Penghubung antara {d}dengan {a}; {d} ⁼ l.Al {a}

Koordinat yang diperumum

(generelized coordinates).

semi-lebar-jalur dari suatu matriks. ^· Matriks "regangan-peralihan" (Bab

4.3)

Kontinuitas derajat

n

(Bab

4.2)

Jumlah kondisi untuk [K) (Bab

15.6)

Matriks redaman atau matriks kendala

(constrain).

Peralihan

Derajat be bas

(degree of freedom)

d.o.f. nodal untuk struktur (d.o.f. global) d.o.f. nodal untuk elemen.

1

E.Es

{D}

[E] {F}

{f}

G [H]

I

[ _I J [J]

k [K]

[k]

[Ka]

[kal L, l I, m, n

[M]

M, N

[m]

MB AND N, NEQ NDOF NUMEL NUMNP 0 [N]

[O] , {O}

P;. ^q;

p

{P} [Q] . {Q}

R q

{R}

{r}

{r}

s

s, t

" T J

[T]

Matriks kekakuan.lentur untuk pelat

Modulus elastis

( E),

modulus sekan

(Es)

(Garn bar

13.

l

0. 1)

Matriks kekakuan elastis (Bab

1.5)

Gaya benda

(body forces)

per satuan volume.

Medan peralihan; {t} ⁼ { _u v w }dalam ruang tiga dimensi.

modulus geser.

digunakan apabila [Q] dipakai momen inersia balok

Matriks satuan {disebutjuga matriks identitas) Determinan dari [J] , disebut juga Jacobian matriks Jacobian

kekakuan pegas. Konduktivitas termal (Bab

17)

Matriks kekakuan struktur (global)

Matriks kekakuan elemen (matriks konduktivitas pada Bab

17).

Matriks kekakuan tegangan struktur (global).

Matriks kekakuan tegangan elemen.

Panjang cosinus arah

Matriks massa struktur (global) Matriks massa elemen

Momen lentur

(M},

gaya membran

(N)

Sama dengan B

Banyaknya persamaan Banyaknya derajat bebas Banyaknya elemen pada struktur Banyaknya titik pada struktur Matriks fungsi bentuk; {f} ⁼ [:N] {d}

}.

pe<t•m• hH digunakan pada Bab

2

Ordy; sebagai contoh

O(h2)

⁼ suku dengan orde

h2•

Matriks kosong, vektor kosong

Gaya terpusat pada titik

i

(Bab I dan

2)

Gay a

Vektor gaya yang bekerja pada titik-titik struktur.

Matriks yang digunakan untuk berbagai. hal. Didefinisikan setiap kali digunakan.

Beban lateral (permukaan atau garis) Residual (sisa) (Bab

15.9;

Bab

18).

Beban total pada titik-titik struktur; {R} ⁼

{P}·

^{+ �} {r}

Gaya-gaya yang bekerja dari elemen terhadap titik-titik (Persamaan

4.3.5).

{r} ^{= -} {r}(Bab

2.4)

Permukaan

(surface)

Arah-arah koordinat, biasanya Cartesian.

Temp�ratur Tebal, Waktu Matriks tr�nsformasi

.(

•

U. Uo u, v. w

v x,y, z x.

y.

z

SIMBOJ

Q'.

a, (3, ^r (3 [r]

0 {e} ,

{e,

{1<}

v

�. ^T/, � II

1T

p

{a}, {ac ip. {<I>}

w

SIMBOI

-'\t\t\1\

�

�

t=

tiap kali

rsamaan

•

U. Uu U, V, W

v x,y,z x ,y. z

Energ1 regangan, energf regangan per satuan volume Komponen-komponen peralihan

Volume

Koordinat Cartesian Koordinat Cartesian lokal

SIMBOL-SIMBOL YUNANI

a a, {3, ^'Y {3

Koefisien ekspansi termal Koordinat luas (Bab 7.9).

Sudut, faktor relaksasi, modulus fundasi, dan sebagainya.

lnversJacobian, [ )

⁼

[J]-1• ,

[rJ

5

{€}

^•

{€0}

{K}

Operator perubahan kecil; sebagai contoh t adalah inkremen waktu.

Operator virtuil (rnaya); sebagai contoh

_ou

adalah peralihan virtuil.

Regangan, regangan awal (Bab 1.6)

v

�. ^17, � n

Tr

p

{a}, {ao}

¢>

{<I>}

w

Vektor kelengkungan (pada'lentur pelat).

Nilai eigen. Pengali Lagrange.

Angka Poisson.

Koordinat isoparametrik (Bab 5).

Fungsional (np

⁼

energi potensial total).

3,1415926536 .. . Rapat massa

.

^'

Tegangan, tegangan awal (Bab 1.6)

Variabel yang bergantung. Sudut meridian pada cangkang (Bab IO).

Vektor gesekan permukaan (Bab 1.3) Frekuensi sudut dalam radian per detik.

SIMBOL-SIMBOL GRAFIS

Vektor gaya atau peralihan

Vektor rotasi atau momen (dengan aturan tangan kanan).

-'\i\i\i\i\i\__.

Pegas atau tumpuan elastis.

Tumpuan rol (menahan gay a-gay a normal positip maupun negatip ).

� Tumpuan sendi (menahan semua gaya, tetapi tidal<. menahan momen).

?ii (

� :t::::==� � Tumpuan jepit (menahan semua gaya dan momen) .

3

1

PENDAHULUAN

1.1 METODE ELEMEN HINGGA

Metode elemen hingga adalah prosedur numerik untuk memecahkan masalah mekanika kontinum dengan ketelitian yang dapat diterima oleh rekayasawan.

Bayangkanlah bahwa tegangan dan peralihan pada suatu struktur dalam Gambar I.

I

harus dicari. J�waban numeriknya tidak _2,kan ada pad a buku manapun. Metodc­

metode klasik menunjukkan bahwa masalah ini berupa persamaan diferensial parsial, akan tetapi jawabannya tidak ada karena geometri dan pernbebanannya terlalu kom­

pleks. Secara praktis,

banyak sekali

masalah yang terlalu kornpleks untuk diperoleh jawaban tertutupnya

(closed form solution).

Untuk itu. diperlukan solusi numerik, dan salah satu yang cukup memadai adalah met ode elemen hingga.

Pada Gambar I.I.

lb

diperlihatkan model elemen hingga. Daerah yang berupa segitiga dan kuadrilateral adalah elemen-elemen hingga. Titik-titik hitam adalah titik simpul

(node)

dimana elemen yang satu berhubungan .dengan lainnya. Suatu jaring

(mesh)

adalah susunan titik simpul dan elemen. Ben tuk jaring pada gambar tersebut terdiri atas elcmen segitiga dan kuadrilateral, ada yang mempunyai titik simpul pada sisinya, dan ada pula yang hanya pada ujungnya. (Informasi mengenai tata letak elemen pada jaring diberikan pada Bab

7.13

dan Apendiks B).

Pada dasarnya, elemen hingga merupakan bagian-bagian kecil dari struktur �ktual.

Akan tetapi, kita tidak dapat mengubah Gambar

I. I.

la menjadi Gambar

I.I.

l

b

hanya dengan membuat potongan sembarang seperti potongan-potongan material yang terikat pada titik-titik kumpul. Apabila terpotong demikian, struk.tur lcrsebut akan sangat rnelemah. Selain_itu, potongan:pot:o�rsebJ1t akao mempunyai kon�i

!£gan@n pada titik-titik--kurnpulnya dan akan cende;ung menjadi turn_pang_tindih at.fill terpisahkan di sepan�otongfil!. �lasnya, pada struktur aktual tidak akan terjadi demikian, jadi elemen hingga harus dapat beraeformasi dengan cara yang terbatas.

Sebagai contoh, apabila ujung-ujung elemen dikendalakan untuk tetaplurus, seperti yang diperlihatkan pada Gambar I.

I.

le, maka elemen yang bersebelahan dengannya tidak akan bertumpang tindih maupun terpisahkan.

Untuk memformulasikan suatu elernen, k.ita harus mencari gaya-gaya titik simpul

(nodal forces)

yang menghasilkan berbagai ragam deformasi elemen. Kita dapat men­

cari gaya-gaya ini dengan teori dasar untuk £.iemen hingga "alami" seperti balok

(beam)

a tau batang

{bar).

Akan tetapi, untuk elemen-elemen Y-ang didefinisikan clengan menggambarkan g_aris-garis pada suatu kontinum,_sepertLyang diperlilrntkan pad a Garn bar

1. 1.

lb dan I. I.le, diperlukan Q_rosedur baru (Bab

3, 4, 5, 8, 9, I 0, 17,

dan

18).

�- Metode elemen hingga tidak dibatasi pada masalah-masalah mekanika struktural (Gamba,r

1.1.2).

Pada Gambar

1.1.2

juga diperlihatkan bagaimana permukaan </> yang

4 •

berubal simpul terpilin dekatar

,y.

v

Gambar hingga 1

gaya-ga\

Di x dan ^· dari </>.

ini me

bagian [!rdefii simpul

x/

(

Gambar

kanika

;am bar letode­

parsial,

1 kom­

ieroleh ik, dan berupa th titik 1 jaring

�rsebut 1! pada 3 letak

�ktuaL

1 hanya

1 1

_yang

1t akan rentrasi lih atau _!!!rjadi :rbatas.

seperti .gannya s

imp\.!!

3t men­

i balok inisikan

�n

10,

17,

·uktural

</> yang

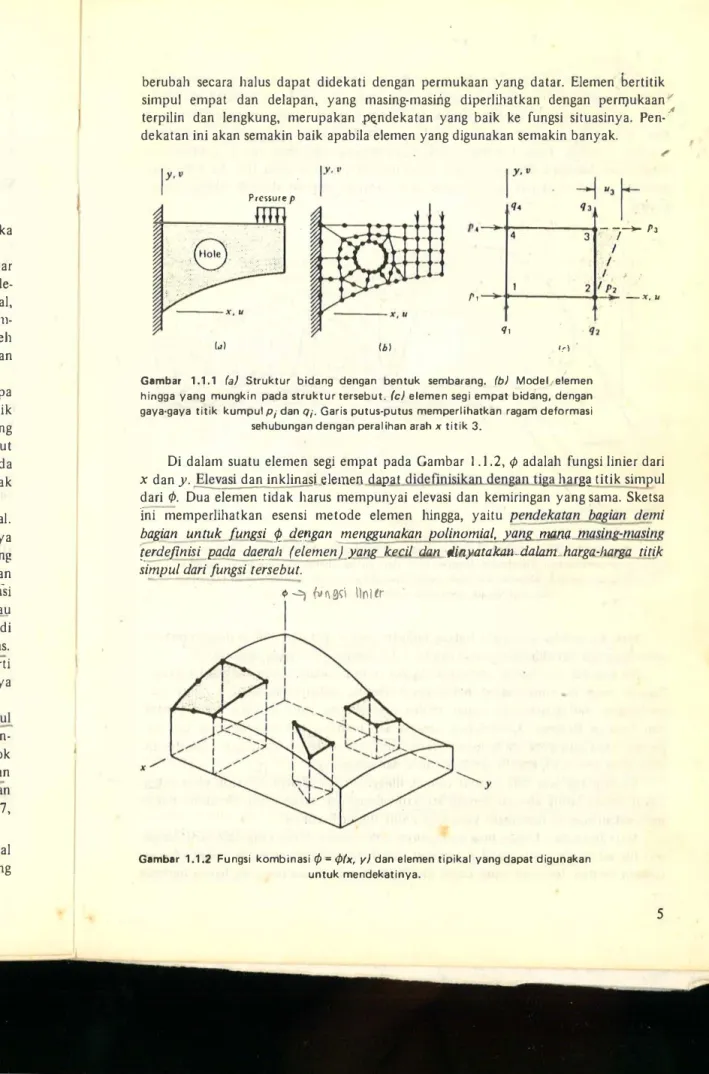
berubah secara halus dapat didekati dengan permukaan yang datar. Elemen bertitik simpul empat dan delapan, yang masing-masing diperlihatkan dengan per!T}ukaan"

terpilin dan lengkung, merupakan .Pxndekatan yang baik ke fungsi situasinya. Pen-"

dekatan ini akan semakin baik apabila elemen yang digunakan semakin banyak.

Pressure p

r.��4 ^_____ 3_. ^-,� ^/'3 I I I 2 I P2 p, ��---.__..;.. ^{-x. u}

'11

1�1 (b) 'r\

Gambar 1.1.1 (a) Struktur bidang dengan bentuk sembarang. (b) Model elemen hingga yang mungkin pada struktur tersebut. (c) elemen segi empat bidang, dengan gaya-gaya titik kumpul P; dan Q;. Garis putus-putus memperlihatkan ragam deformasi

sehubungan dengan peralihan arah x titik 3.

Di dalam suatu elemen segi empat pada Gambar

1.1.2,

</> adalah fungsi linier dari x dan ^{y .}

.fil

evasi dan inklinasj elemen dapat didefinisikan...dengan...Uga harl@_ titik simpul dari </>. Dua elemen tidak harus mempunyai elevasi dan kemiringan yang sama. Sketsa lni memperlihatkan esensi metode elemen hingga, yaitu

pendekatan bagian de_mi bagian untuk fungsi p df:!!gan menggunakan polinomial, yang

mana

masing-masing [!!rdefinisi 12.ada da!!.ah (elemen) yang kecil dan.Jijn)liltakafl-daiam.Jlarga-harga titik simpul dari fungsi tersebut.

-

� � fvf\9\i llnltr

I

Gambar 1.1.2 Fungsi kombinasi </> ^� </>(x, y) dan elemen tipikal yang dapat digunakan untuk mendekatinya.

5

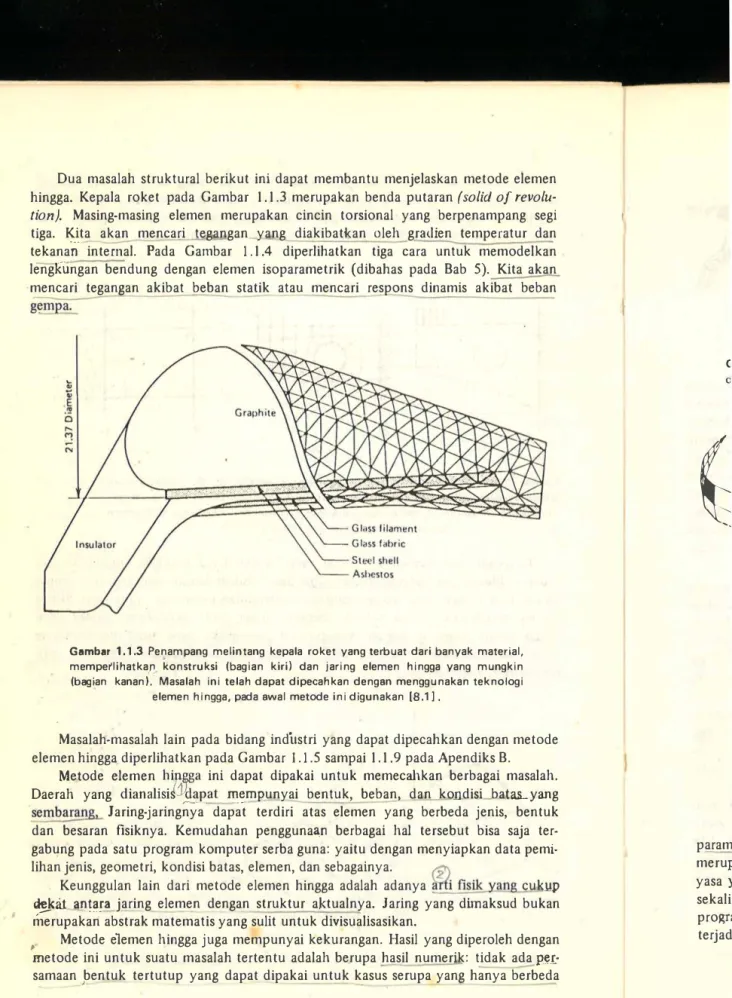
Dua masalah struktural berikut ini dapat membantu menjelaskan metode elemen hingga. Kepala roket pada Gambar

1.1.3

merupakan benda putaran

(solid of revolu­

tion).

Masing-masing elemen merupakan cincin torsional yang berpenampang segi tiga. Kita akan mencari tegangan yang diakibatkan oleh gra<.lien temperatur dan tekana'O internal. Pada Garn bar

1.1.4

diperlihatkan tiga cara untuk memodelkan lengKu"ngan bendung dengan elemen isoparametrik (dibahas pada Bab

5).

Kita akan mencari tegangan akibat beban statik atau mencari respons dinamis akibat beban _{- -- -}

Gambar 1.1.3 Penampang melintang kepala roket yang terbuat dari banyak material, mempe�lihatkap konstruksi (bagian kiri) dan jaring elemen hingga yang mungkin (bagian kanan). Masalah ini telah dapat dipecahkan dengen menggunakan teknologi

elemen hingga, pada ewal metode ini digunakan (8.1).

MasaJah-masalah lain pada bidang industri yang dapat dipecahkan dengan metode elemen hingga diperlihatkan pada Gambar

1.1.5

_sampai

1.1.9

pada Apendiks B.

M.etode elemen hi�a ini dapat dipakai untuk memecahkan berbagai masalah.

Daerah yang dianalisi

�

dapat �unyai bentuk, beban, dan kon.disi bataL)lfillg sembarang, Jaring-jaringnya dapat terdiri atas elemen yang berbeda jenis, bentuk dan besaran fisiknya. Kemudahan penggunaap berbagai hal tersebut bisa saja ter­

gabung pada satu program komputer serba guna: yaitu dengan menyiapkan data pemi- lihan jenis, geometri, kondisi batas, elemen, dan sebagainya. Keunggulan lain dari metode elemen hingga adalah adanya

f2')

lirti fisik_yang cukup

��

jaring elemen dengan struktur aJ<tualnya. Jaring yang dirnaksud bukan merupakan abstrak matematis yang sulit untuk divisualisasikan.

� Metode elemen hingga juga mempunyai kekurangan. Hasil yang diperoleh dengan metode ini untuk suatu masalah tertentu adalah berupa hasil numerik: tidak ada�

samaan ,bentuk tertutup yang dapat dipakai untuk kasus serupa yang hanya berbeda 6

(

0

�

pa ram meru�

yasa) sekali progn terjad

!lemen

revolu-

1g segi ur dan

� a akan

-

be ban

al, :in 1gi

metode nasalah . aL-}!3.flg bentuk

;aja ter­

ta pemi- .g cukup d bukan

i

dengan ada�L­

berbeda

I

(a) (b) (c)

Gambar 1.1.4 Setengah lengkungan bendung, dimodelkan sebagai (a) elemen kua­

drilateral dan (b) segitiga "kuadratik", dan (c) elemen tunggal "kubik" (1.1). Titik­

titik simpul elemen diperlihatkan sebagai titik hitam pada gambar.

Gambar 1.1.5 Alat tekanan dengan perkuatan pada satu kepalanya, untuk tujuan khusus. Kesimetrisan ditunjukkan dengan memodelkan segmen simetris dan mene­

rapkan kondisi batas yang sesuai pada permukaan terpotongnya. (Atas izin A. 0.

Smith Corp. Data System Division, Milwaukee, Wisconsin.)

parameternya. Dengan metode ini komputer beserta program yang dapat dipercaya merupakan suatu keharusan. Selain itu diperlukan juga pengalaman dan intuisi reka­

yasa yang bail<, agar diperoleh bentuk jaring yang memadai untuk setiap kasus. Banyak sekali data yang harus dimasukkan, begitu pula data keluaran yang telah disortir oleh program harus dicek kembali. Sekalipun demil<ian, kekurangan seperti ini bukan hanya terjadi pada metode elemen hingga.

7

Gambar 1.1.6 Model terperinci dari setengah rangka mobil, digunakan untuk mencari deformasi, teganganrfrekuensi alami, dan bentuk ragam. (Atas izin A. 0. Smith Corp.,

Data System Division, Milwaukee, Wisconsin.)

Ringkasan sejarah elemen hingga. Pada tahun

1906

dan tahun-tahun berikutnya, para ahli riset mengusulkan metode "analogi

lattice"

untuk memecahkan masalah kontinum

[ 1.2-1.4]

1. Disini suatu Kontinum didekati dengan jaring yang teratur yang terbentuk oleh batang-batang elastis. Selanjutnya metode ini berkembang menjadi metode untuk menganalisis struktur rangka. Pada tahun 1941, seorang ahli matematik Courant (dalam tulisan yang diterbitkan tahun 1943), mengusulkan in terpolasi polinomial bagian-demi-bagian pada daerah segitiga, sebagai cara untuk mendapatkan solusi numerik pendekatan

[ 1.5].

Courant memperkenalkan metodenya sebagai solusi Rayleigh-Ritz untuk masalah variasional. Inilah yang kita kenal sebagai metode elemen hingga dewasa ini. Apa yang telah dikerjakan Courant tersebut semula <kilupakan orang, sampai pada s_uatu saat para rekayasawan berhasil mengembangkannya.

Pada waktu itu, pendapat para ahli masih dianggap tidak praktis karena memang belum ada komputer yang dapat dipakai untuk melakukan perhitungan. Setelah tahun

1953,

para rekayasawan menuliskan persamaan kekakuan dalam notasi matriks dan dapat memecahkan persamaan tersebut dengan menggunakan bantuan komputer digital [

1.6].

Makall)h klasik yang dituiis oleh Turner, Clough, Martin, dan Topp diterbitkan tahun

'1956 [I. 7].

Dengan makalah ini, ditamba11 tulisan-tulisan lainnya

[ 1.8],

mulailah terjadi kemajuan yang sangat pesat dalam pengembangan metode elemen hingga dalam bidang rekayasa. Nama "elemen hingga" disebutkan pertama kali pada tahun

1960 [i.9].

Sejak tahun

1963

metode ini mulai dikenaJ sebagai sesuatu yang sangat menarik dipelajari oleh cendekiawan. Pada tahun

1967,

_banyak

rekayasawan dan matematikawan yang bekerja dengan metode elemen hingga, tetapi tidak saling memperhatikan [

1.1 O].

(Pada dewasa ini kedua kelompok terse but suda11 saling memperhatikan, akan· tetapi sangat jarang matematikawan yang tertarik dengan rekayasa, begitu pula rekayasawan sering sulit mengerti pendapat matematikawan).

Pada tahun

1961

telah diterbitkan sepuluh makalah mengenai elemen hingga,

134

makalah pada tahun

1966,

_dan

844

pada tahun

1971 [5.10].

Pada tahun

1979,

_dua

dekade setelah aplikasi rekayasa dimulai, jumlah komulatif publikasi mengenai elemen hingga telah melampaui

7000 [ 1.19] .

,,,

) .

8

Nomor di dalrun kurung siku menunju)<kan referensi yang dicantumkan di bagian belakang buku ini.

• •