METODE MATRIK APLIKASI METODE MATRIK UNTUK ANALISA STRUKTUR BALOK

(1)

METODE MATRIK

APLIKASI METODE MATRIK

UNTUK ANALISA STRUKTUR BALOK

PENGERTIAN UMUM

Metode matrik adalah suatu pemikiran baru pada analisa struktur, yang

berkembang bersamaan dengan populernya penggunaan computer

otomatis untuk operasi perhitungan aritmatika.

(2)

HAL UTAMA DALAM ANALISA UNTUK MENENENTUKAN BAIK ITU DEFORMASI ATAUPUN STRESS PADA STRUKTUR, IALAH SAMPAI JAUH MANA SUDAH DIKETAHUI SIFAT KARAKTERISTIK HUBUNGAN GAYA DAN DEFORMASI DARI ELEMEN-ELEMEN STRUKTUR, DAN MEMAKSAKAN TERPENUHINYA SYARAT-SYARAT KOMPATIBILITI DAN KESETIMBANGAN, ADA TIGA HAL YANG

MENDASARI ANALISIS INI, YAITU:

1. kesetimbangan

2. hubungan stress dan strain, atau gaya

dalam dan deformasi

3. kompatibiliti,atau kontinuitas

dari

(3)

DALAM ANALISIS MATRIK DIKENAL ADA DUA CARA :

1.

metode kekakuan (stiffness method, atau

displacement method )

2.

metode fleksibilitas (flexibility method, atau force

(4)

METODE KEKAKUAN

Dengan metode kekakuan ini sebenarnya dicari hubungan gaya dengan

lendutan, dinyatakan secara matematis :

D

K

Q

Q _{= gaya yang timbul pada titik-titik diskrit akibat adanya lendutan.}

D _{= lendutan pada titik-titik diskrit}

(5)

Metode Kekakuan Ini Juga Disebut Metode Lendutan

(Displacement Method), Karena Analisa Dimulai Dengan “

Lendutan” Sehingga Dengan Demikian Urutan Kerjanya Secara

Garis Besar Adalah Sebagai Berikut :

• kompabiliti; yaitu mencari hubungan antara deformasi dengan lendutan, atau secara tegasnya mencari deformasi apa yang terjadi pada elemen-elemen dititik-titik diskrit akibat diberikannya lendutan pada struktur dititik-titik tersebut.

• persamaan hubungan stress dan strain, yaitu mencari hubungan mengenai gaya-gaya dalam yang timbul sebagai akibat adanya deformasi pada elemen-elemen pada struktur tersebut.

• kesetimbangan, langkah terakhir yang menyatakan hubungan gaya luar dititik diskrit dengan gaya-gaya dalam atau mencari berapa besar gaya luar di ujung elemen-elemen yang tepat diimbangi oleh gaya-gaya dalam elemen titik-titik diskrit.

(6)

Metode Kekakuan Ialah Suatu Cara Untuk Analisa Struktur Dimana Dalam Proses Perumusan Dari Analisanya Diambil Lendutan Di Titik-titik Diskrit Sebagai Besaraan “Anu” Yang Hendak Dicari.Dalam Proses Menganalisa Akan Mengenal Beberapa Matrix Yang Penting Sebagai Berikut :



matrik deformasi

suatu matrik yang menyatakan

hubungan kompatibiliti atau hubungan deformasi dan

lendutan :

dimana :

= menyatakan deformasi dari elemen struktur

A

D

A

d

A

= adalah matrik deformasi

(7)

MATRIK KEKOKOHAN INTERNEN , SUATU MATRIX YANG MEMENUHI HOKUM HOOKE DALAM MANA DINYATAKAN HUBUNGAN ANTARA GAYA DAN DEFORMASI :

dimana

:

S

d

S

H

=

menyatakan

gaya dalam elemen

S

=_elemenadalah matrix kekokohan intern

(8)

MATRIX STATIS

, SUATU MATRIX YANG MENYATAKAN

KESETIMBANGAN ANTARA GAYA LUAR DAN GAYA DALAM :

B

Q

=

_B

_H

dimana :

Q

= menytakan gaya luar yang bekerja dititik diskrit

B

= matrix statis

H

= gaya dalam elemen

Maka ketiga matrix di atas digabungkan, maka akan didapatkan hubungan :

D K Q D A S B Q d S B Q H B Q

(9)

DIMANA

ADALAH MATRIX KEKAKUAN STRUKTUR, DENGAN

PENGERTIAN

:

Jadi salah satu tujuan terminal yang penting adalah proses analisa ini

ialah dapat menurunkan matrik kekakuan struktur

K

A

S

B

K

Selanjutnya akan mudah dicapai tujuan akhir, yaitu analisa

lendutan dan gaya dalam elemen.

(10)

DERAJAT KETIDAK-TENTUAN KINEMATIS



Untuk analisa ini akan dimulai dengan mengambil

lendutan di titik-titik diskrit sebagai sasaran yang

harus dihitung.



Untuk mengetahui dimana harus “dipasang” besaran

lendutan yang akan dicari tersebut, maka harus

diketahui dahulu beberapa derajat ketidak tentuan

kinematis atau istilah lainnya derajat kebebasan

(11)



Derajat ketidak-tentuan kinematis ialah suatu

besaran yang menyatakan jumlah komponen

bebas dari lendutan dititik diskrit yang mungkin

terjadiyang berhubungan dengan diberikannya

suatu pembebanan pada struktur. Di bawah ini

diberikan beberapa macam struktur bidang

yang akan ditujukkan berapa derajat

ketidak-tentuan kinematisnya.

(12)

struktur Komponen bebas dari lendutan _{di titik pertemuan} Derajat ketidak-tentuan kinematis D1 _D2 D2 D1 2 2 0 (a) (b) (c)

(13)

struktur Komponen bebas dari lendutan _{di titik pertemuan} Derajat ketidak-tentuan kinematis 6 D1 D2 D3 D6 D4 D5 D1 D2 D3 3 Dengan mengabaikan

deformasi aksial dari eleme D1 D3 D6 D5 D7 D4 7 D1 D2 D3 D4 D6 D5 D7 D8 D9 D10 D11 D12 12 (d) (e) (f) (g)

(14)

Gambar 1.1 derajat ketidak-tentuan kinematis dari

struktur

ditunjukkan

oleh

banyaknya

vector

lendutan yang mungkin terjadi di titik bebas,

dimana arah vector pada gambar menunjukkan

arah vector yang positif.

(15)

DASAR PERHITUNGAN

Dalam bab ini, akan dijelaskan secara mendetail

urut-urutan analisa dari suatu konstruksi bidang (dua

dimensi)

dengan

berdasarkan

pada

metode

kekakuan.

Sekarang terlihat satu konstruksi seperti seperti

ditunjukkan pada gambar 2.(a) selanjutnya akan

diikuti urutan dari proses analisa.

(16)

D1 D2

D3

(b) derajat ketidak-tentuan kinematis : 3

D1 D2

D3

Q1 Q2 Q3

(c) diagram gaya luar ekivalen Q

yang koresponding dengan lendutan D sebagai pengganti darisistem pembebanan pada gambar (a)

EI1 EI2 EI3

L1 L2 L3

(17)

D1

d3 d2

(e) diberikan

D

₁

= 1 satuan

D2 d4 d5

(f) diberikan

_{D =1 satuan}

₂ d6 D3

(g) diberikan

D3

=1 satuan

(18)

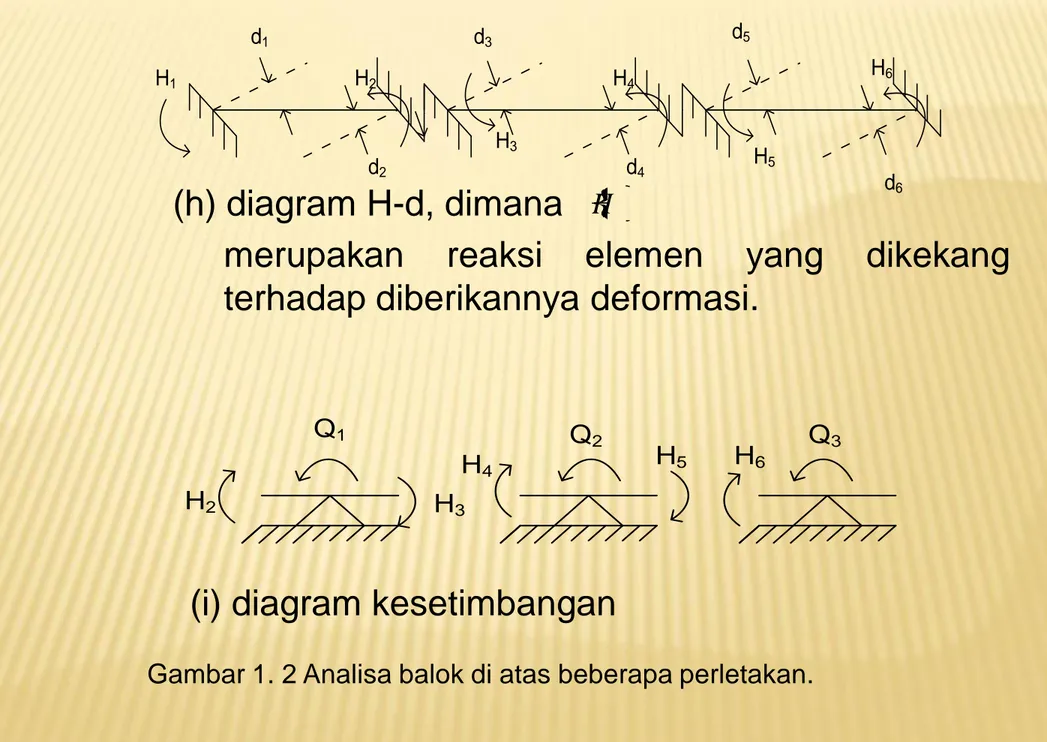
d1 d2 d3 d4 d5 d6 H1 H2 H3 H4 H5 H6

(h) diagram H-d, dimana

H

merupakan

reaksi

elemen

yang

dikekang

terhadap diberikannya deformasi.

Q1 Q₂ Q₃

H2 H₃

H4 H5 H6

(i) diagram kesetimbangan

(19)

Konstruksi Ini Ialah Balok Menerus Di Atas Empat Perletakan, Satu Jepit Dan

Tiga Sendi, Merupakan Suatu Konstruksi Dengan Derajat Ketidak-tentuan

Kinematis Sebesar 3 (Gambar 2.B)



Langkah pertama ialah menyelidiki kompatibilitas dari struktur,

dengan jalan memberikan berturut-turut lendutan



dan

(gambar 2.e, 2.f, dan 2.g).



Mudah dapat kita lihat, bahwa :

1 ,

1

₂ 1

D

₃

1

0 1 3 6 2 5 4 1 3 2 d D d D d d D d d

(20)

atau disusun secara sistematis : 3 6 2 5 2 4 1 3 1 2 1 D d D d D d D d D d d

bila dinyatakan dalam hubungan matrix :

3 2 1 6 5 4 3 2 1 1 0 0 0 1 0 0 1 0 0 0 1 0 0 1 0 0 0 D D D d d d d d d atau

D

A

d

(21)

1

0

1

0

1

0

1

0

1

0

3 2 1 6 5 4 3 2 1

D

d

A

(22)

Langkah kedua ialah menyelidiki hubungan gaya dalam dan deformasi dengan melihat tiap-tiap elemen sebagai bagian yang diskrit, seperti pada gambar 2.h.

Dari sifat elastis elemen,

didapatkan

hubungan :

d1 d2 d3 d4 d5 d6 H1 H2 H3 H4 H5 H6 1 1 2 1 1 1 2 1 1 2 1 1 1 1

3

1

6

1

6

1

3

1 EI

L

H

EI

L

H

d

EI

L

H

EI

L

H

d

(23)

dimana :

1 d

= menyatakan deformasi yang terjadi di ujung elemen

H

=

menyatakan gaya dalam yang ada di ujung elemen,

dalam hal ini momen lentur

diinverskan, akan didapat :

2 1 1 1 1 1 1

2

4 d

L

EI

d

L

EI

H

2 1 1 1 1 1 2

4

2 d

L

EI

d

L

EI

H

4 2 2 3 2 1 3

2

4 d

L

EI

d

L

EI

H

4 2 2 3 2 2 4

4

2 d

L

EI

d

L

EI

H

6 3 3 5 3 3 5

2

4 d

L

EI

d

L

EI

H

6 3 3 5 3 3 6

4

2 d

L

EI

d

L

EI

H

(24)

Bila hubungan ini dinyatakan dalam bentuk matrix, maka : 6 5 4 3 2 1 3 3 3 3 3 3 3 3 2 2 2 2 2 2 2 2 1 1 1 1 1 1 1 1 6 5 4 3 2 1

4

2

0

2

4

0

4

2

0

2

4

0

4

2

0

2

4 d

d

L

EI

L

EI

L

EI

L

EI

L

EI

L

EI

L

EI

L

EI

L

EI

L

EI

L

EI

L

EI

H

(25)

atau :

_H

_S

_d

dimana matrix

S

merupakan matrix

:

3 3 3 3 3 3 3 3 2 2 2 2 2 2 2 2 1 1 1 1 1 1 1 1

4

2

0

2

4

0

4

2

0

2

4

0

4

2

0

2

4 L

EI

L

EI

L

EI

L

EI

L

EI

L

EI

L

EI

L

EI

L

EI

L

EI

L

EI

L

EI

S

6 5 4 3 2 1 d d d d d d

(26)

Jadi Sebenarnya Matrix

Ialah Suatu Matrix Yang Menyatakan

Berapa Besar Gaya Dalam

Yang Timbul Diujung Elemen Bila Di

Titik-titik Tersebut Diberikan Satu Satuan Deformasi .

Langkah ketiga adalah menyelidiki tentang kesetimbangan gaya luar

dan gaya dalam :

Melihat gambar

S

H

d

6 3 5 4 2 5 2 1

H

Q

H

Q

H

Q

(27)

6 5 4 3 2 1 3 2 1

1

0

1

0

1

0 H

H

Q

atau :

H

B

Q

dimana :

6 5 4 3 2 1 3 2 1

1

0

1

0

1

0

H H H H H H

Q

B

(28)

Satu hubungan terminal, adalah mendapatkan hubungan :

D

K

Q

Dimana :

A

S

B

K

untuk mendapatkan lendutan, maka

dapat diinverskan

sebagai :

Q

K

D

1

dimana :

Q

=

menyatakan gaya-gaya luar yang bekerja di titik-titik diskrit.

D

menyatakan

lendutan

di

titik

bersangkutan

yang

berkoresponding dengan gaya

.

(29)

ternyata didapatkan :

T

A

B

prinsip kerja virtual.

Q*

a.gaya luar virtual

D

b. lendutan aktuil

(30)

Misalnya pada konstruksi yang sedang dibahas tersebut

dikerjakan gaya virtual

Q

gambar (1.3a ) sehingga timbul gaya dalam

_H

pada elemennya, maka dari prinsip kerja virtuil akan

didapatkan

hubungan

(yang

dinyatakan

dalam

perkalian matrix).

d

H

D

Q

T

dengan melihat :

T T T

B

H

Q

H

B

Q

D

A

d

(31)

maka persamaan ( ) bisa ditulis ;

D

A

H

D

B

H

T T T

Bila disederhanakan, akan memberikan :

T T A B A B

Dengan demikian persamaan, bisa ditulis :

A

S

A

(32)

Dengan demikian persamaan telah dipermudahkan,

yaitu untuk menurunkan matrix kekakuan

_K

cukup hanya menurunkan dua matrik penbentuknya,

yaitu matrix deformasi

A

dan matrix kekokohan intern elemen S

.

Untuk menghitung gaya dalam digunakan hubungan :

d

S

H

D

A

S

H

atau

(33)

= matrik lendutan dititik diskrit.

D

(34)

APLIKASI

KONSTRUKSI BALOK MENERUS



selanjutnya akan diberikan beberapa contoh

pemakaian metode kekakuan ini pada analisa

struktur.

Contoh 3.1

Di bawah ini akan dibahas secara singkat analisa dengan

metode

kekakuan

dengan

derajat

ketidak-tentuan

kinematik tingkat 1.

(35)

10 m 8 m EI EI 600kg/m A B C

a. konstruksi yang akan dianalisa

b. konstruksi dasar yang dikekang

-5000 +5000 -3200 +3200

(36)

m

kg

M

m

kg

M

CB BC BA AB

.

3200

4 .

600 .

12

1 .

5000

6 .

600 .

12

1

2 2

Momen primer :

D1

d. derajat ketidak-pastian kinematis : 1

Q1=1800kg.m

e. gaya luar ekivalen dititik diskrit yang koresponding

dengan lendutan

.

)

.

(

3200

5000

1

kg

m

Q

(37)

D1 d3 d2

f. diberikan

D

₁

1 satuan

H2 d2 d1 H3 d3 d4 H4

g. diagram

H - d

(38)

H3

H₂

h. diagram kesetimbangan

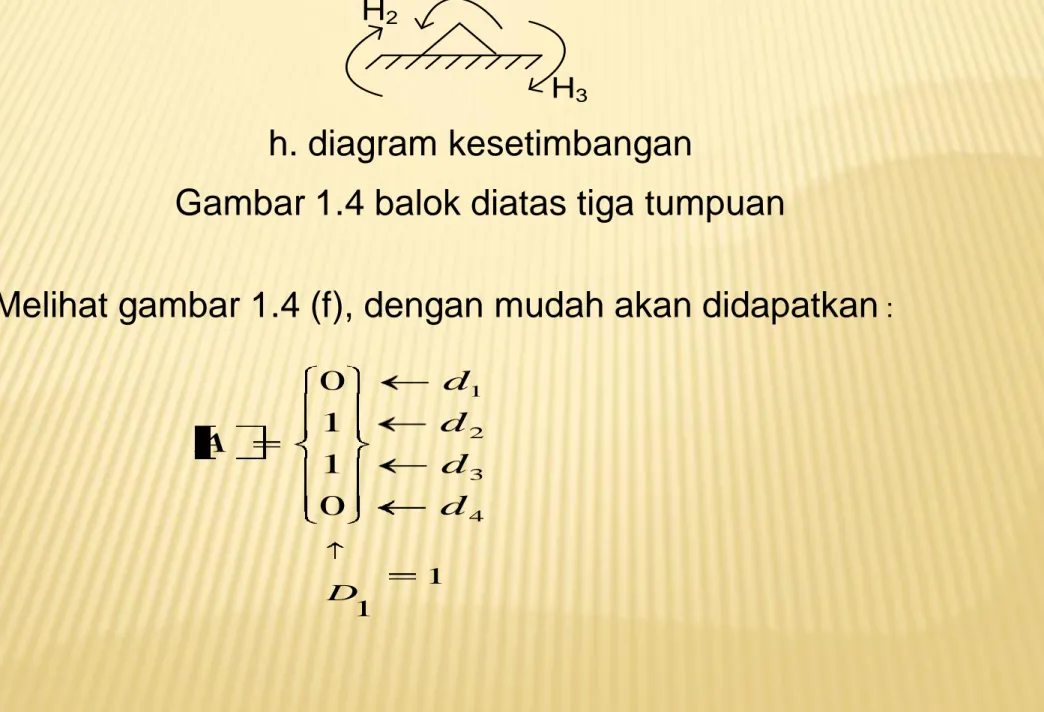
Gambar 1.4 balok diatas tiga tumpuan

Melihat gambar 1.4 (f), dengan mudah akan didapatkan

:

1 1 4 3 2 1 0 1 1 0 D d d d d A

(39)

dari gambar 1.4 (g) :

4 3 2 1 4 3 2 1 8 4 8 2 0 0 8 2 8 4 0 0 0 0 10 4 10 2 0 0 10 2 10 4 d d d d H H H H EI EI EI EI EI EI EI EI S

5 .

0

25 .

0

25 .

0

5 .

0

4 .

0

2 .

0

2 .

0

4 .

0 S

(40)

dari persamaan

:

A

S

A

K

T =

0

1

0

5 .

0

25 .

0

25 .

0

5 .

0

4 .

0

2 .

0

2 .

0

4 .

0 EI

0

1

0

=

₀

_.

₂

₀

_.

₄

₀

_.

₅

₀

_.

₂₅

EI 0 1 1 0

EI

K

EI

K

9 .

0

1

9 .

0

1

(41)

Dengan mengubah gaya Q menjadi gaya titik ekivalen di

ujung elemen (gambar 1.4.c dan e) dan dengan melihat

persamaan (1.25) :

EI

D

EI

D

Q

K

D

2000

1800

9 .

0

1

1 1 1

dari persamaan (1.36) :

D

A

S

H

5 .

0

25 .

0

25 .

0

5 .

0

4 .

0

2 .

0

2 .

0

4 .

0 H

.

2000

25 .

0

5 .

0

4 .

0

2 .

0

(42)

500 1000

800

400

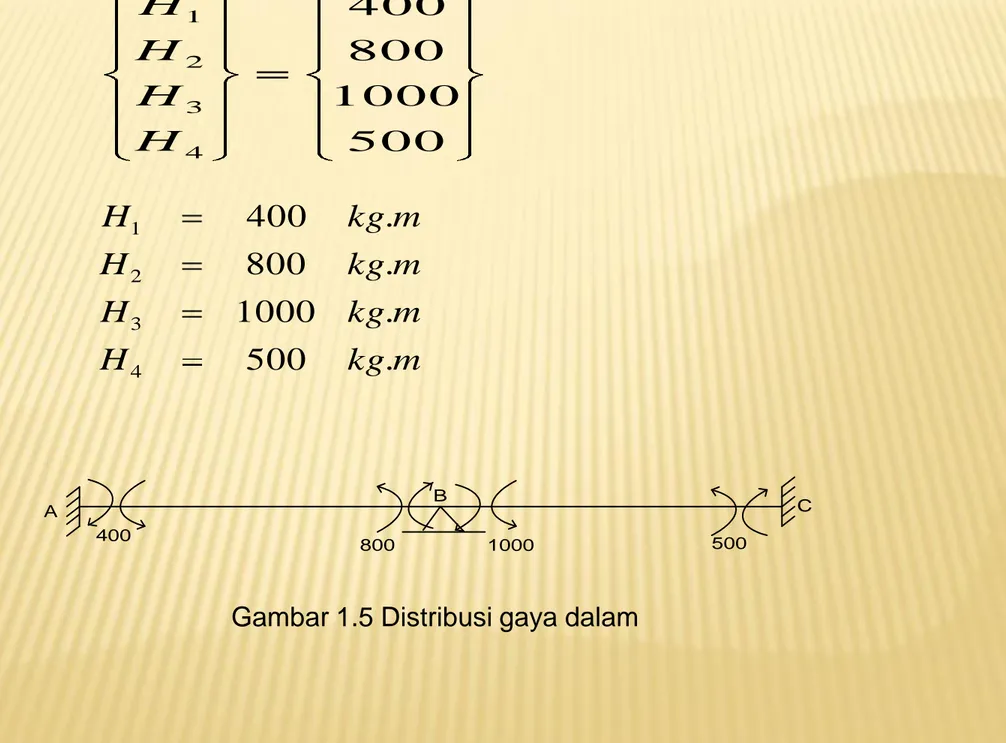
4 3 2 1

H

m

kg

H

m

kg

H

m

kg

H

m

kg

H

.

500 .

1000

.

800 .

400

4 3 2 1 400 800 1000 500 A B C

(43)

hasil yang ditunjukkan oleh gambar 1.5 ialah menyatakan besarnya

momen lentur (dalam hal ini sebagai momen batang, bukan sebagai

momen titik) yang didistribusikan ke batang elemen AB dan BC sesuai

dengan kekakuan masing-masing . jadi gaya dalam

yang didapat

dari hasil perhitungan ini bukan merupakan memen lentur yang

sebenarnya bekerja.

H

Momen lentur

yang sebenarnya bekerja bisa diperoleh dengan

mengurangi gaya dalam dengan momen primer elemen struktur.

H

m

kg

M

m

kg

M

m

kg

M

m

kg

M

C BC BA A

.

2700

)

3200

(

500 .

4200

)

3200

(

1000

.

4200

)

5000

(

800 .

5400

)

5000

(

400

(44)

Penting untuk dicatat pula di sini, bahwa hasil momen akhir

ini juga menyatakan momen batang bukan momen titik.

Contoh 1.2

Sebagai contoh kedua akan dibahas suatau konstruksi

kinematis tertentu seperti pada gambar 1.6 (a).

A C B

4m 6m

EI EI

Q=1000 kg

a. konstruksi yang akan dianalisa dengan beban

(45)

b. struktur dasar yang dikekang

C D1

D2

c. derajat ketidak-tentuan kinematis : 2

(d) diberikan

D

1= 1 satuan d4 d3 d2 d1 D1

(46)

D2 d3 d2

e. diberikan

_D

₂

= 1 satuan

H3 d1 d2 H2 H3 d3 d4 H4

f. diagram H-d

(47)

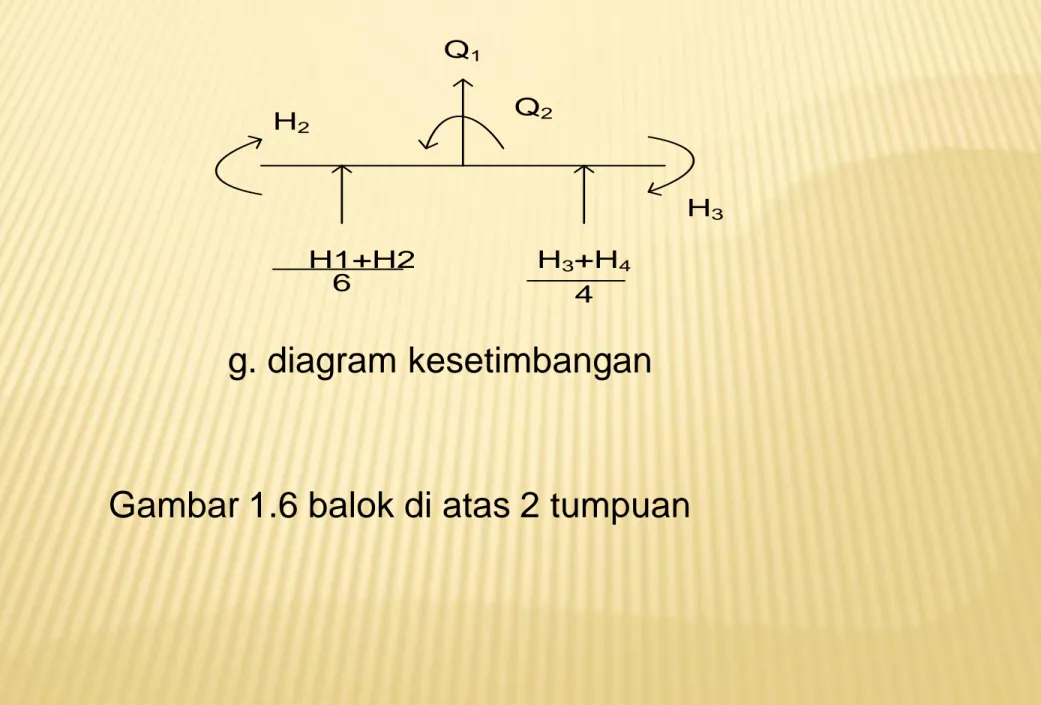
H3+H4 H1+H2 6 ₄ Q₂ Q1 H2 H₃

g. diagram kesetimbangan

(48)

Langkah pertama yang dilakukan ialah menganggap

konstruksi ini terdiri atas dua elemen diskrit. AC dan

CB ( gambar 3.6 b). titik C segai titik diskrit

mempunyai dua derajat kebebasan, yaitu translasi

dan rotasi.

Melihat

gambar

3.6,

akan

didapat

hubungan-hubungan sebagai berikut :

1 2 1 4 3 2 1 0 4 1 1 4 1 1 6 1 0 6 1 D D d d d d A d4 d3 d2 d1 D1

(49)

6 5 4 3 2 1 3 3 3 3 3 3 3 3 2 2 2 2 2 2 2 2 1 1 1 1 1 1 1 1 6 5 4 3 2 1

4

2

0

2

4

0

4

2

0

2

4

0

4

2

0

2

4 d

d

L

EI

L

EI

L

EI

L

EI

L

EI

L

EI

L

EI

L

EI

L

EI

L

EI

L

EI

L

EI

H

(50)

4

2

0

4

2

4

0

6

4

6

2

0

6

2

6

4 EI

S

4

3

2

1

4

3

2

1

2

1

0

2

1

0

3

2

3

1

0

3

1

3

2 EI

(51)

selanjutnya dihitung matrix kekakuan

K

:

A

S

A

K

T

1

2

1

0

2

1

0

3

2

3

1

0

3

1

3

2

0

1

0

4

1

4

1

6

1

6

1 _EI

0

4

1

4

1

6

1

0

6

1 EI

0

4

1

4

1

6

1

0

6

1

2

1

3

2

3

1

8

3

8

3

6

1

6

1

(52)

EI

K

6667

.

1 2083

.

0 2083

.

0 2430

.

0 2430

.

0 2083

.

0 2083

.

0 6667

.

1 3617

.

0

1

EI

K

EI

D

89 .

575

85 .

4607

2 1

selanjutnya akan bisa dihitung gaya dalam :

D

A

S

H

(53)

= EI

1

2

1

0

2

1

0

3

2

3

1

0

3

1

3

2

0

4

1

4

1

6

1

0

6

1

EI EI 89 . 575 85 . 4607 = EI 2 1 8 3 1 8 3 3 2 6 1 3 1 6 1

EI

89 .

575

85 .

4607

(54)

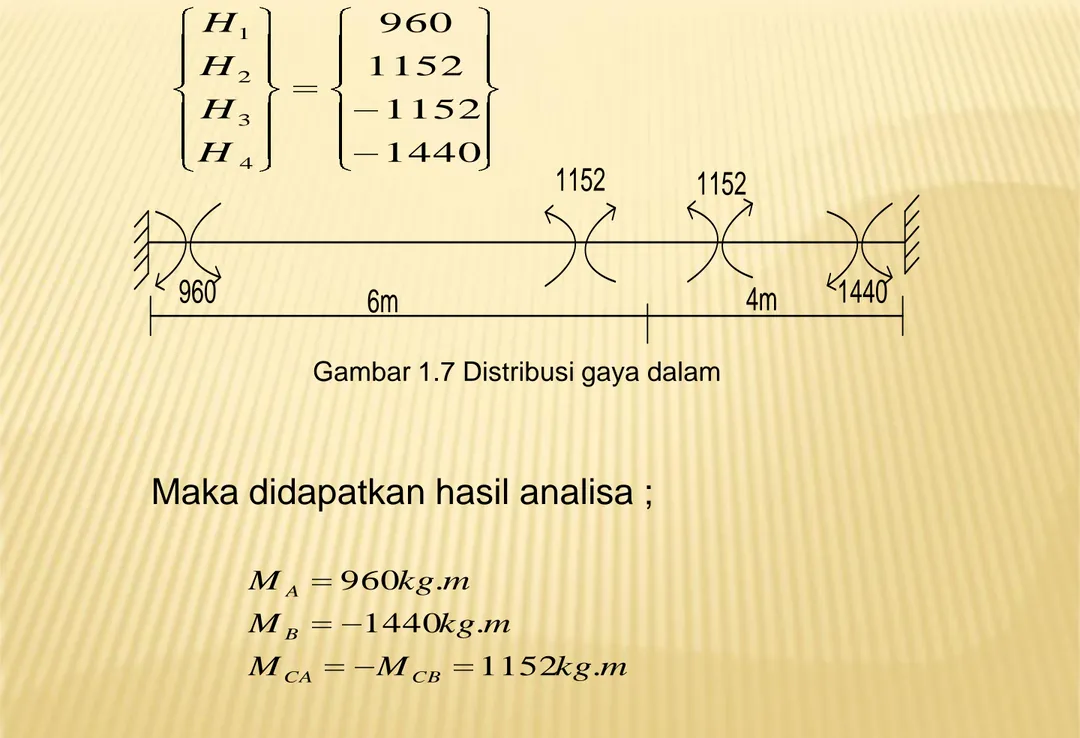
1440 1152 1152 960 4 3 2 1 H H H H

4m

6m

1440

1152

960

Gambar 1.7 Distribusi gaya dalam

Maka didapatkan hasil analisa ;

m kg M M m kg M m kg M CB CA B A . 1152 . 1440 . 960

(55)

Bila dibandingkan hasil ini dengan rumus yang sudah diketahui :

m

kg

M

m

kg

M

B A

.

1440

10

4 .

6 .

1000

.

960

10

4 .

6 .

1000

2 2 2 2

(56)

Contoh 1.3

Pada contoh soal selanjutnya ini, akan diperlihatkan

bagaimana proses analisa bila konstruksi pada contoh

1.2 dikombinasikan dengan suatu perletakan elastis di

titik C.

A B C 4m 6m EI Q=1000 kg k=0.5EI

(a) konstruksi yang akan dianalisa, dengan satu perletakan elastis

dimana k = 0.5 EI

(57)

L L

D1

D2

(b) derajat ketidak-tentuan kinematsi : 2

d4 d3 d2 d1 D1

(c) deberikan

_D

₁

= 1 satuan

(58)

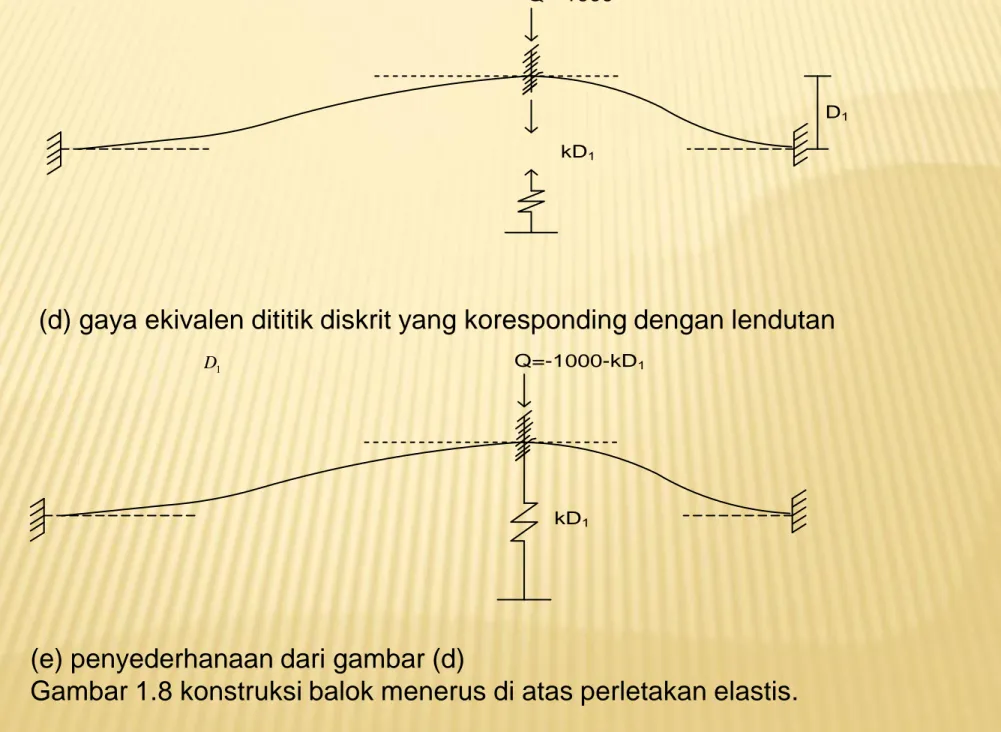
Q=-1000

kD1

D1

(d) gaya ekivalen dititik diskrit yang koresponding dengan lendutan

1

D Q=-1000-kD1

kD1

(e) penyederhanaan dari gambar (d)

(59)

Persoalan pada contoh ini sebenarnya sama dengan contoh 1.2, karena memunyai elemen batang yang sama dengan derajat kebebasan yang sama pula . maka proses analisa tidak akan mendetail dibahas lagi disini, dan langsung akan matrik kekakuan :

EI

K

6667

.

1 2083

.

0 2083

.

0 2430

.

0 2430

.

0 2083

.

0 2083

.

0 6667

.

1 3617

.

0

1

EI

K

Proses selanjutnya akan terlihat adanya perbedaan dengan analisa contoh soal yang lalu, yaitu dalam menetapklan vector gaya yang bekerja, yang disamping ditentukan oleh gaya luar yang dikethui

_Q

_1000kg

_,

(60)

Q

K

D

1 2 1

D

2430

.

0 2083

.

0 2083

.

0 6667

.

1 3617

.

0

1 EI

0 ) 1000 ( kD₁ 1

D

EI

3617

.

0

1 )

1000

(

6667

.

1 .

kD

₁ 1 1 1 1

304 .

2 4608

)

5 .

0 1000

(

3617

.

0 6667

.

1 D

EI

D

EID

EI

D

EI

D

EI

D

7 .

1394

4608

304 .

3

1 1

(61)

))

7 .

1394

5 .

0 1000

(

2083

.

0 (

3617

.

0

1

2

EI

D

EI

D

₂

174 .

3 berdasarkan hasil lendutan

_{D dan}

₁

2

D

yang didapat, bisa dihitung gaya dalam yang timbul

pada elemen struktur.

EI

H

2 1 8 3 1 8 3 3 2 6 1 3 1 6 1

EI

3 .

174

7 .

1394

(62)

9 .

435

7 .

384

7 .

348

5 .

290

4 3 2 1

H

Dengan demikian didapatkan hasil analisa :

m

kg

M

m

kg

M

m

kg

M

m

kg

M

B CB CA A

.

9 .

435 .

7 .

348 .

7 .

348 .

5 .

290

(63)

(64)

KONSTRUKSI PORTAL BIDANG TANPA

PENGGOYANGAN DIMANA DIFORMASI

AKSIAL DIABAIKAN

Dalam hal ini akan dibahas analisa dari konstruksi portal

bidang. Diketahui dua macam konstruksi portal bidang ,

yaitu portal tanpa penggoyangan dan portal dengan

penggoyangan, seperti ditunjukkan oleh gambar 1.2.

Dalam pasal ini akan dicoba dibahas analisa portal bidang

tanpa pergoyangan, dimana deformasi aksial dari

elemen-elemennya diabaikan.

(65)

(a)Portal tanpa penggoyangan.

b. portal menerus tanpa pergoyangan

(66)

(c) portal dengan penggoyangan

(67)

Contoh 1.1

Dalam pasal ini akan dibahas analisa portal bidang

tanpa pergoyangan, dimana deformasi aksial dari

elemen-elemennmya diabaikan.

600kg _600kg Q=300kg/m EI EI 5 m A B C C 2 m 3 m

(a) portal bidang yang akan dianalisa, dengan bentuk konstruksi dan system pembebanan yang simetris

(68)

A

B C

D

( b) struiktur dasar yang dikekang Momen primer :

m

kg

M

_AB

288 .

5

2 .

3 .

600

2 2

m

kg.

432

5

2 .

3 .

600

2 2 BA

M

(69)

m

kg

M

_BC _CB

.

300 .

5

625 .

12

1

₂

m

kg

M

_CD _BA

432 .

m

kg

M

_CD _AB

288 .

A B C D 432 625 625 432 288 288 cMomen primer

(70)

D2

D1

d. derajat ketidak-pastian kinematis : 2

Q1=-193

Q2=-193

(71)

m

kg

Q

m

kg

Q

.

193

432

625 .

193

625

432

2 1 C D1 d3 d2 f. diberikan D =1 satuan

(72)

D2 d5 d4

g. diberikan

D

₂= 1

satuan

H1 d1 H2 H3 d2 d3 _d 4 H4 H5 d5 d6 H6 h. Diagram H-d

(73)

H3 H2 Q1 Q2 H5 H4 (i ) diagram kesetimbangan

Gambar 1.3 Portal simetris

Dengan memperhatikan gambar 1.3 akan didapatkan :

1 1 0 0 1 0 1 0 0 1 0 1 0 0 2 1 6 5 4 3 2 1 D D d d d d d d A

(74)

5 4 5 2 0 0 0 0 5 2 5 4 0 0 0 0 0 0 5 ) 2 ( 4 5 ) 2 ( 2 0 0 0 0 5 ) 2 ( 2 5 ) 2 ( 4 0 0 0 0 0 0 5 4 5 2 0 0 0 0 5 2 5 4 EI S =

5 2EI

6

5

4

3

2

1

2

1

0

1

2

0

4

2

0

2

4

0

2

1

0

1

2

6

5

4

3

2

1

(75)

3 3 3 3 3 3 3 3 2 2 2 2 2 2 2 2 1 1 1 1 1 1 1 1

4

2

0

2

4

0

4

2

0

2

4

0

4

2

0

2

4 L

EI

L

EI

L

EI

L

EI

L

EI

L

EI

L

EI

L

EI

L

EI

L

EI

L

EI

L

EI

S

(76)

Dengan demikian :

A

S

A

K

T

0

1

0

1

0

5 2EI

2

1

0

1

2

0

4

2

0

2

4

0

2

1

0

1

2

0

1

0

1

0

1

0

1

0

5 2EI

1 2 4 2 0 0 0 0 2 4 2 1 0 0 1 0 1 0 0 1 0 1 0 0

K

=

5 2EI

6

2

6

(77)

Dengan mengubah gaya-gaya luar menjadi gaya ekivalen

terpusat di ujung elemen atau di titik-titik diskrit ( 1. 3.c dan e ),

dan dengan melihat persamaan :

Q

K

D

1

4

36

1 .

2

5

2 1

EI

D

193

6

2

6

=

1544

64

5 EI

2 1

D

=

EI

8

965

8

965

(78)

Jadi putaran sudut dititik B dan C ialah sebesar :

EI

D

8

965

2 1

Dari persamaan ( 1.36)

D

A

S

H

=

EI

2

5

2

1

0

1

2

0

4

2

0

2

4

0

2

1

0

1

2

0

1

0

1

0

1

0

1

0

0 EI

EI

8

965

8

965

(79)

4 1934 193 1 0 2 0 4 2 2 4 0 2 0 1 6 5 4 3 2 1 H H H H H H = 25 . 48 5 . 96 5 . 96 5 . 96 5 . 96 25 . 48

Melihat momen primernya pada gambar (1.3.c), maka akan didapat :

m kg M m kg M m kg M m kg M m kg M m kg M D CD CB BC BA AB . 75 . 239 ) 288 ( 25 . 48 . 50 . 528 ) 432 ( 50 . 96 . 50 . 528 ) 625 ( 50 . 96 . 50 . 528 ) 625 ( 50 . 96 . 50 . 528 ) 432 ( 50 . 96 . 75 . 239 ) 288 ( 25 . 48

(80)

(81)

Contoh 1.2 :

Sekarang Akan Dibahas Analisa Portal dengan adanya penahanan kesamping

400kg

q= 600kg/m

A

B

C

D

_2EI

_F

_2EI

_G

_2EI

EI

2.00

1.00

5.00

2.00 1000kg

(82)

A

B

E _F

b. Struktur dasar yang dikekang

Momen primer :

m

kg

M

_ED

400 .

2

800 .

m

kg

M

_EF _FE

.

800 .

5 1250

.

12

1

₂

m

kg

M

_FC _CF

.

600 .

5 1250

.

12

1

₂

m

kg

M

_FB _BF

.

1000

.

4

500 .

8

1

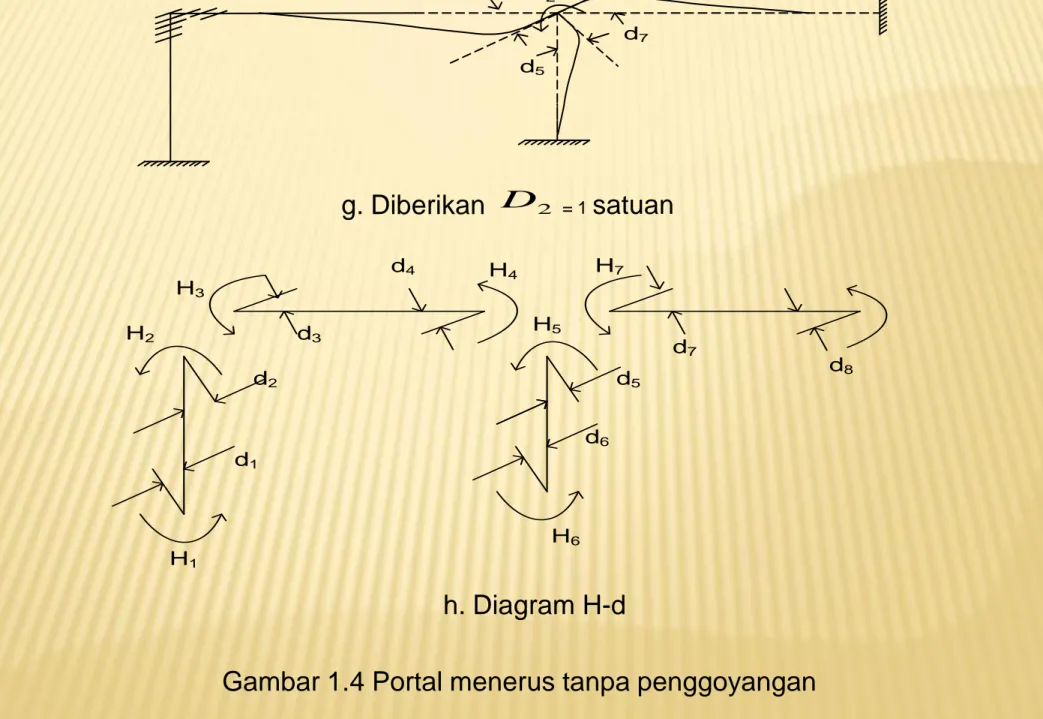
(83)

800 1250 _{1250 1250} 500 1250 500 b. Momen primer D1 D₂

(84)

Q2=-500

Q1=-450

d. Gaya ekivalen Q dititik diskrit yang koresponding dengan lendutan D

D1

d3

d2

(85)

d7 D2 d5 d4 g. Diberikan D2 = 1satuan H3 H2 H1 H6 H4 H7 H5 d1 d2 d3 d4 d5 d6 d7 d8 h. Diagram H-d

(86)

Dimulai dengan menghitung matrik

_A

_dan

S

1

0

1

0

1

0

1

0

1

0

1

0

2 1 8 7 6 5 4 3 2 1

D

d

A

5 ) 2 ( 4 5 ) 2 ( 2 0 0 0 0 0 0 5 ) 2 ( 2 5 ) 2 ( 4 0 0 0 0 0 0 0 0 4 4 4 2 0 0 0 0 0 0 4 2 4 4 0 0 0 0 0 0 0 0 5 ) 2 ( 4 5 ) 2 ( 2 0 0 0 0 0 0 5 ) 2 ( 2 5 ) 2 ( 4 0 0 0 0 0 0 0 0 5 4 5 2 0 0 0 0 0 0 5 2 5 4 EI S

(87)

8 7 6 5 4 3 2 1 18 8 0 0 0 0 0 0 8 16 0 0 0 0 0 0 0 0 5 10 0 0 0 0 0 0 5 10 0 0 0 0 0 0 0 0 8 16 0 0 0 0 0 0 8 16 0 0 0 0 0 0 0 0 8 4 0 0 0 0 0 0 4 8 10 EI

S

Matrik kekakuan struktur dapat dihitung berdasarkan persamaan :

A

S

A

(88)

0

1

0

1

0

1

0

10 EI

18

8

0

8

16

0

5

10

0

5

10

0

8

16

0

8

16

0

8

4

0

4

8

0

1

0

1

0

1

0

1

0

1

0

=

8

16

5

10

16

8

0

8

16

8

4

10 EI

0

1

0

1

0

1

0

1

0

1

0

(89)

K

10 EI

42 8 8 24 1 K

10 EI

944

1 x

24

8

42

12

4

21

236

5 EI

2 1

D

12 4 4 21 236 5 EI

₅₀₀

450

2 1

D

EI

236

5

4200 7450 EI D EI D 236 21000 236 37250 2 1

D

A

S

H

(90)

10 EI

18 8 0 0 0 0 0 0 8 16 0 0 0 0 0 0 0 0 5 10 0 0 0 0 0 0 5 10 0 0 0 0 0 0 0 0 8 16 0 0 0 0 0 0 8 16 0 0 0 0 0 0 0 0 8 4 0 0 0 0 0 0 4 8 0 0 1 0 0 0 1 0 1 0 0 1 0 1 0 0

EI

236 21000

236 37250

8 0 16 0 5 0 10 0 16 8 8 16 0 8 0 4

236 21000

236 37250

(91)

19 . 71 38 . 142 49 . 44 98 . 88 64 . 268 73 . 323 27 . 126 14 . 63 H

Dengan memperhatikan momen primer dari elemen-elemen struktur maka akan didapat :

m

kg

M

_A

63 .

14

0

63 .

14 .

m kg M_EA 126.27 0 126.27 . m kg M_ED 0 ( 800) 800 .

m

kg

M

_EF

323 .

73 (

1250

)

926 .

27 .

.

m

kg

M

_FE

268 .

64 (

1250

)

1518

.

64 .

m

kg

M

_FB

88 .

98 (

500 )

411 .

02 .

m kg M_FC 142.38 ( 1250) 1107.62 . m kg M_B 44.49 ( 500) 544.49 . m kg M_C 71.19 ( 1250) 1321.19 .

(92)

Sekarang ditinjau apakah kesetimbangan dititik-titik pertemuhan terpenuhi : EF ED EA E

M

= -126.27-800+926.27 = 0 (terpenuhi) FC FB FE E

M

= -1518.64 + 411.02 + 1107.62 = 0 (terpenuhi)

(93)

Setelah matrik kekakuan struktur di atas disusun sesuai

dengan kebutuhan yaitu untuk mendapatkan matrik

yang

berukuran 3 x 3, maka dilakukan kondensasi statik.

K oo ot to tt

K

!

Matrik

K

setelah dikakukan kondensasi adalah :

ot

oo

to

tt

x

K

₃

1

(94)

(95)

KONSTRUKSI PORTAL BIDANG DENGAN PERGOYANGAN

DIMANA DEFORMASI AKSIAL DIABAIKAN

Setelah pada pasal yang lalu dibahas analisa portal tanpa

penggoyangan,

sekarang

akan

dicoba

menganalisa

kostruksi portal dengan pergoyangan, dimana deformasi

aksial masih diabaikan.

Contoh 1 :

Di bawah ini diberikan satu contoh analisa portal

sederhana dengan penggoyangan kesamping.

(96)

(97)

(98)

(99)

3 2 1 6 5 4 3 2 1 0 0 4 1 1 0 4 1 1 0 0 0 1 0 0 1 4 1 0 0 4 1 D D D d d d d d d A 4 4 4 2 0 0 0 0 4 2 4 4 0 0 0 0 0 0 4 ) 2 ( 4 4 ) 2 ( 2 0 0 0 0 4 ) 2 ( 2 4 ) 2 ( 4 0 0 0 0 0 0 4 4 4 2 0 0 0 0 4 2 4 4 EI S

(100)

= 2 EI

6

5

4

3

2

1

6 5 4 3 2 1 2 1 0 0 0 0 1 2 0 0 0 0 0 0 4 2 0 0 0 0 2 4 0 0 0 0 0 0 2 1 0 0 0 0 1 2

Selanjutnya bisa dihitung matrik kekakuan struktur

_K

A

S

A

K

T 0 0 4 1 1 0 4 1 1 0 0 0 1 0 0 1 4 1 0 0 4 1 2 1 0 0 0 0 1 2 0 0 0 0 0 0 4 2 0 0 0 0 2 4 0 0 0 0 0 0 2 1 0 0 0 0 1 2 0 1 1 0 0 0 0 0 0 1 1 0 4 1 4 1 0 0 4 1 4 1 2 EI

(101)

0

4

1

0

4

1

0

1

0

1

4

1

0

4

1

2

4

2

0

2

4

2

1

4

3

4

3

0

4

3

4

3

2 EI

K

=

2 EI

6 2 4 3 2 6 4 3 4 3 4 3 4 3 =

8 EI

24 8 3 8 24 3 3 3 3

(102)

63

15

48

15

63

48

512 1248

1 .

8

1

EI

K

63

15

48

15

63

48

512

156

1

EI

K

Setelah

_K

_dan

_K

1

maka besar lendutan dan gaya-gaya dalam akan dapat dengan mudah ditentukan. dihitung,

D

K

1

Q

3 2 1

D

63 15 48 15 63 48 48 48 512 156 1 EI

500

500 1000

(103)

3 2 1

D

EI

156

1 9000

87000

512000

EI

D

₁

3282

.

05 /

EI

D

₂

557 .

69 /

EI

D

₃

57 .

69 /

2 EI

H

2 1 0 0 0 0 1 2 0 0 0 0 0 0 4 2 0 0 0 0 2 4 0 0 0 0 0 0 2 1 0 0 0 0 1 2

0

4

1

0

4

1

0

1

0

1

4

1

0

4

1 EI

EI

/

69 .

57 /

69 .

557 /

05 .

3282

(104)

2

1

0

4

1

2

0

4

1

4

2

0

2

4

0

2

4

3

0

1

4

3

69 .

57

69 .

557

05 .

3282

6

5

4

3

2

1

92 .

1201

07 .

1173

07 .

673

07 .

1173

07 .

673

92 .

951 H

(105)

Dengan memperhatikan momen primer dari elemen-elemen struktur, maka akan didapat :

m

kg

M

_A

951 .

92

0

951 .

92 .

m

kg

M

_CA

673 .

07

0

673 .

07 .

m

kg

M

_CD

1173

.

07 (

500 )

673 .

07 .

m

kg

M

_DC

673 .

07 (

500 )

1173

.

07 .

m

kg

M

_DB

1173

.

07

0 1173

.

07 .

m

kg

M

_B

1201

.

92

0 1201

.

92 .

(106)

Contoh 2

Dibawah ini akan dicoba menganalisa satu portal sederhana dengan

pergoyangan sate arah yaitu mendataryang dikombinasikan dengan pegas, dengan kontanta pegas k. Beban-beban dan ukuran konstruksi diambil sama dengan contoh : 1.

(107)

(108)

Persoalan kekakuan struktur pada contoh soal ini adalah sama dengan contoh 1, jadi proses menghitung kekakuan

K

adalah sama dengan contoh tersebut.

K

8 EI

24 8 3 8 24 3 3 3 3

63

15

48

15

63

48

512

156

1

EI

K

D

_K

1

_Q

3 2 1

D

63 15 48 15 63 48 48 48 512 156 1 EI 500 500 . 1000 k D₁

(109)

D

K

1

Q

3 2 1

D

1 1 1

.

48 9000

48 37000

.

512 512000

156

1 D

k

kD

D

k

EI

)

.

512 512000

(

156

1

1 1

k

D

EI

D

untuk

k

EI

4

1

1 1

3282

.

05 /

EI

08205

D

EI

D

3282

.

05 /

8205

.

1

₁

EI

D

₁

1802

.

82 /

kg

kD

₁

450 .

70

(110)

2

D

.

1802

.

82 /

)

4

1 .

48 87000

(

156

1 EI

EI

D

₂

419 .

01 /

)

/

82 .

1802

.

4

1 .

48 9000

(

156

1

3

EI

D

EI

D

₃

80 .

986 /

D

A

S

H

EI

/

986 .

80 /

01 .

419 /

82 .

1802

1

0

4

3

2

0

4

3

4

2

0

2

4

0

2

4

3

0

1

4

3

2

(111)

55 .

716

04 .

757

04 .

257

04 .

757

04 .

257

55 .

466 H

Dengan memperhatikan momen primer dari elemen-elemen struktur , maka akan didapatkan :

m

kg

M

_A

466 .

55 .

m

kg

M

_CA

257 .

04 .

m

kg

M

_CD

757 .

04 (

500 )

257 .

04 .

m

kg

M

_DC

257 .

04 (

500 )

757 .

04 .

m

kg

M

_DB

757 .

04 .

m

kg

M

_B

716 .

55 .

(112)

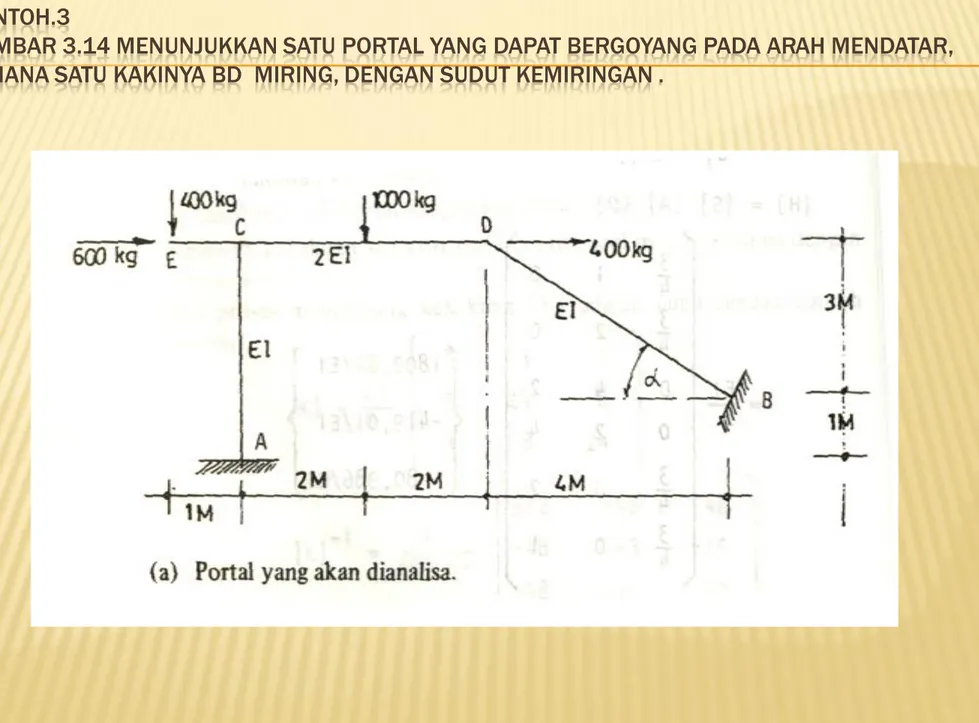
CONTOH.3

GAMBAR 3.14 MENUNJUKKAN SATU PORTAL YANG DAPAT BERGOYANG PADA ARAH MENDATAR, DIMANA SATU KAKINYA BD MIRING, DENGAN SUDUT KEMIRINGAN .

(113)

(114)

(115)

Dengan memperhatikan gambar 3,14 dan memperhatikan bahwa deformasi

aksial akibat diberikannya lendutan dan adalah sama dengan

contoh-contoh yang lalu, maka akan dapat menurunkan

D

2

D

3 matrik dan matrik .

A

_S

3 2 1 6 5 4 3 2 1 0 0 ) 5 )( 3 ( 5 1 0 ) 5 )( 3 ( 5 1 0 ) 4 )( 3 ( 4 0 1 ) 4 )( 3 ( 4 0 1 4 1 0 0 4 1 D D D d d d d d d A

(116)

0 0 3 1 1 0 3 1 1 0 3 1 0 1 3 1 0 1 4 1 0 0 4 1 5 4 5 2 0 0 0 0 5 2 5 4 0 0 0 0 0 0 4 ) 2 ( 4 4 ) 2 ( 2 0 0 0 0 4 ) 2 ( 2 4 ) 2 ( 4 0 0 0 0 0 0 4 4 4 2 0 0 0 0 4 2 4 4 EI S

(117)

10 EI

6 5 4 3 2 1

6

5

4

3

2

1

8

4

0

4

8

0

20

10

0

10

20

0

10

5

0

5

10

Selanjutnya :

A

S

A

K

T

(118)

8

4

0

4

8

0

20

10

0

10

20

0

10

5

0

5

10

0

1

0

1

0

3

1

3

1

3

1

3

1

4

1

4

1 EI

0 0 3 1 1 0 3 1 1 0 3 1 0 1 3 1 0 1 4 1 0 0 4 1 =

4

8

20

10

0

10

20

10

5

4

10

4

15

4

15

10 EI

0

3

1

0

3

1

0

3

1

0

1

3

1

0

1

4

1

0

4

1

(119)

K

28

10

6

10

30

25 .

6

25 .

6

208 .

11

10 EI

18 .

297

58 .

74

5 .

117

58 .

74

82 .

277

115

5 .

117

115

740

17 .

6870

1 .

10

1

EI

K

433 .

0

109 .

0

171 .

0

109 .

0

404 .

0

167 .

0

171 .

0

167 .

0

007 .

1

1 EI

Q

K

D

1 3 2 1

D

433 .

0

109 .

0

171 .

0

109 .

0

404 .

0

167 .

0

171 .

0

167 .

0

007 .

1

1 EI

500

100

34 .

333

(120)

3 2 1

D

EI

/

152 .

284 /

921 .

38 /

823 .

427 D

A

S

H

0 0 3 1 1 0 3 1 1 0 3 1 0 1 3 1 0 1 4 1 0 0 4 1 8 4 0 0 0 0 4 8 0 0 0 0 0 0 20 10 0 0 0 0 10 20 0 0 0 0 0 0 10 5 0 0 0 0 5 10 10 EI EI EI EI / 152 . 284 / 921 . 38 / 823 . 427

(121)

4

0

4

8

0

4

20

10

20

10

0

10

4

15

0

5

4

15

10 EI

EI

/

152 .

284 /

921 .

38 /

823 .

427

790 .

284

451 .

398

560 .

101

514 .

122

513 .

121

973 .

140 H

(122)

Momen akhir :

primer

Momen

H

m

kg

m

kg

m

kg

m

kg

m

kg

m

kg

m

kg

M

B DB DC CD CE CA A

.

790 .

284 .

440 .

389 .

440 .

389 .

487 .

278 .

400 .

513 .

121 .

973 .

140 )

500 (

)

500 (

)

400 (

790 .

284

451 .

398

560 .

101

514 .

221

513 .

121

973 .

140

(123)

KONSTRUKSI RANGKA BATANG DENGAN TITIK HUBUNG

ENGSEL

Pada pasal-pasal yang lalu, telah dibahas analisa struktur dengan sambungan kaku dimana deformasi normal masih diabaikan.

Sekarang akan dapat dianalisa konstruksi rangka batang yang justru dianggap hanya mengalami deformasi normal (aksial) saja.

Sebenarnya proses analisanya adalah sama dengan yang telah dilakukan pada pasal-pasal yang lalu, hanya berbeda pada cara memberikan vector lendutan, dimana hanya ada vector lendutan translasi saja, dan matrik S yang meyatakan hubungan gaya dalam dan deformasi, baik gaya dalam maupun deformasi yang timbul hanyalah bersifat aksial saja. Contoh terlihat di bawah ini.

(124)

(125)

(126)

(127)

Gamnbar 3.15 Konstruksi Rangka Batang

Memperhatikan gambar 3.15, akan dengan mudah dapat ditentukan matrik