時間序列分析–總體經濟與財務金融之應用–

時間序列分析

– 總體經濟與財務金融之應用 _–

共整合與向量誤差修正模型

陳旭昇

2013.12

1 共整合關係

2 共整合與共同隨機趨勢

3 向量誤差修正模型

4 共整合分析

5 共整合分析I: Engle-Granger兩階段程序

6 共整合分析II: Johansen程序

7 共整合分析的實例應用_:利率期限結構

共整合關係

共整合關係

我們將定態時間序列稱為零階整合(integrated of order zero)序列_, 簡稱_I(0)序列_,並以 _{yt ∼I(0)}代表_yt為一個零階整合序列。

如果一個序列經過一階差分後為定態_,則稱此序列稱為一階整合 (integrated of order one)序列_,亦即_I(1)序列_,並以_zt∼I(1)表示 之。

∆z_t= (1−L)z_t ∼I(0), 則_zt∼I(1);同理_,當

∆^dx_t= (1−L^d)x_t ∼I(0), 則_xt為_I(d)序列。

共整合關係

共整合關係

定義₍共整合關係₎

給定_k×1的向量序列_yt,如果_yt∼I(1),且存在一個_k×γ矩陣_β使得 β^′yt ∼I(0)

則我們稱_yt中的_k個序列具共整合關係_,而矩陣_β中的_γ個向量就稱做共整合向量 (cointegrating vectors)。

簡單地說_,共整合關係的意義就是_,將一群_I(1)序列做某一線性組合後變 成一個新序列_,而該新序列竟然變成_I(0)序列_!

共整合關係

例子 _: 貨幣需求函數

m_t=β₀+β₁p_t+β₂y_t+β₃r_t+e_t,

其中_mt,pt,yt以及_rt分別代表 貨幣需求_,物價水準_,實質所得與名目利 率。除了名目利率之外_,其他變數均已取對數。 由於實證上發現

m_t,p_t,y_t與_rt均為_I(1)序列_,而貨幣需求的干擾 e_t =m_t−β₀−β₁p_t−β₂y_t−β₃r_t 必須是_I(0)序列。

共整合關係

例子 _: 貨幣需求函數

如果_et不是定態_,則代表貨幣市場均衡的偏離(deviation)不會消殆。 因 此_,mt,pt,yt與_rt具共整合關係_,且共整合向量為

⎡⎢⎢⎢

⎢⎢⎢⎢

⎢⎣

1

−β₁

−β₂

−β₃

⎤⎥⎥⎥

⎥⎥⎥⎥

⎥⎦

共整合關係

例子 _: 消費函數

C_t=C_t^p+C^t_t,

=β y_t^p+C_t^t,

其中_Ct^p是恆常消費(permanent consumption),為恆常所得 (permanent income)的函數_,Ct^t則是短暫消費(transitory

consumption)。 由於_yt^p_{∼I(1),Ct ∼I(1),}則根據短暫消費的定義_, C_t^t=C_t−β y_t^p

是_I(0)序列。 因此_,Ct與_yt^p具共整合關係_,且共整合向量為

[ 1

−β ]

共整合關係

例子 _: 遠期外匯不偏假說

根據Engel (1996a),在理性預期(rational expectations)與風險中立 (risk neutrality)的假設下_,遠期外匯應為未來匯率的不偏估計式

E_t[s_t+1]= f_t,

其中_st為名目匯率_{, ft}為遠期外匯匯率。 因此_{, FRUH}可以改寫成 s_t+1= f_t+u_t+1, E_t(u_t+1)=0.

給定_{s ∼I(1), f ∼I(1),}則_{u ∼I(0)}。

共整合關係

例子 _: 遠期外匯不偏假說

如果說_ut+1非定態_,亦即_,

u_t+1=u_t+e_t+1,

e_t∼^i.i.d. (0,σ²). 則

s_t+1 = f_t+u_t+1,

= f_t+u_t+e_t+1,

共整合關係

例子 _: 遠期外匯不偏假說

E_t(s_t+1)= f_t+u_t,

代表遠期外匯匯率並沒有包含所有資訊_,或是說市場不具效率性。 因此_, FRUH隱含_ut+1∼I(0),也就是說_st+1與 _ft具共整合關係_,且共整合向量 為

[ 1

−1 ]

相關討論詳見Hakkio and Rush (1989)與Zivot (2000)。

共整合關係

例子 _: 購買力平價說

根據購買力平價_,

q_t =s_t+p^∗_t −p_t

必須是一個定態的數列_,qt∼I(0)。 因此_{, PPP}隱含_st,p^∗

t,與_pt具共整合

關係_,且共整合向量為

⎡⎢⎢⎢

⎢⎢⎢⎣

1 1

−1

⎤⎥⎥⎥

⎥⎥⎥⎦

因此_,檢定購買力平價說有兩種方法_{, (1)}直接對_qt應用單根檢定_{; (2)}檢 定_st,p^∗

t,與_pt是否具共整合關係。

共整合與共同隨機趨勢

共整合與共同隨機趨勢

根據Stock and Watson(1988),考慮

x_t=[ y_t

z_t ]=[ µ_yt+e_yt µ_zt+e_zt ]

其中_µyt與_µzt 為隨機漫步序列(random walk series),e_yt與_ezt為 定態序列(stationary component)。顯而易見地_,yt與_zt均為_I(1) 序列。

假設_yt與_zt具共整合關係_:β^′_xt∼I(0).亦即_, β^′x_t =β₁ y_t+β₂ z_t

共整合與共同隨機趨勢

共整合與共同隨機趨勢

如果_β^′_xt∼I(0),則前一項_{(β1µyt+β2µzt)}必須消失。 也就是說_, β₁µ_yt+β₂µ_zt =0,

或是說

µ_yt= −β2

β₁ µ_zt. 令_{µzt =µt,}我們可以得到

[ y_t z_t ]=⎡⎢

⎢⎢⎣

−β2

β1

1

⎤⎥⎥⎥

⎦µ_t+[ e_yt

e_zt ] (1)

共整合與共同隨機趨勢

共整合與共同隨機趨勢

根據第₍₁₎式_,序列若具有共整合關係_,則它們具有共同的隨機趨勢 (common stochastic trend)。 因此_,「共整合」一詞聽起來很玄_,事實上就 是說序列具有相同的隨機趨勢_,亦步亦趨地一起移動。

共整合與共同隨機趨勢

例子 _: 共整合與共同隨機趨勢

圖_:美國₁年期與10年期的國庫券利率_(TB1Y與TB10Y)以及利差

-4 0 4 8 12 16 20

55 60 65 70 75 80 85 90 95 00 05

TB1Y TB10Y SPREAD

向量誤差修正模型

向量誤差修正模型

考慮一個_VAR(p)模型_,

Φ(L)y_t=ε_t, y_t∈R^k 且 _εt∼^i.i.d. (0, Ω). 亦即

(I−Φ₁L−Φ₂L²− ⋯ −Φ_pL^p)y_t =ε_t.

向量誤差修正模型

向量誤差修正模型

因此_,

y_t=Φ₁y_t−1−Φ₂y_t−2− ⋯ −Φ_py_t−p,

=⎡⎢⎢⎢

⎢⎣

⎛

⎝

p

∑j=1

Φj⎞

⎠L−∑^p

j=2

Φj(1−L)L−∑^p

j=3

Φj(1−L)L²− ⋯

⋯ −∑^p

j=p

Φj(1−L)L^p−1⎤⎥⎥⎥

⎥⎦yt+εt

向量誤差修正模型

向量誤差修正模型

注意到上式可由以下算式驗證_:

(Φ₁+Φ₂+Φ₃⋯ +Φ_p) L

− (Φ₂+Φ₃⋯ +Φ_p) L(1−L)

− (Φ₃⋯ +Φ_p) L²(1−L)

− ⋮ ⋮

− Φ_p L^p−1(1−L) Φ₁L+Φ₂L²+ ⋯ +Φ_pL^p

向量誤差修正模型

向量誤差修正模型

令

D_j=− ∑^p

s=j+1

Φ_s=−(Φ_j+1+Φ_j+2+ ⋯ +Φ_p), 則_yt可以改寫成

y_t=⎡⎢

⎢⎢⎢⎣

∑p j=1

Φ_j⎤⎥

⎥⎥⎥⎦y_t−1+∑^p−1

j=1

D_j∆y_t−j+ε_t

向量誤差修正模型

向量誤差修正模型

左右兩邊都減去_yt−1可得

∆y_t=⎡⎢

⎢⎢⎢⎣−I+∑^p

j=1

Φ_j⎤⎥

⎥⎥⎥⎦y_t−1+∑^p−1

j=1

D_j∆y_t−j+ε_t

=−Φ(1)

´¹¹¹¹¸¹¹¹¹¹¶

Π

y_t−1+∑^p−1

j=1

D_j∆y_t−j+ε_t

=Πy_t−1+∑^p−1

j=1

D_j∆y_t−j+ε_t

向量誤差修正模型

向量誤差修正模型

假設_yt的自積階次最高為一階_{, I(1),}則_∆yt∼I(0)。 如果_∆yt,

∑^p−1j=1 D_j∆y_t−j與_εt均為定態_,則

Πy_t−1 =∆y_t−∑^p−1

j=1

D_j∆y_t−j−ε_t 一定也是定態。

向量誤差修正模型

向量誤差修正模型

根據_Π矩陣的秩_(rank)的性質可以決定三種不同情況。

1 rank(Π)=k,Π為滿秩(full rank)。 因此_,yt−1所有的線性組合都是 定態時間序列_,亦即_yt∼I(0)。 在這種情況下_,我們直接以_yt估計 VAR模型。

2 rank(Π)=0。 因此_,沒有任何一個_yt−1的線性組合是定態時間序 列_,亦即_yt∼I(1),且不存在共整合關係。 在這種情況下_,我們直接以

∆y_t估計_VAR模型。

向量誤差修正模型

向量誤差修正模型

3 rank(Π)=r<k。 因此_,yt−1部分的線性組合是定態時間序列_,更精 確地說_,存在_r個共整合關係_,且_r稱為共整合秩(cointegration rank)。

在第₃種情況下_,稱之為減秩(reduced rank),則我們可以將_Π分解為 Π=αβ^′

其中_α與_β均為_k×r矩陣_,且

rank(α)=rank(β)=r.

向量誤差修正模型

向量誤差修正模型

定理(Granger Representation定理)

給定_yt∈R^k,yt∼I(1)具有_r<k個共整合關係_,若且為若_rank(Π)=r且_Π可以分解 成_Π⁼_αβ^′,其中_β與_α為_k×r矩陣,rank(β)=rank(α)=r且_VAR(p)模型可以寫成 向量誤差修正模型(vector error correction model, VECM),或是稱共整合_VAR模型 (cointegrated VAR model)

∆yt=αβ^′yt−1+^p

−1

∑

j=1

Dj∆yt−j+εt.

向量誤差修正模型

Granger Representation 定理

1 Granger Representation定理告訴我們_,對於任何具共整合關係的 一組序列_,共整合關係與向量誤差修正模型為一體之兩面。

2 由於_Π⁼_−Φ(1),所有長期影響(long-run effects)的資訊已經包含 在_Π矩陣中。

3 Π衡量長期影響_,而_Dj衡量短期影響。

4 β為共整合向量所組成的矩陣。

5 β^′y_t−1稱做 「均衡誤差」(equilibrium error)或是「誤差修正 項」(error correction)。

向量誤差修正模型

例子 _: 誤差修正模型

x_t與_zt有如下向量誤差修正模型 [ ∆xt

∆zt ]=[ −1 1

0 0 ] [ xt−1

zt−1 ] + [ εx t

εz t ] 或是寫成

∆yt=Πyt−1+εt, 其中

y_t=[ xt

z_t ] Π=[ −1 1

0 0 ] 且 _εt=[ εx t

ε_{z t} ]∼(0, Ω).

向量誤差修正模型

例子 _: 誤差修正模型

首先_,我們可以輕易得到

zt=zt−1+εz t,

=

∑t j=1

ε_{z j}+ε_z0,

且

x_t =z_t−1+ε_{x t} =

t−1

∑

j=1

ε_{z j}+ε_z0+ε_{x t},

=(∑^t

j=1

ε_{z j}−ε_{z t}) +ε_z0+ε_{x t},

=

∑t j=1

ε_{z j}+ε_z0+ (ε_{x t}−ε_{z t}).

向量誤差修正模型

例子 _: 誤差修正模型

我們有如下的觀察_,

1 ∑^tj=1ε_{z j}為一隨機趨勢_,所以_xt與_zt都是_I(1)序列。

2 ∑^tj=1ε_{z j}稱為_xt與_zt的共同隨機趨勢。

3 x_t與_zt的某一線性組合可以消除此共同隨機趨勢_:

x_t−z_t=(z_t−1+ε_xt)−(z_t−1+ε_zt)=ε_xt−ε_zt ∼I(0).

4 注意到_Π可以寫成

Π=[ −1 1

]=[ −1

][ 1 −1 ]=αβ^′

共整合分析

共整合分析

共整合分析有兩種主要的程序。 第一種係由Robert Engle以及

Clive Granger所提出_,他們假設變數之間只存在一個共整合關係_,

並且採取兩階段程序_,以第一階段的殘差在第二階段檢定共整合關 係以及建構誤差修正模型。

第二種方法則是由Soren Johansen所提出_,此方法容許多個共整 合關係存在_,並以最大概似法從事檢定與估計。

共整合分析I: Engle-Granger兩階段程序

共整合檢定

Engle and Granger(1987)在只存在一個共整合關係的假設下_,提出一

種兩階段檢定法以檢定一組_I(1)序列是否具有共整合關係。 以兩個序列 x_t與_zt為例_,說明如何執行Engle-Granger檢定。

1 估計共整合關係_:

x_t=β₀+β₁z_t+e_t.

2 對_{eˆt}做_ADF檢定_,

∆ ˆe_t=a₀+a₁eˆ_t−1+∑ⁿ a_i+1∆ ˆe_t−i+ε_t.

共整合分析I: Engle-Granger兩階段程序

共整合檢定

3 欲檢定的假設(hypothesis)為

{ H₀ ∶a₁=0 不具共整合關係 H₁∶a₁ <0 具共整合關係

4 如果我們拒絕虛無假設_,代表_xt與_zt具有共整合關係。 反之_,如果 我們無法拒絕虛無假設_,代表_xt與_zt不具共整合關係₍更精確地說_, 是我們找不到證據支持_xt與_zt具有共整合關係₎。

5 Engle-Granger檢定中的_ADF檢定不能使用傳統的_ADF統計量的

臨界值_,其漸近分配由Phillips and Ouliaris (1990)推導出來。

共整合分析I: Engle-Granger兩階段程序

共整合檢定

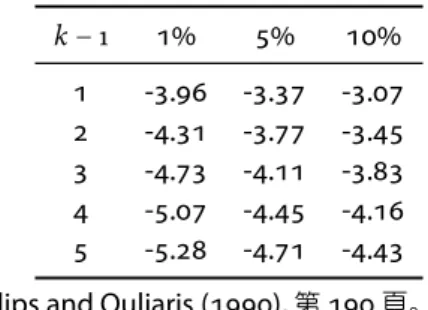
表_:Engle-Granger統計檢定量臨界值

k−1 1% 5% 10%

1 -3.96 -3.37 -3.07 2 -4.31 -3.77 -3.45 3 -4.73 -4.11 -3.83 4 -5.07 -4.45 -4.16 5 -5.28 -4.71 -4.43 參見Phillips and Ouliaris (1990),第₁₉₀頁。

共整合分析I: Engle-Granger兩階段程序

估計共整合關係與向量誤差修正模型

x_t與_zt的向量誤差修正模型為

∆xt=α1+αx[xt−1−β1zt−1]+ ∑

i=1

α₁₁ⁱ∆xt−i+ ∑

i=1

α₁₂ⁱ ∆zt−i+εx t

∆zt=α2+αz[xt−1−β1zt−1]+ ∑

i=1

α₂₁ⁱ ∆xt−i+ ∑

i=1

αⁱ₂₂∆zt−i+εz t

透過第一階段估計出共整合關係後_,令迴歸殘差為 eˆ_t=x_t−βˆ₀+βˆ₁z_t,

共整合分析I: Engle-Granger兩階段程序

估計共整合關係與向量誤差修正模型

Engle and Grangerv(1987)建議估計向量誤差修正模型如下_,

∆x_t=α₁+α_xeˆ_t−1+ ∑

i=1

αⁱ₁₁∆x_t−i+ ∑

i=1

αⁱ₁₂∆z_t−i+ε_{y t},

∆zt=α2+αzeˆt−1+ ∑

i=1

α₂₁ⁱ ∆xt−i+ ∑

i=1

α₂₂ⁱ ∆zt−i+εz t.

1 無論選擇哪一個變數_(xt或_zt)當作共整合關係中的被解釋變數_,理 論上₍大樣本性質₎不會影響我們對是否存在共整合關係的推論_,然 而_,實務上如果樣本數較小_,統計推論會因不同的變數選擇而不同。

共整合分析I: Engle-Granger兩階段程序

估計共整合關係與向量誤差修正模型

2 Engle-Granger兩階段程序無法處理多個共整合關係的存在。

3 兩階段程序可能會不具效率性。 在第一階段估計共整合關係時_,產 生的估計誤差會被帶到下一個階段。

4 由於Engle-Granger兩階段檢定是對殘差做檢定_,是故又稱殘差式

檢定(residual-based tests)。

5 對於共整合關係的估計_,利用_OLS所得到的係數估計式_β^ˆ_0,β^ˆ₁具一 致性_,在某些情況下₍譬如誤差項_et具序列相關₎其_t比率_(t-ratio) 的漸近分配不是標準常態。Stock and Watson (1993)建議一種簡 單的解決方法_:動態OLS (dynamic OLS, DOLS),

x_t =β₀+β₁z_t+ ∑^p

j=−p

δ_j∆z_t−j+e_t.

共整合分析II: Johansen程序

共整合檢定

考慮_VAR(p),

y_t=Φ₁y_t−1+Φ₂y_t−2+ ⋯ +Φ_py_t−p+ε_t. y_t∈R^k 令

D_j=− ∑^p

s=j+1

Φ_s,

Π=−Φ(1)=−(I−Φ1−Φ2− ⋯ −Φp), 則_VAR(p)可以改寫成_VECM

∆yt=Πyt−1+^p

−1

∑j 1

Dj∆yt−j+εt.

共整合分析II: Johansen程序

共整合檢定

給定_yt的階次最高為一。

1 如果_rank(Π)=0,意指沒有任何_yt的線性組合為_I(0),則_yt不存 在共整合關係。此外_,若_rank(Π)=0,則隱含_Π=0(零矩陣_),因此_,

∆y_t=∑^p−1j=1 D_j∆y_t−j+ε_t為_I(0),亦即_yt為_I(1)。

2 如果_rank(Π)=k,意指_yt的所有線性組合都是_I(0),則所有的_yt 都是_I(0)。換句話說_,yt不存在共整合關係。 事實上_,由於

rank(Π)=k,Π矩陣為滿秩(full rank),則_Π矩陣可逆_,且 y_t−1=Π⁻¹∆y_t−Π⁻¹

∑p−1 j=1

D_j∆y_t−j−Π⁻¹ε_t 為定態。

共整合分析II: Johansen程序

共整合檢定

3 如果_rank(Π)=r<k,則_yt存在共整合關係。

因此_,我們可以用_Π矩陣的秩來檢定是否存在共整合關係_,這樣的檢定 方式一般稱為_Johansen檢定(Johansen test)。

性質(矩陣秩的重要性質)

Π矩陣的秩等於其異於零的特性根數目。

假設_Π矩陣的特性根為_λ1,λ2,^⋯_,λk,

1 如果

rank(Π)=0⇒λ1=λ2=⋯=λk=0

⇒log(1−λi)=0 ∀i

共整合分析II: Johansen程序

共整合檢定

2 如果_rank(Π)=r,且假設

{ λ₁,λ₂, . . . ,λ_r ≠0

λr+1=λr+2=...=λk=0 亦即_,

{ log(1−λ_i)≠0 fori=1, 2...r

log(1−λ_i)=0 fori=r+1,r+2, ...k 則_yt存在共整合關係。

共整合分析II: Johansen程序

共整合檢定

實務上_,我們只能透過資料找出估計式_Π,^ˆ 進而找出_rank(Π^ˆ₎。 在給定 rank(Π)=r, Johansen (1988)以最大概似法估計_VECM,亦即_,在 Π=αβ^′的限制下_,估計

∆y_t=Πy_t−1+^p

−1

∑

j=1

D_j∆y_t−j+ε_t,

欲檢定共整合階次_,給定特性根

1>λˆ₁>ˆλ₂> ⋯ >λˆ_r >λˆ_r+1 > ⋯ >ˆλ_k>0,

共整合分析II: Johansen程序

共整合檢定

定義₍跡檢定, Trace Test)

1 檢定之假設為

{ H0∶最大共整合階次為_r(最多只有_r個共整合關係₎ H₁∶最大共整合階次為_k(最多只有_k個共整合關係₎

2 跡檢定量

λtrace(r)=−T

∑k j=r+1

log(1−ˆλj)

如果虛無假設_H0為真,則^ˆ_{λr+1, ˆλr+2}, . . . , ˆλ_k都會很接近零,則跡檢定量_λtrace(r)會 很小。當對立假設成立時_,有更多的_log(1−^ˆ_λj)<0被加進跡檢定量_,由於檢定量前面 乘上一個負號_,亦即在對立假設成立時_,跡檢定量會較大。

共整合分析II: Johansen程序

共整合檢定

定義₍最大特性根檢定, Max Test)

1 檢定之假設為

{ H₀ ∶最大共整合階次為_r(最多只有_r個共整合關係₎ H₁∶最大共整合階次為_r+1(最多只有_r+1個共整合關係₎

2 最大特性根檢定量

λmax(r,r+1)=−Tlog(1−λˆ_r+1) ˆ

共整合分析II: Johansen程序

最大特性根檢定

步驟一:檢定_H0∶r=0vs.H₁∶r=1,如果無法拒絕_H0,代表我們無 法拒絕沒有共整合關係。 反之_,如果我們拒絕_H0,則須執行下一步 驟。

步驟二_:檢定_H0∶r=1vs.H₁∶r=2,如果無法拒絕_H0,代表有一個 共整合關係。 反之_,如果我們拒絕_H0,則須繼續執行_H0∶r=2vs.

H₁∶r=3的檢定_...一直做下去_,直到無法拒絕虛無假設為止。

此兩種檢定量的臨界值可參考Osterwald-Lenum (1992),或是參考 Maddala and Kim (1998)頁₂₁₃的表_6.5。

共整合分析II: Johansen程序

VECM 的設定

關於_VECM的設定_,有以下五種設定。

1 設定_{1, VAR}與_ECM都沒有常數項。

∆y_t=αβ^′y_t−1+^p−1∑

j=1

D_j∆y_t−j+ε_t.

2 設定_{2, VAR}沒有常數項而_ECM有常數項。

∆y_t=α(β^′y_t−1−γ₂) +∑^p−1

j=1

D_j∆y_t−j+ε_t.

共整合分析II: Johansen程序

VECM 的設定

3 設定_{3, VAR}與_ECM都有常數項。

∆y_t =γ₁+α(β^′y_t−1−γ₂) +∑^p−1

j=1

D_j∆y_t−j+ε_t.

4 設定_{4, VAR}有常數項而ECM有常數項與時間趨勢項。

∆y_t=γ₁+α(β^′y_t−1−γ₂−δ₂t) +∑^p−1

j=1

D_j∆y_t−j+ε_t.

共整合分析II: Johansen程序

VECM 的設定

5 設定_{5, VAR}與_ECM都有常數項與時間趨勢項。

∆y_t=γ₁+δ₁t+α(β^′y_t−1−γ₂−δ₂t) +∑^p−1

j=1

D_j∆y_t−j+ε_t.

EViews提供了一個很好的彙整功能。跡檢定與最大特性根檢定可

能會給我們不一致的檢定結果。 遇到這種情況, Johansen and

Juselius(1990)建議採用最大特性根檢定。

共整合分析的實例應用:利率期限結構

實例應用 _: 利率 期限結構

令_Rk,t代表_k年期長期利率_,Rt代表₁年期短期利率_,et代表_I(0)的期 限溢價(term premium)。 根據利率期限結構的預期理論_(the

expectations theory of the term structure of interest rates),長期利率 與短期利率之間的關係為

Rk,t= ∑^kj=1Et(Rt+j) k +et,

其中_,Et(Rt+j)為對於第_t+j期的₁年期短期利率以第_t期的資訊集合所做的預期。

假設_Rt為一隨機漫步序列_:

Rt =Rt−1+ut, u_t ∼^i.i.d. N(0, 1).

共整合分析的實例應用:利率期限結構

實例應用 _: 利率 期限結構

我們知道

E_t(R_1,t+j)=R_t, 因此_,根據以上模型_,

R_k,t= ∑^kj=1E_t(R_t+j) k +e_t,

= ∑^kj=1R_t k +e_t,

= kR_t k +e_t,

共整合分析的實例應用:利率期限結構

實例應用 _: 利率 期限結構

亦即

R_k,t−R_t=e_t∼I(0).

也就是說_,經濟理論告訴我們長期利率與短期利率之間存在共整合關係_, 且共整合向量為

[ 1

−1 ]

關於共整合分析

關於共整合分析

1 根據Clive W. Granger教授之說法_,他當初會發現共整合這個概念是為了證明

「沒有共整合這種現象」。

A colleague, David Hendry, stated that the difference between a pair of integrated series could be stationary. My response was that it could be proved that he was wrong, but in attempting to do so, I showed that he was correct, and generalized it to cointegration, and proved the consequences such as the error-correction representation.

關於共整合分析

關於共整合分析

2 對於共整合分析的適當應用為_:給定一經濟模型_,模型中的_I(1)變數 根據經濟理論在某些線性組合下可為定態_,接下來以共整合檢定驗 證經濟理論。一般常見的不適當做法為隨意找一組_I(1)變數_,做共 整合分析並得到統計上共整合關係_,就冒然宣稱變數之間存在的經 濟關係。統計上的共整合關係只是建議變數之間存在一個看不見的 共同變因_,至於這個共同變因是什麼_,則有賴經濟理論_,經濟制度_,或 是總體經濟環境等之啟迪。

關於共整合分析

關於共整合分析

3 舉例來說_,最常被誤用的概念就是_,錯把統計上的共整合與經濟整合 或是金融整合混在一起。你把不同國家的股票價格₍或是匯率₎找來 做共整合檢定_,發現共整合關係_,然後就下結論說亞洲各國的股票市 場₍外匯市場₎具有相當程度的金融整合_,顯然是不適當的。 除非你 能夠建構一個經濟模型說明金融整合隱含各國股票價格₍或是匯率₎ 有共整合關係_,接下來再以共整合檢定驗證之。

關於共整合分析

關於共整合分析

4 再從另外一個角度來看_,假設各國股票價格為_I(1)序列且存在共整 合關係_;則各國股票報酬為_I(0),自然沒有所謂的共整合關係。 如果 我們貿然地將共整合關係詮釋為金融整合_,則弔詭的是_,同樣的股票 市場_,何以 「價格」 告訴我們有金融整合_,而「報酬」卻又隱含金融整 合不存在_?此外_,另外一個常見的不適當應用_,就是將共整合與市場 效率性混在一起。

關於共整合分析

關於共整合分析

5 共整合分析只能應用在所有序列均為_I(1),要應用共整合分析前_,我 們必須先透過單根檢定確認序列為_I(1),而單根檢定的檢定力已於 第五章討論過,令人堪慮。

6 實務上我們常會碰到研究的變數有的為_I(0),有的為_{I(1), VAR}體系 中有_I(0)與_I(1)序列的混合_,此時應用共整合分析就不恰當。