getdoc26cf. 299KB Jun 04 2011 12:04:11 AM
Teks penuh
Gambar
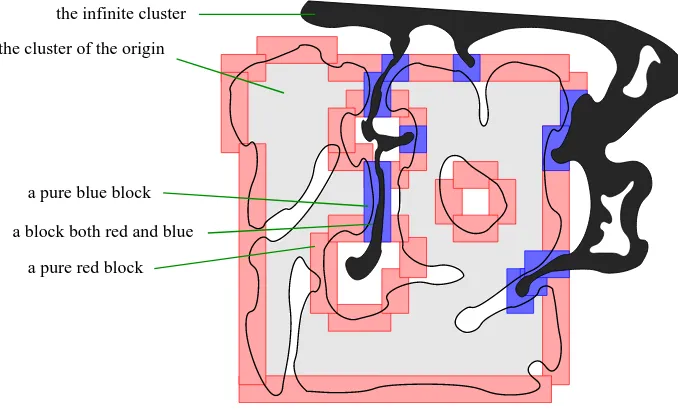
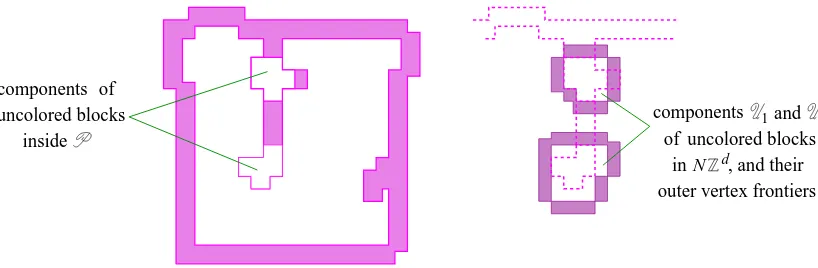
Garis besar
Dokumen terkait
We adapt a regeneration-time argument originally developed by Comets and Zeitouni [ 8 ] for static random environments to prove that, under a space-time mixing property for the
Key words: Random walk among random conductances, functional limit theorems, fractional kinetics, trap models.. AMS 2000 Subject Classification:
Indeed, using estimates for the so-called tan points of the simple random walk, introduced in [1] and subse- quently used in [7, 8], it is possible to prove that, when d ≥ 2, the
We prove a non-standard functional limit theorem for a two dimensional simple random walk on some randomly oriented lattices.. This random walk, already known to be transient, has
Section 2 has some estimates on the potential kernel for random walks in the plane, while Section 3 has the proof of the stochastic calculus results we need.. Theorem 1.1 in the
(ii) the p -th mean exponential convergence of the solution to zero (for all p > 0), and (iii) the exponential integrability of the entries of the kernel K , the exponential
A central limit theorem for random walk in a random environment on marked Galton-Watson trees.. Gabriel
To prove this theorem we extend the bounds proved in [ 2 ] for the continuous time simple random walk on (Γ , µ ) to the slightly more general random walks X and Y defined