Penyelesaian Puzzle Sudoku Menggunakan Pemrograman Linear Integer

(1)

PENYELESAIAN

PUZZLE

SUDOKU MENGGUNAKAN

PEMROGRAMAN LINEAR INTEGER

MUHAMAD FARDAN WARDHANA

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR

(2)

(3)

ABSTRAK

MUHAMAD FARDAN WARDHANA. Penyelesaian Puzzle Sudoku Menggunakan Pemrograman Linear Integer. Dibimbing oleh AMRIL AMAN dan NGAKAN KOMANG KUTHA ARDANA.

Sudoku dapat dipandang sebagai puzzle (teka-teki) dalam matematika. Pemain harus mengisi sebuah matriks n2 × n2 yang berisi beberapa unsur awal yang diberikan, sehingga setiap baris, kolom, dan mini grid n × n berisi masing-masing bilangan bulat 1 sampai n2. Tujuan penelitian ini adalah mengkaji Sudoku tradisional, Sudoku X (Sudoku diagonal) dan menggunakan metode branch and bound, untuk mencari hubungan antara kemungkinan solusi yang muncul dengan ukuran Sudoku, dan banyaknya given yang diberikan. Solusi Sudoku ditentukan dengan menggunakan metode branch and bound yang diimplementasikan pada script m-file. Kami dapat menemukan hubungan antara kemungkinan solusi yang muncul dengan ukuran Sudoku, dan banyaknya given yang diberikan. Di sisi lain, kami tidak dapat menemukan hubungan semacam itu untuk ukuran Sudoku yang umum dan konfigurasi yang umum.

Kata kunci: Sudoku, linear integer, branch and bound

ABSTRACT

MUHAMAD FARDAN WARDHANA. Solving Sudoku Puzzle by Using Linear Integer Programming. Supervised by AMRIL AMAN and NGAKAN KOMANG KUTHA ARDANA.

Sudoku can be viewed as a puzzle in mathematics. Players must fill in a n2 × n2 matrix which is containing some given enteries, so that each row, column, and n × n mini grid contains each integer 1 through n2. The objectives of this research are to study the traditional Sudoku puzzle, Sudoku X puzzle (diagonal Sudoku) and use branch and bound method, to find the relation between the number of possible solution with the size of sudoku, and the number quantity givens. The solutions are determined using branch and bound method that was implemented on m-file script. We can find the relation between the number of possible solution with the size of sudoku, and the number quantity givens. On the other hand, we can not find such relation for general size of sudoku and general configuration.

(4)

(5)

Skripsi

sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains

pada

Departemen Matematika

PENYELESAIAN

PUZZLE

SUDOKU MENGGUNAKAN

PEMROGRAMAN LINEAR INTEGER

MUHAMAD FARDAN WARDHANA

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR

(6)

(7)

Judul Skripsi : Penyelesaian Puzzle Sudoku Menggunakan Pemrograman Linear Integer

Nama : Muhamad Fardan Wardhana

NIM : G54061543

Disetujui oleh

Dr Ir Amril Aman, MSc Pembimbing I

Ir Ngakan Komang Kutha Ardana, MSc Pembimbing II

Diketahui oleh

Dr Toni Bakhtiar, MSc Ketua Departemen

(8)

PRAKATA

Puji dan syukur penulis panjatkan kepada Allah subhanahu wa ta’ala atas segala karunia-Nya sehingga penelitian dengan judul Penyelesaian Puzzle Sudoku Menggunakan Pemrograman Linear Integer dapat diselesaikan.

Terima kasih penulis ucapkan kepada Bapak Dr Ir Amril Aman, MSc dan Bapak Ir Ngakan Komang Kutha Ardana, MSc selaku pembimbing, serta Bapak Dr Ir I Gusti Putu Purnaba, DEA yang telah banyak memberi saran. Ungkapan terima kasih juga disampaikan kepada (alm) ayah, (almh) ibu, istri serta seluruh keluarga, atas segala doa dan kasih sayangnya.

Semoga karya ilmiah ini bermanfaat.

(9)

DAFTAR ISI

PENDAHULUAN 1

Latar Belakang 1

Perumusan Masalah 1

Tujuan Penelitian 2

Ruang Lingkup Penelitian 2

TINJAUAN PUSTAKA 2

Definisi 1 Puzzle (teka-teki) Sudoku 2

Definisi 2 Persamaan Linear 2

Pemrograman Linear 3

Definisi 3 Bentuk Standar Suatu PL 3

Solusi Suatu Pemrograman Linear 3

Definisi 4 Daerah Fisibel 4

Definisi 5 Solusi Basis 4

Definisi 6 Solusi Fisibel Basis 4

Definisi 7 Solusi Optimum 4

Pemrograman Linear Integer 4

Metode Branch and Bound 5

DESKRIPSI DAN PEMODELAN MASALAH 9

Deskripsi Masalah 9

Pemodelan Masalah 9

PEMBAHASAN 13

Contoh Kasus 13

Mencari Solusi Puzzle Sudoku Tradisional pada Matriks 9 × 9 22 Mencari Solusi Puzzle Sudoku X (Sudoku Diagonal) pada Matriks 9 × 9 25 Hubungan Antar Ukuran Sudoku, Banyaknya Unsur Awal, dan Konfigurasi

Sudoku Tradisional. 28

SIMPULAN DAN SARAN 29

Simpulan 29

Saran 29

(10)

DAFTAR GAMBAR

1. Soal Sudoku dengan input data secara acak 1

2. Daerah fisibel PLI (2.5) 7

3. Daerah fisibel untuk Subproblem 2 (x1≥ 4) dan Subproblem 3 (x1≤ 3) 7

4. Seluruh pencabangan pada metode branch and bound untuk

menentukan solusi PLI (2.5) 9

5. Bentuk umum Sudoku ukuran 4 × 4 13

6. Contoh soal Sudoku 4 × 4 16

7. Solusi Sudoku 4 × 4 22

8. Bentuk umum Sudoku ukuran 9 × 9 23

9. Contoh soal Sudoku tradisional 9 × 9 24

10.Solusi Sudoku tradisional ukuran 9 × 9 25

11.Contoh soal puzzle Sudoku yang memiliki banyak solusi (terhingga) 25

12.Contoh soal Sudoku X ukuran 9 ×9 26

13.Solusi Sudoku X ukuran 9 × 9 27

DAFTAR LAMPIRAN

1. Script M-File sudoku.m untuk mencari solusi Sudoku tradisional. 31 2. Script M-File sudokuX.m untuk mencari solusi Sudoku X (Sudoku

diagonal) 33

3. Contoh mencari solusi untuk soal Sudoku ukuran 9 × 9 dengan script

M-File 36

4. Contoh mencari solusi untuk soal Sudoku ukuran 9 × 9 yang memiliki banyak solusi (terhingga) dengan menggunakan script M-File 37 5. Contoh mencari solusi untuk soal Sudoku X ukuran 9 × 9 dengan

menggunakan script M-File 42

6. Contoh mencari solusi untuk soal Sudoku X ukuran 9 × 9 yang memiliki banyak solusi (terhingga) dengan menggunakan script M-File 43 7. Hubungan antar ukuran Sudoku, banyaknya unsur awal, dan

konfigurasi Sudoku tradisional 44

DAFTAR TABEL

(11)

PENDAHULUAN

Latar Belakang

Sudoku adalah sebuah puzzle berdasarkan logika yang pertama kali hadir di Amerika Serikat dengan judul “Number Place” di majalah “Dell Pencil Puzzle & Word Games” di tahun 1979. Pada tahun 1980-an, permainan ini berkembang menjadi popular di Jepang dan telah diganti nama oleh penerbit menjadi “suji wa dokushin ni kagiru”, yang diterjemahkan menjadi “the digits must remain single (angka-angkanya harus tetap tunggal)”. Pada akhirnya diperpendek menjadi ”Sudoku” atau “single number (nomor tunggal) ” (Bartlett, 2008).

Sudoku pada umumnya hadir dalam bentuk matriks 9 x 9. Aturannya mudah: isi dalam matriks sehingga setiap baris, kolom, dan submatriks 3 x 3 yang diisi angka 1 sampai 9 hanya satu kali. Sesuai namanya, maka tidak boleh ada angka/digit yang sama. Hal inilah yang dinamakan dengan “Prinsip keunikan” (Principle of Uniqueness). Setiap puzzle muncul dengan sejumlah nomor yang diberikan. Nomor dan posisinya menentukan tingkat kesulitan permainan ini. Gambar 1 adalah salah satu contoh puzzle Sudoku 9 x 9.

Kesulitan tingkat permainan Sudoku, selain diukur dari besar ukuran matriksnya (n2 × n2), biasanya diukur dari problem perumusan angka-angka awal yang telah diatur posisi dan nilainya. Semakin sedikit angka-angka awal yang diberikan, tentunya akan semakin sulit.

Perumusan Masalah

Sudoku menghasilkan dua pertanyaan menarik secara matematika sebagai berikut: Bagaimana puzzle-puzzle ini bisa diselesaikan secara matematika? dan teknik matematika apa yang bisa digunakan untuk menciptakan dan menyelesaikan puzzle-puzzle Sudoku ini?

(12)

2

Tujuan Penelitian

Di dalam tulisan ilmiah ini akan dipelajari mengenai puzzle (teka-teki) Sudoku, yang selanjutnya disebut dengan Sudoku sebagai sebuah permasalahan pemrograman bilangan bulat (Integer Programming Model). Tujuan dari karya ilmiah ini:

1. Mengkaji Sudoku tradisional menggunakan metode Branch and Bound. 2. Mengkaji Sudoku yang baru (Sudoku diagonal) menggunakan metode

Branch and Bound.

3. Mencari hubungan antar ukuran Sudoku, banyaknya unsur awal, dan konfigurasi pada Sudoku tradisional.

Ruang Lingkup Penelitian

Sudoku memiliki berbagai ukuran. Dalam tulisan ilmiah ini, penulis membatasi pembahasan dan pencarian pola untuk Sudoku berukuran 9 × 9.

TINJAUAN PUSTAKA

Definisi 1 Puzzle (teka-teki) Sudoku

Sudoku adalah sebuah permainan teka-teki angka berbasis logika yang pada umumnya berbentuk matriks 9 × 9 (n2 × n2 dengan n = 3) dan memiliki aturan yang sederhana dengan menyusun bilangan-bilangan 1,2,3, … , n2 pada kotak berjumlah n2 × n2 sehingga setiap kolom, baris, maupun mini grid berukuran 3 × 3 (n × n) hanya boleh terisi dengan bilangan 1 sampai 9 yang berjumlah masing-masing satu.

Definisi 2 Persamaan Linear

Suatu sistem persamaan linear dalam n peubah (variabel) adalah persamaan dengan bentuk

1 1 2 2 ... n n

a x a x  a x b

di mana a a₁, ₂,...,a_n dan b adalah bilangan-bilangan real dan x x₁, ₂,...,x_n adalah peubah. Dengan demikian maka suatu sistem linear dari m persamaan dalam n peubah adalah satu sistem berbentuk:

11 1 12 2 1 1 21 1 22 2 2 2

1 1 2 2 ...

... .

. .

... n n

n n

m m mn n m

a x a x a x b

   

(13)

3 Pemrograman Linear

Pemrograman Linear (PL) adalah suatu masalah optimasi yang memenuhi ketentuan-ketentuan berikut:

a) Tujuan masalah tersebut adalah memaksimumkan atau meminimumkan suatu fungsi linear dari sejumlah variabel keputusan. Fungsi yang akan dimaksimumkan atau diminimumkan ini disebut fungsi objektif.

b) Nilai variabel-variabel keputusannya harus memenuhi suatu himpunan kendala. Setiap kendala harus berupa persamaan linear atau pertidaksamaan linear.

c) Ada pembatasan tanda untuk setiap variabel dalam masalah ini. Untuk sembarang variabel xi, pembatasan tanda menentukan xi harus tak-negatif (xi

≥ 0) atau tidak dibatasi tandanya (unrestricted in sign).

(Winston 2004) Suatu PL mempunyai bentuk standar seperti yang didefinisikan sebagai berikut.

Definisi 3 Bentuk Standar Suatu PL

Suatu pemrograman linear dalam bentuk standar didefinisikan sebagai: Max z (atau min)

s.t.

(2.1)

Dengan mendefinisikan: A = [

] [ ] [ ]

Maka kendala pada (2.1) dapat ditulis dengan sistem persamaan Ax = b (2.2) (Winston 2004) Solusi Suatu Pemrograman Linear

Suatu masalah PL dapat diselesaikan dalam berbagai teknik, salah satunya adalah metode simpleks. Metode ini dapat menghasilkan suatu solusi optimum bagi masalah PL dan telah dikembangkan oleh Dantzig sejak tahun 1947 (Winston 2004), dan dalam perkembangannya merupakan metode yang paling umum digunakan untuk menyelesaikan PL. Metode ini berupa metode iteratif untuk menyelesaikan PL berbentuk standar.

(14)

4

elemennya berupa koefisien variabel nonbasis pada matriks kendala. Dalam hal ini matriks B disebut matriks basis untuk PL (2.2).

Misalkan x dinyatakan sebagai vektor x = dengan x_B adalah vektor variabel basis dan x_N adalah vektor variabel nonbasis, maka Ax = b dapat dinyatakan sebagai:

Ax =

= Bx_B + Nx_N = b (2.3)

Karena matriks B adalah matriks tak singular, maka B memiliki invers, sehingga dari (2.3) x_B dapat dinyatakan sebagai:

x_B = B-1b - B-1Nx_N (2.4)

Kemudian, fungsi objektifnya berubah menjadi: min z =

(Winston 2004) Definisi 4 Daerah Fisibel

Daerah fisibel suatu PL adalah himpunan semua titik yang memenuhi semua kendala dan pembatasan tanda pada PL tersebut.

(Winston 2004) Definisi 5 Solusi Basis

Solusi basis adalah solusi pada PL yang didapatkan dengan mengatur variabel n – m sama dengan nol dan nilai untuk penyelesaiannya adalah dari sisa variabel m. Hal ini mengasumsikan bahwa mengatur variabel n – m sama dengan nol sehingga membuat nilai yang unik untuk sisa variabel m atau sejenisnya, dan kolom-kolom untuk sisa dari variabel m adalah bebas linear.

(Winston 2004) Definisi 6 Solusi Fisibel Basis

Solusi fisibel basis adalah solusi basis pada PL yang semua variabel-variabelnya tak-negatif.

(Winston 2004) Definisi 7 Solusi Optimum

Untuk masalah maksimalisasi, solusi optimum suatu PL adalah suatu titik dalam daerah fisibel dengan nilai fungsi objektif terbesar. Untuk masalah minimisasi, solusi optimum suatu PL adalah suatu titik dalam daerah fisibel dengan nilai fungsi objektif terkecil.

(Winston 2004) Pemrograman Linear Integer

(15)

5 variabel harus berupa integer, maka masalah tersebut dinamakan pure integer programming. Jika hanya sebagian yang harus berupa integer, maka disebut mixed integer programming (MIP). PLI dengan semua variabelnya harus bernilai 0 atau 1 disebut 0-1 PLI.

(Garfinkel & Nemhauser 1972) Metode Branch and Bound

Prinsip dasar metode branch-and-bound adalah memecah daerah fisibel dari masalah relaksasi-PL dengan membuat subproblem-subproblem. Terdapat dua konsep dasar dalam algoritma branch-and-bound.

1. Branch (Cabang)

Branching (pencabangan) adalah proses membagi permasalahan menjadi subproblem-subproblem yang mungkin mengarah ke solusi.

2. Bound (Batas)

Bounding (pembatasan) adalah suatu proses untuk mencari atau menghitung batas atas (dalam masalah minimisasi) dan batas bawah (dalam masalah maksimisasi) untuk solusi optimum pada subproblem yang mengarah ke solusi.

Metode branch-and-bound diawali dari menyelesaikan relaksasi-PL dari suatu pemrograman linear integer. Jika semua nilai variabel keputusan solusi optimum sudah berupa integer, maka solusi tersebut merupakan solusi optimum PLI. Jika tidak, dilakukan pencabangan dan penambahan batasan pada relaksasi-PLnya kemudian diselesaikan.

Winston (2004) menyebutkan bahwa untuk masalah maksimisasi nilai fungsi objektif optimum untuk PLI lebih kecil atau sama dengan nilai fungsi objektif optimum untuk relaksasi-PL, sehingga nilai fungsi objektif optimum relaksasi-PL merupakan batas atas bagi nilai fungsi objektif optimum untuk masalah PLI. Diungkapkan pula oleh Winston (2004) untuk masalah maksimisasi bahwa nilai fungsi objektif optimum untuk suatu kandidat solusi merupakan batas bawah nilai fungsi objektif optimum untuk masalah PLI asalnya. Suatu kandidat solusi diperoleh jika solusi dari suatu subproblem sudah memenuhi kendala integer pada masalah PLI, artinya fungsi objektif dan semua variabelnya sudah bernilai integer.

Sebelumnya akan dibahas terlebih dahulu pengertian subproblem yang terukur. Menurut Winston (2004), suatu subproblem dikatakan terukur (fathomed) jika salah satu kondisi berikut terpenuhi:

a. Subproblem tersebut takfisibel, sehingga tidak dapat menghasilkan solusi optimum bagi PLI.

(16)

6

c. Nilai fungsi objektif optimum untuk subproblem tersebut tidak melebihi batas bawah saat itu (untuk masalah maksimisasi). Suatu subproblem dapat dieliminasi apabila subproblem tersebut takfisibel dan batas bawah kandidat solusi lebih kecil (untuk masalah maksimisasi) dari nilai fungsi objektif optimum untuk subproblem tersebut.

Berikut ini adalah langkah-langkah penyelesaian suatu masalah maksimisasi dengan metode branch-and-bound :

 Langkah 0

Didefinisikan z sebagai batas bawah dari solusi PLI yang optimum. Pada awalnya tetapkan z = − dan i = 0.

 Langkah 1

Subproblem PL(i) dipilih sebagai bagian masalah berikutnya untuk diteliti.

Subproblem PL(i) diselesaikan dan diukur dengan kondisi yang sesuai.

a) Jika PL(i) terukur, maka batas bawah z dapat diperbarui. Batas bawah z dapat

diperbaharui jika solusi PLI yang lebih baik telah ditemukan. Jika tidak, maka bagian masalah (subproblem) baru i dipilih dan langkah 1 diulangi. Jika semua subproblem telah diteliti, maka proses dihentikan.

b) Jika PL(i) tidak terukur, lanjutkan ke langkah 2 untuk melakukan

pencabangan PL(i).

 Langkah 2

Pilih satu variabel xj yang nilai optimumnya, yaitu xj*, tidak memenuhi batasan

integer dalam solusi PL(i). Singkirkan bidang [xj*] xj [xj*]+1 dengan membuat

dua bagian masalah PL yang berkaitan menjadi dua batasan yang tidak dapat dipenuhi secara bersamaan yaitu:

xj ≤ [xj*] dan xj ≥ [xj*]+1,

dengan [xj*] didefinisikan sebagai integer terbesar yang kurang dari atau sama

dengan xj*. Jika PL(i) masih tidak terukur, maka kembali ke Langkah 1.

(Taha 1996) Untuk memudahkan pemahaman mengenai metode branch-and-bound diberikan contoh sebagai berikut:

Contoh 1

Misalkan diberikan PLI sebagai berikut: Maksimumkan z = 5 x1 + 4 x2

terhadap x1 + x2 5

10 x1 + 6 x2

x1, x2 0 dan integer (2.5)

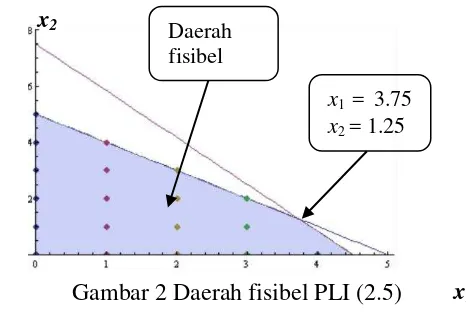
Solusi optimal relaksasi-PL dari masalah PLI (2.5) adalah x1=3.75, x2=1.25,

(17)

7

Langkah berikutnya adalah memartisi daerah fisibel relaksasi-PL menjadi dua bagian berdasarkan variabel yang bernilai pecahan (non-integer). Karena x1=

3.75 dan x2=1.25 variabel bernilai pecahan maka dipilih salah satu variabel,

misalkan x1, sebagai dasar pencabangan. Jika masalah relaksasi-PL dari PLI (2.5)

diberi nama Subproblem 1 dan Subproblem 1 dicabangkan atas x1, maka

pencabangan tersebut menghasilkan 2 subproblem, yaitu:

 Subproblem 2: Subproblem 1 ditambah kendala x1≥ 4

 Subproblem 3: Subproblem 1 ditambah kendala x1≤ 3.

Daerah fisibel untuk kedua subproblem di atas diilustrasikan secara grafis pada Gambar 3.

Setiap titik (solusi) fisibel dari PLI (2.5) termuat dalam daerah fisibel Subproblem 2 atau Subproblem 3. Setiap subproblem ini saling lepas. Sekarang dipilih subproblem yang belum diselesaikan, misalkan dipilih Subproblem 2. Solusi optimal untuk Subproblem 2 ini adalah x1 = 4, x2 = 0.8333 dan z = 23.333.

Karena solusi optimal yang dihasilkan Subproblem 2 bukan solusi integer, maka Subproblem 2 dicabangkan atas x2 sehingga diperoleh dua subproblem lagi, yakni:

 Subproblem 4: Subproblem 3 ditambah kendala x2≥ 1;

Gambar 2 Daerah fisibel PLI (2.5) x2

x1 Daerah

fisibel

x1 = 3.75

x2 = 1.25

Gambar 3 Daerah fisibel untuk Subproblem 2 (x1≥ 4)

dan Subproblem 3 (x1≤ 3)

x1 x2

Subproblem 3

(18)

8

 Subproblem 5: Subproblem 3 ditambah kendala x2≤ 0.

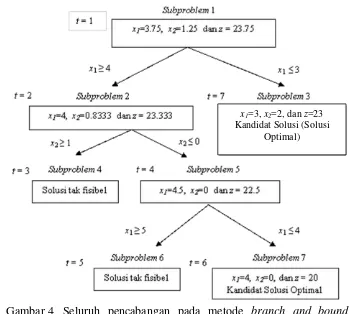
Saat ini subproblem yang belum diselesaikan adalah Subproblem 3, 4 dan 5. Salah satu subproblem dipilih, misalnya dengan aturan LIFO (last in first out). Dengan aturan ini berarti dipilih Subproblem 4 atau Subproblem 5. Subproblem 4 takfisibel maka subproblem ini tidak dapat menghasilkan solusi optimal, yang tersisa adalah Subproblem 3 dan Subproblem 5.

Karena aturan LIFO, dipilih Subproblem 5, yang kemudian menghasilkan solusi optimal x1=4.5, x2=0 dan z=22.5. Karena x1=4.5 bukan integer, maka

dilakukan kembali pencabangan atas x1, sehingga diperoleh:

 Subproblem 6: Subproblem 5 ditambah kendala x1≥5_;

 Subproblem 7: Subproblem 5 ditambah kendala x1≤4.

Misalkan dipilih Subproblem 6. Ternyata Subproblem 6 ini juga takfisibel, sehingga tidak dapat menghasilkan solusi optimal. Dengan demikian subproblem-subproblem yang belum diselesaikan adalah Subproblem 3 dan Subproblem 7. Karena aturan LIFO, dipilih Subproblem 7. Subproblem ini kemudian menghasilkan solusi opimal x1=4, x2= 0, dan z= 20. Dapat dilihat bahwa solusi

optimal subproblem ini semuanya berupa integer, sehingga merupakan kandidat solusi untuk PLI (2.5). Nilai z pada kandidat solusi ini merupakan batas bawah bagi nilai optimal PLI. Penyelesaian Subproblem 3 menghasilkan solusi optimal x1= 3, x2= 2 dan z= 23. Batas bawah yang ditetapkan dari solusi optimal

Subproblem 7 tidak lebih baik dari nilai solusi optimal yang dihasilkan Subproblem 3. Dengan demikian, nilai solusi optimal Subproblem 3, yakni z = 23 menjadi batas bawah yang baru. Semua solusi optimal telah berupa integer dan tidak perlu dilakukan pencabangan kembali, sehingga solusi optimal dari Subproblem 3 merupakan solusi optimal PLI (2.5), yakni x1= 3, x2= 2 dan z= 23.

Pohon pencabangan yang menunjukkan proses penyelesaian masalah PLI (2.5) secara keseluruhan ditunjukkan pada Gambar 4.

(19)

9

DESKRIPSI DAN PEMODELAN MASALAH

Deskripsi Masalah

Untuk mendeskripsikan masalah Sudoku, hal utama yang harus diketahui adalah pada kotak berjumlah n2 × n2 dan akan digunakan kasus Sudoku umum dengan n = 3 sehingga setiap kolom, baris, maupun submatriks berukuran 3 × 3 hanya boleh terisi dengan bilangan 1 sampai 9 yang banyaknya masing-masing satu. Soal Sudoku memiliki variasi yang beragam dan memiliki tingkat kesulitan yang berbeda-beda.

Pemodelan Masalah

Secara matematis, memodelkan Sudoku menggunakan sebuah program linear. Lebih khusus lagi akan dirumuskan oleh formula Binary Integer Linear Programming (BLIP) untuk ukuran puzzle n2 × n2.

Variabel-variabel yang digunakan dalam model untuk penyelesaian puzzle Sudoku:

i = indeks baris pada puzzle Sudoku, j = indeks kolom pada puzzle Sudoku,

{1, 2,3, 4,5, 6, 7,8,9), k

Gambar 4 Seluruh pencabangan pada metode branch and bound untuk menentukan solusi PLI (2.5)

x1=3, x2=2, dan z=23

(20)

10

G = nilai Given.

Untuk memulai, kita definisikan dengan variabel keputusan:

jika elemen ( , ) pada matriks Sudoku berukuran mengandung integer

Selainnya

1 ,

0 ,

{

ijk

i j n n k

x  

Fungsi objektif dan kendala pada Sudoku 9 × 9 (n2 × n2, n = 3) yang memiliki mini grid 3 × 3 (n × n, n = 3).

Min 0T

x

Kendala:

Kendala pertama

Pada kolom Sudoku hanya boleh terisi dengan bilangan 1 sampai 9 tanpa ada pengulangan.

9 1

1, 1: 9, 1: 9...(3.1) ijk

i

x j k



  



Kendala kedua

Pada baris Sudoku hanya boleh terisi dengan bilangan 1 sampai 9 tanpa ada pengulangan.

1

1, 1: 9, 1: 9...(3.2) n

ijk j

x i k



  



Kendala ketiga

Pada mini grid Sudoku hanya boleh terisi dengan bilangan 1 sampai 9 tanpa ada pengulangan.

3 3 3 3 1 3 3 1

1, 1: 9, 1: 3, 1: 3...(3.3) q p

ijk j q i p

x k p q

     

   

 

Kendala keempat

Setiap elemen pada Sudoku harus terisi 9

1

(setiap matriks terisi) 1, 1: 9, 1: 9

ijk k

x i j



  



Kendala kelima

Menentukan nilai Given pada Sudoku 1 ( , , )

ijk

x  i j k G

(21)

11

Dari persamaan (3.1) dapat dijabarkan sebagai berikut: 111 211 311 411 511 611 711 811 911 121 221 321 421 421 621 721 821 921 131 231 331 431 431 631 731 831 931

199 299 399 499 599 699 799 899 999 1,

1,

.

1.

x x x x x x x x x

        

Bentuk umum untuk persamaan (3.1) yaitu:

1

(hanya satu di setiap kolom) 1, 1: , 1:

n ijk i

k

x j n k n



  



Dari persamaan (3.2) sebagai berikut:

111 121 131 141 151 161 171 181 191 211 221 231 241 251 261 271 281 291 311 321 331 341 351 361 371 381 391

919 929 939 949 959 969 979 989 999 1,

1,

.

1.

x x x x x x x x x

        

Bentuk umum dari persamaan (3.2) yaitu:

1

(hanya satu di setiap baris) 1, 1: , 1:

n ijk j

k

x i n k n



  



(22)

12

111 211 311 121 221 321 131 231 331 411 511 611 421 521 621 431 531 631 711 811 911 721 821 921 731 831 931 141 241 341 151 251 351 161 261 361 441 541 6

1, 1, 1, 1,

x x x x x x x x x

x x x

        

  ₄₁ ₄₅₁ ₅₅₁ ₆₅₁ ₄₆₁ ₅₆₁ ₆₆₁

741 841 941 751 851 951 761 861 961 171 271 371 181 281 381 191 291 391 471 571 671 481 581 681 491 591 691 771 871 971 781 881

1, 1, 1, 1,

x x x x x x

x x x x x x x x x

x x x x x

      

        

    x₉₈₁x₇₉₁x₈₉₁x₉₉₁1.

119 219 319 129 229 329 139 239 339 419 519 619 429 529 629 439 539 639 719 819 919 729 829 929 739 839 939 149 249 349 159 259 359 169 269 369 449 549 . . . 1, 1, 1, 1,

x x x x x x x x x

x x

        

 ₆₄₉ ₄₅₉ ₅₅₉ ₆₅₉ ₄₆₉ ₅₆₉ ₆₆₉ 749 849 949 759 859 959 769 869 969

1,

x x x x x x x

x x x x x x x x x

       

        

179 279 379 189 289 389 199 299 399 479 579 679 489 589 689 499 599 699

1, 1,

x x x x x x x x x

        

779 879 979 789 889 989 799 899 999 1.

x x x x x x x x x 

Persamaan di atas di sederhanakan menjadi: 3

1 2 3

1 6

1 2 3

4 9

1 2 3

7 3

4 5 6

1 6

4 5 6

4 9

4 5 6

7 3

7 8 9

1

1; 1 : 9,

i k i k i k i

x x x k

(23)

13 6

7 8 9

4 9

7 8 9

7

1; 1: 9, 1; 1: 9. i k i k i k

i

i k i k i k i

x x x k

         



Persamaan (3.3) memiliki bentuk umum yaitu:

1 1

1, 1: , 1: , 1: (hanya satu di setiap sub matriks) mq mp

ijk j mq m i mp m

x k n p m q m k

     

   

 

PEMBAHASAN

Contoh Kasus

Pada bagian ini akan diberikan contoh kasus dalam penyelesaian Sudoku dengan ukuran 4 × 4 (n2 × n2, n = 2) dan memiliki mini grid 2 × 2 (n × n, n = 2). Misalkan elemen dari baris ke-i dan kolom ke-j adalah x_{i j}_, maka Sudoku secara umum adalah

Penyelesaian Sudoku tersebut menggunakan metode branch and bound memerlukan kendala-kendala sebagai berikut:

4 1

1, 1: 4, 1: 4 ...(4.1)

ijk i

x j k



  



4 1

1, 1: 4, 1: 4...(4.2) ijk

j

x i k



  



1 1

1, 1: 4, 1: 2, 1: 2 mq mp

x k p q

         

 

Sehingga : 2 2 1 1

1, 1: 4...(4.3) ijk j i x k    



2 4 1 3

1, 1: 4...(4.4) ijk j i x k    



4 2 3 1

1, 1: 4...(4.5) ijk j i x k    



(24)

14

4 4 3 3

1, 1: 4...(4.6) ijk j i x k    



4 1

1, 1: 4, 1: 4...(4.7)

ijk k

x i j



  



1 ( , , )

ijk

x  i j k G

Dari persamaan (4.1) diperoleh: 111 211 311 411

121 221 321 421 131 231 331 431 141 241 341 441

1, 1, 1, 1,

x x x x

   

112 212 312 412 122 222 322 422 132 232 332 432 142 242 342 442

1, 1, 1, 1,

x x x x

   

114 214 314 414 124 224 324 424 134 234 334 434 144 244 344 444

1, 1, 1, 1.

x x x x

   

Dari persamaan (4.2) diperoleh : 111 121 131 141

211 221 231 241 311 321 331 341 411 421 431 441

1, 1, 1, 1,

x x x x

   

112 122 132 142 212 222 232 242 312 322 332 342 412 422 432 442

1, 1, 1, 1,

x x x x

   

113 123 133 143 213 223 233 243 313 323 333 343 413 423 433 443

1, 1, 1, 1,

x x x x

   

113 213 313 413 123 223 323 423 133 233 333 433 143 243 343 443

1, 1, 1, 1,

x x x x

   

(25)

15 114 124 134 144

214 224 234 244 314 324 334 344 414 424 434 444

1, 1, 1, 1.

x x x x

   

112 212 122 222 113 213 123 223 114 214 124 224

1, 1, 1, 1.

x x x x

   

312 412 322 422 313 413 323 423 314 414 324 424

1, 1, 1, 1.

x x x x

   

132 232 142 242 133 233 143 243 134 234 144 244

1, 1, 1, 1.

x x x x

   

332 432 342 442 333 433 343 443 334 434 344 444

1, 1, 1, 1.

x x x x

   

211 212 213 214 311 312 313 314 411 412 413 414

1, 1, 1, 1,

x x x x

   

121 122 123 124 221 222 223 224 321 322 323 324 421 422 423 424

1, 1, 1, 1,

x x x x

   

(26)

16

131 132 133 134 231 232 233 234 331 332 333 334 431 432 433 434

1, 1, 1, 1,

x x x x

   

141 142 143 144 241 242 243 244 341 342 343 344 441 442 443 444

1, 1, 1, 1.

x x x x

   

Misalkan diberikan soal Sudoku 4×4:

Dari konfigurasi soal puzzle diatas jika dimasukan ke dalam kendala adalah sebagai berikut:

Dari persamaan (4.1) 111 211 311 411 121 221 321 421 131 231 331 431 141 241 341 441

0 0 0 0 0

0 1 0 0 1

0 0 0 0 0

x x x x

       

112 212 312 412 122 222 322 422 132 232 332 432 142 242 342 442

0 0 0 0 0

1 0 0 0 1

0 0 0 0 0

x x x x

       

114 214 314 414 124 224 324 424 134 234 334 434 144 244 344 444

0 0 0 1 1

0 0 0 0 0

0 0 1 0 1

0 0 0 0 0

x x x x

       

2

3 1

4 3 4 3

Gambar 6 Contoh soal Sudoku 4 × 4

113 213 313 413 123 223 323 423 133 233 333 433 143 243 343 443

0 1 0 0 1 0 0 0 1 1

0 0 0 0 0

0 0 1 0 1

x x x x

       

(27)

17 Dari persamaan (4.2)

111 121 131 141 211 221 231 241 311 321 331 341 411 421 431 441

0 0 0 0 0

0 0 1 0 1

0 0 0 0 0

x x x x

       

112 122 132 142 212 222 232 242 312 322 332 342 412 422 432 442

0 1 0 0 1

0 0 0 0 0

x x x x

       

113 123 133 143 213 223 233 243 313 323 333 343 413 423 433 443

0 0 0 0 0

1 0 0 0 1 0 0 0 1 1 0 1 0 0 1

x x x x

       

114 124 134 144 214 224 234 244 314 324 334 344 414 424 434 444

0 0 0 0 0

0 0 1 0 1 1 0 0 0 1

x x x x

       

Dari persamaan (4.3) 111 211 121 221 112 212 122 222 113 213 123 223 114 214 124 224

0 0 0 0 0

0 0 1 0 1 0 1 0 0 1

0 0 0 0 0

x x x x

       

Dari persamaan (4.4) 311 411 321 421 312 412 322 422 313 413 323 423 314 414 324 424

0 0 0 0 0

0 0 0 1 1 0 1 0 0 1

x x x x

       

Dari persamaan (4.5) 131 231 141 241 132 232 142 242 133 233 143 243 134 234 144 244

0 1 0 0 1

0 0 0 0 0

x x x x

       

(28)

18

Dari persamaan (4.6) 331 431 341 441 332 432 342 442 333 433 343 443 334 434 344 444

0 0 0 0 0

0 0 1 0 1 1 0 0 0 1

x x x x

       

211 212 213 214 311 312 313 314 411 412 413 414

0 0 0 0 0

0 0 1 0 1

0 0 0 0 0

0 0 0 1 1

x x x x

       

121 122 123 124 221 222 223 224 321 322 323 324 421 422 423 424

0 1 0 0 1

0 0 0 0 0

0 0 1 0 1

x x x x

       

131 132 133 134 231 232 233 234 331 332 333 334 431 432 433 434

0 0 0 0 0

1 0 0 0 1 0 0 0 1 1

0 0 0 0 0

x x x x

       

141 142 143 144 241 242 243 244 341 342 343 344 441 442 443 444

0 0 0 0 0

0 0 1 0 1

0 0 0 0 0

x x x x

       

Dari konfigurasi puzzle yang diberikan sudah dapat diketahui given yang diberikan yaitu:

213 1; 414 1; 122 1; 423 1; 231 1; 334 1; 343 1

x  x  x  x  x  x  x 

Kendala di atas memiliki 64 persamaan dan 64 variabel, dan persamaan yang sudah memenuhi kondisi yaitu sebanyak 28 persamaan. Jadi membutuhkan banyak iterasi pada persamaan di atas untuk memperoleh solusi dari puzzle yang diberikan. Oleh karena itu, berdasarkan konsep yang sama, digunakan langkah-langkah yang dapat merealisasikan formulasi tersebut.

Langkah pertama

(29)

19 Untuk k bernilai 1

1 0 1 1 0 1 1 1 1 1 0 0 0 0 1 1

231

: 1

given x 

Untuk k bernilai 2

2 2 2 2 0 2 0 2 2 2 0 0 0 0 2 2

122

: 1

given x 

Untuk k bernilai 3

3 0 3 3 3 3 0 3 3 3 0 3 0 3 3 3

213 423 343

: 1; 1; 1

given x  x  x 

Untuk k bernilai 4

4 0 4 4 0 4 0 4 4 4 4 0 4 0 4 4

414 334

: 1; 1

given x  x 

Langkah kedua

Menentukan kemungkinan pada nilai k berdasarkan konsep hanya boleh ada 1 bilangan angka pada baris, kolom, dan mini grid dengan langkah: jadikan bilangan given sebagai poros; cek baris, kolom, dan mini grid, jika ada yang bernilai k maka ganti dengan angka 0

Kemungkinan k bernilai 1, dengan givenx₂₃ sebagai poros 1 0 0 0 0 0 1 0 1 1 0 0 0 0 0 1 2

3 1

4 3 4 3

2

3 1

4 3 4 3

2

3 1

4 3 4 3

2

3 1

4 3 4 3

1 0 1 1

0 1 1 1

1 1 0 0

(30)

20

Kemungkinan k bernilai 2, dengan givenx₁₂ sebagai poros

0 2 0 0

0 0 0 2

2 0 0 0

0 0 2 2

Kemungkinan k bernilai 3, dengan given: x₂₁;x₄₂;x₃₄ sebagai poros

0 0 3 0

3 0 0 0

0 0 0 3

0 3 0 0

Kemungkinan k bernilai 4, dengan given: x₄₁;x₃₃ sebagai poros

0 0 0 4

0 4 0 4

0 0 4 0

4 0 0 0

Langkah ketiga

Setelah mencari kemungkinan nilai k, barulah memasukan kendala pada semua kemungkinan nilai k.

Kendala: 4

1

1, 1: 4, 1: 4,

ijk i

x j k



  



4 1

1, 1: 4, 1: 4, ijk

j

x i k



  



2 2 1 1

1, 1: 4, ijk j i x k    



2 4 1 3

1, 1: 4, ijk j i x k    



4 2 3 1

1, 1: 4, ijk j i x k    



4 4 3 3

1, 1: 4. ijk j i x k    



Kemungkinan k bernilai 1 4

1 1

1, 1: 4, 1

ij i

x j k



  



2 2 2 2

0 2 0 2

2 2 0 0

0 0 2 2

3 0 3 3

3 3 0 3

0 3 3 3

4 0 4 4

0 4 0 4

4 4 4 0

(31)

21 111 211 311 411

121 221 321 421 131 231 331 431 141 241 341 441

1 0 1 0 2

0 0 1 0 1 0 1 0 0 1 0 0 0 1 1

x x x x

                                4 1 1

1, 1: 4, 1

ij j

x i k



  



111 121 131 141 211 221 231 241 311 321 331 341 411 421 431 441

1 0 0 0 1 0 0 1 0 1

1 1 0 0 2

0 0 0 1 1

x x x x

                                2 2 1 1 1 1, 1 ij j i x k    



111 211 121 221 1 0 0 0 1

x x x x     

2 4 1 1 3 1, 1 ij j i x k    



311 411 321 421 1 0 1 0 0

x x x x     

4 2 1 3 1 1, 1 ij j i x k    



131 231 141 241 0 1 0 0 1

x x x x     

4 4 1 3 3 1, 1 ij j i x k    



331 431 341 441 0 0 0 1 0

x x x x     

Pada iterasi di atas dengan k = 1 diperoleh nilai x_ijkyang memenuhi kondisi yaitu: 111 1; 231 1( ); 441 1; 321 1

x  x  given x  x 

dan selanjutnya iterasi dilanjutkan hingga k = 4, sehingga diperoleh nilai x_ijk, yaitu:

312 1; 122 1( ); 432 1; 242 1 x  x  given x  x 

213 1( ); 423 1( ); 133 1; 343 1( ) x  given x  given x  x  given

(32)

22

Semua solusi dari iterasi persamaan di atas dimasukan ke dalam Sudoku, ditampilkan pada gambar di bawah ini.

Mencari Solusi Puzzle Sudoku Tradisional pada Matriks 9 × 9

Untuk menyelesaikan Sudoku yang berukuran 9 × 9 dengan aturan tradisional, kita bisa menggunakan dengan kendala yang serupa, dengan nilai n=9, dan m=3, sehingga memiliki kendala:

1

(hanya satu di setiap kolom, dengan nilai = 9) 1, 1: , 1:

n ijk i

k n

x j n k n



  



9 1

1, 1: 9, 1: 9,

ijk i

x j k



  



9 2

1, 1: 9, 1: 9,

ijk i

x j k

   



9 9

1, 1: 9, 1: 9.

ijk i

x j k



  



1

(hanya satu di setiap baris dengan nilai =9) 1, 1: , 1:

n ijk j

k n

x i n k n

   



9 1 9 2 9 9

1, 1 : 9, 1 : 9,

1, 1 : 9, 1 : 9. ijk j ijk j ijk j

x i k

           



1 1

1, 1: 9, 1: 3, 1: 3 mq mp

x k p q

     

   

 

1 2 3 4

3 4 1 2

2 1 4 3

4 3 2 1

(33)

23 3 3 1 1 6 3 4 1 9 3 7 1 3 6 1 4

1, 1 : 9,

1, 1 : 9, ijk j i ijk j i ijk j i ijk j i x k x k x k x k                



6 6 4 4 9 6 7 4 3 9 1 7 6 9 4 7 9 9 7 7

1, 1 : 9,

1, 1 : 9. ijk j i ijk j i ijk j i ijk j i ijk j i x k x k x k x k x k                    



9 1

1, 1: 9, 1: 9

ijk k

x i j



  



1 ( , , )

ijk

x  i j k G

[image:33.595.107.395.511.698.2]

Bentuk matriks Sudoku ukuran 9 × 9 secara umum adalah:

(34)

24

Untuk memperoleh solusi dari Sudoku berukuran 9 × 9 menggunakan software MATLAB 7.10.0, dengan membuat algoritma berbentuk script m-file dengan nama sudoku.m (lampiran 1). Contoh soal Sudoku 9 × 9:

Dan diubah ke dalam bentuk matriks, dengan nama matriks M:

0 0 8 0 9 0 5 0 0

0 0 1 0 7 0 4 0 0

0 0 4 0 3 0 6 0 0

0 1 0 0 0 6 0 0 7

0 9 0 0 0 3 0 0 0

0 2 0 0 5 0 0 6 0

0 5 0 0 4 0 0 2 0

0 0 0 8 0 0 0 3 0

6 0 0 1 0 0 0 4 0

M

 

 



 

 

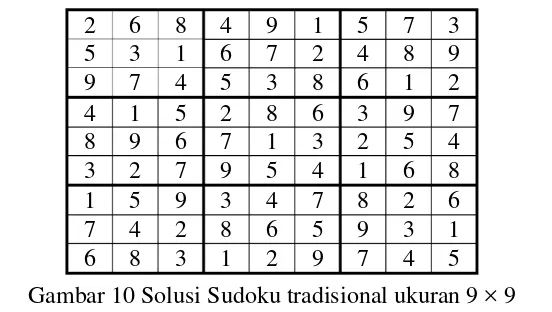
Dan file dari sudoku.m dieksekusi akan memberikan solusi seperti di bawah ini

2 6 8 4 9 1 5 7 3

5 3 1 6 7 2 4 8 9

9 7 4 5 3 8 6 1 2

4 1 5 2 8 6 3 9 7

_ 8 9 6 7 1 3 2 5 4

3 2 7 9 5 4 1 6 8

1 5 9 3 4 7 8 2 6

7 4 2 8 6 5 9 3 1

6 8 3 1 2 9 7 4 5

sol M

 

 



 

 

8 9 5

1 7 4

4 3 6

1 6 7

9 3

2 5 6

5 4 2

8 3

[image:34.595.77.443.85.815.2]

6 1 4

(35)

25 Maka diperoleh Sudoku setiap elemen pada kolom, baris dan sub-matriks terisi oleh angka 1 sampai 9 tanpa ada pengulangan. Gambar di bawah ini merupakan solusi dalam bentuk tabel.

Pada script m-file sudoku.m dapat mengeksekusi soal Sudoku tradisional yang memiliki banyak solusi (terhingga). Output yang diberikan dari m-file ini adalah seluruh solusi. Di bawah ini akan diberikan contoh soal Sudoku yang memiliki banyak solusi yang terhingga.

Soal Sudoku di atas setelah dieksekusi memberikan output (solusi) sebanyak 16 matriks solusi (lampiran 4)

Mencari Solusi Puzzle Sudoku X (Sudoku Diagonal) pada Matriks 9 × 9 Pada bagian pembahasan ini, diperlukan kendala tambahan untuk mencari solusi sudoku X, kendalanya yaitu:

9 1

1, 1: 9

rrk r

x k



 



(diagonal pertama tiap elemennya harus terisi angka 1-9)

111 221 331 441 551 661 771 881 991 1 x x x x x x x x x 

2 6 8 4 9 1 5 7 3

5 3 1 6 7 2 4 8 9

9 7 4 5 3 8 6 1 2

4 1 5 2 8 6 3 9 7

8 9 6 7 1 3 2 5 4

3 2 7 9 5 4 1 6 8

1 5 9 3 4 7 8 2 6

7 4 2 8 6 5 9 3 1

[image:35.595.155.431.140.296.2]

6 8 3 1 2 9 7 4 5

Gambar 10 Solusi Sudoku tradisional ukuran 9 × 9

2 9 4

3 2

4 9 8

6 8 5

2 7

1 5 7 6

6 3

1 8 5

9 1

[image:35.595.124.427.378.529.2]

(36)

26

112 222 332 442 552 662 772 882 992 113 223 333 443 553 663 773 883 993

119 229 339 449 559 669 779 889 999 1 1 .

. .

1

x x x x x x x x x

        

9

(10 ) 1

1, 1: 9

r r k r

x _ k



 



(diagonal kedua tiap elemennya harus terisi angka 1-9)

191 281 371 461 551 641 731 821 911 192 282 372 462 552 642 732 822 912 193 283 373 463 553 643 733 823 913

199 289 379 469 559 649 739 829 919 1

1

.

1

x x x x x x x x x

        

Dengan menambahkan kendala, jadi diperlukan perubahan pada script Sudoku untuk mencari solusi sudoku X. Script m-file Sudoku yang baru diberi nama sudokuX.m (Lampiran 2) untuk mencari solusi Sudoku diagonal. Contoh

permasalahan untuk Sudoku diagonal:

8 6 2 1

9 2 8 7

5 3 9

6 9 1

4 9 1 6 7

8 1 3 2 6 5 9

4 6 2

9 1 2 6

[image:36.595.52.432.36.682.2]

8 6 4 1 2

(37)

27 Bentuk matriks dengan nama matriks M:

0 8 0 0 6 0 2 1 0

0 9 0 2 8 0 0 0 7

0 0 0 0 5 3 9 0 0

6 0 0 0 9 0 0 0 1

0 4 9 0 1 6 7 0 0

8 1 3 0 2 0 6 5 9

4 6 2 0 0 0 0 0 0

9 0 1 0 0 2 0 0 6

0 0 8 6 4 0 1 0 2

M

 

 



 

 

Jika sudokuX.m dieksekusi akan memberikan solusi (lampiran 4), diperoleh solusi Sudoku X dalam bentuk matriks:

5 3 7 4 1 2 8 9 6

6 1 4 9 3 8 2 7 5

9 2 8 5 7 6 1 3 4

3 4 1 7 6 5 9 2 8

_ 2 6 5 8 9 1 7 4 3

8 7 9 2 4 3 6 5 1

1 5 3 6 2 9 4 8 7

7 8 2 1 5 4 3 6 9

4 9 6 3 8 7 5 1 2

sol M

 

 



 

 

Maka solusi dalam bentuk tabel adalah:

5 3 7 4 1 2 8 9 6

6 1 4 9 3 8 2 7 5

9 2 8 5 7 6 1 3 4

3 4 1 7 6 5 9 2 8

2 6 5 8 9 1 7 4 3

8 7 9 2 4 3 6 5 1

1 5 3 6 2 9 4 8 7

7 8 2 1 5 4 3 6 9

[image:37.595.97.487.52.816.2]

4 9 6 3 8 7 5 1 2

(38)

28

Hubungan Antar Ukuran Sudoku, Banyaknya Unsur Awal, dan

Konfigurasi Sudoku Tradisional.

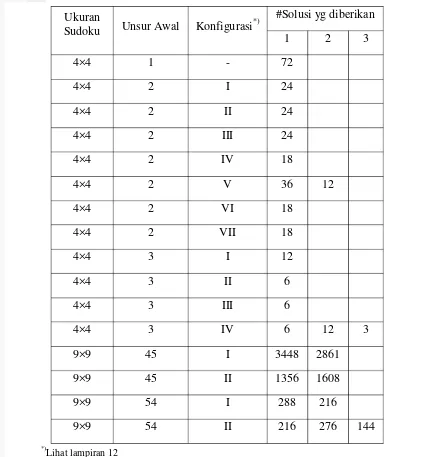
Tabel di bawah ini diberikan gambaran hubungan antar ukuran Sudoku, unsur awal, dan konfigurasi pada Sudoku tradisional. Ukuran Sudoku yang digunakan yaitu: 4 × 4 (n2 × n2, n = 2) dan 9 × 9 (n2 × n2, n = 3), dengan unsur awal yang diberikan beragam :

Pada ukuran Sudoku 4 × 4 dengan pemberian 1 given, 2 given dan 3 given diketahui memiliki beragam solusi, kecuali pemberian 1 given memilik jumlah solusi yang sama (berlaku pada semua konfigurasi Sudoku ukuran 4 × 4). Dengan pemberian 2 given, pada tabel di atas diketahui ada yang memiliki solusi 24, 18,

Ukuran

Sudoku Unsur Awal Konfigurasi

*) #Solusi yg diberikan

1 2 3

4×4 1 - 72

4×4 2 I 24

4×4 2 II 24

4×4 2 III 24

4×4 2 IV 18

4×4 2 V 36 12

4×4 2 VI 18

4×4 2 VII 18

4×4 3 I 12

4×4 3 II 6

4×4 3 III 6

4×4 3 IV 6 12 3

9×9 45 I 3448 2861

9×9 45 II 1356 1608

9×9 54 I 288 216

9×9 54 II 216 276 144

*)

[image:38.595.80.504.196.653.2]

Lihat lampiran 12

(39)

29 36, 12 dengan konfigurasi yang berbeda-beda. Konfigurasi I, II, dan III memiliki variasi solusi yang seragam yaitu sebanyak 24 solusi. Konfigurasi I menempatkan given pada x_1,1 dan x_2,2 dengan x_1,1x_2,2,konfigurasi II menempatkan given pada

1,2

x dan x_1,3 dengan x_1,2 x_1,3, dan konfigurasi III menempatkan given pada x_2,2

dan x_2,3 dengan x_2,2 x_2,3. Sedangkan konfigurasi IV, V dan VI memberikan banyak solusi yang beragam, yaitu: 18, 36, dan 12 (lampiran 12). Untuk konfigurasi IV dan VI menghasilkan solusi yang seragam yaitu 18 solusi, sedangkan untuk konfigurasi V memberikan solusi 36 dan 12 (lampiran 12). Jadi dari beberapa bentuk konfigurasi dengan pemberian 2 given tidak memberikan jumlah solusi yang sama, begitu juga dengan pemberian 3 given pada Sudoku ukuran 4 × 4 memberikan beragam solusi. Hal ini juga terjadi pada Sudoku ukuran 9 × 9 memberikan beragam solusi untuk given yang sama (lampiran 12).

SIMPULAN DAN SARAN

Simpulan

Dalam penulisan karya ilmiah ini telah diperlihatkan pencarian solusi Sudoku dari soal puzzle yang ditentukan, dengan menggunakan metode branch and bound yang diimplementasikan pada script m-file. Pencarian solusi Sudoku diperluas tidak hanya untuk mencari solusi Sudoku tradisional, tetapi dengan penambahan beberapa kendala dan perubahan pada script m-file sehingga bisa menemukan solusi untuk Sudoku diagonal atau dikenal dengan nama Sudoku X. Script m-file pada penulisan karya ilmiah ini telah berhasil memperoleh solusi Sudoku dengan menggunakan metode branch and bound. Dari pembahasan di atas dapat disimpulkan juga bahwa hubungan antar ukuran Sudoku, unsur awal, dan konfigurasi Sudoku tradisional belum dapat menentukan pola keteraturan banyaknya solusi untuk Sudoku ukuran 9 × 9, namun untuk konfigurasi tertentu dapat ditentukan pola keteraturan menentukan banyaknya solusi yang muncul (Sudoku dengan ukuran 4 × 4).

Saran

(40)

30

DAFTAR PUSTAKA

Bartlett AC, Chartier TP, Langville AN, Rankin TD. 2008. An Integer Programming Model for the Sudoku Problem. College of Charleston and Davidson College, (US). [Jurnal]

Garfinkel RS & GL Nemhauser. 1972. Integer Programming, New York.(US): John Willey & Sons.

Leon SJ. 2001. Aljabar Linear dan Aplikasinya. Alit Bondan: Penerjemah, Jakarta. (ID): Erlangga. Terjemahan dari: Linear Algebra With Applications.

Setianto D. 2011. Penjadwalan Kereta Api Menggunakan Pemrograman Linear Integer [Skripsi]. Bogor (ID): Fakultas Matematika dan Ilmu Pengetahuan Alam, Institut Pertanian Bogor.

Taha HA. 1996. Pengantar Riset Operasi. Drs. Daniel Wirajaya: Penerjemah, Jakarta. (ID): Binarupa Aksara. Terjemahan dari: Operations Research.

(41)

31 Lampiran 1 Script m-file sudoku.m untuk mencari solusi Sudoku tradisional.

%created by: Michael Kleder, December 2006 %Script M-File MATLAB 7.10.0

function A=sudoku(M)

if ndims(M)~=2

error('Matriks harus 2 dimensi.')

end

if any((size(M)-[9 9])~=0)

error('Matriks yang dibuat harus memiliki 9 kolom dan 9 baris.')

end

if any(any(M~=floor(M))) || any(abs(M(:)-4.5)>4.5)

error(soal dan solusi merupakan bilangan bulat 1 sampai 9 .')

end

A=0*M;

[M,imp,A]=recurse(M,A);

if imp

error('Tidak ada solusi.')

end

A=A(:,:,2:end);

return

function [M,imp,A]=recurse(M,A)

[M,imp]=deduce(M);

if imp

return

end

z=find(~M(:));

if isempty(z)

A(:,:,end+1)=M;

return

end

impall=zeros(1,9);

for v=1:9 Q=M;

Q(z(1))=v;

[Q,impall(v),A]=recurse(Q,A);

end

imp=all(impall); M=Q;

return

function [M,imp]=deduce(M)

imp=0;

Mprev = 10*M;

while any(M(:)-Mprev(:))

Mprev=M;

N=ones(9,9,9); [i,j]=find(M); for n=1:length(i) N(i(n),j(n),:)=0;

N(i(n),j(n),M(i(n),j(n)))=1; end

(42)

32

if any(any(sum(N,3)<1)) imp=1;

return

end

[i,j]=find(sum(N,3)<2); for n=1:length(i)

if any(any(sum(N,3)<1)) imp=1;

return

end

v = find(N(i(n),j(n),:)); M(i(n),j(n)) = v;

N(:,j(n),v)=0; N(i(n),:,v)=0;

br = floor((i(n)-.5)/3)*3+1; bc = floor((j(n)-.5)/3)*3+1; N(br:br+2,bc:bc+2,v)=0; N(i(n),j(n),v)=1;

end

for i=1:9 for j=1:9

k=find(N(i,j,:)); if length(k)==1 M(i,j)=k; end

end

for i=1:9 for k=1:9

j=find(N(i,:,k)); if length(j)==1 M(i,j)=k; end

end

end for j=1:9

for k=1:9

i=find(N(:,j,k)); if length(i)==1 M(i,j)=k; end

end

for i=[1 4 7] for j=[1 4 7] for k=1:9

Q=N(i:i+2,j:j+2,k); [pr,pc]=find(Q); if length(pr)==1

M(i+pr-1,j+pc-1)=k; end

end

(43)

33 Lampiran 2 Script m-file sudokuX.m untuk mencari solusi Sudoku X (Sudoku

diagonal)

%Script M-File MATLAB 7.10.0

function [A,B]=sudokuX(M)

if ndims(M)~=2

error('Matriks harus 2 dimensi.')

end

if any((size(M)-[9 9])~=0)

error('Matriks yang dibuat harus memiliki 9 kolom dan 9 baris.')

end

if any(any(M~=floor(M))) || any(abs(M(:)-4.5)>4.5)

error('soal dan solusi merupakan bilangan bulat 1 sampai 9.')

end

A=0*M;

[M,imp,A]=recurse(M,A);

if imp

error('Tidak ada solusi.')

end

A=A(:,:,2:end);

C=numel(A)/81;

for sol = 1:C

seq=[1 2 3 4 5 6 7 8 9]; seqver=zeros(1,9);

seqhor=zeros(1,9); for i =1:9

seqver(i)=A(i,i,sol); end

for j =1:9

seqhor(j)=A(j,10-j,sol); end

if (sort(seqver)))==0) && (sum(abs(seq-sort(seqhor)))==0))

B=A(:,:,sol); return

end end

B='Tidak ada solusi untuk sudoku X.';

return

function [M,imp,A]=recurse(M,A)

[M,imp]=deduce(M);

if imp

return

end

z=find(~M(:));

if isempty(z)

A(:,:,end+1)=M;

return

(44)