Regresi Kekar Simpangan Mutlak Terkecil dengan Modifikasi Simpleks

(1)

REGRESI KEKAR SIMPANGAN MUTLAK TERKECIL

DENGAN MODIFIKASI SIMPLEKS

MUHAMMAD YUSUF DWIHARJANGGI

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

(2)

ABSTRAK

MUHAMMAD YUSUF DWIHARJANGGI. Regresi Kekar Simpangan Mutlak Terkecil dengan Modifikasi Simpleks. Dibimbing oleh N.K. KUTHA ARDANA dan RETNO BUDIARTI.

(3)

ABSTRACT

MUHAMMAD YUSUF DWIHARJANGGI. Least Absolute Deviations with Simplex Modification. Supervised by N.K. KUTHA ARDANA and RETNO BUDIARTI

(4)

REGRESI KEKAR SIMPANGAN MUTLAK TERKECIL

DENGAN MODIFIKASI SIMPLEKS

MUHAMMAD YUSUF DWIHARJANGGI

G54103050

Skripsi

sebagai salah satu syarat untuk memperoleh gelar

Sarjana Sains

pada

Departemen Matematika

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

(5)

Judul

: Regresi Kekar Simpangan Mutlak Terkecil dengan Modifikasi

Simpleks

Nama

: Muhammad Yusuf Dwiharjanggi

NIM

: G54103050

Menyetujui

Pembimbing 1

Pembimbing II

Ir. Ngakan Komang Kutha Ardana, M.Sc

Ir. Retno Budiarti, MS

NIP. 19640823 198903 1 001

NIP. 19610729 198903 2 001

Mengetahui

Ketua Departemen Matematika

Dr. Berlian Setiawaty, MS

NIP. 19650505 198903 2 004

(6)

KATA PENGANTAR

Alhamdulillahirobbil’alamin. Penulis mengucapkan syukur kehadirat Allah SWT atas segala limpahan rahmat dan karunia-Nya sehingga karya ilmiah ini berhasil diselesaikan. Penyusunan karya ilmiah ini tidak terlepas dari dukungan dan bantuan dari berbagai pihak. Pada kesempatan ini, penulis juga ingin mengucapkan terimakasih yang sebesar-besarnya kepada:

1. Keluargaku, Bapak, Ibu, Mas Pipin beserta keluarga, sepupu-sepupu , keluarga besar Mbah Dirman dan keluarga besar Bani Sadja’ie, serta almarhum adikku tercinta Rizky. Semoga kelak penulis dapat membanggakan kalian semua.

2. Ir. N. K. Kutha Ardana, M.Sc. selaku dosen pembimbing I dan Ir. Retno Budiarti, MS selaku pembimbing II atas waktu, ilmu yang diberikan dan kesabarannya dalam membimbing penulis. Serta Dra. Farida Hanum, M.Si. selaku dosen penguji. Semoga semua ilmunya dapat bermanfaat bagi penulis.

3. Semua dosen Departemen Matematika, semoga ilmu yang telah diberikan bermanfaat. 4. Pak Yono, Bu Ade, Bu Susi, Mas Bono, Mas Heri, Mas Deni dan seluruh staf pegawai

Departemen Matematika yang membantu dalam memperlancar administrasi akademik bagi penulis di departemen Matematika.

5. Teman-teman satu bimbingan : Boy, Hendra dan Manto, atas bantuan, dukungan, semangat dan saran-sarannya.

6. Teman-teman mathlete angkatan 40 atas keceriaan, dukungan, semangat dan persahabatannya.

7. Adik kelas angkatan 41, 42, 43, 44 dan 45 yang tidak bisa penulis sebutkan satu per satu atas bantuannya dalam menyelesaikan karya ini.

8. Alumni matematika yang telah membantu pencarian literatur, membagi pengalaman, dan saran-sarannya.

9. Teman-teman Alumni Rohis SMA N 89 Jakarta Timur yang mendoakan dan menyemangati. 10. Teman-teman Onigiri Japan Club untuk hiburan dan persahabatannya.

11. Teman-teman UKM Tae Kwon Do IPB, terutama sabeum Billy yang selalu menyemangati. 12. Mas Irfan di Agri FM yang telah meminjamkan printer dan ruangannya..

Penulis menyadari tulisan ini masih memiliki kekurangan dan jauh dari kesempurnaan. Oleh karena itu dibutuhkan kritik dan saran yang membangun dari pembaca.

Semoga karya ilmiah ini bermanfaat bagi kita semua, bagi dunia ilmu pengetahuan khususnya Matematika.

Bogor, Agustus 2011

(7)

RIWAYAT HIDUP

Penulis lahir di Jakarta pada tanggal 16 Agustus 1985 sebagai anak kedua dari tiga bersaudara, anak dari pasangan Djoko Tjatur Nusantara dan Siti Chosiyah. Tahun 1998 penulis lulus dari SDN Rawabebek 2 Bekasi Barat. Tahun 2000 penulis lulus dari SLTPN 172 Jakarta Timur. Tahun 2003 penulis lulus dari SMAN 89 Jakarta Timur dan pada tahun yang sama penulis lulus seleksi masuk IPB melalui jalur Ujian Masuk Perguruan Tinggi Negeri (UMPTN). Penulis memilih jurusan Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam.

(8)

DAFTAR ISI

Halaman

DAFTAR ISI ... vii

DAFTAR GAMBAR ... viii

DAFTAR TABEL ... viii

DAFTAR LAMPIRAN ... ix

I PENDAHULUAN 1.1 Latar Belakang ... 1

1.2 Tujuan ... 1

1.3 Ruang Lingkup ... 1

II LANDASAN TEORI 2.1 Persamaan Regresi... 1

2.2 Regresi Linear ... 2

2.3 Pendugaan Koefisien Regresi Linear ... 2

2.4 Pencilan ... 2

2.5 Regresi Kekar ... 2

2.6 Metode Simpangan Mutlak Terkecil ... 3

2.7 Metode Penyelesaian Simpangan Mutlak Terkecil ... 3

2.8 Metode Modifikasi Simpleks Simpangan Mutlak Terkecil ... 3

2.8.1 Formulasi Masalah dalam Model Simpleks ... 3

2.8.2 Algoritme Simpleks ... 5

III METODELOGI PENELITIAN ... 5

IV HASIL DAN PEMBAHASAN 4.1 Pembangkitan Data ... 61

4.2 Pengolahan Data tanpa Pencilan... 6

4.3 Pengolahan Data dengan Pencilan ... 6

4.4 Penyajian dan Analisis Data tanpa Pencilan... 6

4.5 Penyajian dan Analisis Data dengan Pencilan ... 7

4.5.1 Pencilan Vertikal ... 7

4.5.2 Pencilan Horizontal ... 9

4.6 Penyajian dan Analisis Terhadap Gugus Data Simetrik... 11

V SIMPULAN 4.1 Simpulan ... 13

4.2 Saran ... 13

VI DAFTAR PUSTAKA ... 14

(9)

DAFTAR GAMBAR

Halaman 1 Scatter Plot Kuadrat Terkecil n = 10 tanpa pencilan ... 6 2 Scatter Plot Simpangan Mutlak Terkecil n = 10 tanpa pencilan ... 7 3 Perbandingan Scatter Plot antara OLS (merah) dengan LAD (hijau) pada data tanpa

pencilan ... 7 4 Scatter Plot Kuadrat Terkecil n = 10 dengan pencilan vertikal ... 7 5 Scatter Plot Simpangan Mutlak Terkecil n = 10 dengan pencilan vertikal ... 8 5 Perbandingan Scatter Plot antara OLS (merah) dengan LAD (hijau) pada data dengan

pencilan vertikal ... 8 7 Scatter Plot Kuadrat Terkecil n = 10 dengan pencilan horizontal ... 9 8 Scatter Plot Simpangan Mutlak Terkecil n = 10 dengan pencilan horizontal ... 9 9 Perbandingan Scatter Plot antara OLS (merah) dengan LAD (hijau) pada data dengan

pencilan horizontal ... 10 10 Scatter Plot Kuadrat Terkecil n = 10 dengan pencilan horizontal yang relatif kecil ... 10 11 Scatter Plot Simpangan Mutlak Terkecil n = 10 dengan pencilan horizontal yang relatif

kecil ... 11 12 Perbandingan Scatter Plot antara OLS (merah) dengan LAD (hijau) pada data dengan

pencilan horizontal yang relatif kecil ... 11 13 Scatter Plot Kuadrat Terkecil untuk gugus data simetrik ... 12 14 Scatter Plot Simpangan Terkecil untuk gugus data simetrik ... 12 15 Scatter Plot Simpangan pada solusi garis regresi LAD (hijau), LAD2 (biru) dan LAD3

(merah) gugus data simetrik... 13

DAFTAR TABEL

Halaman 1 Tabel simpleks lengkap untuk masalah linear sederhana ... 4 2 Tabel perbandingan nilai a dan b pada metode Kuadrat Terkecil dan metode Simpangan

Mutlak Terkecil tanpa pencilan ... 7 3 Tabel perbandingan nilai a dan b pada metode Kuadrat Terkecil dengan pencilan

vertikal ... 8 4 Tabel perbandingan nilai a dan b pada metode Simpangan Mutlak Terkecil dengan

pencilan vertikal ... 8 5 Tabel perbandingan nilai a dan b pada metode Kuadrat Terkecil tanpa pencilan dan

dengan pencilan, baik vertikal maupun horizontal ... 9 6 Tabel perbandingan nilai a dan b pada metode Simpangan Mutlak Terkecil tanpa pencilan dan dengan pencilan, baik vertikal maupun horizontal ... 9 7 Tabel perbandingan nilai a dan b pada metode Kuadrat Terkecil tanpa pencilan dan

dengan pencilan, baik vertikal maupun horizontal serta pencilan horizontal yang relatif kecil ... 10 8 Tabel perbandingan nilai a dan b pada metode Simpangan Mutlak Terkecil tanpa pencilan

(10)

DAFTAR LAMPIRAN

Halaman

1 Ilustrasi penghitungan metode modifikasi simpleks Simpangan Mutlak Terkecil ... 16

2 Syntax dalam R language dalam pembangkitan data ... 20

3 Pengolahan data tanpa pencilan dalam R language ... 21

4 Algoritme fungsi rq dalam R language ... 22

5 Pengolahan data dengan pencilan dalam R language ... 24

(11)

1

I

PENDAHULUAN

1.1 Latar Belakang

Penelitian ilmu pengetahuan dan teknologi dewasa ini tidak dapat terlepas dari data dan pengamatan. Data ini kemudian diolah dengan beragam metode untuk pengambilan berbagai keputusan seperti analisis, peramalan dan sebagainya.

Salah satu model yang banyak dipakai adalah model regresi linear. Regresi biasanya digunakan untuk menduga nilai peubah tidak bebas dari nilai peubah bebas yang diketahui. Namun terkadang hasilnya meleset, pada suatu gugus data tertentu. Oleh karena itu banyak diadakan penelitian untuk mencari analisis teknik regresi untuk mendapatkan hasil yang mendekati sebenarnya. Melesetnya dugaan nilai dari hasil metode regresi ini dapat dipengaruhi oleh pencilan atau disebut juga outlier yang menyebabkan koefisiennya menjadi tidak stabil.

Pada model regresi linear tanpa pencilan umumnya dapat diselesaikan dengan menggunakan metode kuadrat terkecil (Ordinary Least of Square yang biasa disebut OLSatau Least of Square yang biasa disebut LS). Metode ini begitu populer karena penggunanya dapat melakukan pendekatan secara kalkulus. Metode ini menghitung penduga peubah takbebas, sehingga jumlah kesalahan kuadrat memiliki nilai terkecil dan jumlah kuadrat jarak vertikal dari titik-titik pengamatan ke garis regresi sekecil mungkin. Namun metode ini

tidak cukup akurat untuk model dengan pencilan, sehingga muncullah suatu kebutuhan akan regresi kekar (robust) yang memiliki ketahanan terhadap nilai-nilai pencilan.

Sejak abad ke-18 banyak bermunculan metode regresi kekar. Salah satu dari metode kekar tersebut adalah least absolute deviations (LAD) atau metode simpangan mutlak terkecil yang datang dari Edgeworth (1887) sebagai solusi dari masalah yang berasal dari pengaruh outliers atau pencilan terhadap OLS.

Penulis akan menggunakan suatu program aplikasi untuk membandingkan model regresi linear antara metode kuadrat terkecil dengan metode simpangan mutlak terkecil.

1.2 Tujuan

1. Mengkaji dan membandingkan metode regresi biasa dan regresi kekar LAD. 2. Mengimplementasikan metode regresi

kekar LAD.

1.3 Ruang Lingkup

Walaupun banyak jenis metode regresi kekar (robust) namun tulisan ini hanya membahas perbandingan metode OLS dengan metode LAD. Adapun metode-metode lain hanya dijelaskan secara singkat ataupun hanya menjadi pembanding.

II

LANDASAN TEORI

2.1 Persamaan Regresi

Menurut Sir Francis Galton, persamaan regresi adalah suatu persamaan matematis yang memungkinkan untuk menduga

nilai-nilai suatu peubah takbebas dari nilai-nilai-nilai-nilai satu atau lebih peubah bebas.

(12)

2

2.2 Persamaan Regresi Linear

Regresi linear dapat dituliskan dalam bentuk :

�=��+� (1) dengan :

� : vektor peubah takbebas berukuran

nx1

� : vektor parameter regresi berukuran

px1

� : matriks peubah bebas berukuran nxp � : vektor galat berukuran nx1

[Myers 1990]

2.3 Pendugaan Koefisien Regresi Linear Metode kuadrat terkecil adalah suatu metode untuk menghitung koefisien regresi sampel (� ) sebagai penduga koefisien regresi populasi (�), sedemikian sehingga jumlah kesalahan kuadrat memiliki nilai terkecil. Secara matematis, dapat dinyatakan sebagai berikut:

Model sebenarnya adalah

�=��+�

Model estimasinya adalah

�=��+ � (2)

Galat (error)adalah

�=� − �� (3)

Jumlah galat kuadrat adalah

��_�_{= (}_{� − ��}₎�₍_{� − ��}₎ ₍₄₎

Jadi metode kuadrat terkecil adalah metode menghitung � sedemikian sehingga persamaan (4) minimum. Caranya adalah dengan membuat turunan parsial mula-mula terhadap � dan menyamakan dengan nol.

��_�₌_��_{� −}₂_��_��_�₊_��_��_��

�(��) �� = 0

�(�� −2��+��)

�� = 0

2��+ 2��= 0

(��)�=฀�� (5)

Kedua ruas dari persamaan (5) dikalikan dengan (��)−1 _{, maka akan diperoleh} dugaan untuk vektor parameter regresi yaitu:

�= (��)−1₍_��_�₎ ₍₆₎

[Rencher & Schaalje 2008]

2.4 Pencilan

Pencilan (outlier) didefinisikan sebagai suatu pengamatan yang tampak bertentangan atau tidak konsisten terhadap pengamatan yang lain.

[Barnett & Lewis 1994]

Metode kuadrat terkecil tidak tahan terhadap data pencilan sehingga diperlukan pendekatan dengan metode lain.

2.5 Regresi Kekar

Regresi kekar adalah suatu regresi yang lebih tahan terhadap data pencilan. Beberapa metode penduga parameter regresi kekar yang dapat digunakan adalah:

1. Metode Kuadrat Terkecil Tertimbang (Weighted Least Square)

2. Metode Simpangan Mutlak Terkecil (Least Absolute Deviation)

3. Metode Median Kuadrat Terkecil (Least Median Square)

4. Metode Kuadrat Terpangkas (Trimmed Square)

[Yaffe 2002]

(13)

3

2.6 Metode Simpangan Mutlak Terkecil

Metode Simpangan Mutlak Terkecil juga bisa disebut dengan istilah least absolute deviations (LAD), least absolute errors

(LAE), least absolute value (LAV), atau juga masalah L1 norm. Namun untuk

mempermudah dalam penulisan karya ilmiah ini, maka untuk selanjutnya penulis akan menggunakan istilah LAD.

Metode Simpangan Mutlak Terkecil mencari suatu model estimasi dari suatu gugus data dengan meminimumkan jumlah simpangan mutlak (sum of absolute error

atau SAE) antara titik-titik dalam fungsi model estimasi dengan titik-titik pada data.

Misalkan suatu gugus data yang terdiri dari

(

x yi, i

)

dengan i=1, 2,,n. Akan

dicari suatu fungsi f sehingga

( )

i i

f x ≈ y

Untuk menduga bentuk fungsi f sejumlah parameter perlu diketahui. Sebagai contoh dalam fungsi linear

( )

i i

f x = +a bx

dengan a dan b parameter yang belum diketahui. Kemudian akan dicari nilainya dengan meminimalkan jumlah simpangan mutlaknya yang dapat dituliskan dalam bentuk

( )

1 min n i i i

S y f x

=

∑

− . (7)

Metode simpangan mutlak terkecil memanfaatkan fakta bahwa garis regresi simpangan mutlak terkecil melewati setidaknya 2 titik data. Kemudian akan didapatkan garis yang terbaik dari semua garis titik data tersebut. Garis yang terbaik ini yang disebut dengan garis regresi simpangan mutlak terkecil.

2.7 Metode Penyelesaian Simpangan Mutlak Terkecil

Untuk menyelesaikan persamaan (7) sudah banyak metode yang dipergunakan antara lain: metode Modifikasi Simpleks, metode Iteratif Kuadrat Terkecil. Walaupun ide dasar dari metode Simpangan Mutlak

Terkecil sekilas terlihat lebih mudah dari metode Kuadrat Terkecil, namun ternyata tidak mudah untuk menghitungnya secara efisien. Hal ini dikarenakan metode Simpangan Mutlak Terkecil tidak memiliki metode penyelesaian secara analitik. Oleh sebab itu pendekatan secara iteratif dibutuhkan untuk menyelesaikannya.

Terdapat beberapa teknik penyelesaian metode Simpangan Mutlak Terkecil antara lain:

1. Metode Modifikasi Simpleks dengan algoritme Barrodale-Roberts.

2. Metode Iteratif Kuadrat Terkecil Terboboti (Iteratively Re-weighted Least Squares).

3. Metode Turunan Langsung Wesolowsky (Wesolowsky’s Direct Descent Method).

4. Metode Pendekatan Maximum Likelihood Li-Arce (Li-Arce’s Maximum Likelihood Approach).

[Pfeil 2006]

Pada penulisan ini akan digunakan penyelesaian yang pertama yaitu dengan menggunakan metode modifikasi simpleks. 2.8 Metode Modifikasi Simpleks

Simpangan Mutlak Terkecil

Metode Modifikasi Simpleks efisien untuk komputasi Simpangan Mutlak Terkecil, termasuk gugus data yang melibatkan banyaknya data yang besar. Metode ini telah diimplementasikan pada paket Software R. Formulasi dan algoritma metode Modifikasi Simpleks sebagai berikut

2.8.1 Formulasi Masalah dalam Model Simpleks

Misalkan terdapat model regresi linear

Y = +α βX +e.

(14)

4

Dalam metode Simpangan Mutlak Terkecil, nilai pendugaan

α

 dan

β

 dipilih sedemikian sehingga jumlah dari nilai mutlak dari sisaan

(

∑

e



_i

)

sekecil mungkin. Dengan demikian nilai dugaan dari Simpangan Mutlak Terkecil

α

 dan

β

 adalah nilai dari a dan b yang meminimumkan persamaan (8). Selisih dari

(

)

i i

y

−

a bx

+

disebut simpangan dari titik (xi,yi) dari garis Y = +a bX



.

Barrodale dan Roberts (1973) melakukan pendekatan untuk menduga garis regresi dengan memisalkan y_i =L A x( , _i)

dan

y

_i

=

f x

( )

_i

=

f

_i yang dapat dituliskan dengan suatu persamaan

( , )

i i i

f

−

L A x

=

e

(8)

yang akan meminimumkan

e

_i . Agar dapat dihitung dengan menggunakan metode simpleks maka

e

_i akan dimisalkan sebagai

i i

u

−

v

. Dengan demikian maka persamaan (8) dapat dituliskan kembali sebagai

( , )

i i i i

f

−

L A x

= −

u

v

(9)

Dalam tulisannya Barrodale dan Roberts (1973) merumuskan secara umum untuk

1

( , )

n

i j ji

j

L A x

a

ϕ

=

∑

dengan i=1, 2,,m . Dengan demikian dalam Barrodale dan Roberts (1973) rumus umumnya dituliskan dalam bentuk

1 n

i j ji i i

j

f

a

ϕ

u

v

=

−

∑

= −

(10)

dengan i=1, 2,,m dan a_j =b_j −c_j

untuk j=1, 2,,n.

Selanjutnya akan dicari suatu solusi optimal dari suatu permasalahan linear

(

)

1

min

m i i i

u

v

=

+

∑

dengan kendala

(

)

, 1 n

i j j j i i i

j

f

b

c

ϕ

u

v

=

∑

−

+ −

,

1, 2, ,

i=  m dan b c u v_j, _j, ,_i _i ≥0.

[Barrodale & Roberts 1973]

Bentuk di atas adalah bentuk umum sedangkan untuk bentuk linear sederhana dapat dituliskan dalam bentuk

(

)

1

min

m i i i

u

v

=

+

∑

dengan kendala

(

0 0

)

0

(

)

1

n

i j j i

j

i i

f

b

c

x

b

c

x

u

v

=

−

+

−

+ −

∑

1, 2, ,

i=  m dan b c u v_j, _j, ,_i _i ≥0

dengan

(

b₀−c₀

)

x₀ adalah a0 yang

merupakan suatu konstanta yang nilainya tetap karena x0 selalu bernilai 1.

Selanjutnya akan dituliskan dalam bentuk tabel simpleks secara lengkap, sebagai berikut

Tabel 1 Tabel simpleks lengkap untuk masalah linear sederhana.

Basis R b0 b1 c0 c1 u1 u2



um v1 v2



vm

u1 y1 x0 x1 -x0 -x1 1 0 0 0 1 0 0 0 u2 y2 x0 x2 -x0 -x2 0 1 0 0 0 1 0 0











um ym x0 xm -x0 -xm 0 0 0 1 0 0 0 1 marginal cost 1 m i i

y

=

∑

0 1 m i

x

=

∑

1 m i i

x

=

∑

0 1 m i

x

=

−

∑

1 m i i

x

=

(15)

5

2.8.2 Algoritme Simpleks

Algoritma simpleks yang digunakan dalam penyelesaian Metode Simpangan Mutlak Terkecil adalah :

1. Tentukan kolom pivot.

Pilihlah kolom pivot dari nilai

marginal cost positif yang terbesar. 2. Tentukan baris pivot.

Pilihlah baris pivot dari nilai paling kecil dari nilai-nilai yang ada dalam kolom pivot yang telah dibagi dengan nilai yang ada di kolom R.

3. Lanjutkan sampai marginal cost dalam kolom pivot menjadi negatif dengan cara mengurangkan nilai-nilai dalam

kolom pivot tersebut dengan titik pivot yang telah dikalikan 2. Selama proses berlangsung maka kolom basis akan berubah, ui menjadi vi.

4. Jika sudah negatif, lakukan pivot, yaitu dengan menukarkan kolom pivot dengan kolom ui. Kemudian baris dalam kolom basis dengan titik pivot akan berubah menjadi b.

5. Ulangi langkah hingga b0 dan

b1berada di dalam kolom basis.

[Barrodale & Roberrts 1973] Untuk lebih jelas dapat dilihat ilustrasinya pada Lampiran 1.

III

METODELOGI PENELITIAN

Metodelogi penelitian dapat diuraikan sebagai berikut:

1. Tahap pembangkitan data.

Tahap ini data dibangkitkan dengan

n = 10 menggunakan R Language

dengan menentukan nilai �, kemudian membangkitkan nilai Xi = i ; i = 1,..,10 dan nilai galat yang menyebar normal, kemudian dilanjutkan membangkitkan nilai unsur-unsur � dari nilai X dan galat yang telah dibangkitkan.

2. Tahap pengolahan data tanpa pencilan. Pada tahap ini data yang telah dibangkitkan diolah dengan dua metode, yaitu: OLS dan LAD.

3. Tahap pembandingan hasil pendugaan parameter dari data tanpa pencilan Pada tahap ini akan dibandingkan hasil dugaan kedua metode. Dugaan parameter yang dihasilkan akan ditampilkan dalam bentuk Scatter Plot.

4. Tahap pengolahan data dengan pencilan. Pada tahap ini data yang telah dibangkitkan kemudian akan diganti dengan data pencilan. Pertama dengan data pencilan vertikal kemudian dengan data pencilan horizontal. Data dengan pencilan tersebut kemudian diolah kembali dengan metode OLS dan LAD. 5. Tahap pembandingan hasil pendugaan

parameter dari data dengan pencilan Sama seperti pada tahap ketiga akan dibandingkan hasil dari dugaan data dengan pencilan pada kedua metode. Dugaan parameter yang dihasilkan akan ditampilkan dalam bentuk Scatter Plot.

(16)

6

IV

HASIL DAN PEMBAHASAN

4.1 Pembangkitan Data

Data dibangkitkan terlebih dahulu dengan bantuan software R language. Prosedur pembangkitan data simulasi dimulai dari tahap menentukan parameter �, kemudian menentukan nilai X sebanyak 10 amatan dan dilanjutkan dengan menentukan nilai � dengan rumus � = X�+�. Langkah terakhir menentukan nilai e dan banyaknya pencilan. Pembangkitan data ini dapat dilihat pada Lampiran 2.

4.2 Pengolahan Data tanpa Pencilan Setelah didapatkan data, selanjutnya data tersebut akan dihitung dengan menggunakan metode OLS dan LAD. Pengolahan dalam R language dapat dilihat pada Lampiran 3.

4.3 Pengolahan Data dengan Pencilan Untuk mengolah data dengan pencilan terlebih dahulu data yang dibangkitkan tadi diganti secara manual, melalui perintah

>data.entry(x,y)

Kemudian untuk data dengan pencilan vertikal didapatkan dengan cara mengganti nilai data y yang kecil dengan nilai yang lebih besar. Sedangkan untuk data dengan pencilan horizontal diperoleh dengan cara mengganti nilai data x yang besar dengan nilai yang lebih besar. Kemudian untuk masing-masing data dengan pencilan vertikal dan horizontal diolah kembali dengan menggunakan metode OLS dan LAD dengan bantuan program R language. Untuk lebih jelasnya dapat dilihat pada Lampiran 5.

4.4 Penyajian dan Analisis Data tanpa Pencilan

Persamaan regresi yang diperoleh dengan menggunakan metode Kuadrat Terkecil yaitu:

-�� = 12.225 + 9.938 �

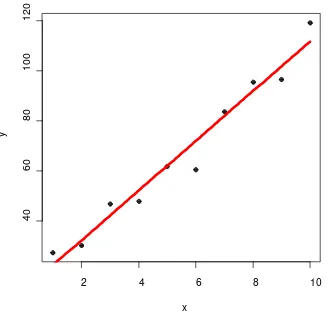
Gambar 1 menunjukkan grafik metode Kuadrat Terkecil untuk data tanpa pencilan.

Gambar 1 Scatter Plot Kuadrat Terkecil untuk n = 10 tanpa pencilan Dengan melihat Gambar 1 dapat dilihat bahwa dengan data yang tanpa pencilan metode Kuadrat Terkecil mampu menampilkan garis regresi tanpa masalah.

Kemudian dengan Metode Simpangan Mutlak Terkecil didapatkan persamaan regresi

��= 8.719 + 10.682�

Gambar 2 menunjukkan grafik regresi dengan menggunakan metode Simpangan Mutlak Terkecil untuk data tanpa pencilan.

2 4 6 8 10

40

60

80

100

120

x

(17)

7

OLS

Gambar 2 Scatter Plot Simpangan Mutlak Terkecil untuk n = 10 tanpa pencilan.

Sama seperti pada metode Kuadrat Terkecil, metode Simpangan Mutlak Terkecil juga menampilkan garis regresi tanpa masalah.

Selanjutnya dari persamaan garis yang didapatkan ini bisa dibandingkan nilai a dan

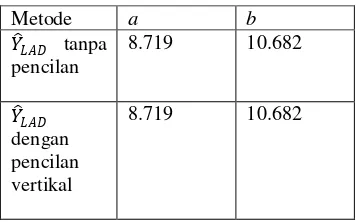
b. Garis regresi metode Kuadrat Terkecil dengan metode Simpangan Mutlak Terkecil. Tabel 2 Tabel perbandingan nilai a dan b

pada metode Kuadrat Terkecil dan metode Simpangan Mutlak Terkecil tanpa pencilan

Metode a b

�� tanpa pencilan

12.225 9.938

8.719 10.682

Dari tabel tersebut terlihat bahwa terdapat perbedaan parameter a dan b pada data tanpa pencilan pada metode OLS dengan LAD. Namun hal ini masih bisa ditoleransi karena apabila diplotkan dalam satu gambar kedua grafik tersebut terlihat berhimpit.

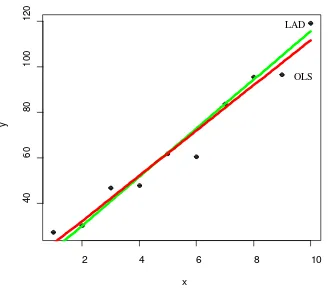
Gambar 3 menunjukkan grafik metode Kuadrat Terkecil dan metode Simpangan Mutlak Terkecil untuk data tanpa pencilan dalam satu plot.

Gambar 3 Perbandingan Scatter Plot antara Metode OLS (merah) dengan LAD (hijau) pada data tanpa pencilan

4.5 Penyajian dan Analisis Data dengan Pencilan

4.5.1Pencilan Vertikal

Misalkan data y ke-1 dari pembangkitan data sebelumnya diganti nilainya dari 27.333 menjadi 200. Kemudian akan dicari persamaan regresinya. Persamaan regresi yang diperoleh dengan menggunakan metode Kuadrat Terkecil yaitu:

-�� = 81.290 + 0.520 �

Gambar 4 menunjukkan grafik metode Kuadrat Terkecil untuk data dengan pencilan vertikal.

Gambar 4 Scatter Plot Kuadrat Terkecil untuk n = 10 dengan pencilan vertikal

Pada Gambar 4 terlihat bahwa garis regresi yang ditampilkan oleh metode Kuadrat Terkecil tidak mewakili mayoritas

2 4 6 8 10

40 60 80 100 120 x y

2 4 6 8 10

40 60 80 100 120 x y

2 4 6 8 10

(18)

8

OLS

titik-titik data. Garis regresi seolah-olah

tertarik ke atas karena data pencilan vertikal. Dari persamaan garis regresi tanpa pencilan dan dengan pencilan metode Kuadrat Terkecil didapatkan perbandingan seperti yang terlihat dalam tabel.

Tabel 3 Tabel perbandingan nilai a dan b

pada metode Kuadrat Terkecil dengan pencilan vertikal

Metode a b

12.225 9.938

�� dengan pencilan vertikal

81.290 0.520

Terlihat perbedaan yang mencolok pada parameter a dan b garis regresi dari data tanpa pencilan dan dengan pencilan vertikal. Baik tabel ataupun gambar, keduanya memperlihatkan bahwa metode Kuadrat terkecil tidak tahan terhadap data pencilan vertikal.

Kemudian dengan Metode Simpangan Mutlak Terkecil didapatkan persamaan garis regresi

��= 8.719 + 10.682 �

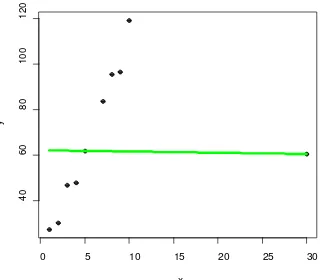
Gambar 5 menunjukkan grafik regresi dengan menggunakan metode Simpangan Mutlak Terkecil untuk data dengan pencilan vertikal.

Gambar 5 Scatter Plot Simpangan Mutlak Terkecil untuk n = 10 dengan pencilan vertikal

Sedangkan pada metode Simpangan Mutlak Terkecil dapat dibandingkan pada tabel berikut.

Tabel 4. Tabel perbandingan nilai a dan b

pada metode Simpangan Mutlak Terkecil dengan pencilan vertikal.

Metode a b

8.719 10.682

Terlihat jelas dengan menggunakan metode Simpangan Mutlak Terkecil persamaan garis regresi yang didapatkan sama antara data tanpa pencilan dengan data dengan pencilan vertikal. Ini berarti bahwa metode Simpangan Mutlak Terkecil lebih tahan terhadap data pencilan vertikal.

Perbedaan antara garis regresi metode Kuadrat Terkecil dengan data pencilan vertikal dan garis regresi metode Simpangan Mutlak Terkecil dengan data pencilan vertikal dapat terlihat dengan memplotkan dua grafik persamaan garis regresi kedua metode tersebut.

Gambar 6 menunjukkan grafik metode Kuadrat Terkecil dan metode Simpangan Mutlak Terkecil untuk data dengan pencilan vertikal dalam satu plot.

Gambar 6 Perbandingan Scatter Plot antara Metode OLS (merah) dengan LAD (hijau) pada data dengan pencilan vertikal

2 4 6 8 10

50 100 150 200 x y

2 4 6 8 10

(19)

9

4.5.2 Pencilan Horizontal

Misalkan pada data bangkitan awal, nilai x ke-6 sebelumnya diganti nilainya dari 6 menjadi 30 sehingga menghasilkan pencilan horizontal. Kemudian dicari persamaan regresinya. Dengan menggunakan metode Kuadrat Terkecil diperoleh:

-�� = 58.486 + 1.063 �

Gambar 7 menunjukkan grafik metode Kuadrat Terkecil untuk data dengan pencilan horizontal.

Gambar 7 Scatter Plot Kuadrat Terkecil untuk n = 10 dengan pencilan horizontal

Dari hasil persamaan-persamaan garis sebelumnya dapat dibuat perbandingan metode Kuadrat Terkecil tanpa pencilan dan dengan pencilan, baik vertikal dan horizontal pada tabel berikut :

Tabel 5 Tabel perbandingan nilai a dan b

pada metode Kuadrat Terkecil tanpa pencilan dan dengan pencilan, baik vertikal maupun horizontal

Metode a b

12.225 9.938

81.290 0.520

�� dengan pencilan horizontal

58.486 1.063

Dari Gambar 7 dan Tabel 5 di atas terlihat bahwa metode Kuadrat Terkecil tidak tahan terhadap pencilan, baik vertikal maupun horizontal.

��฀�� = 62.023 + (−0.053) � Gambar 8 menunjukkan grafik regresi dengan menggunakan metode Simpangan Mutlak Terkecil untuk data dengan pencilan horizontal.

Gambar 8 Scatter Plot Simpangan Mutlak Terkecil untuk n = 10 dengan pencilan horizontal

Selanjutnya dibandingkan pula persamaan-persamaan garis metode Simpangan Mutlak Terkecil yang telah didapatkan sebelumnya pada tabel berikut. Tabel 6 Tabel perbandingan nilai a dan b

pada metode Simpangan Mutlak Terkecil tanpa pencilan dan dengan pencilan baik vertikal maupun horizontal

Metode a b

8.719 10.682

62.023 (-0.053)

0 5 10 15 20 25 30

40 60 80 100 120 x y

0 5 10 15 20 25 30

(20)

10

OLS

Dari Gambar 8 dan tabel 6 ternyata metode Simpangan Mutlak Terkecil memiliki hasil yang sangat jauh berbeda pada data dengan pencilan horizontal. Hal ini mengindikasikan bahwa metode ini tidak tahan pada data dengan pencilan horizontal.

Gambar 9 menunjukkan grafik metode Kuadrat Terkecil dan metode Simpangan Mutlak Terkecil untuk data dengan pencilan horizontal dalam satu plot.

Gambar 9 Perbandingan Scatter Plot antara Metode OLS (merah) dengan LAD (hijau) pada data dengan pencilan horizontal

Ternyata apabila diplotkan dalam satu gambar, garis regresi yang dibuat oleh metode Simpangan Mutlak Terkecil terlihat lebih menyimpang daripada garis regresi metode Kuadrat Terkecil.

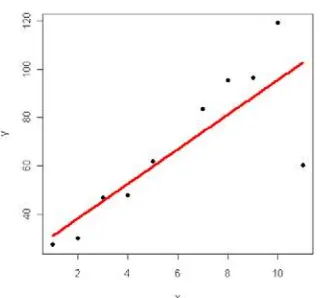
Selanjutnya akan dilakukan pengolahan data pencilan horizontal namun data yang dipilih perbedaannya tidak terlalu besar. Misalkan data x ke-6 dari pembangkitan data tanpa pencilan sebelumnya diganti nilainya dari 6 menjadi 11. Kemudian akan dicari persamaan regresinya. Persamaan regresi yang diperoleh dengan menggunakan metode Kuadrat Terkecil yaitu:

-�� = 23.930 + 7.159�

Gambar 10 menunjukkan grafik metode Kuadrat Terkecil untuk data dengan pencilan horizontal yang relatif kecil.

Gambar 10 Scatter Plot Kuadrat Terkecil untuk n = 10 dengan pencilan horizontal yang relatif kecil Kemudian dibandingkan dengan garis regresi metode Kuadrat Terkecil lainnya, seperti yang terlihat pada tabel berikut. Tabel 7 Tabel perbandingan seluruh nilai a

dan b pada metode Kuadrat Terkecil tanpa pencilan dan dengan pencilan baik vertikal maupun horizontal serta pencilan horizontal yang relatif kecil

Metode a b

12.225 9.938

81.290 0.520

58.486 1.063

�� dengan pencilan horizontal yang relatif kecil

23.930 7.159

Ternyata data pencilan tetap memberikan pengaruh terhadap garis regresi yang dihasilkan oleh metode Kuadrat Terkecil.

��= 18.688 + 8.645 �

0 5 10 15 20 25 30

(21)

11

Gambar 11 menunjukkan grafik regresi dengan menggunakan metode Simpangan Mutlak Terkecil untuk data dengan pencilan horizontal yang relatif kecil.

Gambar 11 Scatter Plot Simpangan Mutlak Terkecil untuk n = 10 dengan pencilan horizontal yang relatif kecil

Selanjutnya dibandingkan pula persamaan-persamaan garis metode Simpangan Mutlak Terkecil yang telah didapatkan sebelumnya pada tabel berikut. Tabel 8 Tabel perbandingan seluruh nilai a

dan b pada metode Simpangan Mutlak Terkecil tanpa pencilan dan dengan pencilan baik vertikal maupun horizontal serta pencilan horizontal yang relatif kecil

Metode a b

8.719 10.682

62.023 (-0.053)

�� dengan pencilan horizontal yang relatif kecil

18.688 8.645

Seperti yang terlihat pada Gambar 11 dan Tabel 8 di atas ternyata metode Simpangan Mutlak Terkecil memiliki hasil

yang berbeda pada data dengan pencilan horizontal. Untuk nilai pencilan horizontal yang kecil pengaruhnya terlihat sedikit sehingga garis regresi masih terlihat mewakili data-data bukan pencilan. Sedangkan untuk nilai pencilan yang besar metode Simpangan Mutlak Terkecil ini sangat dipengaruhi sehingga tidak tahan terhadap data pencilan yang nilainya besar. Hal ini mengindikasikan bahwa metode ini solusinya tidak stabil pada kondisi dimana nilai pencilan horizontalnya besar.

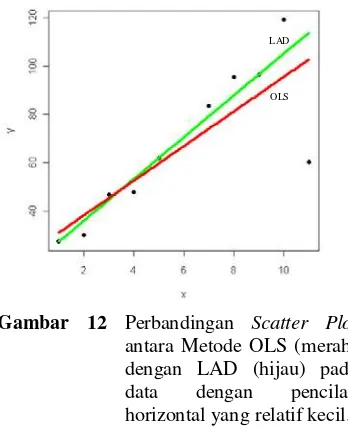
Gambar 12 menunjukkan grafik metode Kuadrat Terkecil dan metode Simpangan Mutlak Terkecil untuk data dengan pencilan horizontal yang relatif kecil dalam satu plot.

Gambar 12 Perbandingan Scatter Plot

antara Metode OLS (merah) dengan LAD (hijau) pada data dengan pencilan horizontal yang relatif kecil. Dari Gambar 12 terlihat bahwa metode Simpangan Mutlak Terkecil masih lebih kekar dibandingkan metode Simpangan Mutlak Terkecil walaupun kedua metode terpengaruh oleh data pencilan namun garis regresi metode Simpangan Mutlak Terkecil masih lebih baik daripada metode Kuadrat terkecil dalam merepresentasikan data-data bukan pencilan.

4.6 Penyajian dan Analisis Terhadap Gugus Data Simetrik.

Terdapat suatu gugus data (x,y) yaitu : {(1,5) , (3,3) , (3,7) , (5,2) , (5,8)} yang akan

(22)

12

dicari garis regresinya dengan menggunakan metode Kuadrat Terkecil dan metode Simpangan Mutlak Terkecil.

Persamaan regresi yang diperoleh dengan menggunakan metode Kuadrat Terkecil yaitu:

�� = 5

Gambar 13 menunjukkan grafik metode Kuadrat Terkecil untuk gugus data tersebut. Perhatikan bahwa garis regresi metode Kuadrat Terkecil juga menjadi garis simetri titik data tersebut, sehingga gugus data tersebut dapat disebut gugus data simetri.

Gambar 13 Scatter Plot Kuadrat Terkecil untuk gugus data simetrik Kemudian dengan metode Simpangan Mutlak Terkecil akan didapatkan persamaan regresi yaitu

�� = 4.25 + 0.75 �

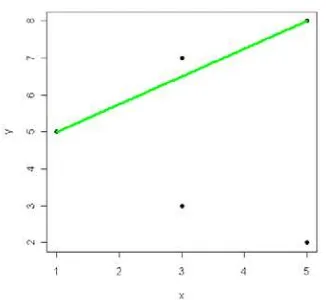
Gambar 14 menunjukkan grafik metode Simpangan Mutlak Terkecil untuk gugus data simetrik.

Gambar 14 Scatter Plot Simpangan Mutlak Terkecil untuk gugus data simetrik

Persamaan regresi dengan metode Simpangan Mutlak Terkecil untuk gugus data simetri ini didapatkan dengan mencari persamaan garis dengan jumlah simpangan mutlak

(

∑

e_i

)

yang paling kecil. Yaitu :

10

i

e =

∑

 (11) Dimisalkan ada dua garis lain yang melalui gugus data simetri ini, yaitu :

�= 5

dan

�= 5.75−0.75 �

Ternyata kedua garis ini juga memiliki jumlah simpangan mutlak terkecil (11) yang sama. Oleh karena itu seluruh garis ini dapat dituliskan kembali sebagai solusi garis regresi dari metode Simpangan Mutlak Terkecil

��฀��2= 5 dan

��3= 5.75−0.75 �

Hal ini juga menunjukan bahwa metode Simpangan Mutlak Terkecil dapat menghasilkan lebih dari satu solusi garis regresi, hal ini terjadi khususnya pada suatu gugus data yang simetri.

(23)

13

Gambar 15 Scatter Plot antara solusi garis regresi LAD (hijau), LAD2 (biru) dan LAD3 (merah) pada gugus data simetrik

Pada Gambar 15 terlihat bahwa garis regresi LAD2 merupakan garis yang sama dengan garis regresi OLS-nya. Sehingga, solusi metode Kuadrat Terkecil merupakan salah satu solusi dari metode Simpangan Mutlak Terkecil. Pada Gambar 15 juga dapat terlihat bahwa sembarang garis yang berada di antara garis regresi LAD (hijau) dan LAD3 (merah) merupakan garis solusi metode Simpangan Mutlak Terkecil.

V

SIMPULAN DAN SARAN

5.1.Simpulan

Secara umum metode Kuadrat Terkecil dan metode Simpangan Mutlak Terkecil memiki hasil yang hampir sama dalam pendugaan parameter untuk data tanpa pencilan.

Akan tetapi pada data yang memiliki pencilan vertikal, metode Simpangan Mutlak Terkecil akan mempunyai dugaan yang lebih baik, karena metode lebih tahan terhadap keberadaan pencilan vertikal daripada metode Kuadrat Terkecil.

Namun, apabila terdapat pencilan horizontal maka kedua metode ini sama-sama tidak menghasilkan penduga yang baik. Oleh sebab, itu diperlukan metode lain yang lebih kekar.

Metode Simpangan Mutlak Terkecil mempunyai beberapa perbedaan bila dibandingkan dengan metode kuadrat terkecil, antara lain: lebih kekar, solusinya tidak stabil dan terdapat kemungkinan lebih dari satu solusi.

5.2.Saran

Pendugaan parameter pada gugus data yang tidak mengandung pencilan (outlier) sebaiknya menggunakan metode Kuadrat Terkecil karena tersedia fasilitas analisis lanjut yang lebih baik, sedangkan untuk gugus data yang mengandung pencilan vertikal hasil penduganya akan lebih baik bila menggunakan metode Simpangan Mutlak Terkecil. Namun apabila ada pencilan horizontal maka disarankan untuk menggunakan metode kekar lainnya.

LAD1

LAD2

(24)

14

DAFTAR PUSTAKA

Barnett, V. and Lewis, T. 1994. Outliers in Statistical Data. New York: John Willey & Sons. Inc.

Barrodale, I. & FDK. Roberts, 1973. “An Improved Algorithm for Discrete L1 Linear Approximation” SIAM

Journal on Numerical Analysis 10, page 839–848.

Myers, R.H. 1990. Classical and Modern Regression with Applications. PWS-KENT Publishing Company, Boston.

Pfeil, W.A. 2006. “Statistical Teaching Aids” An Interactive Qualifying Project Report submitted to the Faculty of the Worcester Polytechnic Institute in partial fulfillment of the requirements for the Degree of Bachelor of Science

Rancher, A.C. & G.B. Schaalje, 2008.

Linear Models in Statistics Second Edition. Hoboken, New Jersey: John Wiley & Sons, Inc.

Rousseuw, P.J. & A.M. Leroy. 1987. Robust Regression and Outlier Detection. John Wiley & Sons, Inc., New York.

Yaffe, R.A. 2002. Robust Regression Analysis: Some Popular Statistical Package Options.

(25)

(26)

16

Lampiran 1. Ilustrasi penghitungan metode modifikasi simpleks Simpangan Mutlak Terkecil

Contoh :

Tentukan pendekatan terbaik untuk regresi linear dari titik-titik data berikut:

S = {(1,1),(2,1),(3,2),(4,3),(5,2)} dengan

y

= +

a bx

Jawab :

Dari data-data di atas bisa didapatkan suatu sistem persamaan :

1

2

1

3

2

4

3

5

2

a b

a

b

a

b

a

b

a

b

+ =

+

=

+

=

+

=

+

=

Kemudian dapat diubah ke dalam tabel simpleks

Tabel lampiran 1. Tabel simpleks untuk ilustrasi

Basis R a b

u1 1 1 1

u2 1 1 2

u3 2 1 3

u4 3 1 4

u5 2 1 5

Marginal cost 9 5 15

sehingga dapat dimulai langkah-langkah penghitungannya yaitu : Langkah 1 : Pilih kolom pivot

Caranya dengan memilih kolom dengan marginal cost tebesar. Pada ilustrasi adalah kolom b.

Langkah 2 : Pilih titik-titik pivot Memilih dengan cara :

 Dapatkan R

� untuk setiap baris. Lihat yang bernilai positif kemudian urutkan dari yang terkecil.  Hitung �� −(2 ×�) sampai bernilai negatif. b yang dipilih sesuai urutan

terkecil positif. 15 – (2 x 5) = 5 5 – (2 x 2) = 1 1 – (2 x 3) = 15

(27)

17

Langkah 3 : Pivoting dengan bantuan uiidentitas.

Tabel lampiran 2. Tabel simpleks untuk menunjukan pemilihan kolom dan titik pivot, serta pembuatan kolom semu ui identitas.

Basis R a b R

�

u1 u2 u3 u4 u5

u1 1 1 1 1 1 0 0 0 0

u2 1 1 2** positif

terkecil 2 1 2

0 1 0 0 0

u3 2 1 3*** positif

terkecil 3 (pivot)

2 3

0 0 1 0 0

u4 3 1 4 3

4

0 0 0 1 0

u5 2 1 5* positif

terkecil 1 2 5

0 0 0 0 1

Kolom pivot

ui identitas

Kemudian buat tabel simpleks baru dengan langkah:

a. Ganti nama baris yang nilai positifnya tadi masih menyisakan hasil yang positif pada perhitungan dilangkah 2 dari ui menjadi vi.

b. Ganti nama kolom pivot b menjadi u3. Kemudian ubah nilai titik pivotnya dengan nilai yang apabila dikalikan dengan titik pivot akan bernilai sama dengan 1.

Misalkan x adalah suatu nilai yang akan membuat titik pivot sama dengan 1.

x . 3 = 1 →x = 1 3

Sedangkan untuk nilai yang lainnya pada kolom pivot lainnya akan dikalikan dengan nilai x.

c. Ganti nama baris pada tabel simpleks lama dengan b dan ubah nilai-nilai pada baris tersebut dengan cara mengkalikan nilai baris u3 dengan nilai x pada langkah b di atas.

d. Ubah nilai lainnya pada tabel pivot lama dengan cara : nilai baris pivot lama yang sekolom dikalikan dengan nilai kolom pivot baru yang sebaris kemudian hasilnya dikurangi nilai pada tabel simpleks lama tersebut.

Misal :

�1R (baru) = [�3R (lama) . �1�3(baru)]− �31R (lama) =� 1 .1

3� − �− 1 3�= −

(28)

18

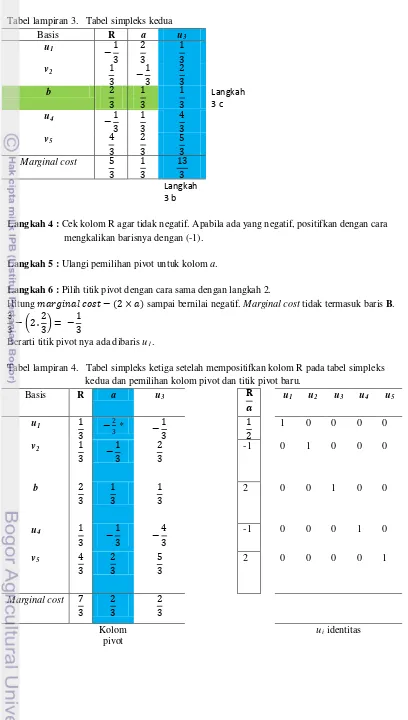
Tabel lampiran 3. Tabel simpleks kedua

Basis R a u3

u1 −1 3 2 3 1 3

v2 1

3 − 1 3 2 3 b 2 3 1 3 1 3 Langkah 3 c u4 −1 3 1 3 4 3

v5 4

3 2 3

5 3 Marginal cost 5

3 1 3 13 3 Langkah 3 b

Langkah 4 : Cek kolom R agar tidak negatif. Apabila ada yang negatif, positifkan dengan cara mengkalikan barisnya dengan (-1).

Langkah 5 : Ulangi pemilihan pivot untuk kolom a.

Langkah 6 : Pilih titik pivot dengan cara sama dengan langkah 2.

Hitung �� −(2 ×�) sampai bernilai negatif. Marginal cost tidak termasuk baris B. 3

3− �2 . 2 3�= −

1 3

Berarti titik pivot nya ada dibaris u1.

Tabel lampiran 4. Tabel simpleks ketiga setelah mempositifkan kolom R pada tabel simpleks kedua dan pemilihan kolom pivot dan titik pivot baru.

Basis R a u3 �

�

u1 u2 u3 u4 u5

u1 1

3 −

2

3 * −

1 3

1 2

1 0 0 0 0

v2 1

3 −

1 3

2 3

-1 0 1 0 0 0

b 2 3 1 3 1 3

2 0 0 1 0 0

u4 1

3 −

1

3 −

4 3

-1 0 0 0 1 0

v5 4

3 2 3

5 3

2 0 0 0 0 1

Marginal cost 7 3 2 3 2 3 Kolom pivot

(29)

19

Langkah 7 : Pivoting dengan bantuan uiidentitas. Buat tabel simpleks baru dengan langkah:

a. Ganti nama kolom a menjadi u1. Kemudian ubah nilai titik pivotnya dengan nilai yang apabila dikalikan dengan titik pivot akan bernilai sama dengan 1.

Misalkan x adalah suatu nilai yang akan membuat titik pivot sama dengan 1.

x . 2

3 = 1 →x = 3 2

b. Ganti nama baris u1menjadi a dan ubah nilainya selain titik pivot dengan mengkalikan nilai u1 dengan x.

c. Ganti nilai-nilai lainnya dengan cara : nilai baris pivot lama yang sekolom dikalikan dengan nilai kolom pivot baru yang sebaris kemudian hasilnya dikurangi nilai pada tabel simpleks lama tersebut.

Misal :

�1R (baru) = [�2R (lama) . �2�1(baru)]− �2R (lama) =� 1

3 . �− 1 2�� −

1 3= −

3 6= −

1 2

Marginal cost tidak menghitung baris a dan b.

Tabel lampiran 5. Tabel simpleks keempat

Basis R u1 u3

a 1 2 3 2 − 1 2 Langkah 3 b v2 −1 2 − 1 2 − 1 2 b −1 2 1 2 − 1 2 u4

−1₂ −1₂ 3₂

v5 -1 1 -2

Marginal cost -2 0 -1

Langkah 3 a

Langkah 8 : Cek kolom R agar tidak negatif. Apabila ada yang negatif, positifkan dengan cara mengkalikan barisnya dengan (-1).

Tabel lampiran 6. Tabel simpleks kelima setelah mempositifkan kolom R.

Basis R u1 u3

a 1 2* 3 2 − 1 2

v2 1

2 1 2 1 2 b 1

2* −

1 2

u4 1

2 1

2 −

3 2

v5 1 -1 2

Dari tabel ke lima didapatkan nilai a dan b. Sehingga

y



= +

a bx

= 1 2 +

(30)

20

Lampiran 2. Syntax dalam R language dalam pembangkitan data. >library(stats)

>n=10

(31)

21

Lampiran 3. Pengolahan data tanpa pencilan dalam R language. >>>Metode OLS

>reg1<-lm(y~x) >reg1

Call:

lm(formula = y ~ x)

Coefficients:

(Intercept) x 12.225 9.938

>>> Plot hasil pengolahan data dengan metode OLS >plot(x,y,pch=19)

>curve(predict(reg1,data.frame(x=x)),add=TRUE,col="red",pch= 20,lwd=4)

>>>Metode LAD

>library(quantreg)

Loading required package: SparseM Package SparseM (0.86) loaded.

To cite, see citation("SparseM")

Attaching package: 'SparseM'

The following object(s) are masked from 'package:base':

backsolve

Package quantreg (4.53) loaded.

To cite, see citation("quantreg") >reg2<-rq(y~x)

>reg2 Call:

rq(formula = y ~ x)

Coefficients:

(Intercept) x 8.719796 10.682301

Degrees of freedom: 10 total; 8 residual

>>>Plot hasil pengolahan data dengan metode LAD

> plot(x,y,pch=19) >

(32)

22

Lampiran 4. Algoritma fungsi rq dalam R language. > rq

function (formula, tau = 0.5, data, subset, weights, na.action,

method = "br", model = TRUE, contrasts = NULL, ...) {

call <- match.call()

mf <- match.call(expand.dots = FALSE)

m <- match(c("formula", "data", "subset", "weights", "na.action"),

names(mf), 0) mf <- mf[c(1, m)]

mf$drop.unused.levels <- TRUE mf[[1]] <- as.name("model.frame") mf <- eval.parent(mf)

if (method == "model.frame") return(mf)

mt <- attr(mf, "terms") weights <- model.weights(mf) Y <- model.response(mf)

X <- model.matrix(mt, mf, contrasts) eps <- .Machine$double.eps^(2/3)

Rho <- function(u, tau) u * (tau - (u < 0)) if (length(tau) > 1) {

if (any(tau < -eps) || any(tau > 1 + eps))

stop("invalid tau: taus should be >= 0 and <= 1")

coef <- matrix(0, ncol(X), length(tau)) rho <- rep(0, length(tau))

fitted <- resid <- matrix(0, nrow(X), length(tau)) for (i in 1:length(tau)) {

z <- {

if (length(weights))

rq.wfit(X, Y, tau = tau[i], weights, method,

...)

else rq.fit(X, Y, tau = tau[i], method, ...) }

coef[, i] <- z$coefficients resid[, i] <- z$residuals

rho[i] <- sum(Rho(z$residuals, tau[i])) fitted[, i] <- Y - z$residuals

}

taulabs <- paste("tau=", format(round(tau, 3))) dimnames(coef) <- list(dimnames(X)[[2]], taulabs) dimnames(resid) <- list(dimnames(X)[[1]], taulabs) fit <- z

fit$coefficients <- coef fit$residuals <- resid fit$fitted.values <- fitted if (method == "lasso")

(33)

23

class(fit) <- c("scadrqs", "rqs") else class(fit) <- "rqs"

} else {

process <- (tau < 0 || tau > 1) fit <- {

if (length(weights))

rq.wfit(X, Y, tau = tau, weights, method, ...)

else rq.fit(X, Y, tau = tau, method, ...) }

if (process)

rho <- list(x = fit$sol[1, ], y = fit$sol[3, ]) else {

dimnames(fit$residuals) <- list(dimnames(X)[[1]], NULL)

rho <- sum(Rho(fit$residuals, tau)) }

if (method == "lasso")

class(fit) <- c("lassorq", "rq") else if (method == "scad")

class(fit) <- c("scadrq", "rq")

else class(fit) <- ifelse(process, "rq.process", "rq")

}

fit$na.action <- attr(mf, "na.action") fit$formula <- formula

fit$terms <- mt

fit$xlevels <- .getXlevels(mt, mf) fit$call <- call

fit$tau <- tau

fit$weights <- weights

fit$residuals <- drop(fit$residuals) fit$rho <- rho

fit$method <- method

fit$fitted.values <- drop(fit$fitted.values) attr(fit, "na.message") <- attr(m, "na.message") if (model)

fit$model <- mf fit

(34)

24

Lampiran 5. Pengolahan data dengan pencilan dalam R language.

DENGAN PENCILAN VERTIKAL

>>>merubah data

>data.entry(x,y)

>>>Metode OLS

> reg3<-lm(y~x) > reg3

Call:

lm(formula = y ~ x)

Coefficients:

(Intercept) x

81.29 0.52

>>> Plot hasil pengolahan data dengan metode OLS > plot(x,y,pch=19)

>

curve(predict(reg3,data.frame(x=x)),add=TRUE,col="red",pch=2 0,lwd=4)

>>>Metode LAD

> reg4<-rq(y~x) > reg4

Call:

rq(formula = y ~ x)

Coefficients:

(Intercept) x 20.619975 9.476251

>>>Plot hasil pengolahan data dengan metode LAD

curve(predict(reg4,data.frame(x=x)),add=TRUE,col="green",pch =20,lwd=4)

(35)

25

DENGAN PENCILAN HORIZONTAL

>>>merubah data

>data.entry(x,y)

>>>Metode OLS > reg5<-lm(y~x) > reg5

Call:

lm(formula = y ~ x)

Coefficients:

(Intercept) x 58.486 1.063

>>>hasil pengolahan data dengan metode OLS > plot(x,y,pch=19)

>

curve(predict(reg5,data.frame(x=x)),add=TRUE,col="red",pch=2 0,lwd=4)

>>>Metode LAD

> reg6<-rq(y~x) > reg6

Call:

rq(formula = y ~ x)

Coefficients:

(Intercept) x 62.02380582 -0.05392116

Degrees of freedom: 30 total; 28 residual

>>>Plot hasil pengolahan data dengan metode LAD

(36)

26

Lampiran 6. Hasil pembangkitan data dan pengantian pencilan.

X Y

Y dengan Pencilan vertikal

X dengan pencilan horizontal 1

X dengan pencilan horizontal 2

1 27.33348 200 1 1

2 30.0844 30.0844 2 2

3 46.78823 46.78823 3 3

4 47.87954 47.87954 4 4

5 61.7542 61.7542 5 5

6 60.40617 60.40617 30 11

7 83.4959 83.4959 7 7

8 95.54018 95.54018 8 8

9 96.49684 96.49684 9 9