Estimasi Parameter Untuk Data Waktu Hidup Yang Berdistribusi Rayleigh Pada Data Tersensor Tipe II Dengan Metode Maksimum Likelihood

ESTIMASI PARAMETER UNTUK DATA WAKTU HIDUP YANG

BERDISTRIBUSI RAYLEIGH PADA DATA TERSENSOR TIPE II

DENGAN METODE MAKSIMUM LIKELIHOOD

SKRIPSI

JULHAIDI

090823045

PROGRAM STUDI SARJANA MATEMATIKA

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

UNIVERSITAS SUMATERA UTARA

ESTIMASI PARAMETER UNTUK DATA WAKTU HIDUP YANG BERDISTRIBUSI RAYLEIGH PADA DATA TERSENSOR TIPE II DENGAN

METODE MAKSIMUM LIKELIHOOD

SKRIPSI

Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains

JULHAIDI 090823045

PROGRAM STUDI SARJANA MATEMATIKA DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

PERSETUJUAN

Judul : ESTIMASI PARAMETER UNTUK DATA WAKTU

HIDUP YANG BERDISTRIBUSI RAYLEIGH PADA DATA TERSENSOR TIPE II DENGAN METODE MAKSIMUM LIKELIHOOD

Kategori : SKRIPSI

Nama : JULHAIDI

Nomor Induk Mahasiswa : 090823045

Program Studi : SARJANA (S1) MATEMATIKA

Departemen : MATEMATIKA

Fakultas : MATEMATIKA DAN ILMU PENGETAHUAN

ALAM (FMIPA) UNIVERSITAS SUMATERA UTARA

Diluluskan di Medan, Juni 2011

Komisi Pembimbing :

Pembimbing II Pembimbing I

Drs. Pasukat Sembiring, M.Si Drs. Marwan Harahap, M.Eng NIP. 195311131985031002 NIP 19461225 197403 1 001

Diketahui Oleh:

Departemen Matematika FMIPA USU Ketua,

Prof. Dr. Tulus, M.Si

PERNYATAAN

ESTIMASI PARAMETER UNTUK DATA WAKTU HIDUP YANG BERDISTRIBUSI RAYLEIGH PADA DATA TERSENSOR TIPE II DENGAN

METODE MAKSIMUM LIKELIHOOD

SKRIPSI

Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.

Medan, Juni 2011

PENGHARGAAN

Bismillahhirrahmanirrahhim, Segala puji dan syukur penulis panjatkan kehadirat ALLAH SWT atas berkat dan limpah-Nya sehingga penulis dapat menyelesaikan Skripsi ini tepat pada waktunya.

Ucapan terima kasih saya sampaikan kepada Bapak Drs. Marwan Harahap, M.Eng dan Drs. Pasukat Sembiring, M.Si selaku pembimbing pada penyelesaian Skripsi ini telah memberikan panduan dan penuh kepercayaan pada penulis dalam menyempurnakan kajian ini. Panduan ringkas, padat dan professional telah diberikan agar penulis dapat menyelesaikan skripsi ini. Serta Bapak Drs. Rachmad Sitepu, M.Si dan Bapak Drs. Suwarno Ariswoyo, M.Si yang telah bersedia menjadi dosen penguji skripsi saya. Terima kasih atas saran dan masukannya.

ABSTRAK

Uji hidup adalah penyelidikan tentang daya tahan hidup suatu unit atau komponen pada keadaan operasional tertentu. Analisis uji waktu hidup adalah salah satu analisis yang digunakan pada dunia industri dan kesehatan. Ada tiga metode yang umum digunakan dalam pengamatan waktu hidup. Sampel lengkap dimana pengamatan berhenti setelah semua sampel yang diamati mati, sensor tipe I pengamatan dilakukan selama unit waktu tertentu, sensor tipe II pengamatan berhenti setelah n kegagalan.Data waktu hidup adalah sampel acak yang mempunyai distribusi peluang. Dengan maksimu likelihood dapat diestimasi bentuk dari parameter waktu hidup dari distribusi peluang waktu hidup itu, dan dalam skripsi ini penulis memakai distribusi Rayleigh dan Sensor tipe II dari data waktu hidup dengan menggunakan maksimum likelihood. Fungsi likelihood dalam mengestimasi Sensor tipe II untuk distribusi Rayleigh adalah

� = ₂

�=1 + ( − ) 2 1 2

ABSTRACT

Life time analysis is one of the statistic analysis which is many use in industry and health. There are three general method which is often used in life time data analysis. Complete sample which is the observation stoped when all the observation failed type I censored the observation stopped during at an unit time, type II censor the observation stoped at n failure. Lifetime data is random sample which is has a probability distribution. With maximum likelihood can be estimate the parameter the form of lifetime data from its probability distribution, and in this thesis writer use a rayleigh distribution and censoring type II of lifetime data and it is estimate by maximum likelihood estimator. The likelihood form of estimating censoring tipe II for rayleigh distribution is

� = ₂

�=1 + ( − ) 2 1 2

Bab 3 Pembahasan dan Hasil 26 3.1 Estimator Parameter Metode Maksimum Likelihood 26 3.2 Data Tersensor Tipe II untuk Distribusi Rayleigh 29

3.3 Contoh Kasus 30

Bab 4 Kesimpulan dan Saran 33

4.1 Kesimpulan 33

4.2 Saran 34

DAFTAR PUSTAKA

DAFTAR GAMBAR

Halaman

Gambar 2.1 Sistem keandalaan seri 16

Gambar 2.2 Sistem keandalan paralel kelebihan aktif 18

Gambar 2.3 Sistem keandalan paralel kelebihan pasif 19

Gambar 2.4 Sistem seri-paralel 19

ABSTRAK

Uji hidup adalah penyelidikan tentang daya tahan hidup suatu unit atau komponen pada keadaan operasional tertentu. Analisis uji waktu hidup adalah salah satu analisis yang digunakan pada dunia industri dan kesehatan. Ada tiga metode yang umum digunakan dalam pengamatan waktu hidup. Sampel lengkap dimana pengamatan berhenti setelah semua sampel yang diamati mati, sensor tipe I pengamatan dilakukan selama unit waktu tertentu, sensor tipe II pengamatan berhenti setelah n kegagalan.Data waktu hidup adalah sampel acak yang mempunyai distribusi peluang. Dengan maksimu likelihood dapat diestimasi bentuk dari parameter waktu hidup dari distribusi peluang waktu hidup itu, dan dalam skripsi ini penulis memakai distribusi Rayleigh dan Sensor tipe II dari data waktu hidup dengan menggunakan maksimum likelihood. Fungsi likelihood dalam mengestimasi Sensor tipe II untuk distribusi Rayleigh adalah

� = ₂

�=1 + ( − ) 2 1 2

ABSTRACT

Life time analysis is one of the statistic analysis which is many use in industry and health. There are three general method which is often used in life time data analysis. Complete sample which is the observation stoped when all the observation failed type I censored the observation stopped during at an unit time, type II censor the observation stoped at n failure. Lifetime data is random sample which is has a probability distribution. With maximum likelihood can be estimate the parameter the form of lifetime data from its probability distribution, and in this thesis writer use a rayleigh distribution and censoring type II of lifetime data and it is estimate by maximum likelihood estimator. The likelihood form of estimating censoring tipe II for rayleigh distribution is

� = ₂

�=1 + ( − ) 2 1 2

BAB 1

PENDAHULUAN

1.1 Latar Belakang

Perkembangan ilmu pengetahuan dan teknologi saat ini berlangsung sangat pesat. Hal ini mendorong manusia untuk terus berupaya memanfaatkan kemajuan teknologi tersebut yang diantaranya diwujudkan melalui penelitian-penelitian. Penelitian yang dilakukan dapat berupa penelitian yang bertujuan untuk menemukan dan menyelesaikan masalah-masalah baru, mengembangkan pengetahuan yang ada maupun penelitian dalam menguji kebenaran suatu pengetahuan. Dalam bidang matematika statistika yang sudah berkembang begitu jauh dengan adanya penemuan berbagai alat analisis untuk berbagai keperluan estimasi, pengujian dan metode peramalan. Uji hidup adalah penyelidikan tentang daya tahan hidup suatu unit atau komponen pada keadaan operasional tertentu.

Fungsi distribusi tahan hidup yang didasarkan pada pengetahuan atau asumsi tertentu tentang distribusi populasinya termasuk dalam fungsi parametrik. Beberapa distribusi yang dapat digunakan untuk menggambarkan waktu hidup antara lain Distribusi Eksponensial, Distribusi Weibull, Distribusi Gamma, Distribusi Rayleigh, dan lain-lain. Di antara beberapa distribusi tersebut, dalam skripsi ini dipilih fungsi tahan hidup berdistribusi Rayleigh dalam penelitian ini

Untuk mengetahui apakah distribusi dari data dalam fungsi tahan hidup yang diasumsikan telah menggambarkan keadaan yang sesungguhnya, diperlukan suatu analisis terhadap data waktu hidup. Langkah untuk menganalisis terhadap fungsi distribusi dari data waktu hidup adalah dengan mengestimasi harga parameter distribusinya.

1.2 Perumusan Masalah

Permasalahan dalam penelitian ini adalah Bagaimana teknik estimasi parameter untuk data waktu hidup yang berdistribusi Rayleigh pada data tersensor tipe II dapat dikerjakan dengan metode maksimum likelihood yang kemudian digunakan untuk memperoleh kehandalan dari suatu sistem yang telah diteliti

1.3 Tinjauan Pustaka

Konsep dasar probabilitas banyak dalam buku Ilmu peluang dan statistika untuk insinyur dan ilmuwan, Walpole, dkk.1998. buku Mathematical Statistics, Mukhopadhyay, Parimal. 2002. dan buku Pendahuluan Teori Kemungkinan dan Statistika, Surjadi, P.A. 1976. Beberapa masalah di dalam probabilitas dapat dikaitkan dengan permasalahan lain seperti uji tahan hidup

Waktu tahan hidup T merupakan variable nonnegative, distribusi peluang dari T dapat dinyatakan dalam tiga cara:

1. Fungsi ketahanan S(t)

2. Fungsi kepadatan peluang f(t)

Ketiga fungsi ini secara matematika saling ekuivalen, artinya jika salah satu dari ketiga fungsi ini sudah di ketahui, maka fungsi yang lainnya dapat ditentukan

Defenisi dari fungsi ketahanan dan fungsi kegagalan adalah sebagai berikut:

Fungsi ketahanan

Pada konsep uji tahan hidup ada juga dibicarakan data tersensor, yaitu data diperoleh sebelum hasil yang diinginkan dari pengamatan terjadi, sedangkan waktu pengamatan telah berakhir atau oleh sebab lain.

Ada tiga macam metode yang sering digunakan dalam eksperimen uji hidup, yaitu sebagai berikut:

1. Sampel lengkap, bila uji dihentikan setelah semua unit gagal atau mati. 2. Sensor tipe I, bila uji dihentikan setelah watu tertentu.

3. Sensor tipe II, bila uji dihentikan setelah di peroleh sejumlah kegagalan tertentu.

Sementara metode untuk mengestimasi harga parameter distribusi dari data dalam fungsi tahan hidup (Survival) adalah dengan menggunakan metode maksimum likelihood.

Metode maksimum likelihood menggunakan nilai dalam ruang parameter Ω yang bersesuaian dengan harga kemungkinan maksimum dari data observasi sebagai estimasi dari parameter yang tidak diketahui.

merupakan fungsi yang dapat diturunkan serta diasumsikan maksimum pada Ω maka dapat terpenuhi. maka fungsi L(θ) dapat dibuat logaritma naturalnya, dengan ketentuan memaksimumkan lnL(θ), sehingga persamaan logaritma natural likelihoodnya adalah

d

 lnL()=0 dθ

Jika fungsi densitas probabilitas bersama dari n variabel random X

1, X2,…,Xn yang

1.4 Tujuan Penelitian

Menyelesaikan persoalan estimator parameter untuk data waktu hidup yang berdistribusi Rayleigh pada data tersensor tipe II dengan Metode Maksimum Likelihood.

1.5 Kontribusi Penelitian

1. Dapat diketahui bahwa Metode Maksimum Likelihood merupakan model estimasi yang dapat digunakan untuk menangani permasalahan data waktu hidup yang berdistribusi Rayleigh pada Data tersensor Tipe II.

2. Menambah wawasan dan memperkaya literatur dalam bidang statistika yang berhubungan dengan fungsi tahan hidup untuk data waktu hidup yang berdistribusi Rayleigh

3. Mengkaji lebih dalam lagi hubungan antara Maksimum likelihood, distribusi Rayleigh dan Data tersensor Tipe II.

4. Diharapkan memberikan manfaat untuk bidang ilmu yang berkaitan dengan uji hidup, seperti bidang kedokteran, pertanian, industri, biologi dan lain-lain.

1.6 Metode Penelitian

1. Mengumpulkan teori-teori probabilitas dan keandalan yang mendukung dalam pelaksanaan penelitian dengan menggunakan metode literature sehingga diperoleh Estimator Maksimum likelihood yang berdistribusi Rayleigh.

2. Kemudian digunakan untuk menghitung nilai estimator dalam data tersensor tipe II.

BAB 2

LANDASAN TEORI

2.1 Ruang Sampel dan Kejadian

2.1.1 Definisi Ruang Sampel

Himpunan semua hasil semua hasil (outcome) yang mungkin muncul pada suatu percobaan disebut ruang sampel dan dinotasikan dengan S.

Tiap – tiap hasil yang mungkin dalam ruang sampel disebut unsur atau anggota ruang sampel tersebut atau disebut juga dengan istilah titik sampel.

Contoh:

Pada percobaan melempar dua mata uang, diperoleh S = {AA, AG, GA, GG}, dengan AA adalah kejadian muncul angka pada lemparan pertama, dan muncul angka pada lemparan kedua; AG adalah kejadian muncul angka pada lemparan pertama, dan muncul gambar pada lemparan kedua; GA adalah kejadian muncul gambar pada lemparan pertama, dan muncul angka pada lemparan kedua; GG adalah kejadian muncul gambar pada lemparan pertama, dan muncul gambar pada lemparan kedua. Titik sampelnya adalah AA, AG, GA, dan GG.

2.1.2 Definisi Kejadian

Kejadian atau peristiwa adalah himpunan bagian dari ruang sampel.

Contoh :

Suatu percobaan yang dilakukan dengan melantunkan sebuah dadu, maka ruang sampelnya: S = {1, 2, 3, 4, 5, 6}. Misalkan A menyatakan suatu kejadian bahwa bilangan genap muncul, maka kejadian A = { 2, 4, 6}, sehingga A merupakan himpunan bagian ruang sampel S, dinotasikan sebagai A ⊂ S.

2.2 Definisi Peluang Suatu Kejadian

Teori peluang mempelajari tentang peluang terjadinya suatu kejadian atau peristiwa. Peluang dinyatakan dalam pecahan atau desimal antara 0 dan 1. bila peluang suatu kejadian bernilai 0, maka kejadian tersebut tidak akan terjadi. Sedangkan bila peluang suatu kejadian bernilai 1, maka kejadian tersebut pasti terjadi. Dalam teori peluang suatu kejadian adalah satu atau beberapa kemungkinan hasil dari suatu tindakan. Tujuan teori peluang adalah menggambarkan dan menaksir rata – rata sedemikian itu dalam bentuk peluang kejadian.

Untuk menentukan Peluang suatu kejadian A, semua bobot titik sampel dalam A dijumlahkan. Jumlah ini dinamakan ukuran A atau peluang A dan dinyatakan dengan P(A). jadi ukuran himpunan ∅ adalah 0 dan ukuran S adalah 1. Peluang didefinisikan dengan menggunakan tiga pendekatan yang berbeda. Ketiga definisi pendekatan tersebut adalah sebagai berikut.

a. Definisi Aksiomatik

Pendekatan aksiomatik peluang berdasar pada tiga postulat sebagai berikut.

Peluang P(A) kejadian A adalah bilangan non negatif yang ditetapkan pada kejadian ini yaitu

P(A) ≥ 0.

Peluang P(B) kejadian B pasti sama dengan 1, yaitu P(B) = 1.

Dan bila kejadian – kejadian A dan B saling asing maka P(A+B) = P(A) + P(B)

b. Definisi Frekuensi Relatif

Pendekatan frekuensi relatif berdasar pada definisi beikut.

Peluang P(A) kejadian A adalah limit dari perbandingan n(A) dengan N, dimana n mendekati tak hingga , sehingga dapat ditulis sebagai berikut.

= lim

→ ( )

�

c. Definisi Klasik

Menurut definisi klasik, Bila suatu percobaan dapat menghasilkan N macam hasil yang berkemungkinan sama dan bila tepat sebanyak n dari hasil berkaitan dengan kejadian A, maka peluang kejadian A adalah

n(A) P(A) = 

N

2.2.1 Definisi Peluang Suatu Kejadian A

Peluang suatu kejadian A adalah jumlah semua titik sampel yang termasuk A. Jadi dinyatakan dengan:

0 ≤ P(A) ≤ 1, P(∅)=0, P(S)=1.

2.2.2 Definisi Peluang Bersyarat

Misalkan A dan B menyatakan dua kejadian dalam koleksi kejadian dalam ruang sampel S, maka peluang bersyarat dari kejadian A bila diberikan kejadian B dinotasikan dengan

P AB

P AB =  dengan PB 0 P B

2.3 Variabel Random dan Distribusi Peluang

2.3.1 Defenisi Variabel Random

Suatu fungsi bernilai real yang harganya ditentukan oleh tiap anggota dalam ruang sampel disebut suatu variabel random

2.3.2 Definisi Variabel Random Diskrit

Jika semua himpunan nilai yang mungkin dari suatu variabel random X merupakan himpunan terbilang (countable set), yaitu { x

1, x2,, ..., xn} atau { x1, x2,, ...}, maka X disebut variabel random diskrit.

2.3.3 Definisi Variabel Random Kontinu

Jika himpunan semua nilai yang mungkin dari suatu variabel random X merupakan selang bilangan real, maka X disebut variabel random kontinu.

2.4 Distribusi Peluang Diskrit dan Kontinu

2.4.1 Defenisi Distribusi Peluang Diskrit

Fungsi f(x) adalah suatu fungsi peluang atau distribusi peluang suatu peubah acak diskrit X bila, untuk setiap hasil x yang mungkin

a. f(x) ≥ 0

b. = 1

c.P(X = x)

Distribus kumulatif F(x) yaitu suatu variabel random diskrit X dengan distribusi peluang f(x) dinyatakan oleh

= = ( ) − ∞< < ∞

2.4.2 Defenisi Distribusi Peluang Kontinu

Fungsi f(x) adalah fungsi padat peluang peubah acak kontinu X, yang didefenisikan atas himpunan semua bilangan real R, bila

b. = 1

∞

−∞

. =

dinamakan fungsi densitas probabilitas dari variabel random kontinu X. Jika variabel random kontinu X memiliki fungsi densitas probabilitas f(x), maka peluang suatu kejadian atau peristiwa A, diberikan oleh

=

�

2.4.3 Definisi Fungsi densitas probabilitas kontinu

Fungsi densitas probabilitas kontinu adalah Suatu fungsi f(x) yang didefinisikan pada selang nilai variabel random X. sehingga fungsi distribusi kumulatifnya dapat dinyatakan sebagai.

=

−∞

2.5 Konsep Dasar Distribusi waktu Hidup

Fungsi-fungsi pada distribusi tahan hidup merupakan suatu fungsi yang menggunakan variable random. Waktu hidup adalah interval waktu yang diamati dari suatu individu saat pertama kali masuk kedalam pengamatan hingga keluar dari pengamatan. Misalnya interval waktu sampai rusaknya suatu barang produksi, matinya suatu makhluk hidup, kambuhnya suatu penyakit, dan lain-lain. Variable random nonnegative waktu hidup biasanya dinotasikan dengan huruf “T’’, dan akan membentuk suatu distribusi.

2.5.1.Fungsi Kepadatan Peluang

Fungsi Kepadatan Peluang adalah probabilitas suatu individu mati atau gagal dalam interval waktu dari t sampai t + t, dengan waktu T merupakan variabel random.

Waktu hidup merupakan variabel random non negatif, sehingga waktu hidup hanya diukur untuk nilai t yang positif, maka diperoleh

Fungsi tahan hidup (Survival) adalah probabilitas suatu individu yang masih dapat bertahan hidup sampai dengan waktu t (t > 0). Jika T merupakan variabel random dari waktu hidup suatu individu dalam interval [0,∞), maka fungsi distribusi kumulatif F(t) untuk distribusi kontinu dengan fungsi densitas probabilitas f(t) dinyatakan sebagai berikut

Oleh karena itu diperoleh fungsi tahan hidup (Survival) yang didefinisikan dengan S(t) = P (T t)

= 1- P (T t)

Dalam beberapa hal, khususnya yang mencakup tahan hidup dari komponen-komponen industri, S(t) ditentukan sebagai fungsi Survival.

Jadi hubungan fungsi densitas probabilitas dengan fungsi tahan hidup (Survival) adalah

(ii). S(∞) = 0 , artinya peluang suatu individu bertahan hidup pada waktu yang tak terhingga adalah 0.

2.5.3. Fungsi Kegagalan (Hazard Function)

Fungsi Kegagalan adalah probabilitas suatu individu mati dalam interval waktu dari t sampai t+Δt, jika diketahui individu tersebut masih dapat bertahan hidup sampai dengan waktu t. fungsi hazard secara matematika dinyatakan sebagai:

= lim

Dari persamaan (2.4) dan (2.6) diperoleh h(t) sebagai berikut:

⇔ − ℎ = ln ( )_�� 0

Karena S(0)=1, maka diperoleh

− ℎ = ln 0

⟺ = − ℎ  t

0

Dari uraian di atas diperoleh hubungan antara f(t), S(t), dan h(t) sebagai berikut:

i) =− ′ (2.8)

ii) ℎ = ( ) ( )

iii) = − ℎ  t

0

Dengan demikian jika fungsi hazard h(t) dari suatu distribusi dalam tahan hidup diketahui, maka f(t), F(t) dan S(t) dapat dicari. Sedangkan fungsi hazard kumulatif didefinisikan dengan

H = ℎ 0

(2.9)

melalui persamaan (2.8) fungsi hazard kumulatif yang dihubungkan dengan fungsi tahan hidup diperoleh

= −�( )

=ℎ − ℎ  dari suatu populasi denga fungsi densitas f(x) maka fungsi densitas probabilitas bersama dari variabel random independen akan diberikan sebagai

1, 2,…, = 1 2 … ( ) fungsi densitas probabilitas dari statistik terurut ke-k, adalah

ℊ = !

−1 ! − ! −

1 _{1− (} − _{jika < <}

2.7Sistem keandalan

Dalam konsep keandalan, juga terdapat beberapa sistem yang dinyatakan untuk membantu memutuskan apakah sistem gagal secara total atau tidak.

Untuk itulah dibwah ini akandiberikan tiga system yang dapat dikatakan sebagai sistem dasar dari keandalan sistem. Yaitu sitem seri, parallel dan gabungan dari seri dengan paralel.

2.7.1 Sistem keandalan seri

Suatu sistem dapat dimodelkan dengan susunan seri jika kompenen-komponen yang ada didalam sistem itu harus bekerja seluruhnya agar sistem tersebut sukses dalam menjalankan fungsinya. Atau denga kata lain bila ada satu komponen saja tidak bekerja, maka akan mengakibatkan system itu gagal menjalankan fungsinya. Secara diagram, system keandalan seri dapat dilihat pada gambar 2.1

Gambar 2.1

Diagram pada gambar diatas sering disebut Diagram Blok Keandalan / Reliability Block Diagram (RDB). Perlu diperhatikan bahwa diagram ini tidak mewakili setiap komponen yang dihubungkan secara seri, tetapi menunjukkan bagaimana komponen-komponen itu diperlakukan dari sudut pandang keandalan.

Jika ada n buah komponen dalam susunan seri dan masing-masing memiliki indeks keandalan _{1, 2,…, ,} seperti terlihat pada gambar 2.1, maka secara umum system keandalan seri dirumuskan sebagai berikut:

= 1 . 2 .…. = � (2.11)

�=1

Sedangkan ekspresi ketidakandalan dari system dengan susunan seri dari n buah komponen adalah

= 1− = 1− _� (2.12)

�=1

Contoh 2.1

Sebuah sistem control terdiri dari lima buah unit dimana semua unit pendukungnya bekerja seluruhnya agar system control tersebut dapat berfungsi. Jika indeks keandalan dari kelima unit masing-masing adalah 0,90; 0,95; 0,87; 0,93; dan 0,90 tentukan indeks keandalan dari sistem kontrol tersebut.

Penyelesaian :

Blok diagram keandalan yang paling mewakili dari system control tersebut adalah blok diagram keandalan dengan susunan seri. Jika keandalan dari masing-masing unit disimbolkan dengan _� maka keandalan dari system control itu adalah

= _� = 0,90 0,95 0,87 0,93 0,90 = 0,622602 5

�=1

Jadi keandalan dari sistem control tersebut adalah 0,622602

2.7.2 Sistem Keandalan Paralel

Pada sistem ini setiap komponen yang mungkin mengalami kerusakan tidak akan mengakibatkan kerusakan sistem secara keseluruhan, dan sering dinamakan fault tolerant( kerusakan yang dapat ditolerir).

Ada dua jenis dari system kendalan paralel ini, yakni kelebihan redundant aktif dan kelebihan pasif.

Pada kelebihan aktif, dua atau lebih unit diletakkan dalam system keandalan paralel dimana secara normal pembagian fungsi dilakukan tetapi unit-unit atersebaut diatur sedemikian hingga jika satu unit atau lebih mengalami kerusakan, maka sisanya dapat menggantikan possisinya. Sebagai contoh adalah dua mesin pesawat terbang yang diaktifkan tetapi tidak menutup kemungkinan pesawat untuk terbang dengan satu mesin, apabila mesin yang satunya mengalami kerusakan.

2.7.2.1 Sistem Keandalan Paralel Kelebihan Aktif

Misalkan ada dua unit (1) dan (2) dihubungkan dalam system parallel seperti gambar dibawah ini.

Gambar 2.2

Sistem akan rusak apabila kedua-duanya mengalami kerusakan. Keandalan system dikalkulasikan sebagai berikut, jika didefenisikan bahwa

= ketidakandalan sistem

Maka

= ₁ ∩ ₂

Dimana adalah kejadian komplemen bebas sehingga diperoleh

= 1− _� (2.13)

�=1

Jika peluang dari kegagalan adalah independent, maka fungsi system keandalannya adalah

= 1− (1− ₁)

�=1

(2.14)

2.7.2.2 Sistem Keandalan Paralel Kelebihan Pasif 1

Pada sistem redundan pasif, unit utama(1) secara normal membawa fungsi secara penuh dan unit siaga (2) dibawa untuk digunakan ketika unit utama mengalami kegagalan.

Secara sederhana, redundan pasif dapat ditunjukkan pada gambar berikut:

Gambar 2.3

Cara untuk menganalisa sistem ini adalah harus mempertimbangkan bahwa system kegagalan waktu adalah variable acak yang mengandung jumlah dari dua variable acak, yakni kegagalan waktu (1) dan kegagalan waktu (2).

Jika ₁ = 2 = exp⁡(−� )

Maka dapat dituliskan :

= 1 +� exp⁡(−� )

2.7.3 Kombinasi Sistem Seri dan Paralel

Kombinasi dari system seri dan paralel dapat di selesaikan dengan menggabungkan masing-masing subsistem ke dalam komponen seri maupun paralel terlebih dahulu.

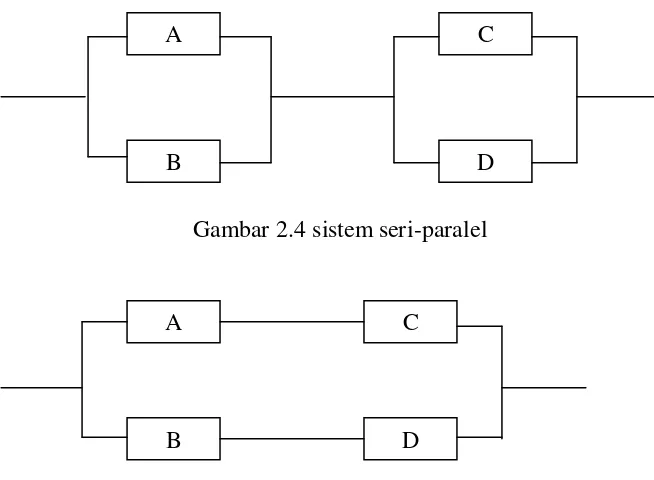
Untuk lebih memahami sistem kombinasi seri dan paralel, akan diberikan contoh gambar seperti berikut ini:

1

Gambar 2.4 sistem seri-paralel

Gambar 2.5 sistem paralel -seri

Dari kedua gambar diatas, gambar (2.4) menunjukkan system kombinasi seri dan paralel. Untuk menyelesaikan sistem gabungan ini pertama-tamakita gabungkan subsistem parelel kedalam bentuk yang sama dengan komponen seri.

Misalkan: = 0.9, = 0.8, = 0.7, dan = 0.6

Maka penyelesaian dapat dituliskan

= 1− 0.1 0.2

= 1−0.02 = 0.98

Dan

= 1− 0.3 0.4

= 1−0.12

= 0.88

Maka keandalan sistem secara keseluruhan adalah

= 0.98 0.88 = 0.8624

A

A C

B D

C

Untuk gambar (2.5) seperti yang ditunjukkan, merupakan system kombinasi paralel-seri. Untuk menyelasaikannya, pertama-tama kita gabungkan subsistem seri ke dalam bentuk yang sama dengan komponen paralel. Untuk pemisalan yang sama dengan diatas, maka diperoleh penyelesaiannya sebagi berikut:

= 0.9 0.7

= 0.63

Dan

= 0.8 0.6

= 0.48

Sehingga keandalan sistem secara keseluruhan adalah

= 1− 1− (1− )

= 1− 1−0.63 (1−0.48)

= 1− 0.37 (0.52) = 1−0.1924

= 0.8076

2.8 Data Tersensor

Dalam penyensoran sering terjadi individu yang diamati tersensor. Masalah penyensoran ini merupakan suatu hal yang membedakan antara uji hidup dengan bidang ilmu statistik yang lain. Data tersensor adalah data yang diperoleh sebelum hasil yang diinginkan dari pengamatan terjadi, sedangkan waktu pengamatan telah berakhir atau oleh sebab lain. Data yang mengalami penyensoran hanya memuat sebagian informasi mengenai variabel random yang diperhatikan, namun berpengaruh terhadap pengertian-pengertian dan perhitungan statistik.

1. Sampel lengkap, dalam uji sampel lengkap eksperimen akan dihentikan jika semua komponen yang diuji telah mati atau gagal. Cara seperti ini mempunyai keuntungan yaitu dapat dihasilkan observasi terurut dari semua komponen yang diuji.

2. Sensor tipe I, semua objek yang diteliti (n) masuk pengujian dalam waktu yang bersamaan, dan pengujian dihentikan setelah batas waktu ₀ yang ditentukan. Kelemahan dari sensor tipe I ini bias terjadi sampai batas waktu ₀ yang ditentukan semua objek masih hidup sehingga tidak diperoleh data tahan hidup dari objek yang diuji.

3. Sensor tipe II, bila uji dihentikan setelah diperoleh sejumlah kegagalan tertentu. data tersensor tipe II merupakan data kematian atau kegagalan yang tidak lengkap (incomplete mortality data) yaitu data waktu kematian atau kegagalan dari r observasi terkecil dalam sampel random yang berukuran n dengan 1 ≤ r ≤ n. Dalam eksperimen menunjukkan penyensoran tipe II lebih sering digunakan sebagai contoh dalam uji hidup dari total observasi sebanyak n, tetapi uji hidup akan berhenti pada waktu observasi sampel mempunyai waktu kematian atau kegagalan ke-r. Oleh karena itu uji hidup ini dapat menghemat waktu dan biaya, karena uji hidup memakan waktu yang lama untuk penyensoran terhadap kegagalan dari observasi. Data tersensor tipe II diperoleh dari penyelidikan terhadap n observasi, sehingga penyensoran berhenti sampai observasi sampel yang mempunyai waktu kematian atau kegagalan ke- r objek tersebut.

2.9 Distribusi Weibull

= ��� �−1_{exp − �} � _{> 0,� > 0,�> 0. 2.14}

Adapun fungsi tahan hidup dan fungsi hazard dari distribusi weibull adalah

= exp −(� )� , > 0 (2.15)

Dan

ℎ = ��(� )�−1 _(2.16)

dimana � > 0,�> 0, > 0.

sedangkan fungsi distribusi dari distribusi weibull adalah

= 1− −(� )2 (2.17)

Dimana � > 0, > 0.

2.10 Distribusi Rayleigh

Dalam beberapa kasus khusus parameter bentuk, β, dari distribusi Weibull diberi

harga β = 2, dikenal sebagai distribusi Rayleigh. Sehingga diperoleh fungsi tahan hidup dari distribusi Rayleigh sebagai berikut.

= −(� )2 � �> 0, > 0. (2.18)

Dan diperoleh fungsi hazard dari distribusi Rayleigh yaitu:

ℎ = 2�2 (2.19)

= 1− ( )

= 1−exp −(� )2

1− = −(� )2

Dari persamaan (2.8) dan (2.18) diperoleh persamaan

= − ( )=− ( − � 2 ₎

(2.20)

Sehingga diperoleh fungsi densitas probabilitas dari distribusi Rayleigh adalah sebagai berikut:

= 2�2 −_{(� )}2 _{> 0,� > 0.}

2.11 Prinsip Dasar Metode Maksimum Likelihood

Metode untuk mengestimasi harga parameter distribusi dari data dalam fungsi tahan hidup (Survival) adalah dengan menggunakan metode maksimum likelihood. Metode maksimum likelihood menggunakan nilai dalam ruang parameter Ω yang bersesuaian dengan harga kemungkinan maksimum dari data observasi sebagai estimasi dari parameter yang tidak diketahui.

Dalam aplikasinya L(θ) menunjukkan fungsi densitas probabilitas bersama dari sampel random. Jika Ω ruang parameter yang merupakan interval terbuka dan L(θ) merupakan fungsi yang dapat diturunkan serta diasumsikan maksimum pada Ω maka persamaan maksimum likelihoodnya adalah

� � � = 0 (2.21)

fungsi L(θ) dapat dibuat logaritma naturalnya, dengan ketentuan memaksimumkan lnL(θ), sehingga persamaan logaritma natural likelihoodnya adalah

�ln� � = 0 (2.22)

Jika fungsi densitas probabilitas bersama dari n variabel random _{1, 2,}…, _,yang diobservasi pada _{1, 2,}…, _, dinotasikan dengan f(. _{1, 2,}…, _,) maka fungsi liklelihood dari himpunan pengamatan _{1, 2,}…, ,dinyatakan sebagai

� � = 1;� 2;� … ;� = 1;�

�=1

(2.23)

Dengan  parameter yang tidak diketahui

Penduga maksimum likelihood dari θ didapat dengan menyelesaikan

persamaan

�ln� � = 0, misalkan ada k parameter yang tidak diketahui, ma ka penduga parameter likelihood dari �_� didapat dengan menyelesaikan

BAB 3

PEMBAHASAN DAN HASIL

3.1 Estimasi Parameter untuk Data Waktu Hidup yang Berdistribusi

Rayleigh pada Data Tersensor Tipe II dengan Metode Maksimum Likelihood

Seringkali data hasil eksperimen tidak diketahui bentuk hubungan fungsional antara variabel-variabel yang mempengaruhi nilai data sampel, sehingga sulit dalam melakukan suatu analisis statistik terhadap populasi yang diamati. Hubungan fungsional ini digambarkan dengan suatu persamaan matematika yang berupa fungsi pendekatan, yaitu fungsi distribusi.

Untuk itu terlebih dahulu dipilih bentuk distribusi dari data dalam fungsi tahan hidup yang diduga, yaitu yang berbentuk parametrik dan data waktu hidup diasumsikan berdistribusi Rayleigh. Kemudian dicari bentuk fungsi parameter yang diwakili data hasil eksperimen tersebut, agar dapat menduga nilai data pada harga selanjutnya. Dalam skripsi ini digunakan metode maksimum likelihood untuk mencari estimasi parameter dari distribusi Rayleigh.

Metode maksimum likelihood menggunakan nilai dalam ruang parameter Ω yang bersesuaian dengan harga kemungkinan maksimum dari data observasi sebagai estimasi dari parameter yang tidak diketahui. Dalam aplikasinya L(θ) menunjukkan fungsi densitas probabilitas bersama dari sampel random. Jika Ω ruang parameter yang merupakan interval terbuka dan L(θ) merupakan fungsi yang dapat diturunkan

serta diasumsikan maksimum pada Ω maka persamaan maksimum likelihoodnya

adalah

�ln� � = 0

diselesaikan maka fungsi L(θ) dapat dibuat logaritma naturalnya, dengan ketentuan ln L(θ) maksimum, sehingga persamaan logaritma natural maksimum likelihoodnya adalah

�ln� � = 0

Penduga maksimum likelihood dari θ didapat dengan menyelesaikan

persamaan

�ln� � = 0, misalkan ada k parameter yang tidak diketahui, ma ka penduga parameter likelihood dari �_� didapat dengan menyelesaikan

��ln� �1,�2,…,� = 0, dengan � = 1, 2, 3,…, .

Misalkan ada n benda yang tahan hidupnya berdistribusi weibull mempunyai f.k.p

= ��� �−1exp − � � > 0,� > 0,� > 0.

Dimana dari distribusi weibull diberi harga �=2 sehingga distribusinya menjadi distribusi Rayleigh

= 2�2 −(� )2 > 0,� > 0.

Jika ₁, 2,… adalah sampel random dari fungsi kepadatan peluang dari

distribusi Rayleigh, maka fungsi likelihoodnya adalah

� :� = ln⁡(2�2_{) − (�}

Dengan menurunkan ln L(t:�) terhadap parameter �, diperoleh

ln�( :�)

Estimator Maksimum likelihood� didapat dengan menyelesaikan persamaan

ln�( :�)

Dan diperoleh

3.2 Data Tersensor Tipe II untuk Distribusi Rayleigh

Misalkan t

1 ≤ t2 ≤... ≤ tr adalah data tersensor tipe II dan merupakan r observasi terkecil dalam sampel random berukuran n dengan r ≤ n dari distribusi Rayleigh untuk data yang tidak dikelompokkan (data tunggal), sehingga diperoleh fungsi densitas probabilitas bersama dari statistik terurut r yang pertama dari sampel random berukuran n dari f( _�) yang kontinu adalah.

1, 2,… =

Fungsi likelihood dari distribusi Rayleigh untuk data tersensor tipe II memiliki bentuk fungsi sebagai berikut

Kemudian ditarik logaritma naturalnya (ln) dari fungsi likelihood (3.6), sehingga diperoleh fungsi log-likelihood dari distribusi Rayleigh sebagai berikut.

= ln ! data tersensor tipe II diperoleh dengan penyelesaian sistem persamaan:

− �2

�(dalam jam ) dari 10 komponen bola lampu pijar tersebut adalah 0.22; 0.50; 0.88; 1.00; 1.32; 1.33; 1.54; 1.76; 2.50; dan 3.00. jadi dari data tersebut dilakukan estimasi parameter distribusi dari data dalam fungsi tahan hidup yang diasumsikan berdistribusi Rayleigh.

Sumber: Buku Reliability in Engineering design. Penyelesaian:

1 = 0.22 2 = 0.50 3 = 0.88 4 = 1.00 5 = 1.32 6 = 1.33

7 = 1.54 8 = 1.76 9 = 2.50 10 = 3.00

n = 13

r = 10

= ₁₀ = 3.00

� = ₂

�=1 + ( − ) 2 1 2

= 10

(0.22)2_{+ (0.50)}2_{+ (0.88)}2_{+ (1.00)}2_{+ (1.32)}2₊⋯_{+ 13}−_{10 . (3.00)}2 1 2

= 10

53.30 1 2

= 0.433

Jadi nilai estimasi parameter untuk  dari distribusi Rayleigh adalah � = 0.433

Dan didapat fungsi kegagalannya, misalkan diberikan ( t = 0.1) sehingga diperoleh

ℎ = ��(� )� −1

= 0.866 ( 0.433) = 0.0375

Jadi setiap komponen dengan 0.1 satuan waktu akan berkurang keandalannya sebesar 0.0375

Dan fungsi tahan hidupnya didadapatkan

= −(� )2

1 = −(0.433(0.1))2

= −(0.433)2

= −0.00187489

= 0.9981

BAB 4

KESIMPULAN DAN SARAN

4.1 Kesimpulan

Berdasarkan hasil penelitian yang telah dilakukan, maka dapat diambil kesimpulan sebagai berikut:

1. Estimator Maksimum Likelihood dari parameter distribusi Rayleigh, untuk data tersensor tipe II adalah

� = ₂

�=1 + ( − ) 2 1 2

Dan Estimator maksimum likelihood dari parameter distribusi Rayleigh yang merupakan bentuk khusus dari distribusi weibull adalah

� =

�2 �=1

1 2

2. Dalam contoh kasus diperoleh h(t) = 0.0375 maka keandalan dari setiap komponen itu akan berkurang 0,0375 atau 3.75% setiap satuan waktu 0.1

4.2 Saran

DAFTAR PUSTAKA

Asmussen, Soren. 1987. Applied Probability and Queues. Denmark: John Wiley and sons, Inc.

Barlow, Richard E. and Proschan, Frank. 1965. Mathematical Theory of Reliability. New York: John Wiley and Sons, Inc.

Barlow , Richard E. and Proschan, Frank. 1981. Statistical Thoery of Reliability and Life Testing. United States of America: Holt, Reinhard and Winston, Inc.

Erlant, R.C and Johnson. N.L. 1980. Survival Models and Data Analysis. New York: John Wiley and Sons. Inc.

Johnson, Richard A. and Wichern, Dean W. 2007. Applied Multivariate Statistical Analysis. Sixth edition. United States of America: Pearson Prentice Hall.

Kapur. K.C. and Lamberson. L. R. 1977. Reliability in Engineering Design. New York: John Wiley and Sons. Inc.

Mukhpadhyay, Parimal. 2002. Mathematical Statistical. Calcuta: Indian Statistical Institude.

Ross, Sheldom M. 1987. Introduction to Probability and Statistics for Engineers and Scientists. Canada: John Wiley and Sons, Inc.

Surjadi, P. A. 1976. Pendahuluan Teori kemungkinan dan Statistika. Bandung: Institut Teknologi Bandung.