Perbandingan Metode Fuzzy Dengan Regresi Linear Berganda Dalam Peramalan Jumlah Produksi (Studi Kasus: Produksi Kelapa Sawit di PT. Perkebunan Nusantara III (PERSERO) Medan Tahun 2011-2012)

(1)

PERBANDINGAN METODE

FUZZY

DENGAN REGRESI

LINEAR BERGANDA DALAM PERAMALAN

JUMLAH PRODUKSI

(Studi Kasus : Produksi Kelapa Sawit di PT. Perkebunan

Nusantara III (PERSERO) Medan Tahun 2011-2012)

SKRIPSI

SISKA ERNIDA WATI

110823009

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

UNIVERSITAS SUMATERA UTARA

(2)

PERBANDINGAN METODE

FUZZY

DENGAN REGRESI

LINEAR BERGANDA DALAM PERAMALAN

JUMLAH PRODUKSI

(Studi Kasus : Produksi Kelapa Sawit di PT. Perkebunan

Nusantara III (PERSERO) Medan Tahun 2011-2012)

SKRIPSI

Diajukan untuk melengkapi tugas dan memenuhi syarat

mencapai gelar Sarjana Sains

SISKA ERNIDA WATI

110823009

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

UNIVERSITAS SUMATERA UTARA

(3)

PERSETUJUAN

Judul : Perbandingan Metode Fuzzy Dengan Regresi Linear Berganda Dalam Peramalan Jumlah Produksi (Studi Kasus: Produksi Kelapa Sawit di PT. Perkebunan Nusantara III (PERSERO) Medan Tahun 2011-2012)

Kategori : Skripsi

Nama : Siska Ernida Wati

Nomor Induk Mahasiswa : 110823009

Program Studi : Sarjana (S1) Matematika

Departemen : Matematika

Fakultas : Matematika Dan Ilmu Pengetahuan Alam Universitas Sumatera Utara

Disetujui di Medan, Juli 2013

Komisi Pembimbing :

Pembimbing 2 Pembimbing 1

Drs. Rachmad Sitepu, M. Si Drs. Djakaria Sebayang, M. Si NIP. 19530418 198703 1 001 NIP. 19511227 198503 1 002

Diketahui/ Disetujui oleh

Departemen Matematika FMIPA USU Ketua,

Prof. Dr. Tulus, M.Si. Ph.D

(4)

PERNYATAAN

PERBANDINGAN METODE FUZZY DENGAN REGRESI LINEAR BERGANDA DALAM PERAMALAN JUMLAH PRODUKSI

(STUDI KASUS: PRODUKSI KELAPA SAWIT DI PT. PERKEBUNAN NUSANTARA III (PERSERO)

MEDAN TAHUN 2011-2012)

SKRIPSI

Saya mengakui bahwa skripsi ini adalah hasil karya sendiri. Kecuali beberapa kutipan dan ringkasan yang masing–masing disebut sumbernya.

Medan, Juli 2013

(5)

PENGHARGAAN

Puji dan syukur penulis panjatkan kepada Tuhan Yang Maha Pemurah dan Maha Penyayang, dengan limpah karunia-Nya penulis dapat meyelesaikan penyusunan skripsi ini dengan judul Perbandingan Metode Fuzzy Dengan Regresi Linear Berganda dalam Peramalan Jumlah Produksi (Studi Kasus: Produksi Kelapa Sawit di PT. Perkebunan Perkebunan Nusantara III (Persero) Medan Tahun 2011-2012).

Terimakasih penulis sampaikan kepada Drs. Djakaria Sebayang, M.Si selaku pembimbing 1 dan Drs. Rachmad Sitepu, M.Si selaku pembimbing 2 yang telah meluangkan waktunya selama penyusunan skripsi ini. Terimakasih kepada Prof. Dr. Tulus, M.Si. Ph.D dan Ibu Dra. Mardiningsih, M.Sc selaku Ketua Departemen dan Sekertaris Departemen Matematika FMIPA-USU Medan, Dekan dan Pembantu Dekan FMIPA USU, seluruh Staff dan Dosen Matematika FMIPA USU, pegawai FMIPA USU dan rekan-rekan kuliah. Akhirnya tidak terlupakan kepada Bapak, Ibu dan keluarga yang selama ini memberikan bantuan dan dorongan yang diperlukan. Semoga Tuhan Yang Maha Esa akan membalasnya.

(6)

MEDAN TAHUN 2011-2012)

ABSTRAK

Kajian ini bertujuan untuk membandingkan hasil suatu peramalan dengan menggunakan metode fuzzy dan regresi linear berganda. Dalam kajian ini, digunakan data produksi kelapa sawit sebagai output atau variabel terikat (Y) dan faktor yang mempengaruhinya yaitu pemupukan, tenaga kerja dan rata-rata curah hujan sebagai input atau variabel bebas X1,X2,X3. Variabel pemupukan (X1)

terdiri atas 3 himpunan fuzzy yaitu: sedikit, standar, dan banyak. Untuk variabel tenaga (X2) terdiri atas 3 himpunan fuzzy yaitu : sedikit, sedang, dan banyak. Dan

untuk variabel rata-rata curah hujan (X3) terdiri atas 3 himpunan fuzzy yaitu:

rendah, standar, dan tinggi. Sementara variabel jumlah produksi (Y) terdiri atas 3 himpunan fuzzy yaitu: berkurang, tetap, dan bertambah. Aturan fuzzy yang digunakan ada 16 aturan. Metode penyelesaian yang digunakan adalah metode

fuzzy Mamdani.Untuk regresi linear berganda diselesaikan dengan menggunakan metode kuadrat terkecil (Least Squares Method). Dengan menunjukkan nilai rata-rata kesalahan relatif dari peramalan setiap metode, diperoleh nilai rata-rata-rata-rata kesalahan relatif metode fuzzy sebesar 0,20748 atau 20,748% dan regresi linear berganda sebesar 0,09383 atau 9,383%. Besarnya nilai tersebut memperlihatkan bahwa nilai rata-rata kesalahan relatif regresi linier berganda lebih kecil daripada metode fuzzy. Maka untuk kasus dengan variabel input dan output dalam penelitian ini dapat disimpulkan bahwa peramalan dengan menggunakan regresi linier berganda lebih baik daripada dengan metode fuzzy.

(7)

THE COMPARISON FUZZY SETS AND MULTIPLE LINEAR REGRESSION FOR PREDICTION OF PRODUCTION

(CASE: PRODUCTION OF PALM OIL IN PT. PERKEBUNAN NUSANTARA III (PERSERO) MEDAN FOR 2011-2012)

ABSTRACT

This study is shown how to compare the result of prediction by using Fuzzy Sets and multiple linear regression. In this study, production of palm oil is used as output or dependent variable (Y), and the manuring, worker, and avarage of rainfall are used as output or independent variable X1, X2, and X3. The manuring

variable (X1) consist of three fuzzy sets : minimum, standard, maximum. For

worker variable (X2) consist of three fuzzy sets : minimum, normal, maximum.

For avarage of rainfall (X3) consist of three fuzzy sets : low, standard, high.

Meanwhile, production of palm oil consist of three fuzzy sets : decrease, permanent, increase. In this study, fuzzy use 16 fuzzy rules. The solution of fuzzy logic use fuzzy-Mamdani Method. Multiple regression linear analysis use least squares method as the solution. By showing the avarage of error relative from both of methods, which for fuzzy set is 0,20748 atau 20,748% and for linear regression is 0,09383 atau 9,383%. It’s value shows that the avarage of error relative from linear regression is smaller than fuzzy set. So for the case where input and output in this study, found the conclusion that prediction with multiple regression linear analysis is better than using fuzzy logic.

(8)

DAFTAR ISI

1.4Tinjauan Pustaka 4

1.5Tujuan Penelitian 5

1.6Kontribusi Penelitian 5

1.7Metode Penelitian 6

BAB II LANDASAN TEORI

2.1 Logika Fuzzy 8

2.1.9 Metode Penegasan (Defuzzifikasi) 17

2.1.10 Sistem Inferensi Fuzzy 18

2.1.11 Sistem Inferensi Fuzzy Mamdani 18

2.2 Analisis Regresi Linear Berganda 20

2.2.1 Pengertian Regresi 20

2.2.2 Analisis Regresi Linear 21

2.2.3 Analisis Regresi Linear Sederhana 23 2.2.4 Analisis Regresi Linier Berganda 26

2.3 Kesalahan Relatif 29

2.4 Variabel 30

BAB 3 PEMBAHASAN DAN HASIL

3.1Penyajian Data 32

(9)

3.3 Perhitungan dengan Menggunakan Regresi Linier Berganda 54 3.4 Perhitungan dan Perbandingan Kesalahan Relatif

yang Dihasilkan dari Setiap Model 60

BAB IV KESIMPULAN DAN SARAN

4.1 Kesimpulan 62

4.2 Saran 63

(10)

DAFTAR GAMBAR

Gambar 2.1 Kurva himpunan fuzzy : kelompok umur 10 Gambar 2.2 Kurva Fungsi Keanggotaan secara tegas 11 Gambar 2.3 Kurva Fungsi Keanggotaan dengan menggunakan konsep fuzzy 12

Gambar 2.4 Representasi Kurva Linear Naik 13

Gambar 2.5 Representasi Kurva Linear Turun 14

Gambar 2.6 Representasi Kurva Segitiga 15

Gambar 2.7 Diagram Pencar 24

Gambar 2.8 Diagram Pencar, Garis Regresi dan Sisa 24 Gambar 3.1 Kurva keanggotaan variabel input pemupukan (X1) 34

Gambar 3.2 Kurva keanggotaan variabel input tenaga kerja (X2) 35

Gambar 3.3 Kurva keanggotaan variabel input rata-rata curah hujan (X3) 36

Gambar 3.4 Kurva keanggotaan variabel output jumlah produksi (Y) 37

Gambar 3.5 Kurva solusi daerah fuzzy 52

(11)

DAFTAR TABEL

Tabel 3.1 Data Jumlah Produksi, Jumlah Pemupukan, Jumlah Tenaga Kerja dan Rata-Rata Curah Hujan pada PT. Perkebunan

(12)

MEDAN TAHUN 2011-2012)

ABSTRAK

Kajian ini bertujuan untuk membandingkan hasil suatu peramalan dengan menggunakan metode fuzzy dan regresi linear berganda. Dalam kajian ini, digunakan data produksi kelapa sawit sebagai output atau variabel terikat (Y) dan faktor yang mempengaruhinya yaitu pemupukan, tenaga kerja dan rata-rata curah hujan sebagai input atau variabel bebas X1,X2,X3. Variabel pemupukan (X1)

terdiri atas 3 himpunan fuzzy yaitu: sedikit, standar, dan banyak. Untuk variabel tenaga (X2) terdiri atas 3 himpunan fuzzy yaitu : sedikit, sedang, dan banyak. Dan

untuk variabel rata-rata curah hujan (X3) terdiri atas 3 himpunan fuzzy yaitu:

rendah, standar, dan tinggi. Sementara variabel jumlah produksi (Y) terdiri atas 3 himpunan fuzzy yaitu: berkurang, tetap, dan bertambah. Aturan fuzzy yang digunakan ada 16 aturan. Metode penyelesaian yang digunakan adalah metode

fuzzy Mamdani.Untuk regresi linear berganda diselesaikan dengan menggunakan metode kuadrat terkecil (Least Squares Method). Dengan menunjukkan nilai rata-rata kesalahan relatif dari peramalan setiap metode, diperoleh nilai rata-rata-rata-rata kesalahan relatif metode fuzzy sebesar 0,20748 atau 20,748% dan regresi linear berganda sebesar 0,09383 atau 9,383%. Besarnya nilai tersebut memperlihatkan bahwa nilai rata-rata kesalahan relatif regresi linier berganda lebih kecil daripada metode fuzzy. Maka untuk kasus dengan variabel input dan output dalam penelitian ini dapat disimpulkan bahwa peramalan dengan menggunakan regresi linier berganda lebih baik daripada dengan metode fuzzy.

(13)

THE COMPARISON FUZZY SETS AND MULTIPLE LINEAR REGRESSION FOR PREDICTION OF PRODUCTION

(CASE: PRODUCTION OF PALM OIL IN PT. PERKEBUNAN NUSANTARA III (PERSERO) MEDAN FOR 2011-2012)

ABSTRACT

This study is shown how to compare the result of prediction by using Fuzzy Sets and multiple linear regression. In this study, production of palm oil is used as output or dependent variable (Y), and the manuring, worker, and avarage of rainfall are used as output or independent variable X1, X2, and X3. The manuring

variable (X1) consist of three fuzzy sets : minimum, standard, maximum. For

worker variable (X2) consist of three fuzzy sets : minimum, normal, maximum.

For avarage of rainfall (X3) consist of three fuzzy sets : low, standard, high.

Meanwhile, production of palm oil consist of three fuzzy sets : decrease, permanent, increase. In this study, fuzzy use 16 fuzzy rules. The solution of fuzzy logic use fuzzy-Mamdani Method. Multiple regression linear analysis use least squares method as the solution. By showing the avarage of error relative from both of methods, which for fuzzy set is 0,20748 atau 20,748% and for linear regression is 0,09383 atau 9,383%. It’s value shows that the avarage of error relative from linear regression is smaller than fuzzy set. So for the case where input and output in this study, found the conclusion that prediction with multiple regression linear analysis is better than using fuzzy logic.

(14)

BAB 1

PENDAHULUAN

1.1Latar Belakang

Ilmu matematika berkembang sangat pesat. Salah satunya adalah dalam kompleksnya bahasa yang menimbulkan kesamaran atau kekaburan. Kesamaran dinyatakan sebagai sebuah bahasa lazim yang diterima dengan arti yang berbeda di setiap tempat. Namun lambat laun ditemukan kesulitan dalam mengambil suatu keputusan. Sehingga untuk membuat suatu keputusan dilakukanlah peramalan

ataupun prediksi.

Selama ini metode peramalan yang lazim digunakan adalah regresi linear. Regresi linear digunakan untuk membentuk suatu persamaan dari beberapa variabel bebas yang dinilai memiliki hubungan dengan variabel tidak bebas. Pada awalnya, regresi linear yang digunakan untuk melihat hubungan antara dua variabel adalah regresi linera sederhana. Namun pada kenyataan sehari-hari sering dijumpai sebuah kejadian yang dipengaruhi oleh lebih dari satu variable, oleh karenanya dikembangkanlah analisis regresi linier berganda. Analisis regresi berganda merupakan pengembangan dari analisis regresi sederhana. Kegunaannya yaitu untuk meramalkan nilai variabel terikat (Y) apabila variabel bebasnya (X) dua atau lebih yakni X1, X2, …., Xi (Algafari, 2000).

Dewasa ini juga telah dikembangkan salah satu metode yang digunakan untuk melakukan analisis sistem yang mengandung ketidakpastian, yaitu logika

(15)

Dalam kehidupan sehari-hari, dapat dijumpai banyak gejala kekaburan. Ambil suatu contoh, dalam suatu kelas seorang guru menyuruh muridnya yang memiliki sepeda angkta tangan, maka dengan mudah murid yang memiliki sepeda akan mengangkat tangannya. Namun ketika guru tersebut menyuruh muridnya yang pandai untuk mengangkat tangannya, maka akan timbul keragu-raguan apakah mereka termasuk kelompok yang pandai atau tidak. Batas antara “punya sepeda” dengan “tidak punya sepeda” adalah jelas dan tegas, tetapi tidak demikian halnya antara “pandai” dan “tidak pandai”. Dengan perkataan lain himpunan para murid yang pandai dan tidak pandai seakan-akan dibatasi secara tidak tegas atau kabur. Maka diperlukan suatu bahasa keilmuan baru yang mampu menangkap ketidaktegasan/kekaburan istilah bahasa sehari-hari yang memadai (Frans Susilo, SJ, 2006).

Bahasa semacam itulah yang diciptakan oleh Lotfi Asker Zadeh, seorang guru besar dari Universitas California. Amerika Serikat pada awal tahun 1965.

Beliau memodifikasi teori himpunan yang lazim digunakan menjadi teori himpunan kabur (fuzzy). Teori ini dapat diaplikasikan dalam berbagai bidang, antara lain algoritma kontrol, diagnosa medis, sistem pendukung keputusan, ekonomi, teknik, psikologi, lingkungan, keamanan dan ilmu pengetahuan (Setiadji, 2009).

Logika fuzzy adalah logika yang menggunakan konsep sifat kesamaran. Sehingga logika fuzzy adalah logika dengan tak hingga banyak nilai kebenaran yang dinyatakan dalam bilangan real dalam selang tertutup [0,1]. Angka 0 dan 1 inilah yang disebut derajat keanggotaan. Dengan kata lain, fungsi keanggotaan

dari suatu himpunan kabur _�̃ dalam semesta X adalah pemetaan _�_�� dari X ke

selang [0,1] yaitu _�_�� _{∶ � →}[0,1]. Nilai fungsi _�_��(�) menyatakan derajat

(16)

Dalam aplikasinya ada tiga metode dalam sistem inferensi fuzzy yang dapat digunakan untuk menentukan jumlah produksi yaitu: metode Tsukamoto,

metode Mamdani dan metode Sugeno (Setiadji, 2009). Dimana dalam setiap metode, variabel X dan variabel Y diasumsikan ke dalam fungsi keanggotaan masing-masing sesuai jenisnya. Namun model inferensi fuzzy yang umum digunakan adalah model fuzzy-Mamdani dan model fuzzy-Sugeno (Thomas Sri Widodo, 2005). Sehingga dalam penelitian ini penulis memilih untuk menggunakan Metode Mamdani sebagai alat untuk meramalkan hasil produksi.

Baik regresi linear ataupun logika fuzzy, masing-masing memiliki variabel bebas (independent) yaitu berupa X1, X2, …, Xn dan variabel terikat (dependent)

yaitu berupa Y. Namun dalam pengerjaannya kedua metode ini memiliki tahap-tahap yang berbeda satu sama lainnya. Oleh karena itu penulis ingin membandingkan penggunaan kedua metode ini sebagai alat peramalan dengan mengambil contoh kasus yang sama. Logika fuzzy yang digunakan adalah metode

Mamdani, sementara untuk metode statistik yang digunakan adalah regresi linear berganda.

Untuk dapat melihat perbedaan penggunaan kedua metode tersebut, maka dalam penelitian ini data yang akan digunakan sebagai contoh kasus adalah data produksi kelapa sawit di PT. Perkebunan Nusantara III. Ada beberapa faktor yang dapat mempengaruhi produksi kelapa sawit. Standar beberapa faktor yang dinilai merupakan syarat tumbuh tanaman kelapa sawit adalah faktor alam dan faktor manusia. Faktor alam misalnya adalah kondisi iklim, curah hujan, bentuk wilayah dan kondisi tanah. Sedangkan unfuk faktor manusia adalah luas areal lahan, jumlah pemupukan, serta jumlah pekerja (Dinas Perkebunan Provinsi Sumatera Utara, 2011).

Dalam penelitian ini, penulis menggunakan faktor yang mempengaruhi produksi kelapa sawit (Y) adalah jumlah pemupukan (X1), tenaga kerja (X2) dan

rata-rata curah hujan (X3). Nantinya kedua metode, baik metode fuzzy-Mamdani

(17)

kelapa sawit di PT. Perkebunan Nusantara III berdasarkan variabel bebasnya. Dari hasil yang diperoleh, akan dilihat metode manakah yang memberikan hasil peramalan/prediksi yang paling dekat dengan data produksi yang telah ada. Berdasarkan uraian di atas, maka penulis memberi tulisan ini dengan judul

“PERBANDINGAN METODE FUZZY DENGAN REGRESI LINEAR

BERGANDA DALAM PERAMALAN JUMLAH PRODUKSI (STUDI KASUS: PRODUKSI KELAPA SAWIT PT. PERKEBUNAN NUSANTARA III (PERSERO) MEDAN TAHUN 2011- 2012)”.

1.2Perumusan Masalah

Perumusan masalah yang akan dibahas adalah membandingkan hasil peramalan dengan penggunaan metode fuzzy dengan regresi linear berganda dalam penentuan jumlah produksi kelapa sawit dengan memperhatikan faktor jumlah pemupukan,

jumlah pekerja dan rata-rata curah hujan.

1.3Batasan Masalah

Agar tidak terlalu luas, maka batasan masalah dalam penelitian ini adalah :

1. Banyaknya variabel yang digunakan hanyalah empat macam yaitu jumlah produksi kelapa sawit, jumlah pemupukan, jumlah pekerja dan rata-rata curah hujan. Faktor lainnya yang mempengaruhi tidak dibahas dalam penelitian ini.

2. Metode yang digunakan adalah metode fuzzy-Mamdani dan regresi linear berganda untuk menentukan jumlah produksi kelapa sawit.

(18)

1.4Tinjauan Pustaka

Dalam penelitian ini, ada beberapa penelitian yang telah dilakukan telebih dahulu yang berhubungan dengan penelitian ini antara lain:

1. Supriyono (2007), dalam penelitiannya membandingkan penggunaan metode

fuzzy dan regresi linear berganda dengan menggunakan data simulasi. Dari penelitian tersebut diperoleh kesimpulan bahwa regresi linear lebih tepat untuk digunakan.

2. Resti Athayani (2009), dalam penelitiannya membandingkan penggunaan metode fuzzy dan regresi linear berganda dengan menggunakan data primer, yaitu data tentang nilai ketidakpuasan konsumen, karakteristik kategori produk, dan kebutuhan mencari variasi pada mahasiswa Universitas Indonesia. Dari penelitian tersebut diperoleh bahwa metode fuzzy lebih tepat untuk digunakan.

3. Nove Maria Sihombing (2010), meneliti tentang faktor-faktor yang

mempengaruhi hasil produksi kelapa sawit pada PT. Perkebunan Nusantara III (PERSERO) Medan antara lain luas lahan, tenaga kerja dan jumlah pemupukan. Dari penelitian tersebut diperoleh hasil bahwa baik luas lahan, tenaga kerja dan jumlah pemupukan sama-sama memberikan pengaruh positif terhadap produksi kelapa sawit.

1.5Tujuan Penelitian

Tujuan dari penelitian ini adalah:

1. Untuk melihat hasil produksi kelapa sawit baik menggunakan perhitungan metode fuzzy-Mamdani maupun analisis regresi linear berganda dengan menggunakan variabel yang sama.

(19)

3. Untuk melihat metode yang paling tepat digunakan dalam meramalkan jumlah produksi kelapa sawit.

1.6Kontribusi Penelitian

Manfaat dari penelitian ini adalah sebagai berikut:

1. Membantu penulis dalam menerapkan ilmu yang telah didapat selama di perkuliahan ke dalam dunia nyata.

2. Menambah pengetahuan penulis tentang persoalan logika fuzzy dan regresi linear berganda.

3. Sebagai dasar dan contoh pengembangan dan penerapan logika fuzzy

khususnya metode Mamdani dan regresi linear berganda.

4. Sebagai bahan masukan bagi pihak PT. Perkebunan III dalam penentuan anggaran produksi kelapa sawit untuk tahun-tahun berikutnya.

1.7 Metode Penelitian

Penelitian ini adalah penelitian dengan menggunakan studi kepustakaan (literature) dengan menggunakan contoh kasus yang dalam hal ini adalah data sekunder. Adapun langkah-langkah dalam penyusunan penelitian ini adalah sebagai berikut:

1. Memahami konsep metode fuzzy-Mamdani dan regresi linear berganda melalui literatur berupa buku-buku, jurnal, maupun internet yang berhubungan dengan penelitian ini.

2. Pengolahan data dalam metode fuzzy dengan menggunakan metode fuzzy -Mamdani.

3. Penurunan persamaan linear berganda dengan menggunakan metode kuadrat terkecil.

(20)

5. Perhitungan dan perbandingan rata-rata jumlah kesalahan relatif (error) untuk tiap nilai peramalan kedua metode tersebut.

(21)

BAB 2

LANDASAN TEORI

2.1 Logika Fuzzy

2.1.1 Pengertian Logika Fuzzy

Suatu kata/istilah dikatakan fuzzy (kabur) apabila kata/istilah tersebut tidak dapat didefenisikan secara tegas, dalam arti tidak dapat ditentukan secara tegas apakah suatu objek tertentu memiliki sifat/ciri yang diungkapkan oleh kata/istilah

tersebut. Sehingga objek itu akan disebut dengan himpunan kabur (fuzzy). Oleh karena itu butuh penegasan terhadap himpunan tersebut (Frans Susilo, SJ, 2006).

(22)

cepat dan sebagainya. Maka diperlukan suatu bahasa keilmuan baru yang mampu menangkap ketidaktegasan/kekaburan istilah bahasa sehari-hari yang memadai (Frans Susilo, SJ, 2006).

Bahasa semacam itulah yang diciptakan oleh Lotfi Asker Zadeh, seorang guru besar dari Universitas California, Amerika Serikat pada awal tahun 1965. Beliau memodifikasi teori himpunan yang lazim digunakan menjadi teori himpunan kabur (fuzzy). Teori ini dapat diaplikasikan dalam berbagai bidang, antara lain algoritma kontrol, diagnosa medis, sistem pendukung keputusan, ekonomi, teknik, psikologi, lingkungan, keamanan dan ilmu pengetahuan (Setiadji, 2009).

Logika fuzzy adalah suatu cara yang tepat untuk memetakan suatu ruang

input ke dalam suatu ruang output. Pada saat ini logika fuzzy sudah banyak diterapkan di berbagai bidang baik di dunia industri maupun penelitian.

Contohnya manajer pergudangan mengatakan kepada manajer produksi seberapa banyak persediaan barang pada akhir minggu ini, kemudian menajer produksi akan menetapkan jumlah barang yang harus diproduksi esok hari. Dengan menggunakan teori himpunan fuzzy logika bahasa dapat diwakili oleh sebuah daerah yang mempunyai jangkauan tertentu yang menunjukkan derajat keanggotaannya (Sri Kusumadewi, 2002).

2.1.2 Variabel Fuzzy

(23)

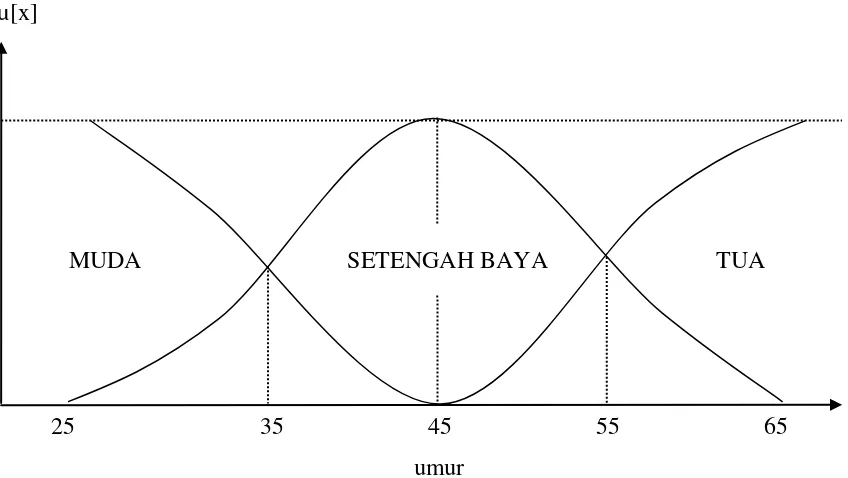
µ[x]

MUDA SETENGAH BAYA TUA

25 35 45 55 65

umur

Gambar 2.1 Kurva himpunan fuzzy : kelompok umur (Sri Kusumadewi, 2002)

Himpunan fuzzy yang dibuat terlihat tumpang tindih dan tiap-tiap himpunan fuzzy

dapat disebut sebagai nilai linguistik yang bersesuaian dalam group yang berbeda, yang dalam hal ini adalah MUDA, SETENGAH BAYA, dan TUA. Sedangkan untuk angka yang merupakan umur dalam tahun, disebut sebagai nilai numerik.

2.1.3 Fungsi Keanggotaan

Ide mengenai “derajat keanggotaan” dalam suatu himpunan diperkenalkan oleh Profesor Zadeh pada tahun 1965 dalam karangan ilmiahnya “Fuzzy Sets”. Dalam karangan tersebut, Zadeh mendefinisikan himpunan kabur dengan menggunakan apa yang disebut fungsi keanggotaan (membership function), yang nilainya berada dalam selang tertutup [0,1] (Frans Susilo, SJ, 2006).

(24)

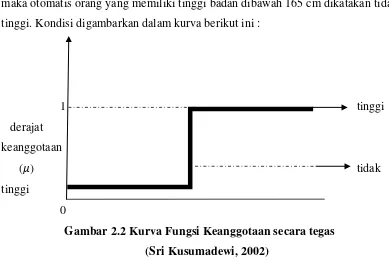
Andaikan seseorang dikatakan tinggi jika memiliki tinggi badan di atas 165 cm, maka otomatis orang yang memiliki tinggi badan dibawah 165 cm dikatakan tidak tinggi. Kondisi digambarkan dalam kurva berikut ini :

1 tinggi

derajat keanggotaan

(_�) tidak

tinggi

0

Gambar 2.2 Kurva Fungsi Keanggotaan secara tegas (Sri Kusumadewi, 2002)

Secara tegas dapat dikatakan bahwa orang yang memiliki tinggi badan di atas 165 cm dikatakan tinggi dengan nilai keanggotaan=1. Sebaliknya apabila seseorang memiliki tinggi beda atau kurang dari atau sama dengan 165 cm, maka secara tegas dikatakan tidak tinggi dengan fungsi keanggotaan = 0. Hal ini menjadi tidak adil, Karena untuk orang yang memiliki tinggi badan 165,1 cm dikatakan tinggi, sedangkan orang yang memiliki tinggi badan 165 cm dikatakan tidak tinggi. Dengan mnggunakan himpunan fuzzy, dapat dibuat suatu fungsi

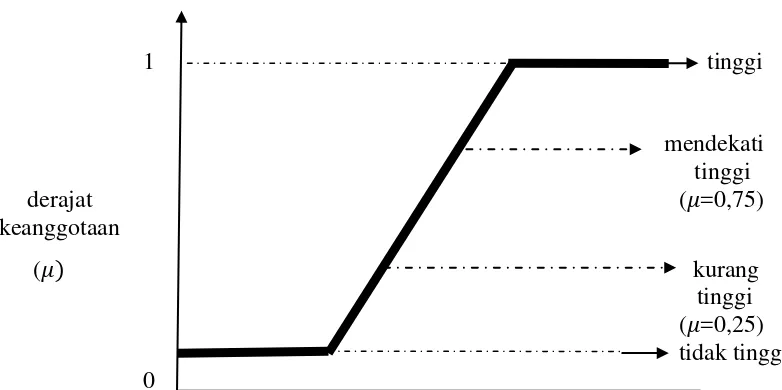
keangotaannya. Orang yang memiliki tinggi 160 cm sudah mendekati tinggi, artinya dia dikatakan tinggi dengan _�=0,75. Sedangkan orang yang memiliki tinggi 130 cm misalnya, dia memang kurang tinggi, artinya dia dikatakan tinggi

(25)

Kondisi tersebut dapat dilihat dalam kurva berikut :

1 tinggi

mendekati tinggi

derajat (_�=0,75)

keanggotaan

(_�) kurang

tinggi (_�=0,25) tidak tinggi 0

Gambar 2.3 Kurva Fungsi Keanggotaan dengan menggunakan konsep fuzzy

(Sri Kusumadewi, 2002)

Fungsi keanggotaan himpunan fuzzy adalah rentang nilai-nilai. Masing-masing nilai mempunyai derajat keanggotaan antara 0 sampai dengan 1. Derajat kenggotaan dinyatakan dengan suatu bilangan real dalam selang tertutup [0,1].

Dengan kata lain, fungsi keanggotaan dari suatu himpunan kabur _�̃ dalam semesta

X adalah pemetaan _�_�� dari X ke selang [0,1] yaitu _�_�� _{∶ � →}[0,1]. Nilai fungsi ��(�) menyatakan derajat keanggotaan unsur x∈X dalam himpunan kabur �̃. Nilai fungsi sama dengan 1 menyatakan keanggotaan penuh, dan nilai fungsi sama dengan 0 menyatakan sama sekali bukan angota himpunan kabur tersebut (Frans Susilo, SJ, 2006).

2.1.4 Representasi Kurva Linear

Pada representasi linear, permukaan digambarkan sebagai suatu garis lurus. Bentuk ini paling sederhana dan menjadi pilihan yang baik untuk mendekati suatu konsep yang kurang jelas (Luh Made Yulyantar, 2011). Ada dua kemungkinan

(26)

a. Representasi Kurva Linear Naik

Yaitu kenaikan himpunan dimulai dari nilai domain yang memiliki nilai keanggotaan nol [0] bergerak ke kanan menuju ke nilai domain yang memiliki derajat keanggotaan yang lebih tinggi.

Fungsi keanggotaan :

Grafiknya adalah seperti berikut :

Gambar 2.4 Representasi Kurva Linear Naik (Sri Kusumadewi, 2002)

b. Representasi Kurva Linear Turun

Yaitu garis lurus yang dimulai dari nilai domain dengan derajat keanggotaan tertinggi pada sisi kiri, kemudian bergerak turun ke nilai domain yang memiliki derajat keanggotaan lebih rendah.

(27)

Grafiknya adalah :

Gambar 2.5 Representasi Kurva Linear Turun (Sri Kusumadewi, 2002)

2.1.5 Representasi Kurva Segitiga

Adalah gabungan antara dua representasi linear (representasi linear naik dan representasi linear turun). Fungsi keanggotaan segitiga ditandai dengan tiga parameter {a,b,c}, yang akan menentukan koordinat x dari tiga sudut.

Fungsi keanggotaan :

µ_A�(x) =�

x−a b−a c−x c−b

0

a≤x≤b b≤ x≤ c x≤ a atau x≥c

(28)

Grafiknya adalah :

Gambar 2.6 Representasi Kurva Segitiga

(Sri Widodo, 2005)

2.1.6 Operator Himpunan Fuzzy

Ada beberapa operasi yang didefinisikan secara khusus untuk mengkombinasi dan memodifikasi himpunan fuzzy. Nilai keanggotaan sebagai hasil dari operasi 2 himpunan sering dikenal dengan nama fire strength atau α–predikat. Ada 3 operator dasar yang diciptakan oleh Zadeh (Luh Made Yulyantar, 2011), yaitu: 1. Operator AND

Operator ini berhubungan dengan operasi interseksi pada himpunan. α– predikat sebagai hasil operasi dengan operator AND diperoleh dengan mengambil nilai keanggotaan terkecil antar elemen pada himpunan-himpunan yang bersangkutan. Operator AND dilambangkan dan didefenisikan sebagai berikut :

µA∩B = min(µA(X), µB(X))

2. Operator OR

Operator ini berhubungan dengan operasi union pada himpunan. α– predikat sebagai hasil operasi dengan operator OR diperoleh dengan mengambil nilai keanggotaan terbesar antar elemen pada himpunan-himpunan yang bersangkutan. Operator OR dilambangkan dan didefenisikan sebagai berikut :

(29)

3. Operator NOT

Operator ini berhubungan dengan operasi komplemen pada himpunan. α– predikat sebagai hasil operasi dengan operator NOT yang diperoleh dengan mengurangkan nilai keanggotaan elemen pada himpunan yang bersangkutan dari 1.

µA’ = 1-µA(X)

2.1.7 Proposisi Fuzzy

Proposisi fuzzy adalah kalimat yang memuat predikat fuzzy, yaitu predikat yang dapat direpresentasikan dengan suatu himpunan fuzzy. Proposisi fuzzy yang mempunyai kebenaran tertentu disebut pernyataan fuzzy. Nilai kebenaran suatu pernyataan fuzzy dapat dinyatakan dengan suatu bilangan riil dalam rentang [0,1]. Nilai kebenaran itu disebut juga derajat kebenaran pernyataan fuzzy. Bentuk

umum suatu proposisi fuzzy adalah:

X adalah A

dengan X adalah suatu variabel linguistik dan A adalah predikat yang menggambarkan keadaan X. Bila Ã adalah himpunan fuzzy yang dikaitkan dengan nilai linguistik A, dan x0 adalah suatu elemen tertentu dalam semesta X

darihimpunan fuzzy Ã, maka x0 memiliki derajat keanggotaan μÃ (x0) dalam

himpunan fuzzy Ã. Derajat kebenaran pernyataan fuzzy “x0adalah A” didefinisikan

sama dengan derajat keanggotaan x0dalam himpunan fuzzy Ã, yaitu μÃ (x0) (Frans

Susilo, 2009).

2.1.8 Implikasi Fuzzy

Jika 2 daerah fuzzy direlasikan dengan implikasi sederhana sebagai berikut: JIKA X adalah A MAKA Y adalah B

transfer fungsi:

(30)

Maka sistem fuzzy dapat berjalan tanpa harus melalui komposisi dan dekomposisi

fuzzy. Nilai output dapat diestimasi secara langsung dari nilai keanggotaan yang berhubungan dengan antesedennya (Sri Kusumadewi, 2002). Ada dua fungsi implikasi yang dapat digunakan, yaitu :

1. Min (minimum), fungsi ini akan memtong output himpunan fuzzy. 2. Dot (product), fungsi ini akan menskala output himpunan fuzzy.

2.1.9 Metode Penegasan (Defuzzifikasi)

Defuzzifikasi atau penegasan merupakan metode untuk memetakan nilai dari himpunan samar ke dalam nilai crisp. Input dari proses defuzifikasi adalah suatu himpunan fuzzy yang diperoleh dari komposisi aturan-aturan fuzzy, sedangkan

output yang dihasilkan merupakan suatu bilangan pada domain himpunan fuzzy

dalam range tertentu. Masukan proses defuzzifikasi adalah himpunan samar.

Terdapat beberapa metode defuzzifikasi (Kusumadewi, 2002) antara lain : 1. Metode Centroid (Composite Moment)

Pada metode ini, penyelesaian crisp diperoleh dengan cara mengambil titik pusat (z*) daerah samar.

Secara umum untuk semesta kontinu dirumuskan dalam persamaan :

z∗ =

(untuk variabel kontinu) (2.4)

z∗ =

(untuk variabel diskrit) (2.5)

2. Metode Bisector

(31)

3. Metode Mean of Maximum (MOM)

Pada metode ini, penyelesaian crisp diperoleh dengan cara mengambil nilai rata- rata domain samar yang memiliki nilai maksimum.

4. Metode Largest of Maximum (LOM)

Pada metode ini, penyelesaian crisp diperoleh dengan cara mengambil nilai terbesar pada domain samar yang memiliki nilai maksimum.

5. Metode Smallest of Maximum (SOM)

Pada metode ini, penyelesaian crisp diperoleh dengan cara mengambil nilai terkecil pada domain samar yang memiliki nilai maksimum.

2.1.10 Sistem Inferensi Fuzzy

Inferensi adalah proses penggabungan banyak aturan berdasarkan data yang tersedia. Terdapat beberapa model Sistem Inferensi Samar (Setiadji, 2009), antara

lain :

1. Model Fuzzy Mamdani 2. Model Fuzzy Sugeno (TSK) 3. Model Fuzzy Tsukamoto

Perbedaan antara ketiga sistem inferensi samar terdapat pada konsekuen dari aturan samar, agregasi dan prosedur defuzzifikasi.

2.1.11 Sistem Inferensi Fuzzy Mamdani

(32)

1. Pembentukan himpunan fuzzy.

Pada Metode Mamdani, baik variabel input maupun variabel output dibagi menjadi satu atau lebih himpunan fuzzy.

2. Aplikasi fungsi implikasi.

Pada Metode Mamdani, fungsi implikasi yang digunakan adalah Min. Secara umum, bentuk model metode fuzzy-Mamdani adalah :

JIKA a1 adalah A1DAN … DAN an adalah An MAKA b is B

dimana A1 … An dan B adalah variabel linguistik, dengan a1… an dan b adalah

skalar. Proposisi yang mengikuti JIKA disebut sebagai antecedent (yang mendahului), sedangkan proposisi yang mengikuti MAKA disebut sebagai konsekuen.

3 Komposisi Aturan.

Apabila sistem terdiri dari beberapa aturan, maka inferensi diperoleh dari kumpulan dan kolerasi antar aturan. Ada 3 metode yang digunakan dalam melakukan inferensi sistem Ada 3 metode yang digunakan dalam melakukan

inferensi sistem fuzzy yaitu: a. Metode Max (Maximum)

Pada metode ini, solusi himpunan fuzzy diperoleh dengan cara mengambil nilai maksimum aturan, kemudian menggunakannya untuk memodifikasi daerah fuzzy, dan mengaplikasikannya ke output dengan menggunakan operator OR (union). Jika semua proposisi telah dievaluasi, maka output akan berisi suatu himpunan fuzzy yang merefleksikan konstribusi dari tiap-tiap proposisi. Secara umum dapat dituliskan:

µsf[Xi] = max(µsf[Xi], µkf [Xi]) (2.6)

dengan:

µsf [Xi] = nilai keanggotaan solusi fuzzy sampai aturan ke-i

µkf [Xi] = nilai keanggotaan konsekuen fuzzy aturan ke-i

b. Metode Additive

Pada metode ini,solusi himpunan fuzzy diperoleh dengan cara melakukan penjumlahan terhadap semua output daerah fuzzy.Secara umum dituliskan:

(33)

dengan:

µsf [Xi] = nilai keanggotaan solusi fuzzy sampai aturan ke-i

µkf [Xi] = nilai keanggotaan konsekuen fuzzy aturan ke-i

c. Metode Probabilistik OR (probor)

Pada metode ini, solusi himpunan fuzzy diperoleh dengan cara melakukan

product terhadap semua output daerah fuzzy. Secara umum dituliskan: µsf [Xi] = ( µsf [Xi]+ µkf [Xi]) - (µsf[Xi] * µkf[Xi])

(2.8) dengan:

µsf[Xi] = nilai keanggotaan solusi fuzzy sampai aturan ke-i

µkf[Xi] = nilai keanggotaan konsekuen fuzzy aturan ke-i

4. Penegasan (defuzzifikasi)

Pada metode mamdani ini akan digunakan metode Centroid (Composite Moment) seperti yang telah dijelaskan sebelumnya.

2.2 Analisis Regresi Linear Berganda

2.2.1 Pengertian Regresi

(34)

Galton disebut dengan “regression to mediocrity”. Dari uraian tersebut dapat disimpulkan bahwa pada umumnya tinggi anak mengikuti tinggi orangtuanya (Sudjana, 1996).

Istilah “ regresi” pada mulanya bertujuan nutuk membuat perkiraan nilai satu variabel (tinggi badan anak) terhadap satu variabel yang lain (tinggi badan orang tua). Pada perkembangan selanjutnya analisis regresi dapat digunakan sebagai alat untuk membuat perkiraan nilai suatu variabel dengan menggunakan beberapa variabel lain yang berhubungan dengan variabel tersebut (Algafari, 2000).

Jadi prinsip dasar yang harus dipenuhi dalam membangun suatu persamaan regresi adalah bahwa antara suatu variabel tidak bebas (dependent variable) dengan variabel-variabel bebas (independent variable) lainnya memiliki sifat hubungan sebab akibat (hubungan kausalitas), baik didasarkan pada teori,

hasil penelitian sebelumnya, maupun yang didasarkan pada penjelasan logis tertentu (Algafari, 2000).

2.2.2 Analisis Regresi Linear

Perubahan nilai suatu variabel tidak selalu terjadi dengan sendirinya, namun perubahan nilai variabel itu dapat disebabkan oleh berubahnya variabel lain yang berhubungan dengan variabel tersebut. Untuk mengetahui pola perubahan nilai suatu variabel yang disebabkan oleh variabel lain diperlukan alat analisis yang memungkinkan untuk membuat perkiraan (prediction) nilai variabel tersebut pada nilai tertentu variabel yang mempengaruhinya (Algafari, 2000).

(35)

Analisis regresi merupakan teknik yang digunakan dalam persamaan matematik yang menyatakan hubungan fungsional antara variabel-variabel. Analisis regresi linier atau regresi garis lurus digunakan untuk:

1. Menentukan hubungan fungsional antar variabel dependen dengan independen. Hubungan fungsional ini dapat disebut sebagai persamaan garis regresi yang berbentuk linier.

2. Meramalkan atau menduga nilai dari satu variabel dalam hubungannya dengan variabel yang lain yang diketahui melalui persamaan garis regresinya.

Analisis regresi tediri dari dua bentuk yaitu : 1. Analisis Regresi Linear Sederhana 2. Analisis Regresi Linear Berganda

Analisis regresi sederhana adalah bentuk regresi dengan model yang bertujuan untuk mempelajari hubungan antara dua variabel, yakni variabel

dependent (terikat) dan variabel independent (bebas). Sedangkan analisis regresi berganda adalah bentuk regresi dengan model yang memiliki hubungan antara satu variabel dependent dengan dua atau lebih variabel independent (Sudjana, 1996).

Variabel independent adalah variabel yang nilainya tidak tergantung dengan variabel lainnya, sedangkan variabel dependent adalah variabel yang nilainya tergantung dari variabel yang lainnya (Algafari, 2000).

Analisis regresi linear dipergunakan untuk menelaah hubungan antara dua variabel atau lebih, terutama untuk menelusuri pola hubungan yang modelnya belum diketahui dengan baik, atau untuk mengetahui bagaimana variasi dari beberapa variabel independen mempengaruhi variabel dependen dalam suatu

fenomena yang komplek. Jika X₁, X₂, ..., Xk adalah variabel-variabel

(36)

(Sujana, 1996). Jika dibuat secara matematis hubungan itu dapat dijabarkan sebagai berikut:

Dimana : Y = f (X₁, X₂, ..., X_k, e) (2.9)

Y adalah variabel dependen (tak bebas) X adalah variabel independen (bebas)

e adalah variabel residu (disturbace term)

2.2.3 Analisis Regresi Linier Sederhana

Regresi linier sederhana digunakan untuk memperkirakan hubungan antara dua variabel di mana hanya terdapat satu variabel/peubah bebas X dan satu peubah tak bebas Y (Drapper & Smith, 1992). Dalam bentuk persamaan, model regresi sederhana adalah :

Yi = β0 + β1Xi + εi (2.10)

dimana : Yi = variabel terikat/tak bebas (dependent)

Xi = variabel bebas (independent)

�0 = jarak titik pangkal dengan titik potong garis regresi pada

sumbu Y (intercept)

�1 = kemiringan (slope) garis regresi

�i = kesalahan (error)

Parameter _�0 dan �1 diduga dengan menggunakan garis regresi. Bentuk

persamaan garis regresi adalah sebagai berikut :

Y

�i = b0 + b1Xi + ei (2.11)

dimana : Y� merupakan penduga titik bagi Yi

b0merupakan penduga titik bagi �0

b1 merupakan penduga titik bagi �1

Pendugaan dilakukan dengan mengambil contoh acak berukuran n dari suatu populasi. Hasil pengamatan berupa pasangan X dan Y sebagai berikut :

(X1,Y1), (X2,Y2), …, (Xk,Yk)

(37)

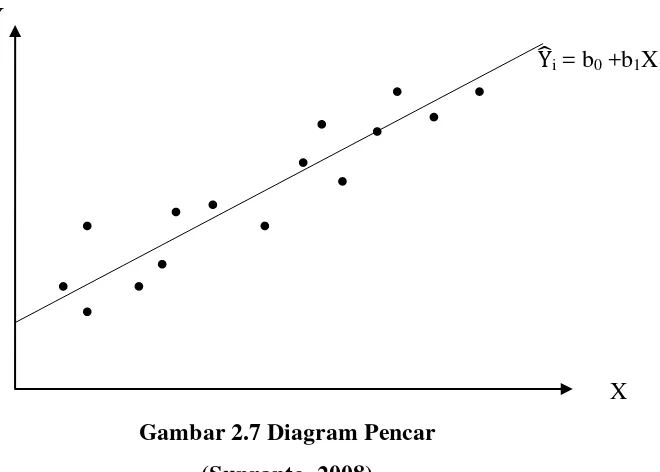
Y

�i = b0 +b1Xi

X

Gambar 2.7 Diagram Pencar (Supranto, 2008)

Dengan demikian diperoleh persamaan regresi linear sederhana sebagai berikut : Yi = b0 + b1Xi + ei (2.12)

Y Yi

Y�_ı = b0 +b1Xi

ei

Y�_ı

b0

X

Gambar 2.8 Diagram Pencar, Garis Regresi dan Sisa (Supranto, 2008)

Pada umumnya Yi tidak sama dengan Y�i,. Perbedaan antara dan dinyatakan

dengan yang disebut dengan sisa (residual). Dalam hal ini:

(38)

Nilai b0dan b1 diperoleh dengan menggunakan metode kuadrat terkecil (least

squares method) (Drapper & Smith). Metode kuadrat terkecil merupakan satu cara

untuk memperoleh b0 dan b1 sebagai perkiraan β0 dan β1, dengan meminimumkan

jumlah kuadrat sisa sebagai berikut:

S = �e2

Agar diperoleh nilai paling minimum maka dilakukan pendiferensialan terhadap b0 kemudian disamakan dengan nol, sebagai berikut :

∂S

demikian juga halnya dengan b1, maka :

(39)

Apabila bentuk persamaan (2.15) dan (2.16) disederhanakan maka nilai koefisien b0 dan b1 dapat diperoleh dengan rumus berikut yaitu :

b₀ =(∑ Yi

n

i=1 )(∑ni=1Xi2)−(∑ni=1Xi)(∑ni=1XiYi)

n∑n_i=1X_i2 −(∑n_i=1X_i)2 (2.17)

�1 = �(∑ ��

�=1 )−(∑��=1��)(∑��=1��)

�(∑�_�=1�2)−(∑�_�=1�_�)2 (2.18)

Untuk menentukan hubungan pengaruh perubahan variabel yang satu terhadap variabel yang lainnya, maka dibutuhkan peranan garis regresi. Selanjutnya, dari hubungan dua variabel ini dapat dikembangkan untuk permasalahan regresi berganda.

2.2.4 Analisis Regresi Linier Berganda

Untuk memperkirakan nilai variabel tak bebas Y, akan lebih baik apabila kita ikut memperhitungkan variabel-variabel bebas lain yang ikut mempengaruhi nilai Y. dengan demikian dimiliki hubungan antara satu variabel tidak bebas Y dengan

beberapa variabel lain yang bebas X₁, X₂, X₃, ..., Xn. Untuk itulah digunakan

regresi linear berganda. Dalam pembahasan mengenai regresi sederhana, simbol yang digunakan untuk variabel bebasnya adalah X. Dalam regresi berganda, persamaan regresinya memiliki lebih dari satu variabel bebas maka perlu

menambah tanda bilangan pada setiap variabel tersebut, dalam hal ini X1, X2,

..., Xn (Sudjana, 1996).

Secara umum persamaan regresi berganda dapat ditulis sebagai berikut :

Yi = β0 +β1 X1i+ β2X2i + . . . + βnXni + εi (2.19)

(Untuk populasi)

Yi = b0 +b1 X1i+ b2X2i + . . . + bnXni + εi (2.20)

(Untuk sampel) dimana : i = 1, 2, . . , n

(40)

Dalam penelitian ini, digunakan empat variabel yang terdiri dari satu

variabel bebas Y dan tiga variabel X yaitu X1, X2dan X3. Maka persamaan

regresi bergandanya adalah :

Yi = b0 + b1X1i + b2X2i + b3X3i + ei (2.21)

Sebagaimana halnya persamaan regresi linear sederhana yang sebelumnya, dengan menggunakan metode kuadrat terkecil, dapat ditentukan nilai b0, b1, b2, ...,

bn dengan terlebih dahulu meminimumkan kuadrat sisanya, maka:

S = �e2

Untuk penelitian ini yang menggunakan tiga variabel bebas X1, X2 dan X3 maka menentukan nilai b0, b1, b2 dab b3 yaitu:

S = �e2

(41)

(42)

Dengan demikian diperolehlah empat buah persamaan untuk menentukan nilai b0,

Kesalahan (error) didefenisikan sebagai selisih antara nilai sebenarnya dengan nilai hasil pengukuran, atau :

Kesalahan = |nilai sebenarnya−nilai pengukuran|

Secara simbolik dinyatakan dengan :

et = |x_s−x_a| (2.29)

dengan : et merupakan kesalahan pengukuran

xs nilai sebenarnya (true value)

xa nilai pengukuran atau nilai pendekatan (aproksimasi)

Kesalahan relatif (relatif error) adalah ukuran kesalahan dalam kaitannya dengan pengukuran. Kesalahan relatif didefenisikan sebagai kesalahan yang dibagi dengan nilai sebenarnya atau secara simbolik dinyatakan dengan :

(43)

Kesalahan relatif juga dapat dilihat besar persentasenya dengan mengalikan dengan 100% (matematikanet.blogspot.com/2009/01/kesalahan.html?m=1).

Untuk melihat rata-rata kesalahan relatif yang terjadi pada suatu data, maka dapat diperoleh dengan membagikan kesalahan relatif yang didapatkan dengan jumlah data yang ada. Secara simbolik dinyatakan dengan :

Rata−rata kesalahan relatif = jumlahkesalahanrelatif

jumlahdata =

er

n (2.31)

2.4 Variabel

Variabel adalah konsep yang mempunyai bermacam-macam nilai. Dengan demikian, variabel adalah objek yang berbentuk apa saja yang ditentukan dengan tujuan untuk memperoleh informasi agar bisa ditarik suatu kesimpulan. Secara teori, defenisi variabel penelitian adalah merupakan suatu objek, atau sifat atau atribut atau nilai dari orang, atau kegiatan yang mempunyai bermacam-macam variasi antara satu dengan lainnya yang ditetapkan dengan tujuan untuk dipelajari

dan ditarik kesimpula

Dalam penelitian ini data tentang variabel-variabel yang digunakan diperoleh dari PT. Perkebunan Nusantara III, Medan. Pertimbangan pemilihan perusahaan adalah karena perusahaan ini telah lama memproduksi kelapa sawit

hingga saat ini. Sebagai sebuah perusahaan perkebunan PT. Perkebunan III selalu berusaha untuk meningkatkan produksi kelapa sawit dengan memperhatikan faktor-faktor yang dapat mempengaruhi pertambahannya. Adapun variabel yang digunakan antara lain :

1. Pemupukan.

(44)

pemeliharaan tanaman untuk mendapatkan pertumbuhan tanaman yang optimal, pada akhirnya memberikan produktivitas yang sesuai pada potensinya. Pemupukan pada dasarnya ditujukan untuk meningkatkan produksi, karena pupuk dianggap vitamin bagi tanah sehingga akan mempengaruhi hasil yang diperoleh. Penggunaan pupuk secara tepat dan teratur akan dapat mempertinggi hasil produksi baik secara kualitas maupun kuantitasnya. Adapun pupuk yang digunakan untuk pertumbuhan kelapa sawit antara lain: NPK (Urea, ZA, SP-36, Rock Phosphate, MOP(KCl)) dan Mg (KIeserit, Dolomite) (Dinas Perkebunan Sumatera Utara, 2011).

2. Tenaga Kerja.

Faktor tenaga kerja memiliki peranan yang sangat penting sebagai pelaksana kegiatan produksi. Peranannya sangat ditentukan terutama oleh kualitas (mutu) disamping kuantitas (jumlah) yang tersedia. Dalam hal ini, yang dikatakan tenaga kerja yaitu mereka yang langsung berfungsi dan ikut serta langsung dalam proses produksi kelapa sawit atau yang biasa disebut karyawan

kebun.

3. Curah Hujan.

Tanaman kelapa sawit dapat tumbuh dengan baik pada suhu udara 270_{C dengan}

suhu maksimum 330_{C dan suhu minimum 22}0_{C sepanjang tahun. Curah hujan}

rata-rata tahunan yang memungkinkan untuk pertumbuhan kelapa sawit adalah

1250-3000 mm yang merata sepanjang tahun, dan curah hujan optimal berkisar

antara 1750-2500 mm. Kelapa sawit lebih toleran dengan curah hujan yang tinggi (misalnya>3000) dibandingkan dengan jenis tanaman lainnya, namun dalam

kriteria klasifikasi kesesuaian lahan, nilai tersebut sudah menjadi faktor pembatas

ringan. Curah hujan <1250 mm sudah merupakan faktor pembatas berat bagi

pertumbuhan kelapa sawit.

4. Hasil produksi

(45)

(46)

BAB 3

PEMBAHASAN DAN HASIL

3.1 Penyajian Data

Dalam penelitian ini, data yang dikumpulkan adalah data mengenai jumlah produksi kelapa sawit dan faktor-faktor yang mempengaruhinya, yaitu sebagai berikut :

1. Jumlah produksi kelapa sawit (ton) 2. Jumlah pemupukan (ton)

3. Jumlah tenaga kerja (orang) 4. Rata-rata curah hujan (mm)

Data yang diambil adalah data yang diperoleh dari PT. Perkebunan Nusantara III (PERSERO), yakni data per bulan tahun 2011-2012 adalah sebagai berikut :

Tabel 3.1 Data Jumlah Produksi, Jumlah Pemupukan, Jumlah Tenaga Kerja dan Rata-Rata Curah Hujan pada PT. Perkebunan Nusantara

III (PERSERO) Medan Tahun 2011-2012

(47)

No. (1) (2) (3) (4) (5) (6)

9 September 7.545 28.067 262 164.580

10 Oktober 20.601 27.991 357 166.786

11 November 32.112 27.958 272 156.176

12 Desember 35.341 27.878 246 135.720

13 2012 Januari 1.179 27.855 93 104.705

14 Februari 2.720 28.080 169 108.837

15 Maret 7.726 28.508 175 128.921

16 April 19.667 28.668 248 124.500

17 Mei 30.512 28.926 206 146.197

18 Juni 42.129 28.848 120 160.045

19 Juli 49.262 28.862 173 188.134

20 Agustus 49.581 28.383 151 160.785

21 September 10.904 28.355 253 178.643

22 Oktober 16.248 28.352 298 167.944

23 November 21.399 28.454 340 160.993

24 Desember 26.670 28.362 236 153.498

(Sumber : PT. Perkebunan (PTPN) III)

3.2 Perhitungan dengan Menggunakan Metode Fuzzy

Dalam metode fuzzy, untuk memperoleh nilai peramalan variabel dependent (Y),

diperlukan beberapa langkah. Adapun prosedur pemrogramannya adalah:

Langkah 1: Menentukan input maupun output yang akan digunakan dalam membangun logika.

Pada kasus ini, ada 4 variabel yang akan digunakan yaitu:

a. Pemupukan (X1) terdiri atas 3 himpunan fuzzy yaitu: SEDIKIT,

STANDAR, BANYAK.

b. Tenaga Kerja (X2) terdiri atas 3 himpunan fuzzy yaitu: SEDIKIT,

SEDANG, BANYAK.

c. Rata-rata Curah Hujan (X3) terdiri atas 3 himpunan fuzzy yaitu: RENDAH,

STANDAR, TINGGI.

(48)

Langkah 2: Menentukan fungsi keanggotaan variabel input X1, X2 , X3 dan output

Y.

Untuk lebih mudah menentukan fungsi keanggotaannya, maka dibuat dalam bentuk kurva terlebih dahulu yaitu :

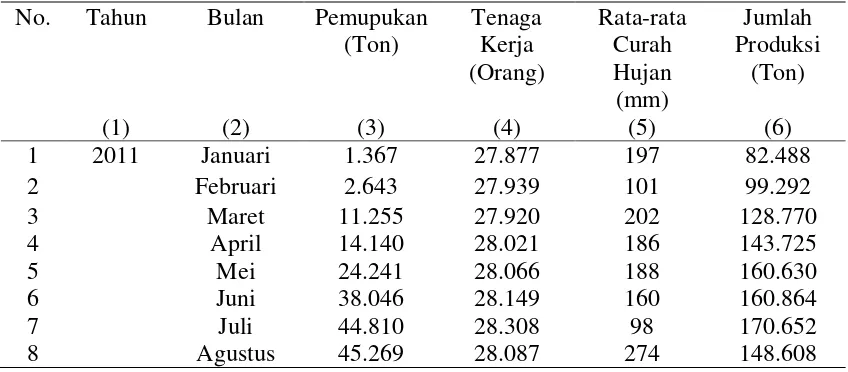
a. Untuk variabel input pemupukan (X1).

Berdasarkan nilai terbesar dan terkecilnya maka bentuk kurvanya adalah sebagai berikut :

SEDIKIT STANDAR BANYAK

1

0 1.179 13.869 20.214 25.380 30.546 36.891 49.581

Gambar 3.1 Kurva keanggotaan variabel input pemupukan (X1)

Maka untuk fungsi keanggotaannya adalah :

(49)

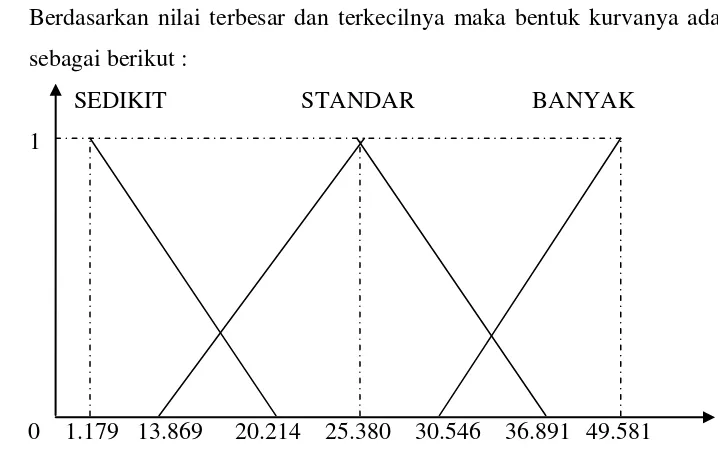
b. Untuk variabel input tenaga kerja (X2).

SEDIKIT SEDANG BANYAK

1

0 27.877 28.139,25 28.270,38 28.401,5 285.32,62 28.663,75 28926

Gambar 3.2 Kurva keanggotaan variabel input tenaga kerja (X2)

(50)

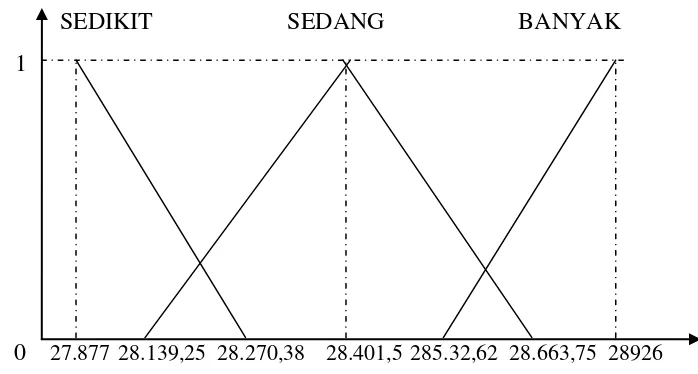
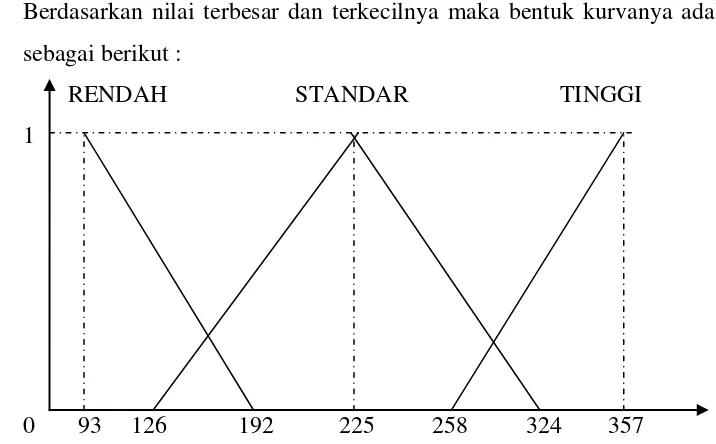
c. Untuk variabel input rata-rata curah hujan (X3).

RENDAH STANDAR TINGGI

1

0 93 126 192 225 258 324 357

Gambar 3.3 Kurva keanggotaan variabel input rata-rata curah hujan (X3)

μ_X₃_RENDAH(x_3i) =�

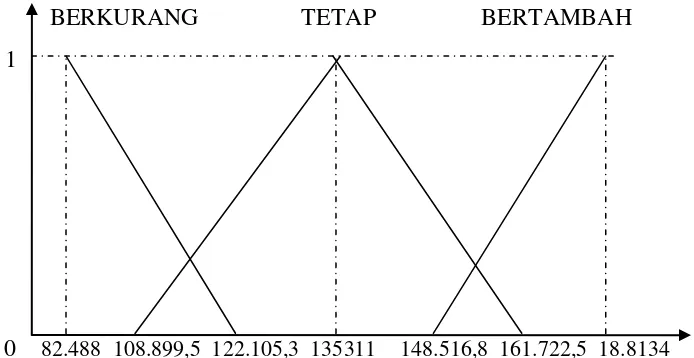
d. Untuk variabel output jumlah produksi (Y).

(51)

BERKURANG TETAP BERTAMBAH 1

0 82.488 108.899,5 122.105,3 135311 148.516,8 161.722,5 18.8134

Gambar 3.4 Kurva keanggotaan variabel output jumlah produksi (Y)

μ_Y_BERKURANG(y_i) =�

Langkah 3 : menyusun aturan fuzzy.

Dalam penelitian ini, aplikasi operator fuzzy yang diasumsikan ada 27 buah aturan

(52)

[R4] Jika X1 SEDIKIT dan X2 SEDANG dan X3 RENDAH maka Y TETAP

[R5] Jika X1 SEDIKIT dan X2 SEDANG dan X3 STANDAR maka Y TETAP

[R6] Jika X1 SEDIKIT dan X2 SEDANG dan X3 TINGGI maka Y BERTAMBAH

[R7] Jika X1 SEDIKIT dan X2 BANYAK dan X3 RENDAH maka Y BERKURANG

[R8] Jika X1 SEDIKIT dan X2 BANYAK dan X3 STANDAR maka Y BERKURANG

[R9] Jika X1 SEDIKIT dan X2 BANYAK dan X3 TINGGI maka Y TETAP

[R10] Jika X1 STANDAR dan X2 SEDIKIT dan X3 RENDAH maka Y TETAP

[R11] Jika X1 STANDAR dan X2 SEDIKIT dan X3 STANDAR maka Y BERTAMBAH

[R12] Jika X1 STANDAR dan X2 SEDIKIT dan X3 TINGGI maka Y BERTAMBAH

[R13] Jika X1 STANDAR dan X2 SEDANG dan X3 RENDAH maka Y BERKURANG [R14] Jika X1 STANDAR dan X2 SEDANG dan X3 STANDAR maka Y TETAP

[R15] Jika X1 STANDAR dan X2 SEDANG dan X3 TINGGI maka Y TETAP

[R16] Jika X1 STANDAR dan X2 BANYAK dan X3 RENDAH maka Y BERTAMBAH

[R17] Jika X1 STANDAR dan X2 BANYAK dan X3 STANDAR maka Y BERTAMBAH [R18] Jika X1 STANDAR dan X2 BANYAK dan X3 TINGGI maka Y BERTAMBAH

[R19] Jika X1 BANYAK dan X2 SEDIKIT dan X3 RENDAH maka Y BERKURANG

[R20] Jika X1 BANYAK dan X2 SEDIKIT dan X3 STANDAR maka Y TETAP

[R21] Jika X1 BANYAK dan X2 SEDIKIT dan X3 TINGGI maka Y TETAP

[R22] Jika X1 BANYAK dan X2 SEDANG dan X3 RENDAH maka Y TETAP

[R23] Jika X1 BANYAK dan X2 SEDANG dan X3 STANDAR maka Y BERTAMBAH

[R24] Jika X1 BANYAK dan X2 SEDANG dan X3 TINGGI maka Y BERTAMBAH

[R25] Jika X1 BANYAK dan X2 BANYAK dan X3 RENDAH maka Y BERKURANG

[R26] Jika X1 BANYAK dan X2 BANYAK dan X3 STANDAR maka Y TETAP

[R27] Jika X1 BANYAK dan X2 BANYAK dan X3 TINGGI maka Y BERTAMBAH

Langkah 4 : Aplikasi aturan fuzzy.

Aturan yang digunakan adalah aturan MIN pada fungsi implikasinya. Sebagai salah satu contoh pembuatan input X1, X2 dan X3 untuk menghasilkan salah satu

output Y, maka diambil salah satu nilai dari data yang tersedia. Apabila diketahui jumlah pemupukan (X1) = 1.367 ton, maka :

μ_X₁_SEDIKIT(1.367) = 20.214−1.367 20.214−1.179=

18.847

(53)

μ_X₁_BANYAK(1.367) = 0

Kemudian diketahui tenaga kerja (X2) = 27.877 orang, maka : μ_X₂_SEDIKIT(27.877) = 1

μ_X₂_STANDAR(27.877) = 0 μ_X

2BANYAK(27.877) = 0

Kemudian diketahui rata-rata curah hujan (X3) = 197 orang, maka : μ_X₂_RENDAH(197) = 0

μ_X₂_STANDAR(197) = 197−126

225−126= 71

99= 0,7172 μ_X₂_TINGGI(197) = 0

Maka untuk aplikasi aturan fuzzy adalah sebagai berikut :

[R1] Jika X1 SEDIKIT* dan X2 SEDIKIT dan X3 RENDAH maka Y BERKURANG. α1 = µ_X₁_SEDIKIT∗∗∩ μ_X

2SEDIKIT ∩ μX3RENDAH = min (μ_X

1Sedikit[1.367] ; μX2Sedikit[27.877] ; μX2Rendah[197]) = min (0,9901 ; 1 ; 0 )

= 0

*X1 SEDIKIT merupakan variabel linguistik

**μ_X₁_SEDIKIT merupakan fungsi keanggotaan dari variabel linguistik

Maka:

Y BERKURANG (y) = 122.105,3−y

122.105,3−82.488= 0

122.105,3 – y = 0

y = 122.105,3

Sehingga:

(54)

[R2] Jika X1 SEDIKIT dan X2 SEDIKIT dan X3 STANDAR maka Y BERKURANG.

122.105,3−82.488= 0,7172

(55)

[R4] Jika X1 SEDIKIT dan X2 SEDANG dan X3 RENDAH maka Y TETAP. α4 = μ_X

1SEDIKIT ∩ μX2SEDANG∩ μX3RENDAH = min (_μ_X

1SEDIKIT[1.367] ; μX2SEDANG[27.877] ; μX3STANDAR[197]) = min (0,9901 ; 1; 0,7172 )

= 0 Maka :

Y TETAP (y) = y−108.899,5

135311−108.899,5= 0

y = 108.899,5 atau

Y TETAP (y) = 161.722,5−y

161.722,5−135.311= 0

y = 161.722,5 Sehingga:

Aturan ke-4: _α4 = 0 maka tidak ada daerah implikasi.

[R5] Jika X1 SEDIKIT dan X2 SEDANG dan X3 STANDAR maka Y TETAP α5 = μ_X

1SEDIKIT ∩ μX2SEDANG∩ μX3STANDAR = min (μ_X

1SEDIKIT[1.367] ; μX2SEDANG[27.877] ; ∩ μX2STANDAR[197]) = min (0,9901 ; 0 ; 0,7172)

= 0 Maka:

Y TETAP (y) = y−108.899,5

135311−108.899,5= 0

y = 108.899,5 atau

Y TETAP (y) = 161.722,5−y

161.722,5−135.311= 0

y = 161.722,5 Sehingga:

(56)

[R6] Jika X1 SEDIKIT dan X2 SEDANG dan X3 TINGGI maka Y BERTAMBAH. α6 = μ_X

1SEDIKIT ∩ μX2SEDANG∩ μX3TINGGI = min (_μ_X

1SEDIKIT[1.367] ; μX2SEDANG[27.877] ; μX3TINGGI[197] ) = min (0,9901 ; 0 ; 0)

= 0 Maka:

Y BERTAMBAH (y) = y−148.516,8

188.134−148.516,8= 0

y = 148.516,8 Sehingga:

Aturan ke-6: α6 = 0 maka tidak ada daerah implikasi.

[R7] Jika X1 SEDIKIT dan X2 BANYAK dan X3 RENDAH maka Y BERKURANG. α7 = μ_X

1SEDIKIT ∩ μX2BANYAK∩ μX3RENDAH

= min (μ_X

1SEDIKIT[1.367] ; μX2BANYAK[27.877] ; μX3RENDAH [197])

= min (0,9901 ; 0 ; 0) = 0

Maka:

122.105,3−82.488= 0 122.105,3 – y = 0

y = 122.105,3 Sehingga:

[R8] Jika X1 SEDIKIT dan X2 BANYAK dan X3 STANDAR maka Y BERKURANG. α8 = μ_X

1SEDIKIT ∩ μX₂BANYAK∩ μX₃STANDAR

= min (μ_X

1SEDIKIT[1.367] ; μX₂BANYAK[27.877] ; μX₃STANDAR[197])

(57)

Maka:

122.105,3−82.488= 0

122.105,3 – y = 0

y = 122.105,3 Sehingga:

[R9] Jika X1 SEDIKIT dan X2BANYAK dan X3 TINGGI maka Y TETAP.

�9 = μ_X

1SEDIKIT ∩ μX2BANYAK∩ μX3TINGGI = min (μ_X

1STANDAR[1.367] ; μX2SEDANG[27.877] ;μX3STANDAR[197]) = min (0,9901 ; 0 ; 0)

= 0 Maka:

Y TETAP (y) = y−108.899,5

135311−108.899,5= 0

y = 108.899,5 atau

Y TETAP (y) = 161.722,5−y

161.722,5−135.311= 0

y = 161.722,5 Sehingga:

[R10] Jika X1 STANDAR dan X2 SEDIKIT dan X3 RENDAH maka Y TETAP.

α10 = _µX₁_STANDAR_∩ _µX₂_SEDIKIT_∩ _µX₃_RENDAH = min (_μ_X

1STANDAR[1.367] ; μX2SEDIKIT[27.877] ;μX3RENDAH[197]) = min (0 ; 1; 0)

= 0 Maka:

Y TETAP (y) = y−108.899,5

135311−108.899,5= 0

(58)

atau

Y TETAP (y) = 161.722,5−y

161.722,5−135.311= 0

y = 161.722,5 Sehingga:

[R11] Jika X1 STANDAR dan X2SEDIKIT dan X3 STANDAR maka Y BERTAMBAH.

α11 = _µX₁_STANDAR_∩ _µX₂_SEDIKIT_∩ _µX₃_STANDAR = min (_μ_X

1STANDAR[1.367] ; μX2SEDIKIT[27.877] ;μX3STANDAR[197]) = min (0 ; 1 ; 0,7172)

= 0 Maka:

188.134−148.516,8= 0

y = 148.516,8 Sehingga:

[R12] Jika X1 STANDAR dan X2 SEDIKIT dan X3 TINGGI maka Y BERTAMBAH. α12 = μ_X

1STANDAR ∩ μX2SEDIKIT∩ μX3TINGGI = min (μ_X

1STANDAR[1.367] ; μX2SEDIKIT[27.877] ; μX3TINGGI [197]) = min (0 ; 1 ; 0)

= 0

Maka:

188.134−148.516,8= 0

y = 148.516,8

Sehingga:

(59)

[R13] Jika X1 STANDAR dan X2 SEDANG dan X3 RENDAH maka Y BERKURANG. α13 = μ_X

1STANDAR ∩ μX2SEDANG∩ μX3RENDAH = min (μ_X

1BANYAK[1.367] ; μX2SEDANG[27.877] ; μX3RENDAH [197]) = min (0 ; 0 ; 0)

= 0 Maka:

122.105,3−82.488= 0

122.105,3 – y = 0

y = 122.105,3 Sehingga:

[R14] Jika X1 STANDAR dan X2SEDANG dan X3 STANDAR maka Y TETAP. α14 = μ_X

1STANDAR ∩ μX2SEDANG∩ μX3STANDAR = min (μ_X

1STANDAR[1.367] ; μX2SEDANG[27.877] ; μX3STANDAR [197]) = min (0 ; 0 ; 0,7172)

= 0 Maka:

Y TETAP (y) = y−108.899,5

135311−108.899,5= 0

y = 108.899,5 atau

Y TETAP (y) = 161.722,5−y

161.722,5−135.311= 0

y = 161.722,5 Sehingga:

[R15] Jika X1STANDAR dan X2 SEDANG dan X3 TINGGI maka Y TETAP. α15 = μ_X

1STANDAR ∩ μX2SEDANG∩ μX3TINGGI = min (μ_X

(60)

= min (0 ; 0 ; 0) = 0

Maka:

Y TETAP (y) = y−108.899,5

135311−108.899,5= 0

y = 108.899,5 atau

Y TETAP (y) = 161.722,5−y

161.722,5−135.311= 0

y = 161.722,5 Sehingga:

[R16] Jika X1 STANDAR dan X2 BANYAK dan X3 RENDAH maka Y BERTAMBAH α16 = μ_X

1STANDAR ∩ μX2BANYAK∩ μX3RENDAH = min (μ_X

1STANDAR[1.367] ; μX2BANYAK[27.877] ; μX3RENDAH [197]) = min (0 ;0 ; 0)

= 0 Maka:

188.134−148.516,8= 0

y = 148.516,8 Sehingga:

[R17] Jika X1 STANDAR dan X2 BANYAK dan X3 STANDAR maka Y BERTAMBAH. α17 = μ_X

1STANDAR ∩ μX2BANYAK∩ μX3STANDAR = min (μ_X

1STANDAR[1.367] ; μX2BANYAK[27.877] ; μX3STANDAR [197])

(61)

Maka :

188.134−148.516,8= 0

y = 148.516,8 Sehingga:

[R18] Jika X1 STANDAR dan X2 BANYAK dan X3 TINGGI maka Y BERTAMBAH. α18 = μ_X

1STANDAR ∩ μX2BANYAK∩ μX3TINGGI = min (μ_X

1STANDAR[1.367] ; μX2BANYAK[27.877] ∩ μX3TINGGI [197])

= (0 ;0 ; 0,7172)

= 0

Maka:

188.134−148.516,8= 0

y = 148.516,8 Sehingga:

[R19] Jika X1 BANYAK dan X2 SEDIKIT dan X3 RENDAH maka Y BERKURANG. α19 = μ_X

1BANYAK ∩ μX2SEDIKIT∩ μX3RENDAH = min (_μ_X

1BANYAK[1.367] ; μX2SEDIKIT[27.877] ∩ μX3RENDAH [197])

= (0 ;1 ; 0)

= 0

Maka:

122.105,3−82.488= 0

122.105,3 – y = 0

y = 122.105,3

Sehingga:

(62)

[R20] Jika X1 BANYAK dan X2 SEDIKIT dan X3 STANDAR maka Y TETAP. α20 = μ_X

1BANYAK ∩ μX2SEDIKIT∩ μX3STANDAR = min (_μ_X

1BANYAK[1.367] ; μX2SEDIKIT[27.877] ∩ μX3STANDAR [197])

= (0 ;1 ;0,7172)

= 0

Maka:

Y TETAP (y) = y−108.899,5

135311−108.899,5= 0

y = 108.899,5 atau

Y TETAP (y) = 161.722,5−y

161.722,5−135.311= 0

y = 161.722,5

Sehingga:

[R21] Jika X1 BANYAK dan X2 SEDIKIT dan X3 TINGGI maka Y TETAP. α21 = μ_X

1BANYAK ∩ μX2SEDIKIT∩ μX3TINGGI = min (μ_X

1BANYAK[1.367] ; μX2SEDIKIT[27.877] ∩ μX3TINGGI [197])

= (0 ;1 ;0) = 0

Maka:

Y TETAP (y) = y−108.899,5

135311−108.899,5= 0

y = 108.899,5 atau

Y TETAP (y) = 161.722,5−y

161.722,5−135.311= 0

y = 161.722,5 Sehingga:

(63)

[R22] Jika X1BANYAK dan X2 SEDANG dan X3 RENDAH maka Y TETAP. α22 = μ_X

1BANYAK ∩ μX2SEDANG∩ μX3RENDAH = min (_μ_X

1BANYAK[1.367] ; μX2SEDANG[27.877] ∩ μX3RENDAH [197])

= (0 ;0 ;0)

= 0

Maka :

Y TETAP (y) = y−108.899,5

135311−108.899,5= 0

y = 108.899,5 atau

Y TETAP (y) = 161.722,5−y

161.722,5−135.311= 0

y = 161.722,5 Sehingga:

[R23] Jika X1 BANYAK dan X2 SEDANG dan X3 STANDAR maka Y BERTAMBAH. α23 = μ_X

1BANYAK ∩ μX2SEDANG∩ μX3STANDAR = min (μ_X

1BANYAK[1.367] ; μX2SEDANG[27.877] ∩ μX3STANDAR [197])

= (0 ;0 ;0)

= 0

Maka:

188.134−148.516,8= 0

y = 148.516,8 Sehingga:

[R24] Jika X1 BANYAK dan X2 SEDANG dan X3 TINGGI maka Y BERTAMBAH. α24 = μ_X

1BANYAK ∩ μX2SEDANG∩ μX3TINGGI = min (μ_X

1BANYAK[1.367] ; μX2SEDANG[27.877] ∩ μX3TINGGI [197])

= (0 ;0 ;0)

(64)

Maka:

188.134−148.516,8= 0

y = 148.516,8 Sehingga:

[R25] Jika X1 BANYAK dan X2 BANYAK dan X3 RENDAH maka Y

BERKURANG

α25 = μ_X

1BANYAK ∩ μX2BANYAK∩ μX3RENDAH = min (μ_X

1BANYAK[1.367] ; μX2BANYAK[27.877] ∩ μX3RENDAH [197])

= (0 ;1 ; 0)

= 0

Maka:

122.105,3−82.488= 0

122.105,3 – y = 0

y = 122.105,3 Sehingga :

Aturan ke-25 : α25 = 0 maka tidak ada daerah implikasi.

[R26] Jika X1BANYAK dan X2BANYAK dan X3STANDAR maka Y TETAP. α26 = μ_X

1BANYAK ∩ μX2BANYAK∩ μX3STANDAR = min (μ_X

1BANYAK[1.367] ; μX2BANYAK[27.877] ∩ μX3STANDAR [197])

= (0 ; 0; 0,7172)

= 0

Maka:

Y TETAP (y) = y−108.899,5

135311−108.899,5= 0

y = 108.899,5 atau

Y TETAP (y) = 161.722,5−y

161.722,5−135.311= 0

(65)

Sehingga:

Langkah 5: Defuzzifikasi pada komposisi aturan Mamdani, yang dalam hal ini menggunakan Metode Centroid. Aturan yang memiliki daerah hasil implikasi adalah aturan ke-2 yakni pada saat Y berkurang yaitu :

μ_Y_BERKURANG(y)

Kemudian dilakukan defuzzifikasi dengan menggunakan metode Centroid

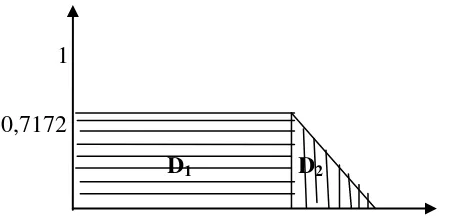
dengan domain kontinu. Untuk menentukan nilai crisp Y, dilakukan dengan membagi satu daerahmenjadi dua bagian D1 dan D2 dengan luas masing-masing

(66)

Kurva luas daerahnya adalah sebagai berikut :

1

0,7172

D1 D2

Gambar 3.5 Kurva solusi daerah fuzzy

Maka untuk rumus Metode Centroid pada persamaan (2.5) yaitu :

z∗ =

Berdasarkan gambar 3.5 yang merupakan gabungan dari dua daerah inferensi, sehingga untuk mempermudah penghitungan maka rumus tersebut menjadi :

z∗ =

Nilai dari M adalah sebagai berikut :

M₁ = � (0,7172) y dy

= (7.850.347.109,0879)−(6.692.093.886,8363)

(67)

Untuk luas setiap daerah adalah :

A1 = (93.691,77) (0,7172) = 67.195,7374

A₁ =(122.105,3−93.691,77) . (0,7172) 2

=(28.413,53) . (0,7172)

2 = 10.189,0919

Maka diperoleh peramalan jumlah produksi untuk bulan Januari =

Y =3.147.843.788,7918 + 1.158.253.222,2517

67.195,7374 + 10.189,0919 = 97.612,025 ton

Demikian seterusnya untuk setiap nilai input X1, X2 dan X3 output Y.

Dengan menggunakan bantuan software Matlab maka akan didapatkan nilai peramalan Y yang disajikan dalam tabel 3.4 berikutnya. Berikut salah satu hasil peramalan Y dengan menggunakan bantuan software Matlab :

(68)

3.3 Perhitungan dengan Menggunakan Regresi Linear Berganda

Pada regresi linear berganda, peramalan nilai variabel dependent (Y) akan ditentukan dengan sebelumnya membentuk sebuah persamaan linear dengan bentuk umum yaitu :

Yi = b0 + b1X1i + b2X2i + b3X3i+ ei

Untuk membentuk persamaan tersebut, maka digunakan metode kuadrat terkecil (last square method) seperti pada pada persamaan (2.24) yaitu :

�Y_i = nb₀+ b₁�X_1i