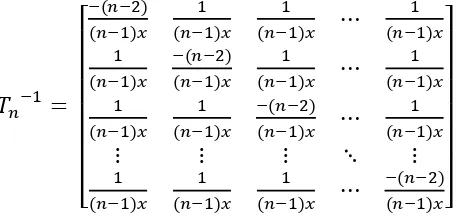Invers Suatu Matriks Toeplitz Menggunakan Metode Adjoin Matriks

(1)

INVERS SUATU MATRIKS TOEPLITZ MENGGUNAKAN METODE ADJOIN MATRIKS

SKRIPSI

BAKTI SIREGAR 090803067

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

(2)

INVERS SUATU MATRIKS TOEPLITZ MENGGUNAKAN METODE ADJOIN MATRIKS

SKRIPSI

Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains

BAKTI SIREGAR 090803067

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

(3)

PERSETUJUAN

Judul : Invers Suatu Matriks Toeplitz Menggunakan Metode Adjoin

Kategori : Skripsi

Nama : Bakti Siregar

Nomor Induk Mahasiswa : 090803067

Program Studi : Sarjana (S1) Matematika

Departemen : Matematika

Fakultas : Matematika dan Ilmu Pengetahuan Alam Universitas Sumatara Utara

:

Diluluskan di Medan, Agustus 2013

Komisi Pembimbing:

Pembimbing 2, Pembimbing 1,

Drs.Sawaluddin, M.IT Prof. Dr. Tulus, M.Si. Ph.D

NIP. 19591231199802 1001 NIP. 196209011988031002

Diketahui / disetujui oleh

Departemen Matematika FMIPA USU

Prof. Dr. Tulus, M.Si. Ph.D

(4)

PERNYATAAN

DETERMINAN DAN INVERS SUATU MATRIKS TOEPLITZ

SKRIPSI

Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.

Medan, Agustus 2013

(5)

PENGHARGAAN

Segala Puji dan syukur kehadirat Allah Yang Maha Kuasa, oleh karena berkat kasih karunia-Nya penulis dapat menyelesaikan skripsi ini dengan sebaik-baiknya

yang berjul “Invers Suatu Matriks Toeplitz Menggunakan Metode Adjoin ” sebagai syarat untuk dapat mencapai gelar Sarjana Sains.

Dengan hormat, saya mengucapkan trima kasih yang sebesar-besarnya kepada Bapak Prof. Dr. Tulus, M.Si selaku pembimbing I dan Bapak Drs. Sawaluddin, M.IT selaku pembimbing II saya yang telah membimbing dan mengarahkan serta kebaikannya untuk meluangkan waktu, tenaga, pikiran dan bantuannya sehingga skripsi saya ini dapat selesai tepat waktu. Saya juga mengucapkan terima kasih kepada:

1. _{Bapak Drs. Pasukat Sembiring, M.si dan Ibu Dra. Mardiningsih, M.Si}

selaku dosen penguji yang telah memberikan masukan dalam penyelesaian skripsi ini.

2. _{Bapak Prof. Dr. Saib Suwilo, Prof. Dr. Iryanto, M.Si, dan Ibu Dra. Esther}

Nababan, M.Si dan Bapak Drs. Ujian Sinulingga, M.si sebagai dosen yang banyak memberi inspirasi dan motivasi dalam proses belajar mengajar di kampus.

3. _{Seluruh Staf Pengajar dan Pegawai Departemen Matematika, Fakultas}

Matematika dan Ilmu Pengetahuan Alam, Universitas Sumatera Utara

4. _{Kepada Ayahanda dan Ibunda saya tercinta serta adik-adik atas dukungan}

moral, doa dan materil yang telah diberikan.

5. _{Seluruh teman-teman di Departemen Matematika khususnya stambuk}

2009 yaitu: Lukas, Siti Sahara, Elisabet, Panca, Rolan Ganda, Doni, Bernat, Budi, Jefri Sihombing, Rianto, Kristian, Valentine, dan semua teman-teman yang tidak dapat disebutkan satu persatu.

Semoga segala bentuk bantuan yang telah diberikan mendapat balasan yang jauh lebih baik dari yang Maha Kuasa.

Sebagai seorang mahsiswa yang menyadari bahwa masih banyak terdapat kekurangan dalam mneyelesaikan skripsi ini. Oleh karena itu kritik dan saran yang membangun sangat diharapkan demi perbaikan tulisan ini. Akhir kata penulis mengucapkan banyak terima kasih.

Medan, Agustus 2013

Penulis

(6)

INVERS SUATU MATRIKS TOEPLITZ MENGGUNAKAN METODE ADJOIN MATRIKS

ABSTRAK

Pencarian invers matriks adalah suatu hal yang biasa dilakukan dalam bidang matematika dan ilmu hitung secara umum. Pada penelitian ini akan dibahas invers suatu matriks toeplitz dengan diagonal nol dan selainnya . Untuk memperoleh invers matriks toeplitz dilakukan dengan mengamati pola rekrusip dari determinan matriks toeplitz berorde hingga dengan

menggunakan metode operasi baris elementer sehingga diperoleh | |

_{dan menentukan invers matriks toeplitz menggunakan metode}

adjoin matriks diperoleh

{

dimana adalah entri-entri yang terletak dibaris ke dan kolom ke .

(7)

DETERMINAN DAN INVERS SUATU MATRIKS TOEPLITZ

ABSTRACT

To obtain the value of the determinant and inverse formula toeplitz matrix is done by observing the pattern rekrusipnya. Then the determinant of a matrix is shown toeplitz T_n is of order 2 × 2 to 7 × 7 by using elementary row operations and showed that matrix inverse toeplitz order 2 × 2 to 5 × 5 matrix using the adjoint method.

{

where the entries is located to the row and column

(8)

DAFTAR ISI

Halaman

Persetujuan i

Pernyataan ii

Penghargaan iii

Abstrak iv

Abstract v

Daftar Isi vi

Daftar Tabel viii

Daftar Gambar ix

Bab I Pendahuluan

1.1 Latar Belakang 1

1.2 Perumusan Masalah 3

1.3 Batasan Masalah 3

1.4 Tujuan Penelitian 4

1.5 ManfaatPenelitian 4

1.6 Metode Penelitian 4

Bab II Landasan Teori

2.1 Matriks 5

2.1.1 Definisi Matriks 5

2.1.2 Jenis – jenis Matriks 6

2.2 Determinan 7

2.2.1 Definisi determinan 7

2.2.2 Definisi Kofaktor Matriks 7

2.2.3 Sifat-sifat Determinan 8

2.2.4 Mencari Determinan Menggunakan Operasi Baris Elementer 8

2.3 Invers Matriks 9

2.3.1 Definisi Invers 9

2.3.2 Sifat-sifat Invers 10

2.3.3 Invers Matriks Dengan Metode Adjoin 10

(9)

Bab III Pembahasan

3.1 Determinan Matriks Toeplitz 12

3.1.1 Determinan Matriks 13

3.2 Determinan Matriks Toeplitz Secara Umum 19

3.2.1 Proposisi 3.1 20

3.2.1 Proposisi 3.2 21

3.2.1 Teorema 3.1 22

3.3 Invers Matriks Toeplitz Secara Umum 23

3.3.1 Teorema 3.2 26

3.3.2 Teorema 3.3 28

3.4 Aplikasi Formula Determinan dan Invers Matriks Toeplitz 30

Bab IV Kesimpulan dan Saran

4.1 Kesimpulan 35

4.2 Saran 36

(10)

DAFTAR TABEL

Halaman

(11)

DAFTAR GAMBAR

Halaman

Gambar 3.1 Determinan matriks toeplitz 31

Gambar 3.2 Invers matriks toeplitz 32

Gambar 3.3 Determinan matriks toeplitz 33

(12)

INVERS SUATU MATRIKS TOEPLITZ MENGGUNAKAN METODE ADJOIN MATRIKS

ABSTRAK

Pencarian invers matriks adalah suatu hal yang biasa dilakukan dalam bidang matematika dan ilmu hitung secara umum. Pada penelitian ini akan dibahas invers suatu matriks toeplitz dengan diagonal nol dan selainnya . Untuk memperoleh invers matriks toeplitz dilakukan dengan mengamati pola rekrusip dari determinan matriks toeplitz berorde hingga dengan

menggunakan metode operasi baris elementer sehingga diperoleh | |

_{dan menentukan invers matriks toeplitz menggunakan metode}

adjoin matriks diperoleh

{

dimana adalah entri-entri yang terletak dibaris ke dan kolom ke .

(13)

DETERMINAN DAN INVERS SUATU MATRIKS TOEPLITZ

ABSTRACT

To obtain the value of the determinant and inverse formula toeplitz matrix is done by observing the pattern rekrusipnya. Then the determinant of a matrix is shown toeplitz T_n is of order 2 × 2 to 7 × 7 by using elementary row operations and showed that matrix inverse toeplitz order 2 × 2 to 5 × 5 matrix using the adjoint method.

{

where the entries is located to the row and column

(14)

BAB 1 PENDAHULUAN

1.1 Latar Belakang

Teori matriks merupakan salah satu cabang ilmu aljabar linier yang menjadi

pembahasan penting dalam ilmu matematika. Sejalan dengan perkembangan ilmu

pengetahuan, aplikasi matriks banyak dijumpai dalam kehidupan sehari-hari, baik

dalam bidang matematika maupun ilmu terapannya. Aplikasi tersebut banyak

dimanfaatkan dalam menyelesaikan masalah-masalah yang berhubungan dengan

kehidupan sehari-hari, misalnya pada aplikasi perbankan yang senantiasa

berhubungan dengan angka-angka, dalam dunia olahraga seperti penentuan

klasemen suatu pertandingan, dalam bidang ekonomi biasa digunakan untuk

menganalisa input dan output seluruh sektor ekonomi (Supranto, 1987).

Dalam teori matriks terdapat berbagai jenis matriks, salah satunya matriks

toeplitz. Matriks toeplitz pada dasarnya mempunyai operasi sama dengan matriks

biasa hanya saja pada matriks toeplitz mempunyai struktur dan sifat yang khusus.

Menurut Robert matriks toeplitz adalah matriks simetris yang sirkulan

dimana setiap unsur pada diagonal utamanya adalah sama dan setiap unsur pada

superdiagonal yang bersesuaian dengan diagonal utamanya juga sama, dapat

diperlihatkan dalam persamaan

[

]

(15)

Secara sederhana matriks toeplitz dapat didefinisikan sebagai berikut:

1. Berbentuk matriks kuadrat yang simetris berorde

2. Semua unsur pada diagonal utama bernilai sama, dinotasikan dengan

untuk dan

3. Semua unsur pada subdiagonal atau unsur diatas diagonal dan dibawah

diagonal utama bernilai sama, dinotasikan dengan untuk dan .

Berdasarkan definisi yang dinyatakan pada persamaan maka

diasumsikan banyak jenis-jenis dari matriks toeplitz. Menurut Salkuyeh (2006)

andaikan suatu matriks toeplitz Tridiagonal berorde adalah

[

]

dimana dan . jika suatu matriks tridiagonal yang diperlihatkan pada

persamaan (1.2) dan dimana adalah bilangan bulat positif, maka

∑

dimana = b+2a√ cos

.

Sianipar.P (2008) dalam jurnalnya menyatakan, jika suatu matriks

kuadrat sedemikian hingga untuk semua dan untuk semua

maka disebut Matriks. Sianpar.P juga menyatakan bahwa syarat cukup untuk menentukan invers matriks ( matriks) adalah det ( ) > 0. Sebenarnya

masih banyak lagi jenis-jenis dari matriks toepitz tetapi tidak harus diperlihatkan

(16)

Pada teori matriks terdapat permasalahan menentukan nilai invers dari

matriks. Sedangkan masalah yang sering muncul dalam mencari invers matriks

biasanya berhubungan dengan ukuran matriks yang akan dicari inversnya.

Semakin besar matriksnya, semakin rumit juga perhitungannya sehingga

dibutuhkan formula yang tepat untuk menentukan invers matriks toeplitz tersebut.

Dengan latar belakang diatas maka penulis merumuskan judul untuk penelitian ini

yakni: “ Invers Suatu Matriks Toeplitz Menggunakan Metode Adjoin”.

1.2 Perumusan Masalah

Andaikan suatu matriks toeplitz yang berdiagonal nol dan selainya

berordo . Secara umum dapat dituliskan pada persamaan (1.3).

[

]

(1.3)

Adapun permasalahan dalam penelitian adalah mengamati pola sehingga

diperoleh formula untuk menetukan determinan matriks , menentukan kofaktor

matriks sehingga dapat diperoleh invers matriks dan bagaimana pembuktian

formula tersebut.

1.3 Batasan Masalah

Penelitian ini hanya menggunakan matriks toeplitz persamaan (1.3) yang

berorde dimana . Menggunakan operasi baris elementer untuk

menentukan determinan matriks dan untuk menentukan invers matriks

(17)

1.4 Tujuan Penelitian

Andaikan adalah suatu matriks toeplitz pada persamaan (1.3) berorde

dimana sehingga yang menjadi tujuan penelitian adalah mendeskripsikan

perolehan formula invers matriks toeplitz dalam teorema serta melakukan

pembuktian formula tersebut.

1.5 Manfaat Penelitian

Manfaat penelitian adalah sebagai bekal pengalaman praktis untuk menentukan

determinan maupun invers matriks toeplitz pada persamaan (1.3) berorde

dimana . Sebagai referensi dalam menambah wawasan tentang metode-metode yang dapat dipergunakan untuk menentukan nilai determinan dan

invers suatu matriks.

1.6 Metodologi Penelitian

Langkah-langkah yang dilakukan untuk meneliti invers matriks toeplits pada

persamaan berorde dimana adalah:

1. Menelaah buku-buku yang berhubungan dengan matriks toeplitz

2. Menentukan nilai determinan matriks toeplitz dengan menggunakan

operasi baris elementer

3. Merumuskan determinan matriks toeplitz kedalam teorema dengan

mengamati pola rekursipnya serta pembuktiannya

4. Merumuskan kofaktor matriks toeplitz kedalam dengan menggunakan

adjoin matriks dan serta pembuktiannya

5. Menentukan invers matriks toeplitz kedalam dengan menggunakan

(18)

BAB 2

LANDASAN TEORI

Pada bab ini akan dipaparkan mengenai konsep dasar tentang matriks meliputi

definisi matriks, jenis-jenis matriks, operasi matriks, determinan, kofaktor, invers

suatu matriks, serta metode yang dapat digunakan untuk mencari nilai determinan

dan invers suatu matriks.

2.1 Matriks

2.1.1 Definisi Matriks

Menurut (Nicholson, 2004) matriks adalah susunan segi empat siku-siku dari

bilangan-bilangan. Bilangan-bilangan dalam susunan tersebut dinamakan entri

dalam matriks. Jadi sebuah matriks berukuran dapat ditulis sebagai

berikut:

( ) [

]

dengan adalah entri-entri yang terletak dibaris ke dan kolom ke .

2.1.2 Jenis-Jenis Matriks

Berikut dipaparkan beberapa jenis matriks yang berhubungan dengan pembahasan

dalam penelitian ini antara lain:

1. Matriks Bujur Sangkar

Matriks bujur sangkar adalah suatu matriks yang banyaknya baris sama

dengan banyaknya kolom, yang dinyatakan dengan dimana dapat ditulis dengan [ ]

(19)

2. Matriks Segitiga-Atas dan Segitiga-Bawah

Matriks segitiga adalah matriks persegi yang entri dibawah atau diatas

garis diagonal utama adalah nol (Zwillinger, 2003).

3. Matriks Simetris

Menurut ( Leon, 2001) suatu matriks berukuran disebut simetris

jika .

4. Minor dan Kofaktor

Misalkan = ( ) adalah matriks bujur sangkar, maka minor entri

dinyatakan oleh | | dan didefinisikan menjadi determinan

sub-matriks yang tetap setelah baris ke-i dan kolomke-j dihapuskan dari .

Bilangan | | dinyatakan oleh dinamakan kofaktor entri (Anton,2004).

5. Matriks Adjoin

(Hefferon, 2012) Matriks adjoin dari matriks berukuran adalah

Adjoin =

[

]

dimana adalah kofaktor-kofaktor dari matriks

6. Matriks Identitas

Leon menyatakan matriks identitas adalah matriks yang

dinotasikan dengan berorde ,

{

(20)

2.2 Determinan

2.2.1 Definisi Determinan

Determinan dari suatu matriks berordo , dinyatakan sebagai det ( ) adalah

skalar yang diasosiasikan dengan matriks dan didefinisikan secara induktif

sebagai :

{

di mana ( ) adalah kofaktor-kofaktor yang diasosiasikan dengan entri-entri dalam baris pertama dari (Leon, 2001).

2.2.2 Definisi Kofaktor Matriks

Suatu matriks kuadrat dengan baris dan kolom dihilangkan baris ke- dan

kolom ke- , maka determinan dari matriks kuadrat dengan baris dan

kolom, yaitu sisa matriks yang tinggal (disebut minor matriks dari elemen

) diberi simbol | |. Apabila pada setiap minor ditambahkan tanda + (plus)

atau – (minus) sebagai tanda pada determinan dan kemudian dinotasikan dengan

simbol: | | maka diperoleh suatu kofaktor elemen yang biasanya diberi simbol . Dengan kata lain kofaktor | |, sehingga setiap elemen mempunyai kofaktor sendiri-sendiri (Anton, 2004).

Nilai determinan matriks sama dengan penjumlahan hasil kali semua

elemen dari suatu baris atau kolom matriks dengan kofaktor masing-masing

yaitu:

a. Dengan menggunakan elemen-elemen baris

ke-det

det ∑ dimana ...,n b. Dengan menggunakan elemen-elemen kolom

ke-det

(21)

2.2.3 Sifat-Sifat Determinan

Berikut ini akan diperlihatkan beberapa sifat-sifat determinan menurut Sianipar

(2008) yakni:

a. Jika setiap elemen suatu baris (kolom) dari determinan suatu matriks

digandakan dengan skalar maka harga determinan menjadi | |.

b. Jika matriks adalah suatu matriks segitiga-atas maupun matriks segitiga-

bawah maka nilai determinannya adalah hasil perkalian setiap elemen

diagonal utamanya

c. Jika matriks diperoleh dari matriks dengan membawa baris ke-

(kolom) menjadi menjadi baris (kolom) yang lain, maka | | | |

d. Jika suatu baris (kolom) merupakan satu atau lebih baris (kolom) dari

suatu matriks kuadrat | | maka | |

e. Determinan dari hasil ganda matriks sama dengan hasil ganda determinan

masing-masing matriks itu, jadi:

| | | || || |

determinan dari jumlah (selisih) beberapa matriks tidak sama dengan

jumlah (selisih) dari masing-masing determinan matriks itu, jadi:

| | | | | | | |

Catatan. Jika determinan suatu matriks kuadrat tingkat sama dengan

nol , maka disebut singular, jika tidak disebut non singular.

2.2.4 Mencari Determinan Menggunakan Operasi Baris Elementer (OBE)

Salah satu cara lain dalam menentukan determinan suatu matriks adalah

dengan mereduksi bentuk matriks tersebut menjadi matriks baru yang mempunyai

penghitungan determinan lebih mudah, misalkan dalam bentuk matriks segitiga,

dimana determinan dari matriks segitiga adalah hasil kali entri-entri pada diagonal

utamanya (Anton, 2004).

Untuk mereduksi sebuah matriks, dapat dilakukan dengan operasi baris

(22)

dan perkalian) yang dikenakan pada setiap unsur dalam suatu baris pada sebuah

matriks. Operasi baris elementer meliputi :

1. Pertukaran baris

2. Perkalian suatu baris dengan konstanta tak nol

3. Penjumlahan suatu baris pada baris yang lain

Secara sederhana determinan suatu matriks merupakan hasil kali setiap

unsur diagonal pada suatu matriks segitiga-atas atau matriks segitiga-bawah.

Sehingga operasi baris elementer pada sebuah matriks akan mempengaruhi nilai

determinannya. Pengaruh operasi baris elementer pada suatu matriks antara lain:

1) Jika ’ adalah matriks yang dihasilkan bila baris tunggal dikalikan oleh

konstanta k, maka det( ’) = k det( )

2) Jika ’ adalah matriks yang dihasilkan bila dua baris dipertukarkan,

maka

det( )= - det( )

3) Jika ’ adalah matriks yang dihasilkan bila kelipatan suatu baris

ditambahkan pada baris lain, maka det( ’) = det( ).

2.3 Invers Matriks

2.3.1 Definisi Invers Matriks

Menurut Zwillinger (2003) suatu matriks bujur sangkar dikatakan dapat dibalik

(invertible) jika terdapat matriks , sehingga sehinga

dinamakan invers dari ditulis . Jika matriks tidak dapat didefinisikan maka dinyatakan sebagai matriks singular. Invers dari didefinisikan sebagai

| | dengan adalah adjoin dari dan | | merupakan nilai

(23)

2.3.2 Sifat-Sifat Invers Matriks

Berikut ini adalah beberapa sifat-sifat dari invers matriks antara lain:

1. Menurut Keith (2004) Jika matrik ataupun adalah invers dari matriks

, maka .

Bukti: Karena adalah invers dari , maka . dengan mengalikan

kedua ruas di sisi kanannya dengan diperoleh . Tetapi

sehingga .

2. Jika dan adalah matriks-matriks yang dapat dibalik dan ukurannya

sama, maka:

a. dapat dibalik

b.

3. Jika A adalah matriks yang dapat dibalik (invertible), maka:

a. dapat dibalik dan =

b. b. Jika , maka mempunyai kebalikan dan

c. dapat dibalik dan untuk

2.3.3 Invers Matriks Dengan Metode Adjoin

Mencari invers suatu matriks dengan mempergunakan adjoin misalnya suatu

matriks kuadrat dengan baris dan kolomnya masing-masing sebesar . Jadi

( ) dan setiap elemen dari matriks mempunyai kofaktor,

yaitu elemen mempunyai kofaktor . Apabila semua kofaktor itu dihitung untuk semua elemen matriks , kemudian dibentuk suatu matriks dengan

kofaktor dari semua elemen matriks sebagai elemennya, maka:

( )

[

]

(24)

Adjoin matriks ialah suatu matriks yang elemen-elemennya terdiri dari

transpose semua kofaktor dari elemen-elemen matriks , yaitu apabila , dimana ialah kofaktor dari elemen , maka adjoint matriks yaitu:

(Supranto, 2003).

Jadi, jelasnya ialah transpose dari matriks kofaktor , yaitu:

( )

[

]

2.3.4 Invers Matriks Dengan Metode Counter

Mencari invers suatu matriks dengan Metode Counter menurut Supranto (2003)

juga menyatakan apabila suatu matriks kuadrat yang non-singular det ,

yaitu dengan baris dan kolom masing-masing sebanyak dan suatu identitas

matriks. Kemudian diletakkan di sebelah kanan matriks , maka diperoleh suatu

matriks yang disebut augemented matriks sebagai berikut: .

Selanjutnya apabila terhadap baris-baris baik dari matriks maupun matriks ,

jelasnya terhadap baris-baris augemented matriks , dilakukan tranformasi

(25)

BAB 3 PEMBAHASAN

Untuk memperoleh invers matriks toeplitz pada persamaan dilakukan

dengan mengamati pola rekrusip dari determinan matriks toeplitz berorde

dengan menggunakan metode operasi baris elementer dan menggunakan metode adjoin matriks untuk memperoleh invers matriks tersebut. Adapun

langkah-langkah untuk menetukan formula invers matriks secara umum adalah

sebagai berikut:

a. Menentukan determinan matriks yang berorde hingga orde ,

dengan menggunakan operasi baris elementer

b. Menentukan formula determinan matriks kedalam teorema dengan

mengamati pola rekursipnya

c. Menentukan invers matriks dengan menggunakan adjoin matriks

d. Mengaplikasikan formula determinan dan invers yang diperoleh dalam

beberapa contoh dan membandingkan hasilnya dengan menggunakan

MATLAB versi 7.5.0.

3.1 Matriks Toeplitz

Andaikan suatu matriks toeplitz yang berdiagonal nol dan selainya

berordo . Secara umum dapat dituliskan pada persamaan (3.1).

[

]

(3.1)

(26)

Untuk menentukan formula determinan matriks toeplitz berorde

dimana maka diperlihatkan determinan matriks yang berorde

hingga orde menggunakan operasi baris elementer sampai matriks

membentuk matriks segitiga-atas, sehingga berdasarkan 2.2.2 mengenai sifat

determinan bagian (b) maka diasumsikan nilai determinan matriks adalah hasil

perkalian diagonal utama matriks tersebut.

Dalam proses operasi baris elementer akan diperlukan beberapa

keterangan sebagai berikut:

a. Notasi adalah pertukaran baris pertama dengan baris

kedua

b. Notasi adalah penjumlahan baris pertama dengan baris

kedua

c. Notasi adalah selisih baris pertama dengan baris kedua

d. Notasi adalah dikalikan dengan baris ke- , dimana adalah

konstanta sembarang dan

3.1.1 Determinan Matriks

Andaikan matriks toeplitz adalah

dimana sehingga dengan menggunakan operasi baris elementer diperoleh

| | | _| |

| maka | | =

Dalam operasi baris elementer matriks terjadi pertukaran baris maka

berdasarkan 2.2.2 mengenai sifat determinan bagian (c) sehingga | | dikali

negatif. Untuk proses iterasi berikutnya sifat determinan 2.2.2 bagian (c) akan

(27)

3.1.2 Determinan Matriks

[ ]

| | |

| |

|

= |

|

maka | |=

Operasi baris elementer pada matriks dilakukan pertukaran baris

pertama dengan baris ketiga karena pertukaran tersebut adalah langkah yang

paling tepat untuk menetukan determinan matriks . Untuk pembuktian

kebenarannya diperlihatkan determinan matriks dengan menggunakan metode

Sarrus adalah

| | |

|

Jika untuk matriks dilakukan operasi pertukaran baris pertama dengan

kedua maka determinannya akan benilai salah dan diperlihatkan sebagai berikut:

| | |

| |

| | |

|

maka terbukti | | = bernilai salah jika

(28)

3.1.3 Determinan Matriks

[ ]

| | | | | | | | | | | | | |

maka | |=

Pada operasi baris elementer matriks dilakukan pertukaran baris

pertama dengan baris ketiga karena pertukaran tersebut adalah langkah yang

paling tepat untuk menentukan determinan matriks . Jika operasi baris

elementer dilakukan dengan pertukaran baris pertama dengan baris kedua atau

pertukaran baris pertama dengan baris keempat akan menemui banyak kendala

dalam menetukan nilai determinannya dan bahkan kemungkinan besar akan

(29)

3.1.4 Determinan Matriks

[ ]

| _{| ||} | | _|| | | || | | _|| || ) || || || ||

maka | | =

Pada operasi baris elementer matriks dilakukan pertukaran baris

pertama dengan baris kelima karena pertukaran tersebut adalah langkah yang

paling tepat untuk menetukan determinan matriks . Jika operasi baris elementer

dilakukan dengan pertukaran baris pertama dengan baris kedua, pertukaran baris

pertama dengan baris ketiga, dan pertukaran baris pertama dan baris keempat akan

ditemukan kesulitan dalam menetukan nilai determinannya. Untuk selanjutnya

dalam menentukan nilai determinan matriks dan diasumsikan langkah yang

dilakukan adalah yang paling tepat untuk operasi baris elementer secara khusus

(30)

3.1.5 Determinan Matriks

[ ]

| |= | | | | | | | | | | | | | | | | | | | | | | | |

Langkah berikutnya dipertukarkan baris kelima dengan baris keenam, sehingga

| | | | | | | | | |

(31)

3.1.6 Determinan Matriks

[ ]

dimana sehingga dengan operasi baris elementer diperoleh | |

| | | | | | | | | | | |

Dengan memperhatikan matriks sebelumnya, jelas terlihat bahwa baris

ketujuh adalah sasaran eliminasi untuk membentuk matriks segitiga atas maka

dilakukan operasi baris sampai dengan sehingga

| | = | | | |

Sifat determinan 2.2.2 bagian (b) menjamin bahwa deteminan matriks

segitiga atas atau matriks segitiga bawah adalah hasil perkalian diagonal

(32)

3.2 Determinan Matriks Toeplitz Secara Umum

Berdasarkan nilai determinan matriks berorde hingga orde yang

[image:32.595.185.485.222.518.2]

deperlihatkan pada 3.1.1 hingga 3.1.6 diperoleh:

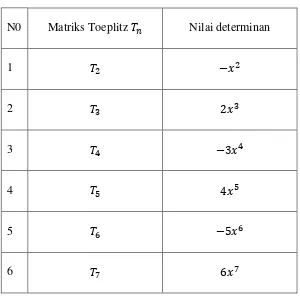
Tabel 3.1 Nilai Determinan Matriks Toeplitz

N0 Matriks Toeplitz Nilai determinan

1

2

3

4

5

6

Pada tabel 3.1 dilakukan pengamatan pola rekursip nilai determinannya

(33)

3.2.1 Proposisi 3.1

Andaikan pada persamaan suatu matriks toeplitz berorde genap

dan diperoleh

| |

Bukti: Pembuktian dilakukan dengan induksi matematika, andaikan adalah matriks toeplitz dengan ordo genap yakni .

a. Untuk diperoleh | |

b. Untuk diperoleh | | | |

c. Untuk diperoleh | | | |

d. dan seterusnya.

| |

. Jadi untuk

dimana berlaku,

| |

| | | |

Sehingga terbukti bahwa | | dimana orde genap berlaku

(34)

3.2.2 Proposisi 3.2

Andaikan pada persamaan suatu matriks toeplitz berorde ganjil

dan diperoleh

| |

Bukti: Pembuktian dilakukan dengan induksi matematika, andaikan adalah matriks toeplitz dengan ordo ganjil yakni

a. untuk diperoleh | |

b. untuk diperoleh | | | |

c. untuk diperoleh | | | |

d. dan seterusnya.

Langakah 2. Asumsikan bahwa | | benar, untuk ganjil maka | | ( ) sehingga pola atau selisih dari

| | | | adalah | _| _||

. Jadi untuk dimana

diperoleh,

| |

| | | | ( )

Sehingga terbukti bahwa | | dimana orde ganjil berlaku

(35)

Berdasarkan hasil pengamatan pada proposisi 3.1 dan proposisi 3.2 diperoleh

kesimpulan yang dinyatakan pada teorema 3.1.

3.2.3 Teorema 3.1:

Andaikan pada persamaan suatu matriks toeplitz berordo dan

bilangan maka nilai determinan matriks adalah

| |

Bukti: Pembuktian dilakukan dengan induksi matematika, andaikan adalah matriks toeplitz dengan ordo

a. untuk diperoleh | |

b. untuk diperoleh | | | |

c. untuk diperoleh | | | |

d. dan seterusnya.

| |

. Jadi

untuk dimana diperoleh,

| |

| | | | ( ₎

(36)

3.3 Invers Matriks Toeplitz Secara Umum

Andaikan matriks toeplitz yang dinyatakan pada persamaan maka invers

matriks toeplitz dinotasikan

| | dimana adjoin matriks

adalah kofaktor-kofaktor dari matriks yang ditransposkan, untuk dan adalah

baris dan kolom dari matriks Secara umum dapat diperlihatkan pada

persamaan | | [ ]

Dimana adalah kofaktor dari matriks pada baris ke- dan kolom ke- . Jika kofator dari matriks pada baris ke- dan kolom ke- .

Untuk memperoleh formula invers matriks toeplitz dilakukan dengan

menggunakan adjoin matriks. Karena proses untuk memperoleh nilai

tidak dapat diperlihatkan secara bersamaan, maka nilai kofaktor-kofaktor dari

matriks diyatakan secara terurut sebagai berikut:

(37)

(38)

|| | | || | | || | | || | | || | | || | | || | | || | | _|| | | || | | | |

Selanjutnya nilai kofaktor-kofaktor dari matriks akan dinyatakan sesuai

baris dan kolom matriks yang disebut dengan adjoin matriks. Matriks kofaktor

dari atau tidak perlu untuk ditransposekan karena kofaktor matriks

toeplitz adalah matriks simetris sehingga maka adjoin

matriks toeplitz adalah

(39)

kofaktor-kofaktor atau adjoin dari matriks toeplitz berorde dan

dapat dinyatakan dengan teorema 3.2.

3.3.1 Teorema 3.2

Andaikan pada persamaan suatu matriks toeplitz berordo dan

maka kofaktor-kofator (adjoin) dari matriks adalah

{| |

dimana kofator dari matriks , untuk adalah baris dan adalah kolom dari matriks .

Bukti: Andaikan adalah suatu matrik toeplitz pada persamaan berdasarkan 2.2.2 definisi kofaktor maka kofaktor dari matriks adalah dengan

mengeliminasi baris ke dan kolom ke diperoleh | | sehingga | | untuk Teorema 3.1 menjamin bahwa kofaktor

| | benar.

Sedangkan untuk membuktikan dengan induksi matematika, andaikan adalah matriks toeplitz dengan ordo

dan

Langkah 1. Diperlihatkan bahwa memiliki pola, untuk setiap dan

a. untuk diperoleh

b. untuk diperoleh c. untuk diperoleh d. dan seterusnya.

(40)

Langakah 2. Asumsikan bahwa benar, untuk maka sehingga pola atau selisih dari adalah

. Jadi untuk dimana

diperoleh,

Sehingga terbukti bahwa dimana adalah kofaktor kofaktor matriks orde dan , berlaku untuk

Pada teorema 3.2 telah diperlihatkan kofaktor-kofaktor matriks secara

umum sehinga invers matriks menggunakan metode adjoin diperoleh

| | [

]

| | [

| |

_|

|

_|

|

_|

(41)

[ | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | ] [ ]

Invers matriks toeplitz pada persamaan berorde dan

dan | | dapat dinyatakan dengan teorema 3.3.

3.3.2 Teorema 3.3

Andaikan suatu matriks toeplitz pada persamaan berode

dimana dan | | adalah bilangan maka invers matriks toeplitz

adalah: {

(42)

Bukti:

Pembuktian dilakukan sesuai dengan definisi invers matriks yakni,

andaikan suatu matriks bujur sangkar berodo dan dapat diperlihatkan

matriks , sehingga maka dikatakan dapat dibalik (invertible) dan dinamakan invers dari adalah

[ ] [ ] [ ] [ ]

Jadi, terbukti bahwa invers dari matriks adalah

(43)

3.4 Aplikasi Formula Deteminan dan Invers Matriks Toeplitz

Berikut ini akan dipaparkan beberapa kasus sebagai aplikasi formula deteminan

dan invers matriks toeplitz yang telah dinyatakan pada teorema 3.1 dan

teorema 3.3 sehingga akan dibuktikan kebenaran formula tersebut dengan

menggunakan software MATLAB 7.5.0.

Andaikan suatu matriks toeplitzberode sebagai berikut

| |

Menentukan nilai determinan suatu matriks toeplitz dimana

dapat ditentukan secara umum tanpa memperhatikan orde dari matriks toeplitz

ganjil atau genap, diperlihatkan pada teorema 3.1 yakni

| | , Sehingga

| |

Determinan matriks dengan menggunakan MATLAB yang

(44)

[image:44.595.115.522.468.702.2]

Gambar 3.1 Determinan Matriks Toeplitz

Dengan menggunakan formula yang diperlihatkan pada teorema 3.3 invers

matriks toeplitz adalah

[

]

| |

(45)

Invers matrikstoeplitz dengan menggunakan MATLAB diperlihatkan

pada gambar 3.2.

Gambar 3.2 Invers Matriks Toeplitz

Andaikan suatu matriks toeplitzberode sebagai berikut

| |

Menentukan nilai determinan suatu matriks toeplitz dimana

dapat ditentukan secara umum tanpa memperhatikan orde dari matriks toeplitz

ganjil atau genap, diperlihatkan pada teorema 3.1 yakni

(46)

Sehingga | |

Determinan matriks dengan menggunakan MATLAB diperlihatkan

[image:46.595.115.343.620.728.2]

pada gambar 3.3.

Gambar 3.3 Determinan Matriks Toeplitz

Dengan menggunakan formula yang diperlihatkan pada teorema 3.3 invers

matriks toeplitz secara umum adalah

[

]

(47)

| |

Invers matriks toeplitz dengan menggunakan MATLAB diperlihatkan

[image:47.595.132.491.84.172.2]

pada gambar 3.4 yakni,

Gambar 3.4 Invers Matriks Toeplitz

Hasil dari contoh kasus matriks toeplitz dan matriks toeplitz menggunakan

teorema 3.1 untuk menentukan determinan serta menggunakan teorema 3.3 untuk

menentuka invers diperoleh nilai yang sama dengan determinan dan invers

(48)

BAB 4

KESIMPULAN DAN SARAN

4.1 Kesimpulan

Hasil dari penelitian tentang invers suatu matriks toeplitz berordo dan

yang dinyatakan dalam pembahasan bab 3 diperoleh beberapa kesimpulan sebagai berikut:

1. Andaikan pada persamaan suatu matriks toeplitz berordo

dan bilangan maka nilai determinan matriks adalah

| |

2. Andaikan pada persamaan suatu matriks toeplitz berordo

dan maka kofaktor-kofator (adjoin) dari matriks adalah

{| |

3. Andaikan suatu matriks toeplitz pada persamaan berode

dimana dan | | adalah bilangan maka invers matriks

toeplitz adalah:

{

(49)

4.2 Saran

Untuk menyelesaikan permasalahan yang berhubungan dengan penggunaan

matriks toeplitz disarankan terlebih dahulu mengetahui struktur atau sifat-sifat

yang dimiliki suatu matriks toeplitz.

Pada skripsi ini, penulis mencari determinan suatu matriks toeplitz dengan

metode Operasi Baris Elementer dan menentukan invers dengan metode Adjoin

Matriks. Bagi pembaca yang ingin membahas kembali masalah yang serupa, maka

disarankan untuk menggunakan metode yang lain atau menggunakan salah satu

(50)

DAFTAR PUSTAKA

Anton, Howard dan Rorres, Chris. 2004. Dasar-Dasar Aljabar Linear. Versi

Aplikasi. Edisi Ketujuh. Jakarta: Erlangga

Gray M. Robert. 2005. Toeplitz And Cirkulan Matrices. Departemen of Electrical

Engenering Stanford, USA.

Jim Hefferon . 2012 . Linear Algebra, Mathematics Saint Michael’s College

Colchester, Vermont USA.

Leon. Steven J, 2001. Aljabar Linear dan Aplikasinya. Edisi Kelima. Jakarta:

Erlangga

Nicholson, W. Keith. 2004. Linear Algebra with Applications, Fourth Edition.

University of Calgary

Salkuyeh, Davod Khojasteh. 2006 Positip Integer Power of the Tridiagonal

Matriks Toeplitz. International Mathematical Forum, Vol 1, no. 22, 1061 -

1065, Mohaghegh Ardabili University. Ardabil, Iran.

Sianipar, P. 2009. Invers Z-Matriks, Bulletin of Mathematics, Vol. 01, No. 01,

114.Medan Indonesia.

Sianipar, P. 2008 Aljabar Linear. Edisi Pertama PT. Intan Dirja Lela, Medan

Indonesia

Supranto, Johannes. 2003. Pengantar Matriks. Jakarta: Rineka Cipta

Zwilinger, D. 2003. Standard Mathematical Tables and Formulae. Chapman