FiniApryanti Page 1
Bagaimana cara menyusun tabel karakter?
Tabel karakter dapat disusun dengan memperhatikan sifat-sifat dari tabel karakter secara
umum. Sifat-sifat tabel karakter beserta contohnya adalah sebagai berikut:
Tabel karakter untuk C2v
Sifat-sifat tabel karakter adalah sebagai berikut:
a. Jumlah total operasi simetri dalam suatu grup disebut sebagai order (h). Untuk
menentukan order suatu grup, jumlahkan banyaknya operasi simetri yang terdaftar pada
baris teratas tabel karakter.
Contoh:
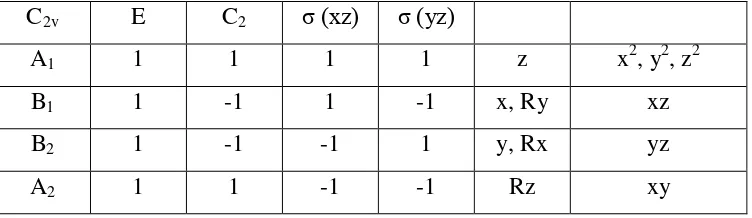
C2v E C2 σ (xz) σ (yz)
Pada tabel karakter C2v di atas, ada empat operasi simetri yang ada, yaitu E (operasi
simetri identitas), C2 (operasi simetri sumbu 180o), σ(xz), dan σ(yz). Dengan demikian
order (h) = 4.
b. Operasi simetri ditata dalam kelas-kelas. Semua operasi simetri dalam satu kelas memiliki
karakter yang sama untuk matriks transformasinya dan dikelompokkan dalam kolom yang
sama dalam tabel karakter.
Contoh:
Pada tabel karakter C2v di atas, ada empat operasi simetri yang diletakkan dalam
kolom-kolom yang berbeda, sehingga dalam tabel karakter tersebut ada empat kolom-kolom.
c. Banyaknya representasi tak tereduksi sama dengan banyaknya kelas-kelas. Hal ini berarti
FiniApryanti Page 2 Contoh:
Tabel karakter C2v memiliki empat baris dan empat kolom.
C2v E C2 σ (xz) σ (yz)
d. Jumlah kuadrat dimensi dari representasi tak tereduksi sama dengan order grup.
Contoh:
e. Bagi representasi tak tereduksi manapun, jumlah kuadrat karakter-karakter sama dengan
FiniApryanti Page 3
A2 1 1 -1 -1
h = 4
= 12 + (12) + ( 12) + 12 = 12 + (-12) + 12 + (-12)
= 12 + (-12)+ (-12)+12 = 12 + 12 + (-12) + (-12) = 4
f. Representasi-representasi tak tereduksi bersifat ortogonal satu sama lain. Jumlah
perkalian karakter-karakter untuk setiap operasi sepasang representasi tak tereduksi
manapun sama dengan nol.
g. Dalam semua grup pasti ada suatu representasi dengan karakter “1” untuk semua operasi.
Contoh:
C2v E C2 σ (xz) σ (yz)
A1 1 1 1 1
B1 1 -1 1 -1
FiniApryanti Page 4
A2 1 1 -1 -1
Setelah memahami sifat-sifat tabel karakter, penyusunan tabel karakter untuk grup
simetri lain dapat dilakukan. Contohnya adalah penyusunan tabel karakter dari grup C4v
berikut:
Langkah pertama:
Menentukan operasi simetri yang ada pada molekul dari grup C4v (disini diambil contoh BrF5).
Dengan menggunakan pengetahuan tentang operasi simetri, kita dapat mengetahui bahwa
BrF5 memiliki operasi simetri E(operasi identitas), 2C4(operasi simetri sumbu 90o),
C2(operasi simetri 180o), 2σv(operasi simetri pencerminan terhadap bidang vertikal), serta 2σd(operasi simetri pencerminan terhadap bidang diagonal).
Langkah kedua:
Data operasi simetri yang telah diketahui disusun dalam baris pertama tabel karakter sesuai
sifat (b):
C4v E 2C4 C2 2σv 2σd
Data bagian tabel di atas dapat diketahui besar orde dengan memanfaatkan sifat (a) tabel
karakter. h= 1 + 2 + 1 + 2 + 2 = 8
Langkah ke-tiga:
dengan menggunakan sifat (c) tabel karakter, jumlah baris dalam tabel karakter dapat
ditentukan, yaitu sama dengan jumlah kolom. Sehingga dapat dibuat kerangka tabel yang
terdiri dari lima kolom dan lima baris :
FiniApryanti Page 5 Langkah ke-empat:
Dengan memanfaatkan sifat (g) tabel karakter, satu baris pada tabel karakter dapat diisi dengan karakter “1” untuk semua operasi.
C4v E 2C4 C2 2σv 2σd
Untuk mengisi baris-baris selanjutnya, dapat digunakan sifat (f) tabel karakter. Untuk
memperoleh nilai nol dari (1x1xa) + (1x2xb) + (1x1xc) + (2x1xd) + (2x1xe), kita harus
bermain logika matematika. Yang pertama, apabila kolom a ke bawah diisi dengan karakter 1,
otomatis kolom c juga harus diisi dengan karakter 1 untuk saling mengilangkan dengan
karakter pada kolom lain yang bernilai -1. Jadi, pada kolom b, d, dan e ke bawah ada tiga
nilai yang mungkin, yaitu 1, -1, dan -1. Untuk penempatanya, bisa digunakan teori kombinasi
sebagai berikut:
Kombinasi yang mungkin untuk karakter 1,-1,-1 ada tiga, yaitu:
FiniApryanti Page 6 Untuk mencari karakter pada kolom p, q, r, s, dan t dapat digunakan sifat (d) tabel karakter.
Untuk operasi simetri E,
12 + 12 + 12 + 12 + p2 = 8
4 + p2 = 8
p2 = 4
p = 2
untuk operasi simetri 2C4,